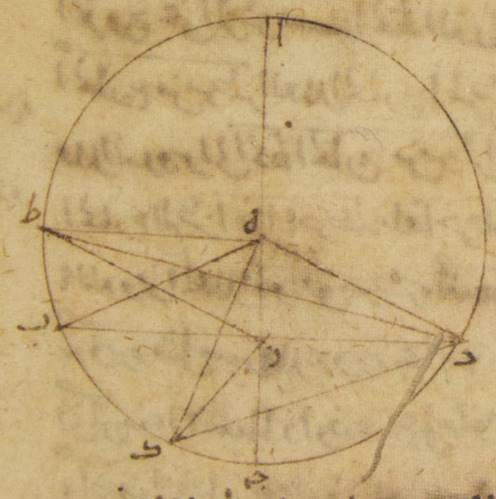Ptolemaeus Arabus et Latinus

بسم الله الرحمن الرحيم

عونك يا واحد

جمل ما في المقالة الثالثة من كتاب بطلميوس المنسوب إلى التعاليم

الأولى: في مقدار زمان السنة؛ الثانية: في وضع جدول لحركات الشمس الوسطى؛ الثالث: في الأصول التي توضع للحركة المستوية التى تجري على الاستدارة؛ الرابعة: في الاختلاف الذي يرى للشمس؛ الخامسة: في النظر في الاختلافات الجزئيّة؛ السادسة: في عمل جدول لأقسام الاختلاف الجزئيّة؛ السابعة: جدول لاختلاف الشمس؛ الثامنة: في حاصل الشمس بحسب حركاتها الوسطى؛ التاسعة: في حساب دوران الشمس؛ العاشرة: في اختلاف الأيّام بلياليها.

/T131/⟨III⟩ ابتداء المقالة الثالثة من كتاب بطلميوس المنسوب إلى التعاليم

فإنّ إنّا لمّا كنّا قد لخّصنا في المقالتين اللتين وضعناهما قبل هذه ما يحتاج على الجملة إلى أن يتقدّم علمه من أمر السماء والأرض بطريق التعاليم.  /H191/وأيضاً من أمر ه: ميل دائرة الشمس التي تمرّ بأوساط البروج وما يلزم فيها من الأمور الجزئيّة في الكرة المنتصبة وفي الكرة المائلة في مسكن مسكن رأينا أنّه قد نتّصل بذلك ونتّبع ما تقدّم وصفه القول في الشمس والقمر والأخبار بما يلزم في حركاتهما وذلك أنّه لم يمكن الوصول إلى علم شيء ممّا يظهر في الكواكب أصلاً دون أن يتقدّم العلم بهذين. وقد نرى أيضاً أنّ العلم بحركة الشمس يتقدّم العلم بأمر القمر وذلك أنّه لن يمكن أيضاً دونه استقصاء العلم بأمر القمر.

⟨III.1⟩ آ: في مقدار زمان السنة

إنّه قد يتقدّم جميع ما يتبيّن من أمر الشمس الوقوف على زمان السنة. وقد يتهيّأ لنا أن نعلم ما وقع بين الأوائل من الاختلاف والشكّ فيما يظهر من أمره ممّا دونوه ه – صح: دوّنوه في كتبهم وخاصّة أبرخس وهو الرجل الذي جمع إلى العناية والاجتهاد إيثار الصدق فإنّ أكثر ما قاد هذا الرجل أيضاً إلى أن وقع في الشكّ والحيرة في هذا الأمر/H192/  أنّه وجد زمان السنة إذا نُظر فيه من قبل العودات التي تكون في الانقلابين والاستوائين والاستواين ثلاث مائة وخمسة وستّين يوماً وأقلّ من زيادة ربع يوم، وإذا نُظر فيه بالقياس إلى الكواكب الثابتة وجد أكثر من هذا المقدار. ومن هنالك وقع في وهمه أنّ كرة الكواكب الثابتة قد يكون منها أيضاً نقلة ما يظنّه في زمانها كما يكون لأكر الكواكب المتحيّرة تلقا الحركة للمدار الأوّل بالدائرة المرسومة مارّة بقطبي الدائرتين جميعاً أعني دائرة معدّل النهار والدائرة المائلة.

فأمّا إن ذلك كذلك والوجه الذي يجري عليه الأمر فيه فإنّا سنبيّنه في كلامنا في الكواكب الثابتة فأنّه ليس يمكن أيضاً /T132/ ولا الوقوف على أمر تلك أصلاً دون أن يتقدّم فيعلم أمر الشمس والقمر. وأمّا في هذا البحث الذي نحن بسبيله فإنّا نرى أنّه ليس ينبغي أن نختبر زمان السنة للشمس بأن نجعل نظرنا في شيء غير عودة الشمس نفسها بقياسها إلى نفسها لا إلى غيرها أعني عودتها التى تكون في الفلك المائل وأنّه ينبغي أن يحدّ زمان السنة بالزمان الذي فيه إذا ابتدأت الشمس من نقطة ما غير متحرّكة من هذه الدائرة ومرّت على الاتصّال ه – خ: حتّى عادت إليها بعينها ونرى أنّ المبادئ الموافقة في مثل هذه العودة أنّما هي فقط النقط من الدائرة التي ذكرناها التي نتبيّنها ه – خ: نفرزها الانقلابان والاستوائان. وذلك أنّا إن ذهبنا في الأمر الواجب إلى ما توجبه التعاليم فلسنا نجد عودة أشدّ موافقة من /H193/ العودة التي تأتي بالشمس إلى شكل واحد بعينه في المكان والزمان إذا نُظر في ذلك بالقياس ↑ خ: أمّا إلى أفق من ↑أفق من↑: خ الآفاق ↑ خ: وإمّا أو إلى دائرة نصف النهار أو ه – خ: وإمّا إلى مقادير الأيّام بلياليها ولا نجد في دائرة البروج مبادئ آخر سوى ما قد حدّه فيها بالعرض نقطتا الانقلابين ونقطتا الاستوائين. وإن تدير الإنسان الأمر الموافق بالوجه الذي هو أشبه بالعلم الطبيعيّ لم نجد عودة أشبه في القياس من العودة التي تأتي بالشمس من حال في الهواء إلى حال مثلها ومن وقت من أوقات السنة إلى وقت مثله ولم نجد مبادئ أولى من المبادئ التي بها تنفصل أوقات السنة ه – خ: الأربعة بعضها من بعض دون غيرها ومع ذلك فإنّ النظر في العودة بالقياس إلى الكواكب الثابتة تُظهر شنعاً لأمور كثيرة ولا سيّما لأنّا نجد كرة هذه الكواكب قد تنتقل نقلة منتظمة تلقا حركة السماء. وذلك أنّه ليس يمنع مانع إذ كان ذلك كذلك أن يقال إنّ مبلغ زمان سنة الشمس هو الزمان الذي فيه تلحق الشمس كوكب زحل مثلاً أو كوكباً ه – خ: آخر من سائر الكواكب المتحيّرة. فتكون على هذا القياس أزمان السنة كثيرة مختلفة. فمن قبل هذه الأشياء رأينا أنّه ينبغي أن يعتقد أنّ زمان السنة للشمس هو الزمان الذي وجد بالأرصاد التي وقعت منذ /H194/ أقصى ما نقدر عليه من المدّة وأقدمها عهداً من أحد الانقلابين أو الاستوائين إلى ذلك المنقلب و ه – خ: أ ⟨يعني أو⟩الاستواء بعينه على الاتّصال.

لكن لمّا كان كأنّه قد يشكّك أبرخس الاختلاف الذي يتوهّم أنّه يقع في مثل هذه العودة نفسها بالأرصاد الدائمة التي كانت مرّة بعد أخرى، فإنّا نروم أن نبيّن بإيجاز أنّه ليس هذا أيضاً ممّا يشكّك وذلك أنّه قد نفرز عندنا أنّ هذه الأزمان ليست غير متساوية من قبل ما وقع لنا نحن أيضاً بالآلات من الرصد المتّصل للانقلابين والاستوائين. فإنّا لسنا نجد هذه الأزمان يخالف الربع اليوم الزائد بشيء له قدر يعتدّ به لكن ربّما تبيّن الشيء اليسير من الاختلاف بقدر ما يمكن من قبل صنعة الآلات ونصبها أن تقع من الزلل. فإذا نحن أيضاً حدسنا وقربنا من الأشياء التي منها تقيس ه – خ: شكّ أبرخس رأينا أنّ الخطاء في هذا الاختلاف هو بأن ينسب إلى الأرصاد أولي.

وذلك أنّه لمّا اقتصّ أوّلاً في كلامه في انتقال نقطتي الانقلابين ونقطتي الاستوائين الانقلابات الصيفيّة والشتويّة التي يظنّ أنّها /T133/ قد رصدت باستقصاء على الولاء اعترف هو نفسه بأنّه لم يقع فيها من الاختلاف ما يوجب من قبلها أن يحكم أنّ في زمان السنة اختلافاً ه – خ وج: وذلك أنّ أبرخس فقد {...} انتقال نقطتي الانقلابين والاستوائين التي رصدها في الانقلابات الصيفيّة والشتويّة يظنّ أنّها قد رصدت {...} أنّ اختلاف ما بينها ليس {...} في طول زمان سنة الشمس {...}.  فإنّه اتّبع ذكره لها بهذا القول. فأمّا بحسب هذه الأرصاد فمن البيّن أنّ اختلافات السنين كانت يسيرة جدّاً. /H195/ وأمّا في الانقلابين فلست (أرفع) بغير راج أو يكون قد ذهب علينا وعلى أرشميدس في الرصد وفي القياس التحصيل إلى مقدار ربع يوم لكن قد يمكن أن يستبين اختلاف زمان السنة من قبل الأرصاد التي وقعت بالحلقة النحاس المنصوبة بإسكندريّة في الرواق  ه – خ: مصر (before في الرواق) المعروف بالمربّع. وهذه الحلقة قد يظنّ أنّها تُبنى عن يوم الاستواء بأنّها في ذلك اليوم تبتدئ تضيء بالشمس بسيطها المقعّر من أحد الجانبين.

ثمّ أنّه يضيف إلى ذلك أوّلاً ذكر أزمان استوائات خريفيّة قد استقصى فيما وصف رصدها. فيقول إنّ الاستواء الخريفيّ كان في السنة السابعة عشر من الدور الثالث من أدوار ه: أظنّ أنّ هذه الأدوار هي أدوار كلّي يستعملها قلبس فهي تنسب إليه والدور منها مبلغه نحواً من سبعين سنة كان يورّخ {بها}. قلبس في اليوم الثلاثين من شهر ماسوري عند مغيب الشمس. وكان بعد ثلاث سنين في سنة عشرين في اليوم الأوّل من الأيّام التي تسمّى اللواحق بالغداة. وكان يجب أن يكون نصف النهار فيكون قد خالف بربع يوم واحد. وكان بعد سنة واحدة في سنة إحدى وعشرين في الساعة السادسة فكان ذلك موافقاً للرصد الذي كان قبله. وكان بعد إحدى عشرة سنة في سنة اثنين وثلاثين في اليوم الثالث من الأيّام اللواحق في نصف الليلة التي يليها اليوم الرابع. وكان يجب أن يكون في غداته، فيكون الاختلاف أنّما كان أيضاً بربع يوم. /H196/ وكان بعد سنة واحدة في سنة ثلاث وثلاثين في اليوم الرابع من الأيّام اللواحق بالغداة. فكان ذلك موافقاً للرصد الذي كان قبله. وكان بعد ثلاث ستّين في سنة ستّ وثلاثين في اليوم الرابع من الأيّام اللواحق بالعشيّ. وكان يجب أن يكون نصف الليل فيكون أنّما خالف أيضاً بالربع فقط.

ثمّ إنّه يذكر بعد ذلك الاستوائات الربيعيّة التي رصدت بمثل ذلك من الاستقصاء البالغ. /T134/ فيقول إنّ الاستواء الربيعيّ كان في سنة اثنتين وثلاثين من الدور الثالث من أدوار قلبس في اليوم السابع والعشرين من الشهر المسمّى ماخيز بالغداة. وإنّ الحلقة التي كانت بإسكندريّة أضاءت بالشمس من الجانبين جميعاً بالسواء في الساعة الخامسة حتّى أنّ هذا الاعتدال أيضاً لمّا رصد في أزمان ه: قال ينبغي أن يكون {مجاز} حتّى {ولو}.  المختلفة وجد يختلف قريباً من خمس ساعات. وإنّ الأرصاد التي كانت بعد هذا إلى سنة سبع وثلاثين كانت موافقة للحصّة التي تبلغ إلى ربع يوم. وإنّ الاستواء الربيعيّ كان بعد إحدى عشرة سنة في سنة ثلاث وأربعين في اليوم التاسع والعشرين من الشهر المسمّى ماخير بعد نصف الليلة التي يتلوها اليوم الثلاثون منه. فكان ذلك مطابقاً للرصد الذي كان في سنة اثنتين وثلاثين وإن ذلك كان أيضاً موافقاً للأرصاد التي كانت في السنين التي بعد هذه إلى سنة خمسين. وذلك أنّ الاستواء الربيعيّ كان في هذه السنة في أوّل يوم من الشهر المسمّى فامانوث عند مغيب الشمس بعد يوم ونصف وقريب من ربع من الوقت الذي كان فيه في سنة ثلاث وأربعين. وذلك هو ما يصيب السبع السنين التي بين تلك السنة وبين هذه لحصّتها.

/H197/ فلم يقع إذن ولا  ه – خ: إذاً في في هذه الأرصاد اختلاف يعتدّ به هذا على أنّه قد يمكن أن يقع الزلل ه - ص: ليس في الأرصاد التي تكون في الانقلابات فقط لكن في التي تكون في الاستوائات أيضاً من قبل الرصد نفسه ويبلغ ذلك الزلل إلى ربع يوم واحد. وذلك أنّه إن زلّ نصب الآلات أو مع ذلك قسمتها عن الصحّة ولو بجزء من ثلاثة آلاف وستّ مائة جزء من أجزاء الدائرة التي تمرّ بقطبي معدّل النهار. فإنّ الشمس تقوم ما هذا مبلغه من العُدول في العرض إذا كانت عند تقاطعي الاستواء إذا تحرّكت ربع جزء في الطول في الدائرة المائلة. فيكون الاختلاف عند ذلك يبلغ إلى قريب من ربع يوم. وقد يقع الزلل أكثر في الآلات التي تنصب بمرّة من غير أن تصحّح بالأرصاد ↑بالأرصاد↑: صح أنفسها لكن تركز في وقت من الأوقات في موضع من المواضع لتبقى على نصبها ذلك زماناً طويلاً بأن ↑بأن↑: صح تحدث في نصبها على طول الزمان زوال لا يشعر به كما قد عرض في الحلق النحاس المنصوب ↑: به عندنا في الملعب الذي يظنّ أن وضعه ه – صح: وضعها في سطح معدّل النهار. Toomer, 134: one can see this in the case of the bronze rings in our Palaestra, which are supposed to be fixed in the plane of the equator. فإنّا رصدنا هذه ↑هذه↑: خ بهذه الحلق فتبيّن لنا أن نصبه ه – صح: نصبها قد بلغ من الزوال وخاصّة أعظم الحلق وأقدمها أنّه ربّما تكررّت أضاءت بسيطاتها المقعرّة في الاستواء الواحد بعينه مرّتين (أيضاً) إلّا أن ما جرى هذا المجرى.

/H198//T135/ فليس يرى ولا أبرخس نفسه فضلاً عن غيره أن شيءاً منه يحقّ أن يتوهّم ↑يتوهّم↑: خ يوجب اختلافاً في أزمان السنين. ه – ج: رأينا الضوء في باطنها في زمان أحد الاعتدالين وهذا ومثله ما لا{...} أبرخس أنّه دلاله على ما يظنّ من اختلاف أزمنة السنين.  ولكنّه لمّا قاس من كسوفات ما من كسوفات القمر ذكر أنّه وجد أنّ اختلاف أزمان السنين إذا قيس بالزمان المتوسّط لم يكن بينه وبينه من الفضل أكثر من نصف وربع يوم واحد. وهذا لعمري ممّا كان يجب أن يضعى إليه لو كان الأمر فيه على ما وصف ولم يكن قد علم أنّه باطل من نفس ما قاله هو. وذلك أنّه يقيس على ذلك بكسوفات قمريّة رصدت وكانت بالقرب من كواكب من الكواكب الثابتة وينظر كم مقدار تقدّم الكوكب المعروف بالسماك الأعزل للنقطة الخريفيّة في كسوف كسوف. ونرى أنّه وجده بذلك في بعض الأوقات كان بعده منها ستّة أجزاء ونصف جزء، وهذا البعد هو أكثر ما وجد هذا الكوكب في زمانه بعيداً عن هذه النقطة، ووجده في بعض الأوقات بينه وبينها خمسة أجزاء وربع جزء وذلك أقلّ ما وجده من البعد بينه وبينها. فيجتمع من ذلك أنّه لمّا كان ليس يمكن أن يكون السماك الأعزل في مثل هذا المقدار اليسير من الزمان يتحرّك هذا المقدار من الحركة فالأولى أن تكون الشمس وهي التي من قبلها يقف على مواضع الكواكب الثابتة ليس تكون عودتها إلى الموضع الذي منه يبتدئ في زمان سواء. ↑سواء↑: واحد وذهب عليه أنّه لمّا كان القياس ↑القياس↑: الحساب ليس يتهيّأ أن يتمّ أصلاً دون أن تحصل ↑تحصل↑: تفرد؛ ه – خ: أن يعلم موضع الشمس في الكسوف. فإنّه هو باستعماله في ذلك في كلّ كسوف الانقلابات والاستوائات التي رصدها باستقصاء في تلك السنين. /H199/ فقد بيّن من ذلك نفسه أنّه إذا قيس بعضها ببعض لم يكن بينها عند المقايسة من الاختلاف شيء غير زيادة حصّة الربع اليوم. ه – خ وج: ومن أخذه الأرصاد بالحقيقة من الانقلابات والاستوائات التي رصدها باستقصاء في تلك السنين يدلّ على أنّ الفضلة التي بين الرصدين لم تكن أكثر من ربع يوم واحد في كلّ سنة ونحن {...} موضع {...} وما فيه. 

ونحن مظهرون ذلك بمثال واحد فنقول إنّه نرى أنّه وجد برصد الكسوف الذي وصف أنّه كان في سنة اثنتين وثلاثين من الدور الثالث من أدوار قلبس السماك الأعزل متقدّماً للنقطة الخريفيّة بستّة أجزاء ونصف ووجده بالرصد الذي كان في سنة ثلاث وأربعين من ذلك الدور بعينه متقدّماً لها بخمسة أجزاء وربع. ولمّا وصف أيضاً على هذا المثال في القياسات التي ذكرها للاستوائين الربيعيّين اللذين رصدا باستقصاء في هاتين السنتين كيما يستخرج بهما موضع الشمس في وسطي زماني الكسوفين ويستخرج من قبل هذين موضعي القمر ويستخرج من قبل موضعي القمر مواضع الكواكب. قال إنّ الاستواء الربيعيّ كان في سنة اثنتين وثلاثين في اليوم السابع والعشرين من الشهر المسمّى ماخير بالغداة وكان في سنة ثلاث وأربعين في اليوم التاسع والعشرين منه بعد نصف الليلة التي يتلوها اليوم الثلاثون فكان هذا الاستواء بعد يومين ونصف وقريب من ربع من اليوم الذي كان فيه في سنة اثنتين وثلاثين وذلك هو مبلغ ما يجتمع من الربع اليوم فقط إذا ألحق بكلّ واحدة من /T136/ الإحدى العشرة السنة التي بين تلك السنة وبين هذه. فإذ كانت عودة الشمس في هذين الاستوائين اللذين وضعهما لم تكن لا في زمان أكثر ولا أقلّ ممّا توجبه الزيادة بالربع اليوم وكان السماك الأعزل لا يمكن أن يسير في مثل هذه السنين اليسيرة /H200/ جزءاً وربع جزء فإنّه من الشنع البين الشناعة أن يستعمل القياسات التي وقعت بتأسيس هذه المبادئ في الطعن على هذه المبادئ أنفسها التي بها كان ثباتها.  ه – خ: بناءها ونترك أن ننسب السبب في الأمر المحال الذي وقع في مبلغ حركة السماك الأعزل وقد يمكن أن يوقع مثل هذا الخطاء أشياء كثيرة (إلى شيء) (سوى الاستوائين فقط اللذين ذكرنا كأنّه قد اجتمع فيهما أنّهما رصدا باستقصاء وبغير استقصاء معاً). وذلك أنّ الأولى أن نظنّ أنّه قد يجوز أن تكون أبعاد القمر في الكسوفات أنفسها من الكواكب القريبة منه لم تخفض جزرها وتدقّق وتجوز أن تكون قياسات زوال القمر ه: يعني اختلاف المنظر بحسب رؤيته في المواضع التي ترى فيها أو قياسات حركة الشمس من نقط الاستواء إلى أوساط أزمان الكسوفات أخذت ↑أخذت↑: صح عن ↑عن↑: خ على غير تحقيق أو على غير استقصاء. ه: {...} نقطتي الاعتدال فقط اللتين منهما بأنّ الرصد على حقيقة أو على غير حقيقة {...} الذي يمكن أن يكون هذا الخطاء من قبله {جهات} كثيرة منها أبعاد القمر {...} لكسوف ممّا يقرب إليه من {...} الكواكب أو من قبل اختلاف المنظر والرؤية إلى القمر وموضعه أو من قبل حركة الشمس من نقطتي الاعتدال إلى أوساط أزمنة الكسوف أو من قبل {...} يقاس ويؤخذ يغير تدقيق وغير حقيقة إلّا. 

إلّا إنيّ أحسب أنّ أبرخس أيضاً نفسه قد علم أنّه ليس في مثل هذه ه – خ: الأشياء ما وجب به أن ينسب إلى الشمس اختلاف ما ثان يعمل عليه وأنّه أنّما أراد لإيثاره الحقّ أن لا يمسك عن شيء ممّا يمكن بوجه من الوجوه أن يدخل الشبه على بعض الناس لا غير. والدليل على ذلك أنّه نفسه فضلاً عن غيره قد استعمل الأصول الموضوعة في أمر الشمس والقمر على أنّ اختلاف في الشمس يوجد واحداً بعينه وهو الذي يعود مع عودة زمان السنة الذي يحسب الانقلابين والاستوائين. /H201/ وإنّا لمّا وضعنا الأدوار المفروضة للشمس متساوية الزمان لم نر الأمور التي تظهر في الكسوفات تخالف أصلاً من قبل ذلك شيء يعتدّ به القياسات التي بنيت على تلك الأصول المفروضة. وقد كان سيلزم  ه – خ: يلزم أن تظهر هذا الاختلاف للحسّ ظهوراً بيّناً لو لم تدرك حقيقة الأمر في اختلاف زمان السنة ولو أنّ الخطاء كان بجزء واحد فقط وذلك ساعتان بالتقريب من ساعات الاستواء.

فمن هذه الأشياء كلّها ومن الأشياء التي منها أدركنا نحن أزمان العودات بأدوار الشمس التي رصدناها مراراً متوالية لسنا نجد مقدار السنة مختلفاً متى نظر فيه بالقياس إلى شيء واحد ولم ينظر فيه مرّة بالقياس إلى نقطتي الانقلابين ونقطتي الاستوائين ومرّة بالقياس إلى الكواكب الثابتة. ولا نجد عودة أليق من العودة التي تأتي فيها الشمس من أحد الانقلابين أو أحد الاستوائين أو من نقطة أخرى أيّ نقطة كانت من الدائرة التي تمرّ بأوساط البروج إلى تلك النقطة بعينها من الرأس. ↑من الرأس↑: خ وبالجملة فإنّا نرى أنّه إنّما ينبغي أن يدلّ على الأشياء الظاهرة بأبسط ما يمكن ه – خ: يكون من الأصول ونقدر ما يكون ما يظهر بالأرصاد لا يوجد فيه شيء يعتدّ به يعايد  ه: يقاوم مثل ذلك الأصل. ه: أعني الرصد بالانقلابات والاستوائات.

فأمّا إنّ زمان السنة إذا نظر فيه بحسب الانقلابين والاستوائين وجد ثلاث مائة وخمسة وستّين يوماً وزيادة أقلّ من ربع يوم فقد بان ذلك لنا ممّا بيّنه أبرخس فضلاً عن غيره. /Η202/ وأمّا بكم هو أقلّ من ربع يوم فليس يمكن /T137/ الوقوف على ذلك محرّراً غاية التحرير إذ كنّا نجد الربع الزائد في السنين الكثيرة ثابتاً على حال واحدة لا تختلف في الحسّ لقلّة الاختلاف فيه. ولذلك صار قد يمكن عند المقايسة التي تقع عليه في زمان طويل أن توجد زيادة الأيّام التي تخرج وهي التي ينبغي أن تقسّم على سنيّ المدّة التي بين الزمانين أيّاماً واحدة بعينها كثرت السنين أو قلّت ه: الأيّام التي تفضل وتجتمع {...} على السنين الكثيرة {...} السنين القليلة التي في مائتين {...} الحصّة واحدة {...} من القسمة للسنة الواحدة.  إلّا أنّ مثل هذه العودة قد يتهيّأ أن تدرك بغاية التقريب من الأمر المستقصى كلّما وجد الزمان الذي بين الرصدين اللذين تقع بينهما المقايسة أطول. وليس هذا أشياء أنّما عرض في هذه العودة فقط بل في جميع العودات الدوريّة أيضاً. وذلك أنّ الزلل الذي يقع من قبل التقصير اللاحق للأرصاد وإن استقصيت واحتيط في أحكامها لمّا كان يسيراً ويكاد يكون واحداً بعينه عندما يدركه الحسّ منه فيما يظهر منه في الزمان الطويل وفيما يظهر منه في الزمان القصير. فإنّه إذا قسم على سنين أقلّ خرج الخطاء في السنة أعظم والمجتمع منه على طول الزمان يعظم أيضاً وإذا قسم على سنين أكثر خرج أقلّ. ولذلك رأينا أنّه قد /H203/ يكتفي بأن ينظر كم مقدار ما يمكن أن {يريدناه} في التقريب من أصول الأدوار الزمان الذي فيما بيننا وبين ما وقع إلينا من الأرصاد القديمة المستقصاة معاً. فتورده ه – ط – صح: فنريده نحن أيضاً عليها ولا نفرط في ذلك فيكون قد أهملنا بإرادتنا ما يجب علينا البحث عنه. فأمّا الطمع في تصحيح  ه – ط: قوله أنّ تصحيح زمان سنة غير {...} على الحقيقة في زمان الدهر كلّه.  ذلك بزمان الدهر كلّه أو بزمان أطول كثيراً من زمان الأرصاد بأضعاف مضاعفة فإنّا نرى أنّ ذلك مجانب لإيثار الحقّ في العلم والمعرفة بالحقائق.

وقد كان يجب من قبل تقادم العهد أن نستعمل أرصاد الانقلابات الصيفيّة التي كانت على عهد ماطن وأوقطيمن والأرصاد التي كانت بعد هذه على عهد أرسطرخس فنقيس بينها ه – ط: أرصاد مبطن وأقطيمن وأرسطراخس وبين الأرصاد التي كانت في زماننا. لكن لمّا كانت بالجملة أرصاد الانقلابات تعسّر أختبارها وكان مع ذلك ما تأدّي إلينا عن تلك الأرصاد أنّما أخذ على غير تدقيق كما يظنّ أنّ أبرخس أيضاً يرى  ه – خ: كان يرى ذلك فإنّا أنصرفنا عن هذه الأرصاد واستعملنا في المقايسة التي قصدنا لها أرصاد الاستوائات وأخترنا من هذه أيضاً طلباً للاستقصاء الأرصاد التي أشار أبرخس إلى أنّها خاصّة كانت منه على غاية التحرير حتّى أنّه يثق بها الثقة كلّها والأرصاد التي كانت منّا نحن بغاية ما يمكن من الاستقصاء الذي لا شكّ فيه بالآلات التي وضعناها لذلك وما أشبهه في أوّل كتابنا هذا. فمن هذه الأرصاد نجد الانقلابين والاستوائين فتقدّم ما يوجبه الربع الزائد  /H204/على الثلاث المائة والخمسة والستّين اليوم في نحو من ثلاث مائة سنة بيوم واحد.

من ذلك أنّ في سنة اثنتين وثلاثين  ه – خ: من الدور الثالث من أدوار قلبس أشار أبرخس إلى /T138/ أنّ الاستواء الخريفيّ فيها رصد خاصّة بغاية الاستقصاء وقال أنّه وجد بالقياس كان في اليوم الثالث من الأيّام اللواحق في نصف الليلة التي يتلوها اليوم الرابع وهذه السنة هي سنة مائة وثمان وسبعين منذ وفاة إسكندر. ورصدنا نحن الاستواء الخريفيّ أيضاً بغاية الاحتياط والتحرّز من الخطاء بعد مائتي سنة وخمس وثمانين سنة في السنة الثالثة لأنطونيس وهي سنة أربع مائة وثلاث وستّين من وفاة إسكندر فوجدناه كان في اليوم التاسع من الشهر المسمّى أثور بعد طلوع الشمس بنحو ساعة. فقد تقدّمت إذن العودة في مائتي سنة وخمس وثمانين سنة تامّة من سنيّ المصريّين وكلّ سنة منها ثلاث مائة يوم ه – ط: إنّ سنين المصريّون هو ما {...}. وخمسة وستّون يوماً بسبعين يوماً وربع يوم وجزء من عشرين جزءاً من يوم بالتقريب مكان الأحد والسبعين اليوم والربع الذي نصب هذه السنين من قبل الربع الزائد فقد تقدّمت إذن العودة الزيادة التي من قبل الربع بيوم واحد إلّا نحواً من جزء من عشرين جزءاً من يوم.

وكذلك أيضاً فإنّ أبرخس يقول إنّ الاستواء الربيعيّ رصد بغاية الاستقصاء في تلك السنة بعينها أعني سنة اثنتين وثلاثين من الدور الثالث من أدوار قلبش فوجد قد كان في اليوم السابع والعشرين من الشهر المسمّى ماخير بالغداة. وهذه السنة هي سنة مائة وثمان وسبعين /H205/ من وفاة إسكندر. ووجدنا نحن الاستواء الربيعيّ بعد مائتين وخمس وثمانين سنة كما قلنا في سنة أربع مائة وثلاث وستّين من وفاة إسكندر كان في اليوم السابع من الشهر المسمّى ماخور بعد منتصف النهار بنحو من ساعة حتّى أنّ هذه الدورة أيضاً قد تقدّمت مثل تلك الأيّام وهي سبعون يوماً وربع يوم وجزء من عشرين جزءاً من يوم بالتقريب مكان الأحد والسبعين اليوم والربع الذي يصيب المائتي السنة والخمس والثمانين السنة بحسب الربع. فقد تقدّمت إذا هاهنا أيضاً عودة الاستواء الربيعيّ الزيادة التي من قبل الربع ↑: يوم يوماً واحداً إلّا نحواً من جزء من عشرين جزءاً من يوم. فيجب من ذلك إذ كانت نسبة الثالث مائة السنة إلى المائتين والخمس والثمانين السنين هي بعينها نسبة يوم واحد إلى يوم واحداً الأجزاء من عشرين جزءاً من يوم أن تجمتع في ثلاث مائة سنة بالتقريب تتقدّم عودة الشمس التي تكون عند نقطتي الاستوائين ما يوجبه زيادة الربع يوماً واحداً. ه – ج: أن تتقدّم عودة الشمس إلى نقطة الاعتدال الأيّام التي تجتمع من الأرباع التامّة بيوم في ثلاث مائة سنة. 

وإن نحن أيضاً طلبنا تقادم العهد فقايسنا بين ما خرج لنا نحن بالقياس الذي استقصيناه بغاية ما يمكن الانقلاب الصيفيّ وبين ما رصد منه على عهد ماطن وأوقطيمن على أنّه لم يحصل رسمه وجدناه ذلك الذي ذكرناه بعينه. فإنّ ذلك الرصد نجده قد كتب أنّه كان ولاية إيسوذيس على أهل أثيبيّة في الشهر المسمّى فامانوث من شهور القبط في اليوم الحادي والعشرين منه في صدر النهار. /H206/ ووجدناه نحن بالقياس الحريز كان في هذه السنة التي ذكرناها أعني سنة أربع مائة وثلاث وستّين {من وفاة} إسكندر في اليوم الحادي عشر من الشهر المسمّى ماسوري بعد منتصف الليلة التي يتلوها اليوم الثاني عشر بنحو من ساعتين. ومبلغ السنين منذ وقت الانقلاب الصيفيّ الذي أثبت أنّه كان على عهد أنسوذيس إلى انقلاب الصيفيّ الذي رصد على عهد أرسطرجس في سنة خمسين من الدور الأوّل من أدوار قلبس على ما قال أيضاً أبرخس مائة سنة واثنتان وخمسون سنة ومن هذه السنة أعني سنة خمسين وهي سنة أربع وأربعين من وفاة إسكندر إلى سنة أربع مائة وثلاث وستّين وهي السنة  ه – ط: السنة الذي رصد هو فيها وبقي {...} من بخت نصر ⟨نبو نصر⟩. التي كان فيها رصدنا نحن أربع مائة سنة وتسع عشرة سنة. ففي السنين /T139/ كلّها التي فيما بين هذين الوقتين وهي خمس مائة سنة وإحدى وسبعون سنة إن كان الانقلاب الصيفيّ الذي رصد على عهد أوقطيمن كان في أوّل اليوم الحادي والعشرين من شهر فامانوث، جميع مازاد في هذه السنين المصريّة التامّة مائة يوم وأربعون يوماً ونصف وثلث يوم بالتقريب، فكان المائة والاثنين والأربعين اليوم والنصف والربع الذي يصيب الخمس المائة السنة الإحدى والسبعين السنة من قبل الربع الزائد. فقد تقدّمت إذن هذه العودة التي وصفنا الزيادة التي يوجبها الربع يومين إلّا جزءاً من اثني عشر جزءاً من يوم. فقد ظهر إذن بهذا الوجه أيضاً أنّ في ستّ مائة سنة بأسرها تتقدّم زمان السنة الزيادة التي يوجبها الربع بنحو من يومين كاملين.

وفي أرصاد آخر أكثر من هذه نجد نحن ذلك بعينه لازماً ونجد أبرخس مراراً كثيرة نعرف ه: يعترف. به من ذلك أنّه في كتابه في زمان السنة لمّا قاس بين الانقلاب الصيفيّ الذي رصده /H207/ أرسطرخس في آخر سنة خمسين من الدور الأوّل من أدوار قلبس.  ه - صح: وبين الانقلاب الصيفيّ أيضاً الذي أخذه هو باستقصاء في آخر سنة ثلاث وأربعين من الدور الثالث من أدوار قلبش. قال هذا القول فمن البيّن إذا أنّ في مائة سنة وخمس وأربعين سنة كان هذا الانقلاب أسرع من الزيادة التي توجبها الربع بنصف الزمان المجتمع من يوم وليلة. وأيضاً في كتابه في الشهور والأيّام الكبيسة لمّا تقدّم فقال إنّ زمان السنة أمّا على رأي آل ميطن وأوقطيمن فثلاث مائة وخمسة وستّون يوماً ومع ذلك ربع يوم وجزء من ستّة وسبعين جزءاً ونصف  ↑ونصف↑: خ من يوم. وأمّا على رأي قلبس فثلاث مائة وخمسة وستّون يوماً وربع يوم فقط. فقد اتّبع ذلك بأن قال بألفاظه نصّاً هذا القول. وأمّا نحن فأمّا نجد شهوراً تامّة محصورة في التسع العشرة السنة عدّتها مثل عدّتها عندهم. وأمّا السنة فنجدها أقلّ أيضاً من الربع بجزء من ثلاثة مائة جزء من يوم بغاية التقريب لمبلغه حتّى يكون في ثلاث مائة سنة ينقض أمّا على رأي ماطن فخمسة أيّام وأمّا على رأي قلبس فيوماً واحداً. ولمّا أجمل أراءه إلّا الشاذّ منها فيما رسمه في كتبه قال هذا القول: وقد وضعتُ في زمان السنة أيضاً مقالة مفردة أبين فيها أنّ سنة الشمس، وذلك يكون الزمان الذي تصير فيه الشمس من أحد الانقلابين إلى ذلك الانقلاب بعينه أو من أحد الاعتدالين إلى ذلك الاعتدال بعينه، تحيط بثلاث مائة وخمسة وستّين يوماً /H208/ وأقلّ من ربع يوم وليلة بجزء من ثلاث مائة جزء من يوم وليلة بالتقريب لا على ما يظنّ أصحاب التعاليم من أنّه يلحق العدّة من الأيّام التي ذكرناها الربع كما هو.

وأمّا إن ما سنح إلى هذه الغاية في مقدار زمان السنة مطابق للمقدار الذي تقدّمنا  /T140/فوضعناه له بحسب عودة الانقلابين والاستوائين فأحسب ذلك قد ظهر بموافقة ما آتينا به الآن لمّا ذكرناه من قبل. وإذا كان ذلك كذلك فإن نحن قسمنا اليوم الواحد على الثلاث مائة سنة أصاب كلّ سنة اثنتا عشرة ثانية فإن نقصنا ذلك من الثلاث مائة والخمسة والستّين يوماً والخمس عشرة الدقيقة التي لحصّة الربع حصل لنا زمان السنة الذي نطلبه ثلاث مائة وخمسة وستّين يوماً  ه: ه وأربع عشرة دقيقة وثمانياً وأربعين ثانية. فهذا مبلغ عدد الأيّام بغاية ما أمكننا من التقريب التي أدركناها ممّا نحن بسبيله.

ومن أجل النظر في أمر الشمس والكواكب الآخر فيما يكون من مسيرها من قبل شيء شيء من الأمور الجزئيّة وهذا أمر قد يسهل تناوله ويكون كالموضوع وضعاً متى أثبت على التفصيل في جداول فإنّا نرى أنّه يجب على صاحب التعاليم أن يجعل قصده وغرضه أن تبيّن أوّلاً أنّ جميع الأشياء التي تظهر في السماء أنّما تجري تحرّكات مستوية على الاستدارة ثمّ يضع جداول مشاكلة موافقة بغاية ما يمكن لمّا قصد له يفرّق بها بين الحركات الجزئيّة المستوية وبين الاختلاف الذي توهّم أوضاع الدوائر التي تلحقها ويتبيّن بها ما تظهر من مسيرهما من قبل اختلاط هذين الأمرين جميعاً واجتماعهما. (وكيما يكون) (هذا الفنّ أخصّ نفعاً ويقرب مأخذه  ه – خ: وأقرب مأخذا عند البراهين أنفسها). ه – صح: وكيما يكون هذا الفنّ أخصّ نفعاً وأقرب مأخذاً عند البراهين أنفسها.
This sentence is not found in Greek version.

⟨III.2⟩ ب: في وضع جداول لحركات الشمس الوسطى There is no new chapter in Greek version.

/Η209/ فنحن واضعون في هذا الموضع صفة حركات الشمس المستوية الجزئيّة على هذا الوجه. أقول إنّه لمّا كنّا قد بيّنا أنّ مبلغ العودة الواحدة ثلاث مائة وخمسة وستّون يوماً وأربع عشرة دقيقة وثمان وأربعون ثانية فإن نحن قسّمنا على هذه العدّة أجزاء دائرة واحدة وهي ثلاث مائة وستّون جزءاً خرج لنا مبلغ حركة الشمس الوسطى في اليوم تسعاً وخمسين دقيقة وثمان ثواني وسبع عشرة ثالثة وثلاث عشرة رابعة  ه: حركة الشمس {...} على رأيه. واثنتي عشرة خامسة وإحدى وثلاثين سادسة بالتقريب فإنّه قد يجزي في هذه القسمة أن يبلغ بالتجزية إلى هذا الموضع.

وأيضاً إذا أخذنا من مبلغ الحركة في اليوم جزءاً من أربعة وعشرين جزءاً حصل لنا مبلغ الحركة في الساعة دقيقتين وسبعاً وعشرين ثانية وخمسين ثالثة وثلاث وأربعين رابعة وثلاث خوامس وسادسة بالتقريب.

وعلى هذا المثال إذا نحن ضاعفنا مبلغ الحركة في اليوم بأيّام شهر واحد وهي ثلاثون يوماً خرج لنا مبلغ الحركة في الشهر الوسطى تسعة وعشرين جزءاً وأربعاً وثلاثين دقيقة وثمان ثواني وستّاً وثلاثين ثالثة وستّاً وثلاثين رابعة وخمس عشرة خامسة وثلاثين سادسة. وإذا نحن ضاعفنا تلك الحركة بأيّام سنة واحدة من سنيّ المصريّين وهي ثلاث مائة وخمسة وستّون يوماً خرج لنا مبلغ الحركة الوسطى  ه – ط: إنّ السنين المصريّة {...} ركب الجداول {...} يوماً تامّ {...} للسنة منها ثلاث مائة وتسعة وخمسين جزءاً وخمس وأربعين دقيقة وأربع وعشرين ثانية وخمس وأربعين ثالثة وإحدى وعشرين رابعة وثمان خوامس ه – صح: وخمساً وثلاثين سادسة.

وإذا ضاعفنا أيضاً الحركة في السنة بثمان عشرة سنة لما سيظهر من تعادل رسم الجدول ونقصنا من ذلك الأدوار التامّة حصل لنا حصّة كلّ ثمان عشرة سنة ثلاث مائة وخمسة وخمسين جزءاً وسبع وثلاثين دقيقة وخمس وعشرين ثانية وستّ وثلاثين ثالثة وعشرين رابعة ه – صح: وأربعاً وثلاثين خامسة وثلاثين سادسة.

فنحن واضعون لحركة الشمس المستوية ثلاثة جداول في كلّ جدول خمسة وأربعون سطراً كما كنّا عملنا وكلّ جدول مقسوم قسمين. فالجدول الأوّل فيه مبلغ الحركات الوسطى التي تصيب السنين المبنيّة على ثمان عشرة سنة، والجدول الثاني فيه /T141/ أوّلاً مبلغها في السنين ثمّ تحتها مبلغها في الساعات، والجدول الثالث فيه أوّلاً مبلغها في الشهور وتحتها مبلغها في الأيّام. وفي هذه الجداول كلّها أعداد الزمان مثبتة في القسم الأوّل من الجدول وما يقسطه  ه: يعادله يوازيه من الأجزاء في القسم الثاني منه على حسب ما يحصل لواحد واحد منها خاصّة. وهكذا رسمنا الجدول.

/H216/ ⟨III.3⟩ ج:  ه: {...} هذا قد {...} لمقابلة في الأصول التي توضع للحركة المستويّة التي تجري على الاستدارة

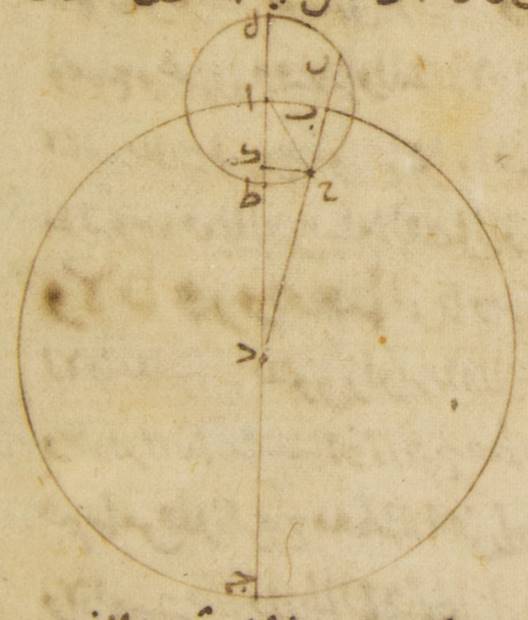
ولمّا كان قد يتلو ذلك أن نبيّن الاختلاف الذي يظهر للشمس، فقد ينبغي أن نتقدّم فنعلم بالجملة أن تنقل ه – خ: (الشمس والقمر و) الكواكب المتحيّرة بحركاتها تلقا حركة السماء وكذلك نقلة الجميع قدماً مستويّة كلّها في طبيعتها على استدارة أعني أنّ الخطوط المستقيمة  ه – خ: (التي هي أبعاد الكواكب من مراكز أفلاكها) التي تتوهّم توهّماً أنّها تدير الكواكب أو أنّها تدير مع الكواكب أفلاكها يفصل فيها كلّها على الإطلاق في الأزمان المتساوية زوايا متساوية عند مراكزها في كلّ واحدة من المدارات. وإنّ الاختلاف الذي يظهر فيها أنّما يكون من قبل  ه – خ – صح: مواضع الأفلاك التي في أكرها الأفلاك مواضع في أكرها أوضاع  التي عليها ه – صح: تتحرّك ومن قبل ترتيبها وأنّه ليس فيما يحالّ من اختلاف نظام ما يظهر فيها ما يلزم منه بالحقيقة شيء مباين لأنّها أبديّة. وإنّ السبب فيما نحالّ من الاختلاف فيها يحتمل أن يرجع إلى أصلين خاصّة أوّلين بسيطين وذلك أنّ حركتها لمّا كانت ترى صح؛ ه – خ – صح: حركات الكواكب التي ترى لو كانت  على فلك يتصوّر في الذهن أنّ مركزه مركز العالم وأنّه في سطح فلك البروج حتّى أنّه لا فرق بين مركزه وبين بصرنا ه – خ – صح: لم يكن يرى لحركاتها اختلاف فلذلك فقد  ه – صح: قد ينبغي أن نظنّ أنّ الكواكب إمّا أن تكون تتحرّك حركاتها على الاستواء على أفلاك ليس مراكزها مركز العالم، وإمّا أن تكون تتحرّك حركاتها على /H217/ أفلاك مركزها مركز العالم إلّا أنّها ليست تتحرّك على هذه الأفلاك على الإطلاق بل على أفلاك أخر تحرّكها تلك الأفلاك ويقال لها أفلاك التداوير. فإنّه قد يظهر أنّه ممكن ↑ممكن↑: يمكن بحسب كلّ واحد من هذين الأصلين أن تبيّن لأبصارنا أنّها في أزمان متساوية يقطع من فلك البروج الذي مركزه مركز العالم قسيّاً غير متساوية.

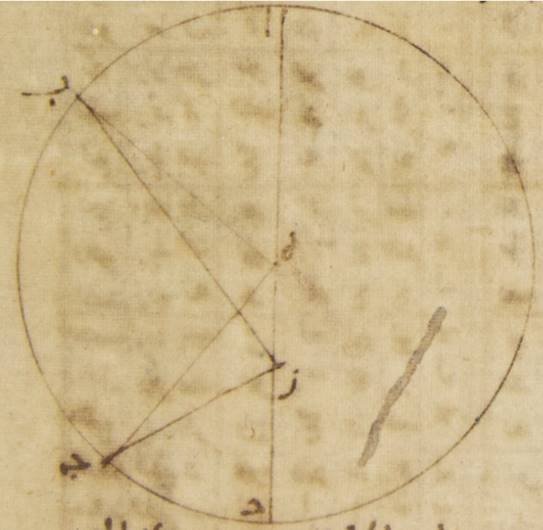
آ: وذلك أنّا إن وضعنا فلكا خارج المركز وتوهّمنا ذلك الفلك الخارج المركز الذي عليه تتحرّك الكوكب باستواء فلك ألف باء جيم دال حول مركز هاء وقطر ألف هاء دال ونقطة زاي على القطر بصرنا حتّى تكون نقطة ألف أبعد البعد من الأرض ونقطة دال أقرب القرب منها. وفصّلنا قوسين متساويتين وهما قوس ألف باء وقوس دال جيم ووصّلنا خطّ باء هاء وخطّ باء زاي وخطّ جيم هاء وخطّ جيم زاي. فقد تبيّن من ذلك أنّ الكوكب يقطع كلّ واحدة من قوسي /T144/ ألف باء، جيم دال في زمان سواء ويظنّ أنّه قد سار قوسين مختلفتين من الدائرة التي ترسم على مركز زاي من قبل أنّ زاوية باء هاء ألف إذ كانت  ↑إذ كانت↑: صح مساوية لزاوية جيم هاء دال فإنّ زاوية باء زاي ألف تكون أصغر من كلّ واحدة منهما وزاوية جيم زاي دال تكون أعظم من كلّ واحدة منهما.

/H218/ ب: فإن وضعنا فلك تدوير وتوهّمنا أنّ الفلك الذي مركزه مركز فلك البروج فلك ألف باء جيم دال حول مركز هاء وقطر ألف هاء جيم وفلك التدوير الذي يدور عليه وهو الذي يتحرّك عليه الكوكب فلك زاي حاء طاء كاف حول مركز ألف.

فقد تبيّن من ذلك على هذه الجهة أيضاً أنّ فلك التدوير إذا سار باستواء على دائرة ألف باء جيم دال من جهة نقطة ألف مثلاً نحو نقطة باء وسار الكوكب أيضاً على هذا المثال في فلك التدوير، فإنّ الكوكب إذا صار على نقطة زاي أو نقطة طاء لم يظهر بينه وبين نقطة ألف، التي هي مركز فلك التدوير، اختلاف وإذا صار على نقطة غيرهما لم يكن ما يظهر كذلك. لكنّه إذا صار على نقطة حاء  ↑حاء↑: ح ظنّ به أنّه قد تحرّك حركة أزيد على الحركة المستوية بقوس ألف حاء، وإذا صار على نقطة كاف ظنّ به على ذلك المثال أنّه قد تحرّك حركة أنقص من الحركة المستوية بقوس ألف كاف.

فأمّا في هذا الأصل الذي وضع فيه الخروج عن المركز فقد يلزم فيه أيضاً أنّ الحركة تكون عند البعد الأبعد أقلّ ما تكون وعند القرب الأقرب أكثر ما تكون، وذلك أنّ  ه: العلّة التي أتى بها عند ذكره الزاويتين أنّما يوجب أن تكون الحركتان اللتان ذكرهما أقلّ من الحركة المستوية وأكثر وإن كان قوله أنّها أقلّ ما يكون وأكثر ما يكون قولاً حقّاً لسبب آخر لم يذكره. زاوية ألف زاي باء (ألف باء) أبداً أصغر من زاوية دال زاي جيم. فأمّا في الأصل الذي وضع فيه فلك التدوير فقد يمكن أن يقع الأمران جميعاً. وذلك أنّ فلك التدوير إن كانت حركته تلقا حركة /H219/ السماء كأنّا قلنا من نقطة ألف نحو نقطة باء، ثمّ كان الكوكب حركته في فلك التدوير على هذا المثال حتّى يكون أيضاً نقلته من البعد الأبعد تلقا حركة السماء، أعني من نقطة زاي نحو نقطة حاء، فإنّ مسيره يلزم أن يكون أطول  ه – خ: أسرع ما يكون عند البعد الأبعد وذلك أنّ /T145/ فلك التدوير والكوكب يكونان حينئذ يتحرّكان إلى جهة واحدة. وإن كانت نقلة الكوكب من بعده الأبعد قدماً في فلك التدوير، أعني من نقطة زاي نحو نقطة كاف، فإنّ الأمر يكون بالعكس، فيكون مسيره عند بعده الأبعد أقصر ه – خ: أبطأ ما يكون وذلك أنّ الكوكب يكون يتحرّك حينئذ إلى ضدّ الجهة التي يتحرّك إليها فلك تدويره.

وإذ كان ذلك كذلك فقد ينبغي أيضاً أن نعلم أنّ ما قد وجد  ه – خ: من الكواكب له فيه ضربان من الاختلاف فقد يمكن أن يكون قد اجتمع فيه المعنيان اللذان وصفناهما جميعاً كما سنبيّن في الكلام فيهما، وما كان أنّما يقع فيه اختلاف واحد وليس يقع فيه غيره من الاختلاف فقد يجري فيه أحد الأصلين اللذين وضعناهما. وإنّ جميع ما يظهر بالعيان على حسب واحد واحد من الأصلين لا فرق فيه  ه – خ: بينهما ولا اختلاف متى كانت النسب محفوظة فيهما جميعاً، أعني متى كانت في الأصل الذي وضع فيه الخروج عن المركز نسبة الخطّ الذي بين المركزين، أعني بين البصر وبين مركز الفلك الخارج المركز، إلى الخطّ الخارج من مركز ه – خ: نصف قطر  الفلك الخارج المركز كنسبة الخطّ الخارج من مركز ه – خ: نصف قطر  فلك التدوير في الأصل الذي وضع فيه فلك التدوير إلى الخطّ الخارج من مركز الفلك الذي يديره ه – خ: نصف قطر الفلك الحامل له ؛ /H220/ وكان أيضاً ه – خ: وأيضاً فأنّ  الزمان الذي فيه يقطع الكوكب  الكوكب↑: جميع الفلك الخارج المركز أخذاً في حركته تلقا حركة السماء ه – خ: من المغرب إلى المشرق  على أنّ هذا الفلك ه: وفلك الخارج المركز  قارٌ غير متحرّك في مثله يكون قطع قطع↑: خ مركز فلك التدوير الفلك الموافق ↑الموافق↑: الذي مركزه للبصر أخذاً أيضاً في حركته تلقا حركة السماء وكان سير الكوكب في فلك تدويره مثل سير فلك تدويره في السرعة لكن حركته في بعده الأبعد يكون قدماً في فلك تدويره.

ونحن مرشدون إلى أنّ هذه الأشياء إذا وضعت على ما وصفنا لزم من ذلك أن يكون ما يظهر أموراً واحدة بأعيانها في كلّ واحد من الأصلين بوجيز من القول تبيّن فيه ما قصدنا له بهذه النسب أنفسها، ثمّ نعدّ ذلك بالأعداد أيضاً التي تبيّنه عليهما فيها في /T146/ اختلاف حركة الشمس. فأقول أوّلاً أوّلاً↑: إنّ بحسب كلّ واحد من الأصلين غاية الفضل بين الحركة المستوية وبين الحركة التي ترى مختلفة وهي التي عندها يتصوّر في الذهن أيضاً المسير الأوسط للكواكب أنّما يكون إذا كان البعد الذي يرى بين الكوكب وبين بعده الأبعد يجوز ربع دائرة، وإنّ الزمان الذي من البعد الأبعد إلى المسير الأوسط الذي ذكرناه أطول من الزمان الذي من المسير الأوسط إلى أقرب القرب. وذلك شيء يلزم دائماً في الأصل الذي يوضع فيه الخروج عن المركز وأمّا في الأصل الذي يوضع فيه فلك التدوير فيلزم متى كانت نقلة الكواكب في أفلاك تداويرها من أبعد أبعادها قُدماً أن يكون الزمان الذي من أقلّ الحركة إلى الحركة الوسطى أطول من الزمان الذي من الحركة الوسطى إلى أكثر الحركة /H221/ من قبل أنّ أقلّ المسير في كلّ واحدة من الجهتين أنّما يكون عند البعد الأبعد. ومتى كان دوران الكواكب في أفلاك تداويرها من البعد الأبعد تلقا حركة السماء كان الأمر بالعكس، أعني أنّ الزمان الذي من أكثر الحركة إلى الحركة الوسطى يكون أطول من الزمان الذي من الحركة الوسطى إلى أقلّ الحركة من قبل أنّ هاهنا أيضاً أكثر المسير أنّما يكون في البعد الأبعد.

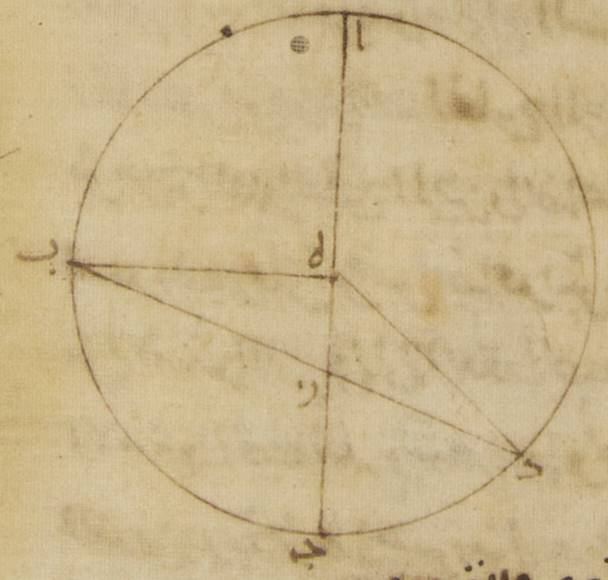
ج: فليكن أوّلاً الفلك الخارج المركز للكوكب فلك ألف باء جيم دال ه – خ: مركز فلك البروج من المغرب إلى المشرق ذلك الزمان أيضاً سواء حركة الكوكب في جهة غير أنّ انتقاله يكون من {...} الكلّ وهي من المشرق إلى المغرب. فلنبيّن باليسير وبالوجيز من القول أنّ {...} جميعاً سواء ومن بعد ذلك {...} حركة الشمس. فأقول أوّلاً إنّ {...} الأصلين يكون الاختلاف {...} وهي الحركة التي {...} مختلفة {...} المعهود إذا {...} إلى {...} من البعد الأبعد إلى {...} هو أطول من الزمان الذي {...} ومن أجل ذلك إمّا على {...} أبداً وإمّا على {...} البعد الأبعد في {...} المشرق إلى المغرب {...} إلى الحركة الوسطى {...} من الزمان الذي من الحركة {...} لأنّ على كلّ واحد من {...} في البعد الأبعد وإذا {...} تدويره من بعده الأبعد إلى {...} تدويره يكون الزمان الذي من الحركة {...} إلى الوسطى أطول من الزمان الذي الحركة الوسطى إلى الحركة {...} لأنّ الحركة {...} حينئذ يكون البعد الأبعد و{...} أوّلاً فلكاً خارج المركز عليه {...}.  حول مركز هاء وقطر ألف هاء جيم وليؤخذ على القطر مركز فلك البروج أعني النقطة التي على البصر ولتكن نقطة زاي ولنجز على نقطة زاي خطّ باء زاي دال على زوايا قائمة على خطّ ألف هاء جيم. ولننزّل أنّ الكوكب في موضعين مرّة على باء ومرّة على دال، ومن البيّن أنّ ما يظهر من البعد يكون حينئذ بينه وبين نقطة ألف التي هي أبعد البعد من كلّ واحد من الجانبين  ه – خ: من فلك البروج ربع دائرة. ه – خ – صح: ودال وباء هما النقطتان اللتان هما عند المجاز الأوسط. فينبغي أن نبيّن أنّ أعظم الفضل بين الحركة المستوية وبين الحركة المختلفة أنّما يكون عند نقطتي باء، دال.

فلنوصل خطّا هاء باء، هاء دال. فقد تبيّن من ذلك أنّ نسبة زاوية هاء باء زاي إلى أربع زوايا قائمة هي /T147/ /H222/ نسبة قوس الفضل الذي من قبل الاختلاف إلى الدائرة بأسرها وذلك أنّ زاوية ألف هاء باء توتّر قوس الحركة المستوية، وزاوية ألف زاي باء توتّر  ه – خ: قوس الحركة التي نحالّ مختلفة، والفضل بينهما زاوية هاء باء زاي.

فأقول أنّه ليس يقوم عند محيط دائرة ألف باء جيم دال على خطّ هاء زاي أعظم من كلّ واحدة من هاتين الزاويتين. فلتقم عند نقطتي طاء، كاف زاويتا هاء طاء زاي، هاء كاف زاي ولنوصل خطّ طاء دال وخطّ كاف دال. فلأنّ كلّ مثلّث فإنّ ضلعه الأطول يوتّر زاويته العظمى، وخطّ طاء زاي أطول من خطّ زاي دال، تكون زاوية طاء دال زاي أيضاً أعظم من زاوية دال طاء زاي وزاوية هاء دال طاء مساوية لزاوية هاء طاء دال، وذلك أنّ خطّ هاء دال أيضاً مساو لخطّ هاء طاء. فزاوية هاء دال زاي إذن بأسرها، أعني زاوية هاء باء دال، أعظم من زاوية هاء طاء زاي. وأيضاً من قبل أنّ خطّ دال زاي أطول من خطّ كاف زاي، تكون زاوية زاي كاف دال أيضاً أعظم من زاوية زاي دال كاف، وزاوية هاء كاف دال بأسرها مساوية لزاوية هاء دال كاف بأسرها من قبل أنّ خطّ هاء كاف أيضاً مساو لخطّ هاء دال. فزاوية هاء دال زاي إذن الباقية أعني زاوية هاء باء زاي أعظم من زاوية هاء كاف زاي. /H223/ فليس يمكن إذن أن تقوم زوايا على الصفة التي تقدّم ذكرها أعظم من الزاويتين اللتين عند نقطتي باء، دال.

وقد تبيّن مع ذلك أيضاً أنّ قوس ألف باء، وهي التي تشتمل على الزمان الذي من أقلّ الحركة إلى الحركة الوسطى،  ه: معنى الحركة الوسطى في هذا الموضع وما شبهه المجاز الأوسط. أعظم من قوس باء جيم، وهي التي تشتمل على الزمان الذي من الحركة الوسطى إلى أكثر الحركة، بالقوسين اللتين تشتملان على الفضل في الاختلاف. وذلك أنّ زاوية ألف هاء باء أعظم من قائمة أعني من زاوية هاء زاي باء بزاوية هاء باء زاي وزاوية باء هاء جيم أصغر منها بتلك الزاوية بعينها.

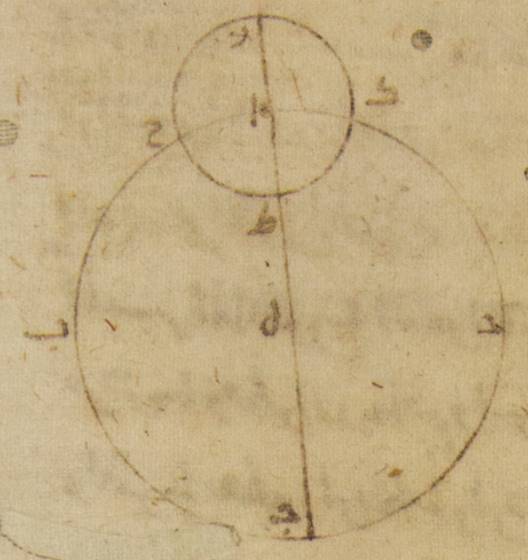
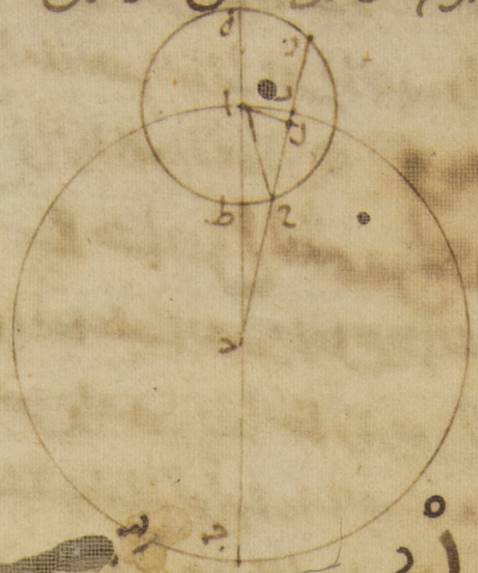
وأيضاً كيما يتبيّن أنّ ذلك بعينه يلزم في الوضع الآخر. ج: ↑ج↑: صح د ليكن الفلك الذي مركزه مركز العالم ألف باء جيم حول مركز دال وقطر ألف دال باء، وليكن فلك التدوير الذي يدور عليه في هذا السطح بعينه فلك هاء زاي حاء حول مركز ألف. ولننزّل كوكباً على نقطة حاء ولتكن هذه منزلته إذ أرى أنّ بعده من ه – خ: موضع البعد الأبعد ه – خ: في فلك البروج ربع دائرة. ولنوصل خطّ ألف حاء وخطّ دال حاء جيم.

فأقول إنّ خطّ دال حاء جيم يماسّ فلك التدوير وإنّ عند ذلك /H224/ يكون أكثر ما يكون من الفضل بين الحركة المستوية وبين الحركة المختلفة. فلأنّ الحركة المستوية من البعد الأبعد تحدّها زاوية هاء ألف حاء، وذلك أنّ حركة الكوكب في فلك تدويره مساوية في السرعة لحركة ه – خ: مركز فلك التدوير في فلك ألف باء جيم. والفضل بين الحركة المستوية وبين الحركة التي تظهر تحدّه زاوية ألف دال حاء. فمن البيّن أنّ فضل زاوية هاء ألف حاء على زاوية ألف دال حاء أعني ↑أعني↑: صح؛ ه – خ: الذي بالفضل ↑بالفضل↑: هو زاوية ألف حاء دال يحدّ البعد  ↑تحدّ البعد↑: صح؛ ه – خ: هو مساو للزاوية التي تحيط بالبعد. الذي يرى بين الكوكب وبين بعده  ↑بعده↑: البعد الأبعد، ه – خ: الذي يرى ولأنّ البعد الذي يرى. إذ كان ذلك ↑إذ كان ذلك↑: صح قد فرض ربع دائرة. فإنّ زاوية ألف حاء دال تكون قائمة ويكون خطّ دال حاء جيم من أجل ذلك مماسّاً لفلك التدوير وهو هاء زاي حاء. فقوس ألف جيم إذاً هي غاية الفضل الذي يلحق من قبل الاختلاف.  ه – خ: بين الحركة الوسطى وبين الحركة التي ترى.

وكذلك  ه – ص – صح: لذلك أيضاً قوس هاء حاء وهي التي تحدّ (في)  ↑(في)↑: صح الحركة التي /T148/ وضعت هاهنا أنّها على فلك التدوير ه – خ: أيضاً  الزمان الذي من أقلّ الحركة إلى الحركة الوسطى أعظم من قوس حاء زاي وهي القوس التي تجوز الزمان الذي من الحركة الوسطى إلى أكثر الحركة بقوس ألف جيم مرتّين. /H225/ وذلك أنّا أن أخرجنا خطّ دال حاء طاء على الاستقامة وأقمنا على خطّ هاء زاي خطّ ألف كاف طاء على زوايا قائمة.

فإنّ زاوية كاف ألف حاء تكون مساوية لزاوية ألف دال جيم، وقوس كاف حاء تكون شبيهة بقوس ألف جيم. وبهذه القوس فضل  ↑فضل↑: صح؛ ه – صح: تفضل قوس هاء كاف حاء على ربع واحد من الدائرة ونقصان ↑ونقصان↑: صح؛ ه – خ – صح: وتنقص قوس زاي حاء عنه. وهذه هي الأشياء التي كان ينبغي أن نبيّنها.

وقد يمكن أن يعلم يقيناً أنّ في الحركات الجزئيّة أيضاً في كلّ واحد من الوضعين تكون في الأزمان المتساوية الأشياء التي يجري الأمر عليها في الحركات المستوية والحركات التي نحالّ بالرؤية. ومع ذلك في التفاضل بينها، أعني الفضل الذي من قبل الاختلاف، أشياء بأعيانها ممّا أنّا واصفه خاصة. ه – خ – وج: وسنبيّن بما نحن واصفوه لكلّ من أراد أن يحيط علماً فإنّ كلّ ما يكون في أصناف الحركات أعني الحركات الوسطى والحركات التي ترى وما بينها من التفاضل الذي هو الاختلاف في الأزمان المتساوية فهو سواء أبداً على كلّ واحد من الأصلين فليكن. 

ه:  ↑ه↑: صح فليكن الفلك الذي مركزه مركز فلك البروج فلك ألف باء جيم حول مركز دال، والفلك الخارج المركز المساوي لفلك ألف باء جيم الموافق المركز فلك هاء زاي حاء حول مركز طاء. والقطر المشترك لهما جميعاً الذي يمرّ بمركز دال ومركز طاء ويمرّ /T149/ بنقطة هاء التي هي أبعد البعد خطّ هاء ألف طاء دال. ولنفرز من الفلك الموافق مركزه قوساً كيف ما وقعت ولتكن قوس ألف باء، ولنجعل نقطة باء مركزاً وببعد طاء دال نرسم فلك تدوير كاف زاي ولنوصل خطّ كاف باء دال.

/H226/ وأقول إنّ الكوكب عند ↑عند↑: في كلّ واحدة من الحركتين يصير إلي نقطة زاي التي هي تقاطع الفلك الخارج المركز وفلك التدوير في زمان سواء لا محالة أعني أنّ القسيّ الثلاث تكون متشابهه وهي قوس هاء زاي من الفلك الخارج المركز وقوس ألف باء من الفلك الموافق مركزه وقوس كاف زاي من فلك التدوير، وإنّ الفضل بين الحركة المستوية وبين الحركة المختلفة والمسير الذي يرى للكوكب يلزم في كلّ واحد من الوضعين أمراً متشابهاً واحداً بعينه.

فليوصل خطّ زاي طاء وخطّ باء زاي وخطّ دال زاي. فلأنّ ذا أربعة أضلاع باء دال طاء زاي أضلاعه المتقابلة متساوية كلّ واحد للمقابل له، أمّا خطّ زاي طاء فلخطّ باء دال وأمّا خطّ باء زاي فلخطّ دال طاء فإنّ ذا أربعة أضلاع باء دال زاي طاء يكون متوازي الأضلاع وذلك أنّ الزوايا المتبادلة تكون (أيضاً) ↑(أيضاً)↑: ص متساوية فالزوايا إذن الثلاث أعني زاوية هاء طاء زاي وزاوية ألف دال باء وزاوية زاي باء كاف متساوية. فيجب من ذلك إذ كانت عند المركز أن تكون القسيّ التي توتّرها متشابهة أعني قوس هاء زاي من الفلك الخارج المركز وقوس ألف باء من الفلك الموافق المركز وقوس كاف زاي من فلك التدوير. {ف}في الحركتين إذن جميعاً يصل الكوكب إلى نقطة واحدة بعينها وهي نقطة زاي في زمان سواء ويرى أنّه قد سار من أبعد بعده قوساً واحدة بعينها من دائرة البروج وهي قوس ألف لام، /H227/ ويتّصل بذلك أنّ الفضل الذي من قبل الاختلاف يكون واحداً بعينه في كلّ واحد من الوضعين؛ وذلك أنّا قد بيّنّا أنّ هذا الفضل تشتمل عليه إمّا في وضع الخروج عن المركز فزاوية دال زاي طاء وإمّا في وضع فلك التدوير فزاوية باء دال زاي، وهاتان الزاويتان تكونان متساويتين متبادلتين لأنّه قد تبيّن أنّ خطّ زاي طاء مواز لخطّ باء دال. ومن البيّن أنّ هذه الأشياء تلزم بعينها في الأبعاد كلّها إذ كان ذو أربعة أضلاع باء دال زاي طاء يكون أبداً متوازي الأضلاع وكان الفلك الخارج المركز أنّما ترسمه حركة الكوكب نفسها في فلك تدويره /T150/ وهذه الأشياء تلزم إذاً اتّفق أن تكون النسب في كلّ واحد من الوضعين متشابهة متساوية.  ه – خ – وج: ولنبيّن أنّ أقدار القسيّ المتشابهة وإن كانت مختلفة الأقدار فإنّ الذي يرى ممّا يعرض فيها مثل الذي يرى في المتساوية الأقدار فنحن

 فأمّا إنّ النسب وإن كانت متشابهة فقط وكانت المقادير التي فيها غير متساوية فقد يلزم أيضاً أن تكون الأشياء التي تظهر أشياء بأعيانها فنحن مبيّنون ذلك على هذا النحو. و: فليكن على هذا المثال الفلك الذي مركزه مركز العالم ألف باء جيم حول مركز دال وقطره الذي عليه يصير الكوكب في أبعد بعده وفي أقرب قربه ألف دال جيم. وليكن فلك تدوير هاء زاي حول مركز باء وبعده من نقطة ألف التي هي أبعد البعد قوس كيف ما وقعت وهي قوس ألف باء. ولتحرّك الكوكب /H228/ قوس هاء زاي فمن البيّن أنّها تكون شبيهة بقوس ألف باء من قبل أنّ العودتين في الدائرتين متساويتان. وليوصل خطّ دال باء هاء وخطّ باء زاي وخطّ دال زاي. فمن البيّن بنفسه أنّ زاويتي ألف دال هاء، زاي باء هاء أبداً متساويتان وإنّ الكوكب أنّما يرى على خطّ دال زاي بحسب وضعنا هذا.

وأقول إن وضعنا أيضاً فلكا خارج المركز كان ذلك الفلك أعظم أو كان أصغر من فلك ألف باء جيم الموافق المركز بعد أن نستثني تشابه النسب (وحده) ↑(وحده)↑: ص وتساوي أزمان العودات أنّها يرى الكوكب على خطّ واحد أيضاً بعينه وهو خطّ دال زاي. فليرسم فلكاً خارج المركز أعظم كما قلنا من ذلك الفلك وليكن حاء طاء حول مركز كاف على خطّ ألف جيم وفلك ه – صح: وفلكاً /T151/ أصغر من ذلك الفلك وليكن لام ميم حول مركز نون على ذلك المثال. ولنخرج على الاستقامة خطّا دال ميم زاي طاء، دال لام ه: ألف حاء وليوصل خطّ طاء كاف وخطّ ميم نون. فلأنّ نسبة خطّ دال باء إلى خطّ باء زاي كخطّ طاء كاف إلى خطّ كاف دال وكخطّ ميم نون إلى خطّ نون دال، /H229/ وزاوية باء زاي دال مساوية لزاوية ميم دال نون من أجل  أجل↑: صح أنّ خطّ دال ألف مواز لخطّ باء زاي، تكون المثلّثات الثلاثة متساوية الزوايا والزوايا التي توتّرها الأضلاع المتناسبة متساوية أعني زاوية باء دال زاي Toomer, p. 151: ZDB وزاوية دال طاء كاف وزاوية دال ميم نون. فخطوط باء دال طاء كاف ميم نون إذن متوازية. فيجب من ذلك أن تكون زوايا ألف دال باء، ألف كاف طاء، ألف نون ميم أيضاً متساوية. ولأنّ هذه الزوايا هي عند مراكز الدوائر، تكون أيضاً القسيّ التي عليها متشابهة، أعني قوس ألف باء وقوس حاء طاء وقوس لام ميم فقد يقطع في زمان سواء. ليس فقط فلك التدوير قوس ألف باء والكوكب قوس هاء زاي، لكن في الدائرتين الخارجتي المركز أيضاً الكوكب يقطع قوس حاء طاء وقوس لام ميم وترى من قبل ذلك أبداً ↑أبداً↑: أنّه على خطّ واحد مستقيم وهو خطّ دال ميم زاي طاء، وذلك أنّه يصير في فلك التدوير على نقطة زاي، وفي الفلك الخارج المركز الأعظم على نقطة طاء، ومن الفلك الخارج المركز الأصغر على نقطة ميم. وكذلك يجري الأمر في جميع الأوضاع.

وقد يلزم أيضاً ه – خ: أن نبيّن بعد هذا أنّه متى  متى↑: صح رئي  ري الكوكب قد فرز قوسين متساويتين من أبعد البعد ومن أقرب القرب كان الفضل الذي من قبل الاختلاف متساوياً في كلّ واحد من الوضعين. وذلك أنّا ↑أنّا↑: أنّه على حسب الأصل الذي يوضع فيه الخروج عن المركز، ز ↑ز↑: صح: إنّ نحن رسمنا فلكا خارج المركز /H230/ وهو ألف باء جيم دال حول مركز هاء وقطر ألف هاء جيم الذي يمرّ بنقطة ألف وهي أبعد البعد، ووضعنا البصر عليه على نقطة زاي وأجزنا على نقطة زاي خطّ باء زاي دال كيف  كيف↑: ما وقع ووصلنا خطّي هاء باء، هاء دال كان المسير الذي ترى متساوياً متقابلاً أعني زاوية ألف زاي باء التي هي للمسير من أبعد البعد /T152/ وزاوية جيم زاي دال التي هي للمسير من أقرب القرب وكان الفضل الذي من قبل الاختلاف شيءاً واحداً بعينه من قبل أنّ خطّ باء هاء مساو لخطّ هاء دال وزاوية هاء باء زاي مساوية لزاوية هاء دال زاي.

فيجب من ذلك أن تكون القوس من أبعد البعد التي للحركة المستوية أعظم من القوس التي ترى وهي القوس التي تحيط بها زاوية ألف زاي باء والقوس من أقرب القرب أصغر من التي ترى وهي التي تحيط بها زاوية جيم زاي دال بفضل واحد بعينه من قبل أنّ زاوية ألف هاء باء أيضاً أعظم من زاوية ألف زاي باء بزاوية زاي باء هاء وزاوية جيم هاء  ↑هاء↑: صح دال أصغر من زاوية جيم زاي دال بزاوية هاء دال زاي.

وعلى حسب الأصل أيضاً الذي يوضع فيه فلك تدوير، ح: إن نحن رسمنا فلكاً موافق المركز كفلك ألف باء جيم حول مركز دال وقطر ألف دال جيم وفلك تدوير كفلك هاء زاي حاء حول مركز ألف وأخرجنا  /H231/خطّ دال حاء باء زاي كيف وقع ووصلنا خطّي ألف زاي، ألف حاء كانت قوس الفضل الذي من قبل الاختلاف وهي قوس ألف باء موضوعة أيضاً واحدة بعينها في الوضعين جميعاً أعني إن كان الكوكب على نقطة زاي، وإن كان على نقطة حاء وزاي بعده سواء من نقطة أبعد البعد من دائرة البروج إذا كان على نقطة زاي ومن نقطة أقرب القرب إذا كان على نقطة حاء. وذلك أنّ القوس الذي يرى من أبعد البعد تحيط بها زاوية دال زاي ألف وذلك  وذاك أنّه قد تبيّن أنّها الزيادة التي تقع بين الحركة المستوية وبين الفضل الذي من قبل الاختلاف والقوس التي ترى من أقرب القرب تحيط بها زاوية زاي حاء ألف وذلك أنّ هذه أيضاً مساوية لزاوية الحركة المستوية التي من أقرب القرب وللفضل الذي من قبل الاختلاف لكن زاوية دال زاي ألف مساوية لزاوية زاي حاء ألف من قبل أنّ خطّ ألف زاي مساو لخطّ ألف حاء.

/T153/ فنجتمع من ذلك أيضاً أنّ الفضل  ه – ص – صح: يفضل واحد بعينه وهو زاوية ألف دال باء ه – ص – صح: تكون
Toomer, p. 153: AD̂H الحركة الوسطى التي عند أبعد البعد أعظم من الحركة التي ترى أعني أنّ زاوية هاء ألف زاي أعظم من زاوية ألف زاي دال /H232/ والحركة الوسطى التي عند أقرب القرب أصغر من الحركة التي ترى التى هي تلك بعينها أعني أنّ زاوية حاء ألف دال أصغر من زاوية ألف حاء زاي. وهذه الأشياء التي كان ينبغي أن نبيّنها.

⟨III.4⟩ د: في الاختلاف الذي يرى للشمس

وإذ تقدّمنا فوطّأنا هذه الأشياء على هذه الصفة فقد ينبغي أن نعلم  نعلم↑: صح أنّه قد يمكن في الاختلاف أيضاً الذي يرى في الشمس كيما يكون واحداً ويكون الزمان  الزمان↑: صح؛ ه – خ – صح: (أن نقدّم القول على الاختلاف الذي يرى للشمس من أجل أنّه واحد أبداً ونجعل الزمان). الذي من أقلّ حركتها إلى حركتها الوسطى أطول أبداً من الزمان الذي من حركتها الوسطى إلى أكثر حركتها. فإنّا نجد هذا المعنى أيضاً موافقاً للأشياء التي ترى أن يكون ↑يكون↑: صح؛ ه – خ – صح: (وقد يمكن أن يكون أمرها) أمره يجري على كلّ واحد من ذينك الأصلين الموضوعين، إلّا أنّه أنّما يجري على طريق وضع فلك تدوير متى كانت حركة الشمس في قوس بعدها الأبعد يكون قدماً. فالأولى أن ينسب هذا الاختلاف إلى الخروج عن المركز إذ إذ↑: صح؛ ه – خ – صح: (فيما نحاول من استخراج النسبة الموجودة) كان هذا الأصل أبسط وكان يتمّ بحركة واحدة لا بحركتين.

ولمّا كان المقدّم في هذا المعنى هو استخراج النسبة الموجودة في خروج دائرة الشمس عن المركز أعني أيّ نسبة هي نسبة الخطّ الذي بين مركز الفلك الخارج المركز وبين المركز الذي على البصر وهو مركز فلك البروج إلى الخطّ الخارج من مركز الفلك الخارج المركز. وأيضاً على أيّ قِطع ه – صح: جزء من فلك البروج توجد النقطة من الفلك الخارج المركز التي هي أبعد البعد. /H233/ فإنّ أبرخس أيضاً قد بيّن هذه الأشياء بعناية لا يشوبها تفريط وذلك أنّه لمّا وضع الزمان الذي من الاستواء الربيعيّ إلى الانقلاب الصيفيّ أربعة وتسعين يوماً ونصف يوم والزمان الذي من الانقلاب الصيفيّ إلى الاستواء الخريفيّ اثنين وتسعين يوماً ونصف يوم، بيّن بهذه الأشياء التي تظهر فقط أنّ الخطّ الذي بين المركزين اللذين نقدّم ذكرهما جزء من أربعة وعشرين جزءاً بالتقريب من الخطّ الخارج من مركز الفلك الخارج المركز وإنّ البعد الأبعد منه يتقدّم الانقلاب الصيفيّ بأربعة وعشرين جزءاً ونصف بالتقريب بالأجزاء التي بها فلك البروج ثلاث مائة وستّون جزءاً. ونحن أيضاً فإنّا وجدنا أزمان هذين الربعين اللذين ذكرناهما والنسبتين اللتين قصدنا لهما قريباً ممّا وصف بعينه في هذا الوقت أيضاً حتّى أنّه قد ظهر  ه – خ: استبان لنا من قبل ذلك أنّ فلك الشمس الخارج المركز يحفظ أيضاً ↑يحفظ أيضاً↑: صح؛ ه – خ – صح: لازم أبداً موضعاً بعينه من نقطتي المنقلبين ومن نقطتي الاستوائين.

ولكيلا يكون هذا الموضع قد أغفل بل يكون هذا المعنى قد وضع ملخّصاً بحسابنا، فنحن أيضاً مبيّنون ما قصدنا له من ذلك في فلك خارج المركز بأن نستعمل تلك الأشياء بأعيانها التي تظهر، وهي كما قلنا أنّ الزمان الذي من الاستواء الربيعيّ إلى الانقلاب الصيفيّ مبلغه أربعة وتسعون يوماً ونصف يوم، والزمان الذي /T154/ من الانقلاب الصيفيّ إلى الاستواء الخريفيّ مبلغه اثنان وتسعون يوماً ونصف يوم. وذلك أنّا قد وجدنا نحن أيضاً بالأرصاد التي كانت منّا /H234/ في سنة أربع مائة وثلاث وستّين من وفاة إسكندر للاستوائين والانقلاب الصيفيّ عدّة أيّام هذين البعدين موافقة لذلك. فإنّا وجدنا كما قلنا الاستواء الخريفيّ كان في اليوم التاسع من الشهر المسمّى أثور بعد طلوع الشمس، والاستواء الربيعيّ في اليوم السابع من الشهر المسمّى ماخور بعد انتصاف النهار، فيجتمع البعد ه – خ: ما بين الرصدين من عدد الأيّام مائة وثمانية وسبعين يوماً وربع يوم، والانقلاب الصيفيّ كان في اليوم الحادي عشر من الشهر المسمّى ماسوري بعد انتصاف الليلة التي يليها اليوم الثاني عشر. فيجتمع هذا البعد أيضاً وهو البعد ه – خ: {...} عدد الأيّام التي  بين الاستواء الربيعيّ وبين الانقلاب الصيفيّ أربعة وتسعين يوماً ونصف يوم ويبقى للبعد بين الانقلاب الصيفيّ وبين الاستواء الخريفيّ الذي يتلوه ما بقي من زمان السنة وهو نحو من اثنين وتسعين يوماً ونصف يوم.

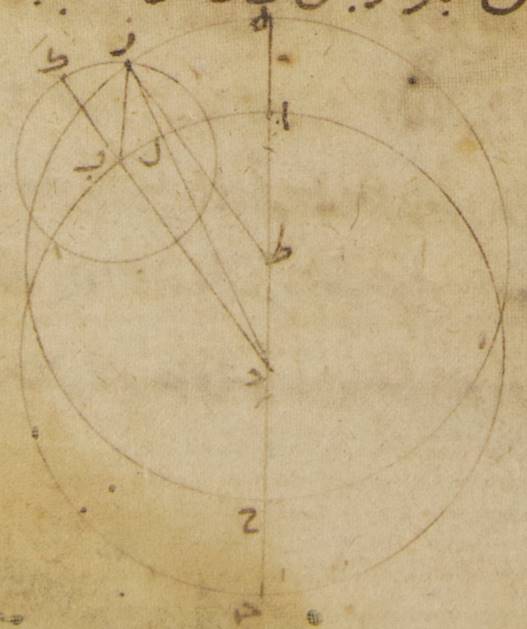
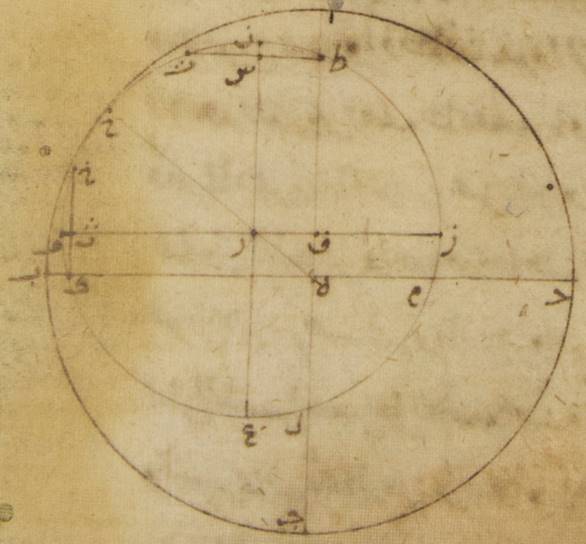
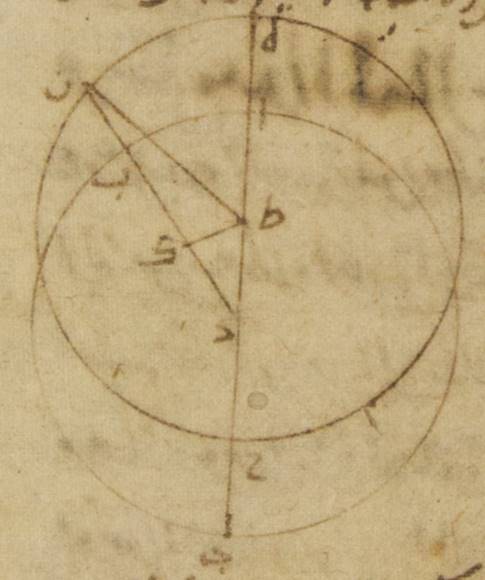
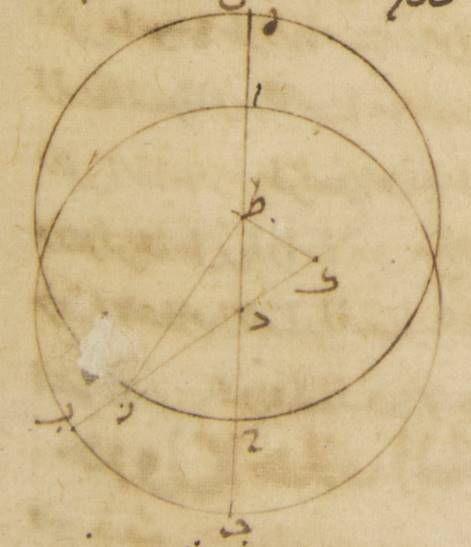
ط: فليكن فلك البروج ألف باء جيم دال حول مركز هاء، ولنخرج فيه قطران يتقاطعان على زوايا قائمة ويمرّان بنقطتي الانقلابين ونقطتي الاستوائين وليكونا ألف جيم وباء دال، ولننزّل نقطة ألف النقطة الربيعيّة ونقطة باء النقطة الصيفيّة والنقطتين الباقيتين على هذا القياس. /T155/ فقد يظهر أنّ مركز الفلك الخارج المركز أنّما يقع فيما بين خطّي هاء ألف، هاء باء من قبل أنّ نصف دائرة ألف باء جيم يشتمل على أكثر من زمان نصف السنة، فهو لذلك يحوز من الفلك الخارج المركز قطعة أكثر من نصف الدائرة وربع دائرة ألف باء أيضاً /Η235/ يشتمل على زمان أكثر ممّا يشتمل عليه ربع دائرة باء جيم ويحوز  ه – خ: فهو يحوز من الفلك الخارج المركز قوساً أعظم من التي يحوزها. وإذا كان ذلك كذلك، فلننزّل أنّ نقطة زاي مركز الفلك الخارج المركز ولنخرج القطر الذي يمرّ بالمركزين وبالبعد الأبعد وليكن هاء زاي حاء. ولنرسم بمركز ه – خ: على مركز زاي وبأيّ بعد اتّفق فلك الشمس الخارج المركز وليكن طاء كاف لام ميم، ولنخرج على نقطة زاي خطّ نون سين عين موازياً لخطّ ألف جيم وخطّ فاء قاف راء موازياً لخطّ باء دال. ولنخرج من نقطة طاء عمود طاء شين تاء على خطّ نون ه – خ: نون سين عين، ومن نقطة كاف عمود كاف ثاء خاء على خطّ فاء قاف راء.

فلمّا كانت الشمس إذا قطعت على الاستواء فلك طاء كاف لام ميم كان قطعها قوس كاف طاء في أربعة وتسعين يوماً ونصف يوم، وقطعها قوس كاف لام في اثنين وتسعين يوماً ونصف يوم. وكانت الشمس تتحرّك على الاستواء في أربعة وتسعين يوماً ونصف ثلاثة وتسعين جزءاً وتسع دقائق بالتقريب بالأجزاء التي بها الدائرة ثلاث مائة وستّون جزءاً وتتحرّك في اثنين وتسعين يوماً ونصف يوم أحد وتسعين جزءاً وإحدى عشرة دقيقة. وجب أن تكون قطعة طاء كاف لام مائة وأربعة وثمانين جزءاً وعشرين دقيقة. /H236/ فمجموع قوس طاء نون وقوس لام عين وهو ما يبقى بعد نصف دائرة نون  ه: فاء عين أربعة أجزاء وعشرين دقيقة. فكلّ واحدة منهما إذن يكون جزئين وعشر دقائق ويكون ضعف قوس طاء نون، وهي قوس طاء نون تاء، بهذه الأجزاء أربعة أجزاء وعشرين دقيقة. فيجب من ذلك أن يكون وترها، وهو خطّ طاء شين تاء، أربعة أجزاء واثنتين وثلاثين دقيقة بالتقريب بالأجزاء التي بها قطر الفلك الخارج المركز مائة وعشرون جزءاً ويكون نصفه، وهو خطّ طاء شين أعني خطّ هاء سين، بهذه الأجزاء جزئين وستّ عشرة دقيقة. وأيضاً لأنّ قطعة طاء نون قاف كاف Greek (Heiberg, p. 236 line 7): ΘNΠK بأسرها ثلاثة وتسعون جزءاً وتسع دقائق، لكن قطعة طاء نون جزئان وعشر دقائق وربع الدئرة نون فاء شطب الكاتب «نون فاء» تسعون جزءاً تبقى قوس كاف فاء تسعاً وخمسين دقيقة ويكون ضعفها وهو قوس كاف فاء خاء جزءاً واحداً وثمانياً وخمسين دقيقة فيكون وترها وهو خطّ كاف ثاء خاء Greek (Heiberg, p. 236 line 11): KΠΧ جزئين وأربع دقائق بالأجزاء التي بها قطر الفلك الخارج المركز مائة وعشرون جزءاً ونصفه وهو خطّ كاف ثاء أعني خطّ زاي سين جزءاً واحداً ودقيقتين. وقد تبيّن أنّ خطّ هاء سين بهذه الأجزاء جزئان وستّ عشرة دقيقة. وإذ كان المربّعان اللذان يكونان من هذين الخطّين إذا جمعا كان منهما المربّع الذي يكون من خطّ هاء زاي يكون خطّ هاء زاي أيضاً في الطول جزئين وتسع وعشرين دقيقة ونصفاً بالتقريب بالأجزاء التي بها الخطّ الخارج من مركز الفلك الخارج المركز ستّون جزءاً. فالخطّ إذن الخارج من مركز الفلك الخارج المركز أربعة وعشرون ضعفاً بالتقريب للخطّ الذي بين مركزه وبين مركز فلك البروج. /H237/ وأيضاً لما كان قد تبيّن أنّ خطّ هاء زاي جزئان وتسع وعشرون دقيقة ونصف بالأجزاء التي كان بها خطّ زاي سين جزءاً واحداً ودقيقتين. فالأجزاء إذن التي بها خطّ هاء زاي الموتّر مائة وعشرون جزءاً فإنّ خطّ سين راء Greek (Heiberg, p. 237 line 3): ZΞ يكون بتلك الأجزاء تسعة وأربعين جزءاً وستّاً وأربعين دقيقة بالتقريب. وتكون القوس التي تقع عليه من الدائرة التي ترسم على مثلّث هاء راء سين Greek (Heiberg, p. 237 line 5): EZΞ القائم الزاوية تسعة وأربعين جزءاً بالأجزاء التي بها الدائرة ثلاث مائة وستّون جزءاً. فزاوية زاء هاء سين Greek (Heiberg, p. 237 line 6): ZEΞ إذن بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً تسعة وأربعون جزءاً وبالأجزاء التي بها (الدائرة) (ثلاث مائة وستّون جزءاً فزاوية راء هاء سين إذن بالأجزاء) أربع زوايا قائمة ثلاث مائة وستّون جزءاً أربعة وعشرون جزءاً وثلاثون دقيقة. وإذ كانت هذه الزاوية عند مركز فلك البروج فإنّ قوس باء حاء، وهي التي بها يتقدّم البعد الأبعد الذي هي نقطة حاء نقطة باء وهي الانقلاب الصيفيّ، أربعة وعشرون جزءاً وثلاثين دقيقة. ويبقى  ه – خ: ومن بعد ذلك لما كان ربعا الدائرة عين زاي وزاي نون Greek (Heiberg, p. 237 line 12,13): ΟΣ, ΣΝ كلّ واحد منهما تسعون جزءاً، وكانت قوس عين لام وقوس طاء نون أيضاً كلّ واحدة منهما جزئين وعشر دقائق، وكانت قوس ميم زاي Greek (Heiberg, p. 237 line 15): ΜΣ تسعاً وخمسين دقيقة  ه – خ: فيجب أن تكون قوس لام ميم ستّة وثمانين جزءاً وإحدى وخمسين دقيقة وقوس ميم طاء ثمانية وثمانين جزءاً وتسعاً وأربعين دقيقة. لكن الشمس تصير على الاستواء ستّة وثمانين جزءاً وإحدى وخمسين دقيقة في ثمانية وثمانين يوماً وثمن يوم وتسير ثمانية وثمانين جزءاً وتسعاً وأربعين دقيقة في تسعين يوماً وثمن يوم بالتقريب. فيجب من ذلك أن تكون الشمس ترى قد سارت قوس جيم دال، وهي القوس التي من /T156/ /H238/ الاستواء الخريفيّ إلى الانقلاب الشتويّ في ثمانية وثمانين يوماً وثمن يوم، وترى قد سارت قوس دال ألف، وهي التي من الانقلاب الشتويّ إلى الاستواء الربيعيّ، في تسعين يوماً وثمن يوم بالتقريب. فقد وجدنا ما قصدنا له على الموافقة لقياس أبرخس. فعلى حسب هذه الأقدار ننظر أوّلاً كم أعظم الفضل بين الحركة المستوية وبين الحركة المختلفة وعند أيّ نقطة يقع هذا الفضل.

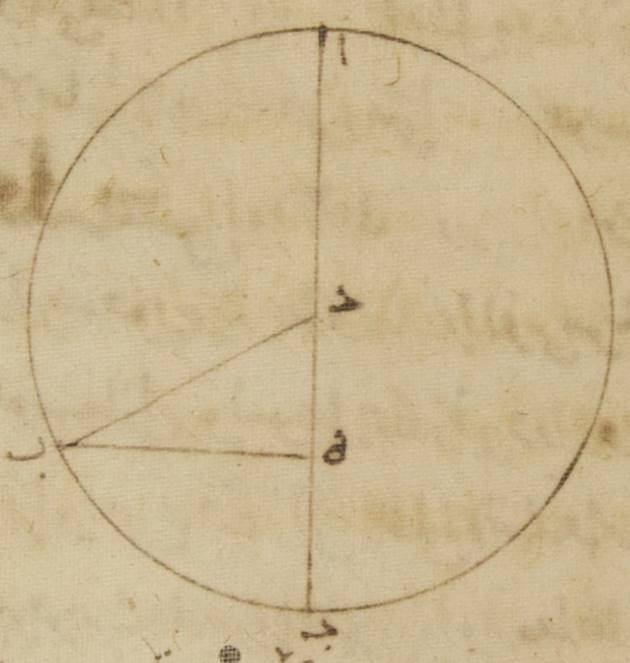
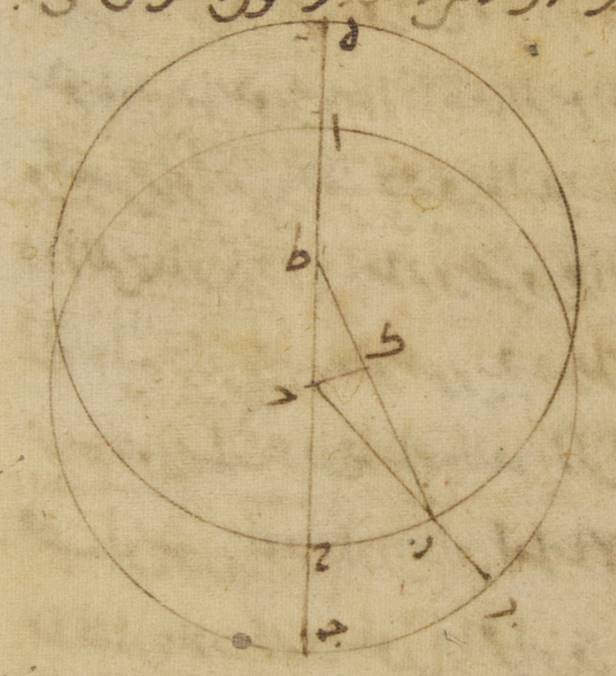
ي: فليكن الفلك الخارج المركز ألف باء جيم حول مركز دال وقطره يمرّ بنقطة ألف وهي أبعد البعد وهو ألف دال جيم وليكن مركز فلك البروج على هذا القطر نقطة هاء. ولنخرج من نقطة هاء خطّ هاء باء على زوايا قائمة على خطّ ألف جيم ولنوصل خطّ دال باء. فلأنّ الأجزاء التي بها خطّ باء دال، وهو الذي من المركز، ستّون جزءاً بتلك الأجزاء، خطّ دال هاء، وهو الذي بين المركزين، جزئان وثلاثون دقيقة على نسبة الأربعة والعشرين. الضعف تكون الأجزاء التي بها وتر باء دال مائة وعشرون جزءاً بها خطّ دال هاء خمسة أجزاء وتكون القوس التي عليه أربعة أجزاء وستّاً وأربعين دقيقة بالتقريب بالأجزاء {التي بها الدائرة} التي ترسم على مثلّث باء دال هاء القائم الزاوية ثلاث مائة وستّون جزءاً. فيجب أن تكون زاوية دال باء هاء أيضاً وهي التي تحيط بأكثر فضل الاختلاف أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فأربعة أجزاء وستّاً وأربعين دقيقة، /H239/ وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فجزئين وثلاثاً وعشرين دقيقة.

وبهذه الأجزاء بعينها زاوية باء هاء دال أيضاً تسعون جزءاً والزاوية المساوية للزاويتين أعني زاوية باء دال ألف اثنان وتسعون جزءاً وثلاث وعشرون دقيقة، وذلك بيّن. ولأنّ الزاويتين عند المركزين أمّا زاوية باء دال ألف فعند مركز الفلك الخارج المركز وأمّا زاوية باء هاء دال فعند مركز الفلك البروج، يحصل لنا أمّا أكثر الفضل الذي من قبل الاختلاف فجزئين وثلاثاً وعشرين دقيقة، وأمّا القسيّ التي عندها تكون كذلك This sentence seems not to occure in Greek (Heiberg, p. 239). ، ه – خ: لذلك أمّا القوس من الفلك الخارج المركز المستوية فاثنتين وتسعين جزءاً وثلاثاً وعشرين دقيقة من البعد الأبعد، وأمّا القوس من فلك البروج التي ترى مختلفة فأجزاء الربع كما بيّنّا من قبل أيضاً شطب الكاتب «أيضاً» وهي تسعون جزءاً. ومن البيّن ممّا تقدّمنا فلخّصناه أنّ في نصف الدائرة أيضاً المقابل لهذا النصف يكون المسير الذي يرى  ه – خ: عند المجاز الأوسط مسيراً وسطاً شطب الكاتب «مسيراً وسطاً» وأكثر فضل الاختلاف على المائتين والسبعين الجزء، ويكون المسير المستوي وهو الذي في الفلك الخارج المركز ه – خ: عن البعد الأبعد على مائتين والسبعة والستّين الجزء والسبع والثلاثين الدقيقة.

/T157/ وكيما نبيّن بالأعداد وأيضاً كما قلنا إنّ هذه الأقدار بأعيانها تحصل في الأصل أيضاً الذي يوضع فيه فلك تدوير متى كانت النسب محفوظة فيه على الجهة التي وصفناها.

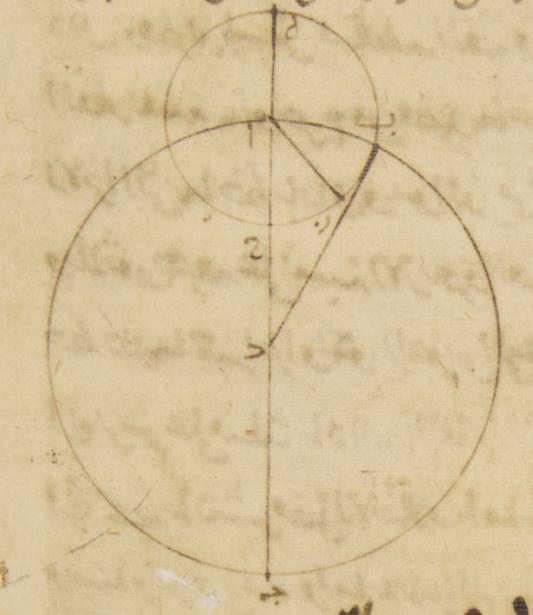
يا: فليكن الفلك الذي مركزه مركز فلك البروج ألف باء جيم حول مركز دال وقطر ألف دال جيم وفلك التدوير هاء زاي حاء حول مركز ألف. ولنخرج من نقطة جيم  شطب الكاتب «جيم»؛ ↑جيم↑: دال خطّ يماسّ فلك التدوير وليكن خطّ دال زاي باء وليوصل خطّ ألف زاي. /H240/ فيصير أيضاً على ذلك المثال في مثلّث ألف دال زاي القائم الزاوية خطّ ألف دال أربعة وعشرين ضعفاً لخطّ ألف زاي فيجب أن تكون أيضاً الأجزاء التي بها وتر ألف دال مائة وعشرون جزءاً بها خطّ ألف زاي خمسة أجزاء وتكون القوس التي عليه أربعة أجزاء وستّاً وأربعين دقيقة بالأجزاء التي بها الدائرة التي ترسم على مثلّث ألف دال زاي القائم الزاوية ثلاث مائة وستّون جزءاً. فزاوية ألف دال زاي إذن أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فهي أربعة أجزاء وستّ وأربعون دقيقة وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فجزئان وثلث وعشرون دقيقة.

فأكثر فضل الاختلاف إذن أعني قوس ألف باء قد وجد من قبل ذلك أيضاً على الموافقة جزئين وثلاثاً وعشرين دقيقة والقوس مختلفة ه – خ: المختلفة إذ كانت زاوية ألف زاي دال القائمة تشتمل عليها تسعون جزءاً، والقوس المستوية وهي التي تشتمل عليها زاوية هاء ألف زاي وجدت أيضاً ه – خ: إذا  اثنين وتسعين جزءاً وثلاثاً وعشرين دقيقة.

⟨III.5⟩ ه:  ه: ب في النظر في الاختلافات الجزئيّة

ولكي يمكنا أن نعرف في كلّ وقت الحركات أيضاً المختلفة /Τ158/ الجزئيّة فنحن مبيّنون أيضاً في كلّ واحد من الأصلين كيف نستخرج متى أعطينا قوساً من هذه القسيّ التي وضعناها باقي القسيّ.

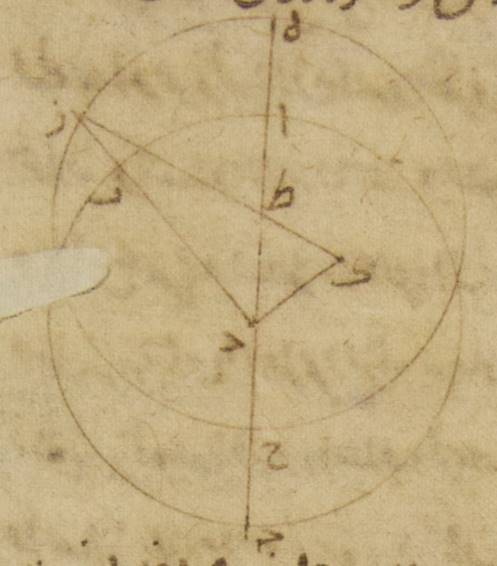
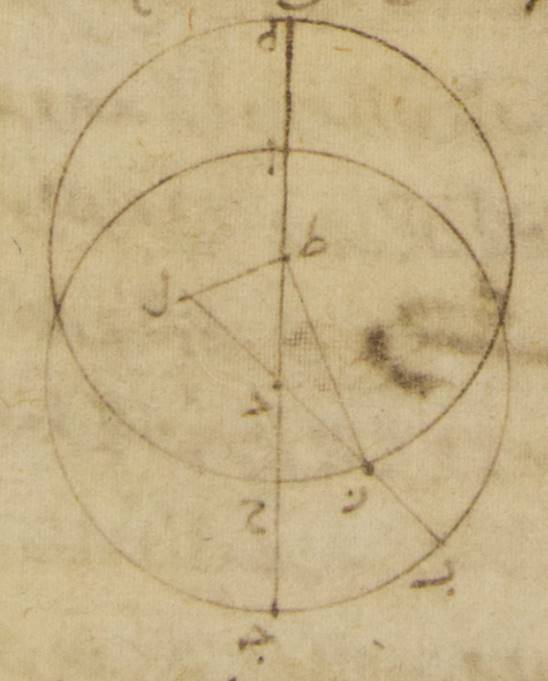
/H241/ يب: فليكن أوّلاً الفلك الذي مركزه مركز فلك البروج ألف باء جيم حول مركز دال، والفلك الخارج المركز هاء زاي حاء حول مركز طاء، والقطر الذي يمرّ بالمركزين وبنقطة هاء، وهي البعد الأبعد، هاء ألف طاء دال. Greek (Heiberg, p. 241, line 6): EAΘDH وليفرز قوس هاء زاي وليوصل خطّ زاي دال وخطّ زاي طاء. ولننزّل أوّلاً أنّ قوس هاء زاي فرضت لنا مثلاً ثلاثين جزءاً. ولنخرج خطّ زاي طاء على الاستقامة ولنخرج إليه من نقطة دال عمود دال كاف. فلأنّ قوس هاء زاي قد فرضت ثلاثين جزءاً، تكون زاوية هاء طاء زاي أيضاً، أعني زاوية دال طاء كاف، أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً، فثلاثين جزءاً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً، فستّون جزءاً. فالقوس إذن التي على خطّ دال كاف ستّون جزءاً بالأجزاء التي بها الدائرة التي ترسم حول مثلث دال طاء كاف القائم الزاوية ثلاث مائة وستّون جزءاً والقوس التي على خطّ طاء كاف ما يبقى لتمام نصف دائرة وهي مائة وعشرون جزءاً. فيكون الخطّان اللذان يوتّرانهما أمّا خطّ دال كاف فستّين جزءاً بالأجزاء التي بها وتر دال طاء مائة وعشرون جزءاً، وأمّا خطّ كاف طاء فبهذه الأجزاء مائة وثلاثة أجزاء وخمساً وخمسين دقيقة. فيجب أن يكون بالأجزاء التي بها خطّ دال طاء جزئان وثلاثون دقيقة وبها خطّ زاي طاء الذي من المركز ستّون جزءاً بها خطّ دال كاف جزءاً واحداً وخمس عشرة دقيقة وبها خطّ كاف طاء جزئين وعشر دقائق، /H242/ وبها خطّ كاف طاء زاي بأسره اثنان وستّون جزءاً وعشر دقائق. ومن قبل أنّ المربّعين اللذين يكونان منهما إذا جمعا كان منهما المربّع الذي من خطّ زاي دال يكون وتر زاي دال اثنين وستّين جزءاً وإحدى عشرة دقيقة بالتقريب بالأجزاء التي بها كان خطّ دال كاف جزءاً واحداً وخمس عشرة دقيقة، فالأجزاء إذن التي بها خطّ زاي دال مائة وعشرون جزءاً يكون بها خطّ دال كاف جزئين وخمساً وعشرين دقيقة وتكون القوس التي عليه جزئين وثمان عشرة دقيقة بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال زاي كاف Greek (Heiberg, p. 242, line 6): ZΔK القائم الزاوية ثلاث مائة وستّون جزءاً. /T159/ فيحب أن تكون زاوية دال زاي كاف أيضاً أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فجزئين وثمان عشرة دقيقة، وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فجزءاً واحداً وتسع دقائق. وهذا إذن يكون حينئذ مبلغ الفضل من قبل الاختلاف وبهذه الأجزاء زاوية هاء طاء زاي ثلاثون جزءاً. فزاوية ألف دال باء إذن الباقية، أعني قوس ألف باء، من فلك البروج ثمانية وعشرون جزءاً وإحدى وخمسون دقيقة. وقد يظهر من ذلك أيضاً أنّا إن أعطينا أيضاً زاوية من هذه الزوايا غير هذه أنّها كانت كان سائر الزوايا معطاة بأن يخرج في مثل هذه الصورة بعينها من نقطة طاء على خطّ زاي دال عمود طاء كاف.

وذلك أنّا إن أنزلنا أنّ قوس ألف باء من فلك البروج معطاة أعني زاوية باء دال ألف Greek (Heiberg, p. 242, line 19): ΘΔL; which is the same angle. كانت من قبل ذلك نسبة خطّ دال طاء إلى خطّ طاء كاف أيضاً معطاة. ولأنّ نسبة خطّ دال طاء إلى طاء زاي معطاة، تكون نسبة طاء زاي إلى طاء كاف أيضاً معطاة. ولذلك تحصل لنا زاوية طاء زاي كاف معطاة، أعني الفضل الذي من قبل الاختلاف، وتحصل أيضاً /H243/ زاوية هاء طاء زاي معطاة، أعني قوس هاء زاي، من الفلك الخارج المركز.

وإن أنزلنا أنّ الفضل الذي من قبل الاختلاف معطا، أعني زاوية طاء زاي دال، فإنّ بالعكس تجب تلك الأشياء بأعيانها. وذلك أنّ نسبة خطّ زاي طاء إلى خطّ طاء كاف تكون من قبل ذلك معطاة، وقد كانت نسبة خطّ زاي طاء إلى خطّ طاء دال منذ أوّل الأمر معطاة. فتكون نسبة خطّ دال طاء إلى خطّ طاء كاف أيضاً معطاة وتصير زاوية طاء دال كاف من قبل ذلك معطاة، أعني قوس ألف باء من فلك البروج وزاوية هاء طاء زاي أعني قوس هاء زاي من الفلك الخارج المركز. The letter ك in this part of the Arabic translation represents Λ (Heiberg, p. 242; corresponding to L in Toomer’s translation, p. 159) and not K! So the translator was not consistent in using the same letters as the original Greek. 

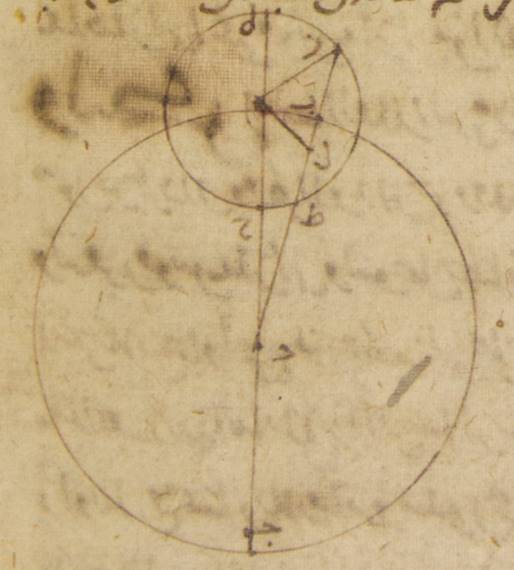
/Τ160/ يد: وليكن أيضاً الفلك الذي مركزه مركز فلك البروج ألف باء جيم حول مركز دال وقطر ألف دال جيم وفلك التدوير الذي على تلك النسبة بعينها هو حاء طاء Greek (Heiberg, p. 243, line 18): EZHΘ حول مركز ألف. ولنفرز قوس هاء زاي ولنوصل خطّا زاي باء دال، زاي ألف. ولننزّل أيضاً أنّ قوس هاء زاي هي تلك الأجزاء أعني ثلاثين جزءاً ولنخرج من نقطة زاي على خطّ ألف هاء عمود زاي كاف. فلأنّ قوس هاء زاي ثلاثون جزءاً، تكون زاوية هاء ألف زاي أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فثلثين جزءاً، وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فستّين جرءاً. فيجب أن تكون القوس التي على خطّ زاي كاف ستّين جزءاً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث ألف زاي كاف القائم الزاوية ثلاث مائة وستّون جزءاً، /H244/ والقوس التي على خطّ ألف كاف ما يبقى لتمام نصف الدائرة وهو مائة وعشرون جزءاً. فيكون إذاً الخطّان اللذان يوتّرانهما أمّا خطّ زاي كاف منهما فستّون جزءاً بالأجزاء التي بها قطر ألف زاي مائة وعشرون جزءاً وأمّا خطّ كاف ألف فبهذه الأجزاء مائة وثلاثة أجزاء وخمساً وخمسين دقيقة. فيجب أن يكون بالأجزاء التي بها وتر ألف زاي جزئان وثلاثون دقيقة وبها خطّ ألف دال، الذي من المركز ستّون جزءاً، بها خطّ زاي كاف جزءاً واحداً وخمس عشرة دقيقة وبها خطّ كاف ألف جزئين وعشر دقائق، وبها خطّ كاف ألف دال بأسره اثنان وستّون جزءاً وعشر دقائق. ومن قبل أنّ المربّعين اللذين يكونان منهما إذا جمعا كان منهما المربّع الذي يكون من خطّ دال زاي يكون خطّ دال زاي أيضاً في الطول اثنين وستّين جزءاً وإحدى عشرة دقيقة بالأجزاء التي بها كان خطّ زاي كاف جزءاً واحداً وخمس عشرة دقيقة. فالأجزاء إذن التي بها وتر زاي دال مائة وعشرون جزءاً يكون بها خطّ زاي كاف جزئين وخمساً وعشرين دقيقة، وتكون القوس التي عليه جزئين {وثمان} عشرة دقيقة بالأجزاء التي بها الدائرة التي ترسم على مثلّث دال زاي كاف القائم الزاوية ثلاث مائة وستّون جزءاً فيجب أن تكون زاوية زاي دال كاف أيضاً أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فجزئين وثمان عشرة دقيقة، وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث وستّون جزءاً فجزءاً واحداً وتسع دقائق. The numbers 1;9 and 2;18 were interchanged by an oversight in Toomer, p. 160 in the last two lines. The Arabic agrees with the Greek (Heiberg, p. 244, lines 22-24). 

/T161/ فيصير إذن هذا أيضاً مبلغ فضل قوس ألف باء الذي من قبل الاختلاف. /H245/ وبهذه الأجزاء كانت زاوية هاء ألف زاي ثلاثين جزءاً. فزاوية ألف زاي دال إذن الباقية أعني القوس من فلك البروج التي ترى ثمانية وعشرون جزءاً وإحدى وخمسون دقيقة على الموافقة للأقدار التي تبيّنت في الخروج عن المركز.

يه: وعلى هذا المثال هاهنا أيضاً إن أعطينا زاوية أخرى، كانت سائر هذه الزوايا معطاة بأن يخرج في مثل هذه الصورة من نقطة ألف على خطّ دال زاي عمود ألف لام. فإنّا إن أنزلنا أيضاً أنّ القوس من فلك البروج التي ترى معطاة، أعني زاوية ألف زاي دال، كانت من قبل ذلك نسبة خطّ زاي ألف إلى خطّ ألف لام معطاة. فلأنّ نسبة خطّ زاي ألف إلى خطّ ألف دال كانت منذ أوّل الأمر معطاة تصير نسبة خطّ دال ألف إلى خطّ ألف لام أيضاً معطاة. ومن قبل ذلك تكون زاوية ألف دال لام Toomer, p. 161: AD̂B معطاة، أعني قوس ألف باء وهي قوس الفضل الذي من قبل الاختلاف، وتكون زاوية هاء ألف زاي معطاة أعني قوس هاء زاي من فلك التدوير.

وإن أنزلنا الفضل الذي من قبل الاختلاف معطا، أعني زاوية ألف دال باء، فإنّ بالعكس على ذلك المثال تصير نسبة خطّ دال ألف إلى خطّ ألف لام من قبل ذلك معطا؛ وقد كانت منذ أوّل الأمر نسبة خطّ دال ألف إلى خطّ ألف زاي معطاة، /H246/ فتصير نسبة خطّ زاي ألف إلى خطّ ألف لام معطاة. ومن قبل ذلك تكون زاوية ألف زاي دال معطاة، أعني القوس من فلك البروج التي ترى، وتكون زاوية هاء ألف زاي معطاة، أعني قوس هاء زاي من فلك التدوير.

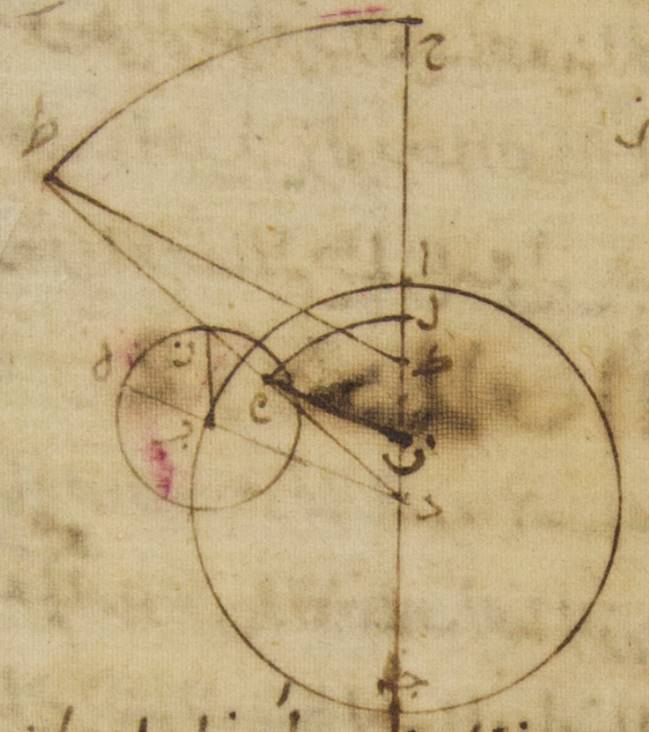
يو: وأيضاً في رسم الفلك الخارج المركز الذي وضعناه لنفرز من لدن نقطة حاء التي هي القرب الأقرب من الفلك الخارج المركز قوس حاء زاي ولننزّل أنّها تلك الأجزاء وهي ثلاثون جزءاً ولنوصل خطّ دال زاي باء وخطّ طاء زاي ولنخرج من نقطة دال على خطّ طاء زاي عمود دال كاف. فلأنّ قوس زاي حاء ثلاثون جزءاً، تكون زاوية زاي طاء حاء أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فثلاثون جزءاً، وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فستّين جزءاً. فيجب أن تكون القوس التي على خطّ دال كاف ستّين جزءاً بالأجزاء التي بها الدائرة التي ترسم حول ↑حول↑: على مثلّث دال طاء كاف القائم الزاوية ثلاث مائة وستّون جزءاً. وتكون القوس التي على خطّ طاء كاف الأجزاء التي تبقى لتمام نصف الدائرة وهي مائة وعشرون جزءاً. فالخطّان إذن اللذان يوتّرانهما أمّا خطّ دال كاف منهما فستّون جزءاً بالأجزاء التي بها القطر، وهو خطّ دال طاء، مائة وعشرون جزءاً وأمّا خطّ كاف طاء فبهذه الأجزاء مائة وثلاثة أجزاء وخمس وخمسون دقيقة. فالأجزاء إذن التي بها وتر دال طاء جزئان وثلاثون دقيقة وبها خطّ طاء زاي الذي من المركز ستّون جزءاً، /H247/ بها خطّ دال كاف جزء واحد وخمس عشرة دقيقة وبها خطّ طاء كاف على ذلك المثال جزئين وعشر دقائق {وبها} خطّ كاف زاي الأجزاء الباقية وهي سبعة وخمسون جزءاً وخمسون دقيقة. وإذا كان المربّعان اللذان يكونان منهما إذا جمعا كان المربّع الذي يكون من خطّ دال زاي صار هذا الخطّ أيضاً في الطول سبعة وخمسين جزءاً وإحدى وخمسين دقيقة بالتقريب بالأجزاء التي كان بها خطّ دال كاف جزءاً واحداً وخمس عشرة دقيقة. فالأجزاء إذن التي بها وتر دال زاي مائة وعشرون جزءاً بها يكون خطّ دال كاف جزئين وأربعاً وثلاثين دقيقة. وتكون القوس التي عليه جزئين وسبعاً وعشرين دقيقة بالأجزاء التي بها الدائرة التي ترسم على مثلّث دال زاي كاف ثلاث مائة وستّون جزءاً. فيجب أن تكون زاوية دال زاي كاف أيضاً أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فجزئان وسبع وعشرون دقيقة، وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فجزءاً واحداً وأربع عشرة دقيقة بالتقريب. /T163/ فهذا إذن مبلغ الفضل الذي من قبل الاختلاف.

ولأنّا قد وضعنا أنّ زاوية زاي طاء حاء بهذه الأجزاء ثلاثون جزءاً، تكون زاوية باء دال جيم بأسرها، أعني قوس جيم باء، من فلك البروج أحداً وثلاثين جزءاً وأربع عشرة دقيقة.

يز: وكذلك أيضاً هاهنا إذا أخرج خطّ باء دال على الاستقامة وأخرج إليه عمود طاء لام. فإنّا إن جعلنا قوس جيم باء من فلك البروج معطاة، أعني زاوية طاء دال لام، كان من قبل ذلك نسبة خطّ دال طاء إلى خطّ طاء لام معطاة. /H248/ ولأنّ نسبة خطّ دال طاء إلى خطّ طاء زاي معطاة منذ أوّل الأمر تصير نسبة خطّ زاي طاء أيضاً إلى خطّ طاء لام معطاة. فيكون قد حصل لنا من قبل ذلك أنّ زاوية طاء زاي دال معطاة، أعني الفضل الذي من قبل الاختلاف، وأنّ زاوية زاي طاء دال معطاة، أعني قوس حاء زاي من الفلك الخارج المركز.

وإن جعلنا الفضل الذي من قبل الاختلاف معطاة، أعني زاوية طاء زاي دال، فإنّ الأمر ينعكس فتكون نسبة خطّ زاي طاء إلى خطّ طاء لام من قبل ذلك معطاة. وإذ كانت نسبة خطّ زاي طاء إلى خطّ طاء دال معطاة منذ أوّل الأمر فإنّ نسبة خطّ دال طاء إلى خطّ طاء لام أيضاً تكون معطاة. ومن أجل ذلك يحصل لنا أنّ زاوية طاء دال لام معطاة، أعني قوس جيم باء من فلك البروج وإنّ زاوية زاي طاء حاء معطاة، أعني قوس حاء زاي من الفلك الخارج المركز.

يح: وعلى هذا المثال أيضاً في الرسم الذي اثبتنا فيه الفلك الموافق المركز وفلك التدوير فيما تقدّم، نفرز من لدن نقطة طاء، وهي البعد الأقرب قوس طاء حاء، ونفرض ثلاثين جزء كما كنّا فرضناها، ونوصل خطّ ألف حاء وخطّ دال حاء باء ونخرج من نقطة حاء عمود حاء كاف على خطّ ألف دال. فنقول أيضاً لأنّ قوس طاء حاء تكون ثلاثين جزءاً، /H249/ تكون زاوية طاء ألف حاء أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فثلثين جزءأً، وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فستّين جزءاً. فيجب أن تكون القوس التي على خطّ حاء كاف ستّين جزءاً بالأجزاء التي بها الدائرة التي ترسم على مثلّث ألف حاء كاف القائم الزاوية ثلاث مائة وستّون جزءاً وتكون القوس التي على خطّ ألف {كاف} الأجزاء الباقية لتمام نصف دائرة وهي مائة وعشرون جزءاً. /T164/ فالخطّان إذاً اللذان يوتّرانهما أمّا خطّ حاء كاف منهما فيكون ستّين جزءاً بالأجزاء التي بها وتر ألف حاء مائة وعشرون جزءاً، وأمّا خطّ ألف كاف فيكون بهذه الأجزاء مائة وثلاثة أجزاء وخمساً وخمسين دقيقة، فالأجزاء إذاً التي بها أمّا خطّ ألف حاء فجزئان وثلاثون دقيقة وخطّ ألف دال، وهو الذي من المركز، ستّون جزءاً، يكون بها خطّ جيم كاف Greek (Heiberg, p. 249, line 14): HK جزءاً واحداً وخمس عشرة دقيقة وخطّ ألف كاف على ذلك المثال جزئين وعشر دقائق وخطّ كاف دال الأجزاء الباقية وهي سبعة وخمسون جزءاً وخمسون دقيقة. وإذ كان المربّعان اللذان يكونان منهما يكون منهما إذا جمعا المربّع الذي يكون من خطّ دال حاء فإنّ خطّ دال حاء نفسه يكون في الطول سبعة وخمسين جزءاً وإحدى وخمسين دقيقة بالتقريب بالأجزاء التي بها كان خطّ كاف حاء جزءاً واحداً وخمس عشرة دقيقة. فالأجزاء إذاً التي بها وتر دال حاء مائة وعشرون جزءاً، يكون بها خطّ حاء كاف جزئين وأربعاً وثلاثين دقيقة. وتكون القوس التي عليه جزئين وسبعاً وعشرين دقيقة بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال حاء كاف القائم الزاوية ثلاث مائة وستّون جزءاً فيجب أن تكون زاوية حاء دال كاف أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فجزئين وسبعاً وعشرين دقيقة، /H250/ وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فجزءاً واحداً وأربع عشرة دقيقة بالتقريب. فهذا إذن مبلغ الفضل الذي من قبل الاختلاف هاهنا أيضاً أعني قوس ألف باء. وإذ كنّا قد وضعنا زاوية حاء ألف كاف Greek (Heiberg, p. 250, line 4): KAH بهذه الأجزاء ثلاثين جزءاً، فإنّ زاوية باء حاء ألف بأسرها، وهي التي تشتمل على القوس من فلك البروج الذي يرى، يكون أحداً وثلاثين جزءاً وأربع عشرة دقيقة على الموافقة للأقدار التي وجدت في الفلك الخارج المركز.

يط: وكذلك أيضاً هاهنا إذا أخرج خطّ ألف لام عموداً على خطّ دال باء. إن نحن جعلنا القوس من فلك البروج معطاة، أعني زاوية ألف حاء لام، صارت من قبل ذلك نسبة خطّ حاء ألف إلى ألف لام معطاة. وإذ كانت نسبة خطّ حاء ألف إلى خطّ ألف دال معطاة منذ أوّل الأمر، فإنّ نسبة خطّ دال ألف أيضاً إلى خطّ لام ألف تكون معطاة. ومن قبل ذلك يحصل لنا أنّ زاوية ألف دال باء، أعني قوس ألف باء، وهي قوس الفضل الذي من قبل الاختلاف، معطاة وأنّ زاوية حاء ألف طاء، GreeK (Heiberg, p. 250, line 22): ΘAH أعني قوس طاء حاء من فلك التدوير، معطاة. وإن نحن أيضاً جعلنا قوس ألف باء، وهي قوس الفضل الذي من قبل /T165/ /H251/ الاختلاف، معطاة أعني زاوية ألف دال باء، فإنّ الأمر يكون بالعكس. فتصير على ذلك المثال نسبة خطّ دال ألف إلى خطّ ألف لام من قبل ذلك معطاة. وإذا كانت نسبة خطّ دال ألف إلى خطّ ألف حاء معطاة منذ أوّل الأمر. فإنّ نسبة خطّ جيم ألف Greek (Heiberg, p. 251, line 4): HA إلى خطّ ألف لام تكون معطاة. ومن قبل ذلك يحصل لنا أنّ زاوية ألف حاء لام معطاة، أعني القوس من فلك البروج، وأنّ زاوية طاء ألف حاء معطاة، أعني قوس طاء حاء من فلك التدوير. فقد آتينا ببيان ما قصدنا له.

⟨III.6⟩ و: في عمل جدول لأقسام الاختلاف الجزئيّة The title does not occur in Heiberg’s Greek text, p. 251, line 10.

ولمّا كان قد يمكن بهذه الأبواب عمل جدول للقسيّ التي تحوّل ه – خ: تقوم بسبب اختلاف المسيرات التي ترى يسهل به تناول مقادير ما تقوم به القسيّ الجزئيّة وكان عمله قد يتهيّأ بها على ضروب شتّى، فإن أحسنها عندنا ما وضع فيه بإزاء القسيّ المستوية التفاضل الذي من قبل الاختلاف لما في ذلك من الموافقة لمّا جرى عليه الأمر في الأصلين الموضوعين لنا أنفسهما ولما فيه من السهولة وسرعة الانتزاع ه – خ: العمل عند حساب واحدة واحدة من الحركات فلذلك من الحركات. فلذلك استعملنا في الأعداد وفي الأقسام الجزئيّة الباب الأوّل من البابين اللذين وضعناهما في كلّ واحد من الأصلين، فحسبنا بالخطوط على مثال ما بيّنّاه ما يصيب كلّ واحدة من القسيّ المستوية من فضل الاختلاف. وقسّمنا على الجملة أمّا الأرباع التي تلي نقط ه – خ: فقط البعد الأبعد في الشمس /H252/ وفي سائر الكواكب فبخمسة عشر خمسة عشر قسماً حتّى يكون ما يوضع بإزائها ستّة ستّة من الأجزاء وأمّا  /T166/الأرباع التي تلي البعد الأقرب فقسّمناها بثلاثين ثلاثين قسماً حتّى يكون أيضاً ما يوضع بإزاء هذه يوضع بإزاء ثلاثة ثلاثة من الأجزاء. وذلك أنّ تفاضل زيادة ما تصيب من اختلاف المسير من قبل حركة الاختلاف الأقسام المتساوية عند نقطة القرب الأقرب أعظم ممّا يكون عند نقطة البعد الأبعد.

⟨III.7⟩ ز: جدول لاختلاف الشمس

فنحن مثبتون جدول اختلاف الشمس كعادتنا في خمسة وأربعين سطراً وقاسموه ثلاثة أقسام أمّا القسمان الأوّلان ففيهما أعداد الحركة المستوية الثلاث مائة والستّون الجزء من ذلك الخمسة عشر السطر الأوّل فيها الربعان اللذان يليان البعد الأبعد ومن ذلك الثلاثون السطر الباقية فيها الربعان اللذان يليان البعد الأقرب. وأمّا القسم الثالث ففيه ما يصيب واحداً واحداً من الأعداد المستوية من أجزاء التفاضل الذي من قبل الاختلاف إلى  ه: أي الزيادة والنقصان. وهكذا رسم الجداول.

/H254/ ⟨III.8⟩ ح: في حاصل الشمس بحسب حركتها الوسطى

وإذ بقي علينا تقييد حاصل حركة الشمس المستوية لما في ذلك من الوقوف علي مسيراتها الجزئيّة في وقت وقت، فنحن واصفون ذلك أيضاً ولازمون أيضاً بالجملة في الشمس وفي سائر الكواكب ما وقفنا عليه من مسيرها بالأرصاد التي تولّيناها بأنفسنا بغاية الاستقصاء ومرتقون منها بتقييدنا حاصلها إلى مبدأ ملك {بختنصر} باستعمالنا الحركات الوسطى التي بيّنّاها. وذلك أنّ أكثر ما في أيدينا ممّا بقي إلى هذه الغاية من الأرصاد القديمة أنّما هي من ذلك الزمان.

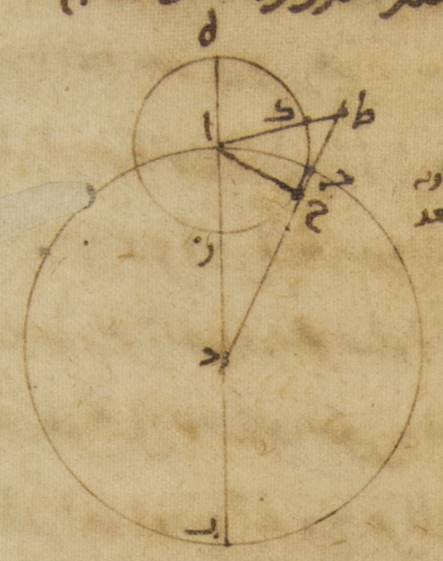
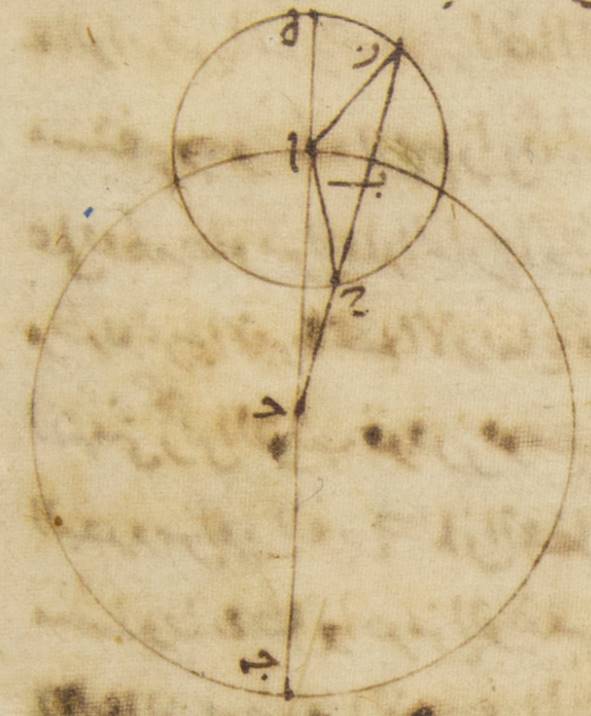
ك: فليكن الفلك الذي مركزه مركز فلك البروج ألف باء جيم حول مركز دال، وفلك الشمس الخارج المركز هاء زاي حاء حول مركز طاء والقطر الذي يمرّ بالمركزين وبنقطة هاء وهي البعد الأبعد هاء ألف حاء جيم. ولننزّل أنّ نقطة باء من فلك البروج النقطة الخريفيّة، ولنوصل خطّ باء زاي دال وخطّ زاي طاء، ولنخرج من نقطة طاء عمود كاف طاء على خطّ زاي دال إذا أخرج على الاستقامة. /H255/ فلأنّ نقطة باء الخريفيّة على مبدأ الميزان ونقطة جيم، وهي البعد الأقرب، على خمسة أجزاء ونصف من الرامي، فقوس باء جيم إذن خمسة وستّون جزءاً وثلاثون دقيقة. فزاوية باء دال جيم إذن، أعني زاوية طاء دال كاف، أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فهي خمسة وستّون جزءاً وثلاثون دقيقة، وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فهي مائة وأحد وثلاثون جزءاً. فيجب أن تكون القوس التي على خطّ طاء كاف مائة وأحداً وثلاثين جزءاً بالأجزاء التي بها الدائرة التي نرسم حول مثلّث دال طاء كاف القائم الزاوية ثلاث مائة وستّون جزءاً ووترها وهو خطّ طاء كاف مائة وتسعة أجزاء واثنتا عشرة دقيقة بالأجزاء التي بها قطر دال طاء مائة وعشرون جزءاً. /T168/ فالأجزاء إذن التي بها خطّ دال طاء خمسة أجزاء، ووتر زاي طاء مائة وعشرون جزءاً، بها يكون أمّا خطّ كاف طاء فأربعة أجزاء وثلاثاً وثلاثين دقيقة وأمّا القوس التي عليه فأربعة أجزاء وعشرين دقيقة بالأجزاء التي بها الدائرة التي ترسم حول مثلّث زاي طاء كاف القائم الزاوية ثلاث مائة وستّون جزءاً.

فيجب أن تكون زاوية طاء زاي دال أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فأربعة أجزاء وعشرون دقيقة، وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فجزئين وعشر دقائق. وقد كانت زاوية باء دال جيم بهذه الأجزاء خمسة وستّين جزءاً وثلاثين دقيقة. فزاوية زاي طاء دال الباقية إذن أعني قوس زاي حاء من الفلك الخارج المركز ثلاثة وستّون جزءاً وعشرون دقيقة. فإذا كانت الشمس إذن في الاستواء الخريفيّ، فإنّها /H256/ تتقدّم بحركتها الوسطى نقطة البعد الأقرب أعني خمسة أجزاء وثلاثين دقيقة من الرامي بثلاثة وستّين جزءاً وعشرين دقيقة وتبعد من نقطة البعد الأبعد أعني من خمسة أجزاء وثلاثين دقيقة من التوأم بحركتها الوسطى تلقا حركة الكلّ مائة وستّة عشر جزءاً وأربعين دقيقة.

وإذ قد علم ذلك وكنّا قد وجدنا في أوائل ما رصدنا من الاستواءات استواءاً خريفيّاً قد استصقى رصده بغاية ما يمكن كان في سنة سبع عشرة من ملك أذريانوس في اليوم السابع من الشهر من شهور المصريين المسمّى أثور بعد منتصف النهار بساعتين بالتقريب من الساعات الاستوائيّة. فمن البيّن أنّ الشمس كان في ذلك الزمان بعدها بحركتها الوسطى من نقطة البعد الأبعد في الفلك الخارج المركز تلقا حركة الكلّ مائة وستّة عشر جزءاً وأربعون دقيقة. لكن ما يجتمع من السنين من ملك بختنصر إلى وفاة إ ه: لا ⟨يعني الإسكندر⟩سكندر أربع مائة وأربع وعشرون سنة من سنيّ المصريّين، ومن وفاة إ ه: لا ⟨يعني الإسكندر⟩سكندر إلى ملك أغسطس مائتان وأربع وتسعون سنة ه: إنّ أوّل تاريخ بخت نصر إلى أوّل تاريخ وفاة الإسكندر تكد سنة 424 مصريّة ومن وفاة الإسكندر إلى ملك أوغسطس رضد سنة 294. ومن منتصف نهار أوّل يوم من الشهر المسمّى توث، فإنّا أنّما نقيّد التحصيلات من منتصف النهار من السنة الأولى من سنيّ المصريّين من ملك أوغسطس إلى ساعتين من ساعات الاستواء مضتاً من منتصف نهار اليوم السابع من الشهر المسمّى أثور من {السنة} السابعة عشر من ملك أذريانوش تكون مائة سنة وإحدى وستّين سنة وستّة وستّين يوماً وساعتين من ساعات الاستواء. فيكون إذن الذي يجتمع من منتصف نهار أوّل يوم من شهر توث من السنة الأولى من سنيّ المصريّين من ملك بختنصر إلى وقت الاستواء الخريفيّ الذي ذكرناه من السنّين المصريّة ثمان مائة سنة وتسعاً وسبعين سنة وستّة وستّين يوماً وساعتين من ساعات الاستواء. /H257/ لكن الشمس تسير في هذا المقدار من الزمان بحركتها الوسطى بعد الأدوار التامّة مائتين وأحد عشر جزءاً وخمساً وعشرين دقيقة بالتقريب. /T169/ فإن نحن إذن زدنا على أجزاء (على) (أجزاء) بعد الشمس من نقطة الأبعد الأبعد من الفلك الخارج المركز في هذا الاستواء الخريفيّ الذي ذكرناه، وهي مائة وستّة عشر جزءاً وأربعون دقيقة أجزاء، دورة واحدة، وهي ثلاث مائة وستّون جزءاً، ونقصنا من المجتمع المائتين والأحد العشر الجزء والخمس والعشرين الدقيقة، وهي الفضلة التي لحقت من قبل الزمان الذي بين الوقتين، صار لنا حاصل الحركة الوسطى في السنة الأولى من سنيّ المصريّين من ملك بختنصر في شهر توث في أوّل يوم منه في منتصف النهار ه: أنّ بعد الشمس كان فيه من نقطة البعد الأبعد في الجهة التي تقابل الجهة التي إليها يجري الكلّ {حركتها المستوية} مائتان وخمسة وستّون جزءاً وخمس عشرة دقيقة. وإنّ حاصلها بالحركة الوسطى كان خمساً وأربعين دقيقة من الحوت.

⟨III.9⟩ ط: في حساب دوران الشمس Ch. 9 is numbered Ch. 8 in Heiberg’ edition, p. 257, line 11.

فكلّما أثرنا أن نعلم مسير الشمس في كلّ زمان من الأرمنة التي نطلب معرفتها، نظرنا ه – خ: معرفته فيها أخذنا  الزمان المجتمع من وقت تحصيل الشمس إلى الزمان الذي طلب بحسب الساعة بإسكندريّة ه – خ: بحساب ساعات إسكندريّة  فأدخلناه في جداول الحركة المستوية، فما كان بإزاء مثل ذلك العدد أضفناه إلى أجزاء الحاصل التي هي مائتان وخمسة وستّون جزءاً وخمس عشرة دقيقة وألقينا من المجتمع الأدوار التامّة وما يبقى ألقينا منه لكلّ برج حقّه. وابتدأنا في ذلك من خمسة أجزاء وثلاثين دقيقة من التوأم ومررنا على توالي البروج، فحيث وقع العدد فهناك يوجد مسير الشمس الأوسط. /H258/ ثمّ تأخذ هذا العدد بعينه، أعني الذي من نقطة البعد الأبعد إلى مسير الشمس الأوسط، فتدخله في جدول الاختلاف وتنظر ما بإزاء ذلك العدد من الأجزاء في القسم الثالث من الجدول. فإن كان العدد قد وقع في القسم الأوّل من الجدول، أعني إن كان مبلغه مائة وثمانين جزءاً وما دون، نقصنا ما بإزائه من الحاصل الذي توجبه الحركة الوسطى؛ وإن كان قد وقع في القسم الثاني من الجدول، أعني إن كان قد جاوز المائة والثمانين، زدنا ما بإزائه على المسير الوسط. فوقفنا بهذا الطريق على موضع الشمس بالحقيقة والرؤية.

⟨III.10⟩ ي: في اختلاف الأيّام بلياليها

فهذه الأشياء تكاد تكون قد آتت على جميع ما ينظر فيه من الممرّ للشمس ه – خ: أمر الشمس  وحدها. وقد يتّصل بها أن نضيف إلى ذلك بإيجاز ما يحتاج إلى أن يتقدّم فيعلم من أمر اختلاف الأيّام بلياليها لأنّ جميع ما وضعناه من الحركات الوسطى في كلّ واحد ممّا وضعناه بالجملة فإنّما ينبغي أن يوجد التفاضل فيه بزيادات متساوية على أنّ أزمان الأيّام كلّها بلياليها متساوية. وينبغي أن نعلم أنّ ذلك ليس كذلك. فنقول أنّ دوران الكلّ إذ كان يجري على الاستواء وعلى قطبي معدّل النهار ه – صح: و ⟨يعني وكانت⟩ كانت هذه العودة أبين ما عرفت به أن ينظر فيها بالقياس إلى الأفق أو إلى دائرة نصف النهار. فمن البيّن أنّ الدورة الواحدة للعالم هي عودة نقطة بعينها من دائرة معدّل النهار إذا ابتدأت /H259/ من جزء ما من الأفق أو من دائرة {نصف} النهار إلى ذلك الجزء بعينه. وإنّ اليوم الواحد بليلته على الإطلاق ه: هذا الذي رسم به اليوم والليلة على الإطلاق بناه على ألّا حركة للشمس وعلى أنّها كالنقطة ولذلك قال هو عودة الشمس أيضاً إذا ابتدأت من جزئاً من الأفق أو من دائرة نصف النهار إلى ذلك الجزء وهذا لا يصحّ إلّا إن كانت الشمس نقطة ثابتة. هو عودة الشمس أيضاً إذا ابتدأت من جزء ما من /T170/ الأفق أو من دائرة نصف النهار. ه: إلى ذلك الجزء فيكون من قبل ذلك اليوم المتسوي بليلته المسير الذي يشتمل على أزمان دورة واحدة لمعدّل النهار وهي ثلاث مائة وستّون زماناً ومع ذلك على تسع وخمسين دقيقة بالتقريب من زمان واحدٍ  ↑واحدٍ↑: صح وهي مبلغ ما تزيده الشمس بحركتها الوسطى؛ ويكون اليوم بليلته المختلف ه – خ: هو المسير الذي يشتمل على أزمان دورة واحدة لمعدّل النهار وهي ثلاث مائة وستّون زماناً ومع ذلك على الأزمان التي تطلع أو تتوسّط السماء مع حركة الشمس المختلفة فهذا القسم من معدّل النهار الذي يلحق ه – صح: أبداً زائداً على الثلاث مائة والستّين الزمان يجب ضرورة أن يكون مختلفاً من قبل ما يرى من اختلاف الشمس.

ومن قبل أنّ القطع المتساوية من فلك البروج ليست تجوز في أزمنة سواء، لا الأفق ولا دائرة نصف النهار، وكلّ واحد من هذين الأمرين فإنّ الفضل الذي يقع من قبله بين العودة المستوية وبين العودة المختلفة لا يقع محسوساً في اليوم الواحد لكنّه إذا اجتمع في أيّام كثيرة بان للحسّ بياناً واضحاً.

فأمّا أكثر الفضل من قبل اختلاف الشمس /H260/ فيكون في البعدين ه – خ: الأوسطين أعني اللذين من إحدى حركتي الشمس الوسطى إلى الآخر. فإنّ الأيّام بلياليها التي يجتمع لما ه – خ: ممّا بين ذلك ه – خ: ذينك تخالف الأيّام المستوية بأربعة أزمان ونصف وربع زمان بالتقريب وتخالف بعضها بعضاً بضعف ذلك وهو تسعة أزمان ونصف زمان من قبل أنّ مسير الشمس أيضاً الذي يرى يخالف مسيرها المستوي أمّا في نصف الدائرة الذي يلي البعد الأبعد فتنقصان أربعة أجزاء ونصف وربع، وأمّا في نصف الدائرة الذي يلي البعد الأقرب فبزيادة مثل هذه الأجزاء.

وأمّا أكثر الفضل ه: {...} الفضل يكون حيث ذكر هو كلام غير محصّل لأنّه قد يكون هناك ويكون في غير ذلك الموضع إلّا أن يكون بطلميوس قد أجزى كلامه في هذا الموضع على ضرب من {...} وهو ظنّي به. وإنّما كان يحتاج إلى أن يقول إنّ أكثر الفضل في أكثر البلدان أن {يكون} كما ذكر.
ه – خ: بين الأيّام من قبل اختلاف ما يطلع مع أجزاء فلك البروج أو ما يغرب معها، فيكون في نصفي الدائرة اللذين يحدّانهما نقطتا الانقلابين. فإنّ هاهنا أيضاً مطالع كلّ واحد من هذين النصفين يخالف الأزمان التي يوجد على الاستواء وهي مائة وثمانون زماناً بالفضل ه – خ: الذي بين أطول ما يكون من النهار أو أقصر ما يكون وبين نهار الاستواء ويخالف المطلعان أحدهما الآخر بالفضل بين أطول ما يكون من النهار أو أطول ما يكون من الليل وبين أقصر {ما} يكون من النهار أو من الليل. وأمّا أكثر فضل من قبل اختلاف ما يتوسّط السماء مع أجزاء فلك البروج فيكون أيضاً في الأبعاد التي تحيط بالبرجين خاصّة اللذين هما جميعاً عن جنبي نقطة من نقطتي الانقلابين أو نقطة من نقطتي الاستوائين. فإنّ البرجين من هذه البروج اللذين يليان جميعاً نقطة من نقطتي الانقلابين يخالفان الأزمان التي توجّه على الاستواء بأربعة أزمان ونصف زمان بالتقريب ويخالفان البرجين الذين يليان جميعاً نقطة من نقطتي الاستواء أيضاً بتسعة أزمان بالتقريب من قبل أنّ هذين ينقصان عن الحصّة الوسطى وذينك يزيدان عليها بقريب من مثل ذلك. /H261/ ولذلك جعلنا مبادئ الأيّام بلياليها في التحصيلات من توسّط الشمس السماء لا من طلوعها ولا من غروبها، وذلك أنّ الفضل الذي يوجد عند الآفاق قد يمكن أن يبلغ ساعات كثيرة، وليس يكون واحداً بعينه في كلّ موضع بل يتغيّر بتغيّر الفضل في أطول ما يكون من الأيّام أو أقصر ما يكون منها /T171/ في كلّ واحد من ميول الكرة، فأمّا الفضل الذي عند دائرة نصف النهار فإنّه واحد بعينه في كلّ مسكن وليس يزيد ولا ه – خ: ينقص عن على أزمان الفضل التي  ه – خ: الذي تجتمع من قبل الاختلاف الذي يلحق الشمس.

ويجتمع من اقتران هذين ه – خ: ومطالع وسط السماء ويجتمع من أكثر الاختلافين أنّ هذين.  الفضلين أعني الفضل الذي من قبل اختلاف الشمس والفضل الذي من قبل ما يتوسّط السماء مع أجزاء فلك البروج أكثر الفضل في الأبعاد التي يجتمع فيها الفضلان اللذان ذكرناهما جميعاً إمّا زائدين معاً وإمّا ناقصين معاً. فيكون القسم خاصّة المنسوب إلى النقصان من الوجهين هو الذي من وسط الدلو إلى ه – خ: {آخر} الميزان ويكون {القسم} المنسوب إلى الزيادة هو الذي من  ه – خ: أوّل العقرب إلى وسط الدلو ه: {...} والقسم المنسوب إلى النقصان من الوجهين هو القسم الذي من وسط الدلو إلى آخر الميزان والقسم المنسوب إلى الزيادة هو الذي {من} أوّل العقرب إلى وسط الدلو.  من قبل أنّ أكثر الفضل في كلّ واحد من هذين القسمين ينبغي إمّا أن يزاد معاً وإمّا أن ينقص معاً. والذي يزاد أو ينقص أمّا من قبل اختلاف الشمس فثلاثة أجزاء  ه – خ: أزمان وثلثي جزء وأمّا من قبل ما يتوسّط السماء فأربعة أزمان وثلثي زمان بالتقريب حتّى يكون أكثر الفضل المجتمع من هذا الاقتران الذي وضعناه للأيّام بلياليها في كلّ واحد من القسمين اللذين ذكرناهما إمّا بالقياس إلى الأيّام المستوية، /H262/ أمّا من الأزمان فثمانية أزمان وثلث زمان وأمّا من الساعات فنصف ساعة وجزء من ثمانية عشر جزءاً من ساعة، وإمّا بقياس بعضها إلى بعض فضعف ذلك وهو من الأزمان ستّة عشر زماناً وثلثا زمان ومن الساعات ساعة وتسع ساعة. وهذا المقدار إن أغفل أمّا في الشمس وفي غيرها فيكاد يكون لا يلحق من قبله في الفحص عمّا يظهر فيها ضرر محسوس؛ وأمّا في القمر فلسرعة حركته قد يقع من الفضل في ذلك شيء له قدر يلحق بثلاثة أخماس جزءاً.

ولكي تقدر متى أعطينا أيّاماً كم كانت أعني بالأيّام ما كان ه: ه منها من منتصف النهار أو منتصف الليل إلى منتصف النهار أو منتصف الليل أن يزدها جملة إلى أيّام مستوية فقد ينبغي أن ننظر حاصل الشمس في أوّل ذلك البعد المعطى للأيّام وحاصلها في آخره في أيّ جزء هو من فلك البروج على حركتها المستوية وعلى حركتها المختلفة ثمّ نعمد إلى بعد أجزاء الحصّة الذي من البعد المختلف أعني الذي يرى إلى البعد الذي يرى ه – الحجّاج: ثمّ من بعد ذلك نأخذ ما بين الموضعين لمسير الشمس المختلف الذي يرى من الأجزاء.  فندخله في المطالع في الكرة المنتصبة وتنظر /H263/ أجزاء أجزاء↑: هذا البعد المختلف كما قلنا مع كم زمان من معدّل النهار يتوسّط السماء فنأخذ الزيادة من ه – خ: تلك الأزمان التي توجد وبين أجزاء البعد المستوي ونحتسب بهذا ه – خ: ونحسب هذا  المقدار الذي يشتمل على أزمان الزيادة ه – خ: كم هو من ساعة من ساعات الاستواء فمتى وجدنا عدد الأزمان أكثر من البعد المستوي زدناه على عدد الأيّام التي أعطيناها، ومتى وجدناه أقلّ منه نقصناه من تلك العدّة فما حصل لنا من الزمان فهو الزمان المحوّل إلى الأيّام المستوية. وهذا هو الذي نستعمله خاصّة في جماعات حركات {القمريّة} الوسطى التي في الجدول. وممّا يسهل فهمه من ذلك أنّه قد يمكن أيضاً استخراج الأيّام الزمانيّة التي توجد مختلفة من قبل الأيّام المستوية بأن نستعمل ما ذكرناه /T172/ من الزيادة والنقصان لأزمان الساعات على عكس ما استعملناه.

وكان حاصل الشمس في حسابنا ه – خ: نحن أعني في السنة الأولى من سنيّ المصريّين من ملك بختنصر في الشهر المسمّى توث في أوّل يوم منه ↑منه↑: منها في منتصف النهار أمّا بحركتها الوسطى على ما بيّنّا قبيل فخمس وأربعون دقيقة من الحوت وأمّا بحركتها المختلفة فثلاثة أجزاء وثمان دقائق بالتقريب من الحوت.

تمّت المقالة الثالثة من كتاب بطلميوس المنسوب إلى التعاليم ↑إلى التعاليم↑: وهو ي أقوال والحمد لله كثيراً على عونه.