Ptolemaeus Arabus et Latinus

بسم الله الرحمن الرحيم

عونك يا واحد

جمل ما في مقالة الخامسة من كتاب بطلميوس المنسوب إلى التعاليم⊙

الأولى: في إعداد ه – خ: اتّخاذ آلة يقاس بها الكوكب ↑: صح خ (الثابتة)؛ الثانية: في الأصل الذي ↑الأصل الذي↑: الأصول التي  يعمل عليه ↑: عليها في اختلاف القمر المضعّف ه – خ: المضاعف؛ الثالثة: في مبلغ الاختلاف الذي يلحق القمر بقياسه إلى الشمس؛ الرابعة: في النسبة التي تحدث عن خروج فلك القمر عن المركز؛ الخامسة: في محاذاة فلك التدوير الذي للقمر⊙ وانحرافه ↑: خ؛ السادسة: كيف نستخرج بطريق الخطوط من قبل الحركات الدوريّة مسير القمر المصحّح؛ السابعة: في صفة عمل جدول لجملة اختلاف القمر؛ الثامنة: جدول لجميع اختلاف القمر؛ التاسعة: في الحساب الكلّي لحركة القمر؛ العاشرة: في أنّه ليس يكون من قبل فلك القمر الخارج المركز اختلاف في الاتّصالات يعتدّ به؛ الحادية عشرة: في اختلاف منظر القمر؛ الثانية عشرة: في صنعة آلات ه – خ: آلة يستخرج بها اختلاف المنظر ه – خ: يعرف بها اختلافُ منظر القمر ؛ الثالثة عشر: في تبيين أبعاد القمر؛ الرابعة عشرة: في قدر أقطار الشمس والقمر والظلّ التي ترى في الاتّصالات؛ الخامسة عشرة: في بعد الشمس وما يتبيّن ببيانه؛ السادسة عشرة: في مقادير الشمس والقمر والأرض؛ السابعة عشرة: في اختلاف المنظر الجزئيّة للشمس والقمر؛ الثامنة عشرة ↑: في: جدول لاختلاف المنظر⊙ التاسعة عشرة: في تقويم اختلاف المنظر⊙

⟨V⟩ /T217/ ابتداء المقالة الخامسة من كتاب بطلميوس المنسوب إلى التعاليم

⟨V.1⟩ آ: في إعداد آلة يقاس بها الكوكب ↑: صح؛ ه – خ: (الكواكب الثابتة)

أمّا فيما ↑: خ ما يحتاج إليه لاتّصالات القمر بالشمس التي تكون عند الاجتماعات والاستقبالات و ↑: *للكسوفات التي تتمّ ه: يكون حدوثها في تلك الأحوال، فإنّا نجد الأصل الذي عمل عليه في الاختلاف الأوّل البسيط مجزيّاً فيه ولو ه – خ: إذا اقتصر على ذلك وحده فاستعمل على ما وصفنا. وأمّا في المسيرات الجزئيّة التي تكون فيها سائر أصناف تشكّل القمر بالقياس إلى الشمس ه – خ: وأمّا في حركات القمر في غير الاجتماعات والاستقبالات من الأشكال ، فلسنا نجد ذلك الأصل كافياً فيها /H351/وذلك أنّه قد يوجد كما قلنا للقمر اختلاف ثان من قبل أبعاده بالقياس إلى الشمس يعود إلى ذلك الاختلاف الأوّل في الاتّصالين جميعاً ويصير على أكثر ما يكون في التربيعين جميعاً. والذي قادنا إلى التنبيه على ذلك والتصديق به ما اثبته أبرخَس من الأرصاد التي وقعت له لمسيرات ه –خ: بمجازات القمر وما وقفنا عليه نحن أنفسنا بالآلة التي اتّخذناها لما يجري هذا المجرى⊙ وإنّا واصف من ذي قيل أمرها كلّه.

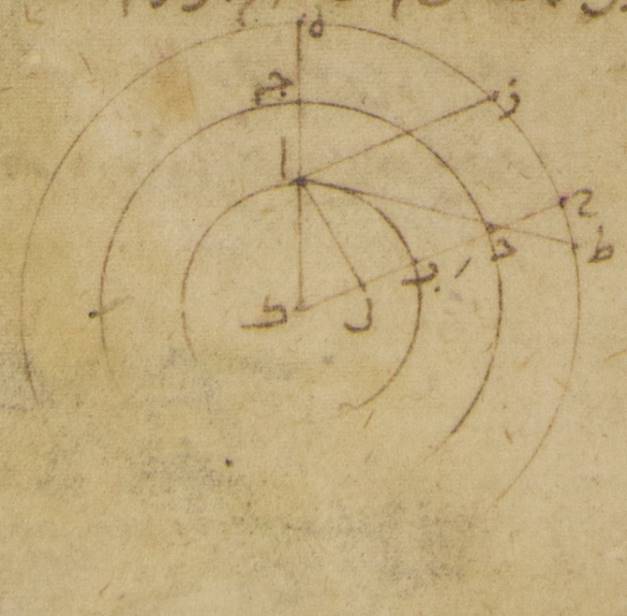
فأقول إنّا اتّخذنا حلقتين مهندمتين على أحكام مربّعتي السطوح مقتدرتي العظم متساويتين متشابهتين من جميع جوانبهما فداخلنا الواحدة في الأخرى على القطر ه – خ: موضعين مقابلين وجعلناهما على زوايا قائمة على بسيطهما حتّى أقمنا الواحدة مقام دائرة البروج، وأقمنا الأخرى مقام دائرة نصف النهار التي تمرّ بقطبي هذه وبقطبي دائرة معدّل النهار. واستخرجنا على هذه الدائرة من قبل ضلع المربّع النقطتين اللتين تحدّان قطبي فلك البروج فأوتدنا فيهما جميعا وتدين أسطوانيّي الشكل ناتئين إلى خارج وإلى داخل. ثمّ أثبتنا في الوتدين من خارج حلقة أخرى /H352/ يماسّ بسيطها المقعّر بسيط الحلقتين الداخلتين المحدّب من جميع الجوانب مماسّة صحيحة ويمكن فيها أن تدار في الطول حول القطبين اللذين ذكرناهما لفلك البروج /T218/{وأثبتنا} في الوتدين أيضاً من داخل على ذلك المثال حلقة أخرى تماسّ أيضاً من جميع جوانبها بسيطها المحدّب بسيط تينك الحلقتين المقعّر مماسّة صحيحة ويحتمل أن تدار في الطول حول ذينك القطبين على مثال الحلقة التي من خارج وقسمنا هذه الحلقة التي من داخل والحلقة أيضاً التي كنّا نقيمها مقام دائرة البروج إلى الأجزاء التي من عادتنا أن نقسم بها محيط الدائرة وهي ثلاث مائة وستّون جزءاً. ثمّ إلى ما أمكن أن نقسم إليه من أجزاء هذه الأجزاء وركّبنا أيضاً {في} هذه الحلقة التي من داخل الحلق تركيباً محكماً حلقة أخرى صغيرة لطيفة فيها ثقبان متقاطران ناشران عن بسيط الحلقة يتهيّأ فيها أن يدار في سطح تلك الحلقة نحو كلّ واحد من القطبين الموصوفين لما يحتاج إليه من رصد أمر العرض.

فلمّا أعددنا ه – صح: أعددنا هذه الحَلَق على هذه الصفة أخذنا على الدائرة التي نتوهّمها مارّة بأقطاب الدائرتين جميعاً من لدن كلّ واحد من قطبي فلك البروج القوس التي تبيّن أنّها بين قطبي فلك البروج وبين قطبي معدّل النهار. /H353/ ثمّ أوتدنا الطرفين اللذين انتهينا إليهما اللذين هما أيضاً متقاطران في حلقة تشبه حلقة نصف النهار التي وصفناها في أوّل هذا الكتاب لقياس القوس التي بين الانقلابين من دائرة نصف النهار كيما يكون إذا نصبت هذه الحلقة على ما نصبت تلك أعني على زوايا قائمة على بسيط الأفق وبحسب ارتفاع القطب الذي يخصّ البلد الذي أنت به وموازية أيضاً لبسيط دائرة نصف النهار التي بالطبع كان مدار الحلق التي في داخلها /T219/حول قطبي معدّل النهار من المشرق إلى المغرب على ما تجري عليه حركة الكلّ الأولى.

فلمّا نصبنا الآلة على هذه الصفة كنّا ننظر فمتى تهيّأ أن تكون الشمس والقمر ظاهرين ه: في نسخة أخرى يتحرّكان معاً فوق الأرض، وضعنا الحلقة التي من خارج حلق القياس على الجزء الذي توجد الشمس فيه في ذلك الوقت بغاية التقريب. وأدرنا الحلقة التي تمرّ بالأقطاب إلى أن يصير تقاطع الحلقتين على جزء الشمس محاذياً للشمس على الحقيقة فتستظلّ الحلقتان جميعاً معاً بأنفسهما أعني حلقة البروج والحلقة التي تمرّ بقطبيها^φ. وإن ه: قصده بهذه الدائرة الخارجة أن نجعل فلك البروج على وضعه بالحقيقة في ذلك الوقت الذي يقيس فيه فإن تهيّأ له ذلك بالشمس فعله على ما وصف وإن لم يتهيّأ له بالشمس صح قضيّته بغيرها من الكواكب على هذه الصفة الثانية. كان الذي به يقاس كوكباً من الكواكب أدرنا الحلقة التي تمرّ بالأقطاب إلى أن يكون أحد الناظرين إذا وضع على أحد جانبي الحلقة التي من خارج في ذلك الجزء الذي فيه الكوكب من فلك البروج رأي أيضاً الكوكب في هذه الحلقة من الجانب الآخر المحاذي لهذا الجانب الذي بإزائه /H354/ كأنّه لاصق ببسيطي الجانبين جميعاً في السطح الذي يمرّ بهما^φ. ثمّ كنّا نعمد إلى الحلقة الأخرى التي من داخل حلق القياس فنديرها نحو القمر أو نحو غيره ممّا نريد قياسه إلى أن يكون مع إثباتنا بالقياس موضع الشمس أو غيرها ممّا بني عليه القياس يرى أيضاً القمر أو ما أردنا غيره من الثقبين جميعاً اللذين على الحلقة اللطيفة المداخلة في هذه الحلقة.

فإنّا بهذا الوجه كنّا نقف على حاصله في الطول على أيّ جزء هو من فلك البروج من قبل تقاطع الحلقة الداخلة التي تحدث بينها وبين أقسام الحلقة المساوية في القوّة لفلك البروج. ونعلم أيضاً كم بعده عنه في الشمال أو في الجنوب في الدائرة التي تمرّ بقطبيه من قبل أقسام تلك الحلقة نفسها التي من داخل وما نجده من البعد فيما بين وسط ه – خ: وأمّا في حركات القمر في غير الاجتماعات والاستقبالات من الأشكال  الثقب الذي فوق الأرض من الحلقة اللطيفة التي تدور فيها وبين الخطّ الذي هو وسط حلقة البروج⊙

/T220/ ⟨V.2⟩ ب: في الأصل الذي يعمل عليه في اختلاف القمر المضعّف

فعند ما كان الأمر يجري في الأصل الذي يعمل عليه في اختلاف القمر المضعّف في رصد هذا الاختلاف على ظاهر ما يوجبه القياس، فإنّا كنّا نجد الأبعاد بين القمر وبين الشمس /H355/ فيما أثبته أبرخس وفيما كنّا نرصده نحن مرّة موافقة لما نخرجه من *الحساب* الأصل الذي وضعناه ومرّة مخالفة له والمخالفة أيضاً ربّما كنا نجدها يسيرة وربّما كنّا نجدها عظيمة. فلمّا أدمنا النظر في نظام هذا الاختلاف وواصلناه وتأمّلناه فضل تأمّل، وقفنا على أنّه أبداً عند الاجتماعات والاستقبالات إمّا ألّا يقع فيه خطاء محسوس وإمّا إن يقع فيه زوال يسير بقدر ما يوجبه اختلافات منظر القمر من الفضل^φ. فأمّا في التربيعين جميعاً، فقل ما يقع فيه من الخطاء أو لا ه – خ – صح: بل لا يقع فيه شيء أصلاً عند ما يكون القمر في البعد الأبعد أو في البعد الأقرب من فلك التدوير وأكثر ما يقع فيه من الخطاء متى كان القمر إذ هو في سيره الوسط يفعل أكثر ما يكون من الفضل أيضاً من قبل الاختلاف الأوّل؛ وإنّ الاختلاف الأوّل إذا كان اختلاف نقصان في أيّ التربيعين كان وجد مكان القمر أقلّ ممّا يوجبه الحساب من النقصان الأوّل، وإذا كان اختلاف زيادة وجد مكانه أزيد على حسب مقدار النقصان الأوّل والزيادة وعلى حسب قياسه في النسبة حتّى أنّ ما حصل في أنفسنا من هذا النظام قادنا إلى أن نروى I think it should be نُرى (i.e., we see). فنعلم أنّ فلك التدوير الذي للقمر يتحرّك أيضاً على فلك خارج المركز فيصير في غاية البعد من الأرض في الاجتماعات والاستقبالات /H356/ ويصير في غاية القرب منها في التربيعين جميعاً. والذي به يتهيّأ لزوم ما وضعناه من ذلك أن نصلح ه – خ: الأصل الأوّل هذا الضرب من الإصلاح.

لنتوهّم الفلك الموافق مركزه لمركز فلك البروج في السطح المائل الذي للقمر يتحرّك قدماً، كما كنّا قلنا من قبل، أيضاً بسبب العرض حول قطبي ه: __ من __ ه
This is a reference to the beginning of Ch. IV.6. فلك البروج بالمقدار الذي به تفضل على الحركة في الطول الحركة في العرض، وأنّ القمر يدور أيضاً في الفلك المسمّى فلك التدوير على أنّه إذا كان في قوس بعده الأبعد كانت نقلته قدماً على لزوم للعودة التي للاختلاف ه – خ: إلى الا  الأوّل. فهذا السطح المائل نضع فيه حركتين مستويتين متضادّتين تكونان جميعاً حول مركز فلك البروج إحداهما تدير مركز فلك التدوير على توالي البروج لازمة للحركة في العرض والأخرى تدير مركز الفلك الخارج المركز الذي يوجد في هذا السطح نفسه ه – خ: بعينه وبعده الأبعد وعلى هذا الفلك يكون أبداً مركز فلك التدوير وإدارتها ه – خ: ته (إدارته i.e.,) قدماً للبروج بمقدار ما يزيد على الحركة في العرض البعد إذا أضعف أعني ه – خ: بالبعد فضل حركة القمر الوسطى في الطول على حركة الشمس حتّى أنّه في اليوم الواحد /H357/ مثلاً يتحرّك مركز فلك التدوير على توالي البروج أجزاء العرض وهي ثلاثة عشر جزءاً وأربع عشرة دقيقة بالتقريب فيرى ه – خ: علي توالي البروج أنّه أنّما قطع أجزاء الطول وهي ثلاثة جزءاً وإحدى عشرة دقيقة من قبل أنّ الدائرة المائلة بأسرها يخطّ قدماً للفضل بينهما وهو ثلاث دقائق ويتحرّك البعد الأبعد من الفلك الخارج المركز إلى ضدّ تلك الجهة أيضاً قدماً أحد عشر جزءاً وتسع دقائق /T221/ وهي الأجزاء التي بها يزيد ضعف البعد، وهو أربعة وعشرون جزءاً وثلاث وعشرون دقيقة، على أجزاء العرض وهي ثلاثة عشر جزءاً وأربع عشرة دقيقة. فإنّه إذا جرى الأمر هذا المجرى كان من تقابل الحركتين جميعاً الذي يكون كما قلنا حول مركز فلك البروج زيادة في بعد الخطّ الذي يمرّ بمركز فلك التدوير على الخطّ الذي يمرّ بمركز الفلك الخارج المركز ه – خ: وعلى البعد الأبعد ومبلغه القوس المركّبة من الثلاثة العشر الجزء والأربع العشرة الدقيقة ومن الأحد عشر الجزء والتسع الدقائق، وهذه القوس تكون ضعف أجزاء البعد ه – خ: بين القمر والشمس وهي أثنا عشر جزءاً وإحدى عشرة دقيقة ونصف بالتقريب. ومن أجل ذلك صار فلك التدوير يقطع الفلك الخارج المركز مرّتين في زمان الشهر ه – خ: القمريّ الوسط على أن توضع العودة التي تتصوّر أنّها يكون له إلى البعد الأبعد من الفلك الخارج المركز يتمّ في أزمان الاجتماعات والاستقبالات التي توجد بالوسط.

آ: ولكي يزداد وقوفنا وفهمنا لأمور هذا الأصل الذي وضعناه، لنتوهّم أيضاً الفلك الذي في السطح المائل للقمر /H358/ الموافق مركزه لمركز فلك البروج ألف باء جيم دال حول مركز هاء وقطر ألف هاء جيم. ولنوضع معاً على أنّ نقطة ألف البعد الأبعد من الفلك الخارج المركز ومركز فلك التدوير والنهاية الشماليّة ومبدأ الحمل ووسط الشمس ففي المسير في يوم واحد. أقول إنّ ه – خ: يكون  السطح بأسره يتحرّك قدماً كأنّك قلت من نقطة ألف نحو نقطة دال حول مركز هاء ثلاث دقائق بالتقريب حتّى أنّ النهاية الشماليّة وهي نقطة ألف ه – صح: تصير على تسعة وعشرين جزءاً وسبع وخمسين دقيقة من الحوت. وأمّا الحركتان المتقابلتان اللتان تكونان باستواء عن ه – خ: على نظير خطّ هاء ألف حول مركز هاء أيضاً الذي هو مركز فلك البروج. فأقول إنّ أمرهما يجري على ذلك المثال في المسير في اليوم فأمّا الخطّ النظير لخطّ هاء ألف الذي يمرّ بمركز الفلك الخارج المركز فيدور باستواء قدماً للبروج كأنّك قلت إلى خطّ هاء دال فينتقل البعد الأبعد من الفلك الخارج المركز إلى نقطة دال، ونرسم حول مركز ه – صح: زاي فلك دال حاء الخارج المركز This sentence cannot be found in the Greek version. وتكون القوس التي قطعها، وهي قوس ألف دال، /T222/ أحد عشر جزءاً وتسع دقائق. وأمّا الخطّ الذي بمركز فلك التدوير فيدور أيضاً باستواء حول مركز هاء على توالي البروج كأنّك قلت إلى خطّ هاء باء فينتقل مركز فلك التدوير إلى نقطة حاء /H359/ وتكون قوس ألف باء التي قطعها ثلاثة عشر جزءاً وأربع عشرة دقيقة حتّى أنّ مركز فلك التدوير، وهو حاء، يرى بينه وبين النهاية الشماليّة، وهي نقطة ألف، ه: من البعد الثلاثة العشر الجزء والأربع عشرة الدقيقة التي للعرض وأمّا من أوّل الحمل فثلاثة عشر جزءاً وإحدى عشرة دقيقة التي هي للطول من قبل أنّ النهاية الشماليّة. في هذا المقدار من الزمان يصير في تسعة وعشرين جزءاً وسبع وخمسين دقيقة من الحوت ويرى بينه وبين نقطة دال، وهي البعد الأبعد، من الفلك الخارج المركز الأجزاء التي تجتمع منها ه – خ: من القوسين جميعاً أعني من قوس ألف دال ومن قوس ألف باء وهي أربعة وعشرون جزءاً وثلاث وعشرون دقيقة وهذه ضعف أجزاء البعد الوسط لليوم الواحد. فعلى هذا الطريق من قبل أنّ الحركتين جميعاً أعني التي تكون بالخطّ الذي يمرّ بنقطة باء والتي تكون بالخطّ الذي يمرّ بنقطة دال تتعاودان في نصف زمان الشهر الوسط عودة واحدة إلى موضع واحد، فمن البيّن أنّ في ربع هذا الزمان بعينه وأيضاً في نصفه وربعه تتقاطران لا محالة، أعني في التربيعين اللذين يوجدان وسطاً. ومن قبل ذلك إذا قاطر مركز فلك التدوير الذي على خطّ هاء باء البعد الأبعد من الفلك الخارج المركز الذي على خطّ هاء دال صار في قربه الأقرب.

وظاهر أنّ هذه الأشياء إذا كانت على ما وصفنا فليس يجب شيء من المخالفة للحركة المستوية من قبل الفلك الخارج المركز نفسه، أعني من قبل أنّ قوس دال باء غير شبيهة بقوس دال حاء /H360/ إذ كان خطّ هاء باء أنّما يقطع بمسيره على الاستواء قوس دال باء من فلك البروج لا قوس دال حاء من الفلك الخارج المركز، من قبل أنّه أنّما يدور حول مركز هاء لا حول مركز زاي، وهو ه – خ: الذي مركز الفلك الخارج المركز. وأنّما يجب الفضل ↑الفضل↑: المخالفة من قبل الاختلاف وحده الذي يكون في فلك التدوير نفسه من قبل أنّه إذا صار في قربه الأقرب زائد أبداً في الفضل الذي من قبل الاختلاف في الزيادة والنقصان بالسواء، وذلك أنّ الزاوية التي تحوزه التي عند البصر تصير في الأوضاع التي هي أقرب أعظم. فنقول الآن إنّه متى كان مركز فلك التدوير على نقطة ألف، وهي البعد الأبعد، لم يكن من قبل الأصل الأوّل شيء من الفضل بالجملة وذلك يكون في الاجتماعات والاستقبالات التي توجد بالوسط.

ب: وذلك أنّا إن رسمنا حول مركز ألف فلك تدوير ميم نون كانت نسبة خطّ هاء ألف إلى خطّ ألف ميم هي النسبة التي تبيّنت بالكسوفات. وإنّ أكثر ما يكون في الفضل متى كان مسير فلك التدوير على نقطة حاء، /H361/ وهي النقطة من الفلك الخارج المركز التي هي أقرب القرب بمنزلة الدائرة التي ترسم مارّة بنقطتي سين، طاء. H361.1: Ξ, Ο. Toomer, p. 222: (as XO here). وذلك أيضاً أنّما يتّفق في التربيعات التي توجد بالوسط. وذلك أنّ نسبة خطّ سين حاء إلى خطّ حاء هاء تكون أعظم من جميع النسب التي تحصل في سائر الأوضاع، وذلك أنّ خطّ سين حاء، الذي من مركز فلك التدوير، هو أبداً سواء وواحد بعينه، وخطّ هاء حاء الذي من مركز الأرض أقصر من كلّ خطّ يوصل بينه وبين الفلك الخارج المركز في غير هذا الموضع⊙

⟨V.3⟩ ج: في مبلغ الاختلاف الذي يلحق القمر بقياسه إلى الشمس

فكيما ↑فكيما: و ننظر كم يكون أكثر الفضل الذي من قبل الاختلاف عندما تكون حركة فلك التدوير من الفلك الخارج المركز في أقرب قربه رصدنا الأبعاد التي ترى بالقياس بين القمر وبين الشمس /T223/ التي يكون بها سيره وسطاً بغاية التقريب، فإنّه أنّما يكون فضل الاختلاف أكثر ما يكون ويكون بعده من الشمس إذا أخذ بالوسط قريباً من ربع الدائرة عند ما يصير فلك التدوير أيضاً من الفلك الخارج المركز في قربه الأقرب، واعتمدنا مع ذلك ألّا يكون للقمر شيء من اختلاف المنظر في الطول.

فإنّ هذه الأشياء إذا اتّفقت وكان البعد في الطول الذي يرى بالقياس موافقاً للبعد الصحيح، /H362/ تهيّأ لذلك الوقوف أيضاً بثقةٍ على الفضل المطلوب الذي للاختلاف الثاني. فلمّا جعلنا نظرنا من أمثال هذه *من* الأرصاد وجدنا أنّ الفلك التدوير متى كان في القرب الأقرب، كان أكثر الفضل الذي للاختلاف أمّا بينه وبين المسير الوسط فسبعة أجزاء وثلثا جزء بالتقريب، وأمّا بينه وبين الاختلاف الأولّ فجزءان وثلثا جزء.

ونحن ذاكرون على طريق المثال رصداً أو رصدين يقف بهما على صحّة هذا التحرير. فنقول إنّا قسنا الشمس والقمر في السنة الثانية من سني أنطونيس في الشهر منها من شهور المصريّين المسمّى فامانوت في اليوم الخامس والعشرين منه بعد طلوع الشمس وقبل انتصاف النهار بخمس ساعات وربع من ساعات الاستواء، فوجدنا الشمس في ثمانية عشر جزءاً ونصف وثلث من الدلو وكان وسط السماء الجزء الرابع من الرامي، ورأينا القمر نازلاً على تسعة أجزاء وثلثين من العقرب وكذلك كانت منزلته ↑منزلته↑: حاصله على الحقيقة من قبل أنّ القمر في أوائل العقرب إذا كان بعده عن دائرة نصف النهار ساعة ونصف بالتقريب نحو المغرب بإسكندريّة لم يكن له اختلاف منظر في الطول محسوساً. والزمان الذي من وقت التحصيلات التي كانت في السنة الأولى من /T224/ سني بختنصر إلى وقت هذا الرصد /H363/ ثمان مائة وخمس وثمانون سنة مصريّة ومائتا يوم وثلاثة أيّام ومن الساعات الاستوائيّة على الإطلاق وعلى الصحّة ↑الصحّة↑: صح ثمان عشرة ساعة ونصف وربع. وبحسب هذا الزمان نجد محصول الشمس أمّا على التوسّط فعلى ستّة عشر جزءاً وسبع وعشرين دقيقة من الدلو، وأمّا على الاستقصاء فعلى ثمانية عشر جزءاً وخمسين دقيقة منه على ما وجدناه بالقياس.

وحاصل القمر يوجد بالوسط في تلك الساعة بالأصل الذي وضع أوّلاً أمّا في الطول فعلى سبعة عشر جزءاً وعشرين دقيقة من العقرب حتّى يكون ه – خ: وكان  بعده الوسط من الشمس قريباً من ربع الدائرة، وأمّا من الاختلاف فعلى سبعة وثمانين جزءاً وتسع عشرة دقيقة من البعد الأبعد من فلك التدوير. وعند هذه الأجزاء أيضاً يكون فضل الاختلاف أكثر ما يكون فقد صار إذن المسير الصحيح أقلّ من المسير المستوي بسبعة أجزاء وثلثي جزء مكان الخمسة الأجزاء التي أوجبها الاختلاف الأوّل.

وكيما يستبين لنا الفضل الذي في أشباه هذا المسير ممّا رصده أبرخس من أمر هذه المسيرات فنحن محضرون ذكر واحد من تلك الأرصاد وهو الذي ذكر أنّه كان في سنة خمسين من الدور الثالث من أدوار قلبس في الشهر منها من شهور المصريّين المسمّى إبيفي في اليوم السادس عشر منه وقد مضى من الساعة الأولى منه ثلثاها. فقال إنّ السير ه – خ: المسير كان مائتين وواحداً وأربعين، وإنّ الشمس وجدت بالقياس في ثمانية أجزاء ونصف وجزء من اثني عشر من جزء من الأسد ورأي القمر حاصلاً على اثني عشر جزءاً وثلث من الثور، وكان حاصله على الحقيقة أيضاً على قريب من هذه الأجزاء. فيصير إذن البعد بين الشمس وبين القمر الذي يوجد على الاستقصاء ستّة وثمانين جزءاً وخمس عشرة دقيقة. لكنّ الشمس إذ كانت في أوائل الأسد فإنّ الساعة من ساعات النهار تكون برودس، وهو الموضع الذي كان فيه هذا الرصد، سبعة عشر زماناً وثلث. /H364/ فالخمس الساعات إذن والثلث الزمانيّة التي قبل انتصاف النهار يكون منها من ساعات الاستواء ستّ ساعات وسدس حتّى يكون /Τ225/ الرصد قبل انتصاف نهار اليوم السادس عشر بستّ ساعات وسدس من ساعات الاستواء، وكان المتوسّط للسماء الجزء التاسع من الثور. فيجتمع هاهنا أيضاً الزمان الذي من التحصيلات في الأصل إلى وقت هذا الرصد ستّ مائة سنة وتسع عشرة سنة مصريّة وثلاث مائة وأربعة عشر يوماً، ومن ساعات الاستواء أمّا على الإطلاق فسبع عشرة ساعة ونصف وثلث، وأمّا على الاستقصاء فسبع عشرة ساعة ونصف وربع. وبحسب هذا الزمان نجد حاصل الشمس بالأصول التي عليها يعمل إذ كانت دائرة نصف النهار التي تمرّ برودس هي التي تمرّ بإسكندريّة أمّا على التوسّط فعلى عشرة أجزاء وسبع وعشرين دقيقة من الأسد، وأمّا على الاستقصاء فعلى ثمانية أجزاء وعشرين دقيقة منه، ونجد حاصل القمر على التوسّط أمّا في الطول فعلى أربعة أجزاء وخمس وعشرين دقيقة من الثور حتّى يكون أيضاً البعد الوسط ه – خ: الذي بين الشمس والقمر قريباً من ربع الدائرة، وأمّا من الاختلاف فعلى مائتين وسبعة وخمسين جزءاً وسبع وأربعين دقيقة من البعد الأبعد من فلك التدوير وعند هذه الأجزاء أيضاً يكون على التقريب أكثر ما يكون من قبل ه – خ: فضل الاختلاف الذي من قبل فلك التدوير. فيجتمع إذن البعد الذي بين القمر على التوسّط وبين الشمس على الحقيقة ثلاثة وتسعون جزءاً وخمساً وخمسين دقيقة. ووجد بالرصد البعد الذي من موضع القمر على الاستقصاء وبين موضع الشمس على الاستقصاء ستّة وثمانين جزءاً وخمس عشرة دقيقة. فصار إذن حاصل القمر الذي يوجد على الحقيقة يزيد على مسيره المستوي سبعة أجزاء أيضاً وثلثي جزء مكان الخمسة الأجزاء التي يوجبها الأصل الأوّل⊙ وقد ظهر أنّ /H365/ هذين الرصدين وإن كان جميعا وقعا في التربيعين الباقيين، فإنّ الرصد الذي كان منّا نحن وُجد ناقصاً عن التقويم بالاختلاف الأوّل بجزئين وثلثي جزء⊙ وأمّا الرصد الذي كان من أبرخس فو{جد} زائداً بهذا المقدار بعينه من قبل أنّ الفضل بأسره الذي من قبل الاختلاف وقع لنا نحن يوجب النقصان ووقع لأبرخس يوجب الزيادة. وقد يوجب بأرصاد أخر أكثر من هذه نظائر لها أكثر الفضل الذي من قبل الاختلاف سبعة أجزاء وثلثي جزء بالتقريب متى كان فلك التدوير من الفلك الخارج المركز في القطع ه – خ – صح: البعد الذي هو أقرب قربه⊙

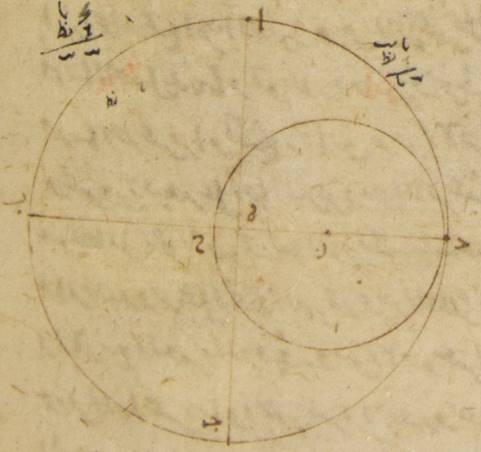
⟨V.4⟩ {د}: ه: ج في النسبة التي تَحدث عن خروج فلك القمر عن المركز

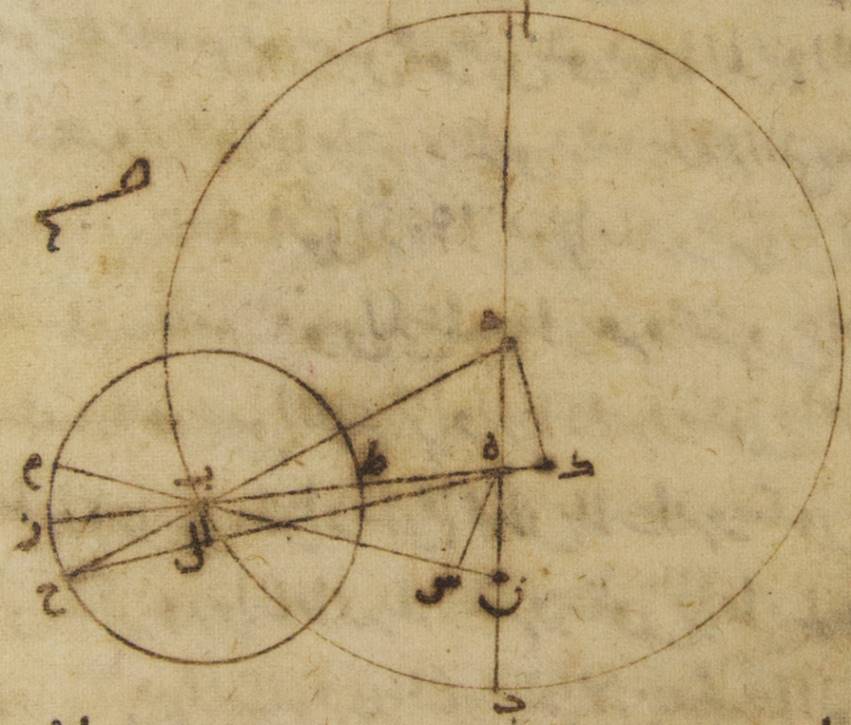
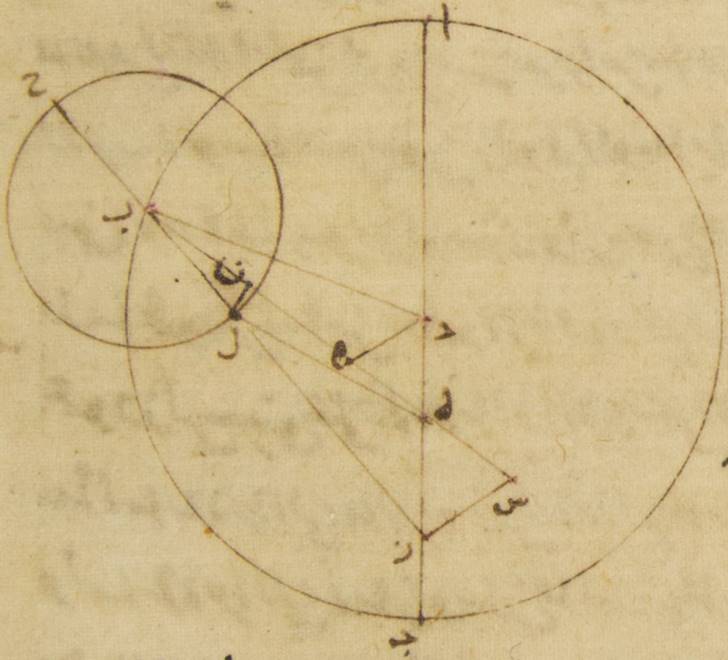
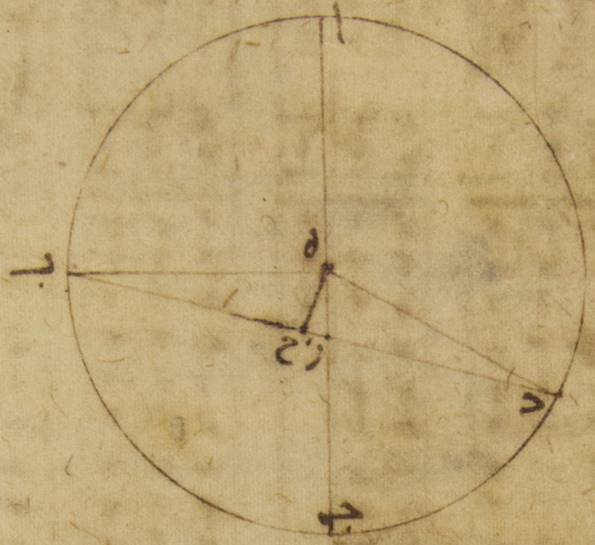
فإذ كان ذلك كذلك فليكن فلك القمر الخارج المركز ألف باء جيم حول مركز دال وقطر ألف دال جيم، ولننزّل أنّ مركز فلك البروج عليه نقطة هاء حتّى تكون نقطة ألف البعد الأبعد من الفلك الخارج المركز ونقطة جيم القرب الأقرب. ولنرسم على مركز جيم فلك التدوير للقمر وليكن زاي حاء طاء ولنخرج خطّ يماسّه ه – صح: وليكن هاء طاء باء وليوصل خطّ جيم طاء.

فلأنّ القمر إذا صار على الخطّ المماسّ لفلك التدوير فحينئذ يكون فضل الاختلاف أكثر ما يكون، /H366/ وقد تبيّن أنّ مبلغ هذا الفضل سبعة أجزاء وثلثا جزء، فواجب أن تكون زاوية جيم هاء طاء إذ هي عند مركز فلك البروج أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فسبعة أجزاء وأربعون دقيقة، وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فخمسة عشر جزءاً وعشرون دقيقة. /T226/ فالقوس أذن التي على خطّ جيم طاء خمسة عشر جزءاً وعشرون دقيقة بالأجزاء التي بها الدائرة التي ترسم حول مثلّث جيم هاء طاء القائم الزاوية ثلاث مائة وستّون جزءاً ووترها وهو خطّ جيم طاء ستّة عشر جزءاً بالتقريب بالأجزاء التي بها خطّ جيم هاء الموتّر مائة وعشرون جزءاً. فيجب أن تكون الأجزاء ه: بالأجزاء التي بها تبيّن أنّ خطّ جيم طاء وهو الذي من مركز فلك التدوير خمسة أجزاء وخمس عشرة دقيقة، وأنّ خطّ هاء ألف الذي بين مركز فلك البروج وبين البعد الأبعد من الفلك الخارج المركز ستّون جزءاً بها خطّ هاء جيم أيضاً، وهو الخطّ الذي بين ذلك المركز نفسه وبين القرب الأقرب من الفلك الخارج المركز، تسعة وثلاثون جزءاً واثنتان وعشرون دقيقة. فقطر ألف جيم إذن بأسره يكون بهذه الأجزاء تسعة وتسعين جزءاً واثنتين وعشرين دقيقة، وخطّ دال ألف، وهو الذي من مركز الفلك الخارج المركز، يكون تسعة وأربعين جزءاً وإحدى وأربعين دقيقة، وخطّ هاء دال، وهو الذي بين مركز فلك البروج وبين مركز الفلك الخارج المركز يكون عشرة أجزاء وتسع عشرة دقيقة. فقد بانت لنا إذن النسبة التي تحصل أيضاً عن الخروج عن المركز⊙

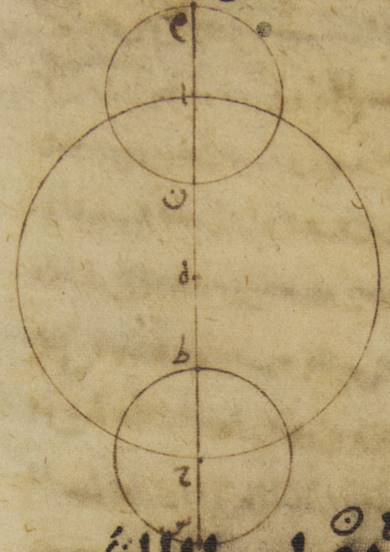
⟨V.5⟩ /H367/ ه: في محاذاة فلك التدوير الذي للقمر ه – خ: في معرفة ميل فلك التدوير وانحرافه؛ ه: في إبن الهيثم قال فحركة {...} فلك التدوير {...} بها البعد الأبعد إلى مسافة {...} المفروضة و{...} هذه الحركة حركة. 

أمّا من قبل ما يظهر في اتّصالات القمر بالشمس وأصناف تشكّله في التربيعات فهذا مبلغ ما يتهيّأ للإنسان أن يتوهّمه من أمر الأصول التي يجري الأمر عليها في الداوئر الموضوعة له. وأمّا من قبل ما يرى من مسيراته الجزئيّة في أبعاده في التسديسات والتثليثات وهي التي فيها يصير فلك التدوير على أخصّ ما يكون ممّا بين البعد الأبعد /T227/ وبين البعد الأقرب ه – خ: فلك التدوير فيما بين البعد الأبعد وبين البعد الأقرب.  من الفلك الخارج المركز، فإنّا نجد أنّه قد يلزم في القمر أمر ما خاصّ بمحاذاة ه – خ: عند ميل فلك التدوير. التدوير↑: خ وانحرافه وذلك أنّه لمّا كان قد يجب أن يوضع بالجملة نقطة واحدة بعينها من أفلاك التداوير إليها أبداً تكون لا محالة عودات ما يتحرّك فيها. وهذه النقطة هي التي نسمّيها «البعد الأبعد المستوي» وهي التي منها ثبتت ه – خ: بُنيت مبادئ أعداد الحركة في فلك التدوير. ومثال ذلك في هذه الصورة التي وضعناها ه – خ: المتقدّمة نقطة زاي وهذه النقطة ونظائرها يحدّها في الوضع الذي يكون فيه فلك التدوير ه – خ: فلك التدوير فيما بين البعد الأبعد وبين البعد الأقرب.  في أبعد الأبعاد أو أقربها من الأفلاك الخارجة المراكز الخطّ المستقيم الذي يخرج مارّاً بالمراكز جميعاً كخطّ ألف دال هاء جيم. Η.367.21: DEΓ; Toomer, p. 227: (DEG here) فأمّا في سائر الأصول كلّها على الإطلاق فلسنا نرى شيءاً /H368/ من الأمور التي تظهر مخالفاً للقول بأنّ ه – خ: لأنّ القطر الذي يمرّ بالبعد الأبعد الذي ذكرناه من فلك التدوير أعني خطّ زاي جيم حاء في سائر مسيرات أفلاك التداوير تحفظ أبداً الوضع الذي يكون فيه على الاستقامة مع الخطّ الذي يديره مركزه على استواء كخطّ هاء جيم هاهنا وأنّه يحاذي أبداً وهذا أمرٌ قد يسبق إلى الظنّ أنّه أمر لازم مركز الحركة المديرة وهو الذي عنده يتجاز أيضاً ه – خ: ويكون ميله أبداً إلى مركز الخطّ المدير الذي يكون عنده في  في الأزمان المتساوية زوايا متساوية للحركة المستوية. وأمّا ه – خ: ما يرى في القمر فإنّ ما يظهر يخالف ذلك وذاك أنّ في مسيرات فلك التدوير فيما بين نقطتي ألف وجيم لا يكون قطر زاي حاء محاذياً لمركز الحركة المديرة وهو نقطة هاء ه – خ: ميل قطر حاء زاي إلى نقطة ه التي هي مركز الاستدارة.  ولا حافظاً للوضع على الاستقامة مع خطّ هاء جيم. فإنّا نجده أبداً حافظاً لمحاذاة نقطة واحدة بعينها من النقط التي على قطر ألف جيم وليست تلك النقطة نقطة هاء، التى هي مركز فلك البروج، ولا نقطة دال، التي هي مركز الفلك الخارج المركز، بل أنّما يحاذي نقطة بعدها من نقطة هاء نحو البعد الأقرب من الفلك الخارج المركز بعد مساو لخطّ دال هاء وهو الخطّ الذي بين المركزين. ونحن مبيّنون أنّ ذلك كذلك بأن نصف أيضاً من أرصاد كثيرة تدلّ على ذلك رصدين هما أقواها في إظهار ما قصدنا له منه أعني رصدين كان فلك التدوير فيهما في أبعاده الوسطى ه – خ: عند البعدين الأوسطين من الفلك الخارج المركز.  /H369/ وكان القمر في البعد الأبعد أو في البعد الأقرب من فلك التدوير من قبل أنّ أكثر ما يكون من الفضل في هذه المحاذيات الموصوفة ه – خ: يعرض أن يكون في هذا الميل الموصوف.  أنّما يكون عند هذه المسيرات وما أشبهها⊙

فنقول إنّ أبرخس كتب أنّه رصد بالآلات برودس الشمس والقمر في سنة مائة وسبع وتسعين من وفاة إسكندر في الشهر من شهور المصريّين منها المسمّى فرموثي في اليوم الحادي عشر منه في ابتداء الساعة الثانية منه. فقال إنّ الشمس وجدت بالقياس في سبعة أجزاء ونصف وربع من الثور، وإنّ مركز القمر رأي حاصلاً ه – خ: نازلاً على أحد وعشرين جزءاً وثلثي جزء من الحوت وكان حاصله على الحقيقة أحداً وعشرين جزءاً وثلث وثمن جزء منه. فكان إذن في هذا الزمان المذكور بعد القمر على الحقيقة من حاصل الشمس على الحقيقة تلقا حركة الكلّ ثلاث مائة وثلاثة عشر جزءاً واثنتين وأربعين دقيقة بالتقريب، لكنّ لأنّ الرصد كان في ابتداء الساعة الثانية وقبل انتصاف النهار من اليوم الحادي عشر بنحو من خمس ساعات زمانيّة وهذه الساعات تكون برودس في ذلك الوقت نحواً من خمس ساعات وثلثي ساعة من ساعات الاستواء /T228/ يحصل الزمان الذي من التحصيلات التي لنا إلى وقت ذلك الرصد ستّ مائة وعشرين سنة من سني المصريّين ومائتين وتسعة عشر يوماً ومن ساعات الاستواء، أمّا على الإطلاق أيضاً فثمان عشرة ساعة وثلثا ساعة، وأمّا على الحقيقة فثمان عشرة ساعة فقط. وفي ذلك ↑وفي ذلك↑: بحسب ذلك الوقت نجد حاصل الشمس بحركتها المستوية على ستّة أجزاء وإحدى وأربعين دقيقة من الثور، وحاصلها على الحقيقة على سبعة أجزاء وخمس وأربعين دقيقة منه، ونجد حاصل القمر بحركته المستوية أمّا في الطول فعلى اثنتي وعشرين جزءاً وثلاث عشرة دقيقة من الحوت، /H370/ وأمّا من الاختلاف فعلى مائة وخمسة وثمانين جزءاً وثلاثين دقيقة من البعد الأبعد ه – خ: بمسيره الوسط من فلك التدوير حتّى يكون أيضاً المجتمع من بعد القمر بحركته المستوية من الشمس بحركتها ه – خ: كتهِ (بحركته i.e.,) الحقيقيّة ثلاث مائة وأربعة وعشر جزءاً وثمانياً وعشرين دقيقة⊙

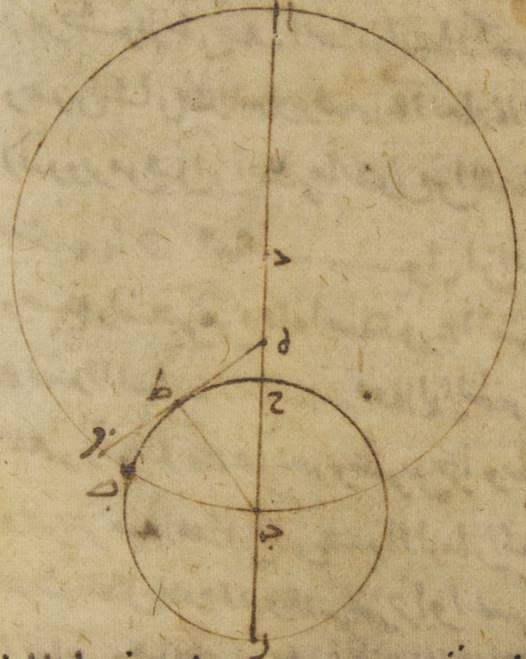
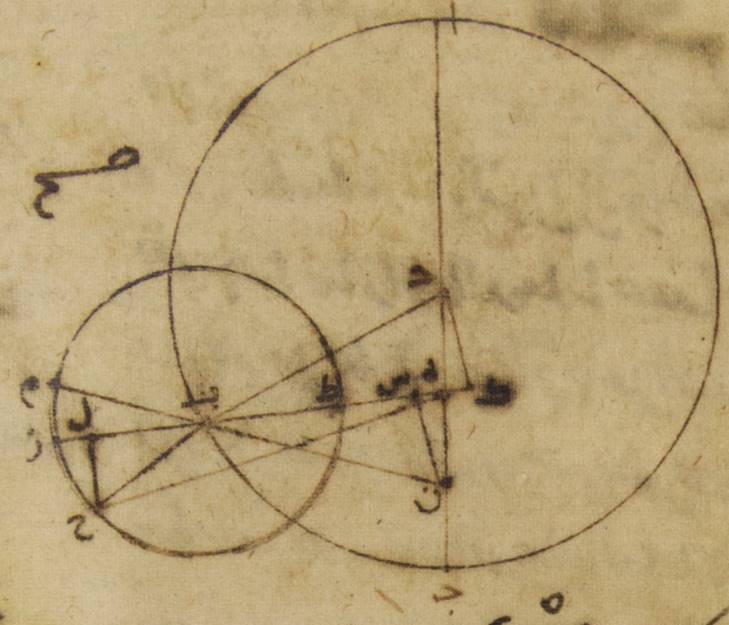
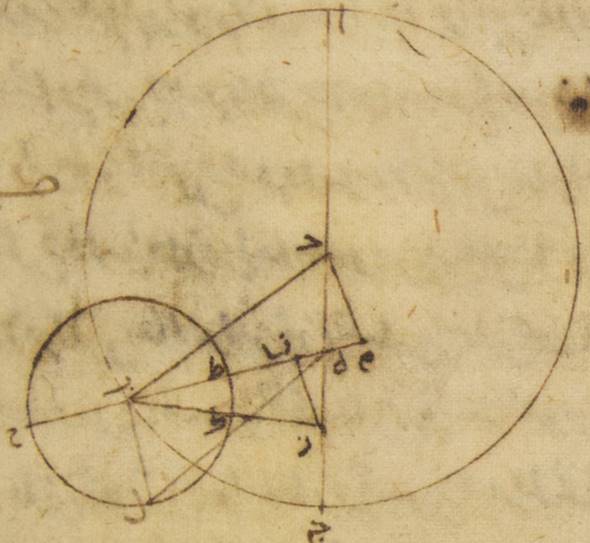
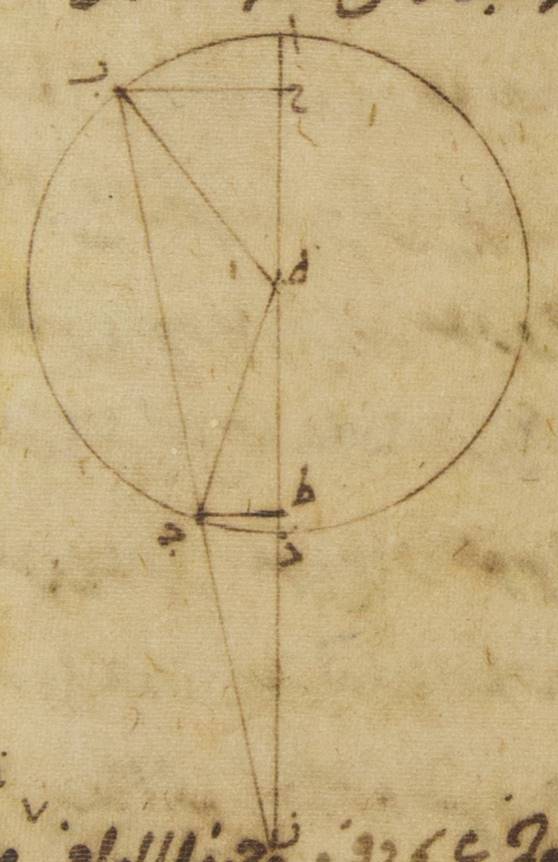
د: فإذ قد وطئت هذه الأشياء فليكن الفلك الخارج المركز للقمر ألف باء جيم حول مركز دال وقطر ألف دال جيم، وليكن في هذا القطر مركز فلك البروج نقطة هاء ولنرسم على مركز باء فلك تدوير القمر وليكن زاي حاء طاء {وليدر} فلك التدوير بالحركة الوسطى التي على توالي البروج من نقطة باء مثلاً إلى نقطة ألف وليدر القمر بحركته في فلك التدوير من نقطة زاي مثلاً إلى نقطة حاء ثمّ إلى نقطة طاء وليوصل خطّا دال باء، هاء طاء طاء↑: باء زاي. فمن قبل أنّ زمان الشهر الوسط يحيط بعودتين لفلك التدوير في الفلك الخارج المركز، وفي هذا الرصد الذي ذكرناه كان بعد القمر بحركته الوسطى من الشمس بحركتها الوسطى ثلاث مائة وخمسة عشر جزءاً واثنتين وثلاثين دقيقة. إن نحن أضعفنا هذه الأجزاء وأسقطنا منه ه – خ: منها أجزاء دائرة حصل لنا البعد كان في ذلك الوقت لفلك التدوير من البعد الأبعد /H371/ من الفلك الخارج المركز إلى توالي البروج مائتين وواحداً وسبعين جزءاً وأربع دقائق. ولذلك تكون زاوية ألف هاء باء أيضاً ما يبقى إلى ه: من أربع زوايا قائمة وهي ثمانية وثمانون جزءاً وستّ وخمسون دقيقة فلنخرج من نقطة دال إلى خطّ هاء باء عمود دال كاف، فلأنّ زاوية دال هاء باء أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فثمانية وثمانون جزءاً وستّ وخمسون دقيقة، وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فمائة وسبعة وسبعون جزءاً واثنتان وخمسون دقيقة. /T229/ تكون أيضاً أمّا القوس التي على خطّ دال كاف فمائة وسبعة وسبعون جزءاً واثنتان وخمسون دقيقة بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال هاء كاف القائم الزاوية ثلاث مائة وستّون جزءاً، وأمّا القوس التي على خطّ هاء كاف فالأجزاء الباقية إلى ↑إلى↑: خ من نصف دائرة وهي جزءان وثمان دقائق. فالخطّان إذن اللذان يوتّرانهما أمّا خطّ دال كاف منهما فتكون مائة وتسعة عشر جزءاً وتسعاً وخمسين دقيقة بالأجزاء التي بها قطر دال هاء مائة وعشرون جزءاً، وأمّا خطّ هاء كاف فجزءان وأربع عشرة دقيقة بهذه الأجزاء. فالأجزاء إذن التي بها أمّا خطّ دال هاء، وهو الذي بين المركزين فعشرة أجزاء وتسع عشرة دقيقة، وأمّا خطّ دال باء وهو الذي من مركز الفلك الخارج المركز فتسعة وأربعون جزءاً وإحدى وأربعون دقيقة تكون بها أيضاً أمّا خطّ دال كاف فعشرة أجزاء وتسع عشرة دقيقة أيضاً بالتقريب، وأمّا خطّ هاء كاف فعلى هذا المثال اثنتا عشرة دقيقة. ولأنّ المربّع الذي من خطّ دال كاف إذا نقص من المربّع الذي من خطّ دال باء كان الباقي المربّع الذي يكون من خطّ باء كاف يحصل لنا خطّ باء كاف أيضاً بهذه الأجزاء ثمانية وأربعين جزءاً وستّاً وثلاثين دقيقة، وخطّ هاء باء بأسره ثمانية وأربعون جزءاً وثمانياً وأربعون دقيقة⊙

/H372/ وأيضاً لأنّ البعد بين القمر بحركته المستوية وبين الشمس بحركتها الحقيقيّة كان ثلاث مائة وأربعة عشر جزءاً وثمانياً وعشرين دقيقة وبعده منها بحركته الحقيقيّة الأجزاء التي وُجدت بالرصد وهي ثلاث مائة وثلاثة عشر جزءاً واثنتان وأربعون دقيقة، لذلك قد يجب أن ينقص الفضل الذي من قبل اختلافه، وهو ستّ وأربعون دقيقة. ومسير القمر المستوي يرى على خطّ هاء باء. فلننزّل أنّ القمر من قبل أنّه كان من فلك التدوير عند بعده الأقرب على نقطة حاء وليوصل خطّا هاء حاء، باء حاء ولنخرج من نقطة باء إلى خطّ هاء حاء إذا أخرج على الاستقامة ه: عمود باء لام. فمن أجل أنّ زاوية باء هاء لام يشتمل على الفضل الذي من قبل اختلاف القمر يكون أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فعلى ذلك المثال ستّاً وأربعين دقيقة، وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فجزءاً واحداً واثنتين وثلاثين دقيقة. ولذلك تكون أمّا القوس التي على خطّ باء لام فجزءاً واحداً واثنتين وثلاثين دقيقة بالأجزاء التي بها الدائرة التي ترسم حول مثلّث هاء باء لام القائم الزاوية ثلاث مائة وستّون جزءاً. وأمّا الخطّ الذي يوتّرها وهو خطّ باء لام فجزءاً واحداً وستّاً وثلاثين دقيقة بالأجزاء التي بها خطّ باء هاء الموتّر مائة وعشرون جزءاً. فيجب أن يكون أيضاً بالأجزاء التي بها أمّا خطّ باء هاء فثمانية وأربعون جزءاً وثمان وأربعون دقيقة وأمّا خطّ باء حاء وهو الذي من مركز فلك التدوير فخمسة أجزاء وخمس عشرة دقيقة بها خطّ باء لام تسع وثلاثون دقيقة فالأجزاء إذن التي بها الخطّ الذي من مركز فلك التدوير وهو خطّ باء حاء مائة وعشرون جزءاً يكون بها أمّا خطّ باء لام أيضاً فأربعة عشر جزءاً واثنتان وخمسون دقيقة وأمّا القوس التي عليه فأربعة عشر جزءاً وأربع عشرة دقيقة بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء حاء لام القائم الزاوية ثلاث مائة وستّون جزءاً. /H373/ فلذلك تكون أمّا زاوية باء حاء لام فأربعة عشر جزءاً وأربع عشرة دقيقة بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً وأمّا زاوية هاء باء ↑هاء باء↑: صح حاء الباقية أمّا بهذه الأجزاء بعينها فاثنا عشر جزءاً واثنتان وأربعون دقيقة، وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فستّة أجزاء وإحدى وعشرون دقيقة. فهذا إذن مبلغ أجزاء قوس حاء طاء من فلك التدوير وهي القوس التي تشتمل على البعد بين القمر وبين البعد الأقرب الصحيح.

ولكنّ لأنّ بعد القمر من البعد الأبعد الوسط كان في زمان ذلك الرصد مائة وخمسة وثمانين جزءاً وثلاثين دقيقة، فمن البيّن أنّ البعد الأقرب الوسط يتقدّم القمر، أعني نقطة حاء. فلتكن نقطة ميم ولنجز ه – خ: وَنُخرُج خطّ باء ميم نون ولنخرج من نقطة هاء عمود هاء سين على هذا الخطّ. فلأنّ قوس طاء حاء قد تبيّن أنّها ستّة أجزاء وإحدى وعشرون دقيقة وقوس حاء ميم قد وضعت الأجزاء التي من البعد الأقرب ه – خ: بين البعد الأقرب الوسط وموضع القمر ، وهي خمسة أجزاء وثلاثون دقيقة، حتّى يكون مجموع قوس طاء ميم أحد عشر جزءاً وإحدى وخمسين دقيقة تكون زاوية هاء باء سين أيضاً أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فأحد عشر جزءاً وإحدى وخمسين دقيقة، وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فثلاثة وعشرون جزءاً واثنتان وأربعون دقيقة. /T230/ فلذلك تكون أمّا القوس التي على خطّ هاء سين فثلاثة وعشرون جزءاً واثنتان وأربعون دقيقة بالمقدار ه: بالأجزاء الذي تكون به الدائرة المحيطة بمثلّث باء هاء سين القائمة الزاوية ثلاث مائة وستّون جزءاً، ويكون وتر هاء سين أربعة وعشرين جزءاً وتسعاً وثلاثين دقيقة بالمقدار ه: بالأجزاء الذي به ↑به↑: بها يكون قطر باء هاء مائة وعشرون جزءاً. فبالمقدار الذي به خطّ باء هاء ثمانية وأربعون جزءاً وثمان وأربعون دقيقة فبه /H374/ يكون خطّ هاء سين عشرة جزءاً ودقيقتين. ولأنّ زاوية ألف هاء باء مائة وسبعة وسبعون جزءاً واثنتان وخمسون دقيقة بالأجزاء التي بها الزاويتان القائمتان ثلاث مائة وستّون جزءاً وزاوية هاء باء نون بتلك الأجزاء ثلاثة وعشرون جزءاً واثنتان وأربعون دقيقة تكون زاوية هاء نون باء الباقية بتلك الأجزاء مائة وأربعة وخمسون جزءاً وعشر دقائق. ولذلك تكون أمّا القوس التي على خطّ هاء سين فمائة وأربعة وخمسون جزءاً وعشر دقائق بالأجزاء التي بها الدائرة التي ترسم حول مثلّث هاء باء ↑باء↑: ن سين القائم الزاية ثلاث مائة وستّون جزءاً وأمّا خطّ هاء سين نفسه فمائة وستّة عشر جزءاً وثمانياً وخمسين دقيقة بالأ{جزاء} التي بها خطّ هاء نون الموتّر مائة وعشرون جزءاً فالأجزاء إذن التي بها أمّا خطّ هاء سين فعشرة أجزاء ودقيقتان، وأمّا خطّ دال هاء وهو الذي بين المركزين فعشرة أجزاء وتسع عشرة دقيقة يكون بها خطّ هاء نون أيضاً عشرة أجزاء وثمان عشرة دقيقة. فقد وجد ه - صح: فقد وُجدَ  إذن الانحراف الذي وقع لخطّ باء ميم، وهو الذي يمرّ بالبعد الأقرب الوسط حتّى حاذى نقطة نون خطّ هاء نون، ه – خ: نقطة نون يقطع خطّ هاء نون.  مساوياً بالتقريب لخطّ دال هاء⊙

وعلى هذا المثال كيما يتبيّن أنّ ذلك بعينه يلزم من الجانب الآخر المقابل لهذا من الفلك الخارج المركز ومن فلك التدوير أخذنا أيضاً من الأبعاد التي رصدها كما قلنا أبرخس بجزيرة رودس الرصد الذي كان منه بالقياس في تلك السنة بعينها وهي سنة مائة وسبع وتسعين من وفاة إسكندر في الشهر منها من شهور المصريّين المسمّى ناوي في اليوم السابع عشر منه على تسع ساعات وثلث. /H375/ فقال إنّه وجد الشمس بهذا الرصد في أحد عشر جزءاً إلّا عشر ه – صح: جُزءٍ من السرطان وإنّ القمر رأي حاصلاً على تسعة وعشرين جزءاً *غايته* غاينه من الأسد. وهذا أيضاً كان مبلغ حاصله على الحقيقة وذاك أنّ برودس إذ كان القمر في أواخر الأسد فليس يقع للقمر اختلاف منظر في الطول بعد نحو من ساعة من انتصاف النهار. ه – خ: إذا كان بعده من فلك نصف النهار قريباً من ساعة واحدة. 

فكان إذن في هذا الزمان الموصوف بعد القمر بحركته الحقيقيّة من الشمس بحركتها الحقيقيّة نحو توالي البروج ثمانية وأربعين جزءاً وستّ دقائق. لكنّ لأنّ الرصد كان بعد ثلاث ساعات وثلث زمانيّة من انتصاف النهار من اليوم السابع السانع عشر من شهر ناوي وهذه الساعات تكون منها في ذلك الوقت برودس من الساعات الاستوائيّة أربع ساعات بالتقريب يكون الزمان الذي من التحصيلات التي لنا إلى وقت ذلك الرصد ستّ مائة وعشرون سنة مصريّة ومائتين وستّة وثمانون يوماً ومن ساعات الاستواء أمّا على الإطلاق فأربعاً وأمّا على الحقيقة فثلاث ساعات وثلثا ساعة. وفي هذا الزمان على ذلك المثال نجد حاصل الشمس بمسيرها المستوي على اثني عشر جزءاً وخمس دقائق من السرطان، وبمسيرها الحقيقيّ على عشرة أجزاء وأربعين دقيقة منه، ونجد حاصل القمر بحركته المستوية أمّا في الطول فعلى سبعة وعشرين جزءاً وعشرين دقيقة من الأسد، فيكون أيضاً ما يجتمع من بعد القمر بحركته المستوية من الشمس على الحقيقة ستّة وأربعين جزءاً وأربعين دقيقة، وأمّا من الاختلاف فنجد بعده من البعد الأبعد الوسط من فلك التدوير ثلاث مائة وثلاثة وثلاثين جزءاً واثنتي عشرة دقيقة.

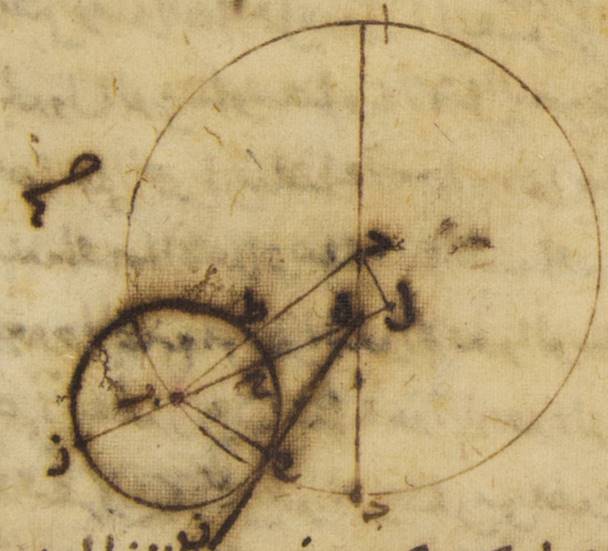
ه: وإذ قد وطئت هذه الأشياء فليكن أيضاً الفلك الخارج المركز للقمر ألف باء جيم ه: ب حول مركز دال /T231/ /H377/ وقطر ألف دال جيم وليكن على هذا القطر مركز فلك البروج نقطة هاء، ولنرسم على نقطة باء فلك تدوير القمر، وليكن ه: فلك زاي حاء طاء، وليوصل خطّا دال باء، هاء طاء باء زاي. فلأنّ البعد الوسط بين الشمس وبين القمر إذا أضعف كان مبلغه تسعين جزءاً وثلاثين دقيقة يكون لما قد تقدّم علمه زاوية ألف هاء باء أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فتسعون جزءاً وثلاثون دقيقة، وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فمائة وأحد وثمانون جزءاً. فإن نحن إذن أخرجنا خطّ باء هاء على الاستقامة وأخرجنا عليه من نقطة دال عمود دال كاف، كانت زاوية دال هاء كاف أيضاً الأجزاء الباقية إلى ↑إلى↑: خ من زاويتين قائمتين وهي مائة وتسعة وسبعون جزءاً. فلذلك تكون أمّا القوس التي على خطّ دال كاف فمائة وتسعة وسبعون جزءاً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال هاء كاف القائم الزاوية ثلاث مائة وستّون جزءاً، /H377/ وأمّا القوس التي على خطّ هاء كاف الباقية من نصف الدائرة فجزءاً واحداً. فالخطّان إذن اللذان يوتّرانهما أمّا خطّ دال كاف منهما فيكون مائة وتسعة عشر جزءاً و تسعاً وخمسين دقيقة بالأجزاء التي بها خطّ دال هاء الموتّر مائة وعشرون جزءاً، وأمّا خطّ هاء كاف فجزءاً واحداً وثلاث دقائق بهذه الأجزاء. فيكون إذاً الأجزاء التي بها أمّا خطّ دال هاء، وهو الخطّ الذي بين المركزين فعشرة أجزاء وتسع عشرة دقيقة، وأمّا خطّ دال باء، وهو الذي من مركز الفلك الخارج المركز، فتسعة وأربعون جزءاً وإحدى وأربعون دقيقة، بها خطّ دال كاف أيضاً عشرة أجزاء وتسع عشرة دقيقة بالتقريب، وخطّ هاء كاف على هذا المثال خمس دقائق. ولأنّ المربّع الذي من خطّ باء دال منقوصاً منه المربّع الذي من خطّ كاف دال يكون الباقي المربّع الذي من خطّ باء كاف فإنّه يصير لنا خطّ باء كاف بأسره ثمانية وأربعين جزءاً وستّاً وثلاثين دقيقة، وخطّ هاء باء الباقي بهذه الأجزاء ثمانية وأربعون جزءاً وإحدى وثلاثون دقيقة⊙

وأيضاً لأنّ البعد بين القمر بحركته المستوية وبين الشمس بحركتها الصحيحة كان ستّة وأربعين جزءاً وأربعين دقيقة، وبعده منها بحركته الصحيحة ثمانية وأربعون جزءاً وستّ دقائق، فيكون واجباً أن يزاد ↑يزاد↑: صح الفضل الذي من قبل الاختلاف وهو جزء وستّ وعشرون دقيقة⊙ فلننزّل أنّ القمر لأنّه كان عند البعد الأبعد من فلك التدوير على نقطة حاء وليوصل خطّا هاء حاء، باء حاء ولنخرج من نقطة باء على خطّ هاء حاء عمود باء لام.

/T232/ فلأنّ زاوية باء هاء لام أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فهي جزء واحد وستّ وعشرون دقيقة، وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فهي جزءان واثنتان وخمسون دقيقة، تكون أيضاً أمّا القوس التي على خطّ باء لام فجزءان واثنتان وخمسون دقيقة بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء هاء لام القائم الزاوية ثلاث مائة وستّون جزءاً، /H378/ وأمّا خطّ باء لام نفسه فجزءان وتسع وخمسون دقيقة بالأجزاء التي بها خطّ هاء باء الموتّر مائة وعشرون جزءاً. فالأجزاء إذن التي بها أمّا خطّ هاء باء فثمانية وأربعون جزءاً وإحدى وثلاثون دقيقة، وأمّا خطّ باء حاء، وهو الذي من مركز فلك التدوير، فخمسة أجزاء وخمس عشرة دقيقة، يكون بها خطّ باء لام أيضاً جزءاً واحداً واثنتا عشرة دقيقة. فلذلك تكون الأجزاء التي بها خطّ باء حاء الموتّر مائة وعشرون جزءاً بها أمّا خطّ باء لام فسبعة وعشرون جزءاً وأربع ه: إنّما يصحّ الحساب فيما بعد على أنّ هذه الدقائق أربع وثلاثون دقيقة ويتبيّن أيضاً ممّا قبل إذا أحرز الحساب فإنّ بطلميوس أنّما كتبه غير محرز لأنّه أسقط ذكر الثواني في قوله أنّ باء لام جزء واحد واثنتا عشرة دقيقة وهي اثنتا عشرة وقربت من ثلث ولم يُسقط استعمال هذه الثواني في نفس الحساب لكثرة ما يلحق عنها ولذلك صار باء لام بالمقدار الآخر سبعة وعشرين جزءاً وأربعاً وثلاثين دقيقة. وثلاثون دقيقة وأمّا القوس التي عليه فستّة وعشرون جزءاً وأربع وثلاثون دقيقة بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء حاء لام القائم الزاوية ثلاث مائة وستّون جزءاً، وأمّا زاوية باء حاء لام إذن فهي ستّة وعشرون جزءاً وأربع وثلاثون دقيقة بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً. وأمّا زاوية زاي باء حاء بأسرها فهي أمّا بهذه الأجزاء فتسعة وعشرون جزءاً وستّ وعشرون دقيقة، وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فأربعة عشر جزءاً وثلاث وأربعون دقيقة.

فهذا إذن مبلغ أجزاء قوس حاء زاي من فلك التدوير التي تشتمل على البعد بين القمر وبين البعد الأبعد الحقيقيّ. لكنّ لما كان بعده من البعد الأبعد الوسط كان في وقت الرصد ثلاث مائة وثلاثة وثلاثين جزءاً واثنتي عشرة دقيقة فإنّا إن أنزلنا أنّ البعد الأبعد الوسط على نقطة ميم ووصلنا خطّ ميم باء نون وأخرجنا عليه من نقطة هاء عمود هاء سين. كانت أمّا قوس حاء زا ↑ي↑ صح ميم بأسرها فالأجزاء الباقية من الدائرة وهي ستّة وعشرون جزءاً وثمان وأربعون دقيقة وأمّا قوس زاي ميم الباقية فاثنا عشر جزءاً وخمس دقائق. فلذلك تكون أمّا زاوية ميم باء زاي، أعني زاوية هاء باء سين، أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فاثنا عشر جزءاً وخمس دقائق، وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فأربعة وعشرون جزءاً وعشر دقائق. فأمّا القوس إذن التي على خطّ هاء سين فهي أربعة وعشرون جزءاً وعشر دقائق بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء هاء سين القائم الزاوية ثلاث مائة وستّون جزءاً، /H379/ وأمّا خطّ هاء سين نفسه فخمسة وعشرون جزءاً وسبع دقائق بالأجزاء التي بها خطّ باء هاء إذ كان موتّراً مائة وعشرون جزءاً. فالأجزاء إذن التي بها أمّا خطّ باء هاء فثمانية وأربعون جزءاً وإحدى وثلاثون دقيقة، وأمّا خطّ دال هاء وهو الذي بين المركزين فعشرة أجزاء وتسع عشرة دقيقة يكون بها خطّ هاء سين أيضاً عشرة أجزاء وثمان دقائق⊙ وأيضاً لأنّ زاوية ألف هاء باء قد وضعت مائة وأحد وثمانون جزءاً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً، وزاوية هاء باء نون قد تبيّن أنّها أربعة وعشرون جزءاً وعشر دقائق، فتبقى زاوية هاء نون باء الباقية بهذه الأجزاء مائة وستّة وخمسون جزءاً وخمسون دقيقة، يصير أيضاً أمّا القوس التي على خطّ هاء سين فمائة وستّة وخمسون جزءاً وخمسون دقيقة بالأجزاء التي بها الدائرة التي ترسم حول مثلّث هاء نون سين القائم الزاوية ثلاث مائة وستّون جزءاً. وأمّا خطّ هاء سين نفسه فمائة وسبعة عشر جزءاً وثلاثاً وثلاثين دقيقة بالأجزاء التي بها خطّ هاء نون إذ كان موتّراً مائة وعشرون جزءاً.

فالأجزاء إذن التي بها أمّا خطّ هاء سين فعشرة أجزاء وثمان دقائق، وأمّا خطّ دال هاء وهو الذي بين المركزين فعشرة أجزاء وتسع عشرة دقيقة يكون بها خطّ هاء نون، أيضاً عشرة أجزاء وعشرين دقيقة. فمن هذه الجهة أيضاً قد قرّر انحراف خطّ ميم باء، ↑ميم باء↑: صح؛ ه –خ: نون باء ميم وهو الذي يمرّ بالبعد الأبعد الوسط، حتّى حاذى نقطة ↑نقطة↑: صح نون وخطّ هاء نون أيضاً مساوياً بالتقريب لخطّ دال هاء، وهو الذي بين المركزين.

وقد نجد هذه النسبة بعينها تحصل على غاية ه – خ: التقريب من أرصاد أخر أكثر من هذه. فيتقرّر من ذلك الأمر الخاصّ في الأصل الذي يعمل عليه في القمر من محاذاة ه – خ: انحراف فلك التدوير /T233/ وهو أنّ مركز فلك التدوير يدور حول مركز فلك البروج، وهو نقطة هاء، وأمّا قطر فلك التدوير الذي يحدّ /H380/ بعده الأبعد الوسط فليس يكون دوره على الاستواء على محاذاة مركز هاء، على ما يكون عليه في سائر الكواكب، لكنّ محاذاته أبد أنّما هي لنقطة زاي ه – خ: انحرافه أبد أنّما يكو {...}  التي هي على بعد مساو في الجهة الأخرى لخطّ دال هاء وهو الذي بين المركزين⊙

⟨V.6⟩ و: كيف يستخرج بطريق الخطوط من قبل الحركات الدوريّة للقمر مسيره الصحيح⊙

وإذ قد بيّنت هذه الأشياء على هذه الصفة وكان يتّصل بذلك أن نضيف إليه الأخبار بالجهة التي يتيهّأ بها في مسيرات القمر الجزئيّة أيضاً إذا أخذنا تحصيلات الحركات الوسطى أن نجد من قبل عدد البعد ومن قبل العدد الذي للقمر في فلك تدويره الفضل ه – خ: الذي من قبل الاختلاف الذي يزاد أو ينقص من المسير الوسط في الطول، فإنّا نقوم ذلك بطريق الخطوط بنظائر ما وصفناه في ↑في↑: خ من المعاني والأشكال^φ. الأشكال↑: خ

و: ومثال ذلك أنّا إن وضعنا في آخر صورة وضعناها تلك الحركات الدوريّة بأعيانها التي للبعد والتي للاختلاف أمّا للبعد ه – صح: فالأجزاء التي اجتمعت من الأضعاف وهي تسعون جزءاً وثلاثون دقيقة، /H381/ وأمّا للاختلاف فأجزاء البعد من البعد الأبعد الوسط من فلك التدوير وهي ثلاث مائة وثلاثة وثلاثون جزءاً واثنتا عشرة دقيقة. وأخرجنا مكان عمود هاء سين عمود نون سين ومكان عمود باء لام عمود حاء لام. فبتلك الأشياء بأعيانها أيضاً من قبل أنّ الزاويتين اللتين عند مركز هاء تكونان معطاتين وموتّري ↑وموتّري↑: صح؛ ه – خ: ووترا دال هاء، هاء نون المتساويتين المتساويتين↑: يان (المتساويان i.e.,) معطيان، سيتبيّن أنّ كلّ واحد من خطّي دال كاف، نون سين عشرة أجزاء وتسع عشرة دقيقة بالتقريب /T234/ بالأجزاء التي بها أمّا خطّ دال باء الذي من مركز الفلك الخارج المركز فتسعة وأربعون جزءاً وإحدى وأربعون دقيقة، وأمّا خطّ باء حاء الذي من مركز الفلك التدوير فخمسة أجزاء وخمس عشرة دقيقة، وأنّ كلّ واحد من خطّي هاء كاف، هاء سين بهذه الأجزاء خمس دقائق. ولذلك يكون أمّا خطّ باء كاف بأسره كما بيّنّا فيما تقدّم بهذه الأجزاء فثمانية وأربعين جزءاً وستّاً وثلاثين دقيقة، وأمّا خطّ باء هاء على ذلك المثال فثمانية وأربعون جزءاً وإحدى وثلاثون دقيقة، وأمّا خطّ باء سين فالأجزاء الباقية وهي ثمانية وأربعون جزءاً وستّ وعشرون دقيقة. فيجب من ذلك إذ كان المربّعان أيضاً اللذان من خطّي باء سين، نون سين مجموعين يكون منهما المربّع الذي من خطّ باء نون أن يحصل لنا هذا الخطّ أيضاً في الطول تسعة وأربعون جزءاً وإحدى وثلاثون دقيقة بالأجزاء التي بها كان خطّ نون سين عشرة أجزاء وتسع عشرة دقيقة. فالأجزاء إذن التي بها خطّ باء نون إذ كان موتّراً مائة وعشرون جزءاً يكون بهذه الأجزاء، /H382/ أمّا خطّ نون سين فخمسة وعشرون جزءاً بالتقريب، فأمّا القوس التي عليه فأربعة وعشرون جزءاً وثلاث دقائق بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء نون سين القائم الزاوية ثلاث مائة وستّون جزءاً. فلذلك تكون زاوية نون باء سين أيضاً أعني زاوية زاي باء ميم أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً، فأربعة وعشرون جزءاً وثلاث دقائق، وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً، فاثنا عشر جزءاً ودقيقة واحدة بالتقريب. فهذا إذن مبلغ أجزاء قوس زاي ميم أيضاً من فلك التدوير.

لكنّ لأنّ نقطة حاء، التي هي موضع القمر، كان بعدها من نقطة ميم، وهي البعد الأبعد الوسط، ما يبقى لتمام دائرة واحدة وهي ستّة وعشرون جزءاً وثمان وأربعون دقيقة، فإنّ قوس حاء زاي الباقية تحصل لنا أربعة عشر جزءاً وسبعاً وأربعين دقيقة *(فلذلك زاوية حاء باء زاي الباقية تحصل لنا أربعة عشر جزءاً وسبعاً وأربعين)* *(دقيقة)*. فلذلك زاوية حاء باء زاي أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً، فهي أربعة عشر جزءاً وسبع وأربعون دقيقة، وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فهي تسعة وعشرون جزءاً وأربع وثلاثون دقيقة. فأمّا القوس إذن التي على خطّ حاء لام فهي تسعة وعشرون جزءاً وأربع وثلاثون دقيقة بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء حاء لام القائم الزاوية ثلاث مائة وستّون جزءاً. وأمّا القوس التي على خطّ لام باء فالأجزاء الباقية إلى نصف دائرة وهي مائة وخمسون جزءاً وستّ وعشرون دقيقة. فالخطّان إذن اللذان يوتّرانهما أمّا خطّ حاء لام منهما فيكون ثلاثين جزءاً وسبعاً وثلاثين دقيقة بالأجزاء التي بها خطّ باء حاء إذا كان موتّراً مائة وعشرون جزءاً، وأمّا خطّ لام باء فبهذه الأجزاء مائة وستّة عشر جزءاً ودقيقتان. فلذلك تكون الأجزاء التي بها أمّا خطّ باء حاء الذي من مركز فلك التدوير فخمسة أجزاء وخمس عشرة دقيقة، وأمّا خطّ باء هاء على ما تبيّن فثمانية وأربعون جزءاً وإحدى وثلاثون دقيقة بها أيضاً، أمّا خطّ حاء لام فجزء واحد وعشرون دقيقة، وأمّا خطّ لام باء على هذا المثال فخمسة أجزاء وخمس دقائق. /H383/ فخطّ هاء باء لام إذن بأسره ثلاثة وخمسون جزءاً وستّ وثلاثون دقيقة بالأجزاء التي بها كان خطّ لام حاء جزءاً واحداً وعشرين دقيقة. ولأنّ أيضاً مجموع المربّعين اللذين منهما يكون منه المربّع الذي من خطّ هاء حاء يحصل لنا خطّ هاء حاء في الطول أيضاً بهذه الأجزاء ثلاثة وخمسين جزءاً وسبعاً ↑وسبعاً↑: خ ط وثلاثين دقيقة فلذلك تكون الأجزاء ه – خ: بالأجزاء التي بها خطّ هاء حاء إذا كان موتّراً مائة وعشرون جزءاً بها أيضاً أمّا خطّ حاء لام فجزءان وتسع وخمسون دقيقة، وأمّا القوس التي عليه فجزءان واثنتان وخمسون دقيقة بالأجزاء التي بها الدائرة التي ترسم حول مثلّث هاء حاء لام القائم الزاوية ثلاث مائة وستّون جزءاً فزاوية حاء هاء لام إذن وهي زاوية الفضل الذي من قبل الاختلاف أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فهي جزءان واثنتان وخمسون دقيقة، وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فهي جزء واحد وستّ وعشرون دقيقة. وذلك ما كنّا قصدنا لتبيينه⊙

⟨V.7⟩ ز: في صفة عمل الجدول ه – خ: جَدولٍ لجملة اختلاف القمر

ولكي نرشد أيضاً لعمل جدول إلى تقويم ↑إلى التقويم↑: لتقويم  الزيادات والنقصانات الجزئيّة بأيسر السعي Toomer, p. 234: by setting a table. ، فإنّا أتممنا الجدول الذي كنّا وضعناه /T235/ في الأصل البسيط بصفوف يتهيّأ بها بسهولة الوقوف على الاختلاف المضعّف أيضاً على الصحّة بأن سلكنا في استخراج ذلك أيضاً بطريق ه – خ: طريق الخطوط. وذلك أنّا زدنا بعد الصفّين الأوّلين اللذين اثبتنا فيهما الأعداد صفّاً ثالثاً أثبتنا فيه /H384/ الزيادات والنقصانات التي تكون بعدد الاختلاف كيما نَنقُل العدد المجتمع من لدن البعد الأبعد الوسط، أعني *من* نقطة ميم، من المسيرات الوسطى إلى البعد الحقيقيّ، أعني *إلى* نقطة زاي. فكما ه – خ: كما بينّا في هذا البعد الذي وضعناه، وهو تسعون جزءاً وثلاثون دقيقة، أنّ قوس زاي ميم اثنا عشر جزءاً ودقيقة واحدة، ولأنّ بعد القمر كان من نقطة ميم وهي البعد الأبعد الوسط ثلاث مائة وثلاثة وثلاثون جزءاً واثنتا عشرة دقيقة وجدنا بعده من نقطة زاي، وهي البعد الحقيقيّ، يجتمع من الأجزاء ثلاث مائة وخمسة وأربعون جزءاً وثلاث عشرة دقيقة، وذلك بيّن، وهذه الأجزاء هي التي بحسبها يجب أن تؤخذ الزيادة ↑: خ أو النقصان اللذين من قبل فلك التدوير من الخطّة ه – خ: الحركة الوسطى *في الطول*. كذلك أيضاً، في سائر أعداد البعد، لمّا أخذنا ه – خ: وكذلك ينبغي أن تؤخذ الأعداد التي للبعد  بتلك الأجزاء بأعيانها التي قلنا فيما تقدّم أنّها معتدلة، كيلا نطيل الكلام، في شيء شيء المقادير التي تحدث عن الزيادة أو النقصان المفروض جعلناها ه – خ: ولكي لا نطيل الكلام في كلّ {...} في الجدول الثالث الزيادات وال{...}  بإزاء الأعداد التي هي لها كلّ واحد بإزاء عدده في الصفّ الثالث. وأمّا الصفوف الباقية، فإنّ الصفّ الرابع {منها} اثبتنا فيه الفضول التي تقدّم وضعها في الجدول الأوّل للاختلاف الذي من قبل فلك التدوير على أنّ أعظم الزيادة أو النقصان أيضاً ه – خ: أنّها يبلغ إلى خمسة أجزاء بالتقريب Toomer, p. 235: 5;1°. Heiberg’s ms. D also omis the “one” (α) minute. على نسبة الستّين الجزء إلى الخمسة الأجزاء والخمس العشرة الدقيقة. والصفّ الخامس منها، اثبتنا فيه زيادات الفضول التي تكون من الاختلاف الثاني على الاختلاف الأوّل على /H385/ أنّ أعظم ما تكون من الزيادة أو النقصان هاهنا أيضاً تجتمع سبعة أجزاء وثلثي جزء على نسبة الستّين الجزء إلى الثمانية الأجزاء حتّى يكون الصفّ الرابع للوضع الذي يكون لفلك التدوير على البعد الأبعد من الفلك الخارج المركز في الاتّصالات، ويكون الصفّ الخامس للزيادات المجتمعة من الاختلاف الذي يكون عند البعد الأقرب من الفلك الخارج المركز في التربيعات.

وكيما يستخرج في المسيرات أيضاً التي بين هذين الصفّين من وضع فلك التدوير الأجزاء التي تصيبها من الزيادات الموضوعة بإزائها على ذلك القياس، فإنّا رسمنا سطر سادساً فيه *من* الدقائق التي ينبغي أن يؤخذ في ه – خ: كلّ واحد من أعداد البعد من العدد الموضوع حيال الصفّ الأوّل *والثاني* فيزاد على الزيادة أو النقصان الذي ه – خ: هو من قبل الاختلاف الأوّل الموضوع في الصفّ الرابع. ونحن واضعون الجهة التي سلكناها في استخراج هذه أيضاً وهي هذه⊙

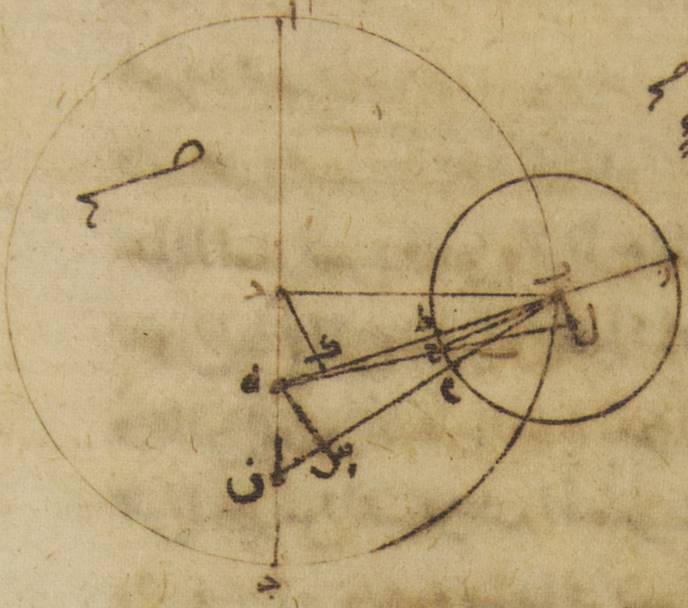
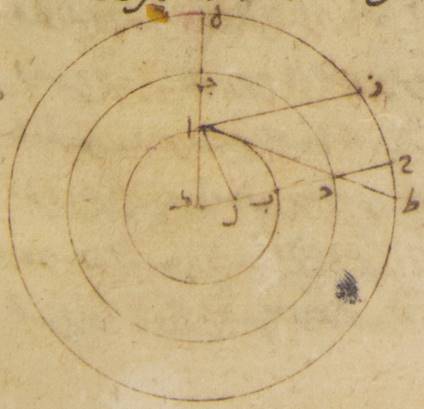
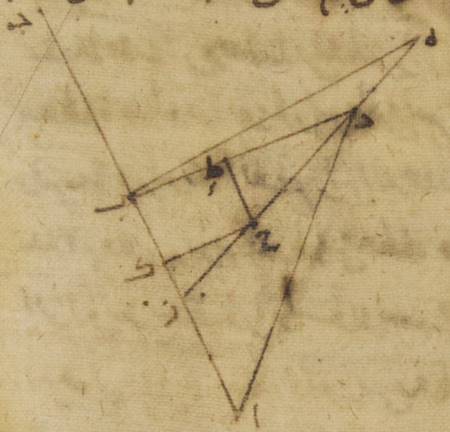
ز: ليكن أيضاً الفلك الخارج المركز للقمر ألف باء جيم حول مركز دال وقطر ألف دال جيم ولننزّل عليه مركز فلك البروج نقطة هاء، ونفصل قوس ألف باء ونرسم على نقطة باء فلك تدوير حاء طاء زاي H385.21: ZHΘK ونخرج خطّ هاء باء زاي، ولننزّل أنّ أجزاء البعد قد فرضت ستّين مثلاً ه – خ: جزءاً حتّى يكون أيضاً لتلك الأشياء بأعيانها التي تقدّم بيانها /H386/ زاوية ألف هاء باء ضعف أجزاء البعد المفروض وهي مائة وعشرون جزءاً. ولنخرج من نقطة دال عمود دال لام على خطّ باء هاء إذا أخرج على الاستقامة وليخرج ه – خ: أيضاً خطّ دال طاء باء. Η386.3: HBKΔ ولننزّل أنّ الخطّ الذي نخرج من مركز هاء إلى القمر، يماسّ فلك التدوير، حتّى يكون فضل الاختلاف على أكثر ما يكون عليه وليكن *خطّ* هاء ميم نون /T236/ وليوصل ↑وليوصل↑: صح خطّ باء ميم. فلأنّ زاوية ألف هاء باء أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فإنّها وضعت مائة وعشرين جزءاً، وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فهي مائتان وأربعون جزءاً تكون زاوية دال هاء لام أيضاً الأجزاء الباقية إلى ↑إلى↑: خ من زاويتين قائمتين وهي مائة وعشرون جزءاً.

فلذلك تكون أمّا القوس التي على خطّ دال لام فمائة وعشرون جزءاً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال هاء لام القائم الزاوية ثلاث مائة وستّون جزءاً، وأمّا القوس التي على خطّ هاء لام فالأجزاء الباقية إلى ↑إلى↑: خ من نصف الدائرة وهي ستّون جزءاً. فالخطّان إذن اللذان يوتّرانهما أمّا خطّ هاء لام منهما فستّون جزءاً بالأجزاء التي بها خطّ دال هاء إذ كان موتّراً مائة وعشرون جزءاً، وأمّا خطّ دال لام فبهذه الأجزاء مائة وثلاثة أجزاء وخمس وخمسون دقيقة. /H387/ فالأجزاء إذن التي بها أمّا خطّ دال هاء فعشرة أجزاء وتسع عشرة دقيقة، وأمّا خطّ دال باء على هذا المثال فتسعة وأربعون جزءاً وإحدى وأربعون دقيقة، يكون بها أمّا خطّ هاء لام فخمسة أجزاء وعشر دقائق بالتقريب، وأمّا خطّ دال لام على هذا المثال فثمانية أجزاء وستّ وخمسون دقيقة. ولأنّ المربّع الذي من خطّ باء دال إذا نقص منه المربّع الذي من خطّ دال لام يكون فيه المربّع الذي من خطّ باء لام، ¹يكون إذاً أمّا خطّ باء هاء لام بأسره فثمانية ه – خ: فهاء لام في الطول ثمانية وأربعون جزءاً وثلاث وخمسون دقيقة، وأمّا خطّ هاء باء الباقي فثلاثة وأربعون جزءاً وثلاث وأربعون دقيقة بالأجزاء التي بها خطّ باء ميم، Toomer, p. 237: MB الذي من مركز فلك التدوير، خمسة أجزاء وخمس عشرة دقيقة. فالأجزاء إذن التي بها خطّ هاء باء إذا كان موتّراً مائة وعشرون جزءاً يكون بها أمّا خطّ باء ميم فأربعة عشر جزءاً وخمس وعشرون دقيقة، وأمّا القوس التي عليه فثلاثة عشر جزءاً وثمان وأربعون دقيقة بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء هاء ميم القائم الزاوية ثلاث مائة وستّون جزءاً. فزاوية باء هاء ميم إذن أيضاً ه: وهي التي تحيط بأكثر ما يكون من فضل الاختلاف أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فإنّها ثلاثة عشر جزءاً وثمان وأربعون دقيقة، وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاثة مائة وستّون جزءاً فإنّها ستّة أجزاء وأربع وخمسون دقيقة. فقد خالف إذن في مسافة هذا البعد الفضل الذي من قبل الاختلاف الأجزاء التي تكون عند البعد الأبعد، وهي خمسة أجزاء ودقيقة واحدة بجزء واحد وثلاث وخمسين دقيقة. لكنّ الفضل بأسره الذي ينتهي عند البعد الأقرب /T237/ جزءان وتسع وثلاثون دقيقة، فالأجزاء إذن التي بها أعظم ما يكون من الاختلاف ستّون دقيقة يكون بها الفضل الذي يصيب الجزء الواحد والثلاث والخمسين الدقيقة اثنتين وأربعين دقيقة وثمانياً وثلاثين ثانية. /H388/ فنضع هذه بإزاء عدد البعد الذي هو مائة وعشرون جزءاً في الصفّ السادس.

وكذلك أيضاً في سائر الأقسام لما حسبنا أيضاً بهذا الباب بعينه الأجزاء التي تستخرج بهذا الطريق التي لزيادة ه – خ: من تفاضل ما بين  الاختلافين وضعنا بإزاء كلّ عدد ما يصيبه من الدقائق والثواني Toomer, p. 237: sixtieths من هذه الزيادة الموصوفة. ومن البيّن أنّ الستّين الدقيقة بأسرها توضع بإزاء العدد الذي هو ضعف أجزاء البعد إذا كان تسعين جزءاً أعني بإزاء مائة وثمانين جزءاً وذلك *في* البعد الأقرب من الفلك الخارج المركز.

ثمّ إنّا أضفنا أيضاً إلى ذلك صفّاً سابعاً أثبتنا فيه مجازات القمر في العرض الذي يكون عن جنبتي فلك البروج في الدائرة التي تمرّ بقطبيه أعني الأجزاء التي تنفرز من هذه الدائرة فيما بين فلك البروج وبين الدائرة المائلة التي على مركزه ه – خ: للقمر الذي مدارها على مركز فلك البروج  في كلّ واحد من مجازاته الجزئيّة في فلكه المائل. واستعملنا في ذلك أيضاً ذلك الطريق بعينه الذي استعملناه حين حسبنا القسيّ التي بين معدّل النهار وبين فلك البروج من الدائرة المرسومة على قطب ه – خ: قطبي معدّل النهار، إلّا إنّا هاهنا بيّنّا الأمر على أنّ القوس التي بين فلك البروج وبين النهاية الشماليّة أو الجنوبيّة من الفلك المائل من الدائرة *التي* من أعظم الدوائر التي ترسم مارّة بأقطاب هاتين الدائرتين جميعاً خمسة أجزاء. وذلك أنّا وجدنا نحن وأبرخس أكثر ما يكون من مجاز القمر عن جنبتي فلك البروج ه – خ: ما هذا مبلغه لما حسبنا ذلك بما يظهر من مجازاته في غاية بعده في الشمال وفي غاية بعده في الجنوب. /H389/ وجميع أيضاً ما يرى في أرصاده التي تكون بالقياس إلى الكواكب *والتي* تكون بالآلات تؤخذ موافقاً مطابقاً لأنّ هذا مبلغ أعظم ما يكون من مجازاته في العرض على ما سنقرّر أيضاً ممّا نحن مبيّنوه فيما بعد. وهكذا رسم الجدول الذي لجملة اختلاف القمر⊙

/H390-1/ ⟨V.8⟩ ح: ه: ب؛ ه – خ: تخطيط جدول لجميع اختلاف القمر

/T238/

/H392/ ⟨V.9⟩ ط: في الحساب الكلّي لحركة القمر

فمتى آثرنا ه – خ: أردنا أن نحسب بهذا الجدول الموضوع لنا حركة اختلاف القمر أخذنا حركات القمر الوسطى بإسكندريّة في الزمان الذي نقصد له /T239/ في الطول وفي البعد وفي الاختلاف وفي العرض على الجهة التي وصفناها. ثمّ أضعفنا أبداً عدد البعد أوّلاً وأسقطنا من ذلك إن كان لنا دورة ثمّ أدخلنا ما يبقى إلى ↑إلى↑: في خ جدول الاختلاف ه – خ: في سطور العدد ونظرنا ما حياله في الصفّ الثالث، فزدناه على الأجزاء الوسطى التي للاختلاف إن كان العدد ↑العدد↑: خ البعد الذي أضعف دون مائة وثمانين جزءاً، ونقصناه منها إن كان العدد الذي أضعف يجاوز المائة والثمانين. والعدد الحقيقيّ الذي يحصل للاختلاف ندخله في ذلك الجدول بعينه ه – خ: فالذي يُحصل من الاختلاف بعد الزيادة والنقصان فهو عدد الاختلاف الحقيقيّ، فندخل عدد الاختلاف الحقيقيّ في ذلك الجدول بعينه في سطور العدد.  وننظر ما بحياله من الزيادة أو النقصان في الصفّ الرابع وما حياله أيضاً من الفضل في الصفّ الخامس فنثبت كلّ واحد من هذين العددين على حدّته، ثمّ نعود بعد ذلك إلى العدد المضعّف ه – خ: الذي هو للبعد الوسط فندخله في تلك الصفوف بأعيانها فما كان حياله من الدقائق ه: ينبغي أن يعلم أنّ أصحّ الدقائق يقع على الثواني أيضاً وعلى ما بعدها. في الصفّ السادس أخذنا بذلك المقدار من الدقائق من الفضل الذي أثبتناه /H393/ فزدناه أبداً على الزيادة أو النقصان المأخوذ من الصفّ الرابع. فما اجتمع من ذلك إن كان العدد الحقيقيّ ه – خ: الذي للاختلاف دون مائة وثمانين جزءاً، نقصناه من الأجزاء الوسطى التي للطول والتي للعرض، وإن كان مجاوزاً للمائة والثمانين زدناه عليها. فما حصل من العدد أمّا عدد الطول فنلقيه من أجزاء حاصل القمر Toomer, p. 239: we add the one for the longitude to the position at epoch. فحيث انتهى العدد هناك نقول إنّ القمر بالحقيقة⊙ وأمّا عدد العرض الذي من النهاية الشماليّة فندخله في ذلك الجدول ه – خ: في سطور العدد فما كان بإزائه من الأجزاء في الصفّ السابع الذي للعرض فذلك هو بعد مركز القمر من فلك البروج في الدائرة ه – خ: التي من أعظم الدوائر التي ترسم مارّة بقطبيه. وإن وجد العدد الذي أدخل ه – خ: في الجدول في الخمسة العشر السطر الأوّل فبعده عنه في الشمال، وإن وجد في السطور التي دونها ه – خ: بعدها فبعده عنه في الجنوب. والصفّ الأوّل من الأعداد فيه مجازه من الشمال إلى الجنوب، والصفّ الثاني فيه مجازه من الجنوب إلى الشمال⊙

/H394/ ⟨V.10⟩ ي: في أنّه ليس يكون من قبل فلك القمر الخارج المركز في الاتّصالات فضل ه – خ: اختلاف يعتدّ به⊙

ولمّا كان قد يلزم أن يقع لبعض الناس الشكّ ويسبق إلى ظنّه أنّه قد يلحق في الاجتماعات أنفسها والاستقبالات و ↑: خ فيالكسوفات التي تكون فيها فضل ما له قدر من قبل فلك القمر الخارج المركز إذ كان ليس أبداً ولا واجباً ضرورة أن يتّفق ه – خ: يكون فيها مركز فلك التدوير على نفس نقطة أبعد البعد، بل قد يمكن أن يكون بعيداً منها بقوس لها قدر، وذلك أنّ الأوضاع التي تكون منها ه – خ: فيها في البعد الأبعد نفسه أنّما يكون في الاتّصالات التي تؤخذ بالوسط وأمّا الاجتماعات والاستقبالات الحقيقيّة فإنّما يؤخذ مع اختلاف كلّ واحد من النيّرين. فنحن ملتمسون الموافقة على أنّ هذا الفضل ليس يمكن أن يلحق منه خطاء له {قدر} في الأمور التي ترى عند الاتّصالات، وإن لم يعتدّ بالفضل الذي من قبل خروج هذا الفلك عن المركز فنحتسب به⊙

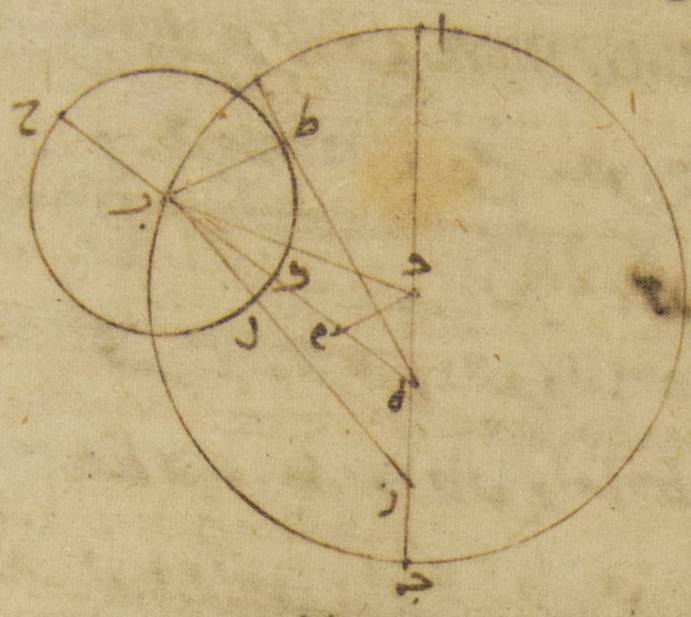
/T240/ ح: فليكن فلك القمر الخارج المركز ألف باء جيم حول مركز دال وقطر ألف دال جيم /H395/ وليؤخذ عليه أمّا مركز فلك البروج فنقطة هاء وأمّا النقطة المقابلة ه: المضارعة بنقطة دال، التي هي نقطة المحاذاة ه – خ: التي إليها {...} فلك {...}. ، فنقطة زاي. ولنفرز من لدن نقطة ألف وهي البعد الأبعد ه – خ: من الفلك الخارج المركز قوس ألف باء، ولنرسم حول نقطة باء فلك تدوير حاء طاء كاف لام، وليوصل خطّ باء دال وخطّ حاء باء كاف هاء وأيضاً خطّ باء لام زاي. فلأنّه قد يمكن أن يزيد مقدار الاختلاف على مقداره عند وضع فلك التدوير على نقطة ألف، وهي البعد الأبعد من وجهين أحدهما من قبل أنّه إذا صار أقرب إلى الأرض Toomer, p. 240: because the epicycle is removed towards the perigee. كانت الزاوية التي تجوزها عند نقطة هاء أعظم، والآخر من قبل أنّ القطر الذي يمرّ بالبعد الأبعد والبعد الأقرب الوسط ليس يكون محاذياً لمركز هاء، بل لنقطة زاي.

وأكثر ما يكون من الفضل أمّا من قبل السبب الأوّل، فإذا كان الفضل أيضاً الذي من قبل اختلاف القمر أكثر ما يكون، وأمّا من قبل السبب الثاني فإذا كان القمر في البعد الأبعد أو البعد الأقرب من فلك التدوير. فمن البيّن أنّه متى اتّفق أن يكون الفضل الذي من قبل السبب الأوّل على أكثر ما يكون، فإنّ الفضل حينئذ الذي من قبل السبب الثاني لا يكون محسوساً أصلاً، وذلك أنّ القمر إذا كان ه: السبب الأوّل هو إذا كان القمر في أوسط مسيره من فلك تدويره. والثاني هو إذا كان في أقرب قربه أو أبعد بعده من فلك التدوير. في هذه الحال يكون على الخطوط /H396/ المماسّة لفلك التدوير، فإنّ الزيادة أو النقصان الذي له مقدار صالح لا يقع منه فضل ه – خ: ويكون عند ذلك اختلاف الزيادة أو النقصان في زمان طويل اختلافاً واحداً لا يقع فيه فضل. . ويكون جائزاً أن يخالف الاتّصال الصحيح الاتّصال الذي يؤخذ وسطاً بالفضلين جميعاً اللذين من قبل اختلاف كلّ ه – خ: الذي من قبل الاختلاف والذي لكلّ.  واحد من النيّرين على أنّ أحدهما بالزيادة والآخر بالنقصان. ومتى اتّفق أن يكون الفضل من قبل السبب الثاني، وهو الذي للمحاذاة، ه – خ: للانحراف أكثر ما يكون كان حينئذ الفضل الذي من قبل السبب الأوّل غير محسوس أيضاً ه – خ: أصلاً لأنّ الفضل بأسره الذي من قبل الاختلاف متى كان القمر في البعد الأبعد أو في البعد الأقرب من فلك التدوير. فأمّا إلّا يكون أصلاً وأمّا إن يكون يسيراً جدّاً وأنّما يخالف الاتّصال الحقيقيّ الاتّصال الذي يؤخذ وسطاً بالفضل فقط الذي من قبل اختلاف الشمس.

/T241/ فلننزّل أنّ الشمس أكثر ما يوجبه من الزيادة الجزأين والثلاث والعشرين الدقيقة، وأنّ القمر أيضاً أكثر ما يوجبه أوّلاً من النقصان الخمسة الأجزاء والدقيقة الواحدة حتّى تكون زاوية ألف هاء باء تشتمل على ضعف جملة هذه السبعة الأجزاء والأربع والعشرين الدقيقة وهي أربعة عشر جزءاً وثمان وأربعون دقيقة. ولنخرج من نقطة هاء خطّ هاء طاء ممّاساً لفلك التدوير، وليوصل عمود باء طاء ولنخرج أيضاً من نقطة دال عمود دال ميم على خطّ باء هاء. فلأنّ زاوية ألف هاء باء أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فإنّها أربعة عشر جزءاً وثمان وأربعون دقيقة، وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فإنّها تسعة وعشرون جزءاً وستّ وثلاثون دقيقة، /H397/ يكون أيضاً أمّا القوس التي على خطّ دال ميم فتسعة وعشرون جزءاً وستّ وثلاثون دقيقة بالأجزاء التي بها الدائرة التي ترسم حول مثّلث دال هاء ميم القائم الزاوية ثلاث مائة وستّون جزءاً وأمّا القوس التي على خطّ هاء ميم فالأجزاء الباقية إلى نصف دائرة وهي مائة وخمسون جزءاً وأربع وعشرون دقيقة فالخطّان إذن اللذان يوتّرانهما أمّا خطّ دال ميم منهما فيكون ثلاثين جزءاً وتسعاً وثلاثين دقيقة بالأجزاء التي بها خطّ دال هاء إذا كان موتّراً مائة وعشرون جزءاً، وأمّا خطّ هاء ميم فيكون بهذه الأجزاء مائة وستّة عشر جزءاً ودقيقة واحدة. فلذلك يكون أيضاً بالأجزاء التي بها أمّا خطّ دال هاء، وهو الذي بين المركزين فعشرة أجزاء وتسع عشرة دقيقة، وأمّا خطّ باء دال، الذي من مركز الفلك الخارج المركز، فتسعة وأربعون جزءاً وإحدى وأربعون دقيقة بها أيضاً أمّا خطّ دال ميم فجزءان وثمان وثلاثون دقيقة، وأمّا خطّ هاء ميم على هذا المثال فتسعة أجزاء وتسع وخمسون دقيقة. ولأنّ المربّع الذي من خطّ باء دال إذا نقص منه المربّع الذي من خطّ دال ميم يكون المربّع الذي من خطّ باء ميم يصير أمّا خطّ باء ميم فتسعة وأربعون جزءاً وسبع وثلاثون دقيقة، وأمّا خطّ باء ميم هاء بأسره فتسعة وخمسون جزءاً وستّ وثلاثون دقيقة بالأجزاء التي بها خطّ باء طاء الذي من مركز فلك التدوير خمسة أجزاء وخمس عشرة دقيقة. فالأجزاء إذن التي بها خطّ هاء باء إذا كان موتّراً مائة وعشرون جزءاً يكون بها أمّا خطّ باء طاء فعشرة أجزاء وأربع وثلاثون دقيقة، وأمّا القوس التي عليه فعشرة أجزاء وستّ دقائق بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء هاء طاء القائم الزاوية ثلاث مائة وستّون جزءاً فزاوية باء هاء طاء إذاً، وهي زاوية أكثر ما يكون من فضل الاختلاف، ه: أكثر ما يكون الاختلاف الذي من قبل مركز الخارج المركز الاجتماعات والاستقبالات دقيقتان. أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فيكون عشرة أجزاء وستّ دقائق، وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فخمسة أجزاء وثلاث دقائق /H398/ مكان الخمسة الأجزاء والدقيقة الواحدة التي تكون إذا كان فلك التدوير على نقطة ألف، وهي البعد الأبعد. فالذي وقع إذن من الفضل الذي من قبل الاختلاف من قبل هذا السبب هو دقيقتان وليس ما يقع بذلك من الخطاء ه – خ: يقع من ذلك الخطاء ما  يلحق بجزء من ستّة عشر جزءاً من ساعة⊙

وأيضاً لننزّل أنّ القمر على نقطة لام وهي البعد الأقرب الوسط حتّى تكون زاوية ألف هاء باء تشتمل على قريب من ضعف اختلاف الشمس وحده وذلك بيّن ومبلغه أربعة أجزاء وستّ وأربعون دقيقة. وليوصل في مثل تلك الصورة خطّ هاء لام وليخرج إلى خطّ باء هاء عمودان أمّا من نقطة لام فعمود لام نون وأمّا من نقطة دال فعمود دال ميم وليخرج من نقطة زاي عمود زاي سين على خطّ هاء باء إذا أخرج على الاستقامة. فلما تقدّم بعينه من قبل أنّ الزاوية التي عند نقطة هاء أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فإنّها أربعة أجزاء وستّ وأربعون دقيقة وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فإنّها تسعة أجزاء واثنتان وثلاثون دقيقة يكون لنا كلّ واحدة من القوسين اللتين على خطّي دال ميم، زاي سين فتسعة أجزاء واثنتان وثلاثون دقيقة بالأجزاء التي بها الدائرتان اللتان ترسمان حول مثلّثي هاء دال ميم، هاء زا سين القائم الزاوية كلّ واحدة منهما ثلاث مائة وستّون جزءاً من قبل أنّ خطّ دال هاء مساو لخطّ هاء زاي The passage cannot be found in the English translation.  /H399/ وأمّا كلّ واحدة من القوسين اللتين على خطّي هاء ميم، هاء سين فالأجزاء الباقية إلى نصفي الدائرتين وهي مائة وسبعون جزءاً وثمان وعشرون دقيقة. فالخطوط إذن التي يوتّرها أمّا كلّ واحد من خطيّ دال ميم، زاي سين منهما فإنّه تسعة أجزاء وتسع وخمسون دقيقة بالأجزاء التي بها كلّ واحد من خطّي دال هاء، هاء زاي إذا كان موتّراً مائة وعشرون جزءاً وأمّا كلّ واحد من خطّي ميم هاء، هاء سين منها فبهذه الأجزاء بأعيانها مائة وتسعة عشر جزءاً وخمس وثلاثون دقيقة. /T242/ فلذلك تكون الأجزاء التي بها أمّا كلّ واحد من خطّي دال هاء، هاء زاي فعشرة أجزاء وتسع عشرة دقيقة، وأمّا خطّ دال باء، الذي من مركز الفلك الخارج المركز، فتسعة وأربعون جزءاً وإحدى وأربعون دقيقة بها، أمّا كلّ واحد من خطّي دال ميم، زاي سين على ذلك المثال فإحدى وخمسون دقيقة وأمّا كلّ واحد من خطّي ميم هاء، هاء سين فبهذه الأجزاء عشرة أجزاء وسبع عشرة دقيقة. ولأنّ المربّع الذي من خطّ باء دال إذا نقص منه المربّع الذي من خطّ دال ميم كان من ذلك المربّع الذي من خطّ باء ميم يكون خطّ باء ميم أيضاً في الطول بهذه الأجزاء قريباً من تسعة وأربعين جزءاً وإحدى وأربعين دقيقة. فلذلك يكون أمّا خطّ باء هاء فتسعة وخمسون جزءاً وثمان وخمسون دقيقة، وأمّا خطّ باء سين بأسره فسبعون جزءاً وخمس عشرة دقيقة (فلذلك يكون أمّا خطّ باء هاء فتسعة وخمسون جزءاً وثمان وخمسون دقيقة وأمّا خطّ باء سين بأسره فسبعون) (جزءاً وخمس عشرة دقيقة) The manuscript repeats this passage by homeoteleuton. بالأجزاء التي بها كان ه: خطّ زاي سين إحدى وخمسين دقيقة. ولذلك بعينه يكون خطّ باء زاي إذا كان موتّراً قريباً من هذه الأجزاء وهي سبعون جزءاً وخمس عشرة دقيقة. ونسبة خطّ باء زاي إلى كلّ واحد من خطّي زاي سين، باء سين كنسبة خطّ باء لام إلى كلّ واحد من خطّي لام نون، باء نون. فلذلك يكون بالأجزاء التي بها أمّا خطّ باء لام، الذي من مركز فلك التدوير، فخمسة أجزاء وخمس عشرة دقيقة. وأمّا خطّ باء هاء على ما تبيّن فتسعة وخمسون جزءاً وثمان وخمسون دقيقة ه – خ: يكون بهذه الأجزاء أمّا خطّ لام نون فأربع دقائق، وأمّا خطّ باء نون فبهذه الأجزاء قريباً من خمسة أجزاء وخمس عشرة دقيقة. /H400/ فخطّ نون هاء الباقي أربعة وخمسون جزءاً وثلاث وأربعون دقيقة بالأجزاء التي بها كان خطّ لام نون أربع دقائق. ولأنّ خطّ هاء لام إذا كان موتّراً يكون من قبل ما تقدّم وضعه ليس بينه وبين أن يكون مبلغه بهذه الأجزاء بأعيانها أربعة وخمسين جزءاً وثلاثاً وأربعين دقيقة فضل، يحصل من ذلك أنّ الأجزاء التي بها خطّ هاء لام إذا كان موتّراً ه – خ: ولأجل ما ذكرنا أنّ وتر لام هاء غير مخالف للأربعة والخمسين الجزء والثلاث والأربعين الدقيقة التي هي خطّ نون هاء إلّا بما لا قدر له يصير إذاً إذا كان قطر لام هاء. مائة وعشرون جزءاً، يكون بها أمّا خطّ لام نون فثمان دقائق بالتقريب، وأمّا القوس التي عليه فثمان دقائق أيضاً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث هاء لام نون القائم الزاوية ثلاث مائة وستّون جزءاً. فزاوية باء هاء لام إذاً، وهي التي بها يخالف القمر من قبل محاذاته لنقطة زاي، أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فإنّها ثمان دقائق، وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فإنّها أربع دقائق. /T243/ فالذي خالف به في هذا الموضع أيضاً الفضل الذي من قبل اختلاف القمر أربع دقائق، ه: أكثر ما يكون الاختلاف الذي من قبل انحراف فلك التدوير في الاجتماعات والاستقبالات أربع دقائق. وليس يوقع ذلك فيما يظهر في الاتّصالات خطاء يعتدّ به إذ كان ليس يلحق منه من الخطاء ولا ثمن ساعة واحدة بالتقريب وكان هذا المقدار غير مستنكر أن يلحق كثيراً من قبل الأرصاد أنفسها.

وإنّما أثبتنا ما اثبتناه من ذلك ليعلم أنّ هذه الفضول أنفسها وإن كانت يسيرة جدّاً فليس يتعذّر حسابها عند النظر في الاتّصالات أيضاً، لكنّه ليس يقع لنا ه: بها خطاء محسوس في البراهين التي أقمناها بكسوفات القمر {الموصوفة} من قبل تركنا استعمال الأصل الذي كمل {بآخره} بفلك خارج المركز⊙

/H401/ ⟨V.11⟩ يا: في اختلاف منظر القمر

أمّا ما يستعمل في إدراك مسيرات القمر الصحيحة فيكاد أن يكون قد آتينا عليه، ولما كان قد يعرض في القمر، ألّا يكون مسيره عند الحسّ فضلاً عن غيره الذي يرى هو مسيره الصحيح بعينه من قبل أنّه ليس قدر الأرض كما قلنا قدر النقطة بالقياس إلى بعد كرته. فقد يجب ضرورة ويتّصل بذلك بسبب سائر ما يظهر ولا سيّما ما يرى في كسوفات الشمس أن نتكلّم في اختلافاته التي من قبلها قد يمكن بمسيراته الصحيحة التي تتوهّم بالقياس إلى مركز الأرض وفلك البروج أن نقوم أيضاً مسيراته التي تحصل من نظر الناظرين أعني من بسيط ما على الأرض ويمكن ضدّ ذلك، أعني استخراج مسيراته الصحيحة من مسيراته التي ترى. ولمّا كان قد يلزم في هذا النظر أنّه ليس يمكن استخراج مقادير اختلافات المنظر الجزئيّة دون أن يكون قدر البعد مفروضاً، وأنّه ليس يمكن استخراج قدر البعد نفسه دون أن يفرض اختلاف ما للنظر. ه – خ: للمنظر فأمّا ما لم يكن له اختلاف منظر محسوس، /H402/ أعني ما كان قياس الأرض إليه قياس المركز فمن البيّن أنّه ليس يمكن، ولا أن يوقف على قدر بعده منها. وأمّا ما كان له اختلاف منظر، مثل القمر، فالذي ه – خ: والذي يتهيّأ فيه هذا الأمر وحده وهو أن يوقف على قدر بعده بإن يعرض أوّلاً اختلاف ما لمنظره من قبل أنّ الرصد لاختلاف ما لمنظره قد يتهيّأ أن يدرك على حياله، وأمّا مقدار بعده فليس يمكن إدراكه على حاله.

فأمّا أبرخس، فإنّه جعل فحصه عن ذلك من قبل الشمس خاصّة. وذلك أنّه لمّا كان قد يلزم من أعراض ما أخر لحقت في الشمس والقمر سنتكلّم فيها فيما بعد أن يكون البعد في واحد [*واحد*] من النيّرين إذا فرض كان البعد في الآخر معلوماً. فإنّه يروم بالتشديد نحو معرفة بعد الشمس أن نبيّن بعد القمر بهذا الوجه فوضع أوّلاً أنّ الشمس يكون لها اختلاف منظر محسوس قليل جدّاً فقط كيما يستخرج بذلك بعدها ثمّ وضع بعد ذلك /T244/ ما وضعه من كسوف الشمس مرّة أنّ الشمس ليس لها اختلاف منظر محسوس أصلاً، ومرّة أنّ لها اختلاف منظر وأنّه أيضاً له مقدار صالح، فلذلك وجد كلامه أيضاً في أقدار بعد القمر مختلفاً بحسب كلّ واحد من الأصلين اللذين وضعهما إذ كان ممثّلاً بالجملة في أمر الشمس هل لها اختلاف منظر أصلاً فضلاً عن مقدار اختلاف منظر إن كان لها⊙

/H403/ ⟨V.12⟩ يب: في صنعة آلة يُستخرج بها اختلاف المنظر

وأمّا نحن فكيلا نستعمل في هذا العلم شيءاً غير بيّن اتّخذنا آلة يمكّنا بها أن نرصد بغاية ما يمكن من الاستقصاء كم مبلغ اختلاف منظر الشمس ه – صح: القمر وكم مقدار بعده إذا كان له اختلاف منظر من النقطة التي على سمت الرأس في الدائرة من أعظم الدوائر التي ترسم مارّة بقطبي الأفق وبه.

فعملنا مسطرتين ذواتي أربع جوانب يكون طول كلّ واحدة منهما ليس بأقلّ من أربع أذرع لنتهيّأ فيها القسمة بأجزاء أكثر، ه – خ: كثيرة وجعلنا لهما ثخناً صالحاً كيلا يلتويان بسبب طولهما بل يكون انبساطهما وامتدادهما على غاية ما يمكن من الحقيقة ويكون كلّ جانب من جوانبهما في غاية الاستقامة. ثمّ حزّرنا ه – خ: خطّطنا في كلّ واحدة منهما في الوسط من أعرض جوانبهما خطّاً مستقيماً وركّبنا في إحدى المسطرتين في طرفيهما جميعاً شطبتين منتصبتين مربّعتين على الخطّ الوسط متساويتين متوازيتين في كلّ واحدة منهما في وسطهما على الحقيقة ثقب، ه – خ: وصيّرنا وسط كلّ واحد من الثقب على حقيقة الخطّ الذي {...} وجعلنا أحد الثقبين وهو الذي كنّا نجعله فيما بعد ممّا يلي البصر دقيقاً، والثقب الآخر وهو الذي كنّا {نجعله} مّما يلي القمر أوسع منه بمقدار ما إذا وضعت إحدى العينين /H404/ على الشطبة التي منها الثقب الأضيق {تهيّأ} أن يرى القمر كلّه بالثقب المحاذي لهذا الثقب الذي في الشطبة الأخرى. ثمّ ثقبنا كلّ واحدة من المسطرتين بالسواء على الخطّين اللذين في الوسط في أحد الطرفين عند الشطبة التي فيها الثقب الأوسع وداخلنا فيهما محوراً يرتبط به جنبا المسطرتين اللتين فيهما الخطّان حتّى يكون كالمركز لهما ويتهيّأ أن يدور فيه المسطرة ذات الشطبتين إلى جميع الجوانب من غير أن يضطرب أو يلتوي. وركزنا إحدى المسطرتين وهي التي ليس فيها شطاباً في قاعدة ثمّ تعلّمنا على الخطّ الذي في وسط كلّ واحدة منهما نقطة ممّا يلي الطرف الذي عند القاعدة بعدها من مركز المحور فيهما جميعاً سواء وأكثر ما يمكن وقسمنا الخطّ الذي ينفرز في المسطرة ذات القاعدة بستّين جزءاً وقسمنا أيضاً هذه الأجزاء بما أمكّنا من الأقسام. ونصبنا أيضاً في هذه المسطرة من خلف عند طرفيها شطبتين كلّ جانبين من جوانبهما هما في جهة واحدة /T245/ يكونان بالقياس إلى خطّ بعينه مستقيم على الاستقامة وبعدهما من جميع الجوانب من خطّ بعينه في الوسط بالسواء كيما نقدر بتعليق شاقول يمرّ بهما أن ينصب تلك المسطرة على بسيط الأفق على زوايا قائمة من غير ميل. وكنّا نتقدّم فنخطّ خطّ نصف النهار /H405/ في بسيط مواز لبسيط ه: لبسيط الأفق في موضع مضيء. ه – خ: مكشوف للشمس ثمّ ننصب هذه الآلة عليه على زوايا قائمة ونجعل جانبي /T246/ المسطرتين اللذين اتّحدا بالمحور إلى جهة الجنوب حتّى يكون هذان الجانبان منهما موازيين ه: في ترجمة الحجّاج السطحان المتطابقان موازيين لخطّ نصف النهار الذي وضعناه، وكنّا ننصب المسطرة ذات القاعدة على زوايا قائمة من غير ميل ولا التواء ونحكم أيضاً نصبها ونستوثق منها، وأمّا المسطرة الأخرى فإنّا كنّا نجعل ممرّها بالمحور سلساً ليتهّيأ أن يدور حوله في بسيط دائرة نصف النهار. واتّخذنا أيضاً مسطرة أخرى صغيرة دقيقة مستقيمة فركّبناها بمسمار لطيف لتكون أيضاً سلسلة المدار في الطرف الذي تلي القاعدة من الخطّ المجزّأ، وجعلنا طولها يلحق بأقصى ما يبلغه طرف الخطّ من المسطرة الأخرى إذا فارقت الأولى الذي بعده مثل بعد ذلك الطرف المركوز فيه المسطرة كيما تكون إذا حرّكنا المسطرة الرقيقة ه: الدقيقة مع هذا الطرف أوقفتنا على البعد الذي يكون بين هذين الطرفين على الاستقامة.

فكنّا نعتمد أن نجعل أرصاد القمر التي نستعملها بهذا الوجه في المسيرات التي تكون له على دائرة نصف النهار نفسها وفي نقطتي الانقلابين من دائرة البروج، وذلك أنّه إذا كانت هذه حالهُ كانت الدوائر العظمى التي ترسم مارّة بقطبي الأفق وبمركز القمر تكاد أن تكون الدوائر بأعيانها التي ترسم مارّة بقطبي فلك البروج وبه وهي التي بحسبها تؤخذ مجازات القمر في العرض. /H406/ ونستخرج من قبل ذلك بعده الصحيح أيضاً من النقطة التي على سمت الرأس من قرب وبأهون سعي. فكنّا ندير المسطرة ذات الشطبتين إلى الجانبين نحو القمر في نفس مسيراته على دائرة نصف النهار إلى أن يرى بالثقبتين جميعاً مركزه في وسط الثقب الأوسع ونتعلّم ه – خ: {تعلّم} على المسطرة الرقيقة ه: الدقيقة البعد الذي حصل عند ذلك بين طرفي الخطّين اللذين في المسطرتين، ثمّ نضعه على الخطّ الذي على المسطرة المنتصبة المقسوم بستّين. فنجد بذلك أجزاء البعد الذي تقدّم ذكره كم هي بالأجزاء التي بها الخطّ الذي من مركز الدائرة التي نرسمها المدار في بسيط دائرة نصف النهار ستّون جزءاً، وذلك بيّن. فنأخذ القوس التي توتّرها الخطّ الذي ذلك مقداره فكانت تكون عندنا قوس بعد مركز القمر الذي يرى في ذلك الوقت من نقطة سمت الرأس في الدائرة العظمى التي ترسم مارّة بقطبي الأفق وبمركز القمر وهذه أيضاً كانت {...} في ذلك الوقت دائرة نصف النهار التي ترسم مارّة بقطبي معدّل النهار وبقطبي فلك البروج بعينها.

وكنّا إذا طلبنا الوقوف الحقيقة على أكثر ما يكون من مجاز القمر في العرض، /H407/ اعتمدنا أن نقيسه إذا كان /T247/ في نقطة الانقلاب الصيفيّ خاصّة وكان أيضاً في النهاية الشماليّة نفسها من دائرته المائلة. وذلك أنّه في هاتين النقطتين أنّما ننفرز في المدّة الطويلة مجازاً واحداً بعينه في العرض عند الحسّ ه – خ: يكون مجازه في العرض في الحسّ طويل المكث بط{...} ، وأنّه إذا كان حينئذ عند النقطة نفسها التي على سمت الرأس في الدائرة الموازية التي تمرّ بإسكندريّة، وهي التي فيها وقعت أرصادنا، كان موضعه الذي يرى وموضعه الحقيقيّ يكاد أن يكون واحداً بعينه. فوجدنا القمر في مثل هذه المسيرات بعد مركزه أبداً من النقطة التي على سمت الرأس جزئين وثمان دقائق بالتقريب حتّى أنّه يكون قد تبيّن بهذا الوجه من الفحص أيضاً أنّ أكثر مجازه في العرض عن جنبتي فلك البروج خمسة أجزاء. وهذه تكاد أن تكون الأجزاء التي بها نزيد الأجزاء التي تبيّن أنّها بين النقطة التي على سمت الرأس وبين معدّل النهار بإسكندريّة وهي ثلاثون جزءاً وثمان وخمسون دقيقة، إذا نقص منها أجزاء البعد الذي يرى، وهي جزءان وثمان دقائق، على الأجزاء التي تبيّن أنّها بين معدّل النهار وبين الانقلاب الصيفيّ وهي ثلاثة وعشرون جزءاً وإحدى وخمسون دقيقة. Toomer, p. 247: if we subtract from this the 2⅛ (which is the apparent distance [of the centre of the moon from the zenith]), the result [28;50 ½]is about 5° greater than the distance from the equator to the summer solstice, which was shown to be 23;51°.

وكنّا إذا طلبنا الوقوف على اختلافات المنظر رصدنا القمر على هذا الوجه أيضاً /H408/ إلّا أنّا كنّا نعتمد أن نرصده إذا اتّفق أن يكون في الانقلاب الشتويّ للأسباب التي تقدّم ذكرها، ولأنّ بعده حينئذ في مسيره إذا كان بالسواء في دائرة نصف النهار من النقطة التي على سمت الرأس إذا كان أكثر ما يكون فإنّ اختلاف منظره يكون أكثر وأبين. فنحن واصفون أيضاً من أرصاد كثيرة وقعت لنا لاختلاف ↑ات؛ ه: لاختلافات المنظر في مثل هذه المسيرات رصداً واحداً يوقف به على طريق حسابه ونبيّن به مع ذلك سائر ما يتّبعه ويتّصل به⊙

⟨V.13⟩ يج: في تبيين أبعاد القمر

فنقول إنّا رصدنا في سنة عشرين من سني أذريانوس في الشهر من شهور المصريّين المسمّى أثور منها في اليوم الثالث عشر منه بعد انتصاف النهار منه بخمس ساعات ونصف وثلث من ساعات الاستواء، وقد كادت الشمس أن تغرب والقمر، *(وهو)* على دائرة نصف النهار. فرأينا مركزه بهذه الآلة بعده من النقطة التي على سمت الرأس خمسين جزءاً ونصفاً وثلاثاً وجزءاً من إثني عشر من جزء. وذلك أنّ البعد على المسطرة الدقيقة كان *على* أحد وخمسين جزءاً ونصف وجزء من اثني عشر من جزء بالأجزاء التي بها قسم الخطّ الذي من مركز دائرة الدور بستّين جزءاً، والخطّ الذي هذا مقداره يوتّر قوساً مبلغها خمسون جزءاً ونصف وثلث وجزء من إثني عشر من جزء بالأجزاء التي بها الدائرة ثلاث مائة وستّون جزءاً. لكنّ الزمان الذي من التحصيلات في السنة الأولى من سني بختنصر إلى وقت هذا الرصد الموصوف ثمان مائة سنة واثنتان وثمانون سنة من سني المصريّين واثنان وسبعون يوماً ومن ساعات الاستواء أمّا على الإطلاق /H409/ فخمس ساعات ونصف وثلث، وأمّا على الحقيقة فخمس ساعات وثلث ساعة. وفي هذا الزمان نجد الشمس يكون حاصلها أمّا على التوسّط فعلى سبعة أجزاء وإحدى وثلاثين دقيقة من الميزان، وأمّا على الحقيقة فعلى خمسة أجزاء وثمان وعشرين دقيقة منه، ونجد حاصل القمر على التوسّط على خمسة وعشرين جزءاً وأربع وأربعين دقيقة من الرامي ونجد البعد ثمانية وسبعين جزءاً وثلاث عشرة دقيقة، ونجد بعده من البعد الأبعد الوسط من فلك التدوير مائتين جزء واثنتين وستّين جزءاً وعشرين دقيقة، وبعده من النهاية الشماليّة في العرض ثلاث مائة وأربعة وخمسين جزءاً وأربعين دقيقة. /T248/ وأضيف إلى ذلك من قبل ما ذكرنا الفضل أيضاً الذي من قبل الاختلاف بعد أن قوم من كلّ وجه من جدوله وهو سبعة أجزاء وستّ وعشرون دقيقة. فيكون موضع القمر على الحقيقة أيضاً في تلك الساعة محصولة أمّا في الطول على ثلاثة أجزاء وعشر دقائق من الجدي، وأمّا في العرض أمّا في دائرته المائلة فعلى جزئين وستّ دقائق من النهاية الشماليّة، وأمّا في الدائرة التي تمرّ بقطبي فلك البروج، وهي الدائرة التي قلنا أنّها تكاد أن تكون في ذلك الوقت دائرة نصف النهار، فعلى أربعة أجزاء وتسع وخمسين دقيقة من فلك البروج في الشمال. لكنّ بعد الثلاثة الأجزاء والعشر الدقائق من الجدي من معدّل النهار في الجنوب في تلك الدائرة بعينها ثلاثة وعشرون جزءاً وتسع وأربعون دقيقة وبعد دائرة معدّل النهار من النقطة التي على سمت الرأس بإسكندريّة في الجنوب على ذلك المثال ثلاثون جزءاً وثمان وخمسون دقيقة. فمركز القمر إذن كان بعده على الحقيقة من النقطة التي على سمت الرأس تسعة وأربعون جزءاً وثمان وأربعون دقيقة وكان يرى بعيداً منها خمسين جزءاً وخمساً وخمسين دقيقة. فقد خالف إذن منظر القمر /H410/ في البعد الذي بحسب هذا المسير الموصوف بجزء واحد وسبع دقائق في الدائرة من أعظم الداوئر التي ترسم مارّة به وبقطبي الأفق إذ كان بعده على الحقيقة من النقطة التي على سمت الرأس تسعة وأربعون جزءاً وثمان وأربعون دقيقة⊙

ي: وإذ فرض ذلك فلنرسم في سطح أعظم الدوائر التي تمرّ بقطبي الأفق وبالقمر حول مركز واحد بعينه، أمّا أعظم دوائر الأرض فدائرة ألف باء، وأمّا الدائرة التي تمرّ بمركز القمر في هذا الرصد فدائرة جيم دال، وأمّا الدائرة التي منزلة الأرض بالقياس إليها منزلة النقطة فدائرة هاء زاي حاء طاء. /T249/ وليكن مركزها جميعاً مشتركاً نقطة كاف والخطّ المستقيم الذي يمرّ بالقطبين اللتين على سمت ه – خ: بالمركز وبسمت الرأس خطّ كاف ألف جيم هاء. ولننزّل أنّ القمر على نقطة دال وبعده على الحقيقة من النقطة التي على سمت الرأس، /H411/ وهي نقطة جيم، الأجزاء التي ذكرنا وهي تسعة وأربعون جزءاً وثمان وأربعون دقيقة. وليوصل خطّ كاف دال حاء وخطّ ألف دال طاء ولنخرج أيضاً من نقطة ألف، وهي التي تكون بصر الناظرين عمود ألف لام على خطّ كاف باء وخطّ ألف زاي موازياً لخطّ كاف حاء.

فمن البيّن أنّ ما وقع لمن ينظر من نقطة ألف من اختلاف منظر القمر هو قوس حاء طاء. فتكون إذن هذه القوس جزءاً واحداً وسبع دقائق على ما استخرج ووقف عليه بالرصد. ومن قبل أنّ فضل قوس زاي طاء على قوس حاء طاء فضل لا يُعتدّ به إذ كان ه – خ: ⟨كا⟩نت منزلة حاصل الأرض بأسرها عند دائرة هاء زاي حاء طاء حاصل ه – خ: منزلة النقطة تكون قوس زاي طاء Toomer, p. 249: ZHΘ أيضاً قريباً من هذه الأجزاء، وهي جزء واحد وسبع دقائق. فلذلك تكون زاوية زاي ألف طاء إذ كان أيضاً لا فرق بين نقطة ألف وبين المركز بالقياس إلى دائرة زاي حاء طاء، Toomer, p. 249: ZΘ أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فجزءاً واحداً وسبع دقائق، وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فجزءان وأربع عشرة دقيقة. وبهذه الأجزاء الزاوية أيضاً المساوية لها، وهي زاوية ألف دال لام، جزءان وأربع عشرة دقيقة. فالقوس إذن التي على خطّ ألف لام جزءان وأربع عشرة دقيقة بالأجزاء التي بها الدائرة التي ترسم حول مثلّث ألف دال لام القائم الزاوية ثلاث مائة وستّون جزءاً، وخطّ ألف لام نفسه جزءان وإحدى وعشرون دقيقة بالأجزاء التي بها خطّ ألف دال إذا كان موتّراً مائة وعشرون جزءاً. ونقصان خطّ دال لام عن خطّ ألف دال نقصان لا يعتدّ به فالأجزاء إذن التي بها خطّ ألف لام جزءان وإحدى وعشرون دقيقة، فخطّ دال لام بها مائة وعشرون جزءاً بالتقريب⊙ /H412/ وأيضاً لأنّه قد وضع أنّ قوس جيم دال تسعة وأربعون جزءاً وثمان وأربعون دقيقة، تكون زاوية جيم كاف دال أيضاً إذ كانت عند مركز الدائرة، أمّا بالأجزاء بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فتسعة وأربعون جزءاً وثمان وأربعون دقيقة، وأمّا بالأجزاء بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فتسعة وتسعون جزءاً وستّ وثلاثون دقيقة. فلذلك تكون أمّا القوس التي على خطّ ألف لام تسعة وتسعون جزءاً وستّ وثلاثون دقيقة بالأجزاء التي بها الدائرة التي ترسم حول مثلّث لام ألف كاف القائم الزاوية ثلاث مائة وستّون جزءاً، وأمّا القوس التي على خطّ لام كاف فالأجزاء الباقية إلى نصف الدائرة وهي ثمانون جزءاً وأربع وعشرون دقيقة. فالخطّان إذاً اللذان يوتّرانهما أمّا خطّ ألف لام فيكون أحداً وتسعين جزءاً وتسعاً وثلاثين دقيقة بالأجزاء التي بها خطّ ألف كاف إذا كان موتّراً مائة وعشرين جزءاً، وأمّا خطّ لام كاف يكون بهذه الأجزاء سبعة وسبعين جزءاً وسبعاً وعشرين دقيقة. فما به ه – خ: فيه المقدار الذي به إذن خطّ ألف كاف ه: جزء واحد، وهو من مركز الأرض، يكون به أمّا خطّ ألف لام فستّ وأربعون دقيقة، وأمّا خطّ كاف لام على هذا المثال فتسع وثلاثون دقيقة.

لكنّ الأجزاء التي كان بها خطّ ألف لام جزئين وإحدى وعشرين دقيقة، تبيّن أنّ خطّ لام دال بها مائة وعشرون جزءاً. فالأجزاء إذن التي بها خطّ ألف لام ستّ وأربعون دقيقة، يكون بها أيضاً خطّ لام دال تسعة وثلاثين جزءاً وستّ دقائق. وبهذه الأجزاء كان خطّ كاف لام على ذلك المثال تسعاً وثلاثين دقيقة. وكان خطّ كاف ألف الذي من مركز الأرض واحداً. فما به إذن خطّ كاف ألف الذي من مركز الأرض واحد، يكون به أيضاً خطّ كاف لام دال بأسره، وهو مشتمل على بعد القمر في ذلك الرصد، تسعة وثلاثون جزءاً وخمس وأربعون دقيقة⊙

يا: وإذ قد تبيّن ذلك فليكن فلك القمر الخارج المركز ألف باء جيم حول مركز دال وقطر ألف دال جيم وليؤخذ عليه أمّا مركز فلك البروج، فنقطة هاء، /H413/ وأمّا نقطة محاذاة فلك التدوير، فنقطة زاي. ولنرسم حول نقطة باء فلك التدوير، حط كاف لام، ولتوصل خطوط حاء باء طاء هاء، باء دال، باء كاف زاي. ولننزّل أنّ القمر كان في هذا الرصد الموصوف على نقطة لام، وليوصل خطّ لام هاء وخطّ لام باء This sentence cannot be found in Toomr's translation. /T250/ ولنخرج إلى خطّ باء هاء من نقطة دال عمود عليه إذا أخرج على الاستقامة This passage is not in Toomer’s translation because he believed that it should be excised from the text, see Toomer p. 250 footnote 48. وليكن دال ميم، ومن نقطة زاي عمود زاي نون.

فلأنّ في وقت الرصد كان عدد البعد ثمانية وسبعين جزءاً وثلاث عشرة دقيقة يكون لما تقدّم العلم به زاوية ألف هاء باء بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً مائة وستّة وخمسين جزءاً وستّاً وعشرين دقيقة؛ ويكون كلّ واحدة من زاويتى نون هاء زاي، دال هاء ميم الباقية من زاويتين قائمتين وهي ثلاثة وعشرون جزءاً وأربع وثلاثون دقيقة، /H414/ فأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فيكون سبعة وأربعين جزءاً وثمان دقائق. فلذلك أمّا القوس التي على كلّ واحد من خطّي دال ميم، زاي نون فسبعة وأربعون جزءاً وثمان دقائق بالأجزاء التي بها الدائرتان اللتان ترسمان حول المثلثين القائمتي الزاويتين الموصوفين ثلاث مائة وستّون جزءاً من أجل أنّ خطّ دال هاء مساو لخطّ هاء زاي، وأمّا القوس التي على كلّ واحد من خطّي هاء ميم، هاء نون فبهذه الأجزاء مائة واثنان وثلاثون جزءاً واثنتان وخمسون دقيقة. فالخطوط إذن التي توتّرها أمّا كلّ واحد من خطّي دال ميم، زاي نون فسبعة وأربعون جزءاً وتسع وخمسون دقيقة بالأجزاء التي بها كلّ واحد من خطّي دال هاء، هاء زاي إذا كان موتّراً مائة وعشرون جزءاً. وأمّا كلّ واحد من خطّي هاء ميم، هاء نون فمائة وعشرة أجزاء بهذه الأجزاء. فلذلك تكون الأجزاء التي بها كلّ واحد من خطّي دال هاء، هاء زاي عشرة أجزاء وتسع عشرة دقيقة، وخطّ دال باء الذي من مركز الفلك الخارج المركز تسعة وأربعون جزءاً وإحدى وأربعون دقيقة، فكلّ واحد من خطّي دال ميم، زاي نون بها أربعة أجزاء وثمان دقائق، وكلّ واحد من خطّي هاء ميم، هاء نون بها تسعة أجزاء وسبع وعشرون دقيقة. ولأنّ المربّع الذي من خطّ باء دال منقوصاً منه المربّع الذي من خطّ دال ميم يكون منه المربّع الذي من خطّ باء ميم يحصل لنا أيضاً أمّا خطّ باء ميم بأسره في الطول بهذه الأجزاء فتسعة وأربعون جزءاً وإحدى وثلاثون دقيقة. وأمّا خطّ باء هاء على هذا المثال فأربعون جزءاً وأربع دقائق، وخطّ باء نون الباقي ثلاثون جزءاً وسبع وثلاثون دقيقة بالأجزاء التي كان بها خطّ زاي نون أربعة أجزاء وثمان دقائق. ولأنّ المربّعين اللذين يكونان منهما يكون منهما إذا جمعا المربّع الذي من خطّ باء زاي يحصل لنا خطّ باء زاي الموتّر في الطول بهذه الأجزاء ثلاثين جزءاً وأربعاً وخمسين دقيقة. /T251/ فالأجزاء إذن التي بها خطّ باء زاي إذا كان موتّراً مائة وعشرون جزءاً يكون بها أمّا خطّ زاي نون فستّة عشر جزءاً ودقيقتان، وأمّا القوس التي عليه فخمسة عشر جزءاً وإحدى وعشرون دقيقة بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء زاي نون القائم الزاوية ثلاث مائة وستّون جزءاً /H415/ فزاوية زاي باء نون إذن أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فإنّها تكون خمسة عشر جزءاً وإحدى وعشرين دقيقة، وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فإنّها تكون سبعة أجزاء وأربعين دقيقة بالتقريب. فهذا إذن مبلغ أجزاء قوس طاء كاف من فلك التدوير.

وأيضاً لانّ في وقت ه: ذلك الرصد كان بعد القمر أمّا من البعد الأبعد الوسط من فلك التدوير فمائتان واثنان وستّون جزءاً وعشرون دقيقة، وأمّا من نقطة كاف، وهي البعد الأقرب الوسط، فالأجزاء الباقية بعد نصف الدائرة، وذلك بيّن، وهي اثنان وثمانون جزءاً وعشرون دقيقة.

تكون أمّا قوس كاف لام فاثنان وثمانون جزءاً وعشرون دقيقة، وأمّا قوس طاء كاف لام بأسرها فتسعون جزءاً. فزاوية طاء باء لام إذن قائمة. ولأنّه قد تبيّن أنّ الأجزاء التي بها أمّا خطّ دال باء الذي من مركز الفلك الخارج المركز فتسعة وأربعون جزءاً وإحدى وأربعون دقيقة وأمّا خطّ باء لام الذي من مركز فلك التدوير فخمسة أجزاء وخمس عشرة دقيقة، فإنّ خطّ هاء باء بها أربعون جزءاً وأربع دقائق، والمربّعين اللذين يكونان منهما يكون منهما إذا جمعا المربّع الذي من خطّ هاء لام يحصل لنا خطّ هاء لام أيضاً في الطول بهذه الأجزاء أربعين جزءاً وخمساً وعشرين دقيقة. فبعد القمر إذن في ذلك الرصد أربعون جزءاً وخمس وعشرون دقيقة بالأجزاء التي بها وضع أمّا ↑أمّا↑: أمّا خطّ باء لام الذي من مركز فلك التدوير فخمسة أجزاء وخمس عشرة دقيقة، وأمّا خطّ هاء ألف الذي من مركز الأرض إلى نقطة البعد الأبعد من الفلك الخارج المركز، وهي نقطة ألف، فستّون جزءاً، وأمّا خطّ هاء جيم الذي من مركز الأرض إلى نقطة البعد الأقرب من الفلك الخارج المركز فتسعة وثلاثون جزءاً واثنتان وعشرون دقيقة.

لكنّ قد تبيّن أنّ بعد القمر في ذلك الرصد، أعني خطّ هاء لام، /H416/ تسعة وثلاثون جزءاً وخمس وأربعون دقيقة بما به الخطّ من مركز الأرض واحد ه – خ: بالمقدار الذي به نصف قطر الأرض جزء واحد . فالأجزاء إذن التي بها أمّا خطّ هاء لام، وهو بعد القمر في وقت الرصد، فتسعة وثلاثون جزءاً وخمس وأربعون دقيقة وأمّا الخطّ الذي من مركز ه – خ: نصف قطر الأرض فجزء واحد، يكون بها أمّا خطّ هاء ألف، و ↑: خ الذيهو البعد ه – خ: بعد القمر الوسط في الاتّصالات، فتسعة وخمسون جزءاً، وأمّا خطّ هاء جيم، وهو البعد الوسط في التربيعات، فثمانية وثلاثون جزءاً وثلاث وأربعون دقيقة، وأمّا الخطّ الذي من مركز فلك التدوير فبهذه الأجزاء خمسة أجزاء وعشر دقائق. وذلك ما قصدنا لتبيينه⊙ وإذ قد بيّنّا بهذا الوجه الذي وصفناه أبعاد القمر، فقد يتّصل بذلك ويتّبعه أن نبيّن معه بعد الشمس. فإنّ ذلك /T252/ أيضاً ممّا يسهل المأخذ فيه بطريق الخطوط إن علمت زيادة مع أبعاد القمر في الاتّصالات مقادير الزوايا التي تكون فيها عند البصر عن أقطار الشمس والقمر والظلّ. فما كان من الطرق المؤدّية إلى ذلك، فظنّ أنّه يستخرج به مساحة النيّرين إمّا بالآلات التي يقع بها العيار بالماء وإمّا بأزمان مطالع الاستواء، فإنّا أنصرفنا ه – خ: اخ{...} عنه وذلك أنّه ليس يمكن بما أشبه ذلك من الأعمال استخراج ما قصدنا به من ذلك على الصحّة ه: في نسخة أخرى {...} هو مبدأ النوع الرابع عشر الذي {...} بعده.
This paragraph is the first paragraph and part of the second paragraph of Chapter 14 in Toomer’s translation. ⊙

⟨V.14⟩ يد: في قدر أقطار الشمس والقمر والظلّ الذي يرى في اتّصالات

/H417/ واتّخذنا نحن أيضاً المقياس الذي وضعه أبرخس بالمسطرة التي طولها أربعة أذرع، وجعلنا رصدنا به فوجدنا قطر الشمس تحيط به زاوية تكاد أن تكون في كلّ موضع ه: يعني بعدت الشمس أو قربت واحدة بعينها من غير أن يقع فيها فضل يعتدّ به من قبل أبعادها، وأمّا قطر القمر فإنّما وجدناه تحيط به هو أيضاً الزاوية بعينها التي تحيط بقطر الشمس في ذلك الوقت فقط الذي يكون فيه في وقت الامتلاء في أكثر ما يكون من البعد من الأرض ه – خ: أعني عند ما يكون في أبعد البعد من فلك التدوير، لا في الوقت الذي يكون فيه في بعده الوسط على ما يلزم من أصول القدماء. ومع ذلك، فإنّا وقفنا على أنّ مقادير الزوايا أنفسها أصغر من المقادير التي أخذناها عنهم بشيء له قدر يُعتدّ به، إلّا أنّ حسابنا لذلك لم نأخذه بأنّا مسّحنا المسطرة، بل بكسوفات ما من كسوفات القمر. وذلك أنّ الوقوف على الوقت الذي فيه يوتّر كلّ واحد من القطرين زاوية سواء متى يكون قد يسهل تناوله من قبل ما عليه هيئة المسطرة، وذلك أنّه ليس يحتاج في مثل ذلك إلى شيء من مساحتنا للمسطرة. وأمّا مقدار هذه الزاوية كم هو فإنّا رأيناه مشكلاً جدّاً وذلك أنّ الإحصاء ه: يعني إحصاه بأن يمسح الذي يكون بإيقاع عرض الشطبة الساترة على /T253/ طول المسطرة الذي بين البصر وبين الشطبة لمّا كان يتكرّر مرّات كثيرة جدّاً أمكن أن تخطّى حقيقة الأمر /H418/ لكن لمّا كان القمر قد وجد مرّة واحدة في أكثر ما يكون من بعده يحدث عند البصر زاوية مساوية لزاوية الشمس فإنّا حسبنا بالكسوفات القمريّة التي رصدت في هذا البعد مقدار الزاوية التي توتّره فوقفنا بذلك مع وقوفنا على هذه الزاوية على زاوية الشمس من قرب وأمّا الجهة التي بها وقفنا على ما وقفنا عليه من ذلك فقد يسهل فهمها بكسوفين أيضاً نصفهما من ذي قبل⊙

فنقول إنّ في سنة خمس من سني نابوفولسرس وكان بعد بختنصر بمائة وسبع وعشرين سنة في الشهر من شهور المصريّين المسمّى أثور منها في اليوم السابع والعشرين منه في الليلة التي {يتلوها} اليوم الثامن والعشرون سنة في آخر الساعة الحادية عشرة منها ببابل، ابتداء القمر ينكسف، وأكثر ما انكسف منه من ناحية الجنوب ربع قطره. فإذ كان ابتداء الكسوف كان بعد انتصاف الليل بخمس ساعات زمانيّة وكان وسط الكسوف بعده بستّ ساعات بالتقريب، وهذه الساعات كانت ببابل في ذلك الوقت خمس ساعات ونصفاً وثلثاً من ساعات الاستواء من قبل أنّ حاصل الشمس على الحقيقة كان على سبعة وعشرين جزءاً وثلاث دقائق من الحمل. فمن البيّن أنّ وسط زمان الكسوف، وهو الوقت الذي فيه كان أكثر ما دخل من قطره في الظلّ، أمّا ببابل فكان بعد انتصاف الليل بخمس ساعات ونصف وثلث من ساعات الاستواء، وأمّا بإسكندريّة أيضاً فبعده بخمس ساعات فقط. والذي يحصل من الزمان منذ وقت التحصيل ه – خ: إلى وقت الكسوف مائة وستّ ↑وستّ↑: خ وتسع وعشرون سنة مصريّة وستّة وثمانون يوماً، /H419/ ومن الساعات الاستوائيّة أمّا على الإطلاق فسبع ↑فسبع↑: ستّ عشرة ساعة، وأمّا بحسب الأيّام بلياليها المستوية فستّ عشرة ساعة ونصف وربع. فلذلك يكون المسير الوسط للقمر في الطول حاصله على خمسة وعشرين جزءاً واثنتين وثلاثين دقيقة من الميزان، وأمّا مسيره الصحيح فعلى سبعة وعشرين جزءاً وخمس دقائق منه. وأمّا بعده من البعد الأبعد من فلك التدوير فثلاث مائة وأربعون جزءاً وسبع دقائق، وأمّا بعده من النهاية الشماليّة في الدائرة المائلة فثمانون جزءاً وأربعون دقيقة.

فظاهر أنّ مركز القمر إذا كان بعده من ه – خ: أحدى العقدتين تسعة أجزاء وثلث جزء في الدائرة المائلة وكان في أبعد ما يكون من البعد وكان مركز الظلّ على الدائرة من أعظم الدوائر التي ترسم مارّة به وعلى زوايا قائمة على الدائرة المائلة، وهذا الوضع هو الذي فيه تكون إظلاماته أعظم ما يكون، فإنّ الذي يقع في الظلّ من قطره ربعه ه – خ: وكان مركز الظلّ في الفلك العظيم المخطو{...} في ذلك البعد على زاوية قائمة من الفلك المائل في الموضع الذي يكون فيه أعظم {...} قطر القمر في الظلّ {...}. ⊙

وأيضاً في سنة سبع من سني فمبوسس، وهي سنة مائتين وخمس وعشرين منذ عهد بختنصر، في الشهر من شهور المصريّين المسمّى فامانوث منها في اليوم السابع عشر منه في الليلة منه التي يتلوها اليوم الثامن عشر قبل انتصاف الليل ساعة واحدة ببابل انكسف من القمر من ناحية الشمال نصف قطره، فكان إذن هذا الكسوف بإسكندريّة قبل انتصاف الليل بساعة ونصف وثلث بالتقريب من ساعات الاستواء. والذي يحصل من الزمان منذ وقت التحصيل ه: إلى وقت الكسوف /T254/ مائتا سنة وأربع وعشرون سنة مصريّة ومائة يوم وستّة وتسعون يوماً، ومن الساعات الاستوائيّة أمّا على الإطلاق فعشر ساعات وسدس وأمّا على الحقيقة فتسع ساعات ونصف وثلث /H420/ من قبل أنّ الشمس كان حاصلها على ثمانية عشر جزءاً واثنتي عشرة دقيقة من السرطان. فلذلك يكون حاصل القمر أيضاً في الطول أمّا على التوسّط فعلى عشرين جزءاً واثنتين وعشرين دقيقة من الجدي، وأمّا على الحقيقة فعلى ثمانية عشر جزءاً وأربع عشرة دقيقة منه، وكان بعده أمّا من البعد الأبعد من فلك التدوير فثمانية وعشرون جزءاً وخمس دقائق، وأمّا من النهاية الشماليّة من الدائرة المائلة فمائتان واثنان وخمسون ه: ستّون جزءاً واثنتا عشرة دقيقة. فهاهنا أيضاً قد ظهر أنّ مركز القمر إذا كان بعده من ه – خ: إحدى العقدتين سبعة أجزاء وأربعة أخماس جزء في الدائرة المائلة، وكان على ذلك المثال في غاية بعده وكان مركز الظلّ وضعه عنده ذلك الوضع الذي ذكرنا، فإنّ الذي يقع من قطر القمر في الظلّ نصفه. ه – خ: وكان مركز الظلّ منه في الموضع الذي ذكرنا أنّ نصف القطر يقع في الظلّ. لكن إذا كان مركز القمر بعده من ه – خ: إحدى العقدتين تسعة أجزاء وثلث جزء في دائرته المائلة. فإنّ بعده من فلك البروج يكون ثمانياً وأربعين دقيقة ونصفاً من جزء واحد في الدائرة من أعظم الداوئر التي ترسم مارّة به وعلى زاوية قائمة على دائرة المائلة وإذا كان بعده من ه – خ: إحدى العقدتين سبعة أجزاء وأربعة أخماس جزء في دائرته المائلة. فإنّ بعده من فلك البروج يكون أربعين دقيقة وثلثين ه – خ: وثلثي دقيقة في الدائرة من أعظم الدوائر التي ترسم مارّة ↑: به وعلى زوايا قائمة على دائرته المائلة. فلأنّ الفضل بين هذين الكسوفين في القمر يشتمل على ربع قطره والفضل /H421/ بين هذين البعدين اللذين وضعناهما لمركزه من فلك البروج، أعني من مركز الظلّ، سبع دقائق ونصف وثلث، فظاهر أنّ قطر القمر بأسره يوتّر قوساً من أعظم الدوائر مبلغها إحدى وثلاثون دقيقة وثلث.

وقد يُفهم من ذلك بسهولة أنّ الخطّ الذي من مركز الظلّ في هذا البعد الأعظم للقمر يوتّر أربعين دقيقة وثلثين، إذ كان مركز القمر لمّا كان بعده من مركز الظلّ هذا المقدار من الدقائق كان قد لقي دائرة الظلّ، إذ كان ما انكسف من القمر كان نصف قطره. وإنّه أصغر من ضعف وثلاثة أخماس الخطّ الذي من مركز القمر الذي هو خمس عشرة دقيقة وثلثان بما لا يعتدّ به. ه – خ: أنّ نصف قطر الظلّ يوتّر أربعين دقيقة وثلثي دقيقة من الجزء الواحد إذا كان في بعد القمر الأعظم إذ كان بعد مركز القمر من مركز الظلّ هذه الأجزاء أعني الأربعين دقيقة والثلثي دقيقة وكان مركز الظلّ على وسط نطاق البروج وكان قد انكسف من القمر نصف قطره وهو الذي دخل منه في دائرة الظلّ. فيكون نصف قطر الظلّ مثل نصف قطر القمر الذي هو خمس عشرة دقيقة وثلثا دقيقة وثلاثة أخماس مثله {...} شيء يصير ليس له كثير قدر. فلمّا وجدنا بهذه الأرصاد وبأرصاد أكثر منها يجري مجراها أنّ هذه المقادير التي وضعناها تكاد أن تكون متّفقة فيها استعملناها في سائر الأمور التي تحتاج إلى النظر فيها من أمر الكسوفات وفي هذا الموضع أيضاً في تبيين بعد الشمس الذي نحن سالكون فيه المذهب الذي سلكه أبرخس بعينه وعاملون فيه على أنّ دوائر /H422/ الشمس والقمر والظلّ التي تحصرها المخروطات ه – خ: يحيط به الشكل الصنوبريّ ليس مقدار صغرها عن ↑عن↑: خ على أعظم الدوائر التي ترسم في أكثرها مقدار يعتدّ به، وكذلك أقطارها على أقطارها⊙

/T255/ ⟨V.15⟩ يه: في بعد الشمس وما يتبيّن ببيانه

فإذ ↑: خ ا (فإذا i.e.,) كانت هذه الأشياء مفروضة وكان أكثر ما يكون بعد القمر في الاتّصالات أربعة وستّين جزءاً وعشر دقائق بالأجزاء التي بها الخطّ الذي من مركز ه – خ: نصف قطر الأرض واحد، إذ كان قد تبيّن أنّ بعده الوسط تسعة وخمسون جزءاً بهذه الأجزاء، وإن (كان) الخطّ الذي من مركز ه – خ: ونصف قطر فلك التدوير خمسة أجزاء وعشر دقائق، فلننظر كم يحصل بعد الشمس أيضاً⊙

يب: فليكن أعظم دوائر الأكر في سطح واحد بعينه، أمّا دائرة كرة الشمس فدائرة ألف باء جيم حول مركز دال، وأمّا دائرة كرة القمر إذا كان في أكثر ما يكون من البعد فدائرة هاء زاي حاء حول مركز طاء، وأمّا الدائرة التي على الأرض فدائرة كاف لام ميم حول مركز نون. وليكن السطحان اللذان يمرّان بالمراكز أمّا السطح الذي يحوي الأرض والشمس منهما فسطح ألف سين جيم، وأمّا السطح الذي يحوي الشمس والقمر فسطح ألف نون جيم، وليكن المحور ه – خ: السهم المشترك لها دال طاء نون سين. ولتكن الخطوط التي تمرّ بمواضع التماسّ، ومن البيّن أنّها تكون متوازية ومساوية لأقطارها عند الحسّ، أمّا لدائرة الشمس فخطّ ألف دال جيم، وأمّا لدائرة القمر فخطّ هاء طاء حاء، /H423/ وأمّا لدائرة الأرض فخطّ كاف نون ميم، وأمّا لدائرة الظلّ الذي يقع فيه القمر في أكثر ما يكون من البعد فخطّ عين فاء قاف حتّى يكون خطّ طاء نون مساوياً لخطّ نون فاء ويكون كلّ واحد منهما أربعة وستّين جزءاً وعشر دقائق بالأجزاء التي بها خطّ نون لام الذي من مركز الأرض واحد.

فقد نحتاج إلى أن نعلم أيّ نسبة هي نسبة خطّ نون دال، ه – خ: {...} نسبة خطّ نون دال الذي وهو بعد الشمس إلى خطّ نون لام، وهو الذي من مركز الأرض. فلنخرج خطّ هاء حاء راء ↑: صح.

ولأنّا قد بيّنّا أنّ قطر القمر في هذا البعد الموصوف في الاتّصالات أعني في أكثر ما يكون من بعده يوتّر قوساً من الدائرة التي ترسم عليه حول مركز الأرض مقدارها إحدى وثلاثون دقيقة وعشرون ثانية بالأجزاء التي بها الدائرة ثلاث مائة وستّون جزءاً، /H424/ تكون زاوية هاء نون حاء على هذا المثال إحدى وثلاثون دقيقة وعشرين ثانية بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً، ويكون نصفها، وهي زاوية طاء نون حاء، بهذه الأجزاء أيضاً إحدى وثلاثين دقيقة وعشرين ثانية بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً. فلذلك تكون أمّا القوس التي على طاء حاء فإحدى وثلاثون دقيقة وعشرون ثانية بالأجزاء التي بها الدائرة التي ترسم حول مثلّث نون حاء طاء القائم الزاوية ثلاث مائة وستّون جزءاً وأمّا القوس التي على خطّ طاء نون فالأجزاء الباقية من نصف الدائرة وهي مائة وتسعة وسبعون جزءاً وثمان وعشرون دقيقة وأربعون ثانية. فالخطّان إذن اللذان يوتّرانهما أمّا خطّ طاء حاء منهما فيكون إثنتين وثلاثين دقيقة وثمانياً وأربعين ثانية بالأجزاء التي بها قطر نون حاء مائة وعشرون جزءاً، وأمّا خطّ نون طاء فبهذه الأجزاء مائة وعشرون جزءاً بالتقريب. فالأجزاء إذن التي بها خطّ نون طاء أربعة وستّون جزءاً وعشر دقائق، يكون بها خطّ طاء حاء سبع عشرة دقيقة وثلاثاً وثلاثين ثانية. وبهذه الأجزاء كان خطّ نون ميم الذي من مركز الأرض جزءاً واحداً. لكنّ لأنّ نسبة خطّ فاء قاف إلى خطّ طاء حاء هي نسبة جزئين وستّ وثلثين دقيقة بالتقريب إلى واحد، يكون خطّ فاء قاف أيضاً بهذه الأجزاء خمساً وأربعين دقيقة وثمانياً وثلاثين ثانية. فالخطّان إذن مجموعان أعني خطّ طاء حاء، وخطّ فاء قاف هما جزء واحد وثلاث دقائق وإحدى عشرة ثانية بالأجزاء التي بها خطّ نون ميم، الذي من مركز الأرض، واحد. لكنّ خطّ فاء قاف وخطّ طاء زاء بأسره مجموعتين (بهما مجموعتين) هما بهذه الأجزاء جزءان من قبل أنّهما مساويان لخطّ نون ميم مرّتين، وذلك أنّهما كلّها كما قلنا متوازية وخطّ نون فاء مساو لخطّ نون طاء. /H425/ فخطّ حاء زاء الباقي يحصل ستّاً وخمسين دقيقة وتسعاً وأربعين ثانية بالأجزاء التي بها خطّ نون ميم واحد. ونسبة خطّ نون ميم إلى خطّ حاء ↑ ح زاي كنسبة خطّ نون جيم إلى خطّ حاء جيم وخطّ نون دال إلى خطّ طاء ↑ ط دال. /T257/ فما به إذن خطّ نون دال واحد، يكون بذلك أمّا خطّ طاء دال H425.4: ΔΘ فستّاً وخمسين دقيقة وتسعاً وأربعين ثانية، وأمّا خطّ طاء نون الباقي بهذه الأجزاء فثلاث دقائق وإحدى عشرة ثانية.

فلذلك يكون بالأجزاء التي بها أمّا خطّ نون طاء فأربعة وستّون جزءاً وعشر دقائق، وأمّا خطّ نون ميم فواحد، بها خطّ نون دال، وهو بعد ↑: صح الشمس، ألف ومائتان وعشرة أجزاء بالتقريب. وكذلك أيضاً من قبل أنّ ما به خطّ نون ميم واحد، فبه قد تبيّن أنّ خطّ فاء قاف خمس وأربعون دقيقة وثمان وثلاثون ثانية، ونسبة خطّ نون ميم إلى خطّ فاء قاف كنسبة خطّ نون سين إلى خطّ قاف سين. فما به إذن خطّ نون سين واحد يكون به أمّا خطّ سين فاء فخمس وأربعون دقيقة وثمان وثلاثون ثانية. وأمّا خطّ فاء نون الباقي بهذه الأجزاء فأربع عشرة دقيقة واثنتان وعشرون ثانية. فالأجزاء إذن التي بها أمّا خطّ فاء نون فأربعة وستّون جزءاً وعشر دقائق، وأمّا خطّ نون ميم الذي من مركز الأرض فواحد، يكون بها أمّا خطّ سين فاء فمائتان وثلاثة أجزاء وخمسون دقيقة بالتقريب، وأمّا خطّ سين نون بأسره فمائتان وثمانية وستّون جزءاً. فقد حصل لنا إذن ما به الخطّ الذي من مركز الأرض واحد، يكون به أمّا بعد القمر الوسط ه: في الاتّصالات فتسعة وخمسون، وأمّا بعد الشمس فألف ومائتان وعشرة أجزاء، وأمّا ما بين مركز الأرض وبين رأس مخروط الظلّ فمائتان وثمانية وستّون جزءاً بهذه الأجزاء⊙

/H426/ ⟨V.16⟩ يو: في مقادير الشمس والقمر والأرض

وممّا يسهل فهمه ويقرب مأخذه النسبة أيضاً بين مقادير أجرام الشمس والقمر والأرض من قبل النسبة بين أقطارها. ↑أقطارها↑: ط وذلك أنّه إذ كان قد تبيّن أنّ ما به خطّ نون ميم الذي من مركز الأرض واحد، يكون به أمّا خطّ طاء حاء الذي من مركز القمر فسبع عشرة دقيقة وثلاث وثلاثون ثانية، وأمّا خطّ نون طاء فأربعة وستّون جزءاً وعشر دقائق وكانت نسبة خطّ نون طاء إلى خطّ طاء حاء كنسبة خطّ نون دال إلى خطّ دال جيم، وقد كان تبيّن أنّ خطّ نون دال بهذه الأجزاء ألف ومائتان وعشرة أجزاء، فإنّ خطّ دال جيم الذي من مركز الشمس يحصل لنا بهذه الأجزاء خمسة أجزاء ونصفاً بالتقريب. فيكون إذن النسب بين أقطارها هي هذه النسب بعينها. فلذلك يكون ما به قطر القمر واحد، فبه أمّا قطر الأرض فثلاثة وخمسان بالتقريب، وأمّا قطر الشمس فثمانية عشر وأربعة أخماس. فقطر الأرض إذن مثل قطر القمر ثلاث مرّات وخمسين، وقطر الشمس مثل قطر القمر ثمان عشرة مرّة وأربعة أخماس /H427/ ومثل قطر الأرض خمس مرّات ونصف بالتقريب. ولذلك أيضاً من قبل أنّ المكعّب الذي يكون من واحد يكون أيضاً واحداً بذلك المقدار، والمكعّب الذي يكون من ثلاثة وخمسين يكون بذلك المقدار تسعة وثلاثين وربعاً بالتقريب، والمكعّب الذي من ثمانية عشر وأربعة أخماس على ذلك المثال ستّة آلاف وستّمائة وأربعة وأربعين ونصفاً بالتقريب، فقد حصل لنا ما به مقدار جرم القمر واحد، يكون به أمّا مقدار جرم الأرض فتسعة وثلاثون وربع، وأمّا مقدار الشمس فستّة آلاف وستمّائة وأربعة وأربعون ونصف. فمقدار جرم الشمس إذن مائة وسبعون مرّة مثل مقدار الأرض بالتقريب⊙

/T258/ ⟨V.17⟩ يز: في اختلاف المنظر ه – خ: المناظر الجزيئّة للشمس والقمر

فإذ قد وُطئت هذه الأشياء على النحو فقد يتّصل بذلك أن نضيف إلى ما بيّنّاه أن نبيّن أيضاً بإيجاز الوجه الذي به يمكن أن نحسب من قبل مقدار أبعاد الشمس والقمر اختلافات المنظر الجزئيّة التي تكون لهما أيّ وجه هو. ونبيّن من ذلك أوّلاً ما نرى منه في الدائرة من أعظم الدوائر التي ترسم مارّة بالنقطة التي على سمت الرأس وبهما وقد {...} إذ كان ما ذكرنا {فعلى} ما وصفنا أن نبيّن أيضاً بإيجاز كيف جهة مأخذ اختلاف المناظر الجزئيّة من أقدار أبعاد الشمس والقمر ونبيّن الاختلافات التي ترى في الفلك العظيم المخطوط عليهما وعلى نقطة سمت الرؤوس. ⊙

/H428/ يج: فليكن في سطح الدائرة من أعظم الدوائر التي تقدّم ذكرها أمّا الدائرة من أعظم الدوائر التي للأرض *أيضاً* فدائرة ألف باء، وأمّا التي على الشمس أو القمر فدائرة جيم دال، وأمّا التي منزلة الأرض عندها منزلة النقطة فدائرة هاء زاي حاء طاء. ومركزها كلّها نقطة كاف والقطر الذي يمرّ *بالنقطتين* *اللتين* على سمت الرأس خطّ كاف ألف جيم هاء. ولنفصل من لدن نقطة جيم التي على سمت الرأس قوس جيم دال على أن يوضع مثلاً ثلاثين جزءاً بالأجزاء التي بها دائرة جيم دال ثلاث مائة وستّون جزءاً وليوصل أيضاً خطّا كاف دال حاء ألف دال طاء، ولنخرج من نقطة ألف خطّ ألف زاي موازياً لخطّ كاف حاء وخطّ ألف لام عموداً عليه.

فلأنّ بعد كلّ واحد من النيّرين وإن كان ليس هو باقياً على حال واحدة لكن الفضل الذي يكون من قبل ذلك لاختلافات المنظر أمّا في الشمس فيسير جدّاً حتّى أنّه يكون غير محسوس من قبل أنّ خروج فلكها عن المركز يسير وبعدها كثير. وأمّا في القمر فيكون بيّنّا محسوساً من قبل /T259/ حركته في فلك التدوير ومن قبل حركة فلك التدوير نفسه على الفلك الخارج المركز إذ كلّ واحد من هذين يحدث من الفضل في الأبعاد ما ليس بيسير. /H429/ فنحن مبيّنون اختلافات المنظر، أمّا للشمس ففي نسبة واحدة وهي نسبة الألف والمائتين والعشرة إلى الواحد، وأمّا للقمر ففي أربع نسب وهي التي بها خاصّة يكون ما نستعمله في الأبواب التي بها نأتي من بعد أسهل سبيلاً. وما أخذناه ↑وما أخذناه↑: خ ونأخذ من هذه الأربعة الأبعاد فإنّ الاثنين الأوّلين منها هما البعدان اللذان ه – خ: أوّلاً البعدين اللذين يكونان له وفلك التدوير في أبعد البعد من الفلك الخارج المركز، أمّا الأوّل منهما فالذي ينتهي فيه ه – خ: القمر إلى البعد الأبعد من فلك التدوير، وقد كان هذا البعد حصل لنا بما تقدّم بيانه أربعة وستّين جزءاً وعشر دقائق بما به الخطّ الذي من مركز الأرض واحد؛ وأمّا الثاني منهما فالذي ينتهي فيه إلى البعد الأقرب من فلك التدوير الذي كان أيضاً حصل بهذه الأجزاء ثلاثة وخمسين جزءاً وخمسين دقيقة⊙ وأمّا الاثنان الباقيان فهما البعدان اللذان يكونان له وفلك التدوير في أقرب القرب من الفلك الخارج المركز، والأوّل أيضاً من هذين هو البعد الذي ينتهي فيه ه – خ: القمر إلى البعد الأبعد من فلك التدوير الذي حصل بما بيّنّاه فيما تقدّم ثلاثة وأربعين جزءاً وثلثاً وخمسين دقيقة بما به الخطّ الذي من مركز الأرض واحد؛ وأمّا الثاني فهو الذي ينتهي فيه إلى البعد الأقرب من فلك التدوير الذي حصل أيضاً بهذه الأجزاء ثلاثة وثلاثين جزءاً وثلاثاً وثلاثين دقيقة. ↑: ؟ فلأنّ قوس جيم دال قد وضعت ثلاثين جزءاً تكون زاوية جيم كاف دال أيضاً أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فثلاثون جزءاً، وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فستّون جزءاً. فلذلك تكون أمّا القوس التي على خطّ ألف لام فستّون جزءاً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث ألف كاف لام القائم الزاوية ثلاث مائة وستّون جزءاً، /H430/ وأمّا القوس الـتي على خطّ كاف لام فالأجزاء الباقية إلى تمام نصف الدائرة وهي مائة وعشرون جزءاً. فالخطّان إذن اللذان يوتّرانهما أمّا خطّ ألف لام منهما فستّون جزءاً بالأجزاء التي بها قطر ألف كاف مائة وعشرون جزءاً، وأمّا خطّ كاف لام بهذه الأجزاء فمائة وثلاثة أجزاء وخمس وخمسون دقيقة. فما به إذن خطّ ألف كاف واحد، يكون به أمّا خطّ ألف لام فثلاثون دقيقة وأمّا خطّ كاف لام فاثنتان وخمسون دقيقة. وبهذه الأجزاء خطّ كاف لام دال أمّا في بعد الشمس فألف ومائتان وعشرة أجزاء، وأمّا في أبعاد القمر أمّا في الحدّ الأوّل فأربعة وستّون جزءاً وعشر دقائق، وأمّا في الحدّ الثاني فثلاثة وخمسون جزءاً وخمسون دقيقة، وأمّا في الحدّ الثالث فثلاثة وأربعون جزءاً وثلاث وخمسون دقيقة، وأمّا في الحدّ الرابع فثلاثة وثلاثون جزءاً وثلاث وثلاثون دقيقة. فخطّ لام دال الباقي أعني خطّ ألف دال إذ كان الاختلاف بينهما لا يعتدّ به يكون أمّا في بعد الشمس فألف ومائتان وتسعة أجزاء وثمان دقائق، وأمّا في أبعاد القمر أمّا في الحدّ الأوّل فثلاثة وستّون جزءاً وثمان عشرة دقيقة، وأمّا في الحدّ الثاني فاثنان وخمسون جزءاً وثمان وخمسون دقيقة، وأمّا في الحدّ الثالث فثلاثة وأربعون جزءاً ودقيقة واحدة، وأمّا في الحدّ الرابع فاثنان وثلاثون جزءاً وإحدى وأربعون دقيقة. فلذلك يكون بالأجزاء التي بها خطّ ألف دال إذا كان موتّراً مائة وعشرون جزءاً، فخطّ ألف لام بها على أن يفهم من قولنا ذلك الترتيب بعينه كيما لا نكرّر المعنى الواحد مراراً كثيرة دقيقتان وتسع وخمسون ثانية، وستّ وخمسون دقيقة واثنتان وخمسون ثانية، وجزء واحد وسبع دقائق وثمان وخمسون ثانية، وجزء واحد وثلاث وعشرون دقيقة وإحدى وأربعون ثانية، وجزء واحد وتسع وخمسون دقيقة⊙ Η430.19: α ν θ (1;50,9) /T260/ فالقوس إذن التي عليه تكون دقيقتين وخمسين ثانية⊙ وأربعاً وخمسين دقيقة وثمان عشرة ثانية، وجزء وأربع دقائق وأربع وخمسون ثانية، وجزءاً وعشرين دقيقة. وجزءاً وخمساً وأربعين دقيقة بالتقريب بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال لام ألف القائم الزاوية ثلاث مائة وستّون جزءاً.

وتكون زاوية ألف دال باء أعني زاوية زاي ألف طاء /H431/ أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فدقيقتان وخمسون ثانية، وأربع وخمسون دقيقة وثمان عشرة ثانية، وجزء وأربع دقائق وأربع وخمسون ثانية، وجزء وعشرون دقيقة، وجزء وخمس وأربعون دقيقة؛ وأمّا الأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فدقيقة واحدة وخمس وعشرون ثانية، وسبع وعشرون دقيقة وتسع ثواني، واثنتان وثلاثون دقيقة وسبع وعشرون ثانية، وأربعون دقيقة، ه – خ: فقط واثنتان وخمسون دقيقة وثلاثون ثانية. فلذلك إذ كان لا فرق بين نقطة ألف وبين مركز كاف، وكانت قوس زاي حاء طاء أعظم من قوس حاء طاء بما لا يعتدّ به من قبل أنّ الأرض بأسرها منزلتها عند دائرة هاء زاي حاء طاء منزلة النقطة تكون قوس حاء طاء أيضاً، وهي قوس اختلاف المنظر بالأجزاء التي بها دائرة ه: هاء زاي حاء طاء ثلاث مائة وستّون جزءاً، أمّا في بعد الشمس فدقيقة واحدة وخمس وعشرون ثانية، وأمّا في أبعاد القمر أمّا في الحدّ الأوّل فسبع وعشرون دقيقة وتسع ثواني، وأمّا في الحدّ الثاني فاثنتان وثلاثون دقيقة وسبع وعشرون ثانية، وأمّا في الحدّ الثالث فأربعون دقيقة، وأمّا في الحدّ الرابع فاثنتان وخمسون دقيقة وثلاثون ثانية. وذلك ما كان يحتاج إلى بيانه⊙

ولمّا حسبنا بهذا الوجه في سائر الأبعاد من النقطة التي على سمت الرأس اختلافات المنظر التي تكون في كلّ واحد من الحدود لستّة أجزاء ستّة أجزاء إلى أن انتهينا إلى التسعين التي هي أجزاء الربع، رسمنا جدولاً لتقويم اختلافات المنظر في خمسة وأربعين سطراً أيضاً مقسوماً بتسعة صفوف. /H432/ فاثبتنا في الصفّ الأوّل التسعين الجزء التي هي أجزاء الربع، ومن البيّن أنّا جعلنا تزييدها The scribe correctd it to تزيّدها. بجزأين جزأين، واثبتنا في الصفّ الثاني ما يصيب كلّ قسم من الدقائق من اختلافات المنظر في الشمس، وفي الصفّ الثالث اختلافات منظر القمر في الحدّ الأوّل، وفي الصفّ الرابع فضل اختلافات المنظر في الحدّ الثاني عليها في الحدّ الأوّل، وفي الصفّ الخامس اختلافات المنظر في الحدّ الثالث، وفي الصفّ السادس فضل اختلافات المنظر في الحدّ الرابع عليها في الحدّ الثالث. مثال ذلك في هذه الثلاثين الجزء التي وضعناها فإنّا نضع بإزائها الدقيقة والخمس والعشرين الثانية التي للشمس، ثمّ بعدها السبع والعشرين الدقيقة والتسع الثواني التي للحدّ الأوّل للقمر، ثمّ بعدها الخمس الدقائق والثمان العشرة الثانية التي بها يفضل الحدّ الثاني على الحدّ الأوّل، ثمّ نضع أيضاً الأربعين الدقيقة التي للحدّ الثالث، ثمّ بعد ذلك الاثني العشرة الدقيقة والثلاثين الثانية التي بها يفضل الحدّ الرابع على الحدّ ↑: صح الثالث⊙

وكيما يوقف بسهولة على اختلافات المنظر أيضاً في الأبعاد التي يتلو بعضها بعضاً فيما بين الأبعاد البعيدة والأبعاد القريبة على حسب تلك الأقسام الجزئيّة من قبل اختلافات المنظر الموضوعة في الحدود الأربعة، توضع الدقائق بإزائها أضعفنا إلى هذه الصفوف ↑: صح الثلاثة. ه – خ: أيضاً صفوفاً ثلاثة. /H433/ فأثبتنا فيها هذه الفصول والوجه الذي سلكناه في حسابها أيضاً هو هذا⊙

يد: ليكن فلك التدوير {للقمر} ألف باء جيم H433.5: ΑΒΓΔ حول مركز هاء ومركز فلك البروج والأرض نقطة زاي. وليوصل خطّ ألف هاء دال زاي، ولنخرج خطّ زاي جيم باء وليوصل خطّا باء هاء، جيم هاء ولنخرج على خطّ ألف دال أمّا من نقطة باء فعمود باء حاء، وأمّا من نقطة جيم فعمود جيم طاء. ولننزّل أوّلاً أنّ القمر بعده من نقطة ألف، التي هي البعد الأبعد على الحقيقة وهو الذي يرى بحسب مركز، ه: زاي قوس ألف باء وهي مثلاً ستّون جزءاً، حتّى تكون أيضاً زاوية باء هاء حاء أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فستّون جزءاً، وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فمائة وعشرون جزءاً. /H434/ /T261/ ومن أجل ذلك تصير القوس التي على خطّ باء حاء مائة وعشرين جزءاً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء هاء حاء القائم الزاوية ثلاث مائة وستّون جزءاً وتصير القوس التي على خطّ هاء حاء الأجزاء الباقية إلى نصف الدائرة وهي ستّون جزءاً. فالخطّان إذن اللذان يوتّرانهما أمّا خطّ باء حاء منهما فيكون مائة وثلاثة أجزاء وخمساً وخمسين دقيقة بالأجزاء التي بها قطر هاء باء مائة وعشرون جزءاً، وأمّا خطّ هاء حاء بهذه الأجزاء فستّون جزءاً. لكنّ إذا كان مركز فلك التدوير وهو نقطة هاء على البعد الأبعد من الفلك الخارج المركز كانت نسبة خطّ هاء زاي إلى خطّ هاء باء نسبة ستّين جزءاً إلى خمسة أجزاء وخمس عشرة دقيقة. فالأجزاء إذن التي بها خطّ هاء باء خمسة أجزاء وخمس عشرة دقيقة، يكون بها أمّا خطّ باء حاء فأربعة أجزاء وثلاث وثلاثون دقيقة، وأمّا خطّ حاء هاء فجزءان وثمان وثلاثون دقيقة، وأمّا خطّ حاء هاء زاي بأسره فاثنان وستّون جزءاً وثمان وثلاثون دقيقة. فلأنّ المربّع الذي من خطّ زاي حاء مع الذي من خطّ حاء باء يكون منه المربّع الذي من خطّ زاي باء يكون هذا الخطّ أيضاً اثنين وستّين جزءاً وثمانياً وأربعين دقيقة بالأجزاء التي بها أمّا خطّ زاي ألف، وهو بعد الحدّ الأوّل، فخمسة وستّون جزءاً وخمس عشرة دقيقة، وأمّا خطّ زاي دال، وهو بعد الحدّ الثاني، فأربعة وخمسون جزءاً وخمس وأربعون دقيقة، وأمّا خطّ ألف دال، وهو فضل ما بين هذين الحدّين، فعشرة أجزاء وثلاثون دقيقة. فالفضل إذن بين البعد عند نقطة باء وبين البعد عند الحدّ الأوّل جزءان وسبع وعشرون دقيقة بالأجزاء التي بها الفضل بأسره عشرة أجزاء وثلاثون دقيقة. فلذلك تكون الأجزاء التي بها /T262/ الفضل بأسره ستّون جزءاً ه – خ – صح: دقيقة بها هذا الفضل Toomer, p. 262: the difference at B. أربعة عشر جزءاً. ه – خ – صح: دقيقة
H434.18:ιδ 0 فنضع إذن هذه الأجزاء في الصفّ السابع في السطر الذي فيه نصف الستّين، أعني حيال ه – ص: إنّما وضعت هذه الدقائق من الفضل {...} الثلاين لأنّ نسبة الثلاثين من ربع {الدائرة} كنسبة الستّين من نصفها. و{...} لمّا لم يكن بدّ من إبقاء الربع على {...} وأحتجنا بعد ذلك هنا في فلك {...} وبعده في الفلك الخارج المركز إلى {...} نصف الدائرة وجب لذلك أنّ {...} قطعة من المربّع الذي لم يكن {...} مقام مثليها من النصف الذي {...} إليه {...} لتقوّي فيها و{...}. الثلاثين، من قبل أنّ الأجزاء أيضاً بأسرها التي وضعت في الصفّ الأوّل من الجدول /H435/ وهي التسعون الجزء أنّما يجوز نصف الأجزاء التي بين نقطة ألف وبين نقطة دال وهي مائة وثمانون جزءاً.

وعلى هذا المثال إن وضعنا أيضاً قوس جيم دال بهذه الأجزاء ستّين جزءاً، نبيّن أنّ خطّ جيم طاء أربعة أجزاء وثلاث وثلاثون دقيقة بالأجزاء التي بها خطّ هاء جيم الذي من المركز خمسة أجزاء وخمس عشرة دقيقة، وأنّ خطّ هاء طاء على هذا المثال جزءان وثمان وثلاثون دقيقة. فخطّ زاي طاء الباقي بهذه الأجزاء سبعة وخمسون جزءاً واثنتان وعشرون دقيقة. ولذلك يكون خطّ زاي جيم الموتّر سبعة وخمسين جزءاً وثلثاً وثلاثين دقيقة. فإذا نقصنا هذه من أجزاء الحدّ الأوّل وهي خمسة وستّون جزءاً وخمس عشرة دقيقة، وجدنا الباقي *وهو* ↑وهو↑: خ سبعة أجزاء واثنتان وأربعون دقيقة ه – خ: وهو من الفضل بأسره أربعاً وأربعين دقيقة. فنضع هذه الدقائق في هذا {الصفّ} بعينه بإزاء عدد الستّين من قبل أنّ قوس ألف باء جيم أيضاً هي مائة وعشرون جزءاً.

وأيضاً نقرّ هذه القسيّ على حالها ولنتوهّم مركز هاء على البعد الأقرب من الفلك الخارج المركز وهذا الوضع هو الذي فيه يكون الحدّ الثالث والحدّ الرابع. فلأنّ في هذا الوضع نسبة خطّ هاء زاي إلى خطّ هاء باء هي نسبة ستّين إلى ثمانية. فالأجزاء إذن التي يكون بها خطّ باء هاء ثمانية /H436/ يحصل بها كلّ واحد من خطّي باء حاء، جيم طاء أيضاً إذا وضعت كلّ واحدة من قوسي ألف باء، جيم دال ستّين جزءاً، ستّة أجزاء وستّ وخمسون دقيقة بالأجزاء التي بها خطّ زاي هاء ستّون جزءاً، ويحصل كلّ واحد من خطّي هاء حاء، هاء طاء بهذه الأجزاء أربعة أجزاء. فمن قبل ذلك إذ ↑: اً كان خطّ زاي حاء يصير بهذه الأجزاء أربعة وستّين جزءاً، وخطّ زاي طاء على هذا المثال ستّة وخمسون جزءاً، يكون لذلك خطّ زاي باء أيضاً الموتّر أربعة وستّين جزءاً وثلثاً وعشرين دقيقة، وخطّ زاي جيم ستّة وخمسين جزءاً وستّاً وعشرين دقيقة بالأجزاء التي بها أمّا خطّ زاي ألف، وهو خطّ الحدّ الثالث، فثمانية وستّون جزءاً، وأمّا خطّ ألف دال، وهو الفضل الذي بينه وبين الحدّ الرابع، فستّة عشر جزءاً. فإن نحن إذن نقصنا الأربعة والستّين الجزء والثالث والعشرين الدقيقة من الثمانية والستّين الجزء بقي لنا ثلاثة أجزاء وسبع وثلاثون دقيقة، وهذه الأجزاء تكون من الفضل بأسره وهو ستّة عشر جزءاً ثلاث عشرة دقيقة وثلثاً وثلاثين ثانية. فنضع هذه على ذلك المثال حيال عدد الثلاثين في الصفّ الثامن.

وإن نحن نقصنا الستّة والخمسين الجزء والستّ والعشرين الدقيقة من هذه الثمانية والستّين الجزء بقي لنا أحد عشر جزءاً وأربع وثلاثون دقيقة وهذه الأجزاء تكون من الفضل بأسره وهو ستّة عشر جزءاً ثلثاً وأربعين دقيقة وأربعاً وعشرين ثانية. فنضعها على هذا المثال بإزاء أعداد الستّين في ذلك الصفّ الثامن أيضاً.

فعلى هذا الوجه نثبت الفضول التي تجتمع من قبل نقلة القمر في فلك التدوير، وأمّا الفضول التي تجتمع من قبل مسير فلك التدوير نفسه في الفلك الخارج المركز، فإنّا نسلك في استخراجها هذه السبيل⊙

/H437/ يه: ليكن الفلك الخارج المركز للقمر ألف باء جيم دال حول مركز هاء وقطر ألف هاء جيم ولنتوهّم عليه مركز فلك البروج نقطة زاي. ولنجز عليه خطّ زاي باء دال H435.3: BZΔ ولننزّل أيضاً أنّ كلّ واحدة من زاويتي باء زاي ألف، جيم زاي دال ستّون جزءاً بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً This passage is not found in the English translation. . وذلك يتّفق أمّا إذا كان مركز فلك التدوير على نقطة باء فإذا كان البعد ه – ص: يعني بعد القمر من الشمس. ثلاثين جزءاً، وأمّا إذا كان على نقطة دال فإذا كان البعد مائة وعشرين جزءاً. وليوصل خطّا باء هاء، هاء دال ولنخرج من نقطة هاء عمود هاء حاء على خطّ باء زاي دال.

/T263/ فلأنّ زاوية باء زاي ألف مائة وعشرون جزءاً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً، تكون القوس أيضاً التي على خطّ هاء حاء مائة وعشرين جزءاً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث هاء زاي حاء القائم الزاوية ثلاث مائة وستّون جزءاً، والقوس التي على خطّ زاي حاء الأجزاء الباقية إلى نصف دائرة وهي ستّون جزءاً. فالخطّان إذن اللذان يوتّرانهما أمّا خطّ هاء حاء منهما فيكون مائة وثلاثة أجزاء وخمساً وخمسين دقيقة /H438/ بالأجزاء التي بها خطّ زاي هاء الموتّر مائة وعشرون جزءاً وأمّا خطّ حاء زاي بهذه الأجزاء فستّون جزءاً. فلذلك يكون بالأجزاء التي بها خطّ هاء زاي، وهو الذي بين المركزين، عشرة أجزاء وتسع عشرة دقيقة، والخطّ الذي من مركز الفلك الخارج المركز تسعة وأربعون جزءاً وإحدى وأربعون دقيقة بها ه: أمّا خطّ هاء حاء ثمانية أجزاء وستّ وخمسون دقيقة، وخطّ زاي حاء بهذه الأجزاء خمسة أجزاء وعشر دقائق. ولأنّ المربّع الذي من خطّ باء هاء منقوصاً منه المربّع الذي من خطّ هاء حاء يكون منه المربّع الذي من خطّ باء حاء، يكون أيضاً كلّ واحد من خطّي باء حاء، دال حاء بهذه الأجزاء ثمانية وأربعين جزءاً وثلثاً وخمسين دقيقة. فلذلك يكون أمّا خطّ زاي باء بأسره فأربعة وخمسون جزءاً وثلاث دقائق بالأجزاء التي بها أمّا خطّ زاي ألف، وهو الذي للحدّين الأولين، فستّون جزءاً، وأمّا خطّ زاي جيم، وهو الذي للحدّين الثانيين، فتسعة وثلاثون جزءاً واثنتان وعشرون دقيقة، وأمّا الفضل بينهما فعشرون جزءاً وثمان وثلاثون دقيقة، وأمّا خطّ زاي دال الباقي فيكون بهذه الأجزاء ثلاثة وأربعين جزءاً. ه – صح: وثلاثاً وأربعين دقيقة. فلأنّ الستّين الجزء يزيد أمّا على الأربعة والخمسين الجزء والثلاث الدقائق فبخمسة أجزاء وسبع وخمسين دقيقة، وهذه تكون من الفضل بأسره الذي هو عشرون جزءاً وثمان وثلاثون دقيقة سبع عشرة دقيقة وثمان عشرة ثانية؛ وأمّا على الثلاثة والأربعين الجزء والثلاث والأربعين الدقيقة فيزيد بستّة عشر جزءاً وسبع عشرة دقيقة، وهذه تكون أيضاً من العشرين الجزء والثمان والثلاثين الدقيقة سبعاً وأربعين دقيقة وإحدى وعشرين ثانية.

فمن البيّن أنّا نصع أمّا السبع العشر الدقيقة والثمان العشر الثانية ففي السطر التاسع حيال عدد الثلاثين الذي للبعد، وأمّا السبع والأربعون الدقيقة والإحدى والعشرون الثانية فنعضها حيال المائة والعشرين، أعني أيضاً حيال الستّين، من قبل أنّ البعد الأقرب إذ كان عند التسعين فإنّ بعد الستّين مساوية قوّته لقوّة بعد المائة والعشرين في المسافة بيننا وبينهما⊙

⟨V.18⟩ يح: في وضع جدول لاختلاف المنظر This title doesn’t exist in the English translation.

/T264/ /H439/ وعلى هذا المثال حسبنا في سائر القسيّ الدقائق التي تكون الفضل ه – خ: للفضل على قياس التفاضلات الثلاث التي وضعناها وفعلنا ذلك لكلّ اثني عشر قسماً وهذه الأقسام تصير أيضاً بستّة ستّة في الأعداد التي في الجدول من قبل أنّ المائة والثمانين الجزء التي من الأبعاد البعيدة إلى الأبعاد القريبة ترى في التسعين الجزء التي للجدول⊙

ووضعنا بإزاء كلّ عدد من الأعداد التي تبيّنت ما يصيبها بقسطها من الدقائق التي حصلت بطريق الخطوط. فأمّا ه – خ: ما بين ذلك من الأقسام، فإنّا جعلنا ما وضعناه بإزائها من الزيادة التي تلحق كلّ ستّة أجزاء على تفاضل متساو إذ كان ليس تلحق الزيادات التي توجد لمّا هذا مقداره فضل فيها ه – خ: فيه من قبل الخطوط ه – خ: (شيء) يعتدّ به لا في الدقائق ولا في اختلافات المنظر أنفسها. /H442-3/ وهكذا رسم الجدول⊙

/T265/

/H444/ ⟨V.19⟩ يط: في تقويم اختلافات المنظر

فإذا آثرنا أن ننظر كم يلحق القمر في كلّ واحد من المسيرات من اختلاف المنظر في الدائرة أوّلاً من أعظم الدوائر التي ترسم مارّة به وبالنقطة التي على سمت الرأس، نظرنا كم ه: من ساعة استوائيّة بعد من دائرة نصف النهار في الإقليم المقصود له. فما وجدناه من الساعات أدخلناه في جدول الزوايا التي للإقليم المقصود له والبرج المقصود له. فأخذنا الأجزاء التي حيال تلك الساعة في الصفّ الثاني إمّا بأسرها وإمّا ما يصيب منها الجزء من ساعة ه – خ: وحصّة ما يصير لأجزاء الساعة من ذلك إن كانت معها أجزاء . فكانت لنا هذه الأجزاء هي بعد القمر من النقطة التي على سمت الرأس في الدائرة العظمى التي ترسم مارّة بهما. فندخلها في جدول اختلافات المنظر ثمّ ننظر في أيّ سطر هي من الصفّ الأوّل، فما كان بإزاء ذلك العدد في الصفوف الأربعة التي بعد صفّ اختلافات منظر الشمس تالية له أعني في الصفّ الثالث والرابع والخامس والسادس اثبتنا كلّ واحد على حياله. ثمّ ه – خ: من بعد ذلك أخذنا عدد ه – خ: مسير الاختلاف المقوّم في تلك الساعة بحسب البعد الأبعد الحقيقيّ إمّا هو نفسه ه – خ: وإن كان أقلّ من مائة وثمانين /H445/ وإمّا إن كان زائداً على المائة والثمانين فما يبقى بعده إلى ثلاث مائة وستّين فنصّفنا أبداً ما يؤخذ من الأجزاء على هذه الصفة، ثمّ أدخلناه في هذه الأعداد بأعيانها ونظرنا كم حيال العدد من الدقائق في الصفّ السابع وفي الصفّ الثامن كلّ واحد على حياله. فما وجدناه منها في الصفّ السابع أخذنا بذلك المقدار من الدقائق من الفضل الذي /T266/ في الصفّ الرابع فزدناه أبداً على اختلاف المنظر الذي في الصفّ الثالث وما وجدناه منها في الصفّ الثامن أخذنا بذلك المقدار من الدقائق من الفضل الذي في الصفّ السادس، فزدناه أبداً أيضاً على اختلاف المنظر الذي في الصفّ الخامس. ونظرنا التفاضل بين هذين الاختلافي المنظر، فاثبتناه ه – خ: ونثبت فضلة ما بين اختلاف المنظرين . ثمّ أخذنا الأجزاء التي هي بعد القمر بحركته الوسطى إمّا من جزء الشمس وإمّا من الجزء المقاطر بجزء الشمس، أيّ البعدين كان أقرب، فأدخلناها في الأعداد التي في الصفّ الأوّل، فما وجدناه من الدقائق حيالها في الصفّ التاسع، وهو الأخير، أخذنا بذلك المقدار من الدقائق من التفاضل بين اختلافي المنظر الذي كنّا اثبتناه فما كان زدناه أبداً على أقلّ التفاضلين، أعني على المقوّم من الصفّ الثالث والصفّ الرابع. فما اجتمع من ذلك كان هو اختلاف منظر القمر في الدائرة العظمى التي ترسم مارّة به وبالنقطة التي على سمت الرأس.

/H446/ وقد يوقف من ذلك بسهولة على اختلاف منظر الشمس في مثل هذا الوضع لمّا يحتاج إليه في كسوفات الشمس من قبل الأجزاء الموضوعة في الصفّ الثاني حيال مقدار القوس التي من النقطة التي على سمت الرأس⊙

وكيما نقوّم أيضاً اختلاف المنظر الذي يكون عند ذلك بالقياس إلى فلك البروج في الطول وفي العرض، فإنّا ندخل أيضاً تلك الساعات الاستوائيّة بأعيانها التي هي بعد القمر من دائرة نصف النهار في ذلك القسم بعينه من جدول الزوايا، ثمّ ننظر ما حيال ذلك العدد من الساعات من الأجزاء أمّا إن كان القمر قبل دائرة نصف النهار فما كان من الأجزاء حياله في الصفّ الثالث، وأمّا إن كان بعد دائرة نصف النهار فما كان حياله في الصفّ الرابع. وإن كانت الأجزاء تسعين وما دون اثبتناها، وإن كانت مجاوزة لتسعين اثبتنا ما يبقى بعدها إلى مائة وثمانين. فإن هذا مبلغ أصغر الزاويتين اللتين في هذا التقاطع بالأجزاء التي بها زاوية واحدة قائمة تسعون جزءاً، ثمّ نضعف ما اثبتناه من الأجزاء بعينه ه: الذي {...} ضعف {...} الضعف {...} وما اثبتناه ممّا *هو ما* يبقى بعد التسعين إلى مائة وثمانين وندخله في جدول الأوتار التي في الدائرة. فأيّ نسبة كانت للخطّ المستقيم الذي يوتّر قوس الأجزاء المضعّفة إلى الخطّ الذي يوتّر القوس الباقية إلى نصف الدائرة، فهي نسبة اختلاف المنظر في العرض إلى اختلاف المنظر في الطول /H447/ من قبل أنّ ما كان هذا مقداره من قسيّ الدوائر فليس بينه وبين الخطوط المستقيمة فرقان. فنضاعف عدد الخطوط المستقيمة التي بإزائها باختلاف المنظر الذي يؤخذ في الدائرة العظمى التي ترسم مارّة بالنقطة التي على سمت الرأس ونقسم ما اجتمع على مائة وعشرين كلّ واحد من العددين على حياله. فما حصل من الأجزاء عند القسمة فهو اختلاف المنظر على حسب العدد المقسوم⊙

وبالجملة أمّا في اختلاف المنظر في العرض فمتى كانت النقطة التي على سمت الرأس في دائرة نصف النهار أميل إلى الشمال من النقطة التي في وسط السماء في ذلك الوقت من فلك البروج فإنّ اختلاف المنظر يكون ممّا يلي الجنوب منه؛ ومتى كانت النقطة التي على سمت الرأس أميل إلى الجنوب من النقطة التي في وسط السماء فإنّ اختلاف المنظر في العرض يكون ممّا يلي الشمال.

وأمّا في اختلاف المنظر في الطول، فلأنّ مقادير الزوايا المثبتة في الجدول أنّما تشتمل على الزاوية التي فيما يلي الشمال من الزاويتين اللتين تحيط بهما قطعة متّصلة /T267/ من فلك البروج ه – خ – صح: مع الفلك العظيم المخطوط على سمت الرؤوس من الجانبين. فإنّ اختلاف المنظر في العرض متى كان ممّا يلي الشمال ثمّ كانت الزاوية التي وصفنا أعظم من قائمة، كان اختلاف المنظر في الطول قدماً للبروج، وإن كانت الزاوية أصغر من قائمة كان تلقا البروج. ومتى كان اختلاف المنظر في العرض ممّا يلي الجنوب كان الأمر بالعكس، إن كانت الزاوية الموصوفة أعظم من قائمة كان اختلاف المنظر في الطول /Η448/ على توالي البروج، وإن كانت أصغر من قائمة كانت قدماً للبروج.

ولم يذهب(؟) علينا أنّا قد استعملنا الأمور التي تقدّم بيانها في الشمس على أنّ الشمس ليس يلحقها من اختلاف المنظر شيء محسوس، وأنّ اختلاف المنظر الذي وقف عليه من بعد ذلك فيها أيضاً قد يوقع في تلك الأمور فضلاً ما. وإنّما فعلنا ذلك لأنّا رأينا الزلل الذي يلحق من قبل هذا فيما يرى ليس مقداره مقدار يعتدّ به حتّى نحوج إلى تغيير شيء ممّا تقدّمنا فاستخرجناه من غير أن يعني بما هذا مقداره من القلّة. وكذلك أيضاً فإنّا قنعنا في اختلافات منظر القمر بالقسيّ والزوايا التي تكون عند فلك البروج عن الدائرة العظمى التي ترسم مارّة بقطبي الأفق مكان القسيّ والزوايا التي تؤخذ عند فلك القمر المائل، لأنّ الفضل الذي يكون من قبل ذلك في الاتّصالات الموجبة للكسوفات غير محسوس، ولأنّا لو وضعنا هذا أيضاً لكان تبيينها منشّراً ه – ظ: منتشراً مفتّناً تعسّر حسابه وذلك أنّ أبعاد القمر من العقدة في كلّ واحد من مسيراته في فلك البروج غير محصّل ه: محصّلة بل هي مختلفة النقلة في المقادير وفي الأوضاع أنفسها.

/H449/ وكيما يسهل فهم ما قصدنا له بقولنا هذا، يو: نضع من فلك البروج قطعة ألف باء جيم ومن الفلك المائل للقمر قطعة ألف دال، وننزّل أنّ العقدة نقطة ألف وأنّ مركز القمر نقطة دال، ولنرسم من نقطة دال على زوايا قائمة على فلك البروج قوس دال باء. وليكن قطب فلك الأفق نقطة هاء، ولنرسم قطعة من أعظم الدوائر تمرّ به وبمركز القمر ولتكن قطعة هاء دال زاي، وقطعة تمرّ به وبنقطة باء ولتكن هاء باء. وليكن اختلاف منظر القمر قوس دال حاء، ولنرسم قطعتين تمرّان بنقطة حاء على زوايا قائمة على قوسي باء دال، باء زاي ولتكونا قوسي حاء طاء حاء كاف حتّى يكون بعداه من العقدة في الطول أمّا الصحيح منهما فقوس ألف باء وأمّا الذي يرى فقوس ألف كاف، وبعداه في العرض من دائرة البروج أمّا الصحيح منهما فقوس باء دال وأمّا الذي يرى فقوس كاف حاء. ويكون اختلاف المنظر الذي يرى من قبل قوس دال حاء بالقياس إلى فلك البروج أمّا في الطول فمساوياً لقوس طاء حاء، وأمّا في العرض فمساوياً لقوس دال طاء.

/H450/ فإذا كانت قوس دال حاء التي هي اختلاف المنظر قد يعلم بما تقدّم وصفه إذا كانت قوس هاء دال معطاة، وكلّ واحدة من قوسي دال طاء، طاء حاء اللتان لاختلاف المنظر تكون معطاة إذا كانت زاوية جيم زاي هاء معطاة. وكنّا نحن قد بيّنّا أنّها ه – خ – ص – صح: آنفاً مبلغ القسيّ والزوايا من الدائرة التي تمرّ بالنقطة التي على سمت الرأس التي تحدث بينها وبين النقط المعطاة من فلك البروج وكان أنّما لنا هاهنا معطا من فلك البروج نقطة باء فقط. فظاهر أنّا نستعمل قوس هاء باء مكان قوس هاء دال، وزاوية جيم باء هاء مكان زاوية جيم زاي هاء⊙

/T268/ فأمّا أبرخس فإنّه قد رام تصحيح ذلك أيضاً إلّا أنّا لسنا نجده أصاب فيما أتى به ه – خ: فيه ولا سلك سبيل القياس أصلاً. أمّا أوّلاً فلأنّه *أنّما* ه – صح: فإنّه أنّما  استعمل بعداً واحداً، وهو بعد ألف دال، لا جميع الأبعاد ولا أكثرها وذلك كان واجباً لازماً لمن آثر استقصاء القول في لطيف الأمور فضلاً عن جليلها. ثمّ ثانياً فلأنّه وقع، وهو لا يشعر، في أشياء أكثر وأقبح ممّا هرب منه. وذلك أنّه لمّا كان هو أيضاً قد كان تقدّم فبيّن القسيّ والزوايا التي توجد عند فلك البروج وأنّ من قبل قوس هاء دال إذا كانت معطاة، تستخرج قوس دال حاء، فإنّ ذلك قد بيّنه في القول الأوّل من اختلافات المنظر ه – خ: المناظر.
The margin contains a sign with unclear meaning. استعمل في /H451/ أنّ قوس هاء دال معطاة قوس هاء زاي وزاوية هاء زاي جيم على أنّهما معطاتان.

فإنّه بهذا الوجه لمّا حسب في القول الثاني قوس زاي دال وضع أنّ قوس هاء دال الباقية معطاة. والذي حاد به عن الصواب أنّه لم يقف على أنّ النقطة المعطاة من فلك البروج أنّما هي نقطة باء لا نقطة زاي، ولذلك تكون المعطاة من القوسين قوس هاء باء لا قوس هاء زاي، والمعطاة من الزاويتين زاوية هاء باء جيم لا زاوية هاء زاي جيم. فلذلك لمّا قصد لإصلاح أمر ما وإن كان جريا(؟) اضطربت عليه أمور شتّى لأنّه قد يقع من ذلك فضل بيّن للحسّ جدّاً فيما بين قسيّ هاء دال وبين قسيّ هاء زاي. وذلك أنّ هذه القسيّ ه: يعني قسيّ هاء دال أخرى من تلك ه: يعني قسيّ هاء زاي كثيراً بأن تكون *غير* معطاة، This passage is a translation of a Greek passage in Heiberg’s edition (451:12-13) which was excised by Toomer (p. 268-269, f.n. 83).  فأمّا الفضل الذي بين قوس باء هاء، التي هي بالحقيقة معطاة، /T269/ وبين قوس هاء دال فأكثر ما يكون منه أنّما يختلف بمقدار قوس باء دال فقط في كلّ واحد من الأبعاد من العقدة.

يز: The numbering of the figures starts to differ. The Arabic figure 17 is not found in Toomer’s translation, but it is found in Heiberg p. 452, left side. The Arabic figure 18 corresponds to Toomer’s figure 17 and is found in Heiberg p. 452 right side. وأمّا ما يلزم من قبل الإصلاح الذي يقع بالجهة الصحيحة فقد يقف عليه عياناً بهذا الطريق ليكن فلك البروج ألف باء جيم ودائرة دال باء هاء عليه على زوايا قائمة والقمر ه – خ: أيضاً إمّا على نقطة دال وإمّا على نقطة هاء وبعده من فلك البروج، وهو ه – خ: الذي هو ألف جيم، Toomer, p. 269: ABG في العرض قوسٌ معطاة كقوس باء دال مثلاً أو قوس باء هاء /H452/ حتّى يكون ما عند نقطة باء من فلك البروج من القسيّ والزوايا من الدائرة التي تمرّ بالنقطة التي على سمت الرأس معطاة ويكون المطلوب ↑: خ بة (المطلوبة i.e.,) أنّما هي القسيّ والزوايا التي تكون بحسب نقطة دال أو نقطة هاء.

يح: فإن كان وضع فلك البروج وضعاً يكون به على زوايا قائمةٍ على الدائرة العظمى التي تمرّ بنقطة زاي، ولننزّل أنّها قطب الأفق، وعلى الدائرة العظمى التي تمرّ بهذه النقطة وبنقطة باء كدائرة زاي باء هاء. H452.9: ZB

فمن البيّن أنّ هذه تطابق قوس دال هاء، وتكون الزاوية التي توخذ بحسب نقطتي دال، هاء لا فرق بينها و بين التي وضعت عند نقطة باء وذاك ↑ذاك↑: لك (ذلكi.e., ) أنّ الزاويتين أيضاً اللتين تحدثان عند فلك البروج بهاتين النقطتين ↑النقطتين↑: صح قائمتان وتكون قوس زاي دال أصغر من قوس زاي باء بقوس باء دال، وقوس زاي هاء أعظم منها بقوس باء هاء، وهما أيضاً معطاتان.

يط: This is figure 18 in Toomer’s translation. وإن طابق فلك البروج، وهو ألف باء جيم، الدائرة العظمى التي ترسم مارّة بالنقطة التي على سمت الرأس، /H453/ ووضعنا قطب الأرض ه – ص – صح: الأفق نقطة ألف ووصلنا قوسي ألف دال، ألف هاء كانتا كانتا↑: نت (كانت i.e.,) هاتان مفارقتين لقوس ألف باء وكانت زاويتا باء ألف دال، باء ألف هاء مخالفتين للزاوية التي كانت أوّلاً قائمة /T270/ إلّا أنّ قوسي ألف دال، ألف هاء تكونان معطاتين إذا أجرينا الكلام فيهما كأنّه في الخطوط المستقيمة إذ كان ليس فيما بين ذلك فضل يعتدّ به من قبل أنّ قوس ألف باء وقوسي باء دال، باء هاء معطاتان فإنّ المربّعات التي منها إذا جمعت كان منها المربّعان اللذان من ألف دال وألف هاء ويتّصل بذلك أن تكون زاويتا باء ألف دال، باء ألف هاء ه – خ: أيضاً معطاتين.

ك: This is figure 19 in Toomer’s translation. وإن كان وضع فلك البروج مائلاً، فإنّا إن وصلنا من نقطة زاي وهي قطب الأفق قسيّ زاي باء، زاي جيم دال، All points “H” in Toomer’s text corresponding to Figure 19 correspond to ج in the Arabic. زاي هاء طاء كانت قوس زاي باء معطاة وزاوية ألف باء زاي، ومن البيّن أنّ قوسي باء دال، باء هاء تكونان معطاتين. والتي تحتاج أن تعلم قوسا زاي دال، زاي هاء وزاويتا ألف جيم زاي، ألف طاء زاي. وقد تعلم هذه أيضاً بأن يخرج عمودان ه – صح: من نقطتي هاء، دال على خطّ زاي باء وهما دال كاف هاء لام.

/H454/ فلأنّ زاوية ألف باء زاي معطاة وزاوية ألف باء هاء ألف باء دال ه – صح: أبداً  قائمة فمثلّثا باء دال كاف، باء لام هاء القائما الزاويتين معطتان ولذلك نسبة قوس باء زاي إلى القوسين اللتين تحيطان بالزاوية القائمة ه – ص: معطاة إذ كانت نسبتها إلى قوسي دال باء، باء هاء الموتّرتين معطاة. فتكون لذلك قوسا زاي دال، زاي هاء الموتّرتان معطاتين، ومن أجل ذلك تكون زاويتا دال زاي كاف، ↑كاف↑: لام هاء زاي لام أيضاً معطاتين وهما فضل الزاويتين المطلوبتين. وذلك أنّ زاوية ألف جيم زاي أعظم من زاوية ألف باء زاي بزاوية جيم زاي باء، Toomer, p. 270: DZB وزاوية ألف طاء زاي أصغر من زاوية ألف باء زاي بزاوية هاء زاي لام. وظاهر أنّه إذا وضع البعد في العرض واحداً بعينه أنّ أكثر الفضل أمّا في الزاويا فيكون إذا كانت نقطة باء هي النقطة نفسها التي على سمت الرأس. وذلك أنّه لمّا كان ليس يكون حينئذ عند نقطة باء ولا زاوية واحدة، فإنّ القسيّ التي بين نقطتي دال هاء وبين النقطة التي على سمت الرأس تحدث مع فلك البروج زوايا قائمة؛ /T271/ وأمّا أكثر الفضل بين القسيّ فيكون الوضع هو هذا الوضع، وذلك أنّه لمّا كان ليس يحدث أيضاً عند نقطة باء ولا قوس واحدة، فإنّ القسيّ التي عند نقطتي دال هاء يكون مقدارها مقدار القسيّ التي تحدث /H455/ من ↑من↑: خ عن مجاز القمر في العرض⊙ إذا كانت ه – ص: كانت الدائرة التي تمرّ بالنقطة التي على سمت الرأس على زوايا قائمة على فلك البروج. وذلك أنّ ه –ص: فإنّ قوسي دال زاي، زاي هاء تخالفان حينئذ قوس زاي باء بالمجاز في العرض بأسره.

وأمّا في سائر الأوضاع إذا كانت قوس دال هاء مائلة على قوس زاي باء، فإنّ ما يجتمع من زيادات القسيّ والزوايا تكون إلى القلّة. ولذلك متى كان بعد القمر في العرض عن فلك البروج خمسة أجزاء، كان أكثر فضل اختلاف المنظر قريباً من عشر دقائق. وذلك أنّ أجزاء أعظم ما يكون من فضل القسيّ، وهي خمسة أجزاء، هذا مبلغ الدقائق التي تقع لها من اختلافات المنظر في أعظم ما يكون من الزيادات وأقلّ ه: يعني أقلّ ما يكون من أبعاد القمر عن مركز الأرض. ما يكون من الأبعاد. ومتى كان بعده ه: يعني بعده في العرض عن منطقة البروج. أعظم ما يكون من ↑من↑: خ في مجازه في كسوفات الشمس، ومبلغ ذلك جزء واحد بالتقريب ونصف جزء، فإنّ فضل اختلاف المنظر يكون بهذه العدّة من الدقائق وهي دقيقة واحدة ونصف دقيقة. وإنّما يتّفق مثل ذلك في الفرد⊙ ه – خ: في الفرط

/T272/ فأمّا طريق *هذا* التصحيح للزوايا وللقسيّ فقد يسهل مأخذه على من آثر استعماله باليسير من القول على هذا النحو⊙

/H456/ فنقول بالجملة إنّا نضعف العدد الذي للزاوية ثم ّ ندخله في جدول الأوتار التي في الدائرة وننظر ما حياله والباقي إلى أجزاء زاويتين قائمتين وهي مائة وثمانون جزءاً فنضاعف كلّ واحد من هذين على حدّته بأجزاء العرض، ثمّ نأخذ من كلّ واحد منهما جزءاً من مائة وعشرين فنثبته. فما حصل من العدد من الزاوية الأولى نقصناه من القوس الموضوعة التي من نقطة سمت الرأس متى كان القمر في الجهة التي فيها النقطة التي على سمت الرأس وزدناه عليها متى كان في الجهة المضادّة لهذه الجهة وما حصل من ذلك ضاعفناه بنفسه وزدناه على ما يكون من أجزاء الزاوية الباقية بعد أن يربّع أيضاً وأخذنا ضلع ما يجتمع وكانت ه – خ: لنا على حسب ما قصدنا له القوس المطلوبة قد حصلت⊙ ه – ص: إنّما دخل بضعف الزاوية المفروضة لكون الزاوية المفروضة أبداً مساوية لزاوية باء هاء لام [ه – صح: أو لزاوية باء دال كاف] التي يجب أن يدخل بضعفها. وإنّما يدخل بضعفها وليس يدخل بها بعينها لأنّ نسبتها من قائمتين كنسبة ضعفها الكائنة عند مركز الدائرة المحيطة بمثلّث باء هاء لام من أربع زوايا قائمة ولمّا كانت نسبة هذه الزاوية التي عند المركز من أربع زوايا قائمة كنسبة القوس التي على باء لام من محيط الدائرة المحيطة بمثلّث باء هاء لام وجب أن يدخل في جداول القسيّ والأوتار بالقوس التي مقدارها مقدار الزاوية التي عند المركز إذ تنوب منابها وتقوم مقا{مها} لأنّ تجزئة الدائرة كتجزئة الأربع زوايا قا{ئمة}.

ثمّ نعمد إلى الأجزاء التي أثبتت من الزاوية الباقية فنضربها في مائة وعشرين ثمّ نقسمها على كلّ واحدة من القوسين اللتين وجدنا على حيالها ونأخذ نصفي القوسين الموضوعين في جدول الخطوط المستقيمة بإزاء العددين اللذين يحصلان، ثمّ ننظر فإن كانت القوس التي قصد بتصحيحها ه – خ: لتحصيلها أعظم من الأولى، زدناه على أجزاء الزاوية الأولى وإن كانت أصغر، نقصناه منها فتحصل لنا الزاوية مصحّحة⊙

/H457/ وكيما يظهر ذلك بمثال ننزّل في تلك الصورة التي تقدّم وضعها أنّ قوسي زاي باء خمسة وأربعون جزءاً وزاوية ألف باء زاي ثلاثون جزءاً بالأجزاء التي بها زاوية قائمة تسعون جزءاً وكلّ واحدة من قوسي ه – خ: مع كلّ واحد من مربّعي  دال باء، باء هاء خمسة أجزاء من العرض.

/T273/ فلأنّ الخطّ المستقيم الذي باء زاي ضعف الثلاثين الجزء أعني بإزاء ستّين جزءاً هو ستّون جزءاً والأجزاء الباقية إلى زاويتين قائمتين وهي مائة وعشرون جزءاً بإزائها، خطّ مستقيم مقداره مائة وأربعة أجزاء بالتقريب تكون نسبة قوس باء لام إلى قوس لام هاء نسبة ستّين إلى مائة وأربعة، وهذه هي ه – خ: هذه وهي  نسبة قوس باء كاف إلى قوس دال كاف بالأجزاء التي بها الموتّرة مائة وعشرون جزءاً. فإذا نحن ضاعفنا كلّ واحد من العددين بأجزاء الموتّرة التي هي خمسة أجزاء وأخذنا جزءاً من مائة وعشرين جزءاً منه حصلت لنا كلّ واحدة من قوسي كاف باء، باء لام بهذه الأجزاء جزئين وثلاثين دقيقة، وكلّ واحدة من قوسي دال كاف، هاء لام على هذا المثال أربعة أجزاء وعشرون دقيقة. فالجزءان والثلاثون الدقيقة أوّلاً إن وضع القمر على نقطة هاء، نقصناها من أجزاء قوس زاي باء، وهي خمسة وأربعون جزءاً، من قبل أنّ بعد القمر في العرض هو في جهة النقطة التي على سمت الرأس، أعني من قبل أنّهما جميعاً إمّا أميل إلى الشمال وإمّا أميل إلى الجنوب من فلك البروج، فتحصل لنا قوس زاي لام إثنين وأربعين جزءاً وثلاثين دقيقة؛ وإن كان القمر على نقطة دال، زدناها على تلك الأجزاء /H458/ لضدّ ما ذكرناه، فتحصل لنا قوس زاي كاف سبعة وأربعين جزءاً وثلاثين دقيقة. فنضيف ما يكون من كلّ واحدة من قوسي ه – خ: ثمّ تجمع كلّ واحد من مربّع  ه – صح: {...} على حيالها إلى ما يكون من كلّ واحدة من قوسي. دال كاف، Toomer, p. 273: ZL لام هاء ⁴أعني ما يكون من أربعة ه: على {...}  أجزاء وعشرين دقيقة إلى ما يكون من ه – خ: مربّع  أثنين وأربعين جزءاً ه – صح: وثلاثين دقيقة [ه: وما يكون (ه – خ: مربّع) من سبعة وأربعين جزءاً وثلاثين دقيقة] ونأخذ ضلع ما يجتمع من ذلك كلّ واحد على حياله فتحصل لنا قوس زاي هاء اثنين وأربعين جزءاً. وستّاً وخمسين H458.6: ZE = μβ βς دقيقة بالتقريب، وقوس زاي دال على هذا المثال سبعة وأربعون جزءاً وأربع وخمسون دقيقة⊙ H458.7: ZD = μζ μδ

ثمّ من بعد ذلك نضاعف الأربعة الأجزاء والعشرين الدقيقة مائة وعشرين مرّة ونقسم ما يجتمع من ذلك على الاثنين والأربعين الجزء والستّ والخمسين الدقيقة H458.9: ZE = μβ βς وعلى السبعة والأربعين الجزء والأربع والخمسين الدقيقة H458.9 = μζ μδ كلّ واحد على حياله فتحصل لنا قوس هاء لام اثني عشر جزءاً وثمان دقائق بالتقريب، بالأجزاء التي بها قوس زاي هاء الموتّر مائة وعشرون جزءاً، وقوس دال كاف عشرة أجزاء ونصفاً وثلثاً بالتقريب بالأجزاء التي بها قوس زاي ذال ه – صح: دال الموتّر مائة وعشرون جزءاً. لكنّ بإزاء الخطّ المستقيم الذي طوله اثنا عشر جزءاً وثمان دقائق، قوس مقدارها أحد عشر جزءاً وثلاثة أخماس جزء، وبإزاء الخطّ المستقيم الذي طوله عشرة أجزاء ونصف وثلث قوس مقدارها عشرة أجزاء وثلث بالتقريب. فنأخذ نصفي هذين العددين فأمّا الخمسة الأجزاء والأربعة الأخماس التي هي أجزاء زاوية هاء زاي لام، فإنّا ننقصها من أجزاء زاوية ألف باء زاي وهي ثلاثون جزءاً، /H459/ من أجل أنّ قوس زاي هاء أصغر من قوس زاي باء. فتحصل لنا زاوية ألف طاء زاي أربعة وعشرين جزءاً وخمس دقائق ه – صح: وخُمُساً ؛ وأمّا الخمسة الأجزاء والسدس التي هي أجزاء زاوية دال زاي كاف ↑كاف↑: لام فإنّا نزيدها على الثلثين الجزء أنفسها من قبل أنّ قوس زاي دال أعظم من قوس زاي باء، فتحصل لنا زاوية ألف جيم زاي خمسة وثلاثين جزءاً وسدس جزء، وذلك ما قصدنا لأن ندلّ على طريقه⊙

تمّت المقالة الخامسة من كتاب بطلميوس المنسوب إلى التعاليم وهي تسعة عشر قولاً. ولواهب العقل الحمد كثيراً كما هو أهله ومستحقّه. ه: بلغ العرض بالأمّ والحمد لله كثيراً على عونه.