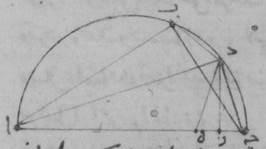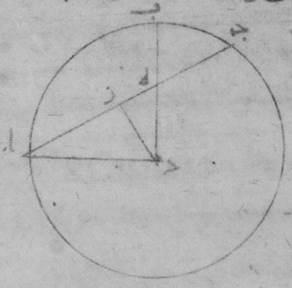بسم الله الرحمن الرحيم

عونك يا واحد

جمل ما في المقالة الأولى من كتاب بطلميوس القلوذي المنسوب إلى التعاليم وهو الكتاب الكبير المعروف بالمجسطي ترجمه من اللسان اليونانيّ إلى اللسان العربيّ لأبي الصقر إسمعيل بن بلبل إسحق بن حنين بن إسحق المتطبّب وصحّحه ثابت بن قرّة الحرّانيّ

وكلّ ما هو في أضعاف هذا الكتاب وفي شيء منه وموقع فيه وفي حواشيه من شرح وتلخيص وإيضاح وتبيين وتسهيل وتقريب واستدراك وتنبيه وإصلاح وتصحيح فهو لثابت بن قرّة الحرّانيّ.

الأولى: صدر الكتاب؛ الثانية: في مراتب أنواع هذا العلم؛ الثالثة: في أنّ السماء كريّة وحركتها أيضاً كريّة؛ الرابعة: في أنّ الأرض بجلّ أجزائها كريّة عند الحسّ بالقياس إلى الكلّ؛ الخامسة: في أنّ الأرض في وسط السماء؛ السادسة: في أنّ الأرض كالنقطة عند السماء؛ السابعة: في أنّ الأرض ليست لها حركة انتقال؛ الثامنة: في أنّ أصناف الحركات الأوّل اللواتي في السماء اثنتان؛ التاسعة: في العلوم الجزئيّة؛ العاشرة: في مقدار الخطوط المستقيمة التي تقع في الدائرة؛ الحادية عشرة: في القوس التي بين الانقلابين؛ الثانية عشرة: فيما يقدّم فيو⟨طّأ للبراهين⟩ على المعاني الكريّة؛ الثالثة عشر: في معرفة القسيّ الجزئيّة من دائرة نصف النهار التي تنفرز فيما بين معدّل النهار وبين فلك البروج؛ الرابعة عشر: في معرفة ما يطلع في الكرة حيث تكون منتصبة من معدّل النهار مع قسيّ فلك البروج المفروضة.

⟨I⟩ ابتداء المقالة الأولى من كتاب بطلميوس المنسوب إلى التعاليم

/T35/ ⟨I.1⟩ آ: صدر الكتاب

نعم ما فعل فيما أرى الذين استقصوا علم الفلسفة، يا سورس، في تقديمهم ه - صح: إفرادهم جزء الفلسفة النظريّ على ↑على↑: عن العمليّ؛ لأنّه وإن كان الجزء العمليّ من قبل أن يكون عمليّاً فهو نظريّ، فإنّ ما يوجد من الخلاف بينهما عظيم ليس من قبل أنّ بعض الفضائل الخلقيّة قد يمكن أن يكون في كثير من الناس بلا تعلّم. وأمّا الأشياء النظريّة فجميعها لا يمكن أن يصير إلى معرفتها أحد بلا تعلّم فقط، لكن من قبل أنّ المؤدّي إلى الغاية المطلوبة أمّا في الجزء العمليّ فكثرة المواظبة على العمل، وأمّا في الجزء النظريّ فالازدياد من النظر. ولذلك رأينا أنّه ينبغي أن يكون إصلاحنا ه: يريد بالإصلاح للعمل إصلاح أخلاق النفس للعمل نتفقّده ه – خ: (نعتقده) بأوهامنا /H5/ لئلّا يزول ولا في يسير من الأمور عن الفحص ↑الفحص↑ خ: التأمل المؤدّي إلى الحال الجميلة المنتظمة ونجعل أكثر تشاغلنا في طلب علم الأشياء النظريّة، لكثرتها وفضل حسنها، ه: جنسها وخاصّة في الأمور التي خصّت بأن سمّيت تعليميّة. فما أحسن ما قسّم أرسطاطاليس الجزء النظريّ إذ قسّمه ه: هذه القسمة موجودة في المقالة الخامسة من كتابه فيما بعد الطبيعة إلى أجناس أوّل ثلاثة إلى الطبيعيّ والتعليميّ والإلهيّ. لأنّ قوام {***} الشيء بالعقل و{***} لصورة النوع الذي به يفارق الشيء غيره {***} ما هو جميع الأشياء من العنصر والصورة والحركة؛ وليس يمكن أن يكون واحد من هذه الثلاثة على الانفراد موجوداً بالفعل، وقد يمكن أن يعقّل كلّ واحد منها دون غيره. فالعلّة الأولى لحركة الكلّ الأولى، إذا توهّمنا الحركة مفردة، رأينا أنّه إله "لا مرئيّ" ولا متحرّك، وسمّينا صنف البحث عنه إلهيّاً، وهذا العقل نعقّله في أعلى علوّ العالم فقط مبايناً ألبتّة للجواهر المحسوسة. /T36/ وأمّا صنف البحث عن الكيفيّة العنصريّة الدائمة التعاقب كالبياض ه – اخ: والحرارة والحلاوة واللين وأشباه ذلك فيسمّى طبيعيّاً؛ والجوهر الذي فيه هذه يوجد على الأكثر في الأشياء التي يعرض لها الفساد التي هي دون كرة القمر. وأمّا الصنف المبيّن عن/H6/ حال الصور وحركات النقلة وهو الذي يبحث عن الشكل والعدد والعظم والمكان والزمان وما أشبه ذلك فيسمّى تعليميّاً. والجوهر الذي فيه هذه كالوسط بين ذينك الجوهرين ليس فقط لأنّه ه – خ: من قبل أنّه قد يعقّل بالحسّ وبغير الحسّ، لكن من قبل أنّه مشترك أيضاً لجميع الأجسام ما يفسد منها وما لا يفسد: فهو فيما يفسد يتغيّر معه في الصورة التي لا تفارق المادّة، وفيما لايفسد أعني في الطبيعة السماويّة تبقى في صورته بلا تغيّر.

فلمّا رأينا أنّ جنسين من الثلاثة الأجناس التي يبحث عنها الجزء النظريّ أنّما يدركان من جهة ما هو أشبه وأجزى لا بالمعرفة الحقيقيّة أمّا الإلهيّ فلاستعلائه ه – خ: فلاستغنائه عن الظهور للحسّ وأن يحاط به، وأمّا الطبيعيّ فلأنّ العنصر غير ثابت الحال خفيّاً؛ ولذلك لم يرج اتّفاق الحكماء فيهما. ورأينا أنّ الجزء التعليميّ فقط إن استقصينا فيه البحث استفدنا به علماً حقّيّاً ثابتاً، لأنّ براهينه تكون بطريق لا شكّ فيه وهي العدد والهندسة دعانا ذلك إلى العناية بهذا العلم كلّه بقدر الطاقة أكثر من جميع الأشياء وخاصّة بعلم الأجرام السماويّة. لأنّ البحث في هذا العلم عن أشياء على حال واحدة دائماً. /H7/ ولذلك يمكن أن يكون هذا العلم في نفسه لثباته وحسن نظامه على حال واحدة دائماً وهذه خاصّة العلم الحقيقيّ. ه – ج: إنّ العلم الحقيقيّ هو الذي {...} دائم على حال واحد{ة} ويمكن أيضاً أن يعيّن على علم الجنسين الآخرين لأنّه يطرق إلى العلم الإلهيّ أكثر من تطريق جميع العلوم، وذلك لأنّا بهذا العلم فقط نقدر على الوصول إلى تصوّر ذلك العقل الذي يكون بلا حركة ولا يشوب ه – خ: ولا سيو{ف} المادة من قبل قربه ه: الهاء التي في قربه راجعة على العلم ممّا يلزم الجواهر المحسوسة المحرِّكة والمحرَّكة التي هي دائمة لا متغيّرة، من ↑من↑ اخ: عن الأدوار ونظام الحركات. وعلم الأجرام السماويّة ينفع في العلم الطبيعيّ منفعة عظيمة لأنّ جمل ه – خ: جلّ خواصّ الجوهر العنصريّ أنّما يتبيّن من خاصّة حركة النقلة لأنّا نعرف أن كان الجرم يفسد أو لا يفسد إذا نظرنا في حركته هل هي على الاستقامة أو على استدارة ونعرف أن كان الجرم ثقيلاً أو خفيفاً أو منفعلاً أو فاعلاً إذا نظرنا في حركته هل هي إلى الوسط أو من الوسط. /T37/ وقد يدعونا أيضاً علم الأجرام السماويّة إلى الفضيلة في العقل والخلق أكثر من جميع العلوم لمّا نرى في الأجسام السماويّة من ثبات الحال وحسن الترتيب والاعتدال وأنّه ليس في شيء من أمرها فضل ولا ما لا يحتاج إليه وتدعونا معرفة هذا الجنس إلى العشق له وتكتسب النفس بذلك عادة وطبيعة لما يشبه هذه الحال.

فنحن ملتمسون أنّما العشق لهذه الحال الثابتة بتعلّمنا ما قد أدركه من ه – اخ: كان قبلنا /H8/ من هذا العلم ممّن استقصى الفحص عنه وبأن نزيد على ذلك بحسب ما أفادنا الزمان الذي فيما بيننا وبينهم. ونجمع كلّ ما قد رأينا أنّه قد وضح إلى هذه الغاية من هذا العلم في كتاب بما يمكن ه – اخ: أمكن من الإيجاز وبقدر ما يستطيع فهمه من قد اتّجه ه – خ: أنجد في هذا العلم قليلاً. ولكي يكون الكتاب تامّاً فإنّا نضع جميع ما ينفع في علم الأجرام السماويّة على النظام الذي ينبغي ولئلّا يطول القول نمرّ ما استقصى الأوائل علمه صفحاً. ونشرح بقدر الطاقة ما لم يدركه الأوائل و ه – اخ: أولم يبلغوا من إدراكه ما ينبغي.

⟨I.2⟩ ب: في مراتب أنواع هذا العلم

إنّ أوّل ما ينبغي أن نبدأ به في هذا الكتاب هو النظر في جملة حال كلّ الأرض عند كلّ السماء. وأوّل ما ينبغي أن نأخذ فيه من أنواعه بعد ذلك طلب العلم بوضع الفلك ه: يعني فلك البروج الدائر المائل والمواضع المسكونة من الأرض ثمّ العلم باختلاف آفاقها على الترتيب الذي هو من قبل العرض. /H9/ فإنّه إذا يقدّم العلم بما ذكرنا كان البحث عمّا سوى ذلك أسهل سبيلاً. والثاني ممّا ينبغي أن نأخذ فيه طلب علم حركة الشمس والقمر وما يلزمهما لأنّه لا يمكن قبل إدراك هذه استقصاء العلم بالكواكب. وآخر ما ينبغي أن نأخذ فيه على ما يشبه النسق القول في الكواكب. وواجب أن نقدّم القول في كرة الكواكب الثابتة /T38/ ثم نلحق بذلك القول في الكواكب الخمسة التي تسمّى المتحيّرة. ونلتمس أن نبيّن كلّ واحد ممّا ذكرنا باستعمالنا الأصول والمبادي التي تؤدّي إلى معرفتها وهي الأشياء الظاهرة البيّنة بالحسّ والأرصاد التي لا شكّ فيها التي رصدها الأوائل والتي رصدنا ↑نا↑ اخ: ت في زماننا ونبنى عليها كلّ ما يتّبعها بطرق البراهين الهندسيّة.

وأمّا الجملة التي تنبغي أن نقدّم فهي أن تبيّن أنّ السماء كريّة، وحركتها كريّة؛ وإنّ شكل الأرض بجلّ أجزائها كريّ في الحسّ؛ وموضعها في وسط كلّ السماء كالمركز؛ وأنّها في البعد والعظم كالنقطة عند كرة الكواكب الثابتة؛/H10/ وأنّه ليست لها حركة انتقال. وسنقدّم قليلاً من القول في تبيين كلّ واحد من هذه للتذكرة.

⟨I.3⟩ ج: في أنّ السماء كريّة وحركتها أيضاً كريّة

إنّ أوّل توهّم القدماء لما ذكرنا أنّما كان لأنّهم رأوا الشمس والقمر وسائر النجوم متحرّكات أبداً من المشارق إلى المغارب وحركتها على دوائر مواز بعضها لبعض، تبدأ من أخفض السفل فترتفع قليلاً قليلاً إلى أرفع العلوّ، كأنّها ترتفع على ↑على↑ صح: عن الأرض، ثمّ تهبط بعد ذلك على تلك النسبة إلى أخفض السفل كأنّها تقع في الأرض وتغيب ألبتّة، ثمّ تمكث بعد ذلك زماناً غائبة ثمّ تطلع أيضاً وتغيب كأنّه ابتداء أخر. ووجدوا هذه الأزمان التي من الطلوع إلى الغروب ومن الغروب إلى الطلوع ومواضع الطلوع والغروب تتكافأ في جلّ الأمر على ترتيب واحد ومثال واحد.

وكان أكثر ما قاد أفكارهم إلى إثبات الحركة الكريّة مدار النجوم الأبديّة الظهور التي ترى مستديرة تجول حول مركز واحد بعينه هو القطب. وذلك أنّ تلك النقطة من الكرة السماويّة واجب أن تكون /H11/ القطب باضطرار: وما كان من النجوم أقرب إلى النقطة يدور في دوائر صغار، وما كان منها أبعد من النقطة يدور في دوائر عظام بقدر القرب والبعد حتّى ينتهى البعد إلى ما يغيب. وما يغيب منها ممّا هو أقرب إلى الأبديّة الظهور فهو أقلّ مكثاً في الغيبة، وما هو أبعد فهو أكثر مكثاً بقدر القرب والبعد. فهذا وشبهه فقط كان أوّل ما سدّد آرائهم وأثبت في أفكارهم أنّ حركة السماء كريّة. ومن بعد ذلك فإنّ النظر الفكريّ قاد إلى فهم سائر ما يتّبع ذلك من قبل أنّ جميع ما يرى فيها من الأمور الظاهرة يدلّ على خلاف ما عليه آراء المخالفين.

وذلك أنّا نهبّ أنّ إنساناً قال إنّ حركة النجوم بالاستقامة إلى ما لا نهاية له، كما قد ظنّ بعض الناس، /T39/ فبأيّ الوجوه إذا يمكن أن نرى كلّ واحد منها في كلّ يوم طالعاً علينا من مطلع واحد؟ وكيف أمكن أن رجعت إلى مطالعها وحركتها بالاستقامة إلى ما لانهاية له؟ وكيف، إن كانت ترجع بالاستقامة، لا ترى راجعة؟ وكيف لا يغيّرها البعد فينقص من نورها وعظمها قليلاً قليلاً ثمّ تغرب بل قد ترى خلاف ذلك أنّها تعظم عند غروبها ثمّ تستتر قليلاً قليلاً كأنّها تنقطع ببسيط الأرض.

وما قد قيل أيضاً من أنّها تسرج ه – اخ: تستسرج من الأرض ثمّ بعد ذلك تطفأ فيها، فإنّه أبعد شيء من الواجب. /H12/ وأنّ نحن سلّمنا أن يكون هذا النظام الجليل الذي في عظم أقدار النجوم وعددها وأبعادها ومواضعها وأزمانها كان عبثاً وباطلاً؛ وأن يكون طبيعة بعض نواحي الأرض موقدة وبعضها مطفئة، بل الموضع الواحد لبعض الناس موقد ولبعضهم مطفئ؛ وأن تكون نجوم ما بأعيانها لبعض الناس موقدة أو مطفأة، ولبعضهم لم توقد بعداً ولم تطفأ: فإن سلّمنا هذا على أنّه ضحكة وسخريّة، فما عسى أن يقول أهل هذا الرأي في النجوم الأبديّة الظهور التي لا تطلع ولاتغرب؟ ولأيّ الأسباب لا تكون النجوم الموقدة المطفأة تطلع وتغرب في كلّ موضع والظاهرة التي لا تطلع ولا تغرب ولا تكون ظاهرة أبداً في كلّ موضع فوق الأرض؟ فإنّه ه – ج: فإنّ تلك النجوم بأعيانها ليست في كلّ المواضع تشرق وتغرب أبداً والظاهرة التي لا تشرق ولا تغرب ليست ظاهرة أبداً في كلّ موضع {***}. ليس لقائل أن يقول إنّ نجوماً بأعيانها توقد وتطفأ عند بعض الناس دائماً ولاتعرض لها ولا واحد من هذين عند بعض الناس. إذ كان قد يوجد عياناً أنّ نجوماً ما بأعيانها في ⟨بعض المواضع⟩ تطلع وتغرب وفي بعضها لا تطلع ولا تغرب.

وجملة، أقول أنّ أيّ الأشكال ادّعاه مدّع في الحركات السماويّة غير الكريّ فبالاضطرار أن تكون الأبعاد التي من الأرض إلى المواضع العلويّة مختلفة حيث ما كانت الأرض موضوعة ه – اخ: وسط الكلّ أو زائلة عن وسط الكلّ وكيف ما كانت. ولذلك كان ينبغي أن يرى عظم أقدار النجوم وأبعاد بعضها من بعض /H13/ مختلفة في الموضع الواحد في كلّ دورة، لأنّها تكون مرّة في بعد أكثر ومرّة في بعد أقلّ. وليس نرى شيأً من ذلك. والذي نرى من الزيادة في عظمها إذا كانت عند الآفاق فليس أنّما نراها كذلك لقربها وقلّة بعدها عند الآفاق، ولكن لأنّ بخار الرطوبة التي تحيط بالأرض يصير فيما بين البصر وبينها فنرى كذلك، كما أنّ ما نلقى في الماء يرى أعظم وكلّما رسب إلى أسفل كان أزيد في عظمه.

وقد يدلّ أيضاً على إثبات الشكل الكريّ أنّه لا يمكن اتّفاق القياسات بالآلات إلّا على هذا الوجه وبهذا الشكل فقط. وإنّ الحركة السماويّة غير عسرة بل هي أسلس الحركات وأسهلها وأسهل الأشكال حركة من /T40/ البسيطات الدائرة ومن المجسّمات الكرة؛ وإنّ الأشكال المختلفة التي ه – ج: قوله: إنّ {...} إحاطتها متساوية {...} منها أكثر زوايا فهو أعظم قدراً. إحاطتها ه – ج: في دوائر متساوية ما هو منها أكثر زوايا فهو أعظم قدراً ولذلك وجب أن ه: تكون الدائرة أعظم السطوح والكرة أعظم المجسّمات والسماء أعظم ممّا سواها ه: يعني أنّ السماء لو لم يكن شكلها كريّاً لكانت إذا كان شكلها كريّاً والإحاطة و{...} أعظم، فلمّا قصد{...} لأن يكون أعظم الأجسام كلّها التي إحاطتها متساوية لإحاطتها جعل شكلها كريّاً. فصارت السماء بذلك أعظم ممّا سواها من الأجسام أعني التي كان يمكن أن تكون إحاطتها مساوية لإحاطتها إلّا إن شكلها غير كريّ. من الأجسام.

وقد نجد السبيل إلى علم ذلك أيضاً من أمور طبيعيّة منها. /H14/ إنّ الأثير، وهو جرم الفلك، ألطف من جميع الأجسام وأشدّ شبهاً بعضه ببعض؛ والذي يشبه أجزاؤه بعضها بعضاً فقد يشبه بسيطه بعضه بعضاً؛ والذي يشبه بسيطه بعضه بعضاً اثنان فقط من المسطوحات الدائرة ومن المجسّمات الكرة. وإذ ليس الأثير سطحاً وأنّما هو مجسّم فقد بقي أن يكون كريّاً. ومنها أنّ جميع الأجرام الأرضيّة التي يعرض لها الفساد فطرت في أشكالها من قطع استدارات مختلفة الأجزاء، وجميع الأجرام السماويّة فطرت في أشكالها كريّة متشابهة الأجزاء. لأنّها لو كانت مسطوحة أو بشكل القصعة لم يكن يراها كلّ من يراها في وقت واحد ومن نواح مختلفة من الأرض مستديرة. فمن أجل ذلك ينبغي أن يكون الأثير المحيط بها إذ هو شبيه بطبيعتها كريّاً ولأنّ أجزائه متشابهة تكون حركته مستديرة باستواء.

⟨I.4⟩ د: في أنّ الأرض بجلّ أجزائها كريّة عند الحسّ بالقياس إلى الكلّ ه: يعني كلّ الأرض أي جملتها

ويستبين لنا أنّ الأرض بجلّ أجزائها كريّة الشكل في الحسّ، من أنّا نرى الشمس والقمر /H15/ وسائر النجوم ليست تطلع وتغيب في كلّ موضع في وقت واحد، ولكن طلوعها على أهل المشرق وغيبوبتها عنهم قبل طلوعها على أهل المغرب وغيبوبتها عنهم. ونعلم ذلك من أنّا نجد أرصاد أزمان الكسوفات، ولاسيّما القمريّة، التي كانت في زمان واحد، لم نجدها الذين أثبتوا ذكرها من القدماء في ساعات متساوية البعد من نصف النهار. ونجد أبداً الساعات التي أثبتها من قاس من المشرقيّين أكثر تأخّراً عن نصف النهار ممّا أثبت ذكره المغربيّون. ولأنّا نجد أيضاً اختلاف الساعات على قدر البعد فيما بين المواضع يجب أن نقول أنّ بسيط الأرض كريّ لأنّ تشابه جلّ أجزاء الأرض في الاستدارة يستر أبداً في المواضع الذي الذي؛ صح: التي يتلو بعضها بعضاً على قياس واحد.

ولو كان شكل الأرض غير كريّ لم يكن كذلك، ويستطيع أن يعلم أيضاً ذلك مّما أقول. لو كانت الأرض مقعّرة، لكانت ترى النجوم تطلع أوّلاً على المغربيّين؛ ولو كانت مسطوحة لكانت تطلع /T41/ على جميع أهل الأرض في وقت واحد؛ ولو كانت مثلّثة أو مربّعة أو شكلاً آخر من الأشكال الكثيرة الزوايا لكانت أيضاً النجوم تطلع في وقت واحد على جميع من يسكن في سطح واحد وعلى خطّ واحد مستقيم. وليس يرى شيء من ذلك. وليست الأرض أيضاً بأسطوانيّة الشكل، بسيط استدارتها إلى المشرق والمغرب،/H16/ وسطحا قاعدتيها إلى قطبي العالم، كما ظنّ قوم أنّه أقرب إلى الإقناع؛ لأنّها لو كانت كذلك لم يكن أحد ممّن يسكن على استدارتها يرى شيأً من النجوم ظاهراً أبداً، بل كانت النجوم إمّا كلّها تطلع وتغرب أبداً على جميعهم، وإمّا كواكب بأعيانها بعدها من واحد واحد من القطبين بعد سواء أبديّة الخفاء عند جميعهم. وقد نرى أنّا كلّما سرنا إلى ناحية الشمال فبقدر إمعاننا فيها يكثّر ما يغيب عنّا من النجوم الجنوبيّة وما يظهر لنا من الشماليّة. فيستبين لنا باستواء ما تستره استدارة الأرض عنّا في هاتين الجهتين إذا قيس بعضه إلى بعض في جميع نواحيها ↑نواحيها↑: النواحي أنّها كريّة.

وكذلك أيضاً إذا نحن سرنا في البحر إلى جبال أو إلى مواضع شامخة مشرفة من أيّ الآفاق وإلى أيّها ه – اخ: كان نرى تزيّدها قليلاً قليلاً كأنّها تطلع من البحر وكأنّها كانت راسبة فيه قبل ذلك؛ فيستبين لنا أنّ ذلك من قبل استدارة بسيط الماء.

⟨I.5⟩ ه: في أنّ الأرض في وسط السماء

ومن بعد علّمنا بهذا، إن طلبنا أن نعلم موضع الأرض، /H17/ وجدنا أنّه إنّما يكون ما ظهر لنا فيها كما نرى إذا نحن أثبتنا موضعها وسط السماء كالمركز في الكرة فقط. لأنّه إن لم يكن كذلك، فلا محالة أن تكون الأرض إمّا خارجة من المحور متساوية البعد من كلّ واحد من القطبين؛ وإمّا ثابتة على المحور مائلة إلى أحد القطبين ⟨وإمّا خارجة من المحور مائلة إلى أحد القطبين⟩. والذي نردّ به على من ادّعى أنّ موضعها هو الأوّل من الثلاثة، فهو ما نصف إن توهّمناها زائلة بأناسٍ عن الوسط إلى فوق أو إلى أسفل، فقد يعرض لهم إذا كانوا في الموضع الذي فيه الكرة منتصبة ألّا يستوي ألبتّة عندهم النهار والليل، لأنّ الأفق يفصل ما فوق الأرض وما تحتها من السماء بغير استواء حينئذ لا محالة؛ وإذا كانوا في الموضع الذي فيه الكرة مائلة، يعرض لهم إمّا أن لا يستوي أيضاً عندهم النهار والليل ألبتّة وإمّا إن كان عندهم استواء ألّا يكون ذلك في المجاز الأوسط بين الانقلاب الصيفيّ والانقلاب الشتويّ، لأنّ هذين البعدين يكونان باضطرار غير متساويين، لأنّ الدائرة التي تقطعها الأفق حينئذ بنصفين ليس هي الدائرة الاستوائيّة التي هي أعظم الدوائر التي تدار على قطبي حركة الكلّ، وإنّما هي واحدة من الدوائر التي توازيها إمّا من التي إلى الشمال منها وإمّا من التي إلى الجنوب. /H18/ وقد ثبت عند جميع الناس أنّ هذين البعدين متساويان في كلّ موضع بما وجدوا من مساواة تزيّد النهار المعتدل في طوله إلى أن ينتهي إلى أطول طوله في /T42/ الانقلابات الصيفيّة للتنقّص في طوله إلى أن ينتهي إلى أقصر قصره في الانقلابات الشتويّة. وإن توهّمنا الأرض زائلة بأناسٍ إلى ناحية المشرق أو المغرب، فقد يعرض لهم أن لا يروا عظم أقدار النجوم ولا أبعادها متساوية على حال واحدة في أفق الصباح وأفق المساء وألّا يكون عندهم الزمان الذي من المشرق إلى وسط السماء مساوياً للزمان الذي من وسط السماء إلى المغرب. وكلّ ذلك خلاف لما يظهر.

والذي نرد به على من ادّعى أنّ موضع الأرض هو الثاني من الثلاثة إذا كانت على المحور ومائلة إلى أحد القطبين. فهو إنّها لو كانت على هذه الصفة لكان بسيط الأفق في كلّ إقليم لا يفصل ما فوق الأرض وما تحتها من السماء بمساواة، بل يفصله باختلاف في وجوه شتّى دائماً وكلّ واحد منها مختلف في نفسه وكلّ واحد عند الآخر. ولم يكن الأفق يمكن أن يفصل السماء بنصفين إلّا حيث تكون الكرة منتصبة فقط وأمّا في الميل الذي يصير أقرب القطبين أبديّ الظهور، فكان يصغّر ما فوق الأرض ويعظّم ما تحتها دائماً ولذلك كان يقطع سطح هذا الأفق الدائرة العظيمة التي تمرّ على أوساط البروج بغير مساواة. /H19/ وذلك ما لا يظهر هكذا، لأنّ جميع الناس يرون ستّة بروج أبداً فوق الأرض ظاهرة والستّة الباقية غائبة؛ ثمّ من بعد ذلك تظهر الستّة الغائبة فوق الأرض وتغيب الستّة الآخر الباقية. فيتبيّن من ذلك أنّ قطع الأفق لدائرة البروج يكون أبداً بنصفين من قبل أنّ كلّ واحد من نصفي هذه الدائرة بكماله، يكون تغيّبه مرّة فوق الأرض ومرّة تحتها.

وبالجملة كان يعرض لو لم يكن وضع الأرض تحت دائرة معدّل النهار، وكان مائلاً إلى أحد القطبين إلى الشمال أو إلى الجنوب إلّا يكون ظّل المقاييس المشرقيّ في استواء النهار مع ظلّ المقاييس المغربيّ على خطّ واحد مستقيم على السطوح الموازية للأفق وقد نرى استوائها على خطّ واحد في كلّ موضع.

ومن هنالك يستبين أنّه لا يثبت إدّعا من ادّعى أنّ موضع الأرض هو الثالث من الثلاثة التي ذكرنا لأنّ كلّ ما نعرض في الموضعين الأوّلين من خلاف ما يظهر يجتمع في الثالث.

وبالجملة أقول أنّه كان يتغيّر ويتبدّل ألبتّة ترتيب الزيادة والنقصان في النهار والليل إن لم تكن الأرض موضوعة في الوسط. ولا يمكن أن تكون الكسوفات القمريّة في كلّ نواحي السماء في مقابلة القمر الشمس على القطر، /H20/ لأنّه كان يكون كثيراً ما لا تستره الأرض في المقابلة لكن في الأبعاد التي تكون أقلّ من نصف دائرة.

⟨I.6⟩ و: في أنّ الأرض كالنقطة عند السماء

إنّ أعظم ما يعلم به أنّ الأرض في الحسّ عند البعد الذي ينتهي إلى فلك الكواكب الثابتة كالنقطة أنّ عظم أقدار النجوم وأبعاد ما بينها ترى في كلّ موضع، في وقت واحد، متساوية متشابهة كما وجدنا بالأرصاد التي كانت لأمور بأعيانها في أقاليم مختلفة في وقت واحد غير مختلفة ولا مغادرة ولاشيء يسير. ووجدنا حكم مقاييس الظلّ في أيّ النواحي وضعت من الأرض، ومراكز ذوات الحلق، كحكم مركز الأرض الحقيقيّ؛ وترى الأشياء التي ترى بالقياس بها ودور الظلّ موافقة للأصول الموضوعة للأشياء التي تظهر كما كانت تكون لو كانت على النقطة الوسطى من الأرض.

والدلالة الواضحة على أنّ هذا كما ذكرنا أنّ السطوح التي تخرج من أبصارنا في كلّ موضع التي تسمّى آفاقاً تقطع أبداً كرة السماء بأسرها بنصفين. /H21/ ولم يكن يمكن أن يكون ذلك لو كان عظم الأرض محسوساً عند بعد السماء وأنّما كان السطح الذي يمرّ على نقطة مركز الأرض وحده فقط يقطع الكرة بنصفين وأمّا في الأصل: فأمّا السطح الذي يمرّ على أيّ موضع كان من بسيط الأرض فإنّه يصير أبداً الأجزاء التي تحت الأرض أعظم من التي فوقها.

⟨I.7⟩ ز: في أنّ الأرض ليست لها حركة انتقال

وبمثل الذي قد استبان به فيما تقدّم أنّ الأرض ليست بخارجة عن المركز يتبيّن أنّه لا يمكن أن يكون للأرض حركة إلى شيء من النواحي ولا نقلة ألبتّة عن موضع المركز لأنّها لو انتقلت لعرضت تلك الأعراض التي كانت تعرض لو كان موضعها غير الوسط. ولذلك رأيت أنّ الفحص عن أسباب الحركة التي إلى الوسط أيضاً فضل بعد أن قد استبان مرّة أنّ الأرض في الوسط من العالم، وأنّ الثقال كلّها ترجحن إليها. وأيسر ما يظهر ممّا يقرب مأخذه في وجود ما ذكرنا أنّ مع الذي قد بيّنا من أنّ شكل الأرض كريّ وموضعها وسط الكلّ /H22/ فإنّ حركات الأجسام الثقال الخاصّيّة لها وجهات الحركة تكون في كلّ وقت وفي كلّ موضع إلى الأرض على زوايا قائمة على السطح الموزون المخرج من موضع السقوط على مماسّة. فبيّن إذ هذا على ما ذكرنا /T44/ أنّها كانت تنتهي بحركتها إلى المركز لو لا أنّ بسيط الأرض يستقبلها ويمنعها، لأنّ الخطّ المستقيم الذي يمرّ على المركز من موضع مماسّة السطح للكرة هو أيضاً على زوايا قائمة على السطح.

وأمّا الذين ظنّوا أنّ من العجب أن لا يكون جسم الأرض محمولاً على شيء ⟨ولا يرسب ولا يسفل⟩ ولا يتحرّك لكثرة ثقله فقد اخطّوا إذ جعلوا القياس بما يعرض لهم لا بما يلزم الكلّ. ولو علموا أنّ قياس الأرض عند الجرم المحيط قياس النقطة والمركز لم يروا هذا عجباً. لأنّهم كانوا يرون أنّه قد يمكن بهذه الجهة أن يكون الذي هو في غاية القلّة بالقياس إلى الذي هو في غاية العظم مستمسكاً من قبل شطب الكاتب «أنّ» الذي هو في غاية العظم متشابه الأجزاء /H23/ حتّى يكون الذي هو في غاية القلّة باقياً في موضعه ويتدافع ما حوله من جميع نواحي الذي هو في غاية العظم تدافعاً متساوياً متشابهاً لأنّ العالم في نفسه ليس له فوق ولا أسفل كما أنّه لا يتوهّم ذلك في الكرة. وأمّا الأجرام التي فيه ه – صح: فيها فبقدر حركاتها الخاصّية الطبيعيّة تذهب الخفيفة منها اللطيفة إلى ظاهر العالم البسيط المحيط، فنظنّ أنّ حركتها إلى فوق عند كلّ قوم لأنّ ما علا الرؤوس المسمّى فوق هو في جهة البسيط المحيط؛ وأمّا الثقيلة الغليظة فتذهب إلى المركز ونظنّ أنّها تقع إلى أسفل، لأنّ ما يلي أرجل جميع الناس المسمّى أسفل هو في جهة مركز الأرض ولذلك تجتمع حول الوسط من مدافعة بعضها لبعض من جميع الجهات مدافعة متساوية متشابهة. ومن أجل ذلك صارت الأشياء الثقال وإن صغرت تلحق كلّيّة الأرض على عظم قدرها عند قدر ما يهوي إليها إذ هي ثابتة قابلة لكلّ ما وقع إليها من جميع النواحي. ولو كانت للأرض وما سواها من الأجسام ه – اخ: الأجرام الثقال حركة واحدة مشتركة، لكانت الأرض بفضل عظمها وثقلها ستسبق كلّ ما سواها ه: فتسفل /H24/ وتخلف الحيوان وما سواه من الأجرام الثقال في الهواء وكانت تنفد سريعاً جميع ما يحيط بها وجرم السماء ألبتّة والتوهّم فقط لهذا وشبهه ضحكة.

إلّا أنّ قوماً لمّا لم يكن عندهم ما تنقضون به هذا الرأي سلّموا ذلك وظنّوا أنّهم إن قالوا إنّ السماء غير متحرّكة وإنّ الأرض متحرّكة على محور واحد من المغرب إلى المشرق وتدور في كلّ يوم دورة واحدة على التقريب؛ أو أنّ السماء والأرض ه: جميعاً متحرّكتان على محور واحد كما ذكرنا /T45/وبقدر ما يلحق إحداهما الأخرى لم يكن شيء ينقض ذلك. وكان قولهم في ظنّهم مقنعاً وذهب عليهم أنّ من قبل ما يظهر من النجوم فليس يمتنع أن يكون ذلك كما ذكروا على التوهّم المطلق، فأمّا من قبل ما يعرض فينا وفي الهواء فيستبين أنّ قولهم أعظم ما يكون من الجهل. وإن نحن سلّمنا لهم ما هو خلاف للطبيعة أن تكون الخفيفة اللطيفة المتشابهة الأجزاء إمّا أن لا تتحرّك ألبتّة وإماّ أن تكون حركتها غير مخالفة لحركة ما يضادّها في الطبيعة على أنّا قد نرى عياناً أنّ الهواء وأشياء آخر أقّل لطفاً منه أسرع تحرّكاً ممّا هو أرضي؛ /H25/ وسلّمنا لهم أيضاً أن تكون للثقيلة الغليظة المختلفة الأجزاء حركة خاصّيّة سريعة متساوية على أنّا قد نرى أنّ الأشياء الأرضيّة عسرة القبول لتحريك غيرها لها. فهم مقرّون أنّ حركة الأرض أسرع من كلّ الحركات اللواتي حولها بعودتها إلى موضعها في مثل هذا الوقت اليسير؛ ولو كان الأمر كذلك لكان جميع ما ليس مستقرّاً عليها يحسّ أبداً متحرّكاً بخلاف حركة الأرض. ولم يكن نرى حركة للسحاب إلى المشرق أبداً ولا لشيء من الطير ولا لشيء ممّا يرمى به لسبق الأرض لكلّ شيء أبداً لسرعة حركتها إلى المشرق، وكان يظنّ أنّ كلّ ما سواها يتحرّك أبداً إلى نواحي المغرب. فإنّهم وإن قالوا إنّ هذا الهواء أيضاً يتحرّك مع الأرض بحركة مساوية لحركتها في السرعة، فإنّه قد يجب أن ترى أبداً حركة الأجرام التي فيه أنقص من حركتها جميعاً؛ فإن قالوا إنّ تلك ه: ثابتة لاصقة في الهواء كالملتحمة تتحرّك معه فقد يلزمها ألّا ترى قدمة ولا متأخّرة: بل تكون ثابتة أبداً ولا يكون لها انتقال ولا تردّد لا في ممرّ ما يمرّ منها ولا في طيران ما يطير ولا في ذهاب ما يرمى به منها. /H26/ وقد نرى كلّ ذلك عياناً وأنّه ليس يلزم ألبتّة شيئاً منها سرعة ولا أبطأ من قبل تحرّك الأرض. فقد يكتفي بما قلنا في الأصول التي تتقدّم باضطرار الأشياء الجزئيّة التي توضع في هذا العلم والأشياء التي تتّبعها على مذهب الإيجاز والاختصار وستثبت وتضح على الكمال الشهادة ه – خ – صح: بشهادة موافقة ما ه – خ: لما؛ ممّا نثبّته فيما بعد ممّا هو مبني عليها لما يظهر. ↑ خ: بالحسّ
The last sentence of this passage is presented as the first sentence of chapter 8 in the English translation.

⟨I.8⟩ ح: في أنّ أصناف الحركات الأوّل اللواتي في السماء اثنتان

ومع ما في الأصل: معما ذكرنا فقد ينبغي أن يكون من جمل ما نقدّم أيضاً أنّ الحركات الأوّل التي في السماء اثنتان. إحداهما التي تحرّك الكلّ أبداً من المشرق إلى المغرب بحال واحدة وأدوار متساوية السرعة وعلى دوائر مواز بعضها لبعض مدارها على قطبي الكرة التي تدير الكلّ باستواء. ويسمّى أعظم هذه الدوائر معدّل النهار لأنّ دائرة الأفق إذ هي من الدوائر العظام تقسّم أبداً هذه الدائرة من بينها بنصفين، فإذا دارت عليها الشمس اعتدل النهار والليل وتساويا عند الحسّ في جميع الأرض. والحركة الأخرى التي تحرّك /H27/ أكر النجوم الجارية إلى خلاف الحركة الأولى على قطبين آخرين لا على قطبيها. وإنّما أثبتنا ما وصفنا لأنّا إذا نظرنا إلى جميع ما في السماء في كلّ يوم رأيناه بالحسّ في اليوم الواحد يطلع ويتوسّط السماء ويغرب على مواضع متشابهة في الصورة موازية لمعدّل النهار، وهذه خاصّة الحركة الأولى. فإذا رصدنا في الأيّام المتوالية رأينا جميع الكواكب سوى الشمس والقمر والكواكب المتحيّرة ثابتاً ↑: بتة أبعاد بعضها من بعض لازمة للمواضع الخاصّيّة بالحركة الأولى على ظاهر الأمر، ورأينا الشمس والقمر والنجوم المتحيّرة تتحرّك حركات مختلفة غير مساو بعضها لبعض إلّا أنّها كلّها بالقياس إلى حركة الكلّ يتحرّك إلى المشرق وإلى النواحي التي تخلفها ورءآها الكواكب الثابتة أبعاد بعضها من بعض التي شطب الكاتب «التي» كان الذي تديرها كرة واحدة.

ولو كانت حركة الكواكب المتحيّرة والشمس والقمر تكون أيضاً على دوائر موازية لمعدّل النهار على قطبي الحركة الأولى /H28/ لكان في إثباتنا أنّ حركة الكلّ حركة واحدة وإنّ هذه الحركة تابعة للحركة الأولى كفاية. وكان من المقنع أن نقول أنّ انتقالها على الخلاف أنّما هو بالظنّ لا بأنّ لها حركة على الخلاف. ولكنّا قد نرى لها مع حركاتها إلى المشرق حركات إلى الشمال والجنوب. ونرى قدر تباعدها فيهما مختلفاً ويكاد أن يظنّ أنّ ميلها ذلك فيهما لأشياء تقذف بها ه – خ: تدفعها و{تضطرّها} إلى ذلك إلّا أنّ ميلها لو كان على هذا الوجه لكان مختلفاً غير منتظم فإذ له ترتيب فقد يجب أن يكون من قبل دائرة مائلة عن معدّل النهار. ومن هنالك نجد هذه الدائرة واحدة بعينها خاصّة للنجوم المتحيّرة. ونجد حركة الشمس ترسمها على الحقيقة وعن جنبي هذه الدائرة وعليها ممرّ القمر والخمسة المتحيّرة، ومجازها من الشمال إلى الجنوب ومن الجنوب إلى الشمال من غير أن يجوز واحد منها مقدار البعد المحدود له عن جنبتيها ولا بالقليل. ولأنّا نرى هذه الدائرة من الدوائر العظام من قبل أنّ ميل الشمس إلى الشمال وإلى الجنوب عن معدّل النهار بقدر واحد، وعلى هذه الدائرة بعينها وعن جنبتيها تكون حركات الكواكب المتحيّرة كلّها إلى المشرق، وجب اضطراراً أن نثبت حركة أخرى ثانية غير حركة الكلّ تكون /H29/ على قطبي هذه الدائرة وعلى خلاف جهة الحركة الأولى.

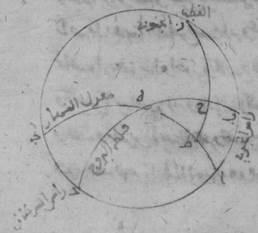
فإذا نحن توهّمنا الدائرة العظيمة المرسومة على أقطاب الدائرتين أعني دائرة معدّل النهار والدائرة المائلة شطب الكاتب حرف «واو»؛ ه – صح: عنها علّمنا باضطرار أنّها تقطع كلّ واحدة من هاتين الدائرتين بنصفين نصفين وعلى زوايا قائمة ووجدنا في الدائرة المائلة أربع نقط: اثنتان منها اللتان يقطعها عليهما /T47/ معدّل النهار كلّ واحدة مقابلة للأخرى تسمّيان معدّلتي النهار إحداهما التي الممرّ عليها من الجنوب إلى الشمال تسمّى ربيعيّة والآخرى التي الممرّ عليها من الشمال إلى الجنوب تسمّى خريفيّة. والنقطتان الباقيتان اللتان تقطعها عليهما الدائرة العظيمة المرسومة على أقطاب الدائرتين كلّ واحدة أيضاً مقابلة للأخرى تسميّان انقلابين ↑ اخ: بيتين إحداهما التي فيما يلي الجنوب من معدّل النهار تسمّى نقطة الانقلاب الشتويّ والأخرى التي فيما يلي الشماليّ من معدّل النهار تسمّى نقطة الانقلاب الصيفيّ.

فمعلوم أنّ الحركة الأولى المحيطة بجميع الحركات الآخر ترسمها فكأنّها ↑: و تجوزها وتحدّها هذه الدائرة العظيمة المرسومة على أقطاب الدائرتين بدورانها وإدارتها معاً الجميع من المشرق إلى المغرب وهي معتمدة على قطبي معدّل النهار كاعتماد الدائرة التي /H30/ تسمّى دائرة نصف النهار عليهما التي ممّا نذكر فقط تنفصل من الدائرة التي ذكرنا المرسومة على أقطاب الدائرتين وهو أنّها ليست مرسومة دائماً على قطبي الدائرة المائلة. ولأنّها أيضاً على زوايا قائمة من الأفق في كلّ وقت تسمّى دائرة نصف النهار من قبل أنّ ما هذا وضعه إذ كان يقطع كلّ واحد من نصفي الكرة السماويّة الذي فوق الأرض والذي تحتها بنصفين صار يحدّ وسطي زماني النهار والليل.

والحركة الثانية الكثيرة الاختلاف تحيط بها الحركة الأولى وتحيط هي بأكر جميع النجوم المتحيّرة وتحرّكها الحركة الأولي التي ذكرنا وتتحرّك هي إلى خلاف ذلك على قطبي الدائرة المائلة اللذين هما ثابتان أبداً في الدائرة التي تحدّ الحركة الأولى أعني الدائرة المرسومة على أقطاب الدائرتين ومتحرّكان معهما ولأزمان في الحركة الثانية التي إلى خلاف الأولى موضعهما من الدائرة العظيمة المدارة بهما المائلة عن معدّل النهار.

⟨I.9⟩ ط: في العلوم الجزئيّة

أمّا جملة ما ينبغي أن نبدأ به من الأصول ونقدّم فهو على قدر ما وصفنا. وإذ نريد أن نبتدئ بالبرهانات على الجزئيّات التي /H31/ أوّلها البرهان الذي يوجد به قدر القوس التي بين القطبين اللذين ذكرنا من الدائرة العظيمة المرسومة على أقطاب الفلكين. قد نرى أنّه يجب باضطرار أن نقدّم القول في معرفة أقدار أوتار أجزاء الدائرة: إذ نريد أن نبيّن ه – اخ: أن نبني البرهان على ما نحن واصفوه من قبل الخطوط.

/T48/ ونتّخذ بعد ذلك لتيسير وجود ما نريد علمه من أقدارها جداول فنجزئ محيط دائرة بثلاث مائة وستّين جزءاً ونجعل تفاضل القسيّ فيها على زيادة نصف جزء نصف جزء ونضيف إليها ما يوتّرها من الأوتار على أنّها أجزاء من مائة وعشرين من القطر لمّا سيتبيّن لنا من سهولته فيما نستعمل من الأعداد. فنبدأ قبل ذلك فنبيّن بأقلّ ما يكون وأبلغه في استخراج ما نريد كيف نعلم /H32/ أقدار الأوتار لئلّا يكون كأنّها إنّما هي موضوعة لنا في الجداول من غير معرفة بها حقيقيّة بل مع وضعها في الجداول يثبت علم أقدارها من طريق الخطوط بأسهل ما يكون. ونتّخذ عدد الستّين في جميع ما يستعمل في أبواب الأعداد ليسهل العمل في الكسور. ونتوخّى في جميع التضعيف والقسمة معرفة ما نريد معرفته بالتقريب حتّى لا يكون ما نقرب ه – اخ: {يبوت} يبعد على الحقيقة بمقدار بيّن للحسّ. This paragraph (ونتّخذ بعد ذلك... بمقدار بيّن للحس) is presented as the first paragraph of chapter 10 in the English translation.

⟨I.10⟩ ي: في مقدار الخطوط المستقيمة التي تقع في الدائرة

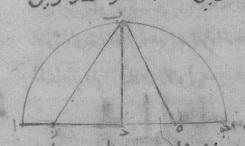
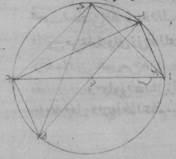
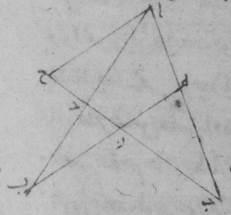
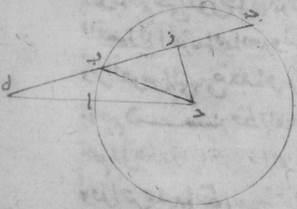
/T48/ ا: فليكن أوّلاً نصف دائرة عليه ألف باء جيم على قطر ألف دال جيم وحول مركز دال. ولنخرج من نقطة دال خطّ دال باء على زوايا قائمة على خطّ ألف جيم ولنقسّم خطّ دال جيم بنصفين على نقطة هاء وليوصل بين ه وباء بخطّ هاء باء ولنفصل من هاء ألف خطّ هاء زاي مساوياً لخطّ هاء باء وليوصل زاي باء.

فأقول إنّ خطّ زاي دال ضلع المعشّر، وخطّ باء زاي ضلع المخمّس. فلأنّ خطّ جيم دال قسّم بنصفين على نقطة هاء وزيد عليه بعض الزيادة وهي خطّ دال زاي، /H33/ فالسطح القائم الزوايا الذي يحيط به خطّا جيم زاي، دال زاي مع مربّع خطّ دال هاء مساو لمربّع خطّ هاء زاي أعني مربع خطّ باء هاء، إذ كان هذا الخطّ مساوياً لخطّ زاي هاء. لكن مربّعي خطّي هاء دال، دال باء مساويان لمربّع خطّ هاء باء. /T49/ فالسطح إذاً الذي يحيط به خطّا جيم زاي، دال زاي مع مربّع خطّ دال هاء مساو لمربّعي خطّي هاء دال، دال باء فإذا أسقط مربّع خطّ هاء دال المشترك ه – خ: إذ كان مشتركاً بقي السطح الذي يحيط به خطّا جيم زاي، زاي دال مساوياً لمربّع خطّ دال باء أعني مربّع خطّ دال جيم.

فخطّ زاي جيم إذا قد انقسم على نسبة ذات وسط وطرفين على نقطة دال. فلأنّ ضلع المسدّس وضلع المعشّر اللذين يرسمان في دائرة واحدة على خطّ واحد مستقيم ينقسمان على نسبة ذات وسط وطرفين وخطّ جيم دال إذ كان من المركز مساو لضلع المسدّس، فخطّ دال زاي إذاً مساو لضلع المعشّر. وعلى هذا المثال، فلأنّ ضلع المخمّس يقوى على ضلع المسدّس وضلع المعشّر المرسومين في دائرة واحدة، /H34/ ومربّع خطّ باء زاي من مثلّث باء دال زاي القائم الزاوية مساو لمربّعي خطّي باء دال، دال زاي وخطّ باء دال ضلع المسدّس وخطّ دال زاي ضلع المعشّر فخطّ باء زاي إذاً مساو لضلع المخمّس.

فلأنّا نضع قطر الدائرة على ما قلنا مائة وعشرين جزءاً يكون من أجل ما قدّمناه خطّ دال هاء إذ كان نصف الخطّ الذي من المركز ثلاثين جزءاً؛ ومربّعه تسع مائة جزء؛ ويكون خطّ دال باء المخرج من المركز ستّين جزءاً؛ ومربّعه ثلاثة آلاف وستّ مائة جزء؛ ويكون مربّع خطّ هاء باء أعني مربع خطّ هاء زاي بهذه الأجزاء أربعة آلاف وخمس مائة؛ فيكون إذاً خطّ هاء زاي سبعة وستّين جزءاً وأربع دقائق وخمساً وخمسين ثانية بالتقريب. فيبقى خطّ دال زاي لتلك الأجزاء سبعة وثلاثين جزءاً وأربع دقائق وخمساً وخمسين ثانية. فضلع المعشّر وهو الذي يوتّر قوساً هي ه – صح: {..} درجة ستّة وثلاثون جزءاً بالأجزاء التي بها الدائرة ثلاث مائة وستّون جزءاً يكون سبعة وثلاثين جزءاً وأربع دقائق وخمساً وخمسين ثانية بالأجزاء التي بها القطر مائة وعشرون جزءاً.

وأيضاً لأنّ خطّ دال زاي سبعة وثلاثون جزءاً وأربع دقائق وخمس وخمسون ثانية ومربّعه ألف وثلاث مائة وخمسة وسبعون جزءاً وأربع دقائق وخمس ه – خ – صح: وأربع عشرة ثانية ومربّع خطّ دال باء هو بتلك الأجزاء ثلاثة آلاف وستّ مائة. وهذان إذا جمعاً كان منهما مربّع خطّ باء زاي. فمربّع خطّ باء زاي أربعة آلاف وتسع مائة وخمسة وسبعون جزءاً وأربع دقائق وخمس ه – خ – صح: وأربع عشرة ثانية يكون خطّ باء زاي في الطول سبعين جزءاً واثنتين وثلاثين دقيقة وثلاث ثواني بالتقريب. /H35/ فيكون إذاً ضلع المخمّس، وهو يوتّر اثنين وسبعين جزءاً بالأجزاء التي بها الدائرة ثلاث مائة وستّون جزءاً، سبعين جزءاً واثنتين وثلاثين دقيقة وثلاث ثواني بالأجزاء التي بها القطر مائة وعشرون جزءاً. وقد استبان من هذا الموضع أنّ ضلع المسدّس، وهو الذي يوتّر ستّين جزءاً وهو مساو للخطّ الذي من المركز، ستّون جزءاً. وعلى هذا المثال لأنّ ضلع المربّع، وهو الذي يوتّر تسعين جزءاً، مثلاً الخطّ الذي من المركز في القوّة. وضلع المثلّث، وهو الذي يوتّر مائة وعشرين جزءاً، ثلاثة أمثال هذا الخطّ في القوّة، ومربّع الخطّ الذي يخرج من المركز ثلاثة آلاف وستّ مائة. ه – صح: جزء نحصل من ذلك أنّ مربّع ضلع المربّع سبعة آلاف ومائتا جزء؛ ومربّع ضلع المثلّث عشرة آلاف وثمان مائة جزء.

/T50/ فيجب من ذلك أن يكون الخطّ المستقيم الذي يوتّر تسعين جزءاً، أربعة وثمانين جزءاً وإحدى وخمسين دقيقة وعشر ثواني بالأجزاء التي بها القطر مائة وعشرون جزءاً. ويكون الخطّ الذي يوتّر مائة وعشرين جزءاً مائة وثلاثة أجزاء بتلك الأجزاء وخمساً وخمسين دقيقة وثلاثاً وعشرين ثانية.

فقد استخرجنا هذه الأوتار بطريق سهل من قرب. وقد يستبين من هذا الموضع أنّه إذا فرض لنا خطوط مستقيمة أمكننا بسهولة أن نعرف أيضاً الخطوط التي توتّر القسيّ الباقية من نصف الدائرة /H36/ لأنّ الذي يجتمع من مربّعي الوترين يكون مثل مربّع القطر. مثال ذلك أنّ الخطّ المستقيم الذي يوتّر ستّة وثلاثين جزءاً قد تبيّن أنّه سبعة وثلاثون جزءاً وأربع دقائق وخمس وخمسون ثانية؛ ومربّعه ألف وثلاث مائة وخمسة وسبعون جزءاً وأربع دقائق وخمس عشرة ثانية؛ ومربّع القطر أربعة عشر ألفاً وأربع مائة. يكون مربّع الخطّ الذي يوتّر الأجزاء الباقية من نصف الدائرة، وهي مائة وأربعة وأربعون جزءاً، الأجزاء الباقية من مربّع القطر، وهي ثلاثة عشر ألفاً وأربعة وعشرون جزءاً وخمس وخمسون دقيقة ه – ⟨صح⟩: وخمس وأربعون ثانية. ويكون هذا الخطّ في الطول بهذه الأجزاء مائة وأربعة عشر جزءاً وسبع دقائق وسبع وثلاثون ثانية بالتقريب وعلى هذا المثال يجري الأمر في سائر الأوتار.

وسنبيّن فيما بعد الوجه الذي به نعرف من هذه الأوتار سائر الأوتار الجزئيّة بعد أن تقدّم فنوطّئ معنى عظيم المنفعة في علمنا هذا. ه: ب

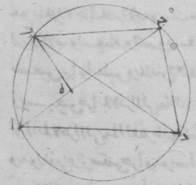
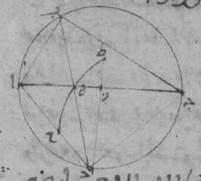
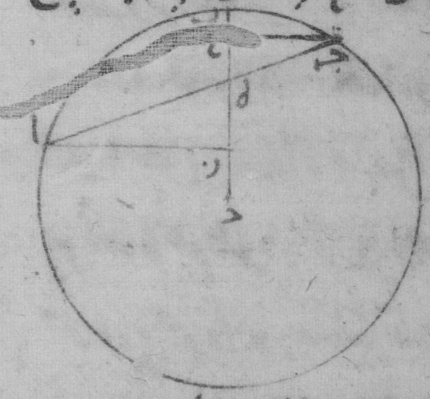
فلتكن دائرة قد رسم فيها ذو أربعة أضلاع ألف باء جيم دال وليوصل خطّا ألف جيم، باء دال.

فينبغي أن نبيّن أنّ السطح القائم الزوايا الذي يحيط به خطّا ألف جيم، باء دال مساو للسطح الذي يحيط به خطّا ألف باء، دال جيم وللسطح الذي يحيط به خطّا ألف دال، باء جيم مجموعين. فلنجعل زاوية ألف باء هاء مساوية لزاوية دال باء جيم. فلأنّ زاوية دال باء جيم مساوية لزاوية ألف باء هاء إن نحن جعلنا زاوية هاء باء دال مشتركة، كانت أيضاً زاوية ألف باء دال مساوية لزاوية هاء باء جيم. /T51/ //H37 وزاوية باء دال ألف مساوية لزاوية باء جيم هاء، وذلك أنّهما يوتّران قوساً واحدة. فمثلّث باء دال ألف إذاً مساوي الزوايا لمثلّث باء جيم هاء. فيجب من ذلك أن تكون نسبة خطّ باء جيم إلى خطّ جيم هاء كنسبة خطّ باء دال إلى خطّ دال ألف. فالسطح إذاً الذي يحيط به خطّا باء جيم، ألف دال مساو للسطح الذي يحيط به خطّا باء دال، جيم هاء. وأيضاً لأنّ زاوية ألف باء هاء مساوية لزاوية هاء باء جيم، وزاوية باء ألف هاء مساوية لزاوية باء دال جيم، فمثلّث ألف باء هاء إذاً مساوي الزوايا لمثلّث باء جيم دال. فنسبة خطّ باء ألف إلى خطّ ألف هاء كنسبة خطّ باء دال إلى خطّ دال جيم. فالسطح إذاً الذي يحيط به خطّا باء ألف، دال جيم مساو للسطح الذي يحيط به خطّا باء دال، هاء ألف. وقد تبيّن أنّ السطح أيضاً الذي يحيط به خطّا باء جيم، دال ألف مساو للسطح الذي يحيط به خطّا باء دال، جيم هاء. والسطح إذاً بأسره الذي يحيط به خطّا ألف جيم، باء دال مساو للسطح الذي يحيط به خطّا ألف باء، دال جيم وللسطح الذي يحيط به خطّا ألف دال، جيم باء مجموعين. وذلك ما كان ينبغي أن نبيّنه.

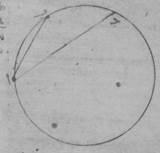
ج: ه: وتر الفضل بين قوسين فإذ تقدّمنا فوضعنا هذا المعنى فليكن نصف دائرة /H38/ ألف باء جيم دال على قطر ألف دال ولنخرج من نقطة ألف خطّا ألف باء، ألف جيم وليكن كلّ واحد منهما معطى بالمقدار من الأجزاء التي بها القطر معطى. ه: معطا ومفروض ومعلوم وموضوع معنا{ه} واحد وليوصل خطّ باء جيم، فأقول إنّ هذا الخّط أيضاً معطى. فليوصل خطّا باء دال، جيم دال.

فمن البيّن أنّ هذين أيضاً معطيان لأنّهما وترا القوسين الباقيتين من نصف الدائرة. فلأنّ في دائرة ذا أربعة أضلاع ألف باء جيم دال، فالسطح الذي يحيط به خطّا ألف باء، جيم دال مع السطح الذي يحيط به خطّا ألف دال، باء جيم مساو للسطح الذي يحيط به خطّا ألف جيم، باء دال، والسطح الذي يحيط به خطّا ألف باء، جيم دال معطا. وأيضاً فإنّ السطح الذي يحيط به خطّا ألف باء، جيم دال معطى والقطر أيضاً معطى. فخطّ باء جيم إذن معطى. فقد بان لنا أنّا إذا أعطينا قوسين وأعطينا وتريهما، كان وتر الفضل بين القوسين معطى.

ومن البيّن أنّه قد يمكننا بهذا الباب أن نرسم وتر قوس اثني عشر جزءاً من التفاضل المعطى بين الأوتار المعطاة بذاتها /H39/ إذ كنّا عالمين بوتر قوس ستّين جزءاً ووتر قوس اثنين وسبعين جزءاً. وأن نرسم أيضاً أوتاراً آخر كثيرة غيره. /T52/ وأيضاً فليكن عرضنا إذا كان في دائرة خطّ مستقيم معطى أن نجد الخطّ الذي يوتّر نصف القوس التي يوتّرها ذلك الخط.

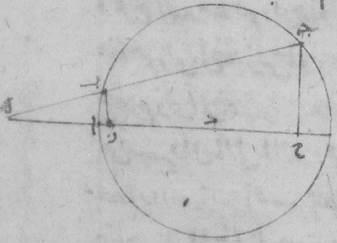
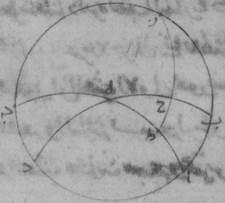
د: فليكن نصف الدائرة ألف باء جيم على قطر ألف جيم وخطّ باء جيم معطى. ونقسّم قوس باء جيم بنصفين على نقطة دال وليوصل خطوط ألف باء، ألف دال، باء دال، دال جيم، ولنخرج من نقطة دال إلى خطّ ألف جيم عمود دال زاي.

أقول إنّ خطّ زاي جيم شطب الكاتب دال هو نصف الفضل بين خطّ ألف باء وبين خطّ ألف جيم. فلنجعل خطّ ألف هاء مساوياً لخطّ ألف باء وليوصل في الأصل: ولنوصل خطّ دال هاء. فلأنّ خطّ ألف باء مساو لخطّ ألف هاء وخطّ ألف دال مشترك، فخطّا ألف باء، ألف دال مساويان لخطّي ألف هاء، ألف دال. وزاوية باء ألف دال مساوية لزاوية هاء ألف دال. فقاعدة باء دال مثل قاعدة ده. لكن خطّ باء دال مثل خطّ دال جيم، فخطّ دال جيم إذن مساو لخطّ دال هاء.

فلأنّ مثلّث دال هاء جيم متساوي الساقين وقد أخرج من رأسه إلى قاعدته عمود د ز، /H40/ فخطّ ه ز مساو لخطّ زاي جيم. شطب الكاتب دال لكن خطّ هاء جيم كلّه هو الفضل بين خطّ ألف باء وبين خطّ ألف جيم. فخطّ ز ج إذن نصف الفضل بين هذين الخطّين.

فلأنّ الخطّ الذي يوتّر قوس باء جيم لمّا كان معطى، كان وتر باقي نصف الدائرة وهو خطّ ألف باء معطى. فخطّ ز ج معطى إذ كان نصف الفضل بين خطّي ألف دال، ه – صح: جيم ألف باء. لكن لمّا كان مثلّث ألف جيم دال القائم الزاوية، قد أخرج فيه عمود دال زاي، فإنّ مثلّث ألف جيم دال القائم الزاوية مساوي الزوايا لمثلّث دال زاي جيم. فتكون نسبة خطّ ألف دال ه – صح: جيم إلى خطّ جيم دال كنسبة خطّ جيم دال إلى خطّ جيم زاي. فالسطح إذا القائم الزوايا الذي يحيط به خطّا ألف جيم، جيم زاي مساو لمربّع خطّ جيم دال. /T53/ فيكون خطّ جيم دال في الطول معطى وهو الذي يوتّر نصف قوس ب ج وذلك ما كان ينبغي أن نبيّنه.

وبهذا الباب أيضاً نستخرج من الخطّ الذي يوتّر اثني عشر جزءاً، الخطّ الذي يوتّر ستّة أجزاء، والخطّ الذي يوتّر ثلاثة أجزاء، والخطّ الذي يوتّر جزءاً ونصفاً، والخطّ الذي يوتّر نصفاً وربع جزء، ونستخرج أيضاً خطوطاً آخر كثيرة جدّاً. فلنصف ذلك إلى القسيّ التي تقدّم العلم بها ونجد بهذا القياس أنّ وتر /H41/ جزء ونصف جزء يكون جزءاً وأربعاً وثلاثين دقيقة وخمس عشرة ثانية بالتقريب بالأجزاء التي بها القطر مائة وعشرون جزءاً ووتر نصف وربع جزء يكون سبعاً وأربعين دقيقة وثمان ثواني بتلك الأجزاء.

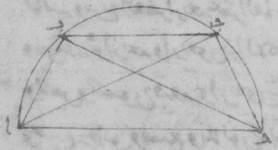
ه: ولتكن أيضاً دائرة ألف باء جيم دال حول قطر ألف دال وعلى نقطة زاي ولنفصل قوسان معطاتان متتاليتان من نقطة ألف ولتكونا قوسي ألف باء، باء جيم. وليوصل خطّا ألف باء، باء جيم يوتّران هاتين القوسين وليكونا أيضاً معطيين.

أقول إنّا أن وصلنا خطّ ألف جيم، كان هذا الخطّ أيضاً معطى.

فلنخرج من نقطة باء قطر الدائرة وليكن باء زاي هاء، ولتوصل خطوط باء دال، جيم دال، جيم هاء، دال هاء. فمن البيّن أنّ بسبب خطّ باء جيم يكون خطّ جيم هاء أيضاً معطى، وبسبب خطّ ألف باء يكون خطّا باء دال، دال هاء معطيين. وبسبب ما تقدّم، لأنّ في دائرة ذا أربعة أضلاع باء جيم دال هاء، وقد أخرج فيه خطّا باء دال، جيم هاء؛ فالسطح القائم الزوايا الذي يحيط به الخطّان المخرجان فيه مساو لمجموع السطحين اللذين يحيط بهما الأضلاع المتقابلة من ذوي ه – اخ: ذي الأربعة الأضلاع. فلأنّ السطح الذي يحيط به خطّا باء دال، جيم هاء معطى يكون السطح الذي يحيط به خطّا باء جيم، دال هاء مع السطح الذي يحيط به خطّا جيم دال، باء هاء معطى. والسطح الذي يحيط به خطّا باء جيم، دال هاء معطى /H42/ وقطر به معطى يكون خطّ جيم دال الباقي معطى. فلذلك يكون أيضاً الخطّ الذي يوتّر القوس الباقية من نصف الدائرة وهو خطّ ألف جيم معطى. وذلك ما كان ينبغي أن نبيّنه.

فيجب عن هذا الشكل أنّه إذا كانت قوسان معطاتان معطاتا الوترين يكون الخطّ الذي يوتّر القوسين جميعاً على التركيب معطى.

فمن البيّن أنّا إذا ركّبنا مع الأوتار المعلومة كلّها وتر جزء ونصف وحسبنا الأوتار التي تصل، فإنّا ه – اخ: فإنّا نرسم ترسم بالجملة كلّ قوس إذا أضعفت /T54/ كان لها ثلث. وتبقى علينا بعد ذلك القسيّ التي بين الأبعاد المتفاضلات بجزء ونصف، وهي في كلّ بعد قوسان، وذلك من قبل أنّ الرسم أنّما نعمله على زيادة نصف جزء نصف جزء. فيجب من ذلك أن يكون إن وجدنا وتر نصف جزء، فإنّه يتمّ لنا به بالتركيب وبالتفاضل الذين بين الخطوط المستقيمة المعطاة المحيطة بالأبعاد معرفة جميع الخطوط المستقيمة الباقية التي فيما بين ذلك أيضاً. لكن لما كنّا إذا أعطينا وتراً ما، كوتر جزء ونصف مثلاً، فإنّ وتر ثلث تلك القوس ليس بمعطى بطريق الخطوط على وجه من الوجوه. ولو قدرنا على ذلك لكنّا سنجد به أيضاً وتر نصف جزء. /H43/ فإنّا نحتال أوّلاً في وجود وتر جزء من قبل وتر جزء ونصف ومن قبل وتر نصف وربع ه: جزء بأن يتقدّم، فنوطّي له شيئاً، وإن كان لا يمكن به تحصيل مقادير هذه الخطوط على الأمر الكلّي، فقد يمكن لنا أن نبلغ به من التدقيق فيها إلى ما ليس بينه وبين المقادير المحصّلة اختلاف.

فأقول إنّا إذا أخرجنا في دائرة خطّين مستقيمين غير متساويين، كانت نسبة الأطول منهما إلى الأقصر أصغر من نسبة القوس التي على الأطول إلى القوس التي على الأقصر.

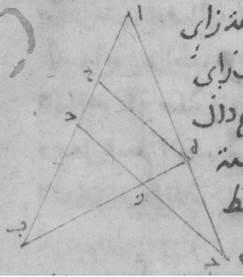
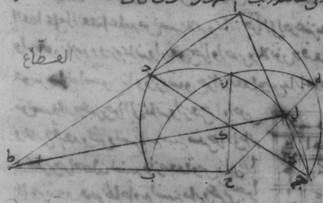
و: فلتكن دائرة ألف باء جيم دال ولنخرج فيها خطّين غير متساويين، خطّ ألف باء أقصرهما وخطّ باء جيم أطولهما. أقول إنّ نسبة خطّ جيم باء إلى خطّ باء ألف أصغر من نسبة قوس جيم باء إلى قوس باء ألف. فلنقسّم زاوية ألف باء جيم بنصفين بخطّ باء دال. ولتوصل خطوط ألف هاء جيم، ألف دال، جيم دال. فلأنّ زاوية ألف باء جيم قسّمت بنصفين بخطّ باء هاء دال، فخطّ جيم دال مساو لخطّ ألف دال /H44/ وخطّ جيم هاء أطول من خطّ هاء ألف. /T55/ فلنخرج من نقطة دال إلى خطّ ألف هاء جيم عمود دال زاي. فلأنّ خطّ ألف دال أطول من خطّ هاء دال وخطّ هاء دال أطول من خطّ دال زاي، فالدائرة إذن التي ترسم على مركز دال وببعد دال هاء تقطع خطّ ألف دال وتتجاوز خطّ دال زاي. فلترسم ولتكن دائرة حاء هاء طاء ولنخرج إليها خطّ دال زاي طاء. فلأنّ قطاع دال هاء طاء أعظم من مثلّث دال هاء زاي، ومثلّث دال هاء ألف أعظم من قطاع دال حاء هاء، ه: بلغ العرض للأمّ فنسبة مثلّث دال هاء زاي إذاً إلى مثلّث دال هاء ألف أصغر من نسبة قطاع دال هاء طاء إلى قطاع دال هاء حاء. لكن نسبة مثلّث دال هاء زاي إلى مثلّث دال هاء ألف كنسبة خطّ هاء زاي إلى خطّ هاء ألف، ونسبة قطاع دال هاء طاء إلى قطاع دال هاء حاء كنسبة زاوية زاي دال هاء إلى زاوية هاء دال ألف. فنسبة خطّ زاي هاء إلى خطّ هاء ألف أصغر من نسبة زاوية زاي دال هاء إلى زاوية هاء دال ألف. فبالتركيب إذن تكون نسبة خطّ زاي ألف إلى خطّ ألف هاء أصغر من نسبة زاوية زاي دال ألف إلى زاوية ألف دال هاء. وإذا أضعفنا المقدّمين /H45/ تكون نسبة خطّ جيم ألف إلى خطّ ألف هاء أصغر من نسبة زاوية جيم دال ألف إلى زاوية ألف دال هاء. وبالتفصيل تكون نسبة خطّ جيم هاء إلى خطّ هاء ألف أصغر من نسبة زاوية جيم دال هاء إلى زاوية هاء دال ألف، لكن نسبة خطّ جيم هاء إلى خطّ هاء ألف كنسبة خطّ جيم باء إلى خطّ باء ألف، ونسبة زاوية جيم دال باء إلى زاوية باء دال ألف كنسبة قوس جيم باء إلى قوس باء ألف. فنسبة خطّ جيم باء إذاً إلى خطّ باء ألف أصغر من نسبة قوس جيم باء إلى قوس باء ألف. وذلك ما كان ينبغي أن نبيّنه.

ز: فإذ قد وضعنا ذلك، فلتكن دائرة ألف باء جيم ولنخرج فيها خطّا ألف باء، ألف جيم ولنضع أوّلاً خطّ ألف باء يوتّر نصفاً وربع جزء وخطّ ألف جيم يوتّر جزءاً واحداً.

فلأنّ نسبة خطّ جيم ألف إلى خطّ ألف باء أصغر من نسبة قوس جيم ألف إلى قوس ألف باء وقوس ألف جيم مثل قوس ألف باء ومثل ثلثها. فخطّ جيم ألف إذن أقلّ من مثل وثلث خطّ باء ألف. /T56/ لكن قد تبيّن أن خطّ ألف باء سبع وأربعون دقيقة وثمان ثواني بالأجزاء التي بها القطر مائة وعشرون جزءاً. فخطّ ألف جيم إذن أقلّ من جزء ودقيقتين وخمسين ثانية بتلك الأجزاء. وذلك أنّ هذه مثل سبع وأربعين دقيقة وثمان ثواني ومثل ثلثها بالتقريب. /H46/ ولننزّل أيضاً في هذه الصورة بعينها أنّ خطّ ألف باء يوتّر جزءاً واحداً وخطّ ألف جيم يوتّر جزءاً ونصفاً. فلذلك بعينه لأنّ قوس ألف جيم مثل قوس ألف باء ومثل نصفها، فخطّ جيم ألف أقلّ من مثل ونصف خطّ باء ألف. لكنّا قد بيّنّا أنّ خطّ ألف جيم جزء وأربع وثلاثون دقيقة وخمس عشرة ثانية بالأجزاء التي بها القطر مائة وعشرون جزءاً. فخطّ ألف باء إذن أكثر من جزء ودقيقتين وخمسين ثانية بتلك الأجزاء، فإنّ الجزء والربع والثلاثين الدقيقة والخمس العشرة الثانية مثل هذه ومثل نصفها.

فإذ قد تبيّن أنّ وتر جزء واحد أكثر وأقلّ من شيء بعينه، فمن البيّن أنّ هذا ه: في ترجمة إسحق من غير إصلاح ثابت بن قرّة: فإذ قد تبيّن أنّ وتر جزء واحد من القوس مرّة أقلّ من جزء ودقيقتين وخمس ثانية وأربعين ثالثة ومرّة أكثر من جزء ودقيقتين وخمسين ثانية فالأقلّ والأكثر {…} الأربعين ثالثة فتبيّن أنّه ينبغي لنا أن نجد وتر الجزء الواحد من القوس جزءاً واحداً من الوتر ودقيقتين وخمسين ثانية وعشرين ثالثة بالأجزاء. الوتر أيضاً جزء ودقيقتان وخمسون ثانية بالتقريب بالأجزاء التي بها القطر مائة وعشرون جزءاً. ونعرف بسبب ما تقدّم بيانه وتر نصف جزء فنجده إحدى وثلاثين دقيقة وخمساً وعشرين ثانية بالتقريب بتلك الأجزاء. ويتمّ لنا كما قلنا سائر الأبعاد الباقية إمّا من تركيب نصف جزء مع جزء ونصف مثلاً إذ كان البعد الأوّل فنتبيّن وتر جزأين، وإمّا من فضل ثلاثة أجزاء ه – اخ: على نصف جزء فيكون وتر جزأين ونصف معطا وكذلك يجري الأمر في سائر الأوتار الباقية.

/H47/ فالعلم بالخطوط التي تقع في الدائرة بهذا الوجه خاصّة أرى أنّه يسهل أمره. ولكي يكون لنا كما قلنا مقادير هذه الخطوط المستقيمة موضوعة ميسّرة لمّا تدعونا إليه الحاجة في كلّ واحد من الأعمال، فنحن واضعون جداول في كلّ جدول منها خمسة وأربعون سطراً إذ كان هذا المقدار معتدلاً. فالقسم الأوّل من الجداول فيه مقادير القسيّ المتفاضلات بنصف جزء نصف جزء. والقسم الثاني فيه مقادير الخطوط المستقيمة التي توتّر تلك القسيّ من المائة والعشرين الجزء التي جزي بها القطر. والقسم الثالث فيه الجزء من الثلاثين من التفاضل بين الخطوط المستقيمة التي توتّر القسيّ المتفاضلة بنصف جزء نصف جزء حتّى يكون إذا علّمنا الحصّة الوسطى لدقيقة واحدة. وذلك غير مخالف عند الحسّ لمّا عليه الأمر بالحقيقة قدّرنا بسهولة على أن نحسب به حصص المقادير التي تقع في ه – اخ – ⟨صح⟩: بين أجزاء النصف.

وممّا يسهل فهمه أنّا بهذه الأبواب بأعيانها التي تقدّمنا فوضعناها أن شكّكنا وتحيّرنا في خطاء عساه أن يقع من الكاتب في شيء من الخطوط المرسومة في الجدول، قد يمكّننا بسهولة أن نقف عليه و نصلحه، إمّا من قبل وتر ضعف القوس المشكوك فيها وإمّا من قبل التفاضل بينه وبين غيره من الخطوط المعطاة وإمّا من قبل الخطّ الذي يوتّر القوس الباقية من نصف الدائرة. وهكذا رسم الجداول:

/T61/ /H64/ ⟨I.11⟩ يا: في القوس التي بين الانقلابين

فإذ قد وضعنا مقادير الخطوط المستقيمة التي تقع في الدائرة، فأوّل ما ينبغي أن نبيّنه، على ما قلنا، كم مقدار ميل الدائرة المائلة التي تمرّ على أوساط البروج عن دائرة معدّل النهار، أعني أيّ نسبة هي نسبة الدائرة العظمى التي تمرّ بالقطبين جميعاً اللذين وضعناهما إلى القوس التي تنفرز من هذه الدائرة بين القطبين. ومن البيّن أنّ هذه القوس هي البعد بين النقطة التي على دائرة معدّل النهار وبين كلّ واحد من الانقلابين. وقد يدرك ذلك بآلة نتّخذها بسيطة على هذه الصفة. نعمل دائرة من نحاس معتدلة في مقدارها، مهندمة محكمة الهندام مربّعة البسيط. فنقيمها مقام دائرة نصف النهار ونقسّمها بالأقسام التي وضعنا أعظم الدوائر مقسومة بها وهي ثلاث مائة وستّون جزءاً، ونقسّم هذه أيضاً إلى ما أمكن فيها أن ينقسم. ثمّ نجعل في جوف هذه الدائرة دائرة أخرى صغيرة لطيفة مطابقة لتلك الدائرة /T62/ مطابقة يمكن معها أن يبقى وجها الدائرتين على سطح واحد، وأن تدور الدائرة الصغرى في الدائرة العظمى في سطح واحد بعينه إلى الشمال وإلى الجنوب بلا مانع يمنعها. ونجعل في جزئين متقاطرين على أحد وجهي /H65/ الدائرة الصغرى شظيّتين صغيرتين متساويتين متواجهتين مواجهتين لمركز الدائرتين، ونضع في الوسط بالحقيقة من عرضيهما مقياسين دقيقين يلقيان وجه الدائرة العظمى المقسومة. فإذا احتجنا إلى استعمال هذه الآلة نصبناها نصباً محكماً على عمود معتدل في قدره واثبتنا قاعدته في موضع مكشوف للسماء. ه – خ – صح: للشمس ورمنا أن يكون ذلك الموضع غير زائل عن بسيط الأفق حتّى يكون بسيط الدائرتين قائماً على بسيط الأفق على زوايا قائمة ويكون موازياً لبسيط دائرة نصف النهار. أمّا الأوّل من هذين فيحكم بالشاقول إذا علّق من النقطة التي تصير بعد على سمت الرأس، وقوّم بما يصير تحت الآلة إلى أن يلقى النقطة المقاطرة لها. وأمّا الثاني منهما فيحكم بأن يوجد خطّ نصف النهار في البسيط الذي العمود قائم عليه ووجود ذلك سهل وتميل الدائرتين إلى الجانبين إلى أن يرى بسيطهما موازياً لذلك الخطّ. فكنّا إذا نصبنا الآلة على هذه الصفة، رصدنا تباعد الشمس إلى الشمال والجنوب بأن ندير الدائرة الداخلة في أنصاف النهار /H66/ حتى تستظلّ الشظيّة السفلى كلّها بالشظيّة العليا كلّها. فإذا كان ذلك، دلّنا طرفا المقياسين على مقدار بعد جزء مركز الشمس في وقت الرصد من النقطة التي على سمت الرأس في دائرة نصف النهار.

وقد كان يقع لنا رصد ذلك أسهل من ذلك الباب. وذلك أنّا كنّا نتّخذ مكان الدائرتين لبنة من حجر أو من خشب مربّعة ليس فيها اعوجاج، صالحة العرض والثخن، يمكن أن يقوم في الأصل: تقوم على حرفها واحد وجهيها شديد الملاسة صقيل. ونجعل في هذا الوجه نقطة ما من النقط التي عند زواياها مركزاً ونرسم به ربع دائرة ونخرج من النقطة التي على المركز إلى القوس التي رسمناها الخطّين اللذين يحيطان بالزاوية القائمة التي يوتّرها ذلك الربع. ونقسّم على ذلك المثال هذه القوس بالتسعين الجزء ونقسّم الأجزا بأجزائها. ثمّ نعمد بعد ذلك إلى أحد الخطّين وهو الذي كنّا نصيره فيما بعد قائماً على زوايا قائمة على بسيط الأفق ونصير وضعه فيما يلي الجنوب، فنوتّد في طرفيه وتدين أسطوانيين صغيرين قائمين عليه على زوايا قائمة متساويين من جميع جوانبهما مهندمين هنداماً واحداً. فيكون أحدهما على نقطة المركز نفسها في الوسط بالحقيقة، والآخر عند الطرف الأسفل من الخطّ المستقيم. /H67/ ثمّ نقيم هذا الجانب المرسوم من اللبنة موازياً لخطّ نصف النهار المخرج في البسيط ه – صح: الموضوع حتّى يكون هو أيضاً موازياً في وضعه لبسيط دائرة نصف النهار. ثمّ نجعل الخطّ الذى يمرّ بالوتدين بشاقول يمرّ بهما قائماً بالحقيقة على زوايا قائمة على بسيط الأفق غير مائل عنه بأن نضع تحت اللبنة أيضاً أشياء لطيفة تقوّمها فتصلح الخلل فيها. ثمّ كنّا نرصد على ذلك المثال في أنصاف النهار الظلّ الذي يحدث من الوتد الذي عند المركز بأن نضع شيأً عند القوس المرسومة ليكون موضع الظلّ أبين ثمّ نعلّم على وسطه ونأخذ الجزء الذي يقع عليه من قوس ربع الدائرة فيستدلّ به على ممرّ الشمس في العرض على دائرة نصف النهار.