〈XIII〉 ابتداء المقالة الثالثة عشرة من كتاب بطلميوس المنسوب إلى التعاليم⊙
قال وإذ بقي علينا بعد في علم أمر الكواكب الخمسة المتحيّرة شيئان أحدهما علم ما يحدث من المسير في العرض بمسيرها في فلك البروج ه: يعني عن جنبي فلك البروج والآخر النظر في أبعاد ظهورها واختفاءاتها بالقياس إلى الشمس وكانت الأبعاد في العرض لواحد واحد منها يجب هاهنا أيضًا أن يتقدّم العلم بها لأنّها قد تقع من قبل هذا المعنى أيضًا في ظهورها واختفاءاتها اختلافات لها قدر فنحن مقدّمون أوّلًا أيضًا وصف الأصول العامّيّة المشتركة لها التي عليها العمل في ميول أفلاكها⊙
〈XIII.1〉 آ: في الأصول التي عليها يعمل في مسيرات الكواكب الخمسة المتحيّرة في العرض⊙
لمّا كان كلّ واحد من هذه الكواكب قد نجده يفعل اختلافين في العرض أيضًا كما يفعل في الطول جزأين من الاختلاف أحدهما بحسب أجزاء فلك البروج من قبل الفلك الخارج المركز والآخر بحسب الشمس ومن قبل فلك تدويره فإنّا نضع بهذا السبب في هذه الكواكب كلّها الفلك الخارج المركز مائلًا عن سطح فلك البروج وفلك التدوير مائلًا عن سطح الفلك الخارج المركز إذ كان ليس يلحق كما قلنا من قبل ذلك شيء من التغيّر يعتدّ به لا في المسير في الطول ولا في تبيين الاختلافات فيما هذا مبلغه من الميل على ما سنبنيه عليه فيما بعد ولمّا كنّا قد وجدنا بالأرصاد الجزئيّة في واحد واحد منها أنّه متى كان عدد الطول المعدّل وعدد الاختلاف المعدّل كلّ واحد منهما {...} ه: {...} بعد ربع دائرة أمّا عدد الطول المعدّل فمن النهاية الشماليّة أو من النهاية الجنوبيّة من الفلك الخارج المركز وأمّا عدد الاختلاف فمن البعد الأبعد الذي له خاصّةً فإنّ هذه الكواكب ترى في نفس سطح فلك البروج فإنّا نضع بهذا السبب ميول أفلاكها الخارجة ↑: المائلة المراكز على مركز فلك البروج كما عملنا في القمر وعلى ↑: بحسب أقطارها التي تمرّ بالنهايات الشماليّة أو الجنوبيّة ونضع ميول أفلاك تداويرها على ↑: بحسب أقطارها المحاذية لمركز فلك البروج وهي الأقطار التي عليها يوجد البعد الأبعد والبعد الأقرب الذي يرى من كل واحد منها ورصدنا أيضًا في هذه الثلاثة الكواكب المتحيّرة وهي زحل والمشتري والمرّيخ أنّه متى كان مسيرها في الطول في القسم الأبعد من الأرض من الفلك الخارج المراكز فإنّها أبدًا ترى أبعد في الشمال وبعدها في الشمال إذا كان مسيرها في البعد الأقرب من أفلاك تدويرها (يكون أكثر من بعدها إذا كان مسيرها في البعد الأقرب من أفلاك تدويرها) يكون أكثر من بعدها إذا كان مسيرها في البعد الأبعد منها وذلك هو غاية بعدها ومتى كان مسيرها في الطول في القسم من الفلك الخارج المركز الأقرب من الأرض كان الأمر بضدّ ذلك قريب أميل إلى الجنوب عن فلك البروج وأنّ النهايات الشماليّة من أفلاكها الخارجة المراكز أمّا في كوكب زحل وكوكب المشتري فهي في مبادئ برج الميزان وأمّا في كوكب المرّيخ فإنّها في أواخر برج السرطان ويكاد أن يكون في نفس البعد الأبعد حتّى إنّه يجتمع من ذلك أنّ الأفلاك الخارجة المراكز أنفسها ما كان من نواحيها على الأجزاء التي ذكرناها من فلك البروج فإنّها مائلة نحو الشمال وما كان من نواحيها على الأجزاء المقاطرة لها فإنّها مائلة نحو الجنوب بمثل ذلك المقدار من الميل⊙ فأمّا أفلاك التداوير فإنّ البعد الأقرب منها هو أبدًا في الجهة التي إليها ميل الأفلاك الخارجة المراكز وأقطارها التي هي على زوايا قائمة على أقطارها التي تمرّ بالبعد الأبعد منها تكون أبدًا موازية لسطح فلك البروج⊙ ورصدنا أيضًا في كوكب الزهرة وكوكب عطارد أنّه متى كان مسيرهما في الطول في ناحية البعد الأبعد أو البعد الأقرب من الفلك الخارج المركز فحينئذ تكون أمّا حركتها في البعد الأقرب من فلكي تدويرهما فغير مغادرة بشيء في العرض لحركتها في البعد الأبعد لكنّهما يكونان على مثال واحد إمّا أميل إلى الشمال عن فلك البروج وإمّا أميل إلى الجنوب أمّا في الزهرة فأميل إلى الشمال أبدًا وأمّا في عطارد فضدّ ذلك أعني أنهما أميل إلى الجنوب أبدًا وأمّا ما مسيرهما في أعظم أبعادهما من الشمس فإنّ أحوالهما تخالف بعضها بعضًا غاية الخلاف أعني الحال الصباحيّة للحال المسائيّة وتخالف أيضًا أحوال فلكي تدويرهما إذا كانا في البعد الأبعد أو البعد الأقرب أعني باختلاف أحوالهما الاختلاف الذي يكون من قبل الفلك الخارج المركز إلى ضدّ الجهة بالسويّة فيكون البعد الثاني المسائيّ الذي هو أعظم البعد أمّا في كوكب الزهرة ففي البعد الأبعد من الفلك الخارج المركز أميل إلى الشمال وفي البعد الأقرب أميل إلى الجنوب وأمّا في كوكب عطارد فبضدّ ذلك أمّا في البعد الأبعد فأميل إلى الجنوب وأمّا في البعد الأقرب فأميل إلى الشمال ومتى كان مسيرهما المعدّل في الطول في العقدتين فحينئذ تكون الأبعاد التي مبلغها من البعد الأبعد أو البعد الأقرب عن جنبي فلكي تدويرهما ربع دائرة جميعًا وفي فلك البروج ويكون مسيرهما في البعد الأقرب على غاية ما يكون من المخالفة بمسيرهما في البعد الأبعد ويكون مثله أمّا في كوكب الزهرة أمّا إذا كان في العقدة التي في نصف الدائرة الذي للنقصان فإلى الجنوب وأمّا إذا كان في العقدة المضادّة لهذه فإلى الشمال وأمّا في كوكب عطارد فبضدّ ذلك أمّا في العقدة التي في نصف الدائرة الذي للنقصان فإلى الشمال وأمّا في العقدة المضادّة لها فإلى الجنوب حتّى إنّه يجتمع من هذه الأشياء أيضًا أنّ ميول فلكيهما الخارجة المركز يتحرّكان ويعودان في حركتهما بعودة أدوار فلكي تدويرهما حتّى إنّ هذين إذا كانا في العقدتين صارا معهما في سطح واحد بعينه وهو سطح فلك البروج وأمّا في البعد الأبعد أو البعد الأقرب أمّا في كوكب الزهرة فإنّه يجعل فلك تدويره في غاية البعد في الشمال وأمّا في كوكب عطارد فإنّه يجعل فلك تدويره في غاية البعد في الجنوب فأمّا فلكا تدويرهما فإنّهما يفعلان ضربين من الاختلاف فيميلان القطرين اللذين يمرّان بالبعدين الأبعدين اللذين يريان غاية ميلهما متى كانا في عقدتي الفلكين الخارجي المركز ويخرقان القطرين القائمين على زوايا قائمة على هذين القطرين غاية ما يكون من انحرافهما فإنّا بهذا الاسم فرقنا بين هذا الميل وبين ذلك الميل إذا كانا في البعد الأبعد أو البعد الأقرب من الفلكين الخارجي المركز ويفعلان ضدّ ذلك أعني أنّهما يجعلان ذينك القطرين في سطح الفلك الخارج المركز متى كانا في البعد الأبعد أو البعد الأقرب منه ويجعلان هذين القطرين في سطح فلك البروج متى كانا في العقدتين اللتين تقدّم ذكرهما⊙
〈XIII.2〉 ب: في الوجه الذي عليه يجري الأمر في حركة هذه الميول والانحرافات بحسب هذه الأصول التي وضعت⊙
والذي يجتمع جملةً من هذه الأصول هو على هذه الصفة إلّا أنّ الأفلاك الخارجة المراكز للكواكب الخمسة المتحيّرة هي مائلة على سطح فلك البروج وعلى مركز فلك البروج لكنّ ميلها في هذه الكواكب الثلاثة أعني زحل والمشتري والمرّيخ ثابت على حال واحدة يكون معها المسيران المتقاطران لأفلاك تدويرهما ينتقلان في العرض في الجهتين المتضادّتين وأمّا في الزهرة وعطارد فإنّهما ينتقلان بنقلة فلكي تدويرهما إلى جهة واحدة بعينها في العرض أمّا في الزهرة فإلى الشمال أبدًا وأمّا في عطارد فإلى الجنوب أبدًا وأنّ أفلاك التداوير أمّا أقطارها التي تمرّ بالبعد الأبعد منها الذي يرى فإنّها إذا صارت في سطح الفلك الخارج المركز ابتدأت ابتداءًا ما من ذلك الموضع تتحرّك عن دوائر صغار كأنّا قلنا إنّها موضوعة بالقرب عند أطرافها التي هي البعد الأقرب وهذه الدوائر معادلة لمبلغ الزوال في العرض وهي على زوايا قائمة على سطوح الأفلاك الخارجة المراكز ومراكزهما موضوعة فيها وتتحرّك على استواء وعلى اللزوم للمسيرات في الطول من أحد ه: أحد المبدأين اللذين على تقاطع هذه السطوح وسطوح أفلاك التدوير نحو الشمال بحسب الأصل الذي يعمل عليه وتقود معها سطوح أفلاك التدوير أمّا في دورانها في الربع الأوّل فإلى النهاية الشماليّة وذلك بيّن وأمّا في الربع الثاني فإلى سطح الفلك الخارج المركز من الرأس وأمّا في الربع الثالث فإلى النهاية الجنوبيّة وأمّا في العودة الباقية فإلى السطح الذي كانت فيه مبداول الأمر وأنّ ابتداء هذه المفارقة وعودتها أمّا في زحل والمشتري والمرّيخ فتكون من التقاطع الذي على العقدة المصعدة وأمّا في الزهرة فتكون من البعد الأقرب من الفلك الخارج المركز وأمّا في عطارد فتكون من البعد الأبعد من الفلك الخارج المركز وأمّا أقطار أفلاك التدوير القائمة على زوايا قائمة على الأقطار التي تقدّم ذكرها فإنّها في الكواكب الثلاثة تبقى كما قلنا أبدًا موازيةً لسطح فلك البروج وإن انحرفت عنه كان انحرافها لا قدر له يعتدّ به فأمّا في عطارد والزهرة فإنّها أيضًا إذا صارت في سطح فلك البروج ابتدأت ابتداءًا ما من ذلك الموضع تتحرّك عن دوائر صغار كأنّها موضوعة عند أطرافها التالية وهذه الدوائر معادلة أيضًا لمبلغ الزوال في العرض وهي على زوايا قائمة على سطح فلك البروج ومراكزها موضوعة على الأقطار الموازية لسطح فلك البروج ويتحرّك حركةً مساويةً في السرعة لتلك الأقطار الأخر من أحد المبدأين اللذين على تقاطع هذه الدوائر الصغار وسطوح أفلاك التدوير نحو الشمال أيضًا بحسب الأصل الذي يعمل عليه وتستوثق معها أطراف هذه الأقطار الموصوفة التي تلي المساء على مثل ذلك الترتيب بعينه الذي تقدّم ذكره وذلك بيّن وأنّ في هذه الأقطار أيضًا يكون مبدأ المفارقة والعودة النظيرة أمّا في كوكب الزهرة فمن العقدة التي على نصف الدائرة الذي للزيادة وأمّا في كوكب عطارد فمن العقدة التي على نصف الدائرة الذي للنقصان إلّا أنّه قد ينبغي أن يعلم أوّلًا من أمر هذه الدوائر الصغار التي عليها تكون تنتقل أفلاك التدوير أنّها أيضًا تنقسم بنصفين عن السطوح التي نقول فيها إنّ حولها تكون تنتقل الميول فإنّ بهذا الوجه وحده يتهيّأ أن تكون مسيراتها في العرض في الجانبين متساوية فأمّا دورانها بحسب الحركة المستوية فليس يكون حول المركز الذي لها خاصّةً بل على مركز آخر وهو الذي يفعل بقياسه إلى الدائرة الصغيرة مثل ذلك الخروج عن المركز الذي يفعله الكوكب في الطول بقياسه إلى فلك البروج وذلك أنّ العودات إذا وضع زمانها مساويًا في فلك البروج وفي الدائرة الصغيرة ووضعنا أيضًا المسيرات في الأرباع في كلّ واحد منها يطابق بعضها بعضًا على حسب ما يرى فإنّ دوران الدائرة الصغيرة إن كان على المركز الذي لها خاصّةً لم يتهيّأ ما ذكرناه أصلًا من قبل أنّ المسيرات في الدائرة الصغرى في كلّ واحد من الأرباع تكون أزمانها متساويةً وتكون مسيرات فلك التدوير في فلك البروج وهي المسيرات التي ترى غير متساوية الأزمان من قبل الفلك الخارج المركز الموضوع في كلّ واحد منها وإن كان على مركز موضعه مثل موضع مركز الفلك الخارج المركز وفي أرباع تتطابق من فلك البروج ومن الدائرة الصغيرة فإنّ عودات الميول تتمّ في أزمان متساوية⊙ ولا يظنّنّ أحد أنّ هذه الأصول وما أشبهها عسر وقوعها بأن يجعل نظره فيما قلنا ↑: قبلنا من الأشياء التي تتّخذ بالحيلة ولطف الصنعة وصعوبتها وعسر وقوعها وذلك أنّه ليس ينبغي أن يقاس على الأمور الإلهيّة بالأمور الإنسيّة ولا أن يقصد لتصحيح ما هذا مبلغ جلالة خطره نتناول المثالات له من الأمور التي هي في غاية البعد من الشبه به فإنّه لا شيء أبعد شبهًا عن الأشياء التي هي أبدًا على مثال واحد من الأشياء التي ليست كذلك ولا في وقت من الأوقات ولا أبعد شبهًا عن الأشياء التي تعتورها العوائق من كلّ جهة من الأشياء التي لا يلحقها عائق لأمر غيرها ولا من أنفسها بل إنّما ينبغي أن يلتمس بغاية ما يمكن أن يطابق بالحركات التي في السماء أبسط ما يكون من الأصول التي يجري أمرها عليها وإن لم يتهيّأ ذلك التمس من الأصول ما يمكن أن يكون يسوغ به ويلتئم فإنّا إن وجدنا بجهة من الجهات كلّ واحد من الأشياء التي يرى فيها لازمًا لتلك الأصول التي توضع لها غير مغادر لها لم يكن لاستنكار أن يكون ممكن أن يكون مثل هذا التركيب والاشتباك قد لحق الحركات السماويّة موضع إذ كان ليس فيها طبيعة مانعة ولا عائقة أصلًا بل طبيعتها موافقة لأن تطاوع وتوالي وتنقاد للحركات الطبيعيّة لكلّ واحد منها وإن كانت متضادّةً حتّى إنّها كلّها تقوى على أن تنفذ في الصبيبات كلّها على الإطلاق التي منها قوامها ويظهر فعلها فيها وإنّ سهولة السلوك ليست إنّما هي في الدوائر الجزئيّة فقط بل في الأكر أنفسها أيضًا وهي مجاور دورانها فإنّ اشتباك هذه أيضًا في الحركات المختلفة وركوب بعضها على بعض حتّى تتطابق أمّا في التماثيل الذي نتّخذها نحن فإنّا نجده صعبًا عسر المرام وإذا التمس فيها أن تكون الحركة لا مانع لها وأمّا في لسماء فإنّا نجد الحركة ليس يمنعها ولا يعوقها ↑: يفوقها هذا الاختلاط من جهة من الجهات أصلًا ومعنى البسيط أيضًا نفسه في الأجرام السماويّة ليس إنّما ينبغي أن يحكم عليه من الأجرام التي قبلنا التي يظنّ أنّها بهذه الصفة إذ كنّا نجد البسيط فينا أنفسنا ليس هو بعينه البسيط في كلّ شيء على مثال واحد فيكون إذا سلكنا هذا الطريق من النظر لم نر أنّ شيئًا ممّا يكون في السماء بسيط ولا الحال نفسها التي للحركة الأولى التي لا تتغيّر فضلًا عن غيرها من قبل أنّ هذا المعنى نفسه أعني أن يكون الشيء في كلّ زمان على مثال واحد ليس هو فينا إنّما هو صعب عسر بل غير ممكن أصلًا فأمّا في الطبائع التي في السماء نفسها وفي حركاتها التي لا تتغيّر فليس ذلك بصعب ولا عسر فإنّا بهذا الوجه يتبيّن لنا أنّها كلّها بسيطة وأنّها أحرى بذلك من الأشياء التي قبلنا ممّا نظنّ به أنّه بهذه الصفة إذ ليس يمكن أن يتوهّم أنّه ينالها في دورانها ضرب من الكلال ولا مشقّة بوجه من الوجوه⊙
〈XIII.3〉 جـ: في مقدار ميل ميل وانحراف انحراف
أمّا جملة الأمر في موضع ميل الدوائر في مرتبته فمن هذه الأشياء يمكن الإنسان أن يستخرجه حتّى يقف عليه وأمّا المقادير الجزئيّة في كلّ واحد من هذه الكواكب للقسيّ التي تجوزها الميول من الدائرة التي ترسم مارّةً بقطبي الدائرة المائلة على سطح فلك البروج القائمة عليه على زوايا قائمة وهي الدائرة التي نحسبها ترى المسيرات في العرض فقد يسهل حسابها في الزهرة وعطارد من قبل المسيرات التي ترى في العرض في الأوضاع المفروضة وذلك أنّه متى كانت حركاتهما في الطول في البعد الأبعد أو في البعد الأقرب من فلكيهما الخارجيّ المركز فإنّه إن كان مسير الكوكبين في البعد الأقرب أو في البعد الأبعد من فلكي تدويرهما كان الأمر فيهما كما قلنا وذلك شيء وقفنا عليه برصدنا لهما وهما بالقرب من هذين الموضعين وهو أنّهما يريان أميل إلى الشمال أو إلى الجنوب عن فلك البروج بالسواء أمّا كوكب الزهرة فإلى الشمال أبدًا ينحو من سدس جزء واحد أكثره وأمّا كوكب عطارد فإلى الجنوب أبدًا بنصف وربع جزء واحد حتّى إنّه يظهر من ذلك أنّ ميل فلك ه: فلك فلك من فلكيهما أيضًا الخارجيّ المركز هذا مقداره وإن كان مسيرهما في أبعادهما العظمى عن الشمس فإنّهما جميعًا يريان أميل إلى الشمال أو إلى الجنوب عن البعدين الأعظمين المضادّين لهما بنحو من خمسة أجزاء على الأمر الوسط في القياس من قبل أنّ كوكب الزهرة يرى يفعل بهذه المضادّة التي ذكرناها في العرض بأقلّ من خمسة أجزاء في البعد الأبعد من الفلك الخارج المركز وأكثر من خمسة أجزاء في القرب الأقرب منه بما لا يعبأ به وكوكب عطارد يرى يختلف في ذلك لنصف جزء أكثره حتّى إنّ انحرافات فلك التدوير في أحد جانبي السطحين اللذين فيهما الفلكان الخارجا المركزين يوتر على الأمر الوسط في القياس نحوًا من جزأين ونصف جزء من الدائرة القائمة على زوايا قائمة على فلك البروج ومن قبل هذه الانحرافات توجد مقادير الزوايا التي تحدث عن انحراف فلكي التدوير على الفلكين الخارجي المركزين كما سيظهر فيما سنبيّنه فيما بعد من أمرها كيلا نقطع في العاجل اتّصال الكلام الذي نقوله في ميول الكواكب الخمسة عامّةً⊙ ومتى كانت حركتاهما في الطول المعتدلتين في العقدتين في قريب من الأبعاد الوسطى وأمّا كوكب الزهرة فإنّ مسيره متى كان في البعد الأبعد من فلك تدويره فإنّه يرى أميل إلى الجنوب أو إلى الشمال عن فلك البروج بجزء واحد ومتى كان مسيره في البعد الأوّل منه فإنّه يرى أميل بستّة أجزاء وثلث بالتقريب حتّى إنّ ميل فلك تدويره من قبل ذلك يكون يجوز من الدائرة التي ترسم على قطبيه على الصفة التي ذكرناها جزأين ونصف جزء فإنّا نجد من قبل الاختلاف في فلك تدويره في الأبعاد الوسطى أنّ هذا المقدار من الأجزاء أمّا في البعد الأبعد من فلك التدوير فيوتر زاوية عند البصر مبلغها جزء واحد ودقيقتان وأمّا في البعد الأقرب فيوتر زاوية مبلغها ستّة أجزاء واثنتان وعشرون دقيقةً وأمّا كوكب عطارد فإنّ مسيره متى كان في البعد الأبعد من فلك تدويره فإنّ ميله إلى الجنوب وإلى الشمال عن فلك البروج يكون جزءًا واحدًا ونصف وربع جزء على ما يوقف عليه من ذلك بالحساب المأخوذة من قبل ظهوراته القريبة من هذا الموضع ومتى كان مسيره في البعد الأقرب فإنّ ميله يكون أربعة أجزاء بالتقريب حتّى إنّ ميل فلك التدوير يكون من قبل هذه ستّة أجزاء وربع جزء فإنّا نجد أيضًا من قبل الاختلاف في فلك تدويره في الأبعاد التي للميول العظمى أعني إذا كان الطول المعدّل بعده من البعد الأبعد ربع دائرة أنّ هذا المقدار من الأجزاء يوتر زاويةً عند البصر أمّا في البعد الأبعد من فلك تدويره فمبلغها جزء واحد وستّ وأربعون دقيقةً وأمّا في البعد الأقرب منه فمبلغها أربعة أجزاء وخمس دقائق⊙ وأمّا في الكواكب الثلاثة الباقية وهي زحل والمشتري والمرّيخ فليس يقدر الإنسان أن يقف بسهولة بهذا الطريق على مقدار الميول فيها لأنّ الصفّين جميعًا فيها هما أبدًا مختلطان أعني ما يكون منها من قبل الفلك الخارج المركز وما يكون منها من قبل فلك التدوير لكنّا نفصّل كلّ واحد من صنفي الميول من الآخر من قبل الأرصاد أيضًا للمسيرات في العرض التي كانت لها في البعد الأقرب وفي البعد الأبعد من الأفلاك الخارجة المراكز وهي أفلاك التدوير بهذا الوجه⊙ آ: فليكن في السطح القائم الزاوية على زوايا قائمة على سطح فلك البروج الفصل المشترك بينه وبين سطح فلك البروج خطّ ألف باء والفصل المشترك بينه وبين سطح الفلك الخارج المركز خطّ جيم دال ونقطة هاء مركز فلك البروج في الفصل المشترك بين السطوح ولنرسم حول نقطة جيم وهي البعد الأبعد من الفلك الخارج المركز وحول نقطة دال وهي القرب الأقرب في السطح الموضوع دائرتي زاي حاء طاء كاف لام ميم نون سين متساويتين كالدائرتين اللتين تمرّان بأقطاب أفلاك التداوير ولنمل عليهما سطحا فلكي التدوير بخطّ حاء جيم كاف وخطّ ميم دال سين بمقدار الزاويتين اللتين عند نقطتي جيم دال ومن البيّن أنّهما متسا متساويتان ولنوصل بين نقطة هاء التي هي مركز فلك البروج وعليها البصر وبين البعدين الأبعدين وبين البعدين الأقربين من فلكي التدوير أمّا بينهما وبين البعدين الأبعدين فبخطّي هاء حاء هاء ميم وأمّا بينهما وبين البعدين الأقربين فبخطّي هاء كاف هاء سين ومن البيّن أنّ نقطتي كاف سين تشتملان على المسيرين المتساويين إلى طرف الليل ونقطتي حاء ميم تشتملان على المسيرين الاجتماعيين فأمّا في كوكب المرّيخ فإنّا أخذنا المسيرات التي تكون له في العرض في أحوال طرف الليل التي تكون له في البعد الأبعد من الفلك الخارج المركز أعني التي تكون على نقطة كاف من فلك التدوير وفي أحوال طرف الليل التي تكون له في البعد الأقرب من الفلك الخارج المركز أعني التي تكون على نقطة سين من فلك التدوير لأنّ الفضل في هذه المسيرات بيّن جدًّا للّمس فوجدناه يبعد عن فلك البروج أمّا في أحوال طرف الليل التي في البعد الأبعد فأربعة أجزاء وثلث في الشمال وأمّا في أحوال طرف الليل التي في البعد الأقرب فسبعة أجزاء في الجنوب بالتقريب حتّى إنّ زاوية ألف هاء كاف تكون أيضًا أربعة أجزاء وثلث بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا وتكون زاوية باء هاء سين بهذه الأجزاء الباقية سبعة أجزاء ؞ وإ قد قد وطّئت هذه الأشياء فإنّا نجد الزاوية التي يحيط بها ميل الفلك الخارج المركز أعني زاوية ألف هاء جيم والزاوية التي يحيط بها ميل فلك التدوير أعني زاوية جيم حاء زاي بهذا الوجه لمّا كان ممّا يسهل فهمه من قبل الاختلافات التي بيّنّاها للمرّيخ إن كان من زوايا المسير التي عند البصر يوترها عند البعد الأقرب من أفلاك التدوير قسيّ متساوية فإنّ نسبة المسيرات التي تكون بها القسيّ التي عند البعد الأبعد من الفلك الخارج المركز إلى المسيرات التي يكون بها على القسيّ التي عند البعد الأٌقرب منه كنسبة خمسة أجزاء بالتقريب إلى تسعة أجزاء وكانتا قوسا طاء كاف نون سين متساويين فإنّ نسبة زاوية جيم هاء كاف إلى زاوية دال هاء سين تكون كنسبة خمسة أجزاء إلى تسعة أجزاء فلذلك من قبل أنّ زاويتي ألف هاء كاف باء هاء سين معلومتان فإنّ نسبة زاوية جيم هاء كاف إلى زاوية دال هاء سين معلومة وأنّ زاوية ألف هاء جيم مساوية لزاوية باء هاء دال إن نحن نظرنا كم جزء التفاضل بين جملتي المقدارين من التفاضل بين عددي النسبة وأخذنا مثل ذلك الجزأين كل واحد من عددي النسبة حصل لنا مبلغ كل واحد من المقدارين اللذين بينهما خاصّةً وقفت النسبة وذلك يبيّن بباب صغير من الأبواب العدديّة فلأنّ المقدارين أحدهما أربعة أجزاء وثلث جزء والآخر سبعة أجزاء والفضل بينهما جزءان وثلثا جزء والنسبة هي نسبة خمسة أجزاء إلى تسعة أجزاء والفضل بين هذين العددين أربعة أجزاء والجزأين والثلثي الجزء جزؤهما من الأربعة الأجزاء الثلثان إن نحن أخذنا من الخمسة الأجزاء ومن التسعة الأجزاء مثل هذا الجزء حصلت لنا زاوية دال هاء سين بهذه الأجزاء ستّة أجزاء وزاوية دال هاء كاف ثلاثة أجزاء وثلث وكانت كل واحدة من زاويتي ألف هاء جيم باء هاء دال الباقيتين وهما زاويتا ميل الفلك الخارج المركز على حسب ما يلزم جزءًا واحدًا ويحصل من ذلك قوس طاء كاف أيضًا وهي قوس ميل فلك التدوير جزأين وربع لأنّ هذا مبلغ ما تشتمل عليه من الأجزاء على التقريب في جدول الاختلاف هذه المقادير التي وقفنا عليها الزاويتين جيم هاء كاف دال هاء سين⊙ وأمّا في زحل والمشتري فإنّا لمّا كنّا نجد مسيراتهما التي تكون في قسمي البعد الأبعد من فلكيهما الخارجي المركز من لا يخالف في الحس مسيراتهما التي تكون في قسمي البعد الأقرب منهما المقاطرة أيضًا لتلك المسيرات فإنّا حسبنا ما قصدنا له من أمرهما على كلّ واحدة ه: يعني إذا كان فلك التدوير في البعد الأبعد من الفلك الخارج المركز وإذا كان في البعد الأقرب منه وكان الكوكب مرّةً في البعد الأبعد من فلك تدويره ومرّةً في القرب الأقرب من الجهتين من قبل المقايسة بين مسيراتهما في البعد الأبعد من فلكي تدويرهما وبين مسيراتهما في البعد الأقرب منه ومبلغ البعد على ما وقفنا عليه من الأرصاد الجزئيّة لهما أمّا في المسيرات التي تكون في الظهور وفي الاختفاء فأكثر ما تكون إلى الشمال وإلى الجنوب أمّا في زحل فجزأين بالتقريب وأمّا في المشتري فجزءًا واحدًا وأمّا في المسيرات التي تكون في أحوال طرف الليل أمّا في زحل
 فإلى ثلاثة أجزاء وأمّا في المشتري فإلى جزأين ه: {...} يريد ثلاثة أجزاء فما دون وجزأين فما دون (فلمّا كان قد يظهر) (من قبل الاختلاف الذي لهذه) المسيرات التي تكون في أحوال) (طرف الليل أمّا في زحل فإلى) (ثلاثة أجزاء وأمّا في المشتري) (فإلى جزأين) فلمّا كان قد يظهر من قبل الاختلاف الذي لهذه المسيرات أيضًا أنّ الزوايا التي عند البصر التي توترها في البعد الأبعد والبعد الأقرب من فلك التدوير قسيّ متساوية ما كان منها يحدث عن المسيرات في البعد الأبعد فإنّ نسبتها إلى الزوايا التي تحدث عن المسيرات في البعد الأقرب أمّا في كوكب زحل فنسبة ثمانية عشر جزءًا إلى ثلاثة وعشرين جزءًا وأمّا في كوكب المشتري فنسبة تسعة وعشرين جزءًا إلى ثلاثة وأربعين جزءًا وكانتا قوس زاي حاء طاء كاف من فلك التدوير متساويين فإنّ نسبة زاوية زاي هاء حاء إلى زاوية زاي هاء كاف تكون أمّا في كوكب زحل فنسبة ثمانية عشر جزءًا إلى ثلاثة وعشرين جزءًا وأمّا في كوكب المشتري فنسبة تسعة وعشرين جزءًا إلى ثلاثة وأربعين جزءًا لكنّ زاوية حاء هاء كاف إذ كانت فضل ما بين المسيرين في العرض في الكوكبين جميعًا تحصل جزءًا واحدًا فإذا قسم إذن هذا الجزء الواحد بالنسبتين المذكورتين حصلت لنا زاوية زاي هاء حاء أمّا في زحل فستًّا وعشرين دقيقةً وأمّا في المشتري فأربعًا وعشرين دقيقةً وحصلت زاوية زاي هاء كاف أمّا في زحل فأربعًا وثلاثين دقيقةً وأمّا في المشتري فستًّا وثلاثين دقيقةً فتكون زاوية ألف هاء جيم الباقية وهي زاوية ميل الفلك الخارج المركز يحصل أمّا في زحل فجزأين وستًّا وعشرين دقيقةً وأمّا في المشتري فجزءًا واحدًا وأربعًا وعشرين دقيقةً إلّا أنّا اخترنا فاستعملنا مكان هذين العددين عدد جزأين ونصف وعدد جزء ونصف طلبًا للتسهيل في العمل فمن قبل ذلك تجتمع قوس طاء كاف أيضًا وهي قوس ميل فلكي التدوير أمّا في زحل فأربعة أجزاء ونصف جزء وأمّا في المشتري فجزأين ونصف جزء وذلك أنّ هذا المقدار من الأجزاء في واحد واحد منهما في جداول الاختلاف يحيط أيضًا على التقريب بالمقدارين اللذين وفّقنا عليهما الزاويتين زاي هاء حاء زاي هاء كاف وهذه هي الأشياء التي كنّا قصدنا لوجودها⊙
فإلى ثلاثة أجزاء وأمّا في المشتري فإلى جزأين ه: {...} يريد ثلاثة أجزاء فما دون وجزأين فما دون (فلمّا كان قد يظهر) (من قبل الاختلاف الذي لهذه) المسيرات التي تكون في أحوال) (طرف الليل أمّا في زحل فإلى) (ثلاثة أجزاء وأمّا في المشتري) (فإلى جزأين) فلمّا كان قد يظهر من قبل الاختلاف الذي لهذه المسيرات أيضًا أنّ الزوايا التي عند البصر التي توترها في البعد الأبعد والبعد الأقرب من فلك التدوير قسيّ متساوية ما كان منها يحدث عن المسيرات في البعد الأبعد فإنّ نسبتها إلى الزوايا التي تحدث عن المسيرات في البعد الأقرب أمّا في كوكب زحل فنسبة ثمانية عشر جزءًا إلى ثلاثة وعشرين جزءًا وأمّا في كوكب المشتري فنسبة تسعة وعشرين جزءًا إلى ثلاثة وأربعين جزءًا وكانتا قوس زاي حاء طاء كاف من فلك التدوير متساويين فإنّ نسبة زاوية زاي هاء حاء إلى زاوية زاي هاء كاف تكون أمّا في كوكب زحل فنسبة ثمانية عشر جزءًا إلى ثلاثة وعشرين جزءًا وأمّا في كوكب المشتري فنسبة تسعة وعشرين جزءًا إلى ثلاثة وأربعين جزءًا لكنّ زاوية حاء هاء كاف إذ كانت فضل ما بين المسيرين في العرض في الكوكبين جميعًا تحصل جزءًا واحدًا فإذا قسم إذن هذا الجزء الواحد بالنسبتين المذكورتين حصلت لنا زاوية زاي هاء حاء أمّا في زحل فستًّا وعشرين دقيقةً وأمّا في المشتري فأربعًا وعشرين دقيقةً وحصلت زاوية زاي هاء كاف أمّا في زحل فأربعًا وثلاثين دقيقةً وأمّا في المشتري فستًّا وثلاثين دقيقةً فتكون زاوية ألف هاء جيم الباقية وهي زاوية ميل الفلك الخارج المركز يحصل أمّا في زحل فجزأين وستًّا وعشرين دقيقةً وأمّا في المشتري فجزءًا واحدًا وأربعًا وعشرين دقيقةً إلّا أنّا اخترنا فاستعملنا مكان هذين العددين عدد جزأين ونصف وعدد جزء ونصف طلبًا للتسهيل في العمل فمن قبل ذلك تجتمع قوس طاء كاف أيضًا وهي قوس ميل فلكي التدوير أمّا في زحل فأربعة أجزاء ونصف جزء وأمّا في المشتري فجزأين ونصف جزء وذلك أنّ هذا المقدار من الأجزاء في واحد واحد منهما في جداول الاختلاف يحيط أيضًا على التقريب بالمقدارين اللذين وفّقنا عليهما الزاويتين زاي هاء حاء زاي هاء كاف وهذه هي الأشياء التي كنّا قصدنا لوجودها⊙
〈XIII.4〉 د: صفة عمل جداول للمسيرات الجزئيّة في العرض
فمن هذه الأشياء حصلت لنا المقادير الكليّة للميول العظمى للأفلاك الخارجة المراكز ولأفلاك التدوير وكيما نقدر أن نستخرج بسهولة في كلّ وقت المسيرات في العرض في الأبعاد الجزئيّة أيضًا اتّخذنا جداول للكواكب الخمسة المتحيّرة في كلّ جدول منها من السطور مثل ما في كلّ جدول من جداول الاختلاف وصفوفه خمسة فالصفّان الأوّلان من هذه الصفوف فيهما الأعداد كما في تلك الصفوف وأمّا الصفوف الثوالث ففيهما الأبعاد في العرض عن فلك البروج التي تصيب أقسام أفلاك التدوير الجزئيّة في الميول العظمى أنفسها أمّا في كوكب الزهرة وكوكب عطارد ففي العقدتين من الأفلاك الخارجة المراكز وأمّا في الكواكب الثلاثة الباقية ففي النهايات الشماليّة من الأفلاك الخارجة المراكز والصفوف الروابع أيضًا في هذه الثلاثة فيها ما يصيب من الأبعاد النظائر لتلك نحو النهايات الجنوبيّة من الأفلاك الخارجة المراكز مضافًا إلى ذلك في هذه الثلاثة الكواكب أكثر ما يكون أيضًا من تباعد أفلاكها الخارجة المراكز في الشمال وفي الجنوب وكان حسابنا لهذه الأقسام أمّا في كوكب الزهرة وكوكب عطارد فبباب أيضًا واحد على هذا النحو ب: ليكن في السطح القائم على زوايا قائمة على سطح فلك البروج أمّا خطّ ألف باء جيم فالفضل المشترك بينه وبين سطح فلك البروج وأمّا خطّ دال باء هاء فالفضل المشترك بينه وبين سطح فلك التدوير وليكن مركز فلك البروج نقطة ألف ومركز فلك التدوير نقطة باء وليكن خطّ ألف باء بعد فلكي تدوير هذين الكوكبين في ميولهما العظمى ولنرسم حول نقطة باء فلك تدوير هذين الكوكبين في ميولهما العظمى ولنرسم حول نقطة باء فلك تدوير دال زاي هاء حاء ولنوصل قطر زاي باء حاء قائمًا على زوايا قائمة على خطّ دال هاء ولننزل أنّ سطح فلك التدوير أيضًا قائم على زوايا قائمة على السطح الموصوف ↑: الموضوع، ه: يعني للقائم على فلك البروج حتّى تكون جميع الخطوط المخرّجة على زوايا قائمة على خطّ دال هاء في سطح فلك التدوير موازية لسطح فلك البروج ما خلا خطّ زاي حاء وحده فإنّه يكون في سطح فلك البروج وليكن قصدنا إذا أعطينا نسبة خطّ ألف باء إلى خطّ باء هاء ومقدار الميل أعني زاوية ألف باء هاء أن نجد مسيرات هذين الكوكبين في العرض متى كان مثلًا بعدهما من نقطة هاء وهي البعد الأقرب من فلك التدوير خمسةً وأربعين جزءًا بالأجزاء التي بها فلك التدوير ثلاث مائة وستّون جزءًا وذلك أنّا نختار أن نبيّن الفضول التي تكون في المسيرات في الطول من قبل ما هذا مبلغه من الميل وهذه الفضول يجب أن تكون في موضع من المسيرات التي فيما بين نقطة هاء وهي البعد الأقرب وبين نقطة زاي ونقطة حاء تخالف غاية ما تكون من مخالفتها من قبل أنّ المسيرات التي ذكرناها موافقة للمسيرات التي تكون خلوًّا ه: يقول التي تكون لو لم يكن لفلك التدوير ميل أصلًا من الميل فلنفصّل قوسًا مقدارها الأجزاء التي ذكرناها وهي خمسة وأربعون جزءًا ولتكن قوس هاء طاء ولنخرج على خطّ باء هاء عمود طاء كاف وعلى سطح فلك البروج عمودا كاف لام طاء ميم ولنوصل خطوط طاء باء لام ميم ألف ميم ألف طاء فمن البيّن من قرب أنّ ذا أربعة أضلاع لام كاف طاء ميم متوازي الأضلاع قائم الزوايا من قبل أنّ خطّ كاف طاء موازٍ لسطح فلك البروج ومن البيّن أيضًا أنّ الزيادة أو النقصان في الطول تشتمل عليه زاوية لام ألف ميم وفي المسير في العرض تشتمل عليه زاوية طاء ألف ميم لأنّ زاويتي ألف لام ميم ألف ميم طاء تكونان أيضًا قائمتين من قبل أنّ خطّ ألف ميم أيضًا يقع في سطح فلك البروج فأمّا مقادير المسيرات المطلوبة في كل واحد من الكوكبين اللذين تقدّم ذكرهما كم تحصل فقد ينبغي الآن أن نبيّن ذلك ونبتدئ من كوكب الزهرة⊙ فنقول إنّ قوس هاء طاء إذ كانت خمسةً وأربعين جزءًا بالأجزاء التي بها فلك التدوير ثلاث مائة وستّون جزءًا فإنّ زاوية هاء باء طاء إذ كانت عند مركز فلك التدوير تكون أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فخمسة وأربعون جزءًا وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فتسعون جزءًا فتكون لذلك كلّ واحدة من القوسين أيضًا اللتين تكونان على خطّي باء كاف كاف طاء تسعين جزءًا بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء طاء كاف القائم الزاوية ثلاث مائة وستّون جزءًا فكلّ واحد إذن من الخطّين اللذين يوترانهما أربعة وثمانون جزءًا واثنتان وخمسون دقيقةً بالأجزاء التي بها موتر باء طاء مائة وعشرون جزءًا فلذلك تكون أيضًا الأجزاء التي بها أمّا موتر باء طاء وهو مركز فلك التدوير ثلاثة وأربعون جزءًا وعشر دقائق وأمّا خطّ ألف باء وهو خطّ البعد الأوسط فستّون جزءًا لأنّ في هذا البعد خاصّةً يكون ميل فلك التدوير الأعظم فإنّ كلّ واحد من خطّي باء كاف كاف طاء بها ثلاثون جزءًا واثنتان وثلاثون دقيقةً وأيضًا لأنّ زاوية ألف باء هاء وهي زاوية الميل وضعت أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزأين وثلاثين دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فخمسة أجزاء تكون أيضًا القوس التي تكون على خطّ لام كاف خمسة أجزاء بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء لام كاف القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ باء لام الأجزاء الباقية إلى نصف دائرة وهي مائة وخمسة وسبعون جزءًا فالخطّان إذن اللذان يوترانهما أمّا خطّ كاف لام منهما فيكون خمسة أجزاء وأربع عشرة دقيقةً بالأجزاء التي بها موتر باء كاف مائة وعشرون جزءًا وأمّا خطّ باء لام منهما فيكون بهذه الأجزاء مائةً وتسعة عشر جزءًا وثلاثًا وخمسين دقيقةً فلذلك يجب أن تكون الأجزاء التي بها أيضًا موتر باء كاف ثلاثون
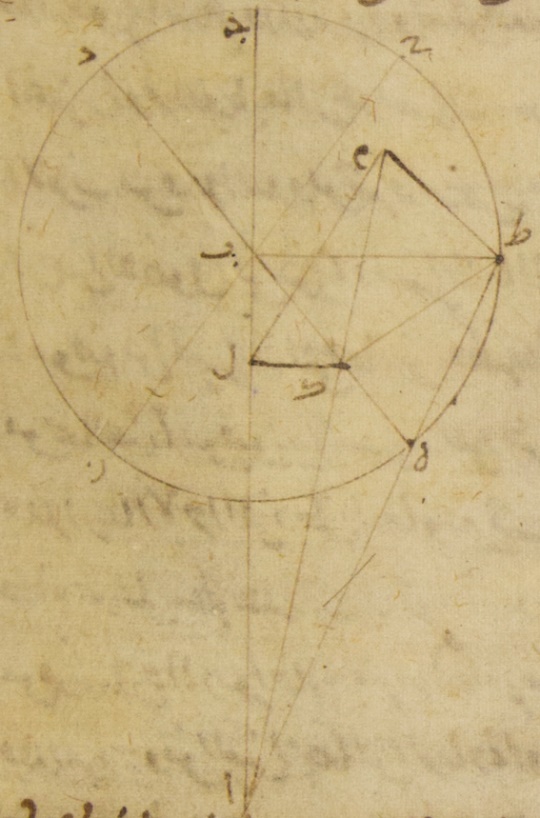 جزءًا واثنتان وثلاثون دقيقةً وخطّ ألف باء ستّون جزءًا فإنّ خطّ كاف لام يكون بها جزءًا واحدًا وعشرين دقيقةً ويكون خطّ باء لام بهذه الأجزاء ثلاثين جزءًا وثلاثين دقيقةً ويكون خطّ ألف لام الأجزاء الباقية وهي تسعة وعشرون جزءًا وثلاثون دقيقةً وبهذه الأجزاء خطّ لام ميم إذ كان مساويًا لخطّ كاف طاء ثلاثون جزءًا واثنتان وثلاثون دقيقةً فيجب من ذلك أن يجتمع موتر ألف ميم بهذه الأجزاء اثنين وأربعين جزءًا وسبعًا وعشرين دقيقةً فالأجزاء إذن التي بها موتر ألف جيم مائة وعشرون جزءًا يكون بها أمّا خطّ لام ميم فستّة وثمانون جزءًا وتسع عشرة دقيقةً وأمّا زاوية لام وهي زاوية النقصان أو الزيادة في الطول حينئذ فتكون أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فاثنان وتسعون جزءًا وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فستّة وأربعون جزءًا وعلى هذا المثال لأنّ الأجزاء التي بها خطّ ألف ميم اثنان وأربعون جزءًا وسبع وعشرون دقيقةً فإنّ بها خطّ باء ميم إذ كان مساويًا لخطّ كاف لام جزء واحد وعشرون دقيقةً وإذا جمع ما يكون منهما كان منه ما يكون من خطّ ألف طاء يكون خطّ ألف طاء أيضًا ه: أيضًا في الطول بهذه الأجزاء اثنين وأربعين جزءًا وتسعًا وعشرين دقيقةً فالأجزاء إذن التي بها موتر ألف طاء مائة وعشرون جزءًا يكون بها أمّا خطّ طاء ميم فثلاثة أجزاء وستًّا وأربعين دقيقةً وأمّا زاوية طاء ألف ميم وهي زاوية التباعد في العرض فتكون أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فثلاثة أجزاء وستّ وثلاثون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزءًا واحدًا وثمانيًا وأربعين دقيقةً فنثبت ذلك في الصفّ الثالث من جدول الزهرة في السطر الذي فيه عدد المائة والخمسة والثلاثين الجزء جـ: وكيما نعتبر ما يقع من الفضل من قبل ذلك الزيادة أو النقصان في الطول لنرسم مثل هذه الصورة على أنّ فلك التدوير فيها غير مائل
جزءًا واثنتان وثلاثون دقيقةً وخطّ ألف باء ستّون جزءًا فإنّ خطّ كاف لام يكون بها جزءًا واحدًا وعشرين دقيقةً ويكون خطّ باء لام بهذه الأجزاء ثلاثين جزءًا وثلاثين دقيقةً ويكون خطّ ألف لام الأجزاء الباقية وهي تسعة وعشرون جزءًا وثلاثون دقيقةً وبهذه الأجزاء خطّ لام ميم إذ كان مساويًا لخطّ كاف طاء ثلاثون جزءًا واثنتان وثلاثون دقيقةً فيجب من ذلك أن يجتمع موتر ألف ميم بهذه الأجزاء اثنين وأربعين جزءًا وسبعًا وعشرين دقيقةً فالأجزاء إذن التي بها موتر ألف جيم مائة وعشرون جزءًا يكون بها أمّا خطّ لام ميم فستّة وثمانون جزءًا وتسع عشرة دقيقةً وأمّا زاوية لام وهي زاوية النقصان أو الزيادة في الطول حينئذ فتكون أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فاثنان وتسعون جزءًا وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فستّة وأربعون جزءًا وعلى هذا المثال لأنّ الأجزاء التي بها خطّ ألف ميم اثنان وأربعون جزءًا وسبع وعشرون دقيقةً فإنّ بها خطّ باء ميم إذ كان مساويًا لخطّ كاف لام جزء واحد وعشرون دقيقةً وإذا جمع ما يكون منهما كان منه ما يكون من خطّ ألف طاء يكون خطّ ألف طاء أيضًا ه: أيضًا في الطول بهذه الأجزاء اثنين وأربعين جزءًا وتسعًا وعشرين دقيقةً فالأجزاء إذن التي بها موتر ألف طاء مائة وعشرون جزءًا يكون بها أمّا خطّ طاء ميم فثلاثة أجزاء وستًّا وأربعين دقيقةً وأمّا زاوية طاء ألف ميم وهي زاوية التباعد في العرض فتكون أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فثلاثة أجزاء وستّ وثلاثون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزءًا واحدًا وثمانيًا وأربعين دقيقةً فنثبت ذلك في الصفّ الثالث من جدول الزهرة في السطر الذي فيه عدد المائة والخمسة والثلاثين الجزء جـ: وكيما نعتبر ما يقع من الفضل من قبل ذلك الزيادة أو النقصان في الطول لنرسم مثل هذه الصورة على أنّ فلك التدوير فيها غير مائل  فلأنّا بيّنّا أنّ كلّ واحد من خطّي باء كاف كاف طاء ثلاثون جزءًا واثنتان وثلاثون دقيقةً بالأجزاء التي بها خطّ ألف باء ستّون جزءًا حتّى إنّ خطّ ألف كاف تكون الأجزاء الباقية وهي تسعة وعشرون جزءًا وثمان وعشرون دقيقةً والذي يكون من هذا الخطّ ومن خطّ كاف طاء إذا جمعا كان منه المربّع الذي من خطّ ألف طاء يكون خطّ ألف طاء أيضًا في الطول بهذه الأجزاء اثنين وأربعين جزءًا وستًّا وعشرين دقيقةً فالأجزاء إذن التي بها موتر ألف طاء مائة وعشرون جزءًا يكون بها أمّا خطّ كاف طاء فستّة وثمانون جزءًا وإحدى وعشرون دقيقةً وأمّا زاوية طاء ألف كاف وهي زاوية الزيادة أو النقصان في الطول فتكون أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فاثنان وتسعون جزءًا وثلاث دقائق وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فستّة وأربعون جزءًا ودقيقتان بالتقريب وقد كان بيّن في الميل أنّ مبلغها بهذه الأجزاء ستّة وأربعون جزءًا فقد نقص إذا عدّد الزيادة أو النقصان من قبل ميل فلك التدوير دقيقتين وذلك ما قصدنا أن نجد⊙ د: ولنرسم أيضًا لتبيين المسيرات في كوكب عطارد مثل تلك الصورة التي قبل هذه على أنّ قوس هاء طاء توضع أجزاءها تلك الأجزاء بأعيانها وهي خمسة وأربعون جزءًا حتّى إنّ كلّ واحد من خطّي باء كاف كاف طاء يجتمع أيضًا أربعة وثمانين جزءًا واثنتين وخمسين دقيقةً بالأجزاء التي بها موتر باء طاء مائة وعشرون جزءًا فالأجزاء إذن التي بها خطّ باء طاء وهو من مركز فلك التدوير اثنان وعشرون جزءًا وثلاثون دقيقةً وخطّ ألف باء وهو خطّ البعد في ميوله العظمى ستّة وخمسون جزءًا وأربعون دقيقةً فإنّا قد بيّنّا هذه الأشياء كلّها أيضًا يكون بها كلّ واحد من خطّي باء كاف كاف طاء أيضًا خمسة عشر جزءًا وخمسًا وخمسين دقيقةً وأيضًا لأنّ زاوية ألف باء هاء وهي زاوية ميل فلك التدوير أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءا فإنّها وضعت بها ستّة أجزاء وخمس عشرة دقيقةً فأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فاثنا عشر جزءًا وثلاثون دقيقةً وتكون أيضًا القوس التي تكون على خطّ لام كاف اثني عشر جزءًا وثلاثين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء لام كاف القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ باء لام الأجزاء الباقية إلى نصف دائرة وهي مائة وسبعة وستّون جزءًا وثلاثون دقيقةً فخطّ كاف لام إذن من الخطّين اللذين يوترانهما ثلاثة عشر جزءًا وأربع دقائق بالأجزاء التي بها موتر باء كاف مائة وعشرون جزءًا وخطّ باء لام منهما بهذه الأجزاء مائة وتسعة عشر جزءًا وسبع عشرة دقيقةً فيجب من ذلك أن تكون الأجزاء التي تبيّن أنّ خطّ باء كاف بها خمسة عشر جزءًا وخمسون دقيقةً ووضع خطّ ألف باء بها ستّة وخمسون جزءًا وأربعون دقيقةً تكون بها أمّا خطّ كاف لام فجزءًا واحدًا وأربعًا وأربعين دقيقةً وأمّا خطّ باء لام فعلى ذلك المثال خمسة عشر جزءًا وتسعًا وأربعين دقيقةً ويكون خطّ ألف لام الباقي بهذه الأجزاء أربعين جزءًا وإحدى وخمسين دقيقةً لكنّ خطّ لام ميم إذ كان مساويًا لخطّ كاف طاء فهو بهذه الأجزاء خمسة عشر جزءًا وخمس وخمسون دقيقةً فلأنّ المربّع الذي من خطّ ألف لام مع المربّع الذي من خطّ لام ميم يكون منهما الذي من خطّ ألف ميم فإنّ هذا الخطّ أيضًا يحصل لنا في الطول ثلاثةً وأربعين جزءًا وخمسين دقيقةً بالأجزاء التي بها خطّ لام ميم خمسة عشر جزءًا وخمس وخمسون دقيقةً فالأجزاء إذن التي بها موتر ألف ميم مائة وعشرون جزءًا يكون بها أمّا خطّ لام ميم فثلاثة وأربعون جزءًا وأربع وثلاثون دقيقةً وأمّا زاوية لام ألف ميم وهي زاوية الزيادة أو النقصان في الطول فتكون أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فاثنان وأربعون جزءًا وثلاثون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فواحد وعشرون جزءًا وسبع عشرة دقيقةً ⊙ وعلى هذا المثال لأنّ الأجزاء التي بها خطّ ألف ميم ثلاثة وأربعون جزءًا وخمسون دقيقةً يصير بها خطّ طاء ميم إذ كان مساويًا لخطّ كاف لام جزءًا واحدًا وأربعًا وأربعين دقيقةً وما يكون منهما إذا جمع يكون منه المربّع الذي من خطّ ألف طاء فإنّ هذا الخطّ أيضًا
فلأنّا بيّنّا أنّ كلّ واحد من خطّي باء كاف كاف طاء ثلاثون جزءًا واثنتان وثلاثون دقيقةً بالأجزاء التي بها خطّ ألف باء ستّون جزءًا حتّى إنّ خطّ ألف كاف تكون الأجزاء الباقية وهي تسعة وعشرون جزءًا وثمان وعشرون دقيقةً والذي يكون من هذا الخطّ ومن خطّ كاف طاء إذا جمعا كان منه المربّع الذي من خطّ ألف طاء يكون خطّ ألف طاء أيضًا في الطول بهذه الأجزاء اثنين وأربعين جزءًا وستًّا وعشرين دقيقةً فالأجزاء إذن التي بها موتر ألف طاء مائة وعشرون جزءًا يكون بها أمّا خطّ كاف طاء فستّة وثمانون جزءًا وإحدى وعشرون دقيقةً وأمّا زاوية طاء ألف كاف وهي زاوية الزيادة أو النقصان في الطول فتكون أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فاثنان وتسعون جزءًا وثلاث دقائق وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فستّة وأربعون جزءًا ودقيقتان بالتقريب وقد كان بيّن في الميل أنّ مبلغها بهذه الأجزاء ستّة وأربعون جزءًا فقد نقص إذا عدّد الزيادة أو النقصان من قبل ميل فلك التدوير دقيقتين وذلك ما قصدنا أن نجد⊙ د: ولنرسم أيضًا لتبيين المسيرات في كوكب عطارد مثل تلك الصورة التي قبل هذه على أنّ قوس هاء طاء توضع أجزاءها تلك الأجزاء بأعيانها وهي خمسة وأربعون جزءًا حتّى إنّ كلّ واحد من خطّي باء كاف كاف طاء يجتمع أيضًا أربعة وثمانين جزءًا واثنتين وخمسين دقيقةً بالأجزاء التي بها موتر باء طاء مائة وعشرون جزءًا فالأجزاء إذن التي بها خطّ باء طاء وهو من مركز فلك التدوير اثنان وعشرون جزءًا وثلاثون دقيقةً وخطّ ألف باء وهو خطّ البعد في ميوله العظمى ستّة وخمسون جزءًا وأربعون دقيقةً فإنّا قد بيّنّا هذه الأشياء كلّها أيضًا يكون بها كلّ واحد من خطّي باء كاف كاف طاء أيضًا خمسة عشر جزءًا وخمسًا وخمسين دقيقةً وأيضًا لأنّ زاوية ألف باء هاء وهي زاوية ميل فلك التدوير أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءا فإنّها وضعت بها ستّة أجزاء وخمس عشرة دقيقةً فأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فاثنا عشر جزءًا وثلاثون دقيقةً وتكون أيضًا القوس التي تكون على خطّ لام كاف اثني عشر جزءًا وثلاثين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء لام كاف القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ باء لام الأجزاء الباقية إلى نصف دائرة وهي مائة وسبعة وستّون جزءًا وثلاثون دقيقةً فخطّ كاف لام إذن من الخطّين اللذين يوترانهما ثلاثة عشر جزءًا وأربع دقائق بالأجزاء التي بها موتر باء كاف مائة وعشرون جزءًا وخطّ باء لام منهما بهذه الأجزاء مائة وتسعة عشر جزءًا وسبع عشرة دقيقةً فيجب من ذلك أن تكون الأجزاء التي تبيّن أنّ خطّ باء كاف بها خمسة عشر جزءًا وخمسون دقيقةً ووضع خطّ ألف باء بها ستّة وخمسون جزءًا وأربعون دقيقةً تكون بها أمّا خطّ كاف لام فجزءًا واحدًا وأربعًا وأربعين دقيقةً وأمّا خطّ باء لام فعلى ذلك المثال خمسة عشر جزءًا وتسعًا وأربعين دقيقةً ويكون خطّ ألف لام الباقي بهذه الأجزاء أربعين جزءًا وإحدى وخمسين دقيقةً لكنّ خطّ لام ميم إذ كان مساويًا لخطّ كاف طاء فهو بهذه الأجزاء خمسة عشر جزءًا وخمس وخمسون دقيقةً فلأنّ المربّع الذي من خطّ ألف لام مع المربّع الذي من خطّ لام ميم يكون منهما الذي من خطّ ألف ميم فإنّ هذا الخطّ أيضًا يحصل لنا في الطول ثلاثةً وأربعين جزءًا وخمسين دقيقةً بالأجزاء التي بها خطّ لام ميم خمسة عشر جزءًا وخمس وخمسون دقيقةً فالأجزاء إذن التي بها موتر ألف ميم مائة وعشرون جزءًا يكون بها أمّا خطّ لام ميم فثلاثة وأربعون جزءًا وأربع وثلاثون دقيقةً وأمّا زاوية لام ألف ميم وهي زاوية الزيادة أو النقصان في الطول فتكون أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فاثنان وأربعون جزءًا وثلاثون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فواحد وعشرون جزءًا وسبع عشرة دقيقةً ⊙ وعلى هذا المثال لأنّ الأجزاء التي بها خطّ ألف ميم ثلاثة وأربعون جزءًا وخمسون دقيقةً يصير بها خطّ طاء ميم إذ كان مساويًا لخطّ كاف لام جزءًا واحدًا وأربعًا وأربعين دقيقةً وما يكون منهما إذا جمع يكون منه المربّع الذي من خطّ ألف طاء فإنّ هذا الخطّ أيضًا 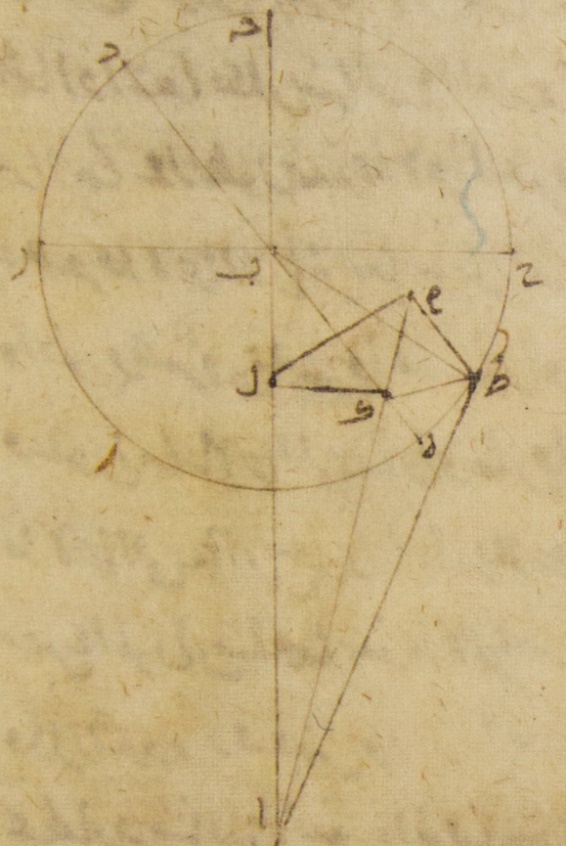 يحصل لنا في الطول بهذه الأجزاء ثلاثةً وأربعين جزءًا واثنتين وخمسين دقيقةً فالأجزاء إذن التي بها خطّ ألف طاء مائة وعشرون جزءًا فيكون بها أمّا خطّ طاء ميم فأربعة أجزاء وأربع وأربعون دقيقةً وأمّا زاوية طاء ألف ميم وهي زاوية التباعد في العرض فتكون أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فأربعة أجزاء واثنتان وثلاثون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزأين وستّ عشرة دقيقةً فنثبت ذلك أيضًا في الصفّ الثالث من جدول كوكب عطارد في ذلك السطر بعينه الذي فيه عدد المائة والخمسة
يحصل لنا في الطول بهذه الأجزاء ثلاثةً وأربعين جزءًا واثنتين وخمسين دقيقةً فالأجزاء إذن التي بها خطّ ألف طاء مائة وعشرون جزءًا فيكون بها أمّا خطّ طاء ميم فأربعة أجزاء وأربع وأربعون دقيقةً وأمّا زاوية طاء ألف ميم وهي زاوية التباعد في العرض فتكون أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فأربعة أجزاء واثنتان وثلاثون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزأين وستّ عشرة دقيقةً فنثبت ذلك أيضًا في الصفّ الثالث من جدول كوكب عطارد في ذلك السطر بعينه الذي فيه عدد المائة والخمسة  والثلاثين الجزء ه: ولنرسم أيضًا سبب اعتبار عدد الزيادة أو النقصان في تلك الصورة التي ليس فيها الميل فلأنّه قد تبيّن أنّ الأجزاء التي بها خطّ ألف باء ستّة وخمسون جزءًا وأربعون دقيقةً فإنّ كلّ واحد من خطّي طاء كاف كاف باء بها خمسة عشر جزءًا وخمس وخمسون دقيقةً ومن البيّن أنّ خطّ ألف كاف يبقى بهذه الأجزاء أربعين جزءًا وخمسًا وأربعين دقيقةً والمربّع الذي من خطّ ألف كاف مع المربّع الذي من خطّ كاف طاء يكون منه الذي من خطّ ألف طاء فإنّ هذا الخطّ أيضًا يحصل لنا في الطول ثلاثةً وأربعين جزءًا وخمسًا وأربعين دقيقةً بالأجزاء التي بها خطّ طاء كاف خمسة عشر جزءًا وخمس وخمسون دقيقةً فالأجزاء إذن التي بها موتر ألف طاء مائة وعشرون جزءًا يكون بها أمّا خطّ طاء كاف فثلاثة وأربعون جزءًا وثلاثون دقيقةً وأمّا زاوية كاف ألف طاء وهي زاوية الزيادة أو النقصان في الطول فتكون أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فاثنان وأربعون جزءًا وأربعون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فأحد وعشرون جزءًا وعشرون دقيقةً وقد كان تبيّن في الميل أنّ مبلغها بهذه الأجزاء أحد وعشرون جزءًا وسبع عشرة دقيقةً فقد نقص إذن هاهنا أيضًا عدد الزيادة أو النقصان في الطول من قبل ميل فلك التدوير ثلاث دقائق وهذه هي الأشياء التي كنّا قصدنا لوجودها⊙ أمّا مسيرات هذين الكوكبين في العرض في الميول العظمى فبهذا الوجه الذي وصفناه عملنا ما عملناه فيها من قبل أنّ هذه المسيرات تكون والفلك الخارج المركز في سطح فلك البروج نفسه فأمّا مسيرات الكواكب الثلاثة الباقية فإنّا عملنا ما عملناه فيها بمعنى صورته غير هذه الصورة من قبل أنّ الميول العظمى لأفلاكها الخارجة المراكز تتّفق معها الميول العظمى لأفلاك تدويرها فيلزم من ذلك أن تكون مسيراتها في العرض التي تجتمع من الميلين جميعًا محسوبة معًا⊙ و: فليكن أيضًا في السطح الذي على زوايا قائمة على سطح فلك البروج أمّا الفصل المشترك بينه وبين سطح فلك البروج فخطّ ألف باء وأمّا الفصل المشترك بينه وبين فلك التدوير فخطّ دال جيم هاء ولننزل أنّ مركز فلك البروج نقطة ألف ومركز فلك التدوير نقطة جيم ولنرسم حول نقطة جيم فلك تدوير دال زاي هاء حاء على أن يكون قطر زاي جيم حاء من الخطوط التي تخرج على زوايا قائمة على خطّ دال هاء في سطح الفلك الخارج المركز وموازيًا لسطح فلك البروج فأمّا سائر تلك الخطوط فتكون موازيةً للسطحين اللذين ذكرناهما جميعًا ولنقرّر قوس هاء طاء على ذلك المثال على أنّها خمسة وأربعون جزءًا ولنخرج من نقطة طاء وهو موضع الكوكب عمود طاء كاف على خطّ هاء جيم ومن نقطتي طاء لام أيضًا على سطح فلك البروج عمود ألف كاف باء طاء لام ولنوصل خطوط باء لام ألف لام ألف طاء وليكن قصدنا أن نجد عدد الزيادة أو النقصان في الطول وهو الذي تشتمل عليه زاوية باء ألف كاف والمسير في العرض وهو الذي تشتمل عليه زاوية لام ألف طاء فلنخرج على خطّ ألف جيم أيضًا من نقطة لام عمود كاف ميم ولنوصل خطّا جيم طاء ألف لام وليوضع من أجل ما تقدّم بيانه كلّ واحد من خطّي جيم كاف كاف طاء أربعةً وثمانين جزءًا واثنتين وخمسين دقيقةً بالأجزاء التي بها موتر جيم طاء مائة وعشرون جزءًا فلأنّه قد تبيّن في كوكب زحل أوّلًا أنّ الخطّ الذي من مركز فلك تدويره ستّة أجزاء وثلاثون دقيقةً بالأجزاء التي بها البعد الوسط ستّون جزءًا يكون أيضًا كلّ واحد من خطّي جيم كاف كاف طاء أربعة أجزاء وستًّا وثلاثين دقيقةً بالأجزاء التي بها موتر جيم طاء ستّة أجزاء وثلاثون دقيقةً ولأنّ زاوية ألف جيم دال وهي زاوية ميل فلك التدوير وضعت أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فأربعة أجزاء وثلاثون دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فتسعة أجزاء تكون أيضًا أمّا القوس التي تكون على خطّ كاف ميم فتسعة أجزاء بالأجزاء التي بها الدائرة التي ترسم حول مثلّث جيم كاف ميم القائم الزاوية ثلاث مائة وستّون جزءًا وأمّا القوس التي على خطّ جيم ميم فالأجزاء الباقية لتمام نصف دائرة وهي مائة وأحد وسبعون جزءًا فخطّ كاف ميم إذن من الخطّين اللذين يوترانهما يكون تسعة أجزاء وخمسًا وعشرين دقيقةً فالأجزاء التي بها موتر جيم كاف مائة وعشرون جزءًا وخطّ جيم ميم منهما يكون بهذه الأجزاء مائة وتسعة عشر جزءًا وثمانيًا وثلاثين دقيقةً فالأجزاء التي بها خطّ جيم كاف أربعة أجزاء وستّ وثلاثون دقيقةً يكون بها أمّا خطّ كاف ميم فاثنتان وعشرون دقيقةً وأمّا خطّ جيم ميم فعلى هذا المثال أربعة أجزاء وخمسًا وثلاثين دقيقةً لكنّ خطّ ألف جيم في الميل الأعظم في نصف الدائرة الأبعد وهو خطّ البعد في مبادئ الميزان يجتمع من قبل المعاني التي تقدّمنا فبيّنّاها في الاختلافات بهذه الأجزاء اثنين وستّين جزءًا وعشر دقائق فيبقى خطّ ألف ميم الباقي منه سبعةً وخمسين جزءًا وخمسًا وثلاثين دقيقةً بالأجزاء التي بها خطّ ميم كاف اثنان وعشرون دقيقةً ومن أجل ذلك يكون موتر ألف لام بهذه الأجزاء سبعةً وخمسين جزءًا وخمسًا وثلاثين دقيقةً فالأجزاء إذن التي بها موتر ألف لام مائة وعشرون جزءًا يكون بها أمّا خطّ كاف ميم فستًّا وأربعين دقيقةً وأمّا زاوية كاف ألف ميم فأربعًا وأربعين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وقد وضعت زاوية باء ألف جيم وهي زاوية ميل الفلك الخارج المركز أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزأين وثلاثين دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فخمسة أجزاء فزاوية باء ألف كاف إذن بأسرها خمسة أجزاء وأربع وأربعون دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فتكون القوس أيضًا التي على خطّ زاي لام خمسة أجزاء وأربعًا وأربعين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء ألف لام القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ ألف باء الأجزاء الباقية لتمام نصف دائرة وهي مائة وأربعة وسبعون جزءًا وستّ عشرة دقيقةً فخطّ باء طاء إذن من الخطّين اللذين يوترانهما ستّة أجزاء بالأجزاء التي بها موتر ألف كاف مائة وعشرون جزءًا وخطّ ألف باء منهما بهذه الأجزاء مائة وتسعة عشر جزءًا وإحدى وخمسين دقيقةً فلذلك تكون الأجزاء التي بها خطّ ألف لام سبعة وخمسون جزءًا وخمس وثلاثون دقيقةً فإنّ خطّ باء كاف بها جزءان وثلاث وخمسون دقيقةً ه - صح: فلذلك تكون الأجزاء التي بها خطّ ألف لام سبعة وخمسون جزءًا وخمس وثلاثون دقيقةً فإنّ خطّ باء كاف بها جزءان وثلاث وخمسون دقيقةً وخطّ ألف باء على ذلك المثال سبعة وخمسون جزءًا وإحدى وثلاثون دقيقةً وبهذه الأجزاء يصير خطّ باء لام أيضًا إذ هو مساوٍ لخطّ كاف طاء أربعة أجزاء وستًّا وثلاثين دقيقةً ولأنّ المربّع الذي من خطّ ألف باء مع الذي من خطّ باء لام يكون منهما الذي من خطّ ألف لام يحصل لنا هذا الخطّ أيضًا في الطول بهذه الأجزاء سبعةً وخمسين جزءًا واثنتين وأربعين دقيقةً وعلى هذا المثال لأنّ خطّ لام طاء إذ كان مساويًا لخطّ باء كاف يصير بهذه الأجزاء جزأين وثلاثًا وخمسين دقيقةً والمربّع الذي من خطّ ألف لام مع الذي من خطّ لام طاء يكون منهما الذي من خطّ ألف طاء فإنّ هذا الخطّ أيضًا يحصل لنا في الطول بهذه الأجزاء سبعةً وخمسين جزءًا وستًّا وأربعين دقيقةً فلذلك تكون الأجزاء التي بها موتر ألف طاء مائة وعشرون جزءًا فإنّ خطّ طاء لام بها خمسة أجزاء وتسع وخمسون دقيقةً فزاوية طاء ألف لام وهي زاوية التباعد في العرض أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فخمسة أجزاء وأربع وأربعون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزءان واثنتان وخمسون دقيقةً فنثبت ذلك في الصفّ الثالث من جدول زحل في حيال عدد المائة والخمسة والثلاثين الجزء في سطره⊙ فأمّا في الميل الأعظم الذي يكون في نصف الدائرة الأقرب فلأنّ خطّ ألف جيم وهو خطّ البعد في مبادئ الحمل يجتمع سبعةً وخمسين جزءًا وأربعين دقيقةً بالأجزاء التي تبيّن أنّ خطّ كاف ميم بها ه: بها اثنتان وعشرون دقيقةً وأنّ خطّ جيم ميم على ذلك المثال أربعة أجزاء وخمس وثلاثون دقيقةً ومن أجل ذلك يصير خطّ ألف ميم الباقي ثلاثةً وخمسين جزءًا وخمس دقائق وبهذه الأجزاء يكون موتر ألف لام أيضًا إذ مبلغ ما يفوته أعظم من خطّ ألف ميم لا يعبأ به ثلاثة وخمسون جزءًا وخمس دقائق ه - صح: وبهذه الأجزاء يكون موتر ألف لام أيضًا إذ مبلغ ما يفوته أعظم من خطّ ألف ميم لا يعبأ به ثلاثة وخمسون جزءًا وخمس دقائق فالأجزاء إذن التي بها موتر ألف لام مائة وعشرون جزءًا يكون بها أمّا خطّ كاف ميم فخمسون دقيقة وأمّا زاوية كاف ألف ميم فثمان وأربعون دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وبهذه الأجزاء وضعت زاوية باء ألف جيم أيضًا خمسة أجزاء فزاوية باء ألف لام إذن بأسرها خمسة أجزاء وثمان وأربعون دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فتكون لذلك القوس التي تكون على خطّ باء كاف خمسة أجزاء وثمان وأربعون دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث ألف باء كاف القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ ألف باء الأجزاء الباقية إلى تمام نصف دائرة وهي مائة وأربعة وسبعون جزءًا واثنتا عشرة دقيقةً فخطّ باء كاف إذن من الخطّين اللذين يوترانهما يصير ستّة أجزاء وأربع دقائق بالأجزاء التي بها موتر ألف لام مائة وعشرون جزءًا وخطّ ألف باء منهما يكون بهذه الأجزاء مائة وتسعة عشر جزءًا وإحدى وخمسين دقيقةً فالأجزاء إذن التي بها خطّ ألف لام ثلاثة وخمسون جزءًا وخمس دقائق يكون بها أمّا خطّ باء كاف فجزأين وإحدى وأربعين دقيقةً وأمّا خطّ ألف باء فعلى هذا المثال ثلاثة وخمسون جزءًا ودقيقة واحدة
والثلاثين الجزء ه: ولنرسم أيضًا سبب اعتبار عدد الزيادة أو النقصان في تلك الصورة التي ليس فيها الميل فلأنّه قد تبيّن أنّ الأجزاء التي بها خطّ ألف باء ستّة وخمسون جزءًا وأربعون دقيقةً فإنّ كلّ واحد من خطّي طاء كاف كاف باء بها خمسة عشر جزءًا وخمس وخمسون دقيقةً ومن البيّن أنّ خطّ ألف كاف يبقى بهذه الأجزاء أربعين جزءًا وخمسًا وأربعين دقيقةً والمربّع الذي من خطّ ألف كاف مع المربّع الذي من خطّ كاف طاء يكون منه الذي من خطّ ألف طاء فإنّ هذا الخطّ أيضًا يحصل لنا في الطول ثلاثةً وأربعين جزءًا وخمسًا وأربعين دقيقةً بالأجزاء التي بها خطّ طاء كاف خمسة عشر جزءًا وخمس وخمسون دقيقةً فالأجزاء إذن التي بها موتر ألف طاء مائة وعشرون جزءًا يكون بها أمّا خطّ طاء كاف فثلاثة وأربعون جزءًا وثلاثون دقيقةً وأمّا زاوية كاف ألف طاء وهي زاوية الزيادة أو النقصان في الطول فتكون أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فاثنان وأربعون جزءًا وأربعون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فأحد وعشرون جزءًا وعشرون دقيقةً وقد كان تبيّن في الميل أنّ مبلغها بهذه الأجزاء أحد وعشرون جزءًا وسبع عشرة دقيقةً فقد نقص إذن هاهنا أيضًا عدد الزيادة أو النقصان في الطول من قبل ميل فلك التدوير ثلاث دقائق وهذه هي الأشياء التي كنّا قصدنا لوجودها⊙ أمّا مسيرات هذين الكوكبين في العرض في الميول العظمى فبهذا الوجه الذي وصفناه عملنا ما عملناه فيها من قبل أنّ هذه المسيرات تكون والفلك الخارج المركز في سطح فلك البروج نفسه فأمّا مسيرات الكواكب الثلاثة الباقية فإنّا عملنا ما عملناه فيها بمعنى صورته غير هذه الصورة من قبل أنّ الميول العظمى لأفلاكها الخارجة المراكز تتّفق معها الميول العظمى لأفلاك تدويرها فيلزم من ذلك أن تكون مسيراتها في العرض التي تجتمع من الميلين جميعًا محسوبة معًا⊙ و: فليكن أيضًا في السطح الذي على زوايا قائمة على سطح فلك البروج أمّا الفصل المشترك بينه وبين سطح فلك البروج فخطّ ألف باء وأمّا الفصل المشترك بينه وبين فلك التدوير فخطّ دال جيم هاء ولننزل أنّ مركز فلك البروج نقطة ألف ومركز فلك التدوير نقطة جيم ولنرسم حول نقطة جيم فلك تدوير دال زاي هاء حاء على أن يكون قطر زاي جيم حاء من الخطوط التي تخرج على زوايا قائمة على خطّ دال هاء في سطح الفلك الخارج المركز وموازيًا لسطح فلك البروج فأمّا سائر تلك الخطوط فتكون موازيةً للسطحين اللذين ذكرناهما جميعًا ولنقرّر قوس هاء طاء على ذلك المثال على أنّها خمسة وأربعون جزءًا ولنخرج من نقطة طاء وهو موضع الكوكب عمود طاء كاف على خطّ هاء جيم ومن نقطتي طاء لام أيضًا على سطح فلك البروج عمود ألف كاف باء طاء لام ولنوصل خطوط باء لام ألف لام ألف طاء وليكن قصدنا أن نجد عدد الزيادة أو النقصان في الطول وهو الذي تشتمل عليه زاوية باء ألف كاف والمسير في العرض وهو الذي تشتمل عليه زاوية لام ألف طاء فلنخرج على خطّ ألف جيم أيضًا من نقطة لام عمود كاف ميم ولنوصل خطّا جيم طاء ألف لام وليوضع من أجل ما تقدّم بيانه كلّ واحد من خطّي جيم كاف كاف طاء أربعةً وثمانين جزءًا واثنتين وخمسين دقيقةً بالأجزاء التي بها موتر جيم طاء مائة وعشرون جزءًا فلأنّه قد تبيّن في كوكب زحل أوّلًا أنّ الخطّ الذي من مركز فلك تدويره ستّة أجزاء وثلاثون دقيقةً بالأجزاء التي بها البعد الوسط ستّون جزءًا يكون أيضًا كلّ واحد من خطّي جيم كاف كاف طاء أربعة أجزاء وستًّا وثلاثين دقيقةً بالأجزاء التي بها موتر جيم طاء ستّة أجزاء وثلاثون دقيقةً ولأنّ زاوية ألف جيم دال وهي زاوية ميل فلك التدوير وضعت أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فأربعة أجزاء وثلاثون دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فتسعة أجزاء تكون أيضًا أمّا القوس التي تكون على خطّ كاف ميم فتسعة أجزاء بالأجزاء التي بها الدائرة التي ترسم حول مثلّث جيم كاف ميم القائم الزاوية ثلاث مائة وستّون جزءًا وأمّا القوس التي على خطّ جيم ميم فالأجزاء الباقية لتمام نصف دائرة وهي مائة وأحد وسبعون جزءًا فخطّ كاف ميم إذن من الخطّين اللذين يوترانهما يكون تسعة أجزاء وخمسًا وعشرين دقيقةً فالأجزاء التي بها موتر جيم كاف مائة وعشرون جزءًا وخطّ جيم ميم منهما يكون بهذه الأجزاء مائة وتسعة عشر جزءًا وثمانيًا وثلاثين دقيقةً فالأجزاء التي بها خطّ جيم كاف أربعة أجزاء وستّ وثلاثون دقيقةً يكون بها أمّا خطّ كاف ميم فاثنتان وعشرون دقيقةً وأمّا خطّ جيم ميم فعلى هذا المثال أربعة أجزاء وخمسًا وثلاثين دقيقةً لكنّ خطّ ألف جيم في الميل الأعظم في نصف الدائرة الأبعد وهو خطّ البعد في مبادئ الميزان يجتمع من قبل المعاني التي تقدّمنا فبيّنّاها في الاختلافات بهذه الأجزاء اثنين وستّين جزءًا وعشر دقائق فيبقى خطّ ألف ميم الباقي منه سبعةً وخمسين جزءًا وخمسًا وثلاثين دقيقةً بالأجزاء التي بها خطّ ميم كاف اثنان وعشرون دقيقةً ومن أجل ذلك يكون موتر ألف لام بهذه الأجزاء سبعةً وخمسين جزءًا وخمسًا وثلاثين دقيقةً فالأجزاء إذن التي بها موتر ألف لام مائة وعشرون جزءًا يكون بها أمّا خطّ كاف ميم فستًّا وأربعين دقيقةً وأمّا زاوية كاف ألف ميم فأربعًا وأربعين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وقد وضعت زاوية باء ألف جيم وهي زاوية ميل الفلك الخارج المركز أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزأين وثلاثين دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فخمسة أجزاء فزاوية باء ألف كاف إذن بأسرها خمسة أجزاء وأربع وأربعون دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فتكون القوس أيضًا التي على خطّ زاي لام خمسة أجزاء وأربعًا وأربعين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء ألف لام القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ ألف باء الأجزاء الباقية لتمام نصف دائرة وهي مائة وأربعة وسبعون جزءًا وستّ عشرة دقيقةً فخطّ باء طاء إذن من الخطّين اللذين يوترانهما ستّة أجزاء بالأجزاء التي بها موتر ألف كاف مائة وعشرون جزءًا وخطّ ألف باء منهما بهذه الأجزاء مائة وتسعة عشر جزءًا وإحدى وخمسين دقيقةً فلذلك تكون الأجزاء التي بها خطّ ألف لام سبعة وخمسون جزءًا وخمس وثلاثون دقيقةً فإنّ خطّ باء كاف بها جزءان وثلاث وخمسون دقيقةً ه - صح: فلذلك تكون الأجزاء التي بها خطّ ألف لام سبعة وخمسون جزءًا وخمس وثلاثون دقيقةً فإنّ خطّ باء كاف بها جزءان وثلاث وخمسون دقيقةً وخطّ ألف باء على ذلك المثال سبعة وخمسون جزءًا وإحدى وثلاثون دقيقةً وبهذه الأجزاء يصير خطّ باء لام أيضًا إذ هو مساوٍ لخطّ كاف طاء أربعة أجزاء وستًّا وثلاثين دقيقةً ولأنّ المربّع الذي من خطّ ألف باء مع الذي من خطّ باء لام يكون منهما الذي من خطّ ألف لام يحصل لنا هذا الخطّ أيضًا في الطول بهذه الأجزاء سبعةً وخمسين جزءًا واثنتين وأربعين دقيقةً وعلى هذا المثال لأنّ خطّ لام طاء إذ كان مساويًا لخطّ باء كاف يصير بهذه الأجزاء جزأين وثلاثًا وخمسين دقيقةً والمربّع الذي من خطّ ألف لام مع الذي من خطّ لام طاء يكون منهما الذي من خطّ ألف طاء فإنّ هذا الخطّ أيضًا يحصل لنا في الطول بهذه الأجزاء سبعةً وخمسين جزءًا وستًّا وأربعين دقيقةً فلذلك تكون الأجزاء التي بها موتر ألف طاء مائة وعشرون جزءًا فإنّ خطّ طاء لام بها خمسة أجزاء وتسع وخمسون دقيقةً فزاوية طاء ألف لام وهي زاوية التباعد في العرض أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فخمسة أجزاء وأربع وأربعون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزءان واثنتان وخمسون دقيقةً فنثبت ذلك في الصفّ الثالث من جدول زحل في حيال عدد المائة والخمسة والثلاثين الجزء في سطره⊙ فأمّا في الميل الأعظم الذي يكون في نصف الدائرة الأقرب فلأنّ خطّ ألف جيم وهو خطّ البعد في مبادئ الحمل يجتمع سبعةً وخمسين جزءًا وأربعين دقيقةً بالأجزاء التي تبيّن أنّ خطّ كاف ميم بها ه: بها اثنتان وعشرون دقيقةً وأنّ خطّ جيم ميم على ذلك المثال أربعة أجزاء وخمس وثلاثون دقيقةً ومن أجل ذلك يصير خطّ ألف ميم الباقي ثلاثةً وخمسين جزءًا وخمس دقائق وبهذه الأجزاء يكون موتر ألف لام أيضًا إذ مبلغ ما يفوته أعظم من خطّ ألف ميم لا يعبأ به ثلاثة وخمسون جزءًا وخمس دقائق ه - صح: وبهذه الأجزاء يكون موتر ألف لام أيضًا إذ مبلغ ما يفوته أعظم من خطّ ألف ميم لا يعبأ به ثلاثة وخمسون جزءًا وخمس دقائق فالأجزاء إذن التي بها موتر ألف لام مائة وعشرون جزءًا يكون بها أمّا خطّ كاف ميم فخمسون دقيقة وأمّا زاوية كاف ألف ميم فثمان وأربعون دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وبهذه الأجزاء وضعت زاوية باء ألف جيم أيضًا خمسة أجزاء فزاوية باء ألف لام إذن بأسرها خمسة أجزاء وثمان وأربعون دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فتكون لذلك القوس التي تكون على خطّ باء كاف خمسة أجزاء وثمان وأربعون دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث ألف باء كاف القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ ألف باء الأجزاء الباقية إلى تمام نصف دائرة وهي مائة وأربعة وسبعون جزءًا واثنتا عشرة دقيقةً فخطّ باء كاف إذن من الخطّين اللذين يوترانهما يصير ستّة أجزاء وأربع دقائق بالأجزاء التي بها موتر ألف لام مائة وعشرون جزءًا وخطّ ألف باء منهما يكون بهذه الأجزاء مائة وتسعة عشر جزءًا وإحدى وخمسين دقيقةً فالأجزاء إذن التي بها خطّ ألف لام ثلاثة وخمسون جزءًا وخمس دقائق يكون بها أمّا خطّ باء كاف فجزأين وإحدى وأربعين دقيقةً وأمّا خطّ ألف باء فعلى هذا المثال ثلاثة وخمسون جزءًا ودقيقة واحدة
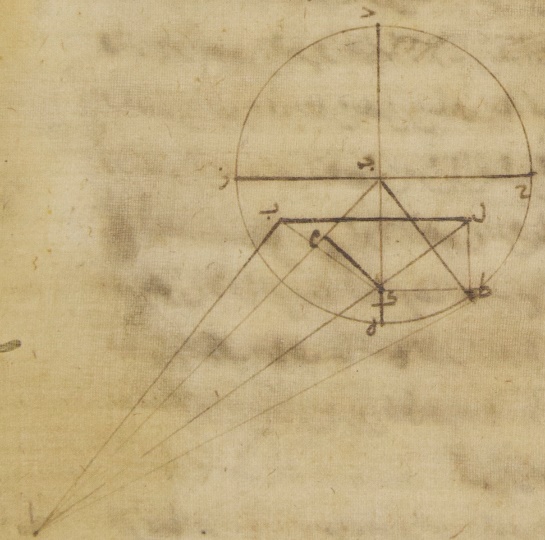 ولأنّ المربّع الذي من خطّ ألف باء مع الذي من خطّ باء لام يكون منهما الذي من خطّ ألف لام وبهذه الأجزاء يتبيّن أنّ خطّ باء لام أربعة أجزاء وستّ وثلاثون دقيقةً يحصل لنا خطّ ألف لام أيضًا في الطول بهذه الأجزاء ثلاثة وخمسين جزءًا وثلاث عشرة دقيقةً فالأجزاء إذن التي بها موتر ألف لام مائة وعشرون جزءًا يكون بها أمّا خطّ باء لام فعشرة أجزاء وثلاث وعشرون دقيقةً وأمّا زاوية باء ألف لام وهي زاوية الزيادة أو النقصان في الطول أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فتسعة أجزاء وستّ وخمسون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فأربعة أجزاء وثمان وخمسون دقيقةً وأيضًا لأنّ الأجزاء التي بها خطّ ألف لام ثلاثة وخمسون جزءًا وثلاث عشرة دقيقةً يصير بها خطّ طاء لام أيضًا إذ كان مساويًا لخطّ كاف باء جزأين وإحدى وأربعين دقيقةً والمربّعان اللذان منهما إذا جمعا كان منهما المربّع الذي من خطّ ألف طاء فإنّ هذا الخطّ أيضًا يحصل لنا في الطول بهذه الأجزاء ثلاثة وخمسين جزءًا وسبع عشرة دقيقةً فالأجزاء إذن التي بها موتر ألف طاء مائة وعشرون جزءًا يكون بها أمّا خطّ طاء لام فستّة أجزاء وثلاث دقائق وأمّا زاوية طاء ألف لام وهي زاوية التباعد في العرض أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فخمسة أجزاء وستّ وأربعون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزأين وثلاثًا وخمسين دقيقةً فنثبت ذلك أيضًا في الصفّ الرابع من جدول زحل بإزاء عدد المائة والخمسة والثلاثين الجزء⊙ ز: وكيما نستعمل الاعتبار أيضًا لأعداد الزيادة أو النقصان في الطول في الميل الأقرب فلنرسم أيضًا الشكل الذي ليس فيه شيء من الميل فلأنّ الأجزاء التي بها خطّ ألف دال وهو خطّ البعد حينئذ سبعة وخمسون جزءًا وأربعون دقيقةً قد وضع بها خطّ كاف لام كلّ واحد من خطّي جيم كاف كاف طاء أربعة أجزاء وستًّا وثلاثين دقيقةً ويكون خطّ ألف كاف الباقي بهذه الأجزاء ثلاثةً وخمسين جزءًا وأربع دقائق والمربّع الذي منه مع المربّع الذي من خطّ كاف طاء يكون منهما الذي من خطّ ألف طاء يحصل لنا خطّ ألف طاء
ولأنّ المربّع الذي من خطّ ألف باء مع الذي من خطّ باء لام يكون منهما الذي من خطّ ألف لام وبهذه الأجزاء يتبيّن أنّ خطّ باء لام أربعة أجزاء وستّ وثلاثون دقيقةً يحصل لنا خطّ ألف لام أيضًا في الطول بهذه الأجزاء ثلاثة وخمسين جزءًا وثلاث عشرة دقيقةً فالأجزاء إذن التي بها موتر ألف لام مائة وعشرون جزءًا يكون بها أمّا خطّ باء لام فعشرة أجزاء وثلاث وعشرون دقيقةً وأمّا زاوية باء ألف لام وهي زاوية الزيادة أو النقصان في الطول أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فتسعة أجزاء وستّ وخمسون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فأربعة أجزاء وثمان وخمسون دقيقةً وأيضًا لأنّ الأجزاء التي بها خطّ ألف لام ثلاثة وخمسون جزءًا وثلاث عشرة دقيقةً يصير بها خطّ طاء لام أيضًا إذ كان مساويًا لخطّ كاف باء جزأين وإحدى وأربعين دقيقةً والمربّعان اللذان منهما إذا جمعا كان منهما المربّع الذي من خطّ ألف طاء فإنّ هذا الخطّ أيضًا يحصل لنا في الطول بهذه الأجزاء ثلاثة وخمسين جزءًا وسبع عشرة دقيقةً فالأجزاء إذن التي بها موتر ألف طاء مائة وعشرون جزءًا يكون بها أمّا خطّ طاء لام فستّة أجزاء وثلاث دقائق وأمّا زاوية طاء ألف لام وهي زاوية التباعد في العرض أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فخمسة أجزاء وستّ وأربعون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزأين وثلاثًا وخمسين دقيقةً فنثبت ذلك أيضًا في الصفّ الرابع من جدول زحل بإزاء عدد المائة والخمسة والثلاثين الجزء⊙ ز: وكيما نستعمل الاعتبار أيضًا لأعداد الزيادة أو النقصان في الطول في الميل الأقرب فلنرسم أيضًا الشكل الذي ليس فيه شيء من الميل فلأنّ الأجزاء التي بها خطّ ألف دال وهو خطّ البعد حينئذ سبعة وخمسون جزءًا وأربعون دقيقةً قد وضع بها خطّ كاف لام كلّ واحد من خطّي جيم كاف كاف طاء أربعة أجزاء وستًّا وثلاثين دقيقةً ويكون خطّ ألف كاف الباقي بهذه الأجزاء ثلاثةً وخمسين جزءًا وأربع دقائق والمربّع الذي منه مع المربّع الذي من خطّ كاف طاء يكون منهما الذي من خطّ ألف طاء يحصل لنا خطّ ألف طاء  أيضًا في الطول ثلاثةً وخمسين جزءًا وستّ عشرة دقيقةً فتكون لذلك الأجزاء أيضًا التي بها موتر ألف طاء مائة وعشرون جزءًا فإنّ خطّ كاف طاء بها عشرة أجزاء واثنتان وعشرون دقيقةً فزاوية طاء ألف كاف وهي زاوية الزيادة أو أو النقصان في الطول تكون أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فتسعة أجزاء وأربع وخمسون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فأربعة أجزاء وسبع وخمسون دقيقةً وقد كان تبيّن أنّ مبلغها في الميلين بهذه الأجزاء أربعة أجزاء وثمان وخمسون دقيقةً فقد زاد إذًا عند الزيادة أو النقصان من قبل الميلين جميعًا دقيقة واحدة وهذه هي الأشياء التي قصدنا لوجودها ح: ثمّ لنرسم أوّلًا الصورة التي فيها الميلان المشتملة على النسب التي بيّنت في المشتري حتّى تكون الأجزاء التي بها خطّ جيم طاء الذي من مركز فلك التدوير أحد عشر جزءًا وثلاثين دقيقةً فيها كلّ واحد من خطّي جيم كاف كاف طاء يجتمع ثمانية أجزاء وثمان دقائق فلأنّ زاوية ألف جيم هاء وهي زاوية ميل فلك التدوير أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فإنّها وضعت جزأين وثلاثين دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فخمسة أجزاء تكون أيضًا القوس التي تكون على خطّ كاف ميم خمسة أجزاء بالأجزاء التي بها الدائرة التي ترسم حول مثلّث جيم كاف ميم القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ جيم ميم الأجزاء الباقية إلى تمام نصف دائرة وهي مائة وخمسة وسبعون جزءًا فخطّ كاف ميم إذن من الخطّين اللذين يوترانهما خمسة أجزاء وأربع عشرة دقيقةً بالأجزاء التي بها موتر جيم كاف مائة وعشرون جزءًا وخطّ جيم ميم بهذه الأجزاء مائة وتسعة عشر جزءًا وثلاث وخمسون دقيقةً فتكون لذلك الأجزاء التي بها أمّا خطّ جيم كاف فثمانية أجزاء وثمان دقائق وأمّا خطّ ألف جيم وهو خطّ ألف جيم وهو خطّ {...} في مبادئ الميزان اثنان وستّون جزءًا وثلاثون دقيقةً فإنّ خطّ كاف ميم بها إحدى وعشرون دقيقةً وخطّ جيم ميم على هذا المثال ثمانية أجزاء وثمان دقائق وخطّ ميم ألف الباقي أربعة وخمسون جزءًا واثنتان وعشرون دقيقةً فموتر ألف لام إذن إذ كان إنّما هو أعظم من خطّ ميم ألف بما لا يُعبأُ به فهو أيضًا بهذه الأجزاء أربعة وخمسون جزءًا واثنتان وعشرون دقيقةً فالأجزاء إذن التي بها خطّ لام كاف مائة وعشرون جزءًا يكون بها أمّا خطّ كاف ميم فستًّا وأربعين دقيقةً وأمّا زاوية كاف ألف ميم فأربعًا وأربعين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وقد كانت لنا زاوية باء ألف جيم وهي زاوية ميل الفلك الخارج المركز أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزءًا واحدًا وثلاثين دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فثلاثة أجزاء فزاوية باء ألف لام إذن بأسرها ثلاثة أجزاء وأربع وأربعون دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فتكون لذلك القوس التي تكون على خطّ كاف باء ثلاثة أجزاء وأربعًا وأربعين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء ألف لام القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ ألف باء الأجزاء الباقية لتمام نصف دائرة وهي مائة وستّة وسبعون جزءًا وستّ عشرة دقيقةً فخطّ كاف باء إذن من الخطّين اللذين يوترانهما ثلاثة أجزاء وأربع وأربعون دقيقةً بالأجزاء التي بها موتر ألف لام مائة وعشرون جزءًا وخطّ ألف باء منهما بهذه الأجزاء مائة وتسعة عشر جزءًا وستّ وخمسون دقيقةً فتكون لذلك الأجزاء التي بها خطّ ألف لام أربعة وخمسون جزءًا واثنتان وعشرون دقيقةً فإنّ خطّ كاف باء بها جزء واحد وستّ وأربعون دقيقةً وخطّ ألف باء على هذا المثال أربعة وخمسون جزءًا وعشرون دقيقةً وبهذه الأجزاء من أجل ما تقدّم بيانه خطّ باء لام ثمانية أجزاء وثمان دقائق ولأنّ المربّعين اللذين من هذين الخطّين إذا جمعا كان منهما المربّع الذي من خطّ ألف لام فإنّ هذا الخطّ أيضًا يحصل لنا في الطول بهذه الأجزاء أربعة وخمسين جزءًا وستًّا وخمسين دقيقةً وعلى هذا المثال لأنّ خطّ لام طاء بهذه الأجزاء جزء واحد وستّ وأربعون دقيقةً والمربّعين اللذين من هذين الخطّين إذا جمعا كان منهما الذي من خطّ ألف طاء فإنّ خطّ ألف طاء أيضًا يحصل لنا في الطول بهذه الأجزاء أربعةً وخمسين جزءًا وثمانيًا وخمسين دقيقةً فتكون لذلك الأجزاء التي بها موتر ألف طاء مائة وعشرون جزءًا فإنّ خطّ لام طاء بها ثلاثة أجزاء واثنتان وخمسون دقيقةً وزاوية طاء ألف لام وهي زاوية التباعد في العرض أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فثلاثة أجزاء واثنتان وأربعون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزء واحد وإحدى وخمسون دقيقةً فنثبت ذلك أيضًا في الصفّ الثالث من جدول كوكب المشتري بإزاء عدد المائة والخمسة والثلاثين الجزء وكذلك أيضًا من قبل أنّ خطّ ألف جيم وهو خطّ البعد في مبادئ الحمل يجتمع سبعةً وخمسين جزءًا وثلاثين دقيقةً بالأجزاء التي بيّنّا أنّ خطّ كاف ميم بها إحدى وعشرون دقيقةً وأنّ خطّ جيم ميم على هذا المثال ثمانية أجزاء وثمان دقائق حتّى يكون خطّ ألف ميم الباقي أعني خطّ ألف لام إذ لا يعتدّ بزيادته عليه بهذه الأجزاء يبقى تسعةً وأربعين جزءًا واثنتين وعشرين دقيقةً ومن أجل ذلك تكون الأجزاء التي بها موتر ألف لام مائة وعشرون جزءًا فإنّ خطّ كاف ميم يصير بها إحدى وخمسين دقيقةً وتصير زاوية كاف ألف ميم تسعًا وأربعين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فإنّ زاوية باء ألف لام بأسرها تجتمع بهذه الأجزاء ثلاثة أجزاء وتسعًا وأربعين دقيقةً فلذلك تكون القوس أيضًا التي تكون على خطّ كاف باء ثلاثة أجزاء وتسعًا وأربعين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث كاف ألف باء القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ ألف باء الأجزاء الباقية إلى تمام نصف دائرة وهي مائة وستّة وسبعون جزءًا وإحدى عشرة دقيقةً فخطّ باء كاف إذن من الخطّين اللذين يوترانهما ثلاثة أجزاء وتسع وخمسون دقيقةً بالأجزاء التي بها موتر ألف لام مائة وعشرون جزءًا وخطّ ألف باء منهما بهذه الأجزاء مائة وتسعة عشر جزءًا وستّ وخمسون دقيقةً فلذلك تكون الأجزاء أيضًا التي بها خطّ ألف لام تسعة وأربعون جزءًا واثنتان وعشرون دقيقةً فإنّ خطّ كاف باء يكون بها جزءًا واحدًا وتسعًا وثلاثين دقيقةً ويكون خطّ ألف باء على ذلك المثال تسعةً وأربعين جزءًا وعشرين دقيقةً ومن أجل ذلك من قبل أنّ خطّ باء لام بهذه الأجزاء ثمانية أجزاء وثمان دقائق فإنّ المربّعين اللذين يكونان منهما إذا جمعا كان منهما الذي يكون من خطّ ألف لام فإنّ هذا الخطّ أيضًا يحصل لنا في الطول خمسون جزءًا فلذلك تكون الأجزاء التي بها أيضًا موتر ألف كاف مائة وعشرون جزءًا فإنّ خطّ
أيضًا في الطول ثلاثةً وخمسين جزءًا وستّ عشرة دقيقةً فتكون لذلك الأجزاء أيضًا التي بها موتر ألف طاء مائة وعشرون جزءًا فإنّ خطّ كاف طاء بها عشرة أجزاء واثنتان وعشرون دقيقةً فزاوية طاء ألف كاف وهي زاوية الزيادة أو أو النقصان في الطول تكون أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فتسعة أجزاء وأربع وخمسون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فأربعة أجزاء وسبع وخمسون دقيقةً وقد كان تبيّن أنّ مبلغها في الميلين بهذه الأجزاء أربعة أجزاء وثمان وخمسون دقيقةً فقد زاد إذًا عند الزيادة أو النقصان من قبل الميلين جميعًا دقيقة واحدة وهذه هي الأشياء التي قصدنا لوجودها ح: ثمّ لنرسم أوّلًا الصورة التي فيها الميلان المشتملة على النسب التي بيّنت في المشتري حتّى تكون الأجزاء التي بها خطّ جيم طاء الذي من مركز فلك التدوير أحد عشر جزءًا وثلاثين دقيقةً فيها كلّ واحد من خطّي جيم كاف كاف طاء يجتمع ثمانية أجزاء وثمان دقائق فلأنّ زاوية ألف جيم هاء وهي زاوية ميل فلك التدوير أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فإنّها وضعت جزأين وثلاثين دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فخمسة أجزاء تكون أيضًا القوس التي تكون على خطّ كاف ميم خمسة أجزاء بالأجزاء التي بها الدائرة التي ترسم حول مثلّث جيم كاف ميم القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ جيم ميم الأجزاء الباقية إلى تمام نصف دائرة وهي مائة وخمسة وسبعون جزءًا فخطّ كاف ميم إذن من الخطّين اللذين يوترانهما خمسة أجزاء وأربع عشرة دقيقةً بالأجزاء التي بها موتر جيم كاف مائة وعشرون جزءًا وخطّ جيم ميم بهذه الأجزاء مائة وتسعة عشر جزءًا وثلاث وخمسون دقيقةً فتكون لذلك الأجزاء التي بها أمّا خطّ جيم كاف فثمانية أجزاء وثمان دقائق وأمّا خطّ ألف جيم وهو خطّ ألف جيم وهو خطّ {...} في مبادئ الميزان اثنان وستّون جزءًا وثلاثون دقيقةً فإنّ خطّ كاف ميم بها إحدى وعشرون دقيقةً وخطّ جيم ميم على هذا المثال ثمانية أجزاء وثمان دقائق وخطّ ميم ألف الباقي أربعة وخمسون جزءًا واثنتان وعشرون دقيقةً فموتر ألف لام إذن إذ كان إنّما هو أعظم من خطّ ميم ألف بما لا يُعبأُ به فهو أيضًا بهذه الأجزاء أربعة وخمسون جزءًا واثنتان وعشرون دقيقةً فالأجزاء إذن التي بها خطّ لام كاف مائة وعشرون جزءًا يكون بها أمّا خطّ كاف ميم فستًّا وأربعين دقيقةً وأمّا زاوية كاف ألف ميم فأربعًا وأربعين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وقد كانت لنا زاوية باء ألف جيم وهي زاوية ميل الفلك الخارج المركز أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزءًا واحدًا وثلاثين دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فثلاثة أجزاء فزاوية باء ألف لام إذن بأسرها ثلاثة أجزاء وأربع وأربعون دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فتكون لذلك القوس التي تكون على خطّ كاف باء ثلاثة أجزاء وأربعًا وأربعين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء ألف لام القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ ألف باء الأجزاء الباقية لتمام نصف دائرة وهي مائة وستّة وسبعون جزءًا وستّ عشرة دقيقةً فخطّ كاف باء إذن من الخطّين اللذين يوترانهما ثلاثة أجزاء وأربع وأربعون دقيقةً بالأجزاء التي بها موتر ألف لام مائة وعشرون جزءًا وخطّ ألف باء منهما بهذه الأجزاء مائة وتسعة عشر جزءًا وستّ وخمسون دقيقةً فتكون لذلك الأجزاء التي بها خطّ ألف لام أربعة وخمسون جزءًا واثنتان وعشرون دقيقةً فإنّ خطّ كاف باء بها جزء واحد وستّ وأربعون دقيقةً وخطّ ألف باء على هذا المثال أربعة وخمسون جزءًا وعشرون دقيقةً وبهذه الأجزاء من أجل ما تقدّم بيانه خطّ باء لام ثمانية أجزاء وثمان دقائق ولأنّ المربّعين اللذين من هذين الخطّين إذا جمعا كان منهما المربّع الذي من خطّ ألف لام فإنّ هذا الخطّ أيضًا يحصل لنا في الطول بهذه الأجزاء أربعة وخمسين جزءًا وستًّا وخمسين دقيقةً وعلى هذا المثال لأنّ خطّ لام طاء بهذه الأجزاء جزء واحد وستّ وأربعون دقيقةً والمربّعين اللذين من هذين الخطّين إذا جمعا كان منهما الذي من خطّ ألف طاء فإنّ خطّ ألف طاء أيضًا يحصل لنا في الطول بهذه الأجزاء أربعةً وخمسين جزءًا وثمانيًا وخمسين دقيقةً فتكون لذلك الأجزاء التي بها موتر ألف طاء مائة وعشرون جزءًا فإنّ خطّ لام طاء بها ثلاثة أجزاء واثنتان وخمسون دقيقةً وزاوية طاء ألف لام وهي زاوية التباعد في العرض أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فثلاثة أجزاء واثنتان وأربعون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزء واحد وإحدى وخمسون دقيقةً فنثبت ذلك أيضًا في الصفّ الثالث من جدول كوكب المشتري بإزاء عدد المائة والخمسة والثلاثين الجزء وكذلك أيضًا من قبل أنّ خطّ ألف جيم وهو خطّ البعد في مبادئ الحمل يجتمع سبعةً وخمسين جزءًا وثلاثين دقيقةً بالأجزاء التي بيّنّا أنّ خطّ كاف ميم بها إحدى وعشرون دقيقةً وأنّ خطّ جيم ميم على هذا المثال ثمانية أجزاء وثمان دقائق حتّى يكون خطّ ألف ميم الباقي أعني خطّ ألف لام إذ لا يعتدّ بزيادته عليه بهذه الأجزاء يبقى تسعةً وأربعين جزءًا واثنتين وعشرين دقيقةً ومن أجل ذلك تكون الأجزاء التي بها موتر ألف لام مائة وعشرون جزءًا فإنّ خطّ كاف ميم يصير بها إحدى وخمسين دقيقةً وتصير زاوية كاف ألف ميم تسعًا وأربعين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فإنّ زاوية باء ألف لام بأسرها تجتمع بهذه الأجزاء ثلاثة أجزاء وتسعًا وأربعين دقيقةً فلذلك تكون القوس أيضًا التي تكون على خطّ كاف باء ثلاثة أجزاء وتسعًا وأربعين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث كاف ألف باء القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ ألف باء الأجزاء الباقية إلى تمام نصف دائرة وهي مائة وستّة وسبعون جزءًا وإحدى عشرة دقيقةً فخطّ باء كاف إذن من الخطّين اللذين يوترانهما ثلاثة أجزاء وتسع وخمسون دقيقةً بالأجزاء التي بها موتر ألف لام مائة وعشرون جزءًا وخطّ ألف باء منهما بهذه الأجزاء مائة وتسعة عشر جزءًا وستّ وخمسون دقيقةً فلذلك تكون الأجزاء أيضًا التي بها خطّ ألف لام تسعة وأربعون جزءًا واثنتان وعشرون دقيقةً فإنّ خطّ كاف باء يكون بها جزءًا واحدًا وتسعًا وثلاثين دقيقةً ويكون خطّ ألف باء على ذلك المثال تسعةً وأربعين جزءًا وعشرين دقيقةً ومن أجل ذلك من قبل أنّ خطّ باء لام بهذه الأجزاء ثمانية أجزاء وثمان دقائق فإنّ المربّعين اللذين يكونان منهما إذا جمعا كان منهما الذي يكون من خطّ ألف لام فإنّ هذا الخطّ أيضًا يحصل لنا في الطول خمسون جزءًا فلذلك تكون الأجزاء التي بها أيضًا موتر ألف كاف مائة وعشرون جزءًا فإنّ خطّ 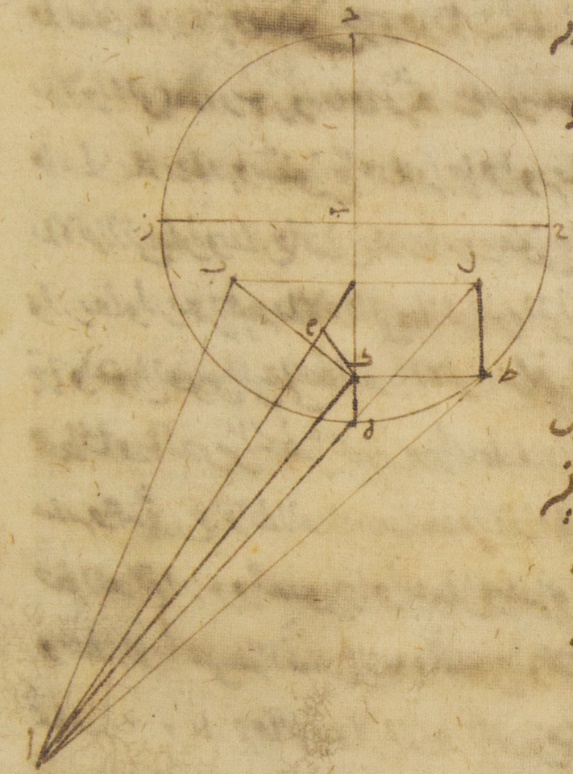 باء لام بها تسعة عشر جزءًا وإحدى وثلاثون دقيقةً وزاوية باء ألف لام وهي زاوية الزيادة أو النقصان في الطول أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فثمانية عشر جزءًا وأربع وأربعون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فتسعة أجزاء واثنتان وعشرون دقيقةً ؞ وأيضًا لأنّ الأجزاء التي بها خطّ ألف لام خمسون جزءًا فإنّ خطّ طاء لام يصير بها جزءًا واحدًا وتسعًا وثلاثين دقيقةً وإذا جمع المربّعان اللذان يكونان منهما كان منهما المربّع الذي يكون من خطّ ألف طاء فإنّ خطّ ألف طاء أيضًا يحصل لنا في الطول بهذه الأجزاء خمسين جزءًا ودقيقتين فالأجزاء إذن التي بها موتر ألف طاء مائة وعشرون جزءًا يكون بها أمّا خطّ لام طاء فثلاثة أجزاء وسبع وخمسون دقيقةً وأمّا زاوية طاء ألف لام وهي زاوية التباعد في العرض أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فثلاثة أجزاء وستّ وأربعون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزءًا واحدًا وثلاثًا وخمسين دقيقةً فنثبت ذلك أيضًا في الصفّ الرابع من جدوله بإزاء عدد المائة والخمسة والثلاثين الجزء⊙
باء لام بها تسعة عشر جزءًا وإحدى وثلاثون دقيقةً وزاوية باء ألف لام وهي زاوية الزيادة أو النقصان في الطول أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فثمانية عشر جزءًا وأربع وأربعون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فتسعة أجزاء واثنتان وعشرون دقيقةً ؞ وأيضًا لأنّ الأجزاء التي بها خطّ ألف لام خمسون جزءًا فإنّ خطّ طاء لام يصير بها جزءًا واحدًا وتسعًا وثلاثين دقيقةً وإذا جمع المربّعان اللذان يكونان منهما كان منهما المربّع الذي يكون من خطّ ألف طاء فإنّ خطّ ألف طاء أيضًا يحصل لنا في الطول بهذه الأجزاء خمسين جزءًا ودقيقتين فالأجزاء إذن التي بها موتر ألف طاء مائة وعشرون جزءًا يكون بها أمّا خطّ لام طاء فثلاثة أجزاء وسبع وخمسون دقيقةً وأمّا زاوية طاء ألف لام وهي زاوية التباعد في العرض أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فثلاثة أجزاء وستّ وأربعون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزءًا واحدًا وثلاثًا وخمسين دقيقةً فنثبت ذلك أيضًا في الصفّ الرابع من جدوله بإزاء عدد المائة والخمسة والثلاثين الجزء⊙ 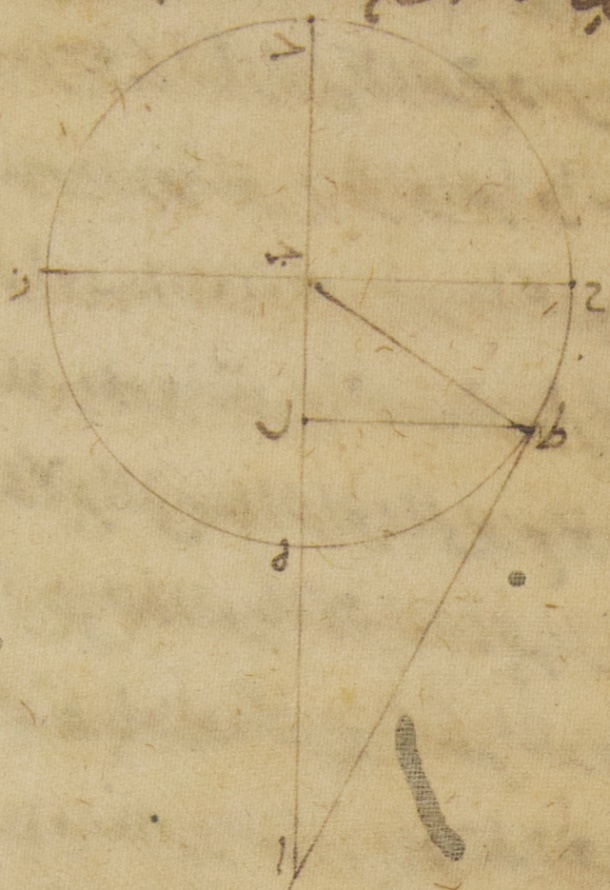 ط: ولنرسم بسبب اعتبار عدد الزيادات أو النقصانات في الطول الصورة المعرّاة من الميل فلأنّ في هذا البعد المفروض الأجزاء التي بها كلّ واحد من خطّي طاء كاف جيم كاف ثمانية أجزاء وثمان دقائق فإنّ خطّ ألف جيم بأسره سبعة وخمسون جزءًا وثلاثون دقيقةً وخطّ ألف لام الباقي بهذه الأجزاء تسعة وأربعون جزءًا واثنتان وعشرون دقيقةً والمربّع الذي يكون من هذا الخطّ مع الذي يكون من خطّ كاف طاء يكون منهما الذي يكون من خطّ ألف طاء فإنّ هذا الخطّ أيضًا يحصل لنا في الطول بهذه الأجزاء خمسين جزءًا ودقيقتين فتكون لذلك الأجزاء أيضًا التي بها موتر ألف طاء مائة وعشرون جزءًا وثلاثون دقيقةً وزاوية طاء ألف كاف وهي زاوية الزيادة أو النقصان في الطول أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فستّة عشر جزءًا واثنتان وأربعون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فتسعة أجزاء وإحدى وعشرون دقيقةً وقد كان بيّن أنّ مبلغها في الميل بهذه الأجزاء تسعة أجزاء واثنتان وعشرون دقيقةً فقد زاد إذن عدد الزيادة أو النقصان في الطول من قبل الميلين مجموعين دقيقةً واحدةً فقط وهذه هي الأشياء التي كنّا قصدنا لوجودها يے: ثمّ من بعد ذلك لنرسم بسبب تبيين هذه المعاني في كوكب المرّيخ لصورة التي فيها الميلان ولتجتمع أيضًا كلّ واحد من خطّي جيم كاف كاف طاء سبعةً وعشرين جزءًا وستًّا وخمسين دقيقةً بالأجزاء التي بها خطّ جيم طاء وهو الذي من مركز فلك التدوير تسعة وثلاثون جزءًا وثلاثون دقيقةً فلأنّ زاوية ألف جيم هاء وهي زاوية ميل فلك التدوير قد كانت لنا أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزأين وخمس عشرة دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فأربعة أجزاء وثلاثون دقيقةً تكون أيضًا القوس التي على خطّ كاف ميم أربعة أجزاء وثلاثين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث جيم ميم كاف القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ جيم ميم الأجزاء الباقية إلى تمام نصف دائرة وهي مائة وخمسة وسبعون جزءًا وثلاثون دقيقةً فخطّ كاف ميم إذن من الخطّين اللذين يوترانهما أربعة أجزاء وثلاث وأربعون دقيقةً (وهي مائة وخمسة وسبعون جزءًا وثلاثون دقيقةً) بالأجزاء التي بها موتر جيم كاف مائة وعشرون جزءًا وخطّ جيم ميم منهما بهذه الأجزاء مائة وتسعة عشر جزءًا وأربع وخمسون دقيقةً فيجب لذلك أن تكون أيضًا الأجزاء التي بها أمّا خطّ جيم كاف فسبعة وعشرون جزءًا وستّ وخمسون دقيقةً وأمّا خطّ ألف جيم وهو خطّ أعظم البعد فستّة وثلاثون جزءًا فإنّ خطّ كاف ميم بها جزء واحد وستّ دقائق وخطّ جيم ميم على هذا المثال سبعة وعشرون جزءًا وأربع وخمسون دقيقةً وخطّ ألف ميم الأجزاء الباقية وهي ثمانية وثلاثون جزءًا وستّ دقائق فلذلك يكون موتر ألف لام أيضًا بهذه الأجزاء ثمانيةً وثلاثين جزءًا وسبع دقائق فالأجزاء إذن التي بها موتر ألف كاف مائة وعشرون جزءًا يكون بها خطّ كاف ميم ثلاثة أجزاء وثمانيًا وعشرين دقيقةً وتكون زاوية كاف ألف ميم ثلاثة أجزاء وتسع عشرة دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وقد كانت لنا زاوية باء ألف جيم وهي زاوية ميل الفلك الخارج المركز أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزءًا واحدًا وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فجزأين فزاوية باء ألف لام إذن بأسرها تجتمع بهذه الأجزاء خمسة أجزاء وتسع عشرة دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فيجب لذلك أن تكون أيضًا القوس التي تكون على خطّ كاف باء خمسة أجزاء وتسع عشرة دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث ألف باء كاف القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ ألف باء الأجزاء الباقية إلى تمام نصف دائرة وهي مائة وأربعة وسبعون جزءًا وإحدى وأربعون دقيقةً فخطّ باء كاف إذن من الخطّين اللذين يوترانهما خمسة أجزاء وأربع وثلاثون دقيقةً بالأجزاء التي بها موتر ألف كاف مائة وعشرون جزءًا وخطّ ألف باء منهما بهذه الأجزاء مائة وتسعة عشر جزءًا واثنتان وخمسون دقيقةً فيجب لذلك أن تكون الأجزاء أيضًا التي بها خطّ ألف لام ثمانية وثلاثون جزءًا وسبع دقائق فإنّ خطّ كاف باء بها جزء واحد وستّ وأربعون دقيقةً وخطّ ألف باء على هذا المثال ثمانية وثلاثون جزءًا وخمس دقائق وبهذه الأجزاء خطّ باء لام أيضًا سبعة وعشرون جزءًا وستّ وخمسون دقيقةً ولأنّ المربّع الذي يكون من خطّ ألف باء مع الذي يكون من خطّ باء لام يكون منهما الذي يكون من خطّ ألف لام فإنّ هذا الخطّ أيضًا يحصل لنا في الطول سبعةً وأربعين جزءًا وأربع عشرة دقيقةً وعلى هذا المثال لأنّ خطّ طاء لام بهذه الأجزاء جزء واحد وستّ وأربعون دقيقةً والمربّع الذي يكون من خطّ ألف لام مع الذي يكون من خطّ لام طاء يكون منهما الذي يكون من خطّ ألف طاء فإنّ هذا الخطّ أيضًا يحصل لنا في الطول بهذه الأجزاء سبعة وأربعون جزءًا وستّ عشرة دقيقةً فيجب لذلك أن تكون الأجزاء أيضًا التي بها موتر ألف طاء مائة وعشرون جزءًا فإنّ خطّ طاء لام بها أربعة أجزاء وتسع وعشرون دقيقةً وزاوية طاء ألف لام وهي زاوية التباعد في العرض أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فأربعة أجزاء وثمان عشرة دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزءان وتسع دقائق فنثبت ذلك أيضًا في السطر الثالث من جدول المرّيخ بإزاء عدد المائة والخمسة والثلاثين الجزء وكذلك أيضًا في الميلين اللذين يكونان في أقلّ البعد من قبل أنّ خطّ ألف جيم أربعة وخمسون جزءًا بالأجزاء التي بها تبيّن أنّ خطّ كاف ميم جزء واحد وستّ دقائق وأنّ خطّ جيم ميم على هذا المثال سبعة وعشرون جزءًا وأربع وخمسون دقيقةً حتّى إنّ خطّ ألف ميم يبقي الأجزاء الباقية وهي ستّة وعشرون جزءًا وستّ دقائق ويجتمع موتر ألف لام بهذه الأجزاء ستّةً وعشرين جزءًا وسبع دقائق فالأجزاء إذن التي بها موتر ألف لام مائة وعشرون جزءًا يكون بها أمّا خطّ كاف ميم فخمسة أجزاء وثلاث دقائق وأمّا زاوية كاف ألف ميم فأربعة أجزاء وتسع وأربعون دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا ومن أجل ذلك تكون أيضًا زاوية باء ألف لام بأسرها بهذه الأجزاء ستّة أجزاء وتسعًا وأربعين دقيقةً فيجب لذلك أن تكون القوس التي تكون على خطّ باء كاف ستّة أجزاء وتسعًا وأربعين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث ألف باء كاف القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ ألف باء الأجزاء الباقية لتمام نصف دائرة وهي مائة وثلاثة وسبعون جزءًا وإحدى عشرة دقيقةً فخطّ باء كاف من الخطّين اللذين يوترانهما يكون سبعة أجزاء وثمان دقائق بالأجزاء التي بها موتر ألف لام مائة وعشرون جزءًا وخطّ ألف باء منهما بهذه الأجزاء مائة وتسعة عشر جزءًا وسبعًا وأربعين دقيقةً فيجب لذلك أن تكون الأجزاء أيضًا التي بها خطّ ألف كاف ستّةً وعشرين جزءًا وسبع دقائق فإنّ خطّ كاف بها جزء واحد وثلاث وثلاثون دقيقةً وخطّ ألف باء على هذا المثال ستّة وعشرون جزءًا وأربع دقائق وبهذه الأجزاء أيضًا خطّ باء لام سبعة وخمسون جزءًا وستّ وخمسون دقيقةً
ط: ولنرسم بسبب اعتبار عدد الزيادات أو النقصانات في الطول الصورة المعرّاة من الميل فلأنّ في هذا البعد المفروض الأجزاء التي بها كلّ واحد من خطّي طاء كاف جيم كاف ثمانية أجزاء وثمان دقائق فإنّ خطّ ألف جيم بأسره سبعة وخمسون جزءًا وثلاثون دقيقةً وخطّ ألف لام الباقي بهذه الأجزاء تسعة وأربعون جزءًا واثنتان وعشرون دقيقةً والمربّع الذي يكون من هذا الخطّ مع الذي يكون من خطّ كاف طاء يكون منهما الذي يكون من خطّ ألف طاء فإنّ هذا الخطّ أيضًا يحصل لنا في الطول بهذه الأجزاء خمسين جزءًا ودقيقتين فتكون لذلك الأجزاء أيضًا التي بها موتر ألف طاء مائة وعشرون جزءًا وثلاثون دقيقةً وزاوية طاء ألف كاف وهي زاوية الزيادة أو النقصان في الطول أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فستّة عشر جزءًا واثنتان وأربعون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فتسعة أجزاء وإحدى وعشرون دقيقةً وقد كان بيّن أنّ مبلغها في الميل بهذه الأجزاء تسعة أجزاء واثنتان وعشرون دقيقةً فقد زاد إذن عدد الزيادة أو النقصان في الطول من قبل الميلين مجموعين دقيقةً واحدةً فقط وهذه هي الأشياء التي كنّا قصدنا لوجودها يے: ثمّ من بعد ذلك لنرسم بسبب تبيين هذه المعاني في كوكب المرّيخ لصورة التي فيها الميلان ولتجتمع أيضًا كلّ واحد من خطّي جيم كاف كاف طاء سبعةً وعشرين جزءًا وستًّا وخمسين دقيقةً بالأجزاء التي بها خطّ جيم طاء وهو الذي من مركز فلك التدوير تسعة وثلاثون جزءًا وثلاثون دقيقةً فلأنّ زاوية ألف جيم هاء وهي زاوية ميل فلك التدوير قد كانت لنا أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزأين وخمس عشرة دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فأربعة أجزاء وثلاثون دقيقةً تكون أيضًا القوس التي على خطّ كاف ميم أربعة أجزاء وثلاثين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث جيم ميم كاف القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ جيم ميم الأجزاء الباقية إلى تمام نصف دائرة وهي مائة وخمسة وسبعون جزءًا وثلاثون دقيقةً فخطّ كاف ميم إذن من الخطّين اللذين يوترانهما أربعة أجزاء وثلاث وأربعون دقيقةً (وهي مائة وخمسة وسبعون جزءًا وثلاثون دقيقةً) بالأجزاء التي بها موتر جيم كاف مائة وعشرون جزءًا وخطّ جيم ميم منهما بهذه الأجزاء مائة وتسعة عشر جزءًا وأربع وخمسون دقيقةً فيجب لذلك أن تكون أيضًا الأجزاء التي بها أمّا خطّ جيم كاف فسبعة وعشرون جزءًا وستّ وخمسون دقيقةً وأمّا خطّ ألف جيم وهو خطّ أعظم البعد فستّة وثلاثون جزءًا فإنّ خطّ كاف ميم بها جزء واحد وستّ دقائق وخطّ جيم ميم على هذا المثال سبعة وعشرون جزءًا وأربع وخمسون دقيقةً وخطّ ألف ميم الأجزاء الباقية وهي ثمانية وثلاثون جزءًا وستّ دقائق فلذلك يكون موتر ألف لام أيضًا بهذه الأجزاء ثمانيةً وثلاثين جزءًا وسبع دقائق فالأجزاء إذن التي بها موتر ألف كاف مائة وعشرون جزءًا يكون بها خطّ كاف ميم ثلاثة أجزاء وثمانيًا وعشرين دقيقةً وتكون زاوية كاف ألف ميم ثلاثة أجزاء وتسع عشرة دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وقد كانت لنا زاوية باء ألف جيم وهي زاوية ميل الفلك الخارج المركز أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزءًا واحدًا وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فجزأين فزاوية باء ألف لام إذن بأسرها تجتمع بهذه الأجزاء خمسة أجزاء وتسع عشرة دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فيجب لذلك أن تكون أيضًا القوس التي تكون على خطّ كاف باء خمسة أجزاء وتسع عشرة دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث ألف باء كاف القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ ألف باء الأجزاء الباقية إلى تمام نصف دائرة وهي مائة وأربعة وسبعون جزءًا وإحدى وأربعون دقيقةً فخطّ باء كاف إذن من الخطّين اللذين يوترانهما خمسة أجزاء وأربع وثلاثون دقيقةً بالأجزاء التي بها موتر ألف كاف مائة وعشرون جزءًا وخطّ ألف باء منهما بهذه الأجزاء مائة وتسعة عشر جزءًا واثنتان وخمسون دقيقةً فيجب لذلك أن تكون الأجزاء أيضًا التي بها خطّ ألف لام ثمانية وثلاثون جزءًا وسبع دقائق فإنّ خطّ كاف باء بها جزء واحد وستّ وأربعون دقيقةً وخطّ ألف باء على هذا المثال ثمانية وثلاثون جزءًا وخمس دقائق وبهذه الأجزاء خطّ باء لام أيضًا سبعة وعشرون جزءًا وستّ وخمسون دقيقةً ولأنّ المربّع الذي يكون من خطّ ألف باء مع الذي يكون من خطّ باء لام يكون منهما الذي يكون من خطّ ألف لام فإنّ هذا الخطّ أيضًا يحصل لنا في الطول سبعةً وأربعين جزءًا وأربع عشرة دقيقةً وعلى هذا المثال لأنّ خطّ طاء لام بهذه الأجزاء جزء واحد وستّ وأربعون دقيقةً والمربّع الذي يكون من خطّ ألف لام مع الذي يكون من خطّ لام طاء يكون منهما الذي يكون من خطّ ألف طاء فإنّ هذا الخطّ أيضًا يحصل لنا في الطول بهذه الأجزاء سبعة وأربعون جزءًا وستّ عشرة دقيقةً فيجب لذلك أن تكون الأجزاء أيضًا التي بها موتر ألف طاء مائة وعشرون جزءًا فإنّ خطّ طاء لام بها أربعة أجزاء وتسع وعشرون دقيقةً وزاوية طاء ألف لام وهي زاوية التباعد في العرض أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فأربعة أجزاء وثمان عشرة دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزءان وتسع دقائق فنثبت ذلك أيضًا في السطر الثالث من جدول المرّيخ بإزاء عدد المائة والخمسة والثلاثين الجزء وكذلك أيضًا في الميلين اللذين يكونان في أقلّ البعد من قبل أنّ خطّ ألف جيم أربعة وخمسون جزءًا بالأجزاء التي بها تبيّن أنّ خطّ كاف ميم جزء واحد وستّ دقائق وأنّ خطّ جيم ميم على هذا المثال سبعة وعشرون جزءًا وأربع وخمسون دقيقةً حتّى إنّ خطّ ألف ميم يبقي الأجزاء الباقية وهي ستّة وعشرون جزءًا وستّ دقائق ويجتمع موتر ألف لام بهذه الأجزاء ستّةً وعشرين جزءًا وسبع دقائق فالأجزاء إذن التي بها موتر ألف لام مائة وعشرون جزءًا يكون بها أمّا خطّ كاف ميم فخمسة أجزاء وثلاث دقائق وأمّا زاوية كاف ألف ميم فأربعة أجزاء وتسع وأربعون دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا ومن أجل ذلك تكون أيضًا زاوية باء ألف لام بأسرها بهذه الأجزاء ستّة أجزاء وتسعًا وأربعين دقيقةً فيجب لذلك أن تكون القوس التي تكون على خطّ باء كاف ستّة أجزاء وتسعًا وأربعين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث ألف باء كاف القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ ألف باء الأجزاء الباقية لتمام نصف دائرة وهي مائة وثلاثة وسبعون جزءًا وإحدى عشرة دقيقةً فخطّ باء كاف من الخطّين اللذين يوترانهما يكون سبعة أجزاء وثمان دقائق بالأجزاء التي بها موتر ألف لام مائة وعشرون جزءًا وخطّ ألف باء منهما بهذه الأجزاء مائة وتسعة عشر جزءًا وسبعًا وأربعين دقيقةً فيجب لذلك أن تكون الأجزاء أيضًا التي بها خطّ ألف كاف ستّةً وعشرين جزءًا وسبع دقائق فإنّ خطّ كاف بها جزء واحد وثلاث وثلاثون دقيقةً وخطّ ألف باء على هذا المثال ستّة وعشرون جزءًا وأربع دقائق وبهذه الأجزاء أيضًا خطّ باء لام سبعة وخمسون جزءًا وستّ وخمسون دقيقةً 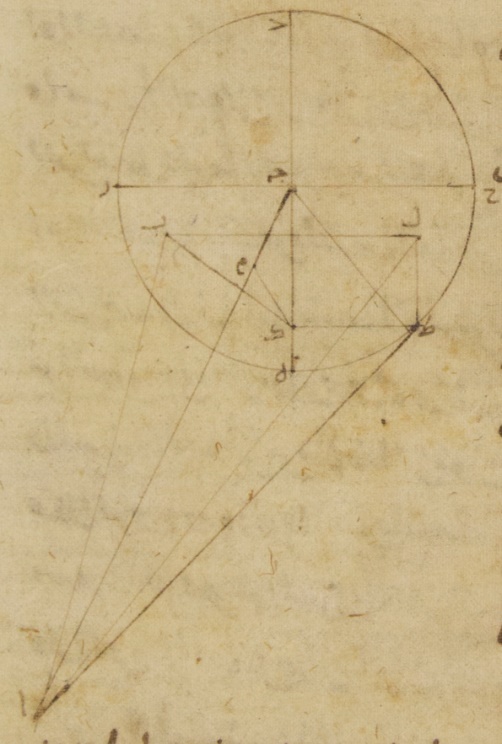 ولأنّ المربّع الذي من خطّ ألف باء مع الذي من خطّ باء لام يكون منه الذي من خطّ ألف لام فإنّ هذا الخطّ يحصل لنا في الطول ثمانيةً وثلاثين جزءًا واثنتي عشرة دقيقةً فالأجزاء إذن التي بها موتر ألف كاف مائة وعشرون جزءًا يكون بها خطّ باء لام سبعةً وثمانين جزءًا ه - صح: واثنتي عشرة دقيقةً فالأجزاء إذن التي بها موتر ألف كاف مائة وعشرون جزءًا يكون بها خطّ باء لام سبعةً وثمانين جزءًا وخمسًا وأربعين دقيقةً وتكون زاوية باء ألف كاف وهي زاوية الزيادة أو النقصان في الطول أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فأربعة وتسعون جزءًا وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا سبعة وأربعون جزءًا وعلى هذا المثال لأنّ الأجزاء التي بها خطّ ألف لام ثمانية وثلاثون جزءًا واثنتي عشرة دقيقةً يصير بها خطّ طاء لام أيضًا جزءًا واحدًا وثلاثًا وثلاثين دقيقةً فإذا جمع المربّعان اللذان يكونان من هذين الخطّين كان منهما المربّع الذي يكون من خطّ طاء ألف فإنّ هذا الخطّ أيضًا يحصل لنا في الطول بهذه الأجزاء ثمانية وثلاثون جزءًا وأربع عشرة دقيقةً فيجب لذلك أن تكون الأجزاء التي بها أيضًا موتر طاء ألف مائة وعشرون جزءًا فإنّ خطّ لام طاء بها أربعة أجزاء واثنتان وخمسون دقيقةً وزاوية طاء ألف لام وهي زاوية التباعد في العرض أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فأربعة أجزاء وأربعون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزءان وعشرون دقيقةً فنثبت ذلك أيضًا في الصفّ الرابع من الجدول بإزاء ذلك العدد بعينه الذي للمائة والخمسة والثلاثين الجزء⊙ يا: وبسبب الاعتبار أيضًا لعدد الزيادات أو النقصانات في الطول إن نحن رسمنا الصورة المعرّاة من الميلين صارت في أقلّ البعد وهو الموضع الذي فيه خاصّةً يجب ضرورةً أن يكون الفضل محسوسًا نسبة خطّ ألف دال إلى كلّ واحد من خطّي جيم كاف كاف طاء نسبة أربعة وخمسين جزءًا إلى سبعة وعشرين جزءًا وستّ وخمسين دقيقةً حتّى يكون قبل ذلك خطّ ألف كاف يبقي الأجزاء الباقية وهي ستّة وعشرون جزءًا وأربع دقائق ويجتمع موتر ألف طاء بهذه الأجزاء ثمانيةً وثلاثين جزءًا واثنتي عشرة دقيقةً فمن أجل ذلك تكون الأجزاء أيضًا التي بها موتر ألف طاء مائة وعشرون جزءًا فإنّ خطّ طاء كاف يصير أيضًا بها سبعةً وثمانين جزءًا وخمسًا وأربعين دقيقةً وتكون زاوية طاء ألف كاف وهي زاوية الزيادة أو النقصان في الطول أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فأربعة وتسعون جزءًا وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فسبعة وأربعون جزءًا وهذا هو مقدار ما كان
ولأنّ المربّع الذي من خطّ ألف باء مع الذي من خطّ باء لام يكون منه الذي من خطّ ألف لام فإنّ هذا الخطّ يحصل لنا في الطول ثمانيةً وثلاثين جزءًا واثنتي عشرة دقيقةً فالأجزاء إذن التي بها موتر ألف كاف مائة وعشرون جزءًا يكون بها خطّ باء لام سبعةً وثمانين جزءًا ه - صح: واثنتي عشرة دقيقةً فالأجزاء إذن التي بها موتر ألف كاف مائة وعشرون جزءًا يكون بها خطّ باء لام سبعةً وثمانين جزءًا وخمسًا وأربعين دقيقةً وتكون زاوية باء ألف كاف وهي زاوية الزيادة أو النقصان في الطول أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فأربعة وتسعون جزءًا وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا سبعة وأربعون جزءًا وعلى هذا المثال لأنّ الأجزاء التي بها خطّ ألف لام ثمانية وثلاثون جزءًا واثنتي عشرة دقيقةً يصير بها خطّ طاء لام أيضًا جزءًا واحدًا وثلاثًا وثلاثين دقيقةً فإذا جمع المربّعان اللذان يكونان من هذين الخطّين كان منهما المربّع الذي يكون من خطّ طاء ألف فإنّ هذا الخطّ أيضًا يحصل لنا في الطول بهذه الأجزاء ثمانية وثلاثون جزءًا وأربع عشرة دقيقةً فيجب لذلك أن تكون الأجزاء التي بها أيضًا موتر طاء ألف مائة وعشرون جزءًا فإنّ خطّ لام طاء بها أربعة أجزاء واثنتان وخمسون دقيقةً وزاوية طاء ألف لام وهي زاوية التباعد في العرض أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فأربعة أجزاء وأربعون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزءان وعشرون دقيقةً فنثبت ذلك أيضًا في الصفّ الرابع من الجدول بإزاء ذلك العدد بعينه الذي للمائة والخمسة والثلاثين الجزء⊙ يا: وبسبب الاعتبار أيضًا لعدد الزيادات أو النقصانات في الطول إن نحن رسمنا الصورة المعرّاة من الميلين صارت في أقلّ البعد وهو الموضع الذي فيه خاصّةً يجب ضرورةً أن يكون الفضل محسوسًا نسبة خطّ ألف دال إلى كلّ واحد من خطّي جيم كاف كاف طاء نسبة أربعة وخمسين جزءًا إلى سبعة وعشرين جزءًا وستّ وخمسين دقيقةً حتّى يكون قبل ذلك خطّ ألف كاف يبقي الأجزاء الباقية وهي ستّة وعشرون جزءًا وأربع دقائق ويجتمع موتر ألف طاء بهذه الأجزاء ثمانيةً وثلاثين جزءًا واثنتي عشرة دقيقةً فمن أجل ذلك تكون الأجزاء أيضًا التي بها موتر ألف طاء مائة وعشرون جزءًا فإنّ خطّ طاء كاف يصير أيضًا بها سبعةً وثمانين جزءًا وخمسًا وأربعين دقيقةً وتكون زاوية طاء ألف كاف وهي زاوية الزيادة أو النقصان في الطول أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فأربعة وتسعون جزءًا وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فسبعة وأربعون جزءًا وهذا هو مقدار ما كان
 تبيّن من قبل الحساب في الميلين من مبلغها فلم يختلف إذن من قبل ميلي الفلكين عند الزيادة أو النقصان في كوكب المرّيخ بشيء أصلًا وذلك ما كنّا قصدنا لوجودها⊙ فأمّا الصفّان الرابعان من جدولي كوكب الزهرة وكوكب عطارد فإنّ فيهما المسيرات في العرض الذي تشتمل عليها الانحرافات العظمى لفلكي تدويرهما وهذه الانحرافات إذن توجد في البعد الأبعد أو في البعد الأقرب من فلكيهما الخارجي المركزين إلّا أنّهما مقودةً على حيالها خلوًّا من الفضل الذي يكون من قبل ميلي فلكيهما الخارجي المركز من قبل أنّه لو خلطنا ما معه لكان يحتاج في ذلك من الجداول إلى أكثر ممّا وضعناه وكان الحساب منها سيكون أصعب من قبل أنّ المسيرات المسائيّة والمسيرات الصباحيّة من شأنها أن تكون غير متساوية وإلّا تكون لا محالة في جهة واحدة بعينها من فلك البروج ومع ذلك فإنّ ميل فلكيهما الخارجي المركز لمّا كان ليس يبقى على حال واحدة فإنّ فضلات التنقّص عن الميول العظمى كانت ستخالف فضلات التنقّص عن الانحرافات العظمى فلمّا أرفدنا الفضل صار يتناول شيء شيء منها أسهل علينا كما سنبيّن من نفس ما يتلو هذا القول يب: فليكن خطّ ألف باء الفصل المشترك لسطحي فلك البروج وفلك التدوير ولننزل أنّ نقطة ألف مركز فلك البروج ونقطة باء مركز فلك التدوير ولنرسم عليه فلك تدوير جيم دال هاء زاي منحرفًا على سطح فلك البروج حتّى تكون الخطوط التي تخرج فيهما قائمة على زوايا قائمة على الفصل المشترك لهما وهو خطّ جيم حاء تجعل الزوايا كلّها التي تكون على نقطة بأعيانها من خطّ جيم حاء متساوية ولنخرج أيضًا خطّ ألف هاء مماسًّا لفلك التدوير وخطّ ألف زاي دال يقطعه كيف ما وقع ولنخرج من نقطة دال هاء
تبيّن من قبل الحساب في الميلين من مبلغها فلم يختلف إذن من قبل ميلي الفلكين عند الزيادة أو النقصان في كوكب المرّيخ بشيء أصلًا وذلك ما كنّا قصدنا لوجودها⊙ فأمّا الصفّان الرابعان من جدولي كوكب الزهرة وكوكب عطارد فإنّ فيهما المسيرات في العرض الذي تشتمل عليها الانحرافات العظمى لفلكي تدويرهما وهذه الانحرافات إذن توجد في البعد الأبعد أو في البعد الأقرب من فلكيهما الخارجي المركزين إلّا أنّهما مقودةً على حيالها خلوًّا من الفضل الذي يكون من قبل ميلي فلكيهما الخارجي المركز من قبل أنّه لو خلطنا ما معه لكان يحتاج في ذلك من الجداول إلى أكثر ممّا وضعناه وكان الحساب منها سيكون أصعب من قبل أنّ المسيرات المسائيّة والمسيرات الصباحيّة من شأنها أن تكون غير متساوية وإلّا تكون لا محالة في جهة واحدة بعينها من فلك البروج ومع ذلك فإنّ ميل فلكيهما الخارجي المركز لمّا كان ليس يبقى على حال واحدة فإنّ فضلات التنقّص عن الميول العظمى كانت ستخالف فضلات التنقّص عن الانحرافات العظمى فلمّا أرفدنا الفضل صار يتناول شيء شيء منها أسهل علينا كما سنبيّن من نفس ما يتلو هذا القول يب: فليكن خطّ ألف باء الفصل المشترك لسطحي فلك البروج وفلك التدوير ولننزل أنّ نقطة ألف مركز فلك البروج ونقطة باء مركز فلك التدوير ولنرسم عليه فلك تدوير جيم دال هاء زاي منحرفًا على سطح فلك البروج حتّى تكون الخطوط التي تخرج فيهما قائمة على زوايا قائمة على الفصل المشترك لهما وهو خطّ جيم حاء تجعل الزوايا كلّها التي تكون على نقطة بأعيانها من خطّ جيم حاء متساوية ولنخرج أيضًا خطّ ألف هاء مماسًّا لفلك التدوير وخطّ ألف زاي دال يقطعه كيف ما وقع ولنخرج من نقطة دال هاء 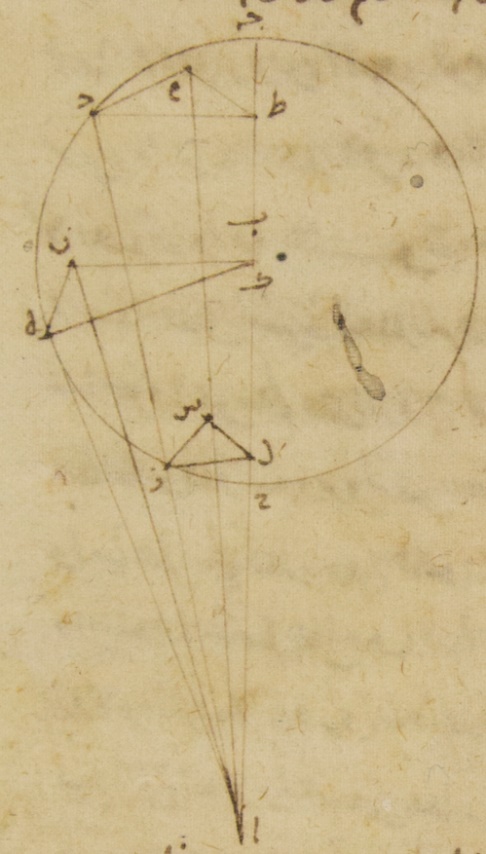 زاي أمّا على خطّ جيم حاء فأعمدة دال طاء هاء كاف زاي لام وأمّا على سطح فلك البروج فأعمدة دال ميم هاء نون زاي سين ولنوصل خطوط طاء ميم كاف نون لام سين وأيضًا خطّا ألف زاي ألف سين ميم فإنّ خطّ ألف سين ميم مستقيم من قبل أنّ الثلاث النقط هي في سطحين أعني في سطح فلك البروج وفي السطح الذي يمرّ بخطّ ألف زاي دال القائم على زوايا قائمة على سطح فلك البروج فمن البيّن في هذا الميل الموصوف أنّ الذي يشتمل على الزيادات أو النقصانات أمّا في الطول لهذين الكوكبين فزاوية طاء ألف ميم وزاوية كاف ألف نون وأمّا في العرض فزاوية دال ألف ميم وزاوية هاء ألف نون فقد ينبغي أن نبيّن أوّلًا أنّ زاوية هاء ألف نون وهي زاوية المسير في العرض التي عند التماسّ أعظم الزوايا كلّها وكذلك زاوية الزيادة أو النقصان في الطول⊙ فنقول لأنّ زاوية هاء ألف كاف أعظم هذه الزوايا كلّها فنسبة خطّ كاف هاء إلى خطّ هاء ألف أعظم من نسبة كلّ واحد من خطّي دال طاء لام زاي إلى كلّ واحد من خطّي دال ألف زاي ألف لكنّ نسبة خطّ كاف هاء إلى خطّ هاء نون كنسبة خطّ طاء دال إلى خطّ دال ميم وكنسبة خطّ لام زاي إلى خطّ زاي سين وذلك أنّ المثلّثات التي بهذه الصفة كلّها متساوية الزوايا كما قلنا والزوايا التي عند نقط ميم زاي سين قائمة فنسبة خطّ نون هاء إذن إلى خطّ هاء ألف أعظم من نسبة كلّ واحد من خطّي ميم دال زاي سين إلى كلّ واحد من خطّي دال ألف زاي ألف وزوايا دال ميم ألف هاء نون ألف زاي سين ألف أيضًا قائمة فزاوية هاء ألف زاي إذن أعظم من زاوية دال ألف ميم ومن البيّن أنّها أيضًا أعظم من الزوايا كلّها التي تكون على هذه الصفة ومن البيّن أيضًا من قرب أنّ الفضول التي تكون للزيادات أو النقصانات في الطول من قبل الانحراف أعظمها الفضل الذي يقع عند المسيرات العظمى التي تكون على نقطة هاء وذلك أنّه تشتمل عليها الزوايا الذي يوتر التفاضل بين خطوط طاء دال كاف هاء لام زاي وبين خطوط طاء ميم كاف نون لام سين ولمّا كانت نسبة كلّ واحد من هذه الخطوط إلى ما به يفضل أيضًا هي نسبة واحدة بعينها فقد يلزم من ذلك أن تكون نسبة التفاضل بين كلّ خطّين من سائر الخطوط النظائر لهذين إلى الخطوط النظائر لخطّ ألف دال ومن البيّن من ذلك أيضًا أنّ نسبة أكثر ما يكون من الزيادة أو النقصان في الطول إلى أعظم ما يكون من المسير في العرض هي النسبة التي تكون في أقسام فلك التدوير كلّها للزيادات أو النقصانات في الطول في كلّ قسم منها إلى المسيرات في العرض ومن أجل أنّ نسبة خطّ كاف هاء إلى خطّ هاء زاي كنسبة الخطوط النظائر لخطّي لام زاي دال طاء كلّها إلى الخطوط النظائر لخطّي زاي سين دال ميم وهذه الأشياء قد أردنا أن نبيّن⊙ فإذ قد تقدّم الإرشاد إلى هذه الأشياء فلننظر أوّلًا كم مقدار الزاوية في كلّ واحد من الكوكبين التي يحدثها انحراف فلك تدويره بعد أن نعمل على ما تقدّمنا فاستخرجناه بدئًا من أنّ كلّ واحد منهما في بعده أكثر ما يكون ميلًا في الشمال أو في الجنوب عن المسيرين المضادين لهما في فلك تدويره البعد الوسط بين أعظم ما يكون من بعده وهو خمسة أجزاء من قبل أنّ كوكب الزهرة يرى زواله في البعد الأقرب وفي البعد الأبعد من الفلك الخارج المركز أكثر وأقلّ من خمسة أجزاء بما لا يعتدّ به وأمّا كوكب عطارد فأكثر وأقلّ من خمسة أجزاء بنحو من نصف جزء يجـ: فليكن |9| أيضًا الفصل المشترك لفلك البروج ولفلك التدوير خطّ ألف باء جيم ولنرسم حول نقطة باء فلك تدوير جيم دال هاء منحرفًا عن سطح فلك البروج على الجهة التي وصفناها وليوصل من نقطة ألف وهي مركز فلك البروج خطّ يماسّ فلك التدوير وليكن خطّ ألف دال وليخرج من نقطة دال أمّا على خطّ جيم باء هاء فعود دال زاي وأمّا على سطح فلك البروج فعمود دال حاء ولتوصل خطوط باء دال زاي حاء ألف حاء ولننزل أنّ زاوية دال ألف حاء تشتمل على نصف التباعد الموصوف في العرض في كلّ واحد من الكوكبين وهو جزءان ونصف بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا وليكن قصدنا أن نجد مقدار انحراف كلّ واحد من فلكي التدوير أعني مقدار زاوية دال زاي حاء ففي كوكب الزهرة لأنّ الأجزاء التي بها الخطّ الذي من مركز فلك التدوير ثلاثة وأربعون جزءًا وعشر دقائق فإنّ البعد الأعظم يكون بها أحدًا وستّين جزءًا وخمس عشرة دقيقةً والبعد الأصغر يكون بها ثمانيةً وخمسين جزءًا وخمسًا وأربعين دقيقةً وما بين هذين أيضًا يصير ستّين جزءًا فإنّ نسبة خطّ ألف باء إلى خطّ باء دال تكون كنسبة ستّين جزءًا إلى ثلاثة وأربعين جزءًا وعشر دقائق ولأنّ المربّع الذي يكون من خطّ باء دال إذا نقص من المربّع الذي يكون من خطّ ألف باء حصل المربّع الذي يكون من خطّ ألف دال فإنّ هذا الخطّ أيضًا يحصل لنا في الطول بهذه الأجزاء أحدًا وأربعين جزءًا وأربعين دقيقةً وعلى هذا المثال لأنّ نسبة خطّ باء ألف إلى خطّ ألف دال كنسبة خطّ باء دال إلى خطّ دال زاي فإنّ خطّ دال زاي أيضًا يحصل لنا بهذه الأجزاء تسعةً وعشرين جزءًا وثمانيًا وخمسين دقيقةً وأيضًا لأنّ زاوية دال ألف حاء وضعت أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزأين وثلاثين دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فخمسة أجزاء تكون أيضًا القوس التي تكون على خطّ دال حاء خمسة أجزاء بالأجزاء التي بها الدائرة التي ترسم حول مثلّث ألف دال حاء القائم الزاوية ثلاث مائة وستّون جزءًا ويكون وترها وهو خطّ دال حاء خمسة أجزاء وأربع عشرة دقيقةً بالأجزاء التي بها موتر ألف دال مائة وعشرون جزءًا فالأجزاء إذن التي بها خطّ ألف دال أحدًا وأربعين جزءًا وأربعين دقيقةً يكون بها خطّ دال حاء أيضًا جزءًا واحدًا وخمسين دقيقةً وبهذه الأجزاء يتبيّن أنّ خطّ دال باء تسعة وعشرون جزءًا وثمان وخمسون دقيقةً فلذلك تكون الأجزاء التي بها موتر دال زاي مائة وعشرون جزءًا فإنّ خطّ دال حاء بها سبعة أجزاء وعشرون دقيقةً وزاوية دال زاي حاء وهي زاوية الانحراف أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فسبعة أجزاء وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فثلاثة أجزاء ونصف لكن لأنّ زيادة زاوية دال ألف زاي على زاوية حاء ألف زاي تشتمل على الفصل الذي يكون للزيادة أو النقصان في الطول فقد يجب أن يحسب هذا الفضل أيضًا بسهولة من قبل ما يستخرج من مقاديرها وذلك أنّه لمّا كان قد تبيّن أنّ الأجزاء التي بها خطّ دال حاء جزء واحد وخمسون دقيقةً فإنّ موتر ألف دال بها أحد وأربعون جزءًا وأربعون دقيقةً وخطّ زاي دال على ذلك المثال تسعة وعشرون جزءًا وثمان وخمسون دقيقةً وكان المربّع الذي يكون من خطّ دال حاء إذا نقص من المربّع الذي يكون من كلّ واحد من خطّي ألف دال دال زاي كان المربّع الذي يكون من كلّ واحد من خطّي ألف حاء زاي فإنّ خطّ ألف حاء أيضًا يحصل لنا في الطول بهذه الأجزاء أحدًا وأربعين جزءًا وسبعًا وثلاثين دقيقةً وخطّ زاي حاء على هذا المثال تسعة وعشرون جزءًا وخمس وخمسون دقيقةً فلذلك قد تكون الأجزاء التي بها موتر ألف حاء مائة وعشرون جزءًا فإنّ خطّ زاي حاء يكون بها ستّةً وثمانين جزءًا وستّ عشرة دقيقةً وزاوية زاي ألف حاء أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فأحدًا وتسعين جزءًا وستًّا وخمسين دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فخمسة وأربعون جزءًا وثمان وخمسون دقيقةً وعلى هذا المثال لأنّ الأجزاء التي بها موتر ألف دال مائة وعشرون جزءًا يصير بها خطّ دال زاي أيضًا ستّةً وثمانين جزءًا وثمان عشرة دقيقةً فإنّ زاوية دال ألف زاي أيضًا يحصل لنا أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فأحدًا وتسعين جزءًا وثمانيًا وخمسين دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فخمسة وأربعون جزءًا وتسع وخمسون دقيقةً فقد نقص إذن عدد الزيادة والنقصان في الطول من قبل الانحراف دقيقةً واحدةً يد: فأمّا في كوكب عطارد فلأنّ الأجزاء التي بها الخطّ الذي من مركز فلك التدوير اثنان وعشرون جزءًا وثلاثون دقيقةً فقد تبيّن أنّ أعظم البعد بها تسعة وستّون جزءًا
زاي أمّا على خطّ جيم حاء فأعمدة دال طاء هاء كاف زاي لام وأمّا على سطح فلك البروج فأعمدة دال ميم هاء نون زاي سين ولنوصل خطوط طاء ميم كاف نون لام سين وأيضًا خطّا ألف زاي ألف سين ميم فإنّ خطّ ألف سين ميم مستقيم من قبل أنّ الثلاث النقط هي في سطحين أعني في سطح فلك البروج وفي السطح الذي يمرّ بخطّ ألف زاي دال القائم على زوايا قائمة على سطح فلك البروج فمن البيّن في هذا الميل الموصوف أنّ الذي يشتمل على الزيادات أو النقصانات أمّا في الطول لهذين الكوكبين فزاوية طاء ألف ميم وزاوية كاف ألف نون وأمّا في العرض فزاوية دال ألف ميم وزاوية هاء ألف نون فقد ينبغي أن نبيّن أوّلًا أنّ زاوية هاء ألف نون وهي زاوية المسير في العرض التي عند التماسّ أعظم الزوايا كلّها وكذلك زاوية الزيادة أو النقصان في الطول⊙ فنقول لأنّ زاوية هاء ألف كاف أعظم هذه الزوايا كلّها فنسبة خطّ كاف هاء إلى خطّ هاء ألف أعظم من نسبة كلّ واحد من خطّي دال طاء لام زاي إلى كلّ واحد من خطّي دال ألف زاي ألف لكنّ نسبة خطّ كاف هاء إلى خطّ هاء نون كنسبة خطّ طاء دال إلى خطّ دال ميم وكنسبة خطّ لام زاي إلى خطّ زاي سين وذلك أنّ المثلّثات التي بهذه الصفة كلّها متساوية الزوايا كما قلنا والزوايا التي عند نقط ميم زاي سين قائمة فنسبة خطّ نون هاء إذن إلى خطّ هاء ألف أعظم من نسبة كلّ واحد من خطّي ميم دال زاي سين إلى كلّ واحد من خطّي دال ألف زاي ألف وزوايا دال ميم ألف هاء نون ألف زاي سين ألف أيضًا قائمة فزاوية هاء ألف زاي إذن أعظم من زاوية دال ألف ميم ومن البيّن أنّها أيضًا أعظم من الزوايا كلّها التي تكون على هذه الصفة ومن البيّن أيضًا من قرب أنّ الفضول التي تكون للزيادات أو النقصانات في الطول من قبل الانحراف أعظمها الفضل الذي يقع عند المسيرات العظمى التي تكون على نقطة هاء وذلك أنّه تشتمل عليها الزوايا الذي يوتر التفاضل بين خطوط طاء دال كاف هاء لام زاي وبين خطوط طاء ميم كاف نون لام سين ولمّا كانت نسبة كلّ واحد من هذه الخطوط إلى ما به يفضل أيضًا هي نسبة واحدة بعينها فقد يلزم من ذلك أن تكون نسبة التفاضل بين كلّ خطّين من سائر الخطوط النظائر لهذين إلى الخطوط النظائر لخطّ ألف دال ومن البيّن من ذلك أيضًا أنّ نسبة أكثر ما يكون من الزيادة أو النقصان في الطول إلى أعظم ما يكون من المسير في العرض هي النسبة التي تكون في أقسام فلك التدوير كلّها للزيادات أو النقصانات في الطول في كلّ قسم منها إلى المسيرات في العرض ومن أجل أنّ نسبة خطّ كاف هاء إلى خطّ هاء زاي كنسبة الخطوط النظائر لخطّي لام زاي دال طاء كلّها إلى الخطوط النظائر لخطّي زاي سين دال ميم وهذه الأشياء قد أردنا أن نبيّن⊙ فإذ قد تقدّم الإرشاد إلى هذه الأشياء فلننظر أوّلًا كم مقدار الزاوية في كلّ واحد من الكوكبين التي يحدثها انحراف فلك تدويره بعد أن نعمل على ما تقدّمنا فاستخرجناه بدئًا من أنّ كلّ واحد منهما في بعده أكثر ما يكون ميلًا في الشمال أو في الجنوب عن المسيرين المضادين لهما في فلك تدويره البعد الوسط بين أعظم ما يكون من بعده وهو خمسة أجزاء من قبل أنّ كوكب الزهرة يرى زواله في البعد الأقرب وفي البعد الأبعد من الفلك الخارج المركز أكثر وأقلّ من خمسة أجزاء بما لا يعتدّ به وأمّا كوكب عطارد فأكثر وأقلّ من خمسة أجزاء بنحو من نصف جزء يجـ: فليكن |9| أيضًا الفصل المشترك لفلك البروج ولفلك التدوير خطّ ألف باء جيم ولنرسم حول نقطة باء فلك تدوير جيم دال هاء منحرفًا عن سطح فلك البروج على الجهة التي وصفناها وليوصل من نقطة ألف وهي مركز فلك البروج خطّ يماسّ فلك التدوير وليكن خطّ ألف دال وليخرج من نقطة دال أمّا على خطّ جيم باء هاء فعود دال زاي وأمّا على سطح فلك البروج فعمود دال حاء ولتوصل خطوط باء دال زاي حاء ألف حاء ولننزل أنّ زاوية دال ألف حاء تشتمل على نصف التباعد الموصوف في العرض في كلّ واحد من الكوكبين وهو جزءان ونصف بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا وليكن قصدنا أن نجد مقدار انحراف كلّ واحد من فلكي التدوير أعني مقدار زاوية دال زاي حاء ففي كوكب الزهرة لأنّ الأجزاء التي بها الخطّ الذي من مركز فلك التدوير ثلاثة وأربعون جزءًا وعشر دقائق فإنّ البعد الأعظم يكون بها أحدًا وستّين جزءًا وخمس عشرة دقيقةً والبعد الأصغر يكون بها ثمانيةً وخمسين جزءًا وخمسًا وأربعين دقيقةً وما بين هذين أيضًا يصير ستّين جزءًا فإنّ نسبة خطّ ألف باء إلى خطّ باء دال تكون كنسبة ستّين جزءًا إلى ثلاثة وأربعين جزءًا وعشر دقائق ولأنّ المربّع الذي يكون من خطّ باء دال إذا نقص من المربّع الذي يكون من خطّ ألف باء حصل المربّع الذي يكون من خطّ ألف دال فإنّ هذا الخطّ أيضًا يحصل لنا في الطول بهذه الأجزاء أحدًا وأربعين جزءًا وأربعين دقيقةً وعلى هذا المثال لأنّ نسبة خطّ باء ألف إلى خطّ ألف دال كنسبة خطّ باء دال إلى خطّ دال زاي فإنّ خطّ دال زاي أيضًا يحصل لنا بهذه الأجزاء تسعةً وعشرين جزءًا وثمانيًا وخمسين دقيقةً وأيضًا لأنّ زاوية دال ألف حاء وضعت أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزأين وثلاثين دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فخمسة أجزاء تكون أيضًا القوس التي تكون على خطّ دال حاء خمسة أجزاء بالأجزاء التي بها الدائرة التي ترسم حول مثلّث ألف دال حاء القائم الزاوية ثلاث مائة وستّون جزءًا ويكون وترها وهو خطّ دال حاء خمسة أجزاء وأربع عشرة دقيقةً بالأجزاء التي بها موتر ألف دال مائة وعشرون جزءًا فالأجزاء إذن التي بها خطّ ألف دال أحدًا وأربعين جزءًا وأربعين دقيقةً يكون بها خطّ دال حاء أيضًا جزءًا واحدًا وخمسين دقيقةً وبهذه الأجزاء يتبيّن أنّ خطّ دال باء تسعة وعشرون جزءًا وثمان وخمسون دقيقةً فلذلك تكون الأجزاء التي بها موتر دال زاي مائة وعشرون جزءًا فإنّ خطّ دال حاء بها سبعة أجزاء وعشرون دقيقةً وزاوية دال زاي حاء وهي زاوية الانحراف أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فسبعة أجزاء وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فثلاثة أجزاء ونصف لكن لأنّ زيادة زاوية دال ألف زاي على زاوية حاء ألف زاي تشتمل على الفصل الذي يكون للزيادة أو النقصان في الطول فقد يجب أن يحسب هذا الفضل أيضًا بسهولة من قبل ما يستخرج من مقاديرها وذلك أنّه لمّا كان قد تبيّن أنّ الأجزاء التي بها خطّ دال حاء جزء واحد وخمسون دقيقةً فإنّ موتر ألف دال بها أحد وأربعون جزءًا وأربعون دقيقةً وخطّ زاي دال على ذلك المثال تسعة وعشرون جزءًا وثمان وخمسون دقيقةً وكان المربّع الذي يكون من خطّ دال حاء إذا نقص من المربّع الذي يكون من كلّ واحد من خطّي ألف دال دال زاي كان المربّع الذي يكون من كلّ واحد من خطّي ألف حاء زاي فإنّ خطّ ألف حاء أيضًا يحصل لنا في الطول بهذه الأجزاء أحدًا وأربعين جزءًا وسبعًا وثلاثين دقيقةً وخطّ زاي حاء على هذا المثال تسعة وعشرون جزءًا وخمس وخمسون دقيقةً فلذلك قد تكون الأجزاء التي بها موتر ألف حاء مائة وعشرون جزءًا فإنّ خطّ زاي حاء يكون بها ستّةً وثمانين جزءًا وستّ عشرة دقيقةً وزاوية زاي ألف حاء أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فأحدًا وتسعين جزءًا وستًّا وخمسين دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فخمسة وأربعون جزءًا وثمان وخمسون دقيقةً وعلى هذا المثال لأنّ الأجزاء التي بها موتر ألف دال مائة وعشرون جزءًا يصير بها خطّ دال زاي أيضًا ستّةً وثمانين جزءًا وثمان عشرة دقيقةً فإنّ زاوية دال ألف زاي أيضًا يحصل لنا أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فأحدًا وتسعين جزءًا وثمانيًا وخمسين دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فخمسة وأربعون جزءًا وتسع وخمسون دقيقةً فقد نقص إذن عدد الزيادة والنقصان في الطول من قبل الانحراف دقيقةً واحدةً يد: فأمّا في كوكب عطارد فلأنّ الأجزاء التي بها الخطّ الذي من مركز فلك التدوير اثنان وعشرون جزءًا وثلاثون دقيقةً فقد تبيّن أنّ أعظم البعد بها تسعة وستّون جزءًا  وأمّا في البعد المقاطر له سبعة وخمسون جزءًا فالبعد الوسط بين هذين يحصل بهذه الأجزاء ثلاثةً وستّين جزءًا وتكون نسبة خطّ ألف باء إلى خطّ باء دال نسبة ثلاثة وستّين جزءًا إلى اثنين وعشرين جزءًا وثلاثين دقيقةً ولأنّ المربّع الذي يكون من خطّ دال باء إذا نقص من الذي يكون من خطّ ألف باء كان المربّع الذي يكون من خطّ ألف دال فإنّ هذا الخطّ أيضًا يحصل لنا في الطول بهذه الأجزاء ثمانيةً وخمسين جزءًا وإحدى وخمسين دقيقةً وعلى هذا المثال لأنّ نسبة خطّ ألف باء إلى خطّ ألف دال كنسبة خطّ باء دال إلى خطّ دال زاي فإنّ خطّ دال زاي
وأمّا في البعد المقاطر له سبعة وخمسون جزءًا فالبعد الوسط بين هذين يحصل بهذه الأجزاء ثلاثةً وستّين جزءًا وتكون نسبة خطّ ألف باء إلى خطّ باء دال نسبة ثلاثة وستّين جزءًا إلى اثنين وعشرين جزءًا وثلاثين دقيقةً ولأنّ المربّع الذي يكون من خطّ دال باء إذا نقص من الذي يكون من خطّ ألف باء كان المربّع الذي يكون من خطّ ألف دال فإنّ هذا الخطّ أيضًا يحصل لنا في الطول بهذه الأجزاء ثمانيةً وخمسين جزءًا وإحدى وخمسين دقيقةً وعلى هذا المثال لأنّ نسبة خطّ ألف باء إلى خطّ ألف دال كنسبة خطّ باء دال إلى خطّ دال زاي فإنّ خطّ دال زاي 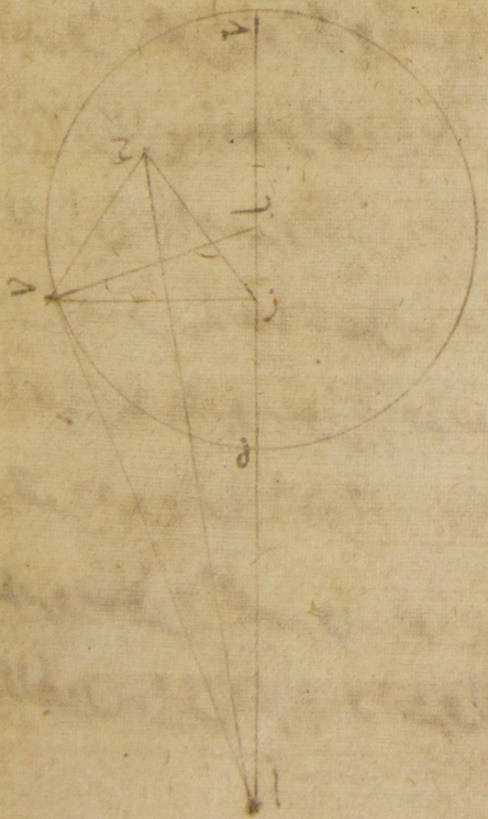 أيضًا يكون بهذه الأجزاء أحدًا وعشرين جزءًا ودقيقةً واحدةً وأيضًا لأنّ زاوية دال ألف حاء قد وضعت خمسة أجزاء بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فإنّ القوس التي تكون على خطّ دال حاء تصير خمسة أجزاء بالأجزاء التي بها الدائرة التي ترسم حول مثلّث ألف دال حاء القائم الزاوية ثلاث مائة وستّون جزءًا ويكون وترها وهو خطّ دال حاء خمسة أجزاء وأربع عشرة دقيقةً بالأجزاء التي بها موتر ألف دال مائة وعشرون جزءًا فالأجزاء إذن التي بها خطّ ألف دال ثمانية وخمسون جزءًا وإحدى وخمسون دقيقةً يكون بها خطّ دال حاء أيضًا جزأين وأربعًا وثلاثين دقيقةً وبهذه الأجزاء تبيّن أنّ خطّ دال زاي أحد وعشرون جزءًا ودقيقة واحدة فلذلك تكون الأجزاء التي بها موتر دال زاي مائة وعشرون جزءًا فإنّ خطّ دال حاء بها أربعة عشر جزءًا وأربعون دقيقةً وزاوية دال زاي حاء وهي زاوية الانحراف أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فأربعة عشر جزءًا وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فسبعة أجزاء وعلى ذلك المثال أيضًا بسبب اعتبار زوايا الزيادة أو النقصان لأنّ الأجزاء أيضًا التي بها خطّ دال حاء جزءان وأربع وثلاثون دقيقةً فإنّ خطّ ألف دال الموتر قد تبيّن أنّه بها ثمانية وخمسون جزءًا وإحدى وخمسون دقيقةً وخطّ دال زاي على هذا المثال أحد وعشرون جزءًا ودقيقة واحدة والمربّع الذي يكون من خطّ دال حاء إذا نقص من المربّعين اللذين يكونان من كلّ واحد من خطّي ألف دال دال زاي كان بذلك المربّعان اللذان يكونان من كلّ واحد من خطّي ألف حاء حاء زاي يحصل لنا أمّا خطّ ألف حاء في الطول فثمانية وخمسون جزءًا وسبع وأربعون دقيقةً وأمّا خطّ زاي حاء بهذه الأجزاء فعشرون جزءًا وثلاث وخمسون دقيقةً فيجب لذلك أن تكون الأجزاء التي بها موتر ألف حاء مائة وعشرون جزءًا فإنّ خطّ زاي حاء بها اثنان وأربعون جزءًا وثمان وثلاثون دقيقةً وزاوية زاي ألف حاء أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فأحد وأربعون جزءًا وثمان وثلاثون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فعشرون جزءًا وتسع وأربعون دقيقةً وكذلك أيضًا لأنّ الأجزاء التي بها موتر ألف دال مائة وعشرون جزءًا يحصل بها خطّ دال زاي اثنين وأربعين جزءًا وخمسين دقيقةً فإنّ زاوية دال ألف زاي أيضًا تحصل لنا أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فأحد وأربعون جزءًا وخمسون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فعشرون جزءًا وخمس وخمسون دقيقةً فقد نقص إذن في هذه أيضًا من قبل الانحراف عدد الزيادة أو النقصان في الطول ستّ دقائق وهذه الأشياء قصدنا لوجودها⊙ فلننظر الآن من بعد ذلك هل نحن إذا وضعنا أنّ هذا مبلغ مقادير الانحرافات وجدنا أعظم المسيرات في العرض في أعظم الأبعاد وأقلّها مواقفًا لما أدركنا منه بالأرصاد يه: ولننزل أيضًا في مثل هذه الصورة بعينها البعد الأعظم أوّلًا لكوكب الزهرة أعني أنّ نسبة خطّ ألف باء إلى خطّ باء دال نسبة أحد وستّين جزءًا وعشر دقائق فمن قبل ذلك لأنّ المربّع الذي يكون من خطّ دال باء إذا نقص من المربّع الذي يكون من خطّ ألف باء كان بذلك المربّع الذي يكون من خطّ ألف دال فإنّ هذا الخطّ أيضًا يحصل بهذه الأجزاء ثلاثة وأربعين جزءًا وسبعًا وعشرين دقيقةً لكنّ نسبة خطّ ألف باء إلى خطّ ألف دال كنسبة خطّ باء دال إلى خطّ دال زاي فخطّ دال زاي إذن يكون بهذه الأجزاء ثلاثين جزءًا وسبعًا وثلاثين دقيقةً وأيضًا لأنّ زاوية دال زاي حاء وهي زاوية الانحراف قد وضعت سبعة أجزاء بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وخطّ دال حاء وضع سبعة أجزاء وعشرين دقيقةً
أيضًا يكون بهذه الأجزاء أحدًا وعشرين جزءًا ودقيقةً واحدةً وأيضًا لأنّ زاوية دال ألف حاء قد وضعت خمسة أجزاء بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فإنّ القوس التي تكون على خطّ دال حاء تصير خمسة أجزاء بالأجزاء التي بها الدائرة التي ترسم حول مثلّث ألف دال حاء القائم الزاوية ثلاث مائة وستّون جزءًا ويكون وترها وهو خطّ دال حاء خمسة أجزاء وأربع عشرة دقيقةً بالأجزاء التي بها موتر ألف دال مائة وعشرون جزءًا فالأجزاء إذن التي بها خطّ ألف دال ثمانية وخمسون جزءًا وإحدى وخمسون دقيقةً يكون بها خطّ دال حاء أيضًا جزأين وأربعًا وثلاثين دقيقةً وبهذه الأجزاء تبيّن أنّ خطّ دال زاي أحد وعشرون جزءًا ودقيقة واحدة فلذلك تكون الأجزاء التي بها موتر دال زاي مائة وعشرون جزءًا فإنّ خطّ دال حاء بها أربعة عشر جزءًا وأربعون دقيقةً وزاوية دال زاي حاء وهي زاوية الانحراف أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فأربعة عشر جزءًا وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فسبعة أجزاء وعلى ذلك المثال أيضًا بسبب اعتبار زوايا الزيادة أو النقصان لأنّ الأجزاء أيضًا التي بها خطّ دال حاء جزءان وأربع وثلاثون دقيقةً فإنّ خطّ ألف دال الموتر قد تبيّن أنّه بها ثمانية وخمسون جزءًا وإحدى وخمسون دقيقةً وخطّ دال زاي على هذا المثال أحد وعشرون جزءًا ودقيقة واحدة والمربّع الذي يكون من خطّ دال حاء إذا نقص من المربّعين اللذين يكونان من كلّ واحد من خطّي ألف دال دال زاي كان بذلك المربّعان اللذان يكونان من كلّ واحد من خطّي ألف حاء حاء زاي يحصل لنا أمّا خطّ ألف حاء في الطول فثمانية وخمسون جزءًا وسبع وأربعون دقيقةً وأمّا خطّ زاي حاء بهذه الأجزاء فعشرون جزءًا وثلاث وخمسون دقيقةً فيجب لذلك أن تكون الأجزاء التي بها موتر ألف حاء مائة وعشرون جزءًا فإنّ خطّ زاي حاء بها اثنان وأربعون جزءًا وثمان وثلاثون دقيقةً وزاوية زاي ألف حاء أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فأحد وأربعون جزءًا وثمان وثلاثون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فعشرون جزءًا وتسع وأربعون دقيقةً وكذلك أيضًا لأنّ الأجزاء التي بها موتر ألف دال مائة وعشرون جزءًا يحصل بها خطّ دال زاي اثنين وأربعين جزءًا وخمسين دقيقةً فإنّ زاوية دال ألف زاي أيضًا تحصل لنا أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فأحد وأربعون جزءًا وخمسون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فعشرون جزءًا وخمس وخمسون دقيقةً فقد نقص إذن في هذه أيضًا من قبل الانحراف عدد الزيادة أو النقصان في الطول ستّ دقائق وهذه الأشياء قصدنا لوجودها⊙ فلننظر الآن من بعد ذلك هل نحن إذا وضعنا أنّ هذا مبلغ مقادير الانحرافات وجدنا أعظم المسيرات في العرض في أعظم الأبعاد وأقلّها مواقفًا لما أدركنا منه بالأرصاد يه: ولننزل أيضًا في مثل هذه الصورة بعينها البعد الأعظم أوّلًا لكوكب الزهرة أعني أنّ نسبة خطّ ألف باء إلى خطّ باء دال نسبة أحد وستّين جزءًا وعشر دقائق فمن قبل ذلك لأنّ المربّع الذي يكون من خطّ دال باء إذا نقص من المربّع الذي يكون من خطّ ألف باء كان بذلك المربّع الذي يكون من خطّ ألف دال فإنّ هذا الخطّ أيضًا يحصل بهذه الأجزاء ثلاثة وأربعين جزءًا وسبعًا وعشرين دقيقةً لكنّ نسبة خطّ ألف باء إلى خطّ ألف دال كنسبة خطّ باء دال إلى خطّ دال زاي فخطّ دال زاي إذن يكون بهذه الأجزاء ثلاثين جزءًا وسبعًا وثلاثين دقيقةً وأيضًا لأنّ زاوية دال زاي حاء وهي زاوية الانحراف قد وضعت سبعة أجزاء بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وخطّ دال حاء وضع سبعة أجزاء وعشرين دقيقةً  بالأجزاء التي بها موتر دال زاي مائة وعشرون جزءًا فالأجزاء إذن التي بها أيضًا خطّ دال زاي ثلاثون جزءًا وسبع وثلاثون دقيقةً وخطّ ألف دال على هذا المثال ثلاثة وأربعون جزءًا وسبع وعشرون دقيقةً يكون بها خطّ دال حاء أيضًا جزءًا واحدًا واثنتين وخمسين دقيقةً فيجب لذلك أن تكون الأجزاء التي بها أيضًا موتر ألف دال مائة وعشرون جزءًا فإنّ خطّ دال حاء بها خمسة أجزاء وتسع دقائق وزاوية دال ألف حاء وهي زاوية الزوال الأعظم في العرض أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فأربعة أجزاء وأربع وخمسون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزأين وسبعًا وعشرين دقيقةً وأمّا في البعد الأصغر فإنّ الأجزاء التي بها خطّ باء دال الذي من مركز فلك التدوير ثلاثة وأربعون جزءًا وعشر دقائق فإنّ خطّ ألف باء قد وضع بها ثمانيةً وخمسين جزءًا وخمسًا وأربعين دقيقةً والمربّع الذي يكون من خطّ دال باء إذا نقص من المربّع الذي يكون من خطّ ألف باء كان بذلك المربّع الذي يكون من خطّ ألف دال فإنّ هذا الخطّ أيضًا يحصل لنا في الطول بهذه الأجزاء تسعةً وثلاثين جزءًا وإحدى وخمسين دقيقةً وعلى ذلك المثال لأنّ نسبة خطّ ألف باء إلى خطّ ألف دال كنسبة خطّ دال باء إلى خطّ دال زاي فإنّ خطّ دال زاي أيضًا يكون بهذه الأجزاء تسعةً وعشرين جزءًا وسبع عشرة دقيقةً لكنّ نسبة خطّ دال زاي إلى خطّ دال حاء قد وضعت كنسبة مائة وعشرين جزءًا إلى سبعة أجزاء وعشرين دقيقةً فالأجزاء إذن التي بها أمّا خطّ زاي دال فسبعة وعشرون جزءًا وسبع عشرة دقيقةً وأمّا خطّ ألف دال على هذا المثال فتسعة وثلاثون جزءًا وإحدى وخمسون دقيقةً يصير بها خطّ دال حاء أيضًا جزءًا واحدًا وسبعًا وأربعين دقيقةً فلذلك تكون الأجزاء أيضًا التي بها موتر ألف دال مائة وعشرون جزءًا فإنّ خطّ دال حاء بها خمسة أجزاء واثنتان وعشرون دقيقةً وزاوية دال ألف حاء وهي زاوية الزوال الأعظم في العرض أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فخمسة أجزاء وثمان دقائق وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزءان وأربع وثلاثون دقيقةً فإذ كان إذن قد وضع الزوال في العرض على النسبة الوسطى جزأين ونصف فإنّ ما يكون منه في البعد الأبعد وجد أقلّ من ذلك بما لا يوقع اختلافًا عند الحسّ وكذلك ما يكون في البعد الأقرب وجد أكثر منه بما لا يحسّ وذلك أنّ الزوال في البعد الأعظم إنّما ينقص ثلاث دقائق فقط والزوال في البعد الأصغر إنّما زاد أربع دقائق وليس هذا المقدار ممّا يمكن أن يلحق ولا يوقف عليه أصلًا بالرصد يو: ثمّ ليوضع |13| أيضًا البعد الأعظم لكوكب عطارد أعني نسبة خطّ ألف باء إلى خطّ باء دال نسبة تسعة وعشرين جزءًا إلى اثنين وعشرين جزءًا وثلاثين دقيقةً حتّى يحصل من قبل تلك الأشياء بأعيانها التي وصفناها قبيل أمّا خطّ ألف دال بهذه الأجزاء فخمسة وستّون جزءًا وأربع عشرة دقيقةً وأمّا خطّ دال زاي على هذا المثال فأحد وعشرون جزءًا وستّ عشرة دقيقةً لكن هاهنا أيضًا لنا زاوية دال زاي حاء وهي زاوية الانحراف موضوعة أربعة عشر جزءًا بالأجزاء التي بها موتر دال زاي مائة وعشرون جزءًا فالأجزاء إذن التي بها أمّا خطّ زاي دال فأحد وعشرون جزءًا وستّ عشرة دقيقةً وأمّا خطّ ألف دال على هذا المثال فخمسة وستّون جزءًا وأربع عشرة دقيقةً يكون بها خطّ دال حاء أيضًا جزأين وستًّا وثلاثين دقيقةً فلذلك تكون الأجزاء أيضًا التي بها موتر ألف دال مائة وعشرون جزءًا
بالأجزاء التي بها موتر دال زاي مائة وعشرون جزءًا فالأجزاء إذن التي بها أيضًا خطّ دال زاي ثلاثون جزءًا وسبع وثلاثون دقيقةً وخطّ ألف دال على هذا المثال ثلاثة وأربعون جزءًا وسبع وعشرون دقيقةً يكون بها خطّ دال حاء أيضًا جزءًا واحدًا واثنتين وخمسين دقيقةً فيجب لذلك أن تكون الأجزاء التي بها أيضًا موتر ألف دال مائة وعشرون جزءًا فإنّ خطّ دال حاء بها خمسة أجزاء وتسع دقائق وزاوية دال ألف حاء وهي زاوية الزوال الأعظم في العرض أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فأربعة أجزاء وأربع وخمسون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزأين وسبعًا وعشرين دقيقةً وأمّا في البعد الأصغر فإنّ الأجزاء التي بها خطّ باء دال الذي من مركز فلك التدوير ثلاثة وأربعون جزءًا وعشر دقائق فإنّ خطّ ألف باء قد وضع بها ثمانيةً وخمسين جزءًا وخمسًا وأربعين دقيقةً والمربّع الذي يكون من خطّ دال باء إذا نقص من المربّع الذي يكون من خطّ ألف باء كان بذلك المربّع الذي يكون من خطّ ألف دال فإنّ هذا الخطّ أيضًا يحصل لنا في الطول بهذه الأجزاء تسعةً وثلاثين جزءًا وإحدى وخمسين دقيقةً وعلى ذلك المثال لأنّ نسبة خطّ ألف باء إلى خطّ ألف دال كنسبة خطّ دال باء إلى خطّ دال زاي فإنّ خطّ دال زاي أيضًا يكون بهذه الأجزاء تسعةً وعشرين جزءًا وسبع عشرة دقيقةً لكنّ نسبة خطّ دال زاي إلى خطّ دال حاء قد وضعت كنسبة مائة وعشرين جزءًا إلى سبعة أجزاء وعشرين دقيقةً فالأجزاء إذن التي بها أمّا خطّ زاي دال فسبعة وعشرون جزءًا وسبع عشرة دقيقةً وأمّا خطّ ألف دال على هذا المثال فتسعة وثلاثون جزءًا وإحدى وخمسون دقيقةً يصير بها خطّ دال حاء أيضًا جزءًا واحدًا وسبعًا وأربعين دقيقةً فلذلك تكون الأجزاء أيضًا التي بها موتر ألف دال مائة وعشرون جزءًا فإنّ خطّ دال حاء بها خمسة أجزاء واثنتان وعشرون دقيقةً وزاوية دال ألف حاء وهي زاوية الزوال الأعظم في العرض أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فخمسة أجزاء وثمان دقائق وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزءان وأربع وثلاثون دقيقةً فإذ كان إذن قد وضع الزوال في العرض على النسبة الوسطى جزأين ونصف فإنّ ما يكون منه في البعد الأبعد وجد أقلّ من ذلك بما لا يوقع اختلافًا عند الحسّ وكذلك ما يكون في البعد الأقرب وجد أكثر منه بما لا يحسّ وذلك أنّ الزوال في البعد الأعظم إنّما ينقص ثلاث دقائق فقط والزوال في البعد الأصغر إنّما زاد أربع دقائق وليس هذا المقدار ممّا يمكن أن يلحق ولا يوقف عليه أصلًا بالرصد يو: ثمّ ليوضع |13| أيضًا البعد الأعظم لكوكب عطارد أعني نسبة خطّ ألف باء إلى خطّ باء دال نسبة تسعة وعشرين جزءًا إلى اثنين وعشرين جزءًا وثلاثين دقيقةً حتّى يحصل من قبل تلك الأشياء بأعيانها التي وصفناها قبيل أمّا خطّ ألف دال بهذه الأجزاء فخمسة وستّون جزءًا وأربع عشرة دقيقةً وأمّا خطّ دال زاي على هذا المثال فأحد وعشرون جزءًا وستّ عشرة دقيقةً لكن هاهنا أيضًا لنا زاوية دال زاي حاء وهي زاوية الانحراف موضوعة أربعة عشر جزءًا بالأجزاء التي بها موتر دال زاي مائة وعشرون جزءًا فالأجزاء إذن التي بها أمّا خطّ زاي دال فأحد وعشرون جزءًا وستّ عشرة دقيقةً وأمّا خطّ ألف دال على هذا المثال فخمسة وستّون جزءًا وأربع عشرة دقيقةً يكون بها خطّ دال حاء أيضًا جزأين وستًّا وثلاثين دقيقةً فلذلك تكون الأجزاء أيضًا التي بها موتر ألف دال مائة وعشرون جزءًا 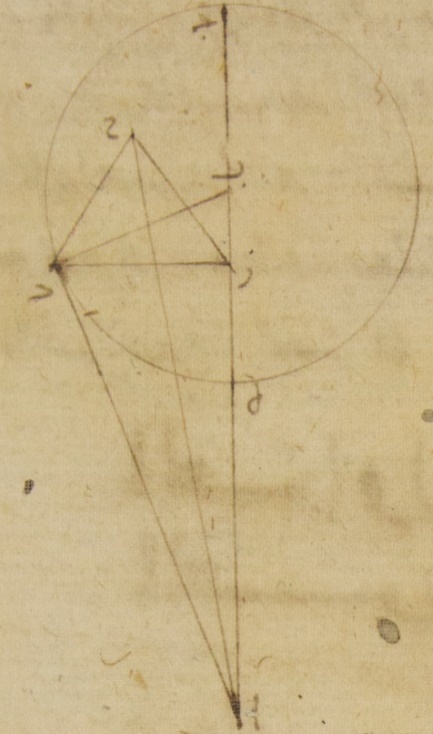 فإنّ خطّ دال حاء بها أربعة أجزاء وسبع وأربعون دقيقةً وزاوية دال ألف حاء وهي زاوية الزوال الأعظم في العرض أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فأربعة أجزاء وأربع وثلاثون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزءان وسبع عشرة دقيقةً وأمّا في البعد الأصغر فإنّ نسبة خطّ ألف باء إلى خطّ باء دال وضعت نسبة سبعة وخمسين جزءًا إلى اثنين وعشرين جزءًا وثلاثين دقيقةً ومن قبل تلك الأشياء بأعيانها أيضًا يكون خطّ ألف دال بهذه الأجزاء اثنين وخمسين جزءًا واثنتين وعشرين دقيقةً ويكون خطّ دال زاي على هذا المثال عشرين جزءًا وأربعين دقيقةً ولأنّ زاي دال من قبل هذه الانحراف بعينه وضعت نسبته إلى خطّ دال حاء نسبة مائة وعشرين جزءًا إلى أربعة عشر جزءًا وأربعين دقيقةً فالأجزاء إذن التي بها خطّ زاي دال عشرون جزءًا وأربعون دقيقةً وخطّ ألف دال على هذا المثال اثنان وخمسون جزءًا واثنتان وعشرون دقيقةً يكون بها خطّ دال حاء جزأين واثنتين وثلاثين دقيقةً فلذلك تكون الأجزاء التي بها أيضًا موتر ألف دال مائة وعشرون جزءًا فإنّ خطّ دال حاء بها خمسة أجزاء وثمان وأربعون دقيقةً وزاوية دال ألف حاء أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فخمسة أجزاء واثنتان وثلاثون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزءان وستّ وأربعون دقيقةً فقد خالف إذن الزوال الأعظم في العرض بحسب المقدار الوسط وقد فرض هاهنا أيضًا جزأين ونصف جزء أمّا الزوال في البعد الأبعد فثلاث عشرة دقيقةً إلى النقصان وأمّا الزوال في البعد الأقرب فبستّ عشرة دقيقةً إلى الزيادة فنحن نستعمل مكان ذلك في تصحيح الحساب من قبل النسبة الوسطى ربع جزء واحد على حسب ما وجدت بالرصد إذ كان لا يقع من قبل ذلك فضل محسوس⊙ ولمّا بيّنت هذه الأشياء وتبيّن أيضًا أنّ نسبة عدد الزيادات أو النقصانات العظمى إلى المسيرات العظمى في العرض كنسبة عدد الزيادات أو النقصانات الجزئية في الطول في سائر أقسام فلك التدوير إلى المسيرات الجزئية في العرض سهل علينا من قبل ذلك إثبات ما أثبتناه في الصفّين الرابعين اللذين وضعناهما في جدولي كوكب الزهرة وكوكب عطارد من المسيرات في العرض المأخوذة من قبل الانحراف إلّا أنّ هذه المسيرات التي أثبتناها أيضًا ه: إنّما هي المسيرات التي تكون من قبل انحراف فلكي تدويرهما وحده المجتمعة كما قلنا من الحصّة الوسطى⊙ فأمّا الفضل الذي يكون من قبل ميل فلكيهما الخارجي المركز وأيضًا من قبل البعد الأبعد والبعد الأقرب لكوكب عطارد فإنّا نصحّحه بسهولة المأخذ في ذلك بالحساب الذي نحن واصفوه بعد هذا وهو أنّه لمّا كان قد تبيّن أنّ في هذه النسب الوسطى الموصوفة أمّا المسير الأعظم في العرض للكوكبين جميعًا الذي يكون عن الميل عن جنبي فلك البروج فجزءان وثلاثون دقيقةً وأمّا أعظم الزيادة أو النقصان في الطول أمّا في كوكب الزهرة فستّة وأربعون جزءًا وأمّا في كوكب عطارد فاثنان وعشرون جزءًا بالتقريب وكان لنا موضوعًا في جدولي اختلافهما حصص الزيادة أو النقصان التي تصيب الأقسام الجزئيّة من فلكي تدويرهما فإنّا ننظر كم جزء هذه الحصص من جمل الزيادة أو النقصان فنأخذ ميل الجزء في كلّ واحد من الكوكبين من الجزأين والثلاثين الدقيقة فما كان أثبتناه في الصفّين الرابعين من جدولي العرض بإزاء تلك الأعداد بأعيانها⊙ وأمّا الصفوف الخوامس فإنّا جعلناها لتعدّل أيضًا ما يكون من الزوال في العرض في سائر المسيرات في الأفلاك الخارجة المراكز بالدقائق المثبتة فيها بإزاء شيء شيء منها وذلك أنّه لمّا كان كما قلنا ما يفعله ميول أفلاك التداوير وانحرافاتها من عودة الزيادة والنقصان بمكان تلك التداوير الصغار بالقرب منها يكون على قياس العودة إلى الفلك الخارج المركز وكانت مقادير هذه الميول والانحرافات كلّها ليس بينها وبين الميل في فلك القمر المائل تفاوت وكانت الزوالات الجزئيّة التي هذا مبلغ ميلها مرتّبةً من أن تكون على نسب تلك أيضًا فكانت تلك الزوالات في القمر مدوّنةً لنا بطريق الخطوط فإنّا أخذنا كلّ واحد من تلك الأعداد المثبتة هناك فضاعفناه اثني عشرة مرّةً لأنّ الحصّة العظمى هناك هي نحو من خمسة أجزاء وهاهنا جعلناه ستّين جزءًا فما يخرج لنا أثبتناه بإزاء العدد الذي هو له في كلّ واحد من الصفوف الخمسة⊙ وهكذا عمل الجداول⊙
فإنّ خطّ دال حاء بها أربعة أجزاء وسبع وأربعون دقيقةً وزاوية دال ألف حاء وهي زاوية الزوال الأعظم في العرض أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فأربعة أجزاء وأربع وثلاثون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزءان وسبع عشرة دقيقةً وأمّا في البعد الأصغر فإنّ نسبة خطّ ألف باء إلى خطّ باء دال وضعت نسبة سبعة وخمسين جزءًا إلى اثنين وعشرين جزءًا وثلاثين دقيقةً ومن قبل تلك الأشياء بأعيانها أيضًا يكون خطّ ألف دال بهذه الأجزاء اثنين وخمسين جزءًا واثنتين وعشرين دقيقةً ويكون خطّ دال زاي على هذا المثال عشرين جزءًا وأربعين دقيقةً ولأنّ زاي دال من قبل هذه الانحراف بعينه وضعت نسبته إلى خطّ دال حاء نسبة مائة وعشرين جزءًا إلى أربعة عشر جزءًا وأربعين دقيقةً فالأجزاء إذن التي بها خطّ زاي دال عشرون جزءًا وأربعون دقيقةً وخطّ ألف دال على هذا المثال اثنان وخمسون جزءًا واثنتان وعشرون دقيقةً يكون بها خطّ دال حاء جزأين واثنتين وثلاثين دقيقةً فلذلك تكون الأجزاء التي بها أيضًا موتر ألف دال مائة وعشرون جزءًا فإنّ خطّ دال حاء بها خمسة أجزاء وثمان وأربعون دقيقةً وزاوية دال ألف حاء أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فخمسة أجزاء واثنتان وثلاثون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فجزءان وستّ وأربعون دقيقةً فقد خالف إذن الزوال الأعظم في العرض بحسب المقدار الوسط وقد فرض هاهنا أيضًا جزأين ونصف جزء أمّا الزوال في البعد الأبعد فثلاث عشرة دقيقةً إلى النقصان وأمّا الزوال في البعد الأقرب فبستّ عشرة دقيقةً إلى الزيادة فنحن نستعمل مكان ذلك في تصحيح الحساب من قبل النسبة الوسطى ربع جزء واحد على حسب ما وجدت بالرصد إذ كان لا يقع من قبل ذلك فضل محسوس⊙ ولمّا بيّنت هذه الأشياء وتبيّن أيضًا أنّ نسبة عدد الزيادات أو النقصانات العظمى إلى المسيرات العظمى في العرض كنسبة عدد الزيادات أو النقصانات الجزئية في الطول في سائر أقسام فلك التدوير إلى المسيرات الجزئية في العرض سهل علينا من قبل ذلك إثبات ما أثبتناه في الصفّين الرابعين اللذين وضعناهما في جدولي كوكب الزهرة وكوكب عطارد من المسيرات في العرض المأخوذة من قبل الانحراف إلّا أنّ هذه المسيرات التي أثبتناها أيضًا ه: إنّما هي المسيرات التي تكون من قبل انحراف فلكي تدويرهما وحده المجتمعة كما قلنا من الحصّة الوسطى⊙ فأمّا الفضل الذي يكون من قبل ميل فلكيهما الخارجي المركز وأيضًا من قبل البعد الأبعد والبعد الأقرب لكوكب عطارد فإنّا نصحّحه بسهولة المأخذ في ذلك بالحساب الذي نحن واصفوه بعد هذا وهو أنّه لمّا كان قد تبيّن أنّ في هذه النسب الوسطى الموصوفة أمّا المسير الأعظم في العرض للكوكبين جميعًا الذي يكون عن الميل عن جنبي فلك البروج فجزءان وثلاثون دقيقةً وأمّا أعظم الزيادة أو النقصان في الطول أمّا في كوكب الزهرة فستّة وأربعون جزءًا وأمّا في كوكب عطارد فاثنان وعشرون جزءًا بالتقريب وكان لنا موضوعًا في جدولي اختلافهما حصص الزيادة أو النقصان التي تصيب الأقسام الجزئيّة من فلكي تدويرهما فإنّا ننظر كم جزء هذه الحصص من جمل الزيادة أو النقصان فنأخذ ميل الجزء في كلّ واحد من الكوكبين من الجزأين والثلاثين الدقيقة فما كان أثبتناه في الصفّين الرابعين من جدولي العرض بإزاء تلك الأعداد بأعيانها⊙ وأمّا الصفوف الخوامس فإنّا جعلناها لتعدّل أيضًا ما يكون من الزوال في العرض في سائر المسيرات في الأفلاك الخارجة المراكز بالدقائق المثبتة فيها بإزاء شيء شيء منها وذلك أنّه لمّا كان كما قلنا ما يفعله ميول أفلاك التداوير وانحرافاتها من عودة الزيادة والنقصان بمكان تلك التداوير الصغار بالقرب منها يكون على قياس العودة إلى الفلك الخارج المركز وكانت مقادير هذه الميول والانحرافات كلّها ليس بينها وبين الميل في فلك القمر المائل تفاوت وكانت الزوالات الجزئيّة التي هذا مبلغ ميلها مرتّبةً من أن تكون على نسب تلك أيضًا فكانت تلك الزوالات في القمر مدوّنةً لنا بطريق الخطوط فإنّا أخذنا كلّ واحد من تلك الأعداد المثبتة هناك فضاعفناه اثني عشرة مرّةً لأنّ الحصّة العظمى هناك هي نحو من خمسة أجزاء وهاهنا جعلناه ستّين جزءًا فما يخرج لنا أثبتناه بإزاء العدد الذي هو له في كلّ واحد من الصفوف الخمسة⊙ وهكذا عمل الجداول⊙
〈XIII.5〉 ه: الجداول المرسومة للمسيرات الجزئيّة في العرض⊙
جدول لعلم العرض |
|||||||||||||
الأعداد المشتركة |
ميول زحل |
ميول المشتري |
|||||||||||
البعد الأبعد وهو في الشمال |
البعد الأقرب وهو في الجنوب |
الدقائق |
البعد الأبعد وهو في الشمال |
البعد الأقرب وهو في الجنوب |
الدقائق |
||||||||
أجزاء |
أجزاء |
أجزاء |
دقائق |
أجزاء |
دقائق |
دقائق |
ثواني |
أجزاء |
دقائق |
أجزاء |
دقائق |
دقائق |
ثواني |
و |
شند |
ب |
د |
ب |
ب |
نط |
لو |
ا |
ز |
ا |
نط |
لو |
|
يب |
شمح |
ب |
ه |
ب |
ج |
نح |
لو |
ا |
ح |
ا |
نح |
لو |
|
يح |
شمب |
ب |
و |
ب |
ج |
نز |
|
ا |
ح |
ا |
و |
نز |
|
كد |
شلو |
ب |
ز |
ب |
د |
ند |
لو |
ا |
ط |
ا |
ز |
ند |
لو |
ل |
شل |
ب |
ح |
ب |
ه |
نب |
|
ا |
ي |
ا |
ح |
نب |
|
لو |
شكد |
ب |
ب |
ز |
مح |
كد |
ا |
يا |
ا |
ط |
مح |
كد |
|
مب |
شيح |
ب |
يا |
ب |
ح |
مد |
كد |
ا |
يب |
ا |
ي |
مد |
كد |
مح |
شيب |
ب |
ب |
ي |
م |
|
ا |
يج |
ا |
يا |
م |
|
|
ند |
شو |
ب |
يد |
ب |
يب |
له |
يب |
ا |
يد |
ا |
يج |
له |
يب |
س |
ش |
ب |
يو |
ب |
يه |
ل |
|
ا |
يو |
ا |
يو |
ل |
|
سو |
رصد |
ب |
يح |
ب |
يح |
كد |
كد |
ا |
يح |
ا |
يح |
كد |
كد |
عب |
رفح |
ب |
كا |
ب |
كا |
كد |
ا |
كا |
ا |
كا |
يح |
كد |
|
عح |
رفب |
ب |
كد |
ب |
كد |
يب |
كد |
ا |
كد |
ا |
كد |
يب |
كد |
فد |
رعو |
ب |
كز |
ب |
كز |
و |
كد |
ا |
كز |
ا |
كز |
و |
كد |
ص |
رع |
ب |
ل |
ب |
ل |
|
|
ا |
ل |
ا |
ل |
|
|
صج |
ب |
لا |
ب |
لا |
ج |
يب |
ا |
لا |
ا |
لا |
ج |
يب |
|
صو |
رسد |
ب |
لج |
ب |
لج |
و |
كد |
ا |
لج |
ا |
لج |
و |
كد |
صط |
رسا |
ب |
لد |
ب |
لد |
ط |
كد |
ا |
لد |
ا |
لد |
ط |
كد |
قب |
رنح |
ب |
لو |
ب |
لو |
يب |
كد |
ا |
لو |
ا |
لو |
يب |
كد |
قه |
رنه |
ب |
لز |
ب |
لز |
يه |
كد |
ا |
لز |
ا |
لز |
يه |
كد |
قح |
رنب |
ب |
لط |
ب |
لط |
يح |
كد |
ا |
لط |
ا |
لط |
يح |
كد |
قيا |
رمط |
ب |
م |
ب |
م |
كا |
كد |
ا |
م |
ا |
م |
كا |
كد |
قيد |
رمو |
ب |
مب |
ب |
مب |
كد |
كد |
ا |
مب |
ا |
مب |
كد |
كد |
قيز |
رمج |
ب |
مج |
ب |
مج |
كز |
يب |
ا |
مج |
ا |
مج |
كز |
يب |
قك |
رم |
ب |
مه |
ب |
مه |
ل |
|
ا |
مه |
ا |
مه |
ل |
|
قكج |
رلز |
ب |
مو |
ب |
مو |
لب |
لو |
ا |
مو |
ا |
مو |
لب |
لو |
قكو |
رلد |
ب |
مز |
ب |
له |
يب |
ا |
مز |
ا |
مح |
له |
يب |
|
قكط |
رلا |
ب |
مط |
ب |
مط |
لز |
لو |
ا |
مط |
ا |
مط |
لز |
لو |
قلب |
ركح |
ب |
ن |
ب |
نا |
م |
|
ا |
ن |
ا |
نا |
م |
|
قله |
ركه |
ب |
نب |
ب |
نج |
مب |
يب |
ا |
نا |
ا |
نج |
مب |
يب |
قلح |
ركب |
ب |
نج |
ب |
ند |
مد |
كد |
ا |
نب |
ا |
ند |
مد |
كد |
قما |
ريط |
ب |
ند |
ب |
نه |
مو |
لو |
ا |
نج |
ا |
نه |
مو |
لو |
قمد |
ريو |
ب |
نه |
ب |
نو |
مح |
كد |
ا |
نه |
ا |
مح |
كد |
|
قمز |
ريج |
ب |
نو |
ب |
نز |
ن |
يب |
ا |
نو |
ا |
نط |
ن |
يب |
قن |
ري |
ب |
نز |
ب |
نح |
نب |
|
ا |
نح |
ب |
|
نب |
|
قنج |
رز |
ب |
نح |
ب |
نط |
نج |
يب |
ا |
نط |
ب |
ا |
نج |
يب |
قنو |
رد |
ب |
نط |
ج |
|
ند |
لو |
ب |
|
ب |
ج |
ند |
لو |
قنط |
را |
ب |
نط |
ج |
ا |
نو |
|
ب |
ا |
ب |
د |
نو |
|
قسب |
قصح |
ج |
|
ج |
ب |
نز |
|
ب |
ب |
ب |
ه |
نز |
|
قسه |
قصه |
ج |
|
ج |
ب |
نز |
مح |
ب |
ب |
ب |
و |
نز |
مح |
قسح |
قصب |
ج |
ا |
ج |
ج |
نح |
لو |
ب |
ج |
ب |
و |
نح |
لو |
قعا |
قفط |
ج |
ج |
ج |
نط |
يب |
ب |
ج |
ب |
ز |
نط |
يب |
|
قعد |
قفو |
ج |
ب |
ج |
د |
نط |
لو |
ب |
د |
ب |
ز |
نط |
لو |
قعز |
قفج |
ج |
ب |
ج |
د |
نط |
مح |
ب |
د |
ب |
ح |
نط |
مح |
قف |
قف |
ج |
ب |
ج |
ه |
س |
|
ب |
د |
ب |
ح |
س |
|
جدول لعلم العرض |
|||||||||||||
الأعداد المشتركة |
ميول المرّيخ |
ميول الزهرة |
|||||||||||
البعد الأبعد وهو في الشمال |
البعد الأقرب وهو في الجنوب |
الدقائق |
الميول |
الانحرافات |
الدقائق |
||||||||
أجزاء |
أجزاء |
أجزاء |
دقائق |
أجزاء |
دقائق |
دقائق |
ثواني |
أجزاء |
دقائق |
أجزاء |
دقائق |
دقائق |
ثواني |
و |
شند |
|
ح |
|
نط |
لو |
ا |
ب |
|
ح |
نط |
لو |
|
يب |
شمح |
|
ط |
|
د |
نح |
لو |
ا |
ا |
|
يو |
نح |
لو |
يح |
شمب |
|
يا |
|
ه |
نز |
|
ا |
|
|
كه |
نز |
|
كد |
شلو |
|
يج |
|
و |
ند |
لو |
|
نط |
|
لج |
ند |
لو |
ل |
شل |
|
يد |
|
ز |
نب |
|
|
نز |
|
ما |
نب |
|
لو |
شكد |
|
|
ط |
مح |
كد |
|
نه |
|
مط |
مح |
كد |
|
مب |
شيح |
|
يح |
|
يب |
مد |
كد |
|
نا |
|
نز |
مد |
كد |
مح |
شيب |
|
كا |
|
م |
|
|
مو |
ا |
ه |
م |
|
|
ند |
شو |
|
كد |
|
يح |
له |
يب |
|
ا |
يج |
له |
يب |
|
س |
ش |
|
كح |
|
كب |
ل |
|
|
ا |
ك |
ل |
|
|
سو |
رصد |
|
لب |
|
كو |
كد |
كد |
|
كط |
ا |
كح |
كد |
كد |
عب |
رفح |
|
لو |
|
ل |
يح |
كد |
|
كج |
ا |
له |
يح |
كد |
عح |
رفب |
|
ما |
|
لو |
يب |
كد |
|
يو |
ا |
مب |
يب |
كد |
فد |
رعو |
|
مو |
|
و |
كد |
|
ح |
ا |
ن |
و |
كد |
|
ص |
رع |
|
نب |
|
مط |
|
|
|
|
ا |
نز |
|
|
صج |
رسز |
|
نه |
|
نب |
ج |
يب |
|
ه |
ب |
|
ج |
يب |
صو |
رسد |
|
نط |
|
نو |
و |
كد |
|
ي |
ب |
ج |
و |
كد |
صط |
رسا |
ا |
ج |
ا |
|
ط |
كد |
|
يه |
ب |
و |
ط |
كد |
قب |
رنح |
ا |
و |
ا |
يب |
كد |
|
ك |
ب |
ط |
يب |
كد |
|
قه |
رنه |
ا |
ي |
ا |
ح |
يه |
كد |
|
ب |
يب |
يه |
كد |
|
قح |
رنب |
ا |
يد |
ا |
يج |
يح |
كد |
|
لب |
ب |
يه |
يح |
كد |
قيا |
رمط |
ا |
يح |
ا |
يح |
كا |
كد |
|
لح |
ب |
يز |
كا |
كد |
قيد |
رمو |
ا |
كج |
ا |
كد |
كد |
كد |
|
ب |
ك |
كد |
كد |
|
قيز |
رمج |
ا |
كح |
ا |
ل |
كز |
يب |
|
ن |
ب |
كب |
كز |
يب |
قك |
رم |
ا |
لد |
ا |
لز |
ل |
|
|
نط |
ب |
كد |
ل |
|
قكج |
رلز |
ا |
ما |
ا |
مد |
لب |
لو |
ا |
ح |
ب |
كو |
لب |
لو |
قكو |
رلد |
ا |
مح |
ا |
نا |
له |
يب |
ا |
يح |
ب |
كز |
له |
يب |
قكط |
رلا |
ا |
ند |
ب |
|
لز |
لو |
ا |
كح |
ب |
كط |
لز |
لو |
قلب |
ركح |
ا |
ب |
ي |
م |
|
ا |
لح |
ب |
ل |
م |
|
|
قله |
ركه |
ب |
ك |
مب |
يب |
ا |
مح |
ب |
ل |
مب |
يب |
||
قلح |
ركب |
يو |
ب |
لب |
مد |
كد |
ا |
نط |
ب |
ل |
مد |
كد |
|
قما |
ريط |
كه |
ب |
مو |
لو |
ب |
يا |
ب |
كط |
مو |
لو |
||
قمد |
ريو |
لد |
ب |
نو |
مح |
كد |
ب |
كج |
ب |
كح |
مح |
كد |
|
قمز |
ريج |
مد |
ج |
ن |
يب |
ب |
مج |
ب |
كو |
ن |
يب |
||
قن |
ري |
ند |
ج |
كط |
نب |
|
ج |
ج |
ب |
كب |
نب |
|
|
قنج |
رز |
ه |
ج |
مو |
نج |
يب |
ج |
كج |
ب |
يح |
نج |
يب |
|
قنو |
رد |
يو |
د |
ط |
ند |
لو |
ج |
مد |
ب |
يب |
ند |
لو |
|
قنط |
را |
كز |
د |
لب |
نو |
|
د |
ه |
ب |
د |
نو |
|
|
قسب |
قصح |
لح |
د |
نه |
نز |
|
د |
كو |
ا |
نه |
نز |
|
|
قسه |
قصه |
مط |
ه |
كد |
نز |
مح |
د |
مط |
ا |
مب |
نز |
مح |
|
قسح |
قصب |
|
ه |
نج |
نح |
لو |
ه |
يج |
ا |
كز |
نح |
لو |
|
قعا |
قفط |
ي |
و |
كا |
نط |
يب |
ه |
لو |
ا |
ط |
نط |
يب |
|
قعد |
قفو |
د |
يد |
و |
لو |
نط |
لو |
ه |
نب |
|
مح |
نط |
لو |
قعز |
قفج |
د |
يح |
و |
نا |
نط |
مح |
و |
|
كه |
نط |
مح |
|
قف |
قف |
د |
كا |
س |
|
و |
كب |
|
|
س |
|
||
جدول لعلم العرض |
|||||||
الأعداد المشتركة |
ميول عطارد |
||||||
الميول |
الانحرافات |
الدقائق |
|||||
أجزاء |
أجزاء |
أجزاء |
دقائق |
أجزاء |
دقائق |
دقائق |
ثواني |
و |
شند |
ا |
|
يا |
نط |
لو |
|
يب |
شمح |
ا |
مد |
|
كب |
نح |
لو |
يح |
شمب |
ا |
مج |
|
لج |
نز |
|
كد |
شلو |
ا |
م |
|
ند |
لو |
|
ل |
شل |
ا |
لو |
|
نه |
نب |
|
لو |
شكد |
ا |
ل |
ا |
و |
مح |
كد |
مب |
شيح |
ا |
كج |
ا |
يو |
مد |
كد |
مح |
شيب |
ا |
ا |
كو |
م |
|
|
ند |
شو |
ا |
ح |
ا |
له |
له |
يب |
س |
ش |
|
نط |
ا |
مد |
ل |
|
سو |
رصد |
|
مط |
ا |
نب |
كد |
كد |
عب |
رفح |
|
لح |
ب |
|
يح |
كد |
عح |
رفب |
|
كو |
ب |
ز |
يب |
كد |
فد |
رعو |
|
يو |
ب |
يد |
و |
كد |
ص |
رع |
|
|
ب |
ك |
|
|
صج |
رسز |
|
ح |
ب |
كج |
ج |
يب |
صو |
رسد |
|
يه |
ب |
كه |
و |
كد |
صط |
رسا |
|
كج |
ب |
كز |
ط |
كد |
قب |
رنح |
|
لا |
ب |
كح |
يب |
كد |
قه |
رنه |
|
م |
ب |
كط |
يه |
كد |
قح |
رنب |
|
مح |
ب |
كط |
يح |
كد |
قيا |
رمط |
|
نز |
ب |
ل |
كا |
كد |
قيد |
رمو |
ا |
و |
ب |
ل |
كد |
كد |
قيز |
رمج |
ا |
يو |
ب |
ل |
كز |
يب |
قك |
رم |
ا |
كه |
ب |
كط |
ل |
|
قكج |
رلز |
ا |
له |
ب |
كح |
لب |
لو |
قكو |
رلد |
ا |
مه |
ب |
كو |
له |
يب |
قكط |
رلا |
ا |
نه |
ب |
كج |
لز |
لو |
قلب |
ركح |
ب |
و |
ب |
ك |
م |
|
قله |
ركه |
ب |
يو |
ب |
يو |
مب |
يب |
قلح |
ركب |
ب |
كز |
ب |
يا |
مد |
كد |
قما |
ريط |
ب |
لز |
ب |
و |
مو |
لو |
قمد |
ريو |
ب |
مز |
ب |
|
مح |
كد |
قمز |
ريج |
ب |
نز |
ا |
نج |
ن |
يب |
قن |
ري |
ج |
ز |
ا |
مو |
نب |
|
قنج |
رز |
ج |
يز |
ا |
لح |
نج |
يب |
قنو |
رد |
ج |
كو |
ا |
كط |
ند |
لو |
قنط |
را |
ج |
لد |
ا |
ك |
نو |
|
قسب |
قصح |
ج |
مب |
ا |
ي |
نز |
|
قسه |
قصه |
ج |
|
نط |
نز |
مح |
|
قسح |
قصب |
ج |
ند |
|
مح |
نح |
لو |
قعا |
قفط |
ج |
نح |
|
لو |
نط |
يب |
قعد |
قفو |
د |
ب |
|
كد |
نط |
لو |
قعز |
قفج |
د |
د |
|
يب |
نط |
مح |
قف |
قف |
د |
ه |
|
|
س |
|
〈XIII.6〉 و: في حساب حركة هذه الكواكب في العرض
وإذ كانت هذه الأشياء على ما وصفنا فإنّ الطريق الذي سلكه في حساب حركة هذه الخمسة الكواكب في العرض هو على ما أنا واصفه أمّا في الكواكب الثلاثة أعني زحل والمشتري والمرّيخ فإنّا ندخل الطول المعدّل إلى أعداد جدول الكوكب الذي له خاصّةً أمّا لكوكب المرّيخ فذلك العدد المعدّل نفسه وأمّا لكوكب المشتري فبعدان ينقص منه عشرين جزءًا وأمّا لكوكب زحل فبعدان يزيد عليه خمسين جزءًا ثمّ ننظر ما بإزائه من الدقائق في الصفّ الخامس من العرض فنثبته وعلى هذا المثال ندخل العدد المعدّل لاختلاف إلى تلك الأعداد بأعيانها فما كان بإزائه من فضل في العرض إن كان الطول المعدّل في السطور الخمسة العشر الأولى فما كان من ذلك في الصفّ الثالث وإن كان في السطور التي بعدها فما كان من ذلك في الصفّ الرابع ضاعفناه بالدقائق التي أثبتناها فما خرج لنا فهو مبلغ بعد لكوكب من فلك البروج إن كان ما أخذ من فضل العرض إنّما أخذ من الصفّ الثالث ففي الشمال وإن كان إنّما أخذ من الصفّ الرابع ففي الجنوب⊙ وأمّا في الزهرة وعطارد فإنّا ندخل أوّلًا عدد الاختلاف المعدّل إلى الأعداد التي في الجدول الحاصر بالكوكب منها ثمّ ننظر ما بإزائه في الصفّ الثالث وفي الصفّ الرابع من العرض فنثبت ما كان منه في الصفّ الثالث وفي الصفّ الرابع كلّ واحد على حياله وعلى وجهه ما خلا ما في الصفّ الرابع لكوكب عطارد فإنّا ننظر فإن كان الطول المعدّل في السطور الخمسة العشر الأولى أنقصنا منه عشرة ثمّ أثبتناه وإن كان في السطور التي دونها زدنا عليه ذلك الجزء بعينه ثمّ أثبتناه ثمّ إنّا بعد ذلك نزيد على الطول المعدّل أبدًا أمّا في كوكب الزهرة فتسعين جزءًا وأمّا في كوكب عطارد فمائتين وسبعين جزءًا ثمّ نسقط دوره إن كان لنا ذلك فما حصل أدخلناه إلى تلك الأعداد بأعيانها فما كان بإزاء ذلك العدد من الدقائق في الصفّ ه: يعني أنّا نأخذ عددًا تكون نسبته إلى ما أخذ من الصفّ الثالث كنسبة الدقائق التي تؤخذ في الصفّ الخامس في العدد الذي أدخل الجدول الخامس أخذنا من الأجزاء المثبتة في الصفّ الثالث بمقدار ذلك فما كان أثبتناه للعرض أمّا إن كان الطول مع الزيادة الموصوفة في السطور الخمسة العشر الأولى إن كان عدد الاختلاف المعدّل في السطور الخمسة العشر الأولى ففي الجنوب وإن كان في السطور التي بعدها ففي الشمال وأمّا إن وقع عدد الطول الذي ذكرناه فيما بعد الخمسة العشر السطر من السطور إن كان عدد الاختلاف الذي ذكرناه في السطور الخمسة العشر السطر الأولى ففي الشمال وإن وقع فيما بعدها من السطور ففي الجنوب ثمّ من بعد ذلك أيضًا نعمد إلى الطول المعدّل أمّا في الزهرة فإيّاه نفسه على الإطلاق وأمّا في عطارد فبعدان نزيد عليه مائةً وثمانين جزءًا فندخله إلى تلك الأعداد بأعيانها فما كان بإزاء هذا العدد أيضًا من الدقائق في الصفّ الخامس أخذنا ممّا أثبت من الصفّ الرابع بذلك المقدار فما حصل أثبتناه للعرض أمّا إن كان كما قلنا الطول الذي أدخل وقع في السطور الخمسة العشر الأولى إن كان العدد المعدّل للاختلاف فيما دون مائة وثمانين جزءًا ففي الشمال وإن كان أكثر من مائة وثمانين جزءًا ففي الجنوب وأمّا إن كان عدد الطول الذي ذكرناه وقع في السطور التي بعد الخمسة العشر السطر إن كان عدد الاختلاف فيما دون مائة وثمانين ففي الجنوب وإن كان أكثر من مائة وثمانين ففي الشمال ثمّ بأخرة نعمد إلى هذه الدقائق أنفسها التي وجدت بإدخالنا الطول ثانيةً فنأخذ منها جزءًا بمقدار ما هي من جزء من الستّين الجزء فما فضل ه: يعني إذا حصل منها عدد وأخذ على حسب ما يوجبه كلّ واحد منها في الشمال أو الجنوب من حضيضه من الباقيتين أو زيادة فيهما أمّا في الزهرة فنأخذ أبدًا سدسه ونثبته في الشمال وأمّا في عطارد فنأخذ أبدًا نصفه وربعه فنثبته في الجنوب فنقف بهذا العمل إذا خلطنا هذه الأعداد الثلاثة التي أثبتناها على مسيرها الذي يرى في العرض بالقياس إلى فلك البروج
〈XIII.7〉 ز: في ظهورات الكواكب الخمسة المتحيّرة واختفاءاتها
وإذ قد قدّم العلم بأخذ زوال الكواكب الخمسة في العرض فقد بقي تتميم ما يحتاج إلى معرفته أيضًا من أمر ظهورات الكواكب واختفاءاتها التي تكون بحسب مواضعها من الشمس فإنّه قد وقع فيها كما بيّنّا أيضًا في علم أمر الكواكب الثابتة أنّ أبعادها من الشمس في فلك البروج تكون غير متساوية على أنحاء شتّى في ظهورها واختفاءاتها لأسباب كثيرة أوّلها لأنّ أعظامها غير متساوية والثاني لأنّ ميول فلك البروج على الآفاق غير متشابهة والثالث من قبل مسيراتها في العرض يز: فإنّا إن توهّمنا أيضًا قطعتين من دائرتين من أعظم الدوائر إحداهما من الأفق وهي قطعة ألف باء والأخرى من فلك البروج وهي قطعة جيم دال وأنزلنا نقطة هاء الفصل المشترك لهما الشرقيّ أو الغربي أيضًا ونقطتي جيم ألف مائلتين نحو الجنوب ونقطة دال مركز الشمس ورسمنا قطعة دال باء زاي من دائرة عظمى تمرّ بمركز الشمس وبقطب الأفق وأنزلنا الكوكب يطلع ويغرب على أفق ألف هاء باء أمّا إذا كان في فلك البروج فعلى نقطة هاء وذلك بيّن وأمّا إذا كان أميل إلى الجنوب فعلى نقطة طاء وأخرجنا إلى فلك البروج من نقطتي حاء طاء عمودي حاء كاف طاء لام حصلت لنا قوس باء دال أيضًا القوس التي متى كانت قوس بعد الشمس تحت الأرض متساويةً لها فذلك الوقت أبدًا هو أوّل وقت يرى فيه الكوكب أو يخفى وذلك أنّ ما تلقيه الشمس من الشعاع على كوكب بعينه من أبعاد متساوية من تحت الأرض إنّما يكون واحدًا بعينه بحسب الدائرة العظمى التي ترسم على هذه الصفة فهذه القوس أوّلًا إذ كان يلزم أن تكون غير متساوية في الكواكب التي ليست بمتساوية فقد يجب ضرورةً وإن كانت سائر الأمور كلّها على حال واحدة أن تكون أيضًا القسيّ من فلك البروج التي توتر الزاوية القائمة أعني الأبعاد النظيرة لبعد هاء دال مختلفةً وما كان منها للكوكب الأعظم كان أصغر وذلك بيّن وما كان منها للكواكب الأصغر كان أعظم وعلى هذا المثال أيضًا وإن كانت قوس باء دال واحدةً بعينها في الكوكب الواحد بعينه إلّا أنّ زاوية باء هاء دال وهي زاوية ميل فلك البروج تختلف إمّا من قبل اختلافات البروج وإمّا من قبل اختلافات المساكن فإنّ قوس بعد هاء دال أيضًا تختلف وتتزيّد عظمها كلّما تنقّصت الزاوية الموصوفة وتقلّ وتصغر كلّما زادت تلك الزاوية وكذلك أيضًا إن زيد على الأمر الأوّل أنّ الميل أيضًا واحد بعينه إلّا أنّ الكوكب لا يكون على فلك البروج نفسه بل إمّا على نقطة حاء التي هي أبعد في الشمال وإمّا على نقطة طاء التي هي أبعد في الجنوب فليس أوّل ظهوره أو اختفائه يكون إذا كان بعده من الشمس قوس دال هاء بل إنّما يكون أوّل ظهوره أو اختفائه أمّا إذا كان أميل إلى الشمال عن فلك البروج فإذا كان بعده قوس دال لام التي هي أصغر من تلك وأمّا إذا كان أميل إلى الجنوب فإذا كان بعده قوس دال هاء لام وهي أكثر من تلك فقد نحتاج إذن ضرورةً في معرفة جزئيّات هذا المعنى أن نفرض أوّلًا مقادير قسيّ باء دال الكليّة في كلّ واحد من الكواكب الخمسة المتحيّرة من قبل الظهورات التي رصدت رصدًا لا يقع معه شكّ وهذه الأرصاد إنّما تتّفق في الصيف وفي برج السرطان من قبل أنّ الهواء في هذا الوقت من أوقات السنة يكون ه: يكون رقيقًا صافيًا ومن قبل أنّ ميول فلك البروج على الآفاق تكون فيه متوسّطةً فقد يجب بالأرصاد الشرقيّة التي جرى أمرها على هذا السبيل من الفحص أنّ في مبدأ السرطان على الأمر الأكثر⊙ أمّا كوكب زحل فيطلع وبعده من موضع الشمس الحقيقي أربعة عشر جزءًا ؞ وأمّا كوكب المشتري فيطلع وبعده على ذلك المثال اثنا عشر جزءًا ونصف وربع جزء ؞ وأمّا كوكب المرّيخ فيطلع وبعده أربعة عشر جزءًا ونصف جزء ؞ وأمّا كوكب الزهرة فيطلع بالعشيّ وبعده خمسة أجزاء وثلثا جزء ؞ وأمّا كوكب عطارد  فيطلع بالعشيّ وبعده على هذا المثال أحد عشر جزءًا ونصف جزء يح: وإذ قد وطّنت هذه الأشياء على هذه الصفة فلنرسم شكل الصورة التي مثّلناها ولا ضير في القسيّ التي هذا مبلغ مقاديرها إن نحن جعلنا النسب طلبًا للتسهيل في العمل في أوتارها إذ كان لا فرق بينها وبين أوتارها في الحسّ⊙ ولتكن نقطة هاء من الفصل المشترك لفلك البروج وللأفق النقطة التي تطلع في هذه الظهورات التي قصدنا لها على مبدأ السرطان للكواكب الثلاثة بالغدوات أعني لزحل والمشتري والمرّيخ وتغرب الزهرة وعطارد بالعشيات وذلك بيّن ولننزل أنّ الإقليم هو الإقليم الذي يمرّ من الشام ببلاد قونيقي وأطول ما يكون النهار هناك أربع عشرة ساعة وربع ساعة استوائيّة وإنّما اخترنا هذا الإقليم لأنّ في هذه الدائرة الموازية خاصّةً وفيما يليها وقعت أكثر الأرصاد وأصحّها أمّا ما وقع فيها من الأرصاد فخليق أن تكون أرصاد الكلدانيّين وأمّا ما وقع فيما يليها فما وقع من الأرصاد في بلاد اللاتين وفي بلاد مصر فلأنّ في هذا الإقليم الذي وضعناه متى طلع مبدأ السرطان فإنّا نجد زاوية باء هاء دال من قبل ما تقدّم بيانه من علم الزوايا يكون مائة وثلاثة أجزاء بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا ونجد من قبل ذلك النسبة التي بين الخطّين المحيطين بزاوية زاوية قائمة نسبة أربعة وتسعين جزءًا إلى خمسة وسبعين جزءًا بالتقريب وبهذه الأجزاء تكون الخطوط الموترة مائة وعشرين جزءًا من جهة علم العرض متى كانت الثلاثة الكواكب دون غيرها تطلع في أوّل السرطان أعني متى كان مسيرها فيما بين البعد الأبعد من أفلاك تداويرها كم كان بعدها من البعد الأبعد بعد أن لا تجاوز برجًا واحدًا فإنّا نجد كوكب زحل وكوكب المشتري يكاد أن يكون على نفس فلك البروج من غير أن يلحق ذلك اختلاف عند الحسّ ونجد كوكب المرّيخ أميل إلى الشمال من فلك البروج بخمس جزء
فيطلع بالعشيّ وبعده على هذا المثال أحد عشر جزءًا ونصف جزء يح: وإذ قد وطّنت هذه الأشياء على هذه الصفة فلنرسم شكل الصورة التي مثّلناها ولا ضير في القسيّ التي هذا مبلغ مقاديرها إن نحن جعلنا النسب طلبًا للتسهيل في العمل في أوتارها إذ كان لا فرق بينها وبين أوتارها في الحسّ⊙ ولتكن نقطة هاء من الفصل المشترك لفلك البروج وللأفق النقطة التي تطلع في هذه الظهورات التي قصدنا لها على مبدأ السرطان للكواكب الثلاثة بالغدوات أعني لزحل والمشتري والمرّيخ وتغرب الزهرة وعطارد بالعشيات وذلك بيّن ولننزل أنّ الإقليم هو الإقليم الذي يمرّ من الشام ببلاد قونيقي وأطول ما يكون النهار هناك أربع عشرة ساعة وربع ساعة استوائيّة وإنّما اخترنا هذا الإقليم لأنّ في هذه الدائرة الموازية خاصّةً وفيما يليها وقعت أكثر الأرصاد وأصحّها أمّا ما وقع فيها من الأرصاد فخليق أن تكون أرصاد الكلدانيّين وأمّا ما وقع فيما يليها فما وقع من الأرصاد في بلاد اللاتين وفي بلاد مصر فلأنّ في هذا الإقليم الذي وضعناه متى طلع مبدأ السرطان فإنّا نجد زاوية باء هاء دال من قبل ما تقدّم بيانه من علم الزوايا يكون مائة وثلاثة أجزاء بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا ونجد من قبل ذلك النسبة التي بين الخطّين المحيطين بزاوية زاوية قائمة نسبة أربعة وتسعين جزءًا إلى خمسة وسبعين جزءًا بالتقريب وبهذه الأجزاء تكون الخطوط الموترة مائة وعشرين جزءًا من جهة علم العرض متى كانت الثلاثة الكواكب دون غيرها تطلع في أوّل السرطان أعني متى كان مسيرها فيما بين البعد الأبعد من أفلاك تداويرها كم كان بعدها من البعد الأبعد بعد أن لا تجاوز برجًا واحدًا فإنّا نجد كوكب زحل وكوكب المشتري يكاد أن يكون على نفس فلك البروج من غير أن يلحق ذلك اختلاف عند الحسّ ونجد كوكب المرّيخ أميل إلى الشمال من فلك البروج بخمس جزء  واحد أكثره فإنّ قوس دال هاء تكون القوس التي بها يبعد من الشمس في فلك البروج كوكب زحل وكوكب المشتري وتكون قوس دال كاف القوس التي بها يبعد كوكب المرّيخ من الشمس لأنّه أبعد في الشمال بقوس كاف حاء وهي اثنا عشرة دقيقةً ولأنّ نسبة قوس كاف حاء إلى قوس كاف هاء نسبة أربعة وتسعين جزءًا إلى خمسة وسبعين جزءًا فإنّ قوس كاف هاء تكون أيضًا بهذه الأجزاء عشر دقائق بالتقريب وقد كانت وضعت قوس دال لام في كوكب المرّيخ أربعة عشر جزءًا ونصف جزء فتكون قوس دال هاء كلّها تجتمع أربعة عشر جزءًا وأربعين دقيقةً وهي في كوكب زحل أربعة عشر جزءًا ؞ وفي كوكب المشتري أربعة عشر جزءًا ونصف وربع جزء ؞ فيجب لذلك من قبل أنّ نسبة قوس هاء دال أيضًا إلى قوس دال باء نسبة مائة وعشرين جزءًا إلى أربعة وتسعين جزءًا أن تكون قوس دال باء أيضًا من الدائرة العظمى التي ترسم مارّةً نقطتي الأفق⊙ يحصل لنا أمّا في كوكب زحل فأحد عشر جزءًا وأمّا في كوكب المشتري فعشرة أجزاء وأمّا في كوكب المرّيخ فأحد عشر جزءًا ونصف جزء بالتقريب ؞ وكذلك أيضًا في الزهرة وعطارد لمّا كان إذا عرف مبدأ السرطان أحدث مع الأفق ميل هذه الزاوية التي وضعناها ومثل هذا الميل وقد كنّا وضعنا أنّ كوكب الزهرة يطلع بالعشيّ في هذا الجزء من فلك البروج وبعده من موضع الشمس الحقيقيّ خمسة أجزاء وثلثا جزء وأنّ كوكب عطارد يطلع بالعشيّ وبعده أحد عشر جزءًا ونصف جزء فحاصل الشمس إذن في طلوعها أمّا على الحقيقة أمّا في كوكب الزهرة فتكون على أربعة عشر جزءًا وثلث جزء من التوأمين ؞ وأمّا في ككب عطارد فعلى ثمانية عشر جزءًا ونصف ؞ وأمّا على التوسّط أمّا في كوكب الزهرة فعلى خمسة وعشرين جزءًا وأمّا في كوكب عطارد فعلى تسعة عشر جزءًا بالتقريب فهذان إذن كانا حاصل الحركة الوسطى في الطول لهذين الكوكبين ومتى كان الطول بهذه الصفة قرباهما في مبدأ السرطان فإنّ كوكب الزهرة يوجد حينئذ بعده من البعد الأبعد من فلك تدويره نحوًا من أربعة عشر جزءًا وكوكب عطارد نحوًا من اثنين وثلاثين جزءًا ؞ يط: فإنّ ذلك يتبيّن بالمعاني التي قدّمنا وضعها في اختلافهما ويلزم من ذلك أن يكون في هذه المسيرات كوكب الزهرة يوجد أميل إلى الشمال عن فلك البروج بجزء واحد ؞ وأمّا كوكب عطارد فبجزء واحد وثلثي جزء بالتقريب لأنّ ذلك مبلغ قوس كاف حاء وذلك بيّن فلذلك من قبل أنّ نسبتها أيضًا إلى قوس هاء كاف نسبة أربعة وتسعين جزءًا إلى خمسة وسبعين جزءًا وهذه النسبة هي أيضًا نسبة جزء واحد إلى نصف وربع جزء ونسبة جزء واحد وثلثي جزء إلى جزء واحد وثلث جزء بالتقريب يحصل لنا قوس هاء كاف أيضًا أمّا في الزهرة فنصف وربع جزء ؞ وأمّا في عطارد فجزءًا واحدًا وثلث جزء وبهذه الأجزاء وضعت أيضًا قوس دال لام وهي القوس التي رأى كلّ واحد منهما أنها بعده من الشمس أمّا في الزهرة فخمسة أجزاء وثلثا جزء ؞ وأمّا في عطارد فأحد عشر جزءًا ونصف جزء فيحصل لنا إذن قوس دال كاف هاء بأسرها أمّا في الزهرة فستّة أجزاء وخمسا جزء ؞ وأمّا في عطارد فاثنا عشر جزءًا ونصف وثلث جزء بالتقريب فلذلك أيضًا من قبل أنّ نسبة قوس هاء دال إلى قوس باء دال نسبة مائة وعشرين جزءًا إلى أربعة وتسعين جزءًا وقد توافق هذه النسبة نسبة ستّة أجزا وخمسي جزء إلى خمسة أجزاء ونسبة اثني عشر جزءًا ونصف وثلث جزء إلى عشرة أجزاء بالتقريب يحصل لنا قوس دال باء أيضًا وهي مقدار البعد الكليّ أمّا في الزهرة فخمسة أجزاء وأمّا في عطارد
واحد أكثره فإنّ قوس دال هاء تكون القوس التي بها يبعد من الشمس في فلك البروج كوكب زحل وكوكب المشتري وتكون قوس دال كاف القوس التي بها يبعد كوكب المرّيخ من الشمس لأنّه أبعد في الشمال بقوس كاف حاء وهي اثنا عشرة دقيقةً ولأنّ نسبة قوس كاف حاء إلى قوس كاف هاء نسبة أربعة وتسعين جزءًا إلى خمسة وسبعين جزءًا فإنّ قوس كاف هاء تكون أيضًا بهذه الأجزاء عشر دقائق بالتقريب وقد كانت وضعت قوس دال لام في كوكب المرّيخ أربعة عشر جزءًا ونصف جزء فتكون قوس دال هاء كلّها تجتمع أربعة عشر جزءًا وأربعين دقيقةً وهي في كوكب زحل أربعة عشر جزءًا ؞ وفي كوكب المشتري أربعة عشر جزءًا ونصف وربع جزء ؞ فيجب لذلك من قبل أنّ نسبة قوس هاء دال أيضًا إلى قوس دال باء نسبة مائة وعشرين جزءًا إلى أربعة وتسعين جزءًا أن تكون قوس دال باء أيضًا من الدائرة العظمى التي ترسم مارّةً نقطتي الأفق⊙ يحصل لنا أمّا في كوكب زحل فأحد عشر جزءًا وأمّا في كوكب المشتري فعشرة أجزاء وأمّا في كوكب المرّيخ فأحد عشر جزءًا ونصف جزء بالتقريب ؞ وكذلك أيضًا في الزهرة وعطارد لمّا كان إذا عرف مبدأ السرطان أحدث مع الأفق ميل هذه الزاوية التي وضعناها ومثل هذا الميل وقد كنّا وضعنا أنّ كوكب الزهرة يطلع بالعشيّ في هذا الجزء من فلك البروج وبعده من موضع الشمس الحقيقيّ خمسة أجزاء وثلثا جزء وأنّ كوكب عطارد يطلع بالعشيّ وبعده أحد عشر جزءًا ونصف جزء فحاصل الشمس إذن في طلوعها أمّا على الحقيقة أمّا في كوكب الزهرة فتكون على أربعة عشر جزءًا وثلث جزء من التوأمين ؞ وأمّا في ككب عطارد فعلى ثمانية عشر جزءًا ونصف ؞ وأمّا على التوسّط أمّا في كوكب الزهرة فعلى خمسة وعشرين جزءًا وأمّا في كوكب عطارد فعلى تسعة عشر جزءًا بالتقريب فهذان إذن كانا حاصل الحركة الوسطى في الطول لهذين الكوكبين ومتى كان الطول بهذه الصفة قرباهما في مبدأ السرطان فإنّ كوكب الزهرة يوجد حينئذ بعده من البعد الأبعد من فلك تدويره نحوًا من أربعة عشر جزءًا وكوكب عطارد نحوًا من اثنين وثلاثين جزءًا ؞ يط: فإنّ ذلك يتبيّن بالمعاني التي قدّمنا وضعها في اختلافهما ويلزم من ذلك أن يكون في هذه المسيرات كوكب الزهرة يوجد أميل إلى الشمال عن فلك البروج بجزء واحد ؞ وأمّا كوكب عطارد فبجزء واحد وثلثي جزء بالتقريب لأنّ ذلك مبلغ قوس كاف حاء وذلك بيّن فلذلك من قبل أنّ نسبتها أيضًا إلى قوس هاء كاف نسبة أربعة وتسعين جزءًا إلى خمسة وسبعين جزءًا وهذه النسبة هي أيضًا نسبة جزء واحد إلى نصف وربع جزء ونسبة جزء واحد وثلثي جزء إلى جزء واحد وثلث جزء بالتقريب يحصل لنا قوس هاء كاف أيضًا أمّا في الزهرة فنصف وربع جزء ؞ وأمّا في عطارد فجزءًا واحدًا وثلث جزء وبهذه الأجزاء وضعت أيضًا قوس دال لام وهي القوس التي رأى كلّ واحد منهما أنها بعده من الشمس أمّا في الزهرة فخمسة أجزاء وثلثا جزء ؞ وأمّا في عطارد فأحد عشر جزءًا ونصف جزء فيحصل لنا إذن قوس دال كاف هاء بأسرها أمّا في الزهرة فستّة أجزاء وخمسا جزء ؞ وأمّا في عطارد فاثنا عشر جزءًا ونصف وثلث جزء بالتقريب فلذلك أيضًا من قبل أنّ نسبة قوس هاء دال إلى قوس باء دال نسبة مائة وعشرين جزءًا إلى أربعة وتسعين جزءًا وقد توافق هذه النسبة نسبة ستّة أجزا وخمسي جزء إلى خمسة أجزاء ونسبة اثني عشر جزءًا ونصف وثلث جزء إلى عشرة أجزاء بالتقريب يحصل لنا قوس دال باء أيضًا وهي مقدار البعد الكليّ أمّا في الزهرة فخمسة أجزاء وأمّا في عطارد  فعشرة أجزاء وهذه الأشياء التي قصدنا لوجودها⊙
فعشرة أجزاء وهذه الأشياء التي قصدنا لوجودها⊙
〈XIII.8〉 ح: في أنّ ما يوجد أيضًا من الخواصّ في ظهورات الزهرة وعطارد واختفاءاتها يوافق الأصول التي وضعت لهما⊙
فأمّا أنّ الأمور الغريبة التي تقع في ظهورات الزهرة وعطارد واختفاءاتهما توجد لازمةً مطابقةً للأصول التي وضعناها لهما أعني أنّ في كوكب الزهرة الزمان الذي من غروبه المسائيّ إلى طلوعه الصباحيّ أمّا متى كان الكوكب في مبادئ الحوت فيكون نحوًا من يومين أكثره وأمّا متى كان الكوكب في مبادئ العذراء فيكون ستّة عشر يومًا وأنّ في كوكب عطارد متى كان خليقًا أن يرى في مبادئ العقرب فإنّ ظهوراته المسائيّة  تخلّ فتبطل فبهذا الوجه نعلم ذلك ك: ولنبدأ أوّلًا بكوكب الزهرة فنضع مثل ذلك الرسم لذي وضعناه للظهورات وننزل أوّلًا أنّ نقطة هاء من فلك البروج النقطة التي على مبدأ الحوت وهذا موضع إذا اتّفق أن يكون فيه كوكب الزهرة في البعد الأقرب من فلك تدويره كان مائلًا عن فلك البروج في الشمال بستّة أجزاء وثلث جزء بالتقريب وننزل أنّ الشكل شكل الغروب المسائيّ وفي هذا الغروب تكون زاوية باء هاء دال تحصل في هذا الإقليم الذي فرضناه مائةً وأربعةً وخمسين جزءًا بالأجزاء التي بها زاويتان قائتان ثلاث مائة وستّون جزءًا وتكون الأجزاء التي بها الموتر ↑: القطر مائة وعشرون جزءًا فإنّ أعظم الخطّين المحيطين بالزاوية القائمة بها مائة وسبعة عشر جزءًا وأصغرهما سبعة وعشرون جزءًا بالتقريب فمن قبل ذلك تكون الأجزاء التي بها خطّ دال باء وهو خطّ البعد الكليّ خمسة أجزاء فإنّ خطّ دال هاء يصير بها خمسة أجزاء وثمان دقائق لكن إذا كان هذا الكوكب أبعد في الشمال عن فلك البروج بستّة أجزاء وثلث جزء لأنّ هذا مبلغ قوس كاف حاء وكانت نسبة مائة وسبعة عشر جزءًا إلى سبعة وعشرين جزءًا هي نسبة سبعة أجزاء وثلث جزء إلى جزء ونصف بالتقريب فإنّ قوس كاف هاء يكون جزءًا واحدًا ونصف جزء وتكون قوس كاف
تخلّ فتبطل فبهذا الوجه نعلم ذلك ك: ولنبدأ أوّلًا بكوكب الزهرة فنضع مثل ذلك الرسم لذي وضعناه للظهورات وننزل أوّلًا أنّ نقطة هاء من فلك البروج النقطة التي على مبدأ الحوت وهذا موضع إذا اتّفق أن يكون فيه كوكب الزهرة في البعد الأقرب من فلك تدويره كان مائلًا عن فلك البروج في الشمال بستّة أجزاء وثلث جزء بالتقريب وننزل أنّ الشكل شكل الغروب المسائيّ وفي هذا الغروب تكون زاوية باء هاء دال تحصل في هذا الإقليم الذي فرضناه مائةً وأربعةً وخمسين جزءًا بالأجزاء التي بها زاويتان قائتان ثلاث مائة وستّون جزءًا وتكون الأجزاء التي بها الموتر ↑: القطر مائة وعشرون جزءًا فإنّ أعظم الخطّين المحيطين بالزاوية القائمة بها مائة وسبعة عشر جزءًا وأصغرهما سبعة وعشرون جزءًا بالتقريب فمن قبل ذلك تكون الأجزاء التي بها خطّ دال باء وهو خطّ البعد الكليّ خمسة أجزاء فإنّ خطّ دال هاء يصير بها خمسة أجزاء وثمان دقائق لكن إذا كان هذا الكوكب أبعد في الشمال عن فلك البروج بستّة أجزاء وثلث جزء لأنّ هذا مبلغ قوس كاف حاء وكانت نسبة مائة وسبعة عشر جزءًا إلى سبعة وعشرين جزءًا هي نسبة سبعة أجزاء وثلث جزء إلى جزء ونصف بالتقريب فإنّ قوس كاف هاء يكون جزءًا واحدًا ونصف جزء وتكون قوس كاف  دال الباقية وهي قوس بعد الكوكب في الغروب المسائيّ عن الشمس إلى ما وراءها ثلاثة أجزاء وثمانيًا وثلاثين دقيقةً كا: وفي مثل هذه الصورة أيضًا لمّا كانت زاوية باء هاء دال تصير في الطلوع الصباحيّ تسعةً وستّين جزءًا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا ومن أجل ذلك تكون الأجزاء التي بها الموتر مائة وعشرون جزءًا فإنّ أصغر الخطّين المحيطين بالزاوية القائمة ثمانية وستّون جزءًا وأعظمهما تسعة وتسعون جزءًا بالتقريب وكانت نسبة ثمانية وستّين جزءًا إلى مائة وعشرين جزءًا هي نسبة خمسة أجزاء إلى ثمانية أجزاء وتسع وأربعين دقيقةً ونسبة الثمانية والستّين الجزء إلى تسعة وتسعين جزءًا هي نسبة ستّة أجزاء وثلث جزء إلى تسعة أجزاء وثلاث عشرة دقيقةً فإنّ قوس دال هاء يحصل لنا بهذه الأجزاء ثمانية أجزاء وتسعًا وأربعين دقيقةً وتحصل قوس كاف هاء وهي قوس الفضل الذي من قبل العرض تسعة أجزاء وثلاث عشرة دقيقةً وتكون قوس دال كاف الباقية ومن البيّن أنّها قوس بعد الكوكب من الشمس إلى خلف أربعًا وعشرين دقيقةً وقد كان بعده منها على هذا المثال إلى خلف في الغروب المسائيّ أيضًا ثلاثة أجزاء وثمانيًا وثلاثين دقيقةً فحركة الكوكب إذن في المدّة التي فيما بين الغروب المسائيّ وبين الطلوع الصباحيّ كانت أقلّ من حركة الشمس في هذه المدّة أعني أقلّ من مسيرها في خاصّ نفسها في الطول بالتقريب بسبب التقدّم الذي من قبل فلك تدويره بثلاثة أجزاء وأربع عشرة دقيقةً فلأنّ الكوكب يساريه هذا المقدار من الأجزاء إلى قدّام على ما يوقف عليه من جدول الاختلاف إذا تحرّك وهو البعد الأقرب من فلك تدويره جزءًا واحدًا وربع جزء والكوكب يقطع ذلك على التوسّط في قريب من يومين فظاهر أنّ هذا يكون مبلغ زمان هذا البعد
دال الباقية وهي قوس بعد الكوكب في الغروب المسائيّ عن الشمس إلى ما وراءها ثلاثة أجزاء وثمانيًا وثلاثين دقيقةً كا: وفي مثل هذه الصورة أيضًا لمّا كانت زاوية باء هاء دال تصير في الطلوع الصباحيّ تسعةً وستّين جزءًا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا ومن أجل ذلك تكون الأجزاء التي بها الموتر مائة وعشرون جزءًا فإنّ أصغر الخطّين المحيطين بالزاوية القائمة ثمانية وستّون جزءًا وأعظمهما تسعة وتسعون جزءًا بالتقريب وكانت نسبة ثمانية وستّين جزءًا إلى مائة وعشرين جزءًا هي نسبة خمسة أجزاء إلى ثمانية أجزاء وتسع وأربعين دقيقةً ونسبة الثمانية والستّين الجزء إلى تسعة وتسعين جزءًا هي نسبة ستّة أجزاء وثلث جزء إلى تسعة أجزاء وثلاث عشرة دقيقةً فإنّ قوس دال هاء يحصل لنا بهذه الأجزاء ثمانية أجزاء وتسعًا وأربعين دقيقةً وتحصل قوس كاف هاء وهي قوس الفضل الذي من قبل العرض تسعة أجزاء وثلاث عشرة دقيقةً وتكون قوس دال كاف الباقية ومن البيّن أنّها قوس بعد الكوكب من الشمس إلى خلف أربعًا وعشرين دقيقةً وقد كان بعده منها على هذا المثال إلى خلف في الغروب المسائيّ أيضًا ثلاثة أجزاء وثمانيًا وثلاثين دقيقةً فحركة الكوكب إذن في المدّة التي فيما بين الغروب المسائيّ وبين الطلوع الصباحيّ كانت أقلّ من حركة الشمس في هذه المدّة أعني أقلّ من مسيرها في خاصّ نفسها في الطول بالتقريب بسبب التقدّم الذي من قبل فلك تدويره بثلاثة أجزاء وأربع عشرة دقيقةً فلأنّ الكوكب يساريه هذا المقدار من الأجزاء إلى قدّام على ما يوقف عليه من جدول الاختلاف إذا تحرّك وهو البعد الأقرب من فلك تدويره جزءًا واحدًا وربع جزء والكوكب يقطع ذلك على التوسّط في قريب من يومين فظاهر أنّ هذا يكون مبلغ زمان هذا البعد  الذي ذكره وذلك موافق لما يرى كب: وفي مثل هذه الصورة أيضًا ننزل أنّ نقطة هاء على مبدأ العذراء وهذا موضع إذا اتّفق أن يكون كوكب الزهرة فيه في البعد الأقرب من فلك تدويره رئي أميل إلى الجنوب عن فلك البروج بقريب من تلك الأجزاء وهي ستّة أجزاء وثلث جزء⊙ ولنضع أوّلًا اختفاءه المسائيّ وعند ذلك زاوية باء هاء دال تسعة وستّون جزءًا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وتكون الأجزاء التي بها الموتر مائة وعشرون جزءًا فإنّ أصغر الخطّين المحيطين بالزاوية القائمة بها ثمانية وستّون جزءًا وأعظمها تسعة وتسعون جزءًا بالتقريب فلأنّ النسب التي تكون هاهنا هي تلك النسب بأعيانها التي كانت في ظهوره الصباحيّ في الحوت وكان البعد في العرض هاهنا هو مثله هناك فإنّ قوس هاء دال يحصل لنا بهذه الأجزاء تسعةً وأربعين جزءًا وتحصل قوس لام هاء وهي قوس الفضل الذي من قبل العرض تسعة أجزاء وثلاث عشرة دقيقةً وتكون قوس دال لام بأسرها وهي قوس بعد الكوكب من الشمس إلى خلف ثمانية عشر جزءًا ودقيقتين والذي يصيب هذا المقدار من الأجزاء وهي أجزاء التقدّم عن موضع الحركة الوسطى للشمس وللكوكب سبعة أجزاء ونصف جزء بالتقريب من البعد الأقرب من فلك التدوير على حسب ما في جدول الاختلاف كما قلنا⊙ كجـ: وكذلك أيضًا إذا كان في الطلوع الصباحيّ الذي يكون لهذا الكوكب في مبادئ العذراء عندما تكون زاوية باء هاء دال مائةً وأربعةً وخمسين جزءًا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا ويكون الأعظم من الخطّين المحيطين بالزاوية مائةً وسبعة عشر جزءًا بالأجزاء التي بها الموتر مائة وعشرون جزءًا والأصغر منهما سبعة وعشرون جزءً وتكون النسب هي تلك النسب أيضًا بأعيانها التي وضعت في الاختفاء المسائيّ في الحوت يحصل لنا بهذه الأجزاء أمّا قوس دال هاء فخمسة أجزاء وثمان دقائق وأمّا قوس هاء لام وهي قوس الفضل الذي من قبل العرض فجزءًا واحدًا وثلاثين دقيقةً وأمّا قوس دال لام بأسرها وهي قوس بعد الكوب من الشمس إلى قدّام ستّة أجزاء وثمان وثلاثون دقيقةً وكان ما تصيب هذه الأجزاء على ذلك النحو من البعد الأقرب من فلك التدوير جزأين ونصف جزء بالتقريب فكوكب الزهرة يتحرّك إذن من الاختفاء المسائيّ إلى الطلوع الصباحيّ هذه الأجزاء كلّها من فلك التدوير وهي عشرة أجزاء وإنّما تقطع هذا المقدار من الأجزاء في قريب من الأيّام التي ذكرنا وهي ستّة عشر يومًا وذلك موافق لما يرى⊙ فإذ قد بيّنت هذه الأشياء فقد ينبغي أن نصرف نظرنا إلى ما يلزم في ظهورات كوكب عطارد التي تخلّ فتبطل ونبدأ أوّلًا بأن نبيّن أنّه متى كان في مبادئ العقرب فإنّ بعده من الشمس إلى خلف ولو كان
الذي ذكره وذلك موافق لما يرى كب: وفي مثل هذه الصورة أيضًا ننزل أنّ نقطة هاء على مبدأ العذراء وهذا موضع إذا اتّفق أن يكون كوكب الزهرة فيه في البعد الأقرب من فلك تدويره رئي أميل إلى الجنوب عن فلك البروج بقريب من تلك الأجزاء وهي ستّة أجزاء وثلث جزء⊙ ولنضع أوّلًا اختفاءه المسائيّ وعند ذلك زاوية باء هاء دال تسعة وستّون جزءًا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وتكون الأجزاء التي بها الموتر مائة وعشرون جزءًا فإنّ أصغر الخطّين المحيطين بالزاوية القائمة بها ثمانية وستّون جزءًا وأعظمها تسعة وتسعون جزءًا بالتقريب فلأنّ النسب التي تكون هاهنا هي تلك النسب بأعيانها التي كانت في ظهوره الصباحيّ في الحوت وكان البعد في العرض هاهنا هو مثله هناك فإنّ قوس هاء دال يحصل لنا بهذه الأجزاء تسعةً وأربعين جزءًا وتحصل قوس لام هاء وهي قوس الفضل الذي من قبل العرض تسعة أجزاء وثلاث عشرة دقيقةً وتكون قوس دال لام بأسرها وهي قوس بعد الكوكب من الشمس إلى خلف ثمانية عشر جزءًا ودقيقتين والذي يصيب هذا المقدار من الأجزاء وهي أجزاء التقدّم عن موضع الحركة الوسطى للشمس وللكوكب سبعة أجزاء ونصف جزء بالتقريب من البعد الأقرب من فلك التدوير على حسب ما في جدول الاختلاف كما قلنا⊙ كجـ: وكذلك أيضًا إذا كان في الطلوع الصباحيّ الذي يكون لهذا الكوكب في مبادئ العذراء عندما تكون زاوية باء هاء دال مائةً وأربعةً وخمسين جزءًا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا ويكون الأعظم من الخطّين المحيطين بالزاوية مائةً وسبعة عشر جزءًا بالأجزاء التي بها الموتر مائة وعشرون جزءًا والأصغر منهما سبعة وعشرون جزءً وتكون النسب هي تلك النسب أيضًا بأعيانها التي وضعت في الاختفاء المسائيّ في الحوت يحصل لنا بهذه الأجزاء أمّا قوس دال هاء فخمسة أجزاء وثمان دقائق وأمّا قوس هاء لام وهي قوس الفضل الذي من قبل العرض فجزءًا واحدًا وثلاثين دقيقةً وأمّا قوس دال لام بأسرها وهي قوس بعد الكوب من الشمس إلى قدّام ستّة أجزاء وثمان وثلاثون دقيقةً وكان ما تصيب هذه الأجزاء على ذلك النحو من البعد الأقرب من فلك التدوير جزأين ونصف جزء بالتقريب فكوكب الزهرة يتحرّك إذن من الاختفاء المسائيّ إلى الطلوع الصباحيّ هذه الأجزاء كلّها من فلك التدوير وهي عشرة أجزاء وإنّما تقطع هذا المقدار من الأجزاء في قريب من الأيّام التي ذكرنا وهي ستّة عشر يومًا وذلك موافق لما يرى⊙ فإذ قد بيّنت هذه الأشياء فقد ينبغي أن نصرف نظرنا إلى ما يلزم في ظهورات كوكب عطارد التي تخلّ فتبطل ونبدأ أوّلًا بأن نبيّن أنّه متى كان في مبادئ العقرب فإنّ بعده من الشمس إلى خلف ولو كان  غاية البعد الذي يكون بينه وبينها لم يمكن أن يرى بالعشيّ كد: فلنضع الصورة التي وضعناها في الظهورات وننزل أنّ نقطة هاء من فلك البروج في مبدأ العقرب وهذا موضع يكون فيه المغيب زاوية باء هاء دال خمسةً وستّين جزءًا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وتكون أصغر الخطّين المحيطين بالزاوية القائمة ثمانية وستّون جزءًا بالأجزاء التي بها الموتر مائة وعشرون جزءًا وأعظم الخطّين تسعة وتسعون جزءًا
غاية البعد الذي يكون بينه وبينها لم يمكن أن يرى بالعشيّ كد: فلنضع الصورة التي وضعناها في الظهورات وننزل أنّ نقطة هاء من فلك البروج في مبدأ العقرب وهذا موضع يكون فيه المغيب زاوية باء هاء دال خمسةً وستّين جزءًا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وتكون أصغر الخطّين المحيطين بالزاوية القائمة ثمانية وستّون جزءًا بالأجزاء التي بها الموتر مائة وعشرون جزءًا وأعظم الخطّين تسعة وتسعون جزءًا  فالأجزاء إذن التي بها قوس باء دال وهي قوس البعد الكلّيّ عشرة أجزاء تكون بها قوس دال هاء سبعة عشر جزءًا وتسعًا وثلاثين دقيقةً لكن إذا كان هذا الكوكب موضعه الموضع الذي وصفناه يكون أميل إلى الجنوب عن فلك البروج بثلاثة أجزاء بالتقريب فذلك من قبل أنّ في هذه النسب الموصوفة الأجزاء أيضًا التي بها قوس لام طاء وهي قوس العرض ثلاثة أجزاء فإنّ قوس لام هاء تكون بها أربعة أجزاء واثنتين وعشرين دقيقةً وتكون قوس دال هاء لام بأسرها بهذه الأجزاء اثنين وعشرين جزءًا بالتقريب فقد يجب أن يكون بعد الكوكب من موضع الشمس الحقيقيّ هذا المقدار من الأجزاء كيما يمكن أن يرى أوّل رؤية لكن لمّا كان أكثر ما يكون بعده من موضع الشمس الحقيقيّ إذا كان في مبادئ العقرب إنّما هو عشرون جزءًا وثمان وخمسون دقيقةً فإنّا قد تقدّمنا فبيّنّا ذلك بالأبواب التي أرشدنا إليها في علم الأبعاد العظمى فظاهر أنّ ما كان كذلك من الظهورات بالواجب يخلّ فيبطل كه: وإن نحن وضعنا أيضًا مثل تلك الصورة التي للظهورات وأنزلنا أنّ نقطة هاء مبدأ الثور في الطلوع الصباحيّ عندما يكون الكوكب بحسب المسيرات الموصوفة أميل إلى الجنوب عن فلك البروج بثلاثة أجزاء وستّ دقائق بالتقريب وتكون النسب الموجودة في المثلّثات القائمة الزوايا هي تلك النسب الموصوفة بأعيانها حصلت أمّا قوس دال هاء سبعة عشر جزءًا وتسعًا وثلاثين دقيقةً بهذه الأجزاء وأمّا قوس لام هاء فأربعة أجزاء وسبع وثلاثون دقيقةً بالأجزاء التي بها قوس طاء لام وهي قوس العرض ثلاثة أجزاء وعشر دقائق وأمّا قوس دال هاء لام بأسرها فاثنين وعشرين جزءًا وستّ عشرة دقيقةً فلذلك نحتاج هاهنا أيضًا أن يكون بعد الكوكب من موضع الشمس الحقيقيّ كيما يرى أوّل رؤية هذا المقدار من الأجزاء ولكن لمّا كان ليس يبعد أكثره فوق الأجزاء التي بيّنّاها وهي اثنان وعشرون جزءًا وثلاث عشرة دقيقةً فبالواجب صارت هذه الظهورات التي تخلّ فتبطل فقد بيّنّا أنّ ما قصدنا له موافق لما يرى وللأصول التي وضعت⊙
فالأجزاء إذن التي بها قوس باء دال وهي قوس البعد الكلّيّ عشرة أجزاء تكون بها قوس دال هاء سبعة عشر جزءًا وتسعًا وثلاثين دقيقةً لكن إذا كان هذا الكوكب موضعه الموضع الذي وصفناه يكون أميل إلى الجنوب عن فلك البروج بثلاثة أجزاء بالتقريب فذلك من قبل أنّ في هذه النسب الموصوفة الأجزاء أيضًا التي بها قوس لام طاء وهي قوس العرض ثلاثة أجزاء فإنّ قوس لام هاء تكون بها أربعة أجزاء واثنتين وعشرين دقيقةً وتكون قوس دال هاء لام بأسرها بهذه الأجزاء اثنين وعشرين جزءًا بالتقريب فقد يجب أن يكون بعد الكوكب من موضع الشمس الحقيقيّ هذا المقدار من الأجزاء كيما يمكن أن يرى أوّل رؤية لكن لمّا كان أكثر ما يكون بعده من موضع الشمس الحقيقيّ إذا كان في مبادئ العقرب إنّما هو عشرون جزءًا وثمان وخمسون دقيقةً فإنّا قد تقدّمنا فبيّنّا ذلك بالأبواب التي أرشدنا إليها في علم الأبعاد العظمى فظاهر أنّ ما كان كذلك من الظهورات بالواجب يخلّ فيبطل كه: وإن نحن وضعنا أيضًا مثل تلك الصورة التي للظهورات وأنزلنا أنّ نقطة هاء مبدأ الثور في الطلوع الصباحيّ عندما يكون الكوكب بحسب المسيرات الموصوفة أميل إلى الجنوب عن فلك البروج بثلاثة أجزاء وستّ دقائق بالتقريب وتكون النسب الموجودة في المثلّثات القائمة الزوايا هي تلك النسب الموصوفة بأعيانها حصلت أمّا قوس دال هاء سبعة عشر جزءًا وتسعًا وثلاثين دقيقةً بهذه الأجزاء وأمّا قوس لام هاء فأربعة أجزاء وسبع وثلاثون دقيقةً بالأجزاء التي بها قوس طاء لام وهي قوس العرض ثلاثة أجزاء وعشر دقائق وأمّا قوس دال هاء لام بأسرها فاثنين وعشرين جزءًا وستّ عشرة دقيقةً فلذلك نحتاج هاهنا أيضًا أن يكون بعد الكوكب من موضع الشمس الحقيقيّ كيما يرى أوّل رؤية هذا المقدار من الأجزاء ولكن لمّا كان ليس يبعد أكثره فوق الأجزاء التي بيّنّاها وهي اثنان وعشرون جزءًا وثلاث عشرة دقيقةً فبالواجب صارت هذه الظهورات التي تخلّ فتبطل فقد بيّنّا أنّ ما قصدنا له موافق لما يرى وللأصول التي وضعت⊙
〈XIII.9〉 ط: في الباب الذي تؤخذ له الأبعاد الجزئيّة من الشمس في ظهورات هذه الكواكب واختفاءاتها⊙
وقد ظهر من ذلك أنّ بالجملة إذا كانت قسيّ باء دال معروضة في واحد واحد من الكواكب وكان مبدأ البروج على تقاطع هاء معطا ومن قبل ذلك تكون زاوية باء هاء دال أيضًا معطاةً فإنّ قوس دال هاء تكون معطاةً  ويكون المسير في العرض الذي يكون للكوكب في هذا البعد أعني قوس كاف حاء أو قوس طاء لام معطاةً ومن أجل ذلك تكون أيضًا قوس كاف هاء أو قوس هاء لام معطاةً ويكون البعد أيضًا الذي يرى معطى أعني قوس دال كاف وقوس دال لام فحسبنا بهذا الوجه كيما لا نطيل الكتاب في هذا الإقليم الوسط الذي ذكرناه وحده لأنّ فيه كفاية في البروج كلّها أيضًا في كلّ واحد من الكواكب الخمسة الأبعاد من موضع الشمس الحقيقي الذي يرى للطلوع وللاختفاء على أنّ الكواكب أنفسها موضوعة في مبادئ البروج وأثبتناها لتسهيل الاستعمال في خمسة جداول للكواكب الخمسة في كلّ جدول منها اثنا عشر سطرًا⊙ فالجداول الثلاثة الأول من هذه السطور لزحل والمشتري والمرّيخ رتّبنا في كلّ جدول منها ثلاثة صفوف وأثبتنا في الصفوف الأول منها مبادئ البروج وفي الصفوف الثواني أبعاد الطلوعات الصباحيّة وفي الصفوف الثوالث أبعاد الغروبات المسائيّة ؞ وأمّا الجدولان الباقيان لكوكب الزهرة وكوكب عطارد فإنّا رتّبناها في خمسة صفوف وأثبتنا في الصفّين الأوّلين على ذلك المثال مبادئ البروج وفي الصفّين الثانيين أبعاد الطلوعات المسائيّة وفي الصفّين الثالثين أبعاد الغروبات المسائيّة وأثبتنا أيضًا في الصفّين الرابعين أبعاد الطلوعات الصباحيّة وفي الصفّين الخامسين أبعاد الغروبات الصباحيّة⊙ ؞ وهكذا صنعة الجداول⊙
ويكون المسير في العرض الذي يكون للكوكب في هذا البعد أعني قوس كاف حاء أو قوس طاء لام معطاةً ومن أجل ذلك تكون أيضًا قوس كاف هاء أو قوس هاء لام معطاةً ويكون البعد أيضًا الذي يرى معطى أعني قوس دال كاف وقوس دال لام فحسبنا بهذا الوجه كيما لا نطيل الكتاب في هذا الإقليم الوسط الذي ذكرناه وحده لأنّ فيه كفاية في البروج كلّها أيضًا في كلّ واحد من الكواكب الخمسة الأبعاد من موضع الشمس الحقيقي الذي يرى للطلوع وللاختفاء على أنّ الكواكب أنفسها موضوعة في مبادئ البروج وأثبتناها لتسهيل الاستعمال في خمسة جداول للكواكب الخمسة في كلّ جدول منها اثنا عشر سطرًا⊙ فالجداول الثلاثة الأول من هذه السطور لزحل والمشتري والمرّيخ رتّبنا في كلّ جدول منها ثلاثة صفوف وأثبتنا في الصفوف الأول منها مبادئ البروج وفي الصفوف الثواني أبعاد الطلوعات الصباحيّة وفي الصفوف الثوالث أبعاد الغروبات المسائيّة ؞ وأمّا الجدولان الباقيان لكوكب الزهرة وكوكب عطارد فإنّا رتّبناها في خمسة صفوف وأثبتنا في الصفّين الأوّلين على ذلك المثال مبادئ البروج وفي الصفّين الثانيين أبعاد الطلوعات المسائيّة وفي الصفّين الثالثين أبعاد الغروبات المسائيّة وأثبتنا أيضًا في الصفّين الرابعين أبعاد الطلوعات الصباحيّة وفي الصفّين الخامسين أبعاد الغروبات الصباحيّة⊙ ؞ وهكذا صنعة الجداول⊙
〈XIII.10〉 يے: الجداول المرسومة لظهورات الكواكب الخمسة المتحيّرة واختفاءاتها
| /237r/ | ||||||||||||||||||||||||||||
جدول ظهورات الكواكب الخمسة واختفائاتها |
||||||||||||||||||||||||||||
البروج الاثناعشر |
لزحل |
للمشتري |
للمرّيخ |
للزهرة |
لعطارد |
|||||||||||||||||||||||
للطلوع الصباحيّ |
للغروب المسائيّ |
للطلوع الصباحيّ |
للغروب المسائيّ |
للطلوع الصباحيّ |
للغروب المسائيّ |
للطلوع الصباحيّ |
للغروب المسائيّ |
للطلوع الصباحيّ |
للغروب المسائيّ |
للطلوع الصباحيّ |
للغروب المسائيّ |
للطلوع الصباحيّ |
للغروب المسائيّ |
|||||||||||||||
أجزاء |
دقائق |
أجزاء |
دقائق |
أجزاء |
دقائق |
أجزاء |
دقائق |
أجزاء |
دقائق |
أجزاء |
دقائق |
أجزاء |
دقائق |
أجزاء |
دقائق |
أجزاء |
دقائق |
أجزاء |
دقائق |
أجزاء |
دقائق |
أجزاء |
دقائق |
أجزاء |
دقائق |
أجزاء |
دقائق |
|
الحمل |
كج |
ل |
يا |
كح |
ك |
ي |
ي |
يط |
كا |
يب |
يا |
ه |
ي |
د |
ط |
ج |
|
ي |
كح |
ط |
نح |
ط |
مج |
كج |
نح |
كج |
لح |
|
الثور |
كا |
نز |
يا |
يط |
و |
ي |
كط |
ك |
يا |
مح |
ه |
ح |
د |
يو |
ط |
م |
ي |
د |
ي |
يه |
كب |
يه |
كب |
يه |
||||
الجوزاء |
يز |
نب |
يب |
كو |
يه |
نا |
يا |
ي |
يز |
كا |
يب |
ل |
ه |
يب |
ه |
ز |
ط |
ز |
لو |
ي |
يح |
يا |
مز |
يح |
|
يو |
مد |
|
السرطان |
يد |
يد |
ب |
يب |
يب |
مو |
يد |
لج |
يد |
لج |
ه |
لو |
ح |
كج |
ه |
نط |
يب |
كب |
يه |
لد |
يد |
د |
يب |
ل |
||||
الأسد |
يا |
لد |
يه |
لد |
ي |
يد |
لا |
يب |
يز |
يط |
و |
يو |
يج |
ج |
ح |
ب |
ه |
ه |
يج |
مج |
يط |
نط |
يا |
كه |
ي |
|||
السنبلة |
ي |
نج |
ي |
يو |
يب |
يا |
مو |
ك |
ه |
ز |
كب |
يح |
ب |
و |
لح |
د |
ند |
يح |
ا |
كج |
ي |
كا |
ط |
نط |
||||
الميزان |
ي |
مح |
يز |
و |
ط |
نز |
يو |
لد |
يا |
لح |
كا |
ز |
نج |
يز |
مج |
ه |
ما |
د |
ند |
كب |
مط |
كج |
يو |
ط |
نا |
ي |
|
|
العقرب |
ي |
نج |
يو |
نج |
ي |
ا |
يو |
يب |
يا |
مح |
ك |
يط |
ح |
يج |
مز |
ه |
كح |
د |
نه |
ا |
كب |
ا |
ط |
ي |
يط |
|||
القوس |
يا |
لد |
يه |
ي |
م |
يد |
لا |
يب |
لد |
يز |
لب |
ز |
مط |
ح |
ا |
د |
لط |
ه |
يو |
يح |
يا |
يز |
كه |
ط |
كه |
يا |
يط |
|
الجدي |
يد |
ب |
يد |
ب |
يب |
مو |
يب |
يد |
مه |
يد |
مه |
و |
د |
ح |
ب |
مج |
و |
له |
يج |
ند |
يب |
ي |
ط |
لو |
يد |
ه |
||
الدلو |
يز |
يب |
كو |
يه |
نا |
يا |
ي |
يز |
له |
يب |
لو |
ه |
نا |
ج |
يو |
|
ل |
ح |
لج |
يا |
ي |
ط |
يب |
كز |
يز |
ن |
||
الحوت |
كا |
نز |
يا |
ما |
يط |
و |
ي |
كط |
ك |
كو |
يا |
مط |
ه |
كب |
ج |
لح |
|
كد |
ي |
يو |
ي |
يا |
ط |
مج |
يط |
يه |
كا |
مو |
جدول ظهورات الكواكب الخمسة واختفائاتها |
||||||||||||||||
البروج الاثناعشر |
للزهرة |
لعطارد |
||||||||||||||
للطلوع الصباحيّ |
للغروب المسائيّ |
للطلوع الصباحيّ |
للغروب المسائيّ |
للطلوع الصباحيّ |
للغروب المسائيّ |
للطلوع الصباحيّ |
للغروب المسائيّ |
|||||||||
أجزاء |
دقائق |
أجزاء |
دقائق |
أجزاء |
دقائق |
أجزاء |
دقائق |
أجزاء |
دقائق |
أجزاء |
دقائق |
أجزاء |
دقائق |
أجزاء |
دقائق |
|
الحمل |
ه |
ي |
د |
ط |
ج |
|
ي |
كح |
ط |
نح |
ط |
مج |
كج |
نح |
كج |
لح |
الثور |
ه |
ح |
د |
يو |
ط |
م |
ي |
د |
ي |
يه |
كب |
يه |
كب |
يه |
||
الجوزاء |
ه |
يب |
ه |
ز |
ط |
ز |
لو |
ي |
يح |
يا |
مز |
يح |
|
يو |
مد |
|
السرطان |
ه |
لو |
ح |
كج |
ه |
نط |
يب |
كب |
يه |
لد |
يد |
د |
يب |
ل |
||
الأسد |
و |
يو |
يج |
ج |
ح |
ب |
ه |
ه |
يج |
مج |
يط |
نط |
يا |
كه |
ي |
|
السنبلة |
ز |
كب |
يح |
ب |
و |
لح |
د |
ند |
يح |
ا |
كج |
ي |
كا |
ط |
نط |
|
الميزان |
ز |
نج |
يز |
مج |
ه |
ما |
د |
ند |
كب |
مط |
كج |
يو |
ط |
نا |
ي |
|
العقرب |
ح |
يج |
مز |
ه |
كح |
د |
نه |
ا |
كب |
ا |
ط |
ي |
يط |
|||
القوس |
ز |
مط |
ح |
ا |
د |
لط |
ه |
يو |
يح |
يا |
يز |
كه |
ط |
كه |
يا |
يط |
الجدي |
و |
د |
ح |
ب |
مج |
و |
له |
يج |
ند |
يب |
ي |
ط |
لو |
يد |
ه |
|
الدلو |
ه |
نا |
ج |
يو |
|
ل |
ح |
لج |
يا |
ي |
ط |
يب |
كز |
يز |
ن |
|
الحوت |
ه |
كب |
ج |
لح |
|
كد |
ي |
يو |
ي |
يا |
ط |
مج |
يط |
يه |
كا |
مو |
〈XIII.11〉 يا: خاتمة الكتاب
فإذ قد استتممنا هذه المعاني أيضًا يا سورس فاستكملنا جميع ما نحتاج أن نرشد إلى علمه في هذا الكتاب بقدر منتهى ه - صح: بقدر منتهى علمي ومبلغ رأيي إلا الشاذّ منها بقدر ما أعاننا عليه الزمان الذي تناهى إلينا على وجود ما نحتاج إلى وجوده من ذلك أو تقويم ما نحتاج إلى تقويمه وتصحيحه منه وبقدر ما يكون ما دوّنّاه منه نافعًا فقط في هذا العلم من غير أن نلتمس به التكبّر ↑: صح والافتخار ↑: صح، ه: التكثير والأنصار فقد يليق ويحسن أن نجعل هذا آخر الكتاب⊙ تمّت المقالة الثالثة عشرة من كتاب بطلميوس المنسوب إلى التعاليم وهي يا قولًا وبتمامها تمّ جميع الكتاب وهو الكتاب المعروف بالمجسطي ولواهب العقل الحمد بلا غاية والشكر بلا نهاية كما هو أهله وذلك في نصف جمادى الآخرة سنة ثماني وسبعين وأربع مائة نسخ من كتاب عورض بنسخة الشيخ أبي القاسم المنجّم الذي كتبه وصحّحه من نسخة الشيخ أبي الحسين ه: هذا أبو الحسين هو عبد الرحمن بن عمر الصوفيّ البزّاز مؤلّف كتاب الكواكب لعضد الدولة أبي شجاع بن ركن الدولة أبي عليّ الصوفيّ رحمه الله.