〈XI〉 ابتداء المقالة الحادية عشرة من كتاب بطلميوس المنسوب إلى التعاليم⊙
〈XI.1〉 آ: في تبيين الخروج عن المركز في المشتري وبعده الأبعد
قال: وإذ قد بيّنّا أدوار الحركات في كوكب المرّيخ واختلافاته وتحصيلاته فنحن الآن متّبعون ذلك بوصف هذه الأشياء أيضًا في كوكب المشتري بذلك الوجه بعينه فنأخذ أوّلًا لتبيين بعده الأبعد ومبلغ خروج فلكه عن المركز ثلثًا من الأحوال التي تسمّى طرف الليل مقاطرةً لمسير الشمس الوسط أحدهنّ رصدناها بآلات القياس في سنة سبع عشرة من سني أذريانوس في شهر إيبفي عند المصريّين في اليوم الأوّل منه في الليلة التي يتلوها اليوم الثاني قبل انتصاف الليل بساعة واحدة وكان الكوكب في ثلاثة وعشرين جزءًا وإحدى عشرة دقيقةً من العقرب⊙ والحال الثانية رصدناها في سنة إحدى وعشرين من سنته في شهر فاوقى في اليوم الثالث عشر منه في الليلة التي يتلوها اليوم الرابع عشر قبل انتصاف الليل بساعتين وكان الكوكب في سبعة أجزاء وأربع وخمسين دقيقةً من الحوت⊙ والحال الثالثة رصدناها في السنة الأولى من سني أنطونيس في شهر أثور في اليوم العشرين منه في الليلة التي يتلوها اليوم الحادي والعشرين بعد خمس ساعات من انتصاف الليل وكان الكوكب في أربعة عشر جزءًا وثلاث وعشرين دقيقةً من الحمل فالبعد إذن من الحال الأولى إلى الحال الثانية كانت مدّته من السنين المصريّة ثلاث سنين ومن الأيّام مائة وستّة أيّام ومن الساعات ثلاث وعشرون ساعةً ومن الأجزاء لمسير الكوكب الذي يرى مائة وأربعة أجزاء وثلاث وأربعون دقيقةً والبعد من الحال الثانية إلى الحال الثالثة كانت مدّته سنةً واحدةً مصريّةً وسبعةً وثلاثين يومًا وسبع
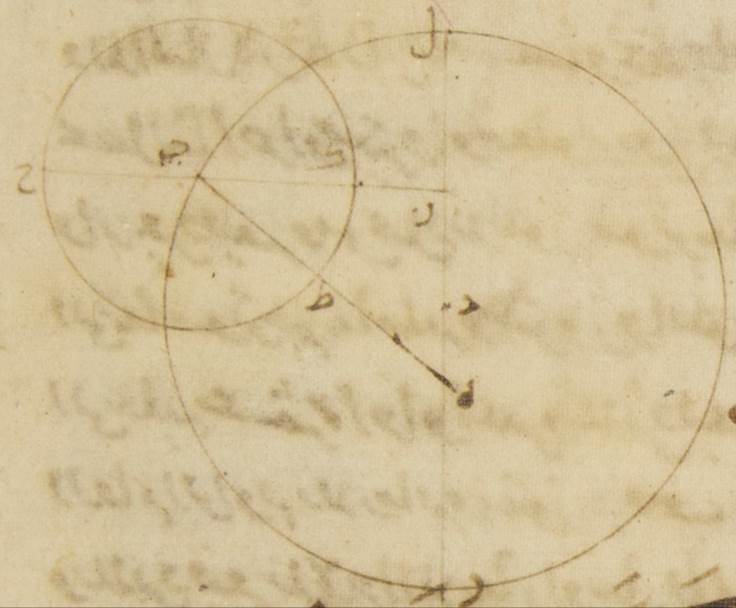
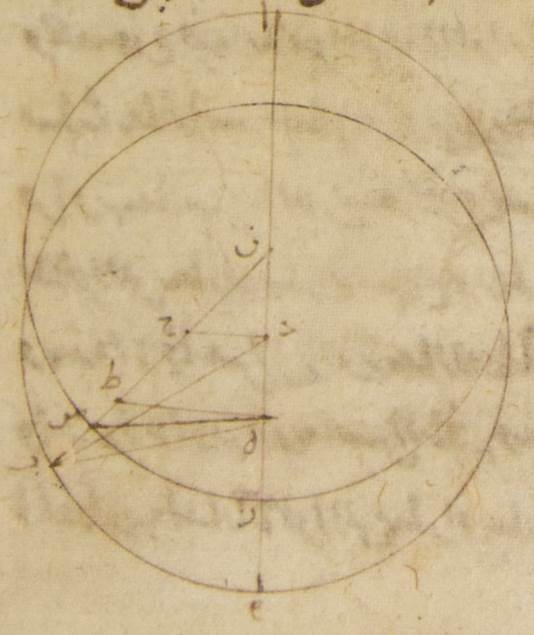
ساعات ومن الأجزاء التي على ذلك المثال ستّةً وثلاثين جزءًا وتسعًا وعشرين دقيقةً والذي يحصل ن المصير الوسط في الطول أمّا لزمان البعد الأوّل فتسعة وتسعون جزءًا وخمس وخمسون دقيقةً وأمّا لزمان البعد الثاني فثلاثة وثلاثون جزءًا وستّ وعشرون دقيقةً فمن هذين البعدين على حسب السبل التي وصفناها في المريخ جعلنا أوّلًا نبيّن الأشياء التي قصدنا للوقوف عليها على أنّ الفلك الخارج المركز أيضًا واحد بهذا الوجه الذي أنا واصفه. آ: ليكن الفلك الخارج المركز ألف باء جيم ولننزل أنّ نقطة ألف النقطة التي عليها كان مركز فلك التدوير في الحال الأولى من أحوال طرف الليل ونقطة باء نقطة الحال الثانية ونقطة جيم نقطة الحال الثالثة ولنوجد داخل فلك ألف باء جيم الخارج المركز نقطة دال مركز فلك البروج ولنوصل خطوط ألف دال باء دال جيم دال ولينفذ خطّ جيم دال هاء ولتوصل خطوط هاء ألف هاء باء ألف باء ولنخرج من نقطة هاء على خطّي ألف دال باء دال عمودا هاء زاي هاء حاء ومن نقطة ألف على خطّ هاء باء عمود ألف طاء فلأنّ قوس باء جيم من الفلك الخارج المركز قد وضعت توتر من فلك البروج ستّةً وثلاثين جزءًا وتسعًا وعشرين دقيقةً تكون زاوية باء دال جيم أيضًا أعني زاوية هاء دال حاء إذ هي عند مركز فلك البروج أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فاثنان وسبعون جزءًا وثمان وخمسون دقيقةً فتكون لذلك القوس أيضًا التي على خطّ هاء حاء اثنين وسبعين جزءًا وثمانيًا وخمسين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث هاء دال حاء القائم الزاوية ثلاث مائة وستّون جزءًا ويكون خطّ هاء حاء أحدًا وسبعين جزءًا وإحدى وعشرين دقيقةً بالأجزاء التي بها خطّ دال هاء الموتر مائةً وعشرين جزءًا وعلى هذا المثال لأنّ قوس باء جيم ثلاثة وثلاثون جزءًا وستّ وعشرون دقيقةً تكون زاوية باء هاء جيم إذ هي عند المحيط ثلاثةً وثلاثين جزءًا وستًّا وعشرين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وتكون زاوية هاء باء حاء الباقية بهذه الأجزاء تسعةً وثلاثين جزءًا واثنتين وثلاثين دقيقةً فتكون لذلك القوس أيضًا التي على خطّ هاء حاء تسعةً وثلاثين جزءًا واثنتين وثلاثين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء هاء حاء القائم الزاوية ثلاث مائة وستّون جزءًا ويكون خطّ هاء حاء أربعين جزءًا وخمسًا وثلاثين دقيقةً بالأجزاء التي بها خطّ باء هاء الموتر مائةً وعشرين جزءًا فالأجزاء إذن التي بها يبين أنّ خطّ هاء حاء أحد وتسعون جزءًا وأحد وعشرون دقيقةً وخطّ هاء دال مائة وعشرون جزءًا يكون بها خطّ هاء باء مائتين وعشرة أجزاء وثمانيًا وخمسين دقيقة وأيضًا لأنّ قوس ألف باء جيم بأسرها من الفلك الخارج المركز قد وضعت توتر من فلك البروج الأجزاء التي تحصل من البعدين مجموعين وهي مائة وأحد وأربعون جزءًا واثنتا عشرة دقيقةً تكون زاوية ألف دال جيم أيضًا إذ هي عند مركز فلك البروج أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فمائة وواحد وأربعون جزءًا واثنتا عشرة دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فمائتان واثنان وثمانون جزءًا وأربع وعشرون دقيقةً وتكون الزاوية التي تليها وهي زاوية ألف دال هاء بهذه الأجزاء سبعةً وسبعين جزءًا وستًّا وثلاثين دقيقةً فتكون لذلك القوس أيضًا التي على خطّ هاء نون سبعةً وسبعين جزءًا وستًّا وثلاثين دقيقةً بالأجزاء التي بها
الدائرة التي ترسم حول مثلّث دال هاء زاي القائم الزاوية ثلاث مائة وستّون جزءًا ويكون خطّ هاء نون خمسةً وسبعين جزءًا واثنتي عشرة دقيقةً بالأجزاء التي بها خطّ دال هاء الموتر مائة وعشرون⊙ وعلى هذا المثال لأنّ قوس ألف باء جيم من الفلك الخارج المركز يحصل مائةً وثلاثةً وثلاثين جزءًا وإحدى وعشرين دقيقة تكون زاوية ألف هاء جيم أيضًا إذ هي عند المحيط مائةً وثلاثةً وثلاثين جزءًا وإحدى وعشرين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وبهذه الأجزاء كانت زاوية ألف دال هاء سبعةً وسبعين جزءًا وستًّا وثلاثين دقيقةً فزاوية هاء ألف زاي الباقية تكون بهذه الأجزاء مائة وتسعة وأربعين جزءًا وثلاث دقائق فتكون لذلك القوس أيضًا التي على خطّ هاء زاي مائة وتسعة وأربعين جزءًا وثلاث دقائق بالأجزاء التي بها الدائرة التي ترسم حول مثلّث ألف هاء زاي القائم الزاوية ثلاث مائة وستّون جزءًا ويكون خطّ هاء زاي مائةً وخمسة عشر جزءًا وتسعًا وثلاثين دقيقةً بالأجزاء التي بها خطّ هاء ألف الموتر ه - صح: الموتر مائة وعشرون جزءًا فالأجزاء إذن التي تبيّن أنّ خطّ هاء زاي بها خمسة وسبعون جزءًا واثنتا عشرة دقيقةً وخطّ هاء دال وضع بها مائة وعشرون جزءًا يكون بها خطّ هاء ألف ثمانيةً وسبعين جزءًا ودقيقتين وأيضًا لأنّ قوس ألف باء من الفلك الخارج المركز تسعة وتسعون جزءًا وخمس وخمسون دقيقةً تكون زاوية ألف هاء باء عند المحيط تسعةً وتسعين جزءًا وخمسًا وخمسين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فتكون لذلك القوس أيضًا التي على خطّ ألف طاء تسعةً وتسعين جزءًا وخمسًا وخمسين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث ألف هاء طاء القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ هاء طاء الأجزاء الباقية لتمام نصف دائرة وهي ثمانون جزءًا وخمس دقائق فخطّ ألف طاء إذن من الخطّين اللذين يوترانهما أحد وتسعون جزءًا واثنتان وخمسون دقيقةً بالأجزاء التي بها خطّ ألف هاء الموتر مائة وعشرون جزءًا وخطّ هاء طاء بهذه الأجزاء سبعة وسبعون جزءًا واثنتا عشرة دقيقةً فتكون لذلك الأجزاء التي بها يبين أنّ خطّ ألف هاء ثمانية وسبعون جزءًا ودقيقتان وخطّ دال هاء مائة وعشرون جزءًا فإنّ بها خطّ ألف طاء تسعة وخمسون جزءًا وأربع وأربعون دقيقةً وخطّ هاء طاء على ذلك المثال خمسون جزءًا واثنتا عشرة دقيقةً وبهذه الأجزاء كان يبين أنّ خطّ هاء باء بأسره مائتا جزء وعشرة أجزاء وثمان وخمسون دقيقةً فخطّ طاء باء الباقي إذن مائة وستّون جزءًا وستّ وأربعون دقيقةً بالأجزاء التي بها خطّ ألف طاء تسعة وخمسون جزءًا وأربع وأربعون دقيقةً والمربّع الذي يكون من خطّ طاء باء خمسة وعشرون ألفًا وثمان مائة وخمسة وأربعون جزءًا وخمسون دقيقةً والذي من خطّ طاء ألف على ذلك المثال ثلاثة آلاف وخمس مائة وثمانية وستّون جزءًا وأربع دقائق فإذا جمع ذلك كان منه المربّع الذي من خطّ ألف باء تسعةً وعشرين ألفًا وأربع مائة وثلاثة عشر جزءًا وتسعًا وخمسين دقيقةً فيكون خطّ ألف باء في الطول مائةً وأحدًا وسبعين جزءًا وثلاثين دقيقةً بالأجزاء التي بها كان خطّ هاء دال مائةً وعشرين جزءًا وخطّ هاء ألف على ذلك المثال ثمانيةً وسبعين جزءًا ودقيقتين لكنّ الأجزاء
التي بها قطر الفلك الخارج المركز مائة وعشرون جزءًا فإنّ خطّ ألف باء بها أحد وتسعون جزءًا واثنتان وخمسون دقيقةً ولذلك أنّه يوتر قوسًا مبلغها تسعة وتسعون جزءًا وخمس وخمسون دقيقةً فالأجزاء إذن التي بها خطّ ألف باء أحد وتسعون جزءًا واثنتان وخمسون دقيقةً وقطر الفلك الخارج المركز مائة وعشرون جزءًا
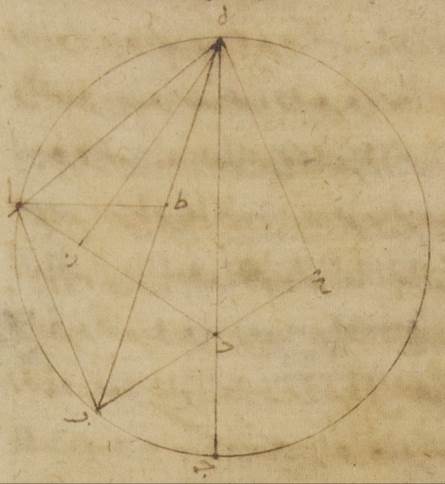 يكون بها خطّ هاء دال أربعةً وستّين جزءًا وسبع عشرة دقيقةً وخطّ هاء ألف أحد وأربعون جزءًا وسبع وأربعون دقيقةً فيجب من ذلك أن تكون القوس التي على خطّ هاء ألف من الفلك الخارج المركز أربعين جزءًا وخمسًا وأربعين دقيقةً وتكون قوس هاء ألف باء جيم بأسرها مائةً وأربعةً وسبعين جزءًا وستّ دقائق فمن قبل ذلك يكون خطّ هاء دال جيم مائةً وتسعة عشر جزءًا وخمسين دقيقةً بالتقريب بالأجزاء التي بها قطر الفلك الخارج المركز مائة وعشرون جزءًا فإنّ قطعة هاء ألف باء جيم أقلّ من نصف دائرة ومن قبل ذلك يقع مركز الفلك الخارج المركز خارجًا منها ب: فلننزل أنّه نقطة كاف وليمرّ عليها وعلى نقطة دال القطر الذي يمرّ بالمركزين وليكن لام كاف دال ميم وليخرج من نقطة كاف على خطّ جيم هاء عمود كاف نون وليخرج إلى نقطة سين فلأنّ الأجزاء التي بها قطر لام ميم مائة وعشرون جزءًا فبها بيّن أنّ جيم هاء بأسره مائة وتسعة عشر جزءًا وخمسون دقيقةً وخطّ هاء دال أربعة وستّون جزءًا وسبع عشرة دقيقةً يكون لنا خطّ جيم دال الباقي بهذه الأجزاء خمسةً وخمسين جزءًا وثلاثًا وثلاثين دقيقةً فلذلك من قبل أنّ السطح القائم الزوايا الذي يحيط به خطّا هاء دال دال جيم مساوٍ للذي يحيط بخ خطّا لام دال دال ميم ويكون الذي يحيط به أيضًا خطّا لام دال دال ميم ثلاثة آلاف وخمس مائة وسبعين جزءًا وستًّا وخمسين دقيقةً بالأجزاء التي بها قطر لام ميم مائة وعشرون جزءًا لكنّ الذي يحيط به خطّا لام دال دال ميم مع المربّع الذي من خطّ دال لام يكون منهما المربّع الذي من نصف القطر أعني خطّ لام كاف فإن نحن إذا نقصنا من المربّع الذي من نصف القطر أعني ثلاثة آلاف وستّ مائة جزء السطح الذي يحيط به خطّا لام دال دال ميم أعني ثلاثة آلاف وخمس مائة وسبعين جزءًا وستًّا وخمسين دقيقةً بقي لنا المربّع الذي من خطّ كاف دال بهذه الأجزاء تسعةً وعشرين جزءًا وأربع دقائق فيحصل لنا إذن خطّ دال لام في الطول وهو الذي بين المركزين بهذه الأجزاء خمسة أجزاء وثلاثًا وعشرين دقيقةً بالتقريب بالأجزاء التي بها خطّ كاف لام الذي من مركز الفلك الخارج المركز ستّون جزءًا وأيضًا لأنّ نصف خطّ جيم هاء أعني خطّ جيم نون تسعة وخمسون جزءًا وخمس وخمسون دقيقةً بالأجزاء التي بها قطر لام ميم مائة وعشرون جزءًا وبهذه الأجزاء تبيّن أنّ خطّ جيم دال خمسة وخمسون جزءًا وثلاث وثلاثون دقيقةً يكون إذن خطّ دال نون الباقي أربعة أجزاء واثنتين وعشرين دقيقةً بالأجزاء التي بها كان خطّ دال كاف خمسة أجزاء وثلاثًا وعشرين دقيقةً فتكون لذلك الأجزاء التي بها خطّ دال لام الموتر مائةً وعشرين جزءًا
يكون بها خطّ هاء دال أربعةً وستّين جزءًا وسبع عشرة دقيقةً وخطّ هاء ألف أحد وأربعون جزءًا وسبع وأربعون دقيقةً فيجب من ذلك أن تكون القوس التي على خطّ هاء ألف من الفلك الخارج المركز أربعين جزءًا وخمسًا وأربعين دقيقةً وتكون قوس هاء ألف باء جيم بأسرها مائةً وأربعةً وسبعين جزءًا وستّ دقائق فمن قبل ذلك يكون خطّ هاء دال جيم مائةً وتسعة عشر جزءًا وخمسين دقيقةً بالتقريب بالأجزاء التي بها قطر الفلك الخارج المركز مائة وعشرون جزءًا فإنّ قطعة هاء ألف باء جيم أقلّ من نصف دائرة ومن قبل ذلك يقع مركز الفلك الخارج المركز خارجًا منها ب: فلننزل أنّه نقطة كاف وليمرّ عليها وعلى نقطة دال القطر الذي يمرّ بالمركزين وليكن لام كاف دال ميم وليخرج من نقطة كاف على خطّ جيم هاء عمود كاف نون وليخرج إلى نقطة سين فلأنّ الأجزاء التي بها قطر لام ميم مائة وعشرون جزءًا فبها بيّن أنّ جيم هاء بأسره مائة وتسعة عشر جزءًا وخمسون دقيقةً وخطّ هاء دال أربعة وستّون جزءًا وسبع عشرة دقيقةً يكون لنا خطّ جيم دال الباقي بهذه الأجزاء خمسةً وخمسين جزءًا وثلاثًا وثلاثين دقيقةً فلذلك من قبل أنّ السطح القائم الزوايا الذي يحيط به خطّا هاء دال دال جيم مساوٍ للذي يحيط بخ خطّا لام دال دال ميم ويكون الذي يحيط به أيضًا خطّا لام دال دال ميم ثلاثة آلاف وخمس مائة وسبعين جزءًا وستًّا وخمسين دقيقةً بالأجزاء التي بها قطر لام ميم مائة وعشرون جزءًا لكنّ الذي يحيط به خطّا لام دال دال ميم مع المربّع الذي من خطّ دال لام يكون منهما المربّع الذي من نصف القطر أعني خطّ لام كاف فإن نحن إذا نقصنا من المربّع الذي من نصف القطر أعني ثلاثة آلاف وستّ مائة جزء السطح الذي يحيط به خطّا لام دال دال ميم أعني ثلاثة آلاف وخمس مائة وسبعين جزءًا وستًّا وخمسين دقيقةً بقي لنا المربّع الذي من خطّ كاف دال بهذه الأجزاء تسعةً وعشرين جزءًا وأربع دقائق فيحصل لنا إذن خطّ دال لام في الطول وهو الذي بين المركزين بهذه الأجزاء خمسة أجزاء وثلاثًا وعشرين دقيقةً بالتقريب بالأجزاء التي بها خطّ كاف لام الذي من مركز الفلك الخارج المركز ستّون جزءًا وأيضًا لأنّ نصف خطّ جيم هاء أعني خطّ جيم نون تسعة وخمسون جزءًا وخمس وخمسون دقيقةً بالأجزاء التي بها قطر لام ميم مائة وعشرون جزءًا وبهذه الأجزاء تبيّن أنّ خطّ جيم دال خمسة وخمسون جزءًا وثلاث وثلاثون دقيقةً يكون إذن خطّ دال نون الباقي أربعة أجزاء واثنتين وعشرين دقيقةً بالأجزاء التي بها كان خطّ دال كاف خمسة أجزاء وثلاثًا وعشرين دقيقةً فتكون لذلك الأجزاء التي بها خطّ دال لام الموتر مائةً وعشرين جزءًا
فخطّ دال نون بها سبعة وتسعون جزءًا وعشرون دقيقةً والقوس التي عليه مائة وثمانية أجزاء وأربع وعشرون دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال كاف نون القائم الزاوية ثلاث مائة وستّون جزءًا فزاوية دال كاف نون إذن ه - صح: إذن أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فإنّها مائة وثمانية أجزاء وأربع وعشرون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فإنّها أربعة وخمسون جزءًا واثنتا عشرة دقيقةً ولأنّها عند مركز الفلك الخارج المركز تكون لنا قوس ميم سين أيضًا أربعةً وخمسين جزءًا واثنتا عشرة دقيقةً بالأجزاء التي بها الفلك الخارج المركز ثلاث مائة وستّون جزءًا لكنّ قوس جيم ميم سين بأسرها إذ هي نصف قوس جيم سين هاء تسعة وثمانون جزءًا وثلاث دقائق فقوس ميم جيم إذن الباقية التي من البعد الأقرب إلى الحال الثالثة من أجزاء طرف الليل يكون اثنين وثلاثين جزءًا وإحدى وخمسين دقيقةً وظاهر أنّ بعد باء جيم إذ كان قد وضع ثلاثةً وثلاثين جزءًا وستًّا وعشرين دقيقةً فإنّ قوس باء ميم الباقية وهي التي من الحال الثانية إلى البعد الأقرب يحصل لنا خمس وثلاثون دقيقةً وبعد ألف باء إذ كان قد وضع تسعةً وتسعين جزءًا وخمسًا وخمسين دقيقةً فإنّ قوس لام ألف الباقية وهي التي من البعد الأبعد
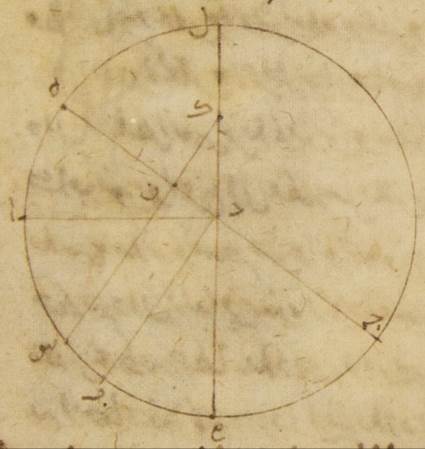 إلى الحال الأولى يحصل لنا تسعةً وسبعين جزءًا وثلاثين دقيقةً فلو كان مركز فلك التدوير إنّما يدور على هذا الفلك الخارج المركز لقد كان سيكتفى باستعمال هذه المقادير إذ كانت لا تغادر لكن لمّا كان على حسب ما يلزم في الأصل الذي عليه يعمل إنّما يدور على دائرة أخرى وهي التي ترسم بمركز يقسم خطّ دال كاف بنصفين وببعد كاف لام فقد يحتاج أيضًا كما احتيج في كوكب المرّيخ إلى أن تحسب أوّلًا الفصول التي تكون للأبعاد التي ترى وإلى أن تتبيّن كم كانت تكون مقاديرها إذا كانت هذه هي أقدار الخروج عن المركز بالتقريب لو لم يكن مركز فلك التدوير يدور على فلك خارج المركز آخر بل على الفلك الأوّل الذي يشتمل على الاختلاف الذي من قبل فلك البروج أعني الفلك الذي يرسم حول مركز كاف جـ: فليكن الآن الفلك الخارج المركز الحامل لمركز فلك التدوير فلك لام ميم حول مركز دال والفلك الذي لحركته المستوية فلأنّ نون سين حول مركز زاي مساويًا لفلك لام ميم وليوصل القطر الذي يمرّ بالمراكز وليكن خطّ باء لام ميم وليوجد عليه مركز فلك البروج أيضًا نقطة هاء ولننزل أوّلًا في الحال الأولى من أحوال طرف الليل مركز فلك التدوير على نقطة ألف ولتوصل خطوط دال ألف هاء ألف زاي ألف سين هاء سين وليخرج من نقطتي دال هاء على خطّ ألف زاي إذا أخرج على الاستقامة عمودا دال حاء هاء طاء فلأنّ زاوية نون زاي سين وهي زاوية مسير المشتري في الطول قد تبيّن أنّها تسعة وسبعون جزءًا وثلاثون دقيقةً بالأجزاء التي بها أربع زوايا
إلى الحال الأولى يحصل لنا تسعةً وسبعين جزءًا وثلاثين دقيقةً فلو كان مركز فلك التدوير إنّما يدور على هذا الفلك الخارج المركز لقد كان سيكتفى باستعمال هذه المقادير إذ كانت لا تغادر لكن لمّا كان على حسب ما يلزم في الأصل الذي عليه يعمل إنّما يدور على دائرة أخرى وهي التي ترسم بمركز يقسم خطّ دال كاف بنصفين وببعد كاف لام فقد يحتاج أيضًا كما احتيج في كوكب المرّيخ إلى أن تحسب أوّلًا الفصول التي تكون للأبعاد التي ترى وإلى أن تتبيّن كم كانت تكون مقاديرها إذا كانت هذه هي أقدار الخروج عن المركز بالتقريب لو لم يكن مركز فلك التدوير يدور على فلك خارج المركز آخر بل على الفلك الأوّل الذي يشتمل على الاختلاف الذي من قبل فلك البروج أعني الفلك الذي يرسم حول مركز كاف جـ: فليكن الآن الفلك الخارج المركز الحامل لمركز فلك التدوير فلك لام ميم حول مركز دال والفلك الذي لحركته المستوية فلأنّ نون سين حول مركز زاي مساويًا لفلك لام ميم وليوصل القطر الذي يمرّ بالمراكز وليكن خطّ باء لام ميم وليوجد عليه مركز فلك البروج أيضًا نقطة هاء ولننزل أوّلًا في الحال الأولى من أحوال طرف الليل مركز فلك التدوير على نقطة ألف ولتوصل خطوط دال ألف هاء ألف زاي ألف سين هاء سين وليخرج من نقطتي دال هاء على خطّ ألف زاي إذا أخرج على الاستقامة عمودا دال حاء هاء طاء فلأنّ زاوية نون زاي سين وهي زاوية مسير المشتري في الطول قد تبيّن أنّها تسعة وسبعون جزءًا وثلاثون دقيقةً بالأجزاء التي بها أربع زوايا
قائمة ثلاث مائة وستّون جزءًا تكون أيضًا الزاوية التي على رأسها وهي زاوية دال زاي حاء أمّا بالأجزاء التي بها أربع زوايا في الأصل: زوا قائمة ثلاث مائة وستّون جزءًا فتسعة وسبعون جزءًا وثلاثون دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فمائة وتسعة وخمسون جزءًا فتكون لذلك أمّا القوس التي على خطّ دال حاء فمائة وتسعة وخمسون جزءًا بالأجزاء التي بها الدائرة المحيطة بمثلّث دال زاي حاء القائم الزاوية ثلاث مائة وستّون جزءًا وأمّا القوس التي على خطّ زاي حاء فالأجزاء الباقية لتمام نصف دائرة وهي أحد وعشرون جزءًا فخطّ دال حاء إذن من الخطّين اللذين يوترانهما يكون مائةً وسعة عشر جزءًا وتسعًا وخمسين دقيقةً بالأجزاء التي بها موتر دال زاي مائة وعشرون جزءًا وخطّ زاي حاء يكون بهذه الأجزاء أحدًا وعشرين جزءًا واثنتين وخمسين دقيقةً فالأجزاء إذن التي بها أمّا خطّ دال نون إذ كان نصف خطّ هاء زاي فجزءان واثنتان وأربعون دقيقةً بالتقريب وأمّا خطّ دال ألف وهو من مركز فلك الخارج المركز ستّون جزءًا يكون بها أمّا خطّ دال حاء فجزءان وتسع وثلاثون دقيقةً وأمّا خطّ زاي حاء على ذلك المثال فثلاثون دقيقةً ولأنّ المربّع الذي من خطّ دال حاء إذا نقص من الذي من خطّ دال ألف يكون المربّع الذي من خطّ ألف حاء يحصل لنا خطّ ألف حاء بهذه الأجزاء تسعةً وخمسين جزءًا وستًّا وخمسين دقيقةً وعلى هذا المثال لأنّ خطّ زاي حاء مساوٍ لخطّ حاء طاء وخطّ هاء طاء ضعف خطّ دال حاء يكون خطّ ألف طاء بأسره ستّين جزءًا وستًّا وعشرين دقيقةً بالأجزاء التي بها خطّ هاء طاء خمسة أجزاء وثمان عشرة دقيقةً ومن قبل ذلك يكون موترًا ألف هاء بهذه الأجزاء ستّين جزءًا وأربعين دقيقةً فالأجزاء إذن التي بها خطّ ألف هاء مائة وعشرون جزءًا يكون بها أمّا خطّ هاء طاء فعشرة أجزاء وتسع وعشرون دقيقةً وأمّا القوس التي عليه فعشرة أجزاء ودقيقة واحدة بالتقريب بالأجزاء التي بها الدائرة التي ترسم حول مثلّث ألف هاء طاء القائم الزاوية ثلاث مائة وستّون جزءًا فتكون لذلك زاوية هاء ألف طاء عشرة أجزاء ودقيقة واحدة بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وأيضًا لأنّ الأجزاء التي بها خطّ هاء طاء خمسة أجزاء وثمان عشرة دقيقةً فإنّ خطّ زاي سين بها إذ كان من مركز الفلك الخارج المركز ستّون جزءًا وخطّ زاي هاء بها جزء واحد ومن البيّن أنّ خطّ سين طاء بأسره يكون بها أحدًا وستّين جزءًا يحصل لنا خطّ هاء سين الموتر أيضًا بهذه الأجزاء أحدًا وستّين جزءًا وأربع عشرة دقيقةً فلذلك تكون الأجزاء التي بها خطّ هاء سين مائة وعشرون جزءًا فإنّ خطّ هاء طاء بها عشرة أجزاء وثلاث وعشرون دقيقةً والقوس التي عليه تسعة أجزاء وخمس
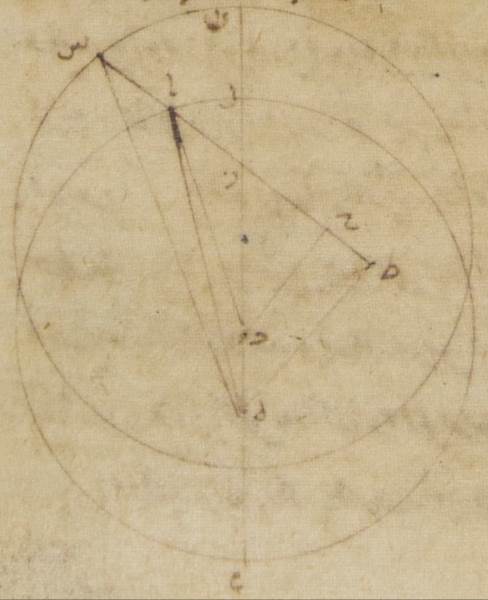 وخمسون دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث هاء طاء سين القائم الزاوية ثلاث مائة وستّون جزءًا فزاوية هاء سين طاء إذن تسعة أجزاء وخمس وخمسون دقيقةً فالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وبهذه الأجزاء تبيّن أنّ زاوية هاء ألف طاء عشرة أجزاء ودقيقة واحدة فزاوية ألف هاء سين الباقية وهي زاوية الفضل المطلوب أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة
وخمسون دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث هاء طاء سين القائم الزاوية ثلاث مائة وستّون جزءًا فزاوية هاء سين طاء إذن تسعة أجزاء وخمس وخمسون دقيقةً فالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وبهذه الأجزاء تبيّن أنّ زاوية هاء ألف طاء عشرة أجزاء ودقيقة واحدة فزاوية ألف هاء سين الباقية وهي زاوية الفضل المطلوب أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة
وستّون جزءًا فإنّها تكون ستّ دقائق وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فتكون ثلاث دقائق لكنّ هذا الكوكب وجد حاصله في الحال الأولى من أحوال طرف الليل وكان يرى على خطّ هاء ألف على ثلاثة وعشرين جزءًا وإحدى عشرة دقيقةً من العقرب فظاهر إذن أنّه لو لم يكن مركز فلك التدوير يتحرّك على فلك لام ميم الخارج المركز لكن على فلك نون سين لقد كان فلك التدوير سيكون على نقطة سين من هذا الفلك وكان الكوكب يوتر على خطّ هاء سين وكان مبلغ الفضل فيه فيما بين الموضعين ثلاث دقائق فكان حاصله يكون على ثلاثة وعشرين جزءًا وأربع عشرة دقيقةً من العقرب⊙ د: وأيضًا في مثل هذا الشكل نضع صورة الحال الثانية من أحوال طرف الليل على أنّها في الشكل متقدّمة قليلًا للبعد الأقرب فلأنّ قوس سين زاي من الفلك الخارج المركز قد تبيّن أنّها خمس وثلاثون دقيقةً تكون زاوية نون زاي سين أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فخمس وثلاثون دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فجزء واحد وعشر دقائق فتكون لذلك أمّا القوس التي على خطّ دال حاء فجزء واحد وعشر دقائق بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال زاي حاء القائم الزاوية ثلاث مائة وستّون جزءًا وأمّا القوس التي على خطّ زاي حاء فما يبقى لتمام نصف دائرة وهو مائة وثمانية وسبعون جزءًا وخمسون دقيقةً فخطّ دال حاء إذن من الخطّين اللذين يوترانهما يكون جزء واحدًا وثلاث عشرة دقيقةً بالأجزاء التي بها خطّ دال زاي الموتر مائة وعشرون جزءًا وخطّ زاي حاء يكون بهذه الأجزاء بالتقريب مائةً وعشرين جزءًا فالأجزاء إذن التي بها أمّا خطّ دال زاي فجزءان واثنتان وأربعون دقيقةً وأمّا خطّ دال باء الذي من مركز الفلك الخارج المركز فستّون جزءًا يكون بها أمّا خطّ دال حاء فدقيقتان وأمّا خطّ زاي حاء فعلى ذلك المثال جزءان واثنتان وأربعون دقيقةً وكذلك خطّ حاء باء إذ كان لا فرق بينه وبين خطّ دال باء الموتر يكون بهذه الأجزاء ستّين جزءًا وأيضًا لأنّ خطّ طاء حاء مساوٍ لخطّ حاء زاي وخطّ هاء طاء ضعف خطّ دال حاء يحصل لنا خطّ طاء باء الباقي سبعة وخمسين جزءًا وثمان عشرة دقيقةً بالأجزاء التي بها خطّ هاء طاء أربع دقائق ومن قبل ذلك يكون موتر هاء باء بهذه الأجزاء سبعةً وخمسين جزءًا وثمان عشرة دقيقةً فلذلك تكون الأجزاء التي بها خطّ هاء باء مائةً وعشرين جزءًا فخطّ هاء طاء بها ثمان دقائق بالتقريب والقوس التي عليه ثمان دقائق وأيضًا فالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء هاء طاء القائم الزاوية ثلاث مائة وستّون جزءًا فزاوية هاء باء طاء إذن ثمان دقائق بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وكذلك أيضًا لأنّ الأجزاء التي بها خطّ زاي سين الذي من مركز الفلك الخارج المركز ستّون جزءًا فخطّ زاي طاء بأسره يبين أنّه خمسة أجزاء وأربع وعشرون دقيقةً يحصل لنا خطّ طاء سين الباقي أربعةً
 وخمسين جزءًا وستًّا وثلاثين دقيقةً بالأجزاء التي بها كان خطّ هاء طاء أربع دقائق ومن قبل ذلك يكون موتر هاء سين بهذه الأجزاء أربعة وخمسين دقيقةً وستًّا وثلاثين ثانيةً فالأجزاء إذن التي بها خطّ هاء سين مائة وعشرون جزءًا يكون بها أمّا خطّ هاء طاء فعشر دقائق بالتقريب وأمّا القوس التي عليه فعشر دقائق بالتقريب بالأجزاء التي بها الدائرة التي ترسم حول مثلّث هاء طاء سين القائم الزاوية ثلاث مائة وستّون جزءًا فلذلك تكون زاوية
وخمسين جزءًا وستًّا وثلاثين دقيقةً بالأجزاء التي بها كان خطّ هاء طاء أربع دقائق ومن قبل ذلك يكون موتر هاء سين بهذه الأجزاء أربعة وخمسين دقيقةً وستًّا وثلاثين ثانيةً فالأجزاء إذن التي بها خطّ هاء سين مائة وعشرون جزءًا يكون بها أمّا خطّ هاء طاء فعشر دقائق بالتقريب وأمّا القوس التي عليه فعشر دقائق بالتقريب بالأجزاء التي بها الدائرة التي ترسم حول مثلّث هاء طاء سين القائم الزاوية ثلاث مائة وستّون جزءًا فلذلك تكون زاوية
هاء سين طاء أيضًا عشر دقائق بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فزاوية باء هاء سين الباقية أمّا بهذه الأجزاء فدقيقتان وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فدقيقة واحدة فظاهر إذن هاهنا أيضًا إذ كان الكوكب في الحال الثانية وقد كان يرى على خطّ هاء باء كان حاصله على سبعة أجزاء وأربع وخمسين دقيقةً من الحوت أنّه لو كان إنّما يرى أيضًا على خطّ هاء سين لكان حاصله على سبعة أجزاء وثلاث وخمسين دقيقةً فقط من الحوت ه: فلنضع أيضًا صورة الحال الثالثة على أنّها متأخّرة في الشكل على القرب الأقرب ولأنّ قوس نون سين من الفلك الخارج المركز قد وضعت اثنين وثلاثين جزءًا وإحدى وخمسين دقيقةً تكون زاوية نون زاي سين أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فاثنان وثلاثون جزءًا وإحدى وخمسون دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فخمسة وستّون جزءًا واثنتان وأربعون دقيقةً فتكون لذلك القوس التي على خطّ دال حاء خمسة وستّين جزءًا واثنتين وأربعين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال زاي حاء القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ زاي حاء ما يبقى لتمام نصف الدائرة وهو مائة وأربعة عشر جزءًا وثمان عشرة دقيقةً فخطّ دال حاء إذن من الخطّين اللذين يوترانهما يكون خمسة وستّين جزءًا وستّ دقائق بالأجزاء التي بها موتر دال زاي مائة وعشرون جزءًا ويكون خطّ زاي حاء بهذه الأجزاء مائة جزء وتسعًا وأربعين دقيقةً فلذلك الأجزاء التي بها أمّا خطّ دال زاي فجزءان واثنتان وأربعون دقيقةً وأمّا خطّ دال جيم الذي من مركز الفلك الخارج المركز فستّون جزءًا يكون بها أمّا خطّ دال حاء فجزءًا واحدًا وستًّا وعشرين دقيقةً وأمّا خطّ زاي حاء فعلى هذا المثال جزأين وستّ عشرة دقيقةً ولأنّ المربّع الذي من خطّ دال حاء إذا نقص من الذي من خطّ حاء دال كان من ذلك المربّع الذي من خطّ جيم حاء يحصل لنا هذا الخطّ أيضًا بهذه الأجزاء تسعةً وخمسين جزءًا وتسعًا وخمسين دقيقةً بالتقريب وعلى هذا المثال لأنّ خطّ طاء حاء مساوٍ لخطّ حاء زاي وخطّ هاء طاء ضعف خطّ دال حاء يحصل لنا خطّ حاء طاء الباقي سبعةً وسبعين جزءًا وثلاثًا وأربعين دقيقةً بالأجزاء التي بها خطّ هاء طاء جزأين وستّ وخمسون دقيقةً ومن قبل ذلك يكون موتر هاء جيم بهذه الأجزاء سبعةً وخمسين جزءًا وسبعًا وأربعين دقيقةً فالأجزاء إذن التي بها خطّ هاء جيم مائة وعشرون جزءًا يكون بها أمّا خطّ هاء طاء فستّة أجزاء وخمس دقائق وأمّا القوس التي عليه فخمسة أجزاء وثمان وأربعون دقيقةً بالتقريب فالأجزاء التي بها الدائرة التي ترسم حول مثلّث جيم هاء طاء القائم الزاوية ثلاث مائة وستّون جزءًا فلذلك تكون زاوية هاء جيم طاء خمسة أجزاء وثمانيًا وأربعين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وكذلك من قبل الأجزاء التي بها خطّ زاي سين الذي من مركز الفلك الخارج المركز ستّون جزءًا فإنّ خطّ زاي طاء بأسره يجتمع بها أربعة أجزاء واثنتين وثلاثين دقيقةً يحصل لنا خطّ سين طاء الباقي خمسةً وخمسين جزءًا وثمانيًا وعشرين دقيقةً بالأجزاء التي بها كان خطّ هاء طاء جزأين وستًّا وخمسين دقيقةً ومن أجل ذلك يكون موتر هاء سين بهذه الأجزاء خمسةً وخمسين جزءًا وثلاثًا وثلاثين دقيقةً فلذلك الأجزاء التي بها خطّ هاء سين مائة وعشرون جزءًا يكون بها أمّا خطّ هاء طاء فستّة أجزاء وعشرون دقيقةً وأمّا القوس التي عليه فتكون ستّة أجزاء ودقيقتين بالأجزاء التي بها الدائرة التي ترسم حول مثلّث هاء طاء سين القائم الزاوية ثلاث مائة وستّون جزءًا فزاوية هاء سين طاء
إذن ستّة أجزاء ودقيقتان بالأجزاء التي بها زاويتان
 قائمتان ثلاث مائة وستّون جزءًا وزاوية جيم هاء سين الباقية أمّا بهذه الأجزاء فأربع عشرة دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فسبع دقائق فلذلك لما كان الكوكب في الحال الثالثة إذ كان يرى على خطّ هاء جيم كان حاصله على أربعة عشر جزءًا وثلاث وعشرين دقيقةً من الحمل فظاهر أنّه لو كان أيضًا على خطّ هاء سين لكان حاصله على أربعة عشر جزءًا وثلاثين دقيقةً من الحمل وقد كان تبيّن أنّ في الحال الأولى كان حاصله سيكون على ثلاثة وعشرين جزءًا وأربع عشرة دقيقةً من العقرب وفي الحال الثانية على سبعة أجزاء وثلاث وخمسين دقيقةً من الحوت فالذي يحصل إذن عليه البعدان اللذان يريان لهذا الكوكب إن لم ينظر فيهما بحسب الفلك الخارج المركز الحامل لمركز فلك التدوير لكن بحسب الفلك الخارج المركز المشتمل على حركته المستوية أمّا البعد بين الحال الأولى وبين الحال الثانية فمائة وأربعة أجزاء وتسع وثلاثون دقيقةً وأمّا البعد بين الحال الثانية وبين الحال الثالثة فستّة وثلاثون جزءًا وسبع وثلاثون دقيقةً فإذا نحن اتّبعنا المعنى ه: يعني الشكل الذي تقدّم بيانه وجدنا الخطّ الذي فيما بين مركز فلك البروج وبين مركز الفلك الخارج المركز المشتمل على حركة فلك التدوير المستوية خمسة أجزاء وثلاثين دقيقةً بالتقريب بالأجزاء التي بها قطر الفلك الخارج المركز مائة وعشرون جزءًا ووجدنا القوس من الفلك الخارج المركز التي بين البعد الأبعد وبين الحال الأولى من أحوال طرف الليل سبعةً وسبعين جزءًا وخمس عشرة دقيقةً والقوس التي بين الحال الثانية وبين البعد الأقرب جزأين وخمسين دقيقةً والقوس التي بين البعد الأقرب وبين الحال الثالثة ثلاثين جزءًا وستًّا وثلاثين دقيقةً وقد يظهر أنّ من هذا الموضع أيضًا استخرجت على الحقيقة المقادير الموصوفة إذ كان التفاضل بين الأبعاد يحصل من هذه المقادير أيضًا موافقًا على التقريب للتفاضل الذي قد تقدّم ذكره من {...} ه: {...} أبعاد الكوكب الذي يرى يوجد بهذه النسب التي استخرجت موافقةً لما وجد منها وذلك يبين ممّا نحن واصفوه⊙ و: لتوضع أيضًا صورة الحال الأولى من أحوال طرف الليل وليكن فيها الفلك الخارج المركز الحامل لمركز فلك التدوير وحده فلأنّ زاوية لام زاي ألف أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فقد تبيّن أنّها سبعة وسبعون جزءًا وخمس عشرة دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فإنّها والزاوية التي على رأسها وهي زاوية دال زاي حاء مائة وأربعة وخمسون جزءًا وثلاثون دقيقةً تكون القوس التي على خطّ دال حاء مائةً وأربعةً وخمسين جزءًا وثلاثين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال زاي حاء القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ زاي حاء ما يبقى لتمام نصف دائرة وهو خمسة وعشرون جزءًا وثلاثون دقيقةً فخطّ دال حاء إذن من الخطّين اللذين يوترانهما مائة وسبعة عشر جزءًا ودقيقتان بالأجزاء التي بها موتر دال نون مائة وعشرون جزءًا
قائمتان ثلاث مائة وستّون جزءًا وزاوية جيم هاء سين الباقية أمّا بهذه الأجزاء فأربع عشرة دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فسبع دقائق فلذلك لما كان الكوكب في الحال الثالثة إذ كان يرى على خطّ هاء جيم كان حاصله على أربعة عشر جزءًا وثلاث وعشرين دقيقةً من الحمل فظاهر أنّه لو كان أيضًا على خطّ هاء سين لكان حاصله على أربعة عشر جزءًا وثلاثين دقيقةً من الحمل وقد كان تبيّن أنّ في الحال الأولى كان حاصله سيكون على ثلاثة وعشرين جزءًا وأربع عشرة دقيقةً من العقرب وفي الحال الثانية على سبعة أجزاء وثلاث وخمسين دقيقةً من الحوت فالذي يحصل إذن عليه البعدان اللذان يريان لهذا الكوكب إن لم ينظر فيهما بحسب الفلك الخارج المركز الحامل لمركز فلك التدوير لكن بحسب الفلك الخارج المركز المشتمل على حركته المستوية أمّا البعد بين الحال الأولى وبين الحال الثانية فمائة وأربعة أجزاء وتسع وثلاثون دقيقةً وأمّا البعد بين الحال الثانية وبين الحال الثالثة فستّة وثلاثون جزءًا وسبع وثلاثون دقيقةً فإذا نحن اتّبعنا المعنى ه: يعني الشكل الذي تقدّم بيانه وجدنا الخطّ الذي فيما بين مركز فلك البروج وبين مركز الفلك الخارج المركز المشتمل على حركة فلك التدوير المستوية خمسة أجزاء وثلاثين دقيقةً بالتقريب بالأجزاء التي بها قطر الفلك الخارج المركز مائة وعشرون جزءًا ووجدنا القوس من الفلك الخارج المركز التي بين البعد الأبعد وبين الحال الأولى من أحوال طرف الليل سبعةً وسبعين جزءًا وخمس عشرة دقيقةً والقوس التي بين الحال الثانية وبين البعد الأقرب جزأين وخمسين دقيقةً والقوس التي بين البعد الأقرب وبين الحال الثالثة ثلاثين جزءًا وستًّا وثلاثين دقيقةً وقد يظهر أنّ من هذا الموضع أيضًا استخرجت على الحقيقة المقادير الموصوفة إذ كان التفاضل بين الأبعاد يحصل من هذه المقادير أيضًا موافقًا على التقريب للتفاضل الذي قد تقدّم ذكره من {...} ه: {...} أبعاد الكوكب الذي يرى يوجد بهذه النسب التي استخرجت موافقةً لما وجد منها وذلك يبين ممّا نحن واصفوه⊙ و: لتوضع أيضًا صورة الحال الأولى من أحوال طرف الليل وليكن فيها الفلك الخارج المركز الحامل لمركز فلك التدوير وحده فلأنّ زاوية لام زاي ألف أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فقد تبيّن أنّها سبعة وسبعون جزءًا وخمس عشرة دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فإنّها والزاوية التي على رأسها وهي زاوية دال زاي حاء مائة وأربعة وخمسون جزءًا وثلاثون دقيقةً تكون القوس التي على خطّ دال حاء مائةً وأربعةً وخمسين جزءًا وثلاثين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال زاي حاء القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ زاي حاء ما يبقى لتمام نصف دائرة وهو خمسة وعشرون جزءًا وثلاثون دقيقةً فخطّ دال حاء إذن من الخطّين اللذين يوترانهما مائة وسبعة عشر جزءًا ودقيقتان بالأجزاء التي بها موتر دال نون مائة وعشرون جزءًا
وخطّ زاي حاء بهذه الأجزاء ستّة وعشرون جزءًا وتسع دقائق فالأجزاء إذن التي بها أمّا خطّ زاي دال فجزءان وخمس وأربعون دقيقةً وأمّا خطّ دال ألف الذي من مركز الفلك الخارج المركز فستّون جزءًا يكون بها أمّا خطّ دال حاء فجزأين وإحدى وأربعين دقيقةً وأمّا خطّ زاي حاء فعلى هذا المثال ستًّا وثلاثين دقيقةً ولمّا تقدّم بيانه بعينه يكون خطّ ألف حاء بهذه الأجزاء تسعةً وخمسين جزءًا وستًّا وخمسين دقيقةً ويكون خطّ ألف طاء بأسره ستّين جزءًا واثنتين وثلاثين دقيقةً فالأجزاء التي بها خطّ هاء طاء إذ هو ضعف دال حاء خمسة أجزاء واثنتان وعشرون دقيقةً
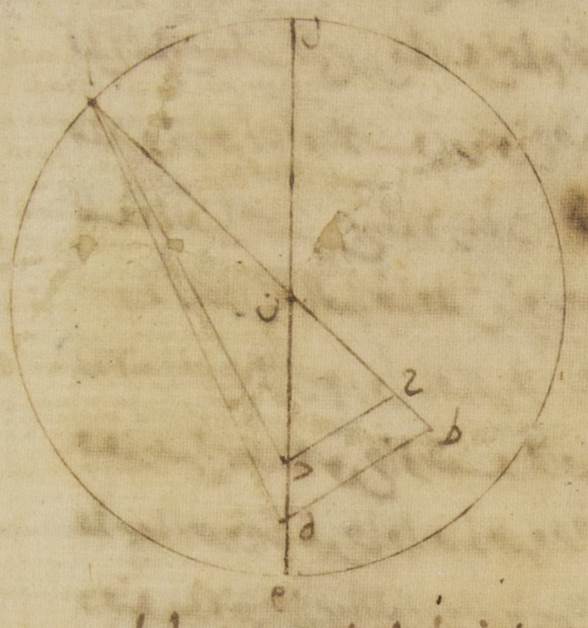 فلذلك يجتمع موتر ألف هاء بهذه الأجزاء ستّين جزءًا وستًّا وأربعين دقيقةً فالأجزاء إذن التي بها خطّ ألف هاء مائة وعشرون جزءًا يكون بها خطّ هاء طاء عشرة أجزاء وستًّا وثلاثين دقيقةً وتكون القوس التي عليه عشرة أجزاء وثمان دقائق بالأجزاء التي بها الدائرة التي ترسم حول مثلّث ألف هاء طاء القائم الزاوية ثلاث مائة وستّون جزءًا فزاوية هاء ألف طاء إذن عشرة أجزاء وثمان دقائق بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وزاوية لام هاء ألف الباقية أمّا بهذه الأجزاء فمائة وأربعة وأربعون جزءًا واثنتان وعشرون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فاثنان وسبعون جزءًا وإحدى عشرة دقيقةً فهذا إذن كان مبلغ أجزاء بعد الكوكب في الحال الأولى من البعد الأبعد في فلك البروج الذي على نقطة لام ز: ولنوضع أوّلًا صورة الحال الثانية فلأنّ زاوية باء زاي ميم أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فقد وضعت جزأين وخمسين دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فخمسة أجزاء وأربعون دقيقةً تكون القوس التي على خطّ دال حاء خمسة أجزاء وأربعين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال زاي حاء القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ زاي حاء الباقي لتمام نصف دائرة وهو مائة وأربعة وسبعون جزءًا وعشرون دقيقةً فخطّ دال حاء إذن من الخطّين اللذين يوترانهما يكون خمسة أجزاء وستًّا وخمسين دقيقةً بالأجزاء التي بها موتر دال زاي مائة وعشرون جزءًا وخطّ زاي حاء بهذه الأجزاء مائة وتسعة عشر جزءًا وإحدى وخمسون دقيقةً فلذلك الأجزاء التي بها أمّا خطّ دال زاي فجزءان وخمس وأربعون دقيقةً وأمّا خطّ دال باء الذي من مركز الفلك الخارج المركز فستّون جزءًا يكون بها أمّا خطّ دال حاء فثمان دقائق وأمّا خطّ زاي حاء فعلى هذا المثال جزأين وخمسًا وأربعين دقيقةً بالتقريب ولذلك بعينه يكون خطّ باء حاء بهذه الأجزاء ستّين جزءًا بالتقريب ويكون خطّ باء طاء الباقي سبعة وخمسين جزءًا وخمس عشرة دقيقةً بالأجزاء التي بها خطّ هاء طاء ستّ عشرة دقيقةً فيجب من ذلك أن يكون موتر هاء باء يجتمع بهذه الأجزاء سبعةً وخمسين جزءًا وخمس عشرة دقيقةً فالأجزاء إذن التي بها خطّ هاء باء مائة وعشرون جزءًا يكون بها خطّ هاء طاء ثلاثًا وثلاثين دقيقةً وتكون القوس التي عليه اثنين وثلاثين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء هاء طاء القائم الزاوية ثلاث مائة وستّون جزءًا فلذلك تكون زاوية هاء باء طاء اثنتين وثلاثين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وتكون
فلذلك يجتمع موتر ألف هاء بهذه الأجزاء ستّين جزءًا وستًّا وأربعين دقيقةً فالأجزاء إذن التي بها خطّ ألف هاء مائة وعشرون جزءًا يكون بها خطّ هاء طاء عشرة أجزاء وستًّا وثلاثين دقيقةً وتكون القوس التي عليه عشرة أجزاء وثمان دقائق بالأجزاء التي بها الدائرة التي ترسم حول مثلّث ألف هاء طاء القائم الزاوية ثلاث مائة وستّون جزءًا فزاوية هاء ألف طاء إذن عشرة أجزاء وثمان دقائق بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وزاوية لام هاء ألف الباقية أمّا بهذه الأجزاء فمائة وأربعة وأربعون جزءًا واثنتان وعشرون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فاثنان وسبعون جزءًا وإحدى عشرة دقيقةً فهذا إذن كان مبلغ أجزاء بعد الكوكب في الحال الأولى من البعد الأبعد في فلك البروج الذي على نقطة لام ز: ولنوضع أوّلًا صورة الحال الثانية فلأنّ زاوية باء زاي ميم أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فقد وضعت جزأين وخمسين دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فخمسة أجزاء وأربعون دقيقةً تكون القوس التي على خطّ دال حاء خمسة أجزاء وأربعين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال زاي حاء القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ زاي حاء الباقي لتمام نصف دائرة وهو مائة وأربعة وسبعون جزءًا وعشرون دقيقةً فخطّ دال حاء إذن من الخطّين اللذين يوترانهما يكون خمسة أجزاء وستًّا وخمسين دقيقةً بالأجزاء التي بها موتر دال زاي مائة وعشرون جزءًا وخطّ زاي حاء بهذه الأجزاء مائة وتسعة عشر جزءًا وإحدى وخمسون دقيقةً فلذلك الأجزاء التي بها أمّا خطّ دال زاي فجزءان وخمس وأربعون دقيقةً وأمّا خطّ دال باء الذي من مركز الفلك الخارج المركز فستّون جزءًا يكون بها أمّا خطّ دال حاء فثمان دقائق وأمّا خطّ زاي حاء فعلى هذا المثال جزأين وخمسًا وأربعين دقيقةً بالتقريب ولذلك بعينه يكون خطّ باء حاء بهذه الأجزاء ستّين جزءًا بالتقريب ويكون خطّ باء طاء الباقي سبعة وخمسين جزءًا وخمس عشرة دقيقةً بالأجزاء التي بها خطّ هاء طاء ستّ عشرة دقيقةً فيجب من ذلك أن يكون موتر هاء باء يجتمع بهذه الأجزاء سبعةً وخمسين جزءًا وخمس عشرة دقيقةً فالأجزاء إذن التي بها خطّ هاء باء مائة وعشرون جزءًا يكون بها خطّ هاء طاء ثلاثًا وثلاثين دقيقةً وتكون القوس التي عليه اثنين وثلاثين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء هاء طاء القائم الزاوية ثلاث مائة وستّون جزءًا فلذلك تكون زاوية هاء باء طاء اثنتين وثلاثين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وتكون
زاوية باء هاء ميم بأسرها أمّا بهذه الأجزاء فستّة أجزاء واثنتا عشرة دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فتكون ثلاثة أجزاء وستّ دقائق فكان بعد الكوكب إذن في الحال الثانية قدمًا للبعد
 الأقرب ثلاثة أجزاء وستّ دقائق وقد كان تبيّن أنّ بعده كان في الحال الأولى متأخّرًا عن البعد الأبعد اثنين وسبعين جزءًا وسبع عشرة دقيقةً فيجتمع إذن البعد من الحال الأولى إلى الحال الثانية التي ترى ما يبقى لتمام نصف دائرة وهو مائة وأربعة أجزاء وثلاث وأربعون دقيقةً وذلك موافق للبعد الذي استخرج ↑: استخرج بالأرصاد ح: فلنضع صورة الحال الثالثة أيضًا فلأنّ زاوية ميم زاي دال أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فقد تبيّن أنّها ثلاثون جزءًا وستّ وثلاثون دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فإنّها أحد وستّون جزءًا واثنتا عشرة دقيقةً تكون القوس التي على خطّ دال حاء أيضًا أحدًا وستّين جزءًا واثنتي عشرة دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال زاي حاء القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ زاي حاء ما يبقى لتمام نصف دائرة وهو مائة وثمانية عشر جزءًا واثنتان وأربعون دقيقةً فخطّ دال حاء إذن من الخطّين اللذين يوترانهما يكون أحدًا وستّين جزءًا وستّ دقائق بالأجزاء التي بها موتر دال زاي مائة وعشرين جزءًا وخطّ زاي حاء بهذه الأجزاء مائة أجزاء وسبع عشرة دقيقةً فلذلك الأجزاء التي بها أمّا خطّ دال زاي فجزءان وخمس وأربعون دقيقةً وأمّا خطّ جيم دال الذي من مركز الفلك الخارج المركز فستّون جزءًا يكون بها أمّا خطّ دال حاء فجزءًا واحدًا وأربعًا وعشرين دقيقةً وأمّا خطّ زاي حاء فعلى هذا المثال جزءان واثنتان وعشرون دقيقةً ولذلك يكون خطّ جيم حاء بهذه الأجزاء تسعةً وخمسين جزءًا وتسعًا وخمسين دقيقةً يكون خطّ حاء طاء الباقي سبعةً وخمسين جزءًا وسبعًا وثلاثين دقيقةً بالأجزاء التي بها يجتمع خطّ هاء طاء جزأين وثمانيًا وأربعين دقيقةً فيصير لذلك موتر هاء جيم سبعةً وخمسين جزءًا وإحدى وأربعين دقيقةً فالأجزاء إذن التي بها خطّ هاء جيم مائة وعشرون جزءًا يكون بها أمّا خطّ هاء طاء فخمسة أجزاء وخمسون دقيقةً وأمّا القوس التي عليه فخمسة أجزاء وأربع وثلاثون دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث جيم هاء طاء القائم الزاوية ثلاث مائة وستّون جزءًا فيكون لذلك أمّا زاوية هاء جيم طاء فخمسة أجزاء وأربع وثلاثون دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وتكون زاوية ميم هاء جيم بأسرها بهذه الأجزاء ستّةً وستّين جزءًا وستًّا وأربعين دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فإنّها تكون ثلاثةً وثلاثين جزءًا وثلاثًا وعشرين دقيقةً فهذا إذن كان مبلغ بعد الكوكب في الحال الثالثة من البعد الأقرب متأخّرًا عنه وقد كان تبيّن أنّ بعده كان في الحال الثانية من هذا البعد الأقرب بعينه متقدّمًا له ثلاثة أجزاء وستّ دقائق فيجتمع إذن البعد الذي يرى من الحال الثانية إلى الحال
الأقرب ثلاثة أجزاء وستّ دقائق وقد كان تبيّن أنّ بعده كان في الحال الأولى متأخّرًا عن البعد الأبعد اثنين وسبعين جزءًا وسبع عشرة دقيقةً فيجتمع إذن البعد من الحال الأولى إلى الحال الثانية التي ترى ما يبقى لتمام نصف دائرة وهو مائة وأربعة أجزاء وثلاث وأربعون دقيقةً وذلك موافق للبعد الذي استخرج ↑: استخرج بالأرصاد ح: فلنضع صورة الحال الثالثة أيضًا فلأنّ زاوية ميم زاي دال أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فقد تبيّن أنّها ثلاثون جزءًا وستّ وثلاثون دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فإنّها أحد وستّون جزءًا واثنتا عشرة دقيقةً تكون القوس التي على خطّ دال حاء أيضًا أحدًا وستّين جزءًا واثنتي عشرة دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال زاي حاء القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ زاي حاء ما يبقى لتمام نصف دائرة وهو مائة وثمانية عشر جزءًا واثنتان وأربعون دقيقةً فخطّ دال حاء إذن من الخطّين اللذين يوترانهما يكون أحدًا وستّين جزءًا وستّ دقائق بالأجزاء التي بها موتر دال زاي مائة وعشرين جزءًا وخطّ زاي حاء بهذه الأجزاء مائة أجزاء وسبع عشرة دقيقةً فلذلك الأجزاء التي بها أمّا خطّ دال زاي فجزءان وخمس وأربعون دقيقةً وأمّا خطّ جيم دال الذي من مركز الفلك الخارج المركز فستّون جزءًا يكون بها أمّا خطّ دال حاء فجزءًا واحدًا وأربعًا وعشرين دقيقةً وأمّا خطّ زاي حاء فعلى هذا المثال جزءان واثنتان وعشرون دقيقةً ولذلك يكون خطّ جيم حاء بهذه الأجزاء تسعةً وخمسين جزءًا وتسعًا وخمسين دقيقةً يكون خطّ حاء طاء الباقي سبعةً وخمسين جزءًا وسبعًا وثلاثين دقيقةً بالأجزاء التي بها يجتمع خطّ هاء طاء جزأين وثمانيًا وأربعين دقيقةً فيصير لذلك موتر هاء جيم سبعةً وخمسين جزءًا وإحدى وأربعين دقيقةً فالأجزاء إذن التي بها خطّ هاء جيم مائة وعشرون جزءًا يكون بها أمّا خطّ هاء طاء فخمسة أجزاء وخمسون دقيقةً وأمّا القوس التي عليه فخمسة أجزاء وأربع وثلاثون دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث جيم هاء طاء القائم الزاوية ثلاث مائة وستّون جزءًا فيكون لذلك أمّا زاوية هاء جيم طاء فخمسة أجزاء وأربع وثلاثون دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وتكون زاوية ميم هاء جيم بأسرها بهذه الأجزاء ستّةً وستّين جزءًا وستًّا وأربعين دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فإنّها تكون ثلاثةً وثلاثين جزءًا وثلاثًا وعشرين دقيقةً فهذا إذن كان مبلغ بعد الكوكب في الحال الثالثة من البعد الأقرب متأخّرًا عنه وقد كان تبيّن أنّ بعده كان في الحال الثانية من هذا البعد الأقرب بعينه متقدّمًا له ثلاثة أجزاء وستّ دقائق فيجتمع إذن البعد الذي يرى من الحال الثانية إلى الحال
الثالثة إذا أجمل ستّةً وثلاثين جزءًا وسبعًا وعشرين دقيقةً
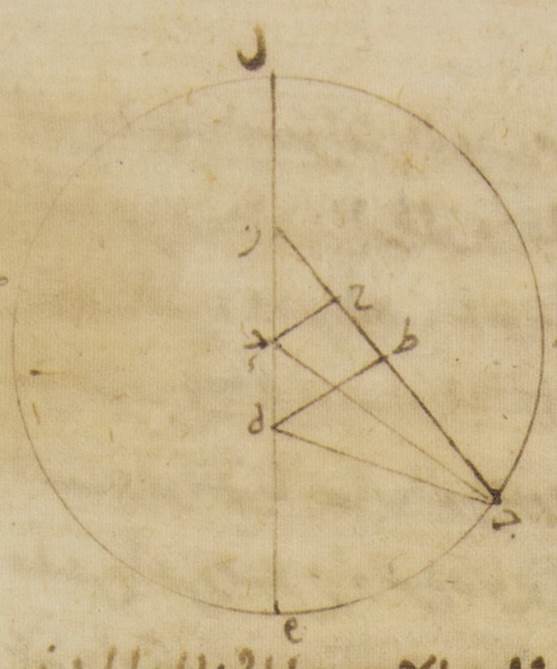 وذلك موافق أيضًا لما رصد⊙ وقد بان من ذلك أنّه كان الكوكب في الحال الثالثة كان حاصله على ما وجد بالرصد على أربعة عشر جزءًا وثلاث وعشرين دقيقةً من الحمل وكان بعده من البعد الأقرب متأخّرًا عنه على ما تبيّن ثلاثة وثلاثون جزءًا وثلاثًا وعشرين دقيقةً فإنّ البعد الأقرب من فلكه الخارج المركز كان حاصله في ذلك الوقت على أحد عشر جزءًا من الحوت والبعد الأبعد على الجزء المقاطر لذلك الجزء وهو الجزء الحادي عشر من العذراء ط: فإذا نحن رسمنا حول مركز دال فلك تدوير حاء طاء كاف كان بيّنًا أنّ المسير الوسط في الطول من البعد الأبعد من الفلك الخارج المركز الذي على نقطة لام يحصل مائتين وعشرة أجزاء وستًّا وثلاثين دقيقةً ومن أجل أنّ زاوية ميم زاي دال قد كان تبيّن أنّها ثلاثون جزءًا وستّ وثلاثون دقيقةً بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا وأنّ قوس طاء كاف من فلك التدوير التي بين نقطة طاء وهي البعد الأقرب وبين نقطة كاف التي عليها الكوكب جزءان وسبع وأربعون دقيقةً من أجل أنّ زاوية جيم هاء راء قد كان تبيّن أنّها خمسة أجزاء وأربع وثلاثون دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فإنّها جزءان وسبع وأربعون دقيقةً ففي وقت الحال الثالثة إذن من أحوال طرف الليل أعني في السنة الأولى من سني
وذلك موافق أيضًا لما رصد⊙ وقد بان من ذلك أنّه كان الكوكب في الحال الثالثة كان حاصله على ما وجد بالرصد على أربعة عشر جزءًا وثلاث وعشرين دقيقةً من الحمل وكان بعده من البعد الأقرب متأخّرًا عنه على ما تبيّن ثلاثة وثلاثون جزءًا وثلاثًا وعشرين دقيقةً فإنّ البعد الأقرب من فلكه الخارج المركز كان حاصله في ذلك الوقت على أحد عشر جزءًا من الحوت والبعد الأبعد على الجزء المقاطر لذلك الجزء وهو الجزء الحادي عشر من العذراء ط: فإذا نحن رسمنا حول مركز دال فلك تدوير حاء طاء كاف كان بيّنًا أنّ المسير الوسط في الطول من البعد الأبعد من الفلك الخارج المركز الذي على نقطة لام يحصل مائتين وعشرة أجزاء وستًّا وثلاثين دقيقةً ومن أجل أنّ زاوية ميم زاي دال قد كان تبيّن أنّها ثلاثون جزءًا وستّ وثلاثون دقيقةً بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا وأنّ قوس طاء كاف من فلك التدوير التي بين نقطة طاء وهي البعد الأقرب وبين نقطة كاف التي عليها الكوكب جزءان وسبع وأربعون دقيقةً من أجل أنّ زاوية جيم هاء راء قد كان تبيّن أنّها خمسة أجزاء وأربع وثلاثون دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فإنّها جزءان وسبع وأربعون دقيقةً ففي وقت الحال الثالثة إذن من أحوال طرف الليل أعني في السنة الأولى من سني
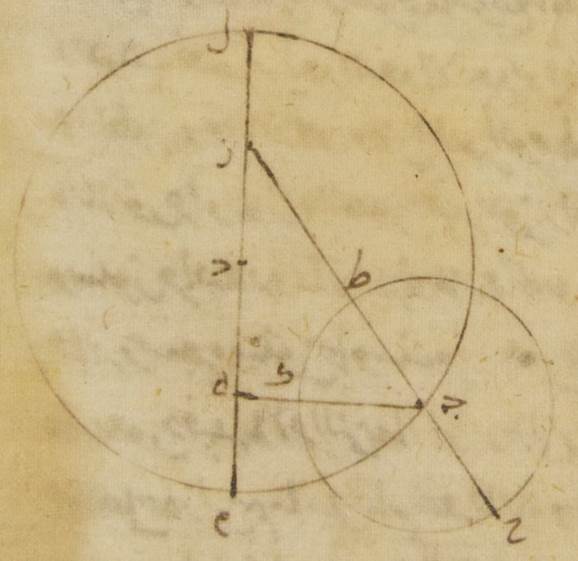 أنطونيس في الشهر المسمّى عند المصريّين أثور في اليوم العشرين منه الليلة التي يتلوها اليوم الحادي والعشرون بعد خمس ساعات من انتصاف الليل كان كوكب المشتري إذا نظر في أمر مسيره الوسط بعده في الطول من البعد الأبعد من الفلك الخارج المركز مائتي جزء وعشرة أجزاء وستًّا وثلاثين دقيقةً أعني أنّ حاصله كان على أحد عشر جزءًا وستّ وثلاثين دقيقةً من الحمل وكان حاصله في الاختلاف على مائة واثنين وثمانين جزءًا وسبع وأربعين دقيقةً من نقطة حاء وهي البعد الأبعد من فلك التدوير⊙
أنطونيس في الشهر المسمّى عند المصريّين أثور في اليوم العشرين منه الليلة التي يتلوها اليوم الحادي والعشرون بعد خمس ساعات من انتصاف الليل كان كوكب المشتري إذا نظر في أمر مسيره الوسط بعده في الطول من البعد الأبعد من الفلك الخارج المركز مائتي جزء وعشرة أجزاء وستًّا وثلاثين دقيقةً أعني أنّ حاصله كان على أحد عشر جزءًا وستّ وثلاثين دقيقةً من الحمل وكان حاصله في الاختلاف على مائة واثنين وثمانين جزءًا وسبع وأربعين دقيقةً من نقطة حاء وهي البعد الأبعد من فلك التدوير⊙
〈XI.2〉 ب: في تبيين مقدار فلك تدوير المشتري
ثمّ من بعد ذلك أخذنا أيضًا لتبيين مقدار فلك تدوير رصدًا كان وقع إلينا بالقياس فيه في السنة الثانية من سني أنطونيس في الشهر المسمّى عند المصريّين ماسوري في اليوم السادس والعشرين منه في الليلة التي يتلوها اليوم السابع والعشرون من قبل طلوع الشمس أعني بعد
خمس ساعات استوائيّة بالتقريب من انتصاف الليل لأنّ مسير الشمس الوسط كان حاصله على ستّة عشر جزءًا وإحدى عشرة دقيقةً من السرطان وكان المتوسّط للسماء في آلة القياس الجزء الثاني من الحمل وكان قياسنا لكوكب المشتري في ذلك الوقت بالكوكب المسمّى الدبران فوجدنا حاصله بالرؤية على خمسة عشر جزءًا ونصف وربع من التوأمين وكان يرى مساويًا في الحاصل لمركز فلك القمر والقمر إذ ذاك أميل إلى الجنوب لكن في تلك الساعة نجد القمر بالحساب الذي تقدّم وصفه حاصله بحركته الوسطى في تسعة أجزاء من التوأمين وبالاختلاف على مائتين واثنين وسبعين جزءًا وخمس دقائق من البعد الأبعد من فلك التدوير ومن أجل ذلك يكون مسيره الحقيقي في أربعة عشر جزءًا وخمسين ه: في نقل الحجّاج أيضًا خمسين دقيقةً وفي نسخة أخرى تسع وخمسون دقيقةً دقيقةً من التوأمين ويكون مسيره الذي يرى بإسكندريّة في خمسة عشر جزءًا ونصف وربع من التوأمين وأيضًا لأنّ الزمان الذي بين الحال الثالثة من أحوال طرف الليل وبين وقت هذا الرصد الذي وضعناه مبلغه سنة واحدة مصريّة ومائتان وستّة وسبعون يومًا والذي تشتمل عليه هذه المدّة فإنّه ليس يقع في ذلك خلاف محسوس وإن حسب على الجليل من الحساب أمّا في الطول فثلاثة وخمسون جزءًا وسبع عشرة دقيقةً وأمّا في الاختلاف فمائتان وثمانية عشر جزءًا وإحدى وثلاثون دقيقةً فإنّا إذا زدنا ذلك على التحصيلات التي بيّنّاها في الحال الثالثة كان لنا في وقت هذا الرصد الحاصل في الطول على مائتي جزء وثلاثة وستّين جزءًا وثلاث وخمسين دقيقةً بالتقريب من البعد الأبعد من الفلك الخارج المركز وحاصل الاختلاف على واحد وأربعين جزءًا وثمان عشرة دقيقةً من البعد الأبعد من فلك التدوير فإذ قد وُطّنت هذه الأشياء على هذه الصفة يے: فلتوضع أيضًا صورة مثل الصورة التي بيّنّا بها هذا المعنى في كوكب المرّيخ وليكن فيها موضع فلك التدوير متأخّرًا عن البعد الأقرب من الفلك الخارج المركز وموضع الكوكب نفسه من بعد البعد الأبعد من فلك التدوير على ما يوافق ما وضعناه هاهنا من المسيرين الوسطين في الطول وفي الاختلاف فلأنّ المسير الوسط في الطول من البعد الأبعد من الفلك الخارج المركز مائتان وستّة وثلاثون جزءًا وثلاث وخمسون دقيقةً تكون زاوية باء زاي جيم أيضًا أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فثلاثة وثمانون جزءًا وثلاث وخمسون دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فمائة وسبعة وستّون جزءًا وستّ وأربعون دقيقةً فلذلك القوس التي على خطّ دال ميم مائة وسبعة وستّون جزءًا وستّ وأربعون دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال زاي ميم القائم الزاوية ثلاث مائة وستّون جزءًا والقوس التي على خطّ زاي ميم ما يبقى لتمام نصف دائرة وهو اثنا عشر جزءًا وأربع عشرة دقيقةً فخطّ دال ميم إذن من الخطّين اللذين يوترانهما مائة وتسعة عشر جزءًا وتسع عشرة دقيقةً بالأجزاء التي بها موتر دال زاي مائة وعشرون جزءًا ولأنّ خطّ زاي ميم بهذه الأجزاء اثنا عشر جزءًا وسبع وأربعون دقيقةً فالأجزاء إذن التي بها أمّا خطّ دال زاي فجزءان وخمس وأربعون دقيقةً وأمّا خطّ دال باء الذي من مركز الفلك الخارج المركز فستّون يكون بها أمّا خطّ دال ميم فجزءان وأربع وأربعون دقيقةً بالتقريب وأمّا خطّ زاي ميم فعلى ذلك المثال ثمان عشرة دقيقةً ولأنّ المربّع الذي من خطّ دال ميم إذا نقص من الذي من خطّ دال باء كان من ذلك المربّع الذي من خطّ باء ميم يكون خطّ ميم باء بهذه الأجزاء تسعةً وخمسين جزءًا وستًّا وخمسين دقيقةً وعلى هذا المثال لأنّ خطّ زاي ميم مساوٍ لخطّ ميم لام وخطّ هاء لام ضعف خطّ دال ميم يكون خطّ
لام باء الباقي تسعةً وخمسين جزءًا وثمانيًا وثلاثين دقيقةً بالأجزاء التي بها يجتمع خطّ هاء لام خمسة أجزاء وثمانيًا وعشرين دقيقةً ومن أجل ذلك يكون خطّ هاء باء الموتر بهذه الأجزاء تسعةً وخمسين جزءًا واثنتين وخمسين دقيقةً فالأجزاء إذن التي بها خطّ هاء باء مائة وعشرون جزءًا يكون بها أمّا خطّ هاء لام فعشرة أجزاء وثمان وخمسون دقيقةً بالتقريب وأمّا القوس التي عليه فعشرة أجزاء وثلاثون دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء هاء لام القائم الزاوية ثلاث مائة وستّون جزءًا فتكون لذلك زاوية باء هاء زاي عشرة أجزاء وثلاثين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وبهذه الأجزاء كانت زاوية باء زاي جيم مائةً وسبعةً وستّين جزءًا وستًّا وأربعين دقيقةً فتكون زاوية باء هاء جيم إذن بأسرها بهذه الأجزاء مائةً وثمانيةً وسبعين جزءًا وستّ عشرة دقيقةً⊙ وأيضًا لأنّ نقطة دال وهي البعد الأقرب كان حاصلها على أحد عشر جزءًا من الحوت بالتقريب وكان الكوكب يرى على خطّ هاء دال وحاصله على خمسة عشر جزءًا وخمس وأربعين دقيقةً من التوأمين تكون زاوية كاف هاء جيم أيضًا أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فأربعة وتسعون جزءًا وخمس وأربعون دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فمائة وتسعة وثمانون جزءًا وثلاثون دقيقةً فزاوية باء هاء كاف الباقية بهذه الأجزاء أحد عشر جزءًا وأربع عشرة دقيقةً بالأجزاء التي بها موتر هاء باء مائة وعشرون جزءًا فالأجزاء إذن التي بها أمّا خطّ هاء باء فتسعة وخمسون جزءًا واثنتان وخمسون دقيقةً وأمّا الخطّ الذي من مركز الفلك الخارج المركز فستّون جزءًا يكون بها خطّ باء زاي خمسة أجزاء وخمسين دقيقةً وعلى هذا المثال لأنّ قوس حاء كاف أحد وأربعون جزءًا وثمان عشرة دقيقةً تكون أيضًا زاوية حاء باء كاف أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فأحد وأربعون جزءًا وثمان عشرة دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فاثنان وثمانون جزءًا وستّ وثلاثون دقيقةً وبهذه الأجزاء كانت زاوية هاء باء زاي أعني زاوية حاء باء طاء عشرة أجزاء وثلاثين دقيقةً فتكون زاوية طاء باء كاف إذن الباقية اثنين وسبعين جزءًا وستّ دقائق وقد كان تبيّن أنّ زاوية طاء هاء كاف
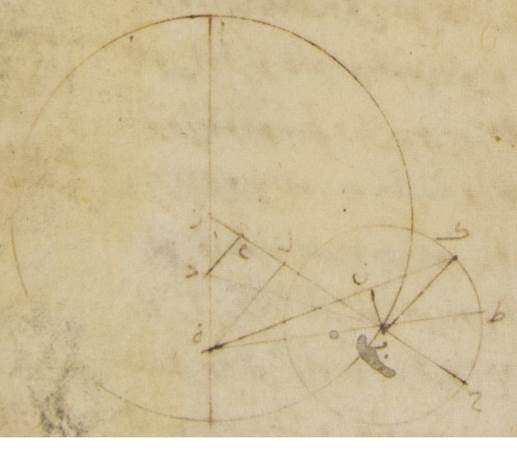 بهذه الأجزاء أحد عشر جزءًا وأربع عشرة دقيقةً فزاوية باء كاف نون إذن الباقية بهذه الأجزاء ستّون جزءًا واثنتان وخمسون دقيقةً فلذلك تكون القوس التي على خطّ باء نون ستّين جزءًا واثنتين وخمسين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء كاف نون القائم الزاوية ثلاث مائة وستّون جزءًا لكنّ خطّ باء نون ستّون جزءًا وسبع وأربعون دقيقةً بالأجزاء التي بها موتر باء كاف مائة وعشرون جزءًا فالأجزاء إذن التي بها أمّا خطّ باء نون فخمسة أجزاء وخمسون دقيقةً وأمّا الخطّ الذي من مركز الفلك الخارج المركز فستّون جزءًا يكون بها خطّ باء كاف الذي من مركز فلك التدوير
بهذه الأجزاء أحد عشر جزءًا وأربع عشرة دقيقةً فزاوية باء كاف نون إذن الباقية بهذه الأجزاء ستّون جزءًا واثنتان وخمسون دقيقةً فلذلك تكون القوس التي على خطّ باء نون ستّين جزءًا واثنتين وخمسين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء كاف نون القائم الزاوية ثلاث مائة وستّون جزءًا لكنّ خطّ باء نون ستّون جزءًا وسبع وأربعون دقيقةً بالأجزاء التي بها موتر باء كاف مائة وعشرون جزءًا فالأجزاء إذن التي بها أمّا خطّ باء نون فخمسة أجزاء وخمسون دقيقةً وأمّا الخطّ الذي من مركز الفلك الخارج المركز فستّون جزءًا يكون بها خطّ باء كاف الذي من مركز فلك التدوير
أحد عشر جزءًا وثلاثين دقيقةً بالتقريب وذلك ما كان يحتاج إلى وجوده⊙
〈XI.3〉 جـ: في تصحيح حركات كوكب المشتري الدوريّة
ثمّ من بعد ذلك أخذنا لأدوار كوكب المشتري أيضًا رصدًا من الأرصاد القديمة التي أتمّت على الاستقصاء الذي لا شكّ فيه قيل فيه نصًّا إنّ في سنة خمس وأربعين على عهد ديونوسيوس في اليوم العاشر من الشهر المسمّى يوناير ه: هذا الاسم مشتقّ من اسم العذراء أي الشهر المنسوب إلى العذراء ستر كوكب المشتري بالغداة الكوكب المسمّى الجبّار الجنوبيّ وهذا الوقت هو في سنة ثلاث وستّين من وفاة الإسكندر في الشهر من شهور المصريّين المسمّى إيبفي في اليوم السابع عشر منه في الليلة التي يتلوها اليوم الثامن عشر في الغلس ونجد الشمس في ذلك الوقت حاصلها بسيرها الوسط على تسعة أجزاء وستّ وخمسين دقيقةً من العذراء لكنّ الكوكب المسمّى الجبّار الجنوبيّ وهو من الكواكب التي حول الفطحة التي في السرطان كان حاصله في وقت رصدنا نحن على أحد عشر جزءًا وثلث جزء من السرطان ومن البيّن أنّه كان حاصله في وقت الرصد الذي وصفناه على سبعة أجزاء وثلاث وثلاثين دقيقةً منه من قبل أنّ الذي يصيب الزمان الذي فيما بين الرصدين وهو ثلاث مائة وثمان وسبعون سنة ثلاثة أجزاء وسبع وأربعون دقيقةً فكوكب المشتري أيضًا كان حاصله في ذلك الوقت من قبل أنّه ستر هذا الكوكب على سبعة أجزاء وثلاث وثلاثين دقيقةً من السرطان وكذلك أيضًا لمّا كان البعد الأبعد في عصرنا كان في أحد عشر جزءًا من العذراء فواجب أن يكون حاصله كان في وقت ذلك الرصد على سبعة أجزاء وثلاث عشرة دقيقةً منها ومن البيّن أنّ هذا الكوكب بالرؤية كان بعده من البعد الأبعد من الفلك الخارج المركز في ذلك الوقت ثلاث مائة جزء وعشرين دقيقةً وكان بعد الشمس بحركتها الوسطى من ذلك البعد الأبعد جزأين وثلاثًا وأربعين دقيقةً⊙ فإذ قد وطّنت هذه الأشياء يا: فلتوضع أيضًا مثل الصورة التي بيّن بها هذا المعنى من أمر المرّيخ ما خلا أنّا نجعلها هاهنا موافقةً للمسيرات التي فرضت في الرصد حتى يكون فيها وضع فلك التدوير الذي حول نقطة باء قبل نقطة ألف التي هي البعد الأبعد وحاصل الشمس بحركتها الوسطى على نقطة لام بعد ذلك البعد الأبعد قليلًا ولذلك يكون أيضًا وضع الكوكب على نقطة طاء بعد نقطة حاء وهي البعد الأبعد من فلك التدوير وتوصل على ذلك المثال أبدًا خطوط زاي باء حاء دال باء باء طاء هاء طاء ويخرج على خطّ دال باء عمود زاي كاف وعلى خطّ هاء طاء عمودا دال ميم باء نون وعلى خطّ باء نون إذا زيد في إخراجه في هذا الموضع عمود دال سين حتّى تحدث الأعمدة سطحًا متوازي الأضلاع قائم الزوايا وهو سطح دال ميم نون سين فلأنّ زاوية ألف هاء طاء إذ تحيط بما يبقى لتمام دائرة واحدة وهي دائرة البروج بعد الثلاث مائة الجزء والعشرين الدقيقة هي تسعة وخمسون جزءًا وأربعون دقيقةً بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا وزاوية ألف هاء لام بهذه الأجزاء جزءان وثلاث وأربعون دقيقةً تكون زاوية لام هاء طاء بأسرها أعني زاوية باء طاء هاء أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فمائة وأربعة وعشرون جزءًا وستّ وأربعون دقيقةً فلذلك تكون القوس التي على خطّ باء نون مائةً وأربعةً وعشرين جزءًا وستًّا وأربعين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء طاء نون القائم الزاوية ثلاث مائة وستّون جزءًا
ويكون خطّ باء نون مائةً وستّة أجزاء وعشرين دقيقةً بالأجزاء التي بها موتر باء طاء مائة وعشرين جزءًا فالأجزاء إذن التي بها خطّ باء طاء الذي من مركز فلك التدوير أحد عشر جزءًا وثلاثون دقيقةً يكون بها خطّ باء نون عشرة أجزاء واثنتي عشرة دقيقةً وأيضًا لأنّ زاوية دال هاء ميم أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فقد وضعت تسعة وخمسين جزءًا وأربعين دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فمائة وتسعة عشر جزءًا وعشرين دقيقةً وزاوية ميم دال هاء الباقية بهذه الأجزاء ستّين جزءًا وأربعين تكون القوس التي على خطّ دال ميم مائة تسعة عشر جزءًا وعشرين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال هاء ميم القائم الزاوية ثلاث مائة وستّون جزءًا ويكون خطّ دال ميم مائة وثلاثة أجزاء وأربعًا وثلاثين دقيقةً بالأجزاء التي بها موتر هاء دال مائة وعشرون جزءًا فالأجزاء إذن التي بها أمّا خط هاء دال فجزءان وخمس وأربعون دقيقةً وأمّا خطّ دال باء الذي من مركز الفلك الخارج المركز فستّون جزءًا يكون بها أمّا خطّ دال ميم فجزأين وثلاث وعشرون دقيقةً وأمّا خطّ باء نون سين بأسره فاثنا عشر جزءًا وخمس وثلاثون دقيقةً بهذه الأجزاء فلذلك الأجزاء التي بها موتر باء دال مائة وعشرون جزءًا يكون بها أمّا خطّ باء نون فخمسة وعشرون جزءًا وعشر دقائق وأمّا القوس التي عليه فأربعة وعشرون جزءًا وأربع عشرة دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء دال سين القائم الزاوية ثلاث مائة وستّون جزءًا فـ{...} باء دال سين إذن أربعة وعشرون جزءًا وأربع عشرة دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون وزاوية باء دال ميم الباقية بهذه الأجزاء مائة وخمسة وخمسون جزءًا وستّ وأربعون دقيقةً وزاوية باء دال هاء بأسرها على ذلك المثال مائتان وستّة عشر جزءًا وستّ وعشرون دقيقةً وزاوية باء دال زاي الباقية أيضًا بهذه الأجزاء مائة وثلاثة وأربعون جزءًا وأربع وثلاثون دقيقةً فلذلك القوس التي على خطّ زاي كاف باء {...} وأربعون جزءًا وأربع وثلاثون دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال زاي كاف القائم الزاوية ثلاث مائة وستّون جزءًا والقوس التي على خطّ دال كاف ما يبقى لتمام نصف دائرة وهو ستّة وثلاثون جزءًا وتسعًا وخمسين دقيقةً بالأجزاء التي بها موتر دال زاي مائة وعشرون جزءًا ويكون خطّ دال قاف بهذه الأجزاء سبعةً وثلاثين جزءًا وإحدى وثلاثين دقيقةً فالأجزاء إذن التي بها أمّا خطّ دال زاي فجزءان وخمس وأربعون دقيقةً وأمّا خطّ دال باء الذي من مركز الفلك الخارج المركز فستّون جزءًا يكون بها أمّا خطّ زاي كاف فجزءان وسبع وثلاثون دقيقةً وأمّا خطّ دال كاف فعلى هذا المثال اثنان وخمسون دقيقةً ويكون خطّ كاف باء الباقي بهذه الأجزاء تسعةً وخمسين جزءًا وثمان دقائق ومن أجل ذلك يكون موتر زاي باء بهذه الأجزاء تسعةً وخمسين جزءًا واثنتي عشرة دقيقةً فلذلك تكون الأجزاء التي بها خطّ زاي باء مائة وعشرون جزءًا فخطّ زاي كاف بها خمسة أجزاء وثمان عشرة دقيقةً والقوس التي عليه خمسة أجزاء وأربع دقائق بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء زاي كاف القائم الزاوية ثلاث مائة وستّون جزءًا فزاوية زاي باء دال إذن خمسة أجزاء وأربع دقائق بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فزاوية ألف زاي باء بأسرها وهي التي تشمل على الحركة المستوية في الطول تكون بهذه الأجزاء مائةً وثمانيةً وأربعين جزءًا وثمانيًا وثلاثين دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فأربعة وسبعون جزءًا وتسع عشرة دقيقةً ولأنّ زاوية حاء باء طاء مع زاوية باء زاي جيم ومع
زاويتي نصف الدائرة إذا جمعت أعني إذا نقص منها ه: يعني من زاوية حبط في هذا الموضع زاوية ألف زاي باء حصلت زاوية ألف هاء لام وهي بهذه الأجزاء جزءان وثلاث وأربعون دقيقةً فإنّ زاوية حاء باء طاء وهي التي تشتمل على مسير الكوكب من البعد الأبعد في فلك التدوير يكون بهذه الأجزاء سبعةً وسبعين جزءًا ودقيقتين فقد تبيّن لنا إذن أنّ في وقت ذلك الرصد الذي وصفناه كان بعد كوكب المشتري إذا نظر فيه بمسيره الوسط في الطول مائتي جزء وخمسةً وثمانين جزءًا وإحدى وأربعين دقيقةً من البعد الأبعد كان في ذلك الوقت في الفلك الخارج المركز أعني أنّ حاصله كان بالحركة الوسطى على اثنين وعشرين جزءًا وأربع وخمسين دقيقةً من التوأمين وكان حاصله في الاختلاف على سبعة وأربعين جزءًا ودقيقتين من البعد الأبعد في فلك التدوير⊙ وقد كنّا بيّنّا أنّ بعده كان في وقت الحال الثالثة من البعد الأبعد في فلك التدوير مائة واثنين وستّين جزءًا وسبع وأربعين دقيقةً فقد فضل له إذن في الزمان الذي بين الرصدين ومبلغه من السنين المصريّة ثلاث مائة
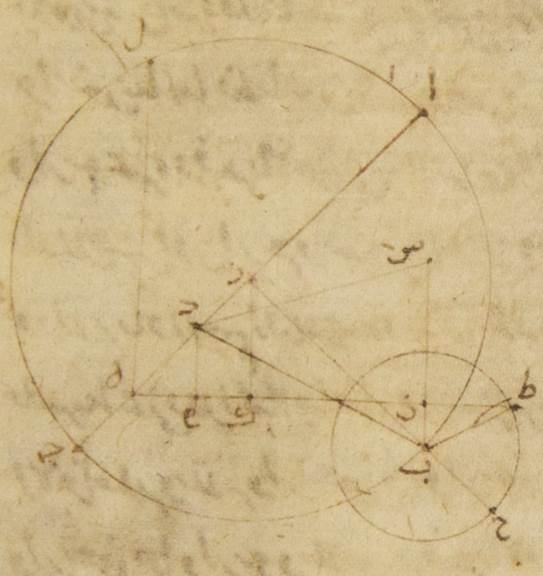 وسبع وسبعون سنةً ومائة وثمانية وعشرون يومًا ينقص نحو من ساعة واحدة بعد الأدوار التامّة للاختلاف وهي ثلاث مائة وخمس وأربعون دورةً ومائة وخمسة أجزاء وخمس وأربعون دقيقةً وذلك أيضًا قريب من فضلة الاختلاف التي توجد تخرج لنا بالحركات الوسطى التي عملناها من قبل أنّا من هذه أنفسها قوّمنا حركته في اليوم بأن قسّمنا الأجزاء التي تحصل من عدّة الأدوار ومن الفضلة على عدّة الأيّام التي تحصل من الزمان الذي فيما بين الرصدين⊙
وسبع وسبعون سنةً ومائة وثمانية وعشرون يومًا ينقص نحو من ساعة واحدة بعد الأدوار التامّة للاختلاف وهي ثلاث مائة وخمس وأربعون دورةً ومائة وخمسة أجزاء وخمس وأربعون دقيقةً وذلك أيضًا قريب من فضلة الاختلاف التي توجد تخرج لنا بالحركات الوسطى التي عملناها من قبل أنّا من هذه أنفسها قوّمنا حركته في اليوم بأن قسّمنا الأجزاء التي تحصل من عدّة الأدوار ومن الفضلة على عدّة الأيّام التي تحصل من الزمان الذي فيما بين الرصدين⊙
〈XI.4〉 د: في تحصيلات أدوار كوكب المشتري
وفي هذا أيضًا لمّا كان الزمان الذي بين السنة الأولى من سني بختنصّر من شهر توث عند المصريّين من اليوم الأوّل منه من انتصاف النهار وبين هذا الرصد القديم الموصوف تكون من السنين المصريّة خمس مائة وستًّا وستّين وثلاث مائة وستّة عشر يومًا ونصف وربع يوم بالتقريب هذا الزمان يحصل فيه من الفضلة أمّا في الطول فمائتان وثمانية وخمسون جزءًا وثلاث عشرة دقيقةً وأمّا في الاختلاف فمائتان وتسعون جزءًا وثمان وخمسون دقيقة. فإنّا إن نقصنا هذين كلّ واحد من نظيره من الحاصلين اللذين وصفناهما في الرصد. كان لنا حاصل كوكب المشتري أيضًا بالحركة الوسطى في ذلك الوقت بعينه الموضوع لتحصيلات سائر الكواكب. أمّا في الطول فعلى أربعة أجزاء وإحدى وأربعين دقيقةً من الميزان. وأمّا في الاختلاف فعلى مائة وستّة وأربعين جزءًا وأربع دقائق من البعد الأبعد في فلك التدوير. ولذلك بعينه يكون أيضًا حاصل البعد الأبعد لفلكه الخارج المركز على جزأين و{...}ـع دقائق من العذراء⊙ ه: {...} لأوّل يوم من ملك قيهابخت {...} ج دقائق من {...} في الاختلاف {..}قيقة من البعد
〈XI.5〉 ه: في تبيين الخروج عن المركز في زحل وبعده الأبعد
وإذ قد بقي في هذا الموضع أن نبيّن الاختلاف والتحصيلات التي توجد في كوكب زحل أيضًا فإنّا أخذنا أيضًا
أوّلًا بسبب النظر في البعد الأبعد ومبلغ خروج الفلك الخارج المركز على المركز كما فعلنا في سائر الكواكب ثلاثة أماكن لهذا الكوكب في الأحوال التي تسمّى طرف الليل كان الكوكب فيها مقاطرًا للشمس بمسيرها الوسط فالأولى من هذه الأحوال لمّا رصدنا الكوكب فيها بآلات القياس في سنة إحدى عشرة من سني أذريانوس في شهر تاجور عند المصريّين في اليوم السابع منه في العشيّة التي يتلوها اليوم الثامن وجدناه في جزء واحدٍ وثلاث عشرة دقيقةً من الميزان وأمّا الحال الثانية فكان رصدنا له فيها في سنة سبع عشرة من سني أذريانوس في شهر إيبفي عند المصريّين في اليوم الثامن عشر منه فأمّا في وقت المقاطرة الصحيحة ومكان الكوكب فيه فإنّا حسبناهما بالمقايسة بينهما وبين ما وقفنا عليه منهما بالأرصاد التي وقعت لنا عند المقاطرة فخرج لنا الوقت بعد أربع ساعات من انتصاف نهار اليوم الثامن عشر وخرج موضع الكوكب في تسعة أجزاء وأربعين دقيقةً من الرامي وأمّا الحال الثالثة فكان رصدنا له في سنة عشرين من سني أذريانوس أيضًا في شهر ماسوري عند المصريّين في اليوم الرابع والعشرين منه وحسبنا وقت المقاطرة الصحيحة على ذلك المثال فوجدناه كان في نصف انتصاف نهار اليوم الرابع والعشرين وحسبنا مكانه فوجدناه في أربعة عشر جزءًا وأربع عشرة دقيقةً من الجدي فهذان البعدان أمّا البعد منهما بين الحال الأولى وبين الحال الثانية فمبلغه ستّ سنين مصريّة وسبعون يومًا واثنان وعشرون ساعةً من أجزاء مسير الكوكب الذي يرى ثمانية وستّون جزءًا وسبع وعشرون دقيقةً وأمّا البعد بين الحال الثانية وبين الثالثة فمبلغه ثلاث سنين وخمسة وثلاثون يومًا وعشرون ساعةً ومن الأجزاء على ذلك المثال أربعة وثلاثون جزءًا وأربع وثلاثون دقيقةً والذي يحصل من أجزاء المسير الوسط في الطول أيضًا على الجليل من الحساب أمّا لزمان البعد الأوّل فخمسة وسبعون جزءًا وثلاث وأربعون دقيقةً وأمّا لزمان البعد الثاني فسبعة وثلاثون جزءًا واثنتان وخمسون دقيقةً⊙ فإذ قد وطّئ هذان البعدان فنحن مبيّنون أيضًا ما قصدنا له بذلك المعنى بعينه وبانون الأمر أوّلًا على أنّ الفلك الخارج المركز واحد بهذا الوجه يب: فلنضع صورةً مثل الصورة التي استعملناها في هذا المعنى من التبيين كيلا نكرّر وصف شيء واحد فلأنّ قوس باء جيم من الفلك الخارج المركز قد وضعت توتر من فلك البروج أربعةً وثلاثين جزءًا وأربعًا وثلاثين دقيقةً تكون زاوية باء دال جيم أيضًا أعني زاوية هاء دال حاء إذ هي عند مركز فلك البروج أمّا بالأجزاء التي بها زاويتان قائمتان ه: قائمتان ثلاث مائة وستّون جزءًا فتسعة وستّون جزءًا وثمان دقائق فيجب لذلك أن تكون القوس التي على خطّ هاء حاء تسعةً وستّين جزءًا وثمان دقائق بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال هاء حاء القائم الزاوية ثلاث مائة وستّون جزءًا ويكون خطّ هاء حاء ثمانية وستّون جزءًا وخمس دقائق بالأجزاء التي بها موتر دال هاء مائة وعشرون جزءًا وعلى هذا المثال لأنّ قوس باء جيم سبعة وثلاثون جزءًا واثنتان وخمسون دقيقةً تكون زاوية باء هاء جيم أيضًا إذ هي عند الخطّ المحيط سبعةً وثلاثين جزءًا واثنتين وخمسين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وتكون زاوية هاء باء حاء الباقية بهذه الأجزاء أحدًا وثلاثين جزءًا وستّ عشرة دقيقةً فيجب لذلك أن تكون القوس التي على خطّ هاء حاء أحدًا وثلاثين جزءًا وستّ عشرة دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء هاء حاء القائم الزاوية ثلاث مائة وستّون جزءًا وأن يكون خطّ هاء حاء اثنتين وثلاثين جزءًا وعشرين دقيقةً
بالأجزاء التي بها موتر باء هاء مائة وعشرون جزءًا فالأجزاء إذن التي بها خطّ هاء حاء على ما تبيّن ثمانية وستّون جزءًا وخمس دقائق وخطّ هاء دال مائة وعشرون جزءًا يكون بها خطّ باء هاء مائتين واثنين وخمسين وإحدى وأربعين دقيقةً⊙ وأيضًا لأنّ قوس ألف باء جيم بأسرها يوتر من فلك البروج الأجزاء المجتمعة من البعدين كليهما وهي مائة وثلاثة أجزاء ودقيقة واحدة تكون زاوية ألف دال جيم أيضًا إذ هي عند مركز فلك البروج مائة وثلاثة أجزاء ودقيقة واحدة بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا ومن قبل ذلك تكون الزاوية التي تتلوها وهي زاوية ألف دال هاء أمّا بهذه الأجزاء فستّة وسبعون جزءًا وتسع وخمسون دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فمائة وثلاثة وخمسون جزءًا وستّ وخمسون دقيقةً فيجب لذلك أن تكون القوس التي على خطّ هاء زاي مائة وثلاثة وخمسين جزءًا وثمانيًا وخمسين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال هاء زاي القائم الزاوية ثلاث مائة وستّون جزءًا ويكون خطّ هاء زاي مائة وستّة عشر جزءًا وخمسًا وخمسين دقيقةً بالأجزاء التي بها موتر دال هاء مائة وعشرون جزءًا وعلى هذا المثال لأنّ قوس ألف باء جيم من الفلك الخارج المركز مبلغها مائة وثلاثة عشر جزءًا وخمس وثلاثون دقيقةً تكون زاوية ألف هاء جيم أيضًا إذ هي عند المحيط مائةً وثلاثة عشر جزءًا وخمسًا وثلاثين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وبهذه الأجزاء كانت زاوية ألف دال هاء مائةً وثلاثةً وخمسين جزءًا وستًّا وخمسين دقيقةً فزاوية هاء ألف زاي إذن الباقية تكون بهذه الأجزاء اثنين وتسعين جزءًا وسبعًا وعشرين دقيقةً فيجب لذلك أن تكون القوس التي على خطّ هاء زاي اثنين وتسعين جزءًا وسبعًا وعشرين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث ألف هاء زاي القائم الزاوية ثلاث مائة وستّون جزءًا ويكون خطّ هاء زاي ستّةً وثمانين جزءًا وتسعًا وثلاثين دقيقةً بالأجزاء التي بها موتر ألف هاء مائة وعشرون جزءًا فالأجزاء إذن التي بها خطّ هاء زاي على ما تبيّن مائة وستّة عشر جزءًا وخمس وخمسون دقيقةً وخطّ هاء دال مائة وعشرون جزءًا يكون بها خطّ هاء ألف مائةً وأحدًا وستّين جزءًا وخمسًا وخمسين دقيقةً وأيضًا لأنّ قوس ألف باء من الفلك الخارج المركز خمسة وسبعون جزءًا وثلاث وأربعون دقيقةً تكون زاوية ألف هاء باء إذ هي عند المحيط خمسةً وسبعين جزءًا وثلاثًا وأربعين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فيجب لذلك أن تكون القوس أيضًا التي على خطّ ألف طاء خمسةً وسبعين جزءًا وثلاثًا وأربعين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث ألف هاء طاء القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ هاء طاء الأجزاء الباقية لتمام نصف الدائرة وهي مائة وأربعة أجزاء وسبع عشرة دقيقةً فخطّ ألف طاء إذن من الخطّين اللذين يوترانهما يكون ثلاثةً وسبعين جزءًا وتسعًا وثلاثين دقيقةً بالأجزاء التي بها موتر هاء ألف مائة وعشرون جزءًا ويكون خطّ هاء طاء بهذه الأجزاء أربعةً وتسعين جزءًا وخمسًا وأربعين دقيقةً فيجب لذلك أن تكون الأجزاء التي بها خطّ ألف هاء على ما تبيّن مائة وأحد وستّون جزءًا وخمس وخمسون دقيقةً وخطّ دال هاء مائة وعشرون جزءًا فخطّ ألف طاء بها تسعة وتسعون جزءًا وثلاث وأربعون دقيقةً وخطّ هاء طاء على ذلك المثال مائة وسبعة وعشرون جزءًا وإحدى وخمسون دقيقةً وبهذه الأجزاء كان تبيّن أنّ خطّ هاء باء بأسره مائتان واثنان وخمسون جزءًا وإحدى وأربعون دقيقةً فخطّ طاء باء إذن الباقي مائة وأربعة وعشرون جزءًا وخمسون دقيقةً بالأجزاء التي بها خطّ ألف طاء سبعة وتسعون جزءًا وثلاث وأربعون دقيقةً
لكنّ المربّع الذي من خطّ طاء باء خمسة عشر ألفًا وخمس مائة وثلاثة وثمانون جزءًا واثنتان وعشرون دقيقةً والمربّع الذي من خطّ ألف طاء على ذلك المثال تسعة آلاف وثمان مائة وسبعة وسبعون جزءًا وثلاث دقائق وإذا جمع ذلك كان منه المربّع الذي من خطّ ألف باء خمسة وعشرون ألفًا وأربع مائة وستّون جزءًا وخمس وعشرون دقيقةً فيكون إذن خطّ ألف باء في الطول مائةً وتسعةً وخمسين جزءًا وأربعًا وثلاثين دقيقةً بالأجزاء التي بها كان خطّ هاء دال مائة وعشرين جزءًا وخطّ هاء ألف على ذلك المثال مائة وأحد وستّون جزءًا وخمس وخمسون دقيقةً لكنّ الأجزاء التي بها قطر الفلك الخارج المركز مائة وعشرون جزءًا فإنّ خطّ ألف باء بها ثلاثة وسبعون جزءًا وتسع وثلاثون دقيقةً وذلك أنّه يوتر قوسًا مبلغها خمسة وسبعون جزءًا وثلاث وأربعون دقيقةً فالأجزاء إذن التي بها خطّ ألف باء ثلاثة وسبعون جزءًا وتسع وثلاثون دقيقةً وقطر الفلك الخارج المركز مائة وعشرون جزءًا يكون بها أمّا خطّ هاء دال فخمسة وخمسون جزءًا وثلاث وعشرون دقيقةً وأمّا خطّ هاء ألف فأربعة وسبعون جزءًا وثلاث وأربعون دقيقةً فيجب لذلك أن يكون قوس هاء ألف أيضًا من الفلك الخارج المركز سبعةً وسبعين جزءًا ودقيقةً واحدةً وتكون قوس هاء ألف باء جيم بأسرها مائة وتسعين جزءًا وستًّا وثلاثين دقيقةً ومن البيّن أنّ قوس جيم هاء الباقية تكون مائةً وتسعةً وستّين جزءًا وأربعًا وعشرين دقيقةً ولذلك يكون خطّ جيم دال هاء مائةً وتسعة عشر جزءًا وثمانيًا وعشرين دقيقةً بالتقريب بالأجزاء التي بها قطر الفلك الخارج المركز مائة وعشرون جزءًا يجـ: فلنوجد مركز الفلك الخارج المركز في داخل قطعة هاء ألف جيم إذ كانت أعظم من نصف دائرة ولتكن نقطة كاف ولنجر عليه وعلى نقطة جيم قطر الفلك الخارج المركز الذي يمرّ بكلي المركزين وليكن خطّ لام كاف دال ميم ولنخرج من نقطة كاف على خطّ جيم هاء عمود كاف زاي ولنخرج إلى نقطة سين فلأنّ الأجزاء التي بها قطر لام ميم مائة وعشرون جزءًا فخطّ هاء جيم بأسره قد تبيّن أنّه بها مائة وتسعة عشر جزءًا وثمان وعشرون دقيقةً وخطّ هاء دال خمسة خمسون جزءًا وثلاث وعشرون دقيقةً فإنّ خطّ دال جيم الباقي يحصل لنا بهذه الأجزاء أربعةً وستّين جزءًا وخمس دقائق فيجب لذلك من قبل أنّ السطح القائم الزوايا الذي يحيط به خطّا جيم دال دال هاء مساوٍ للقائم الزوايا الذي يحيط به خطّا لام دال دال ميم والذي يحيط به خطّا جيم دال دال هاء ثلاثة آلاف وخمس مائة وتسعة وأربعون جزءًا وتسع دقائق فيجب من ذلك أن يكون لنا السطح القائم الزوايا الذي يحيط به خطّا لام دال دال ميم أيضًا ثلاثة آلاف وخمس مائة وتسعةً وأربعين جزءًا وتسع دقائق لكنّ السطح القائم الزوايا الذي يحيط به خطّا لام دال دال ميم مع المربّع الذي من خطّ دال لام يكون منهما المربّع الذي من نصف القطر أعني خطّ لام كاف فإن
 نحن إذن نقصنا من المربّع الذي من نصف القطر وذلك يكون ثلاثة آلاف وستّ مائة جزء ثلاثة آلاف وخمس مائة وتسعة وأربعين جزءًا وتسع دقائق بقي لنا المربّع الذي من خطّ دال لام بهذه الأجزاء خمسين جزءًا وإحدى وخمسين دقيقةً فيحصل لنا خطّ دال كاف في الطول وهو الخطّ الذي فيما بين المركزين سبعة أجزاء وثمان دقائق بالتقريب بالأجزاء التي بها قطر الفلك الخارج المركز مائة وعشرون جزءًا⊙ وأيضًا لأنّ نصف خطّ جيم هاء أعني خطّ هاء زاي تسعة وخمسون جزءًا وأربع وأربعون دقيقةً بالأجزاء التي بها قطر لام ميم مائة وعشرون جزءًا وقد تبيّن أنّ خطّ هاء دال بهذه
نحن إذن نقصنا من المربّع الذي من نصف القطر وذلك يكون ثلاثة آلاف وستّ مائة جزء ثلاثة آلاف وخمس مائة وتسعة وأربعين جزءًا وتسع دقائق بقي لنا المربّع الذي من خطّ دال لام بهذه الأجزاء خمسين جزءًا وإحدى وخمسين دقيقةً فيحصل لنا خطّ دال كاف في الطول وهو الخطّ الذي فيما بين المركزين سبعة أجزاء وثمان دقائق بالتقريب بالأجزاء التي بها قطر الفلك الخارج المركز مائة وعشرون جزءًا⊙ وأيضًا لأنّ نصف خطّ جيم هاء أعني خطّ هاء زاي تسعة وخمسون جزءًا وأربع وأربعون دقيقةً بالأجزاء التي بها قطر لام ميم مائة وعشرون جزءًا وقد تبيّن أنّ خطّ هاء دال بهذه
الأجزاء خمسة وخمسون جزءًا وثلاث وعشرون دقيقةً فإنّ خطّ دال زاي الباقي يحصّل لنا أربعة أجزاء وإحدى وعشرين دقيقةً بالأجزاء التي بها كان خطّ دال كاف سبعة أجزاء وثمان دقائق فيجب لذلك أن تكون الأجزاء التي بها موتر دال لام مائة وعشرون جزءًا فإنّ خطّ دال زاي بها ثلاثة وسبعون جزءًا وإحدى عشرة دقيقةً والقوس التي عليه خمسة وسبعون جزءًا وعشر دقائق بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال كاف نون القائم الزاوية ثلاث مائة وستّون جزءًا فزاوية دال كاف زاي إذن أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فإنّها خمسة وسبعون جزءًا وعشر دقائق وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فإنّها سبعة وثلاثون جزءًا وخمس وثلاثون دقيقةً ولأنّها عند مركز الفلك الخارج المركز يحصل لنا قوس سين ميم سبعة وثلاثين جزءًا وخمسًا وثلاثين دقيقةً لكنّ قوس جيم سين إذ هي نصف قوس جسم سين هاء فإنّها أربعة وثمانون جزءًا واثنتان وأربعون دقيقةً فقوس جيم لام الباقية إذن التي من البعد الأبعد إلى الحال
 الثالثة تكون سبعة وخمسين جزءًا وثلاثًا وأربعين دقيقةً وبهذه الأجزاء وضعت قوس باء جيم سبعة وثلاثين جزءًا واثنتين وخمسين دقيقةً فقوس لام باء الباقية إذن وهي التي من البعد الأبعد إلى الحال الثانية يكون تسعة عشر جزءًا وإحدى وخمسين دقيقةً وعلى هذا المثال لأنّ قوس ألف باء وضعت خمسة وسبعين جزءًا وثلاثًا وأربعين دقيقةً فإنّ قوس ألف لام الباقية وهي التي من الحال الأولى إلى البعد الأبعد خمسة وخمسون جزءًا واثنتان وخمسون دقيقةً يد: فلأنّ مركز فلك التدوير ليس على هذا الفلك الخارج المركز أيضًا يدور لكن على الفلك الذي يرسم على مركز وسط نقطتي دال لام ويبعد خطّ كاف لام حسبنا بحسب ما يلزم من ذلك مثل ما فعلنا في سائر الكواكب الفضول التي يكون بين هذه الأبعاد وبين الأبعاد التي ترى في فلك البروج على أنّ هذه هي النسب بالتقريب إن نقل مسير فلك التدوير إلى الفلك الخارج المركز الذي وصفناه الذي به يكون الاختلاف الذي يلزم من قبل فلك البروج وذلك أنّا نضع الصورة في نظير هذا المعنى من التبيين في الحال الأولى على أنّ الكوكب موضوع في الشكل أمام نقطة لام وهي البعد الأبعد فلأنّ زاوية نون زاي سين وهي زاوية المسير المستوي في الطول أعني زاوية دال زاي حاء أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فقد تبيّن أنّها خمسة وخمسون جزءًا واثنتان وخمسون دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فإنّها مائة وأحد عشر جزءًا وأربع وأربعون دقيقةً تكون القوس أيضًا التي على خطّ دال حاء مائةً وأحد عشر جزءًا وأربعًا وأربعين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال زاي حاء القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ زاي حاء ما يبقى لتمام نصف دائرة وهو ثمانية وستّون جزءًا وستّ عشرة دقيقةً فخطّ دال حاء إذن من الخطّين اللذين يوترانهما تسعة وتسعون جزءًا وعشرون دقيقةً بالأجزاء التي بها موتر دال نون مائة وعشرون جزءًا وخطّ زاي حاء بهذه الأجزاء سبعة وستّون جزءًا وعشرون دقيقةً فيجب لذلك أن تكون الأجزاء التي بها أمّا خطّ دال زاي وهو الذي بين المركزين ثلاثة أجزاء وأربع وثلاثون دقيقةً وأمّا خطّ دال ألف وهو الذي من مركز الفلك الخارج المركز ستّون جزءًا فيها
الثالثة تكون سبعة وخمسين جزءًا وثلاثًا وأربعين دقيقةً وبهذه الأجزاء وضعت قوس باء جيم سبعة وثلاثين جزءًا واثنتين وخمسين دقيقةً فقوس لام باء الباقية إذن وهي التي من البعد الأبعد إلى الحال الثانية يكون تسعة عشر جزءًا وإحدى وخمسين دقيقةً وعلى هذا المثال لأنّ قوس ألف باء وضعت خمسة وسبعين جزءًا وثلاثًا وأربعين دقيقةً فإنّ قوس ألف لام الباقية وهي التي من الحال الأولى إلى البعد الأبعد خمسة وخمسون جزءًا واثنتان وخمسون دقيقةً يد: فلأنّ مركز فلك التدوير ليس على هذا الفلك الخارج المركز أيضًا يدور لكن على الفلك الذي يرسم على مركز وسط نقطتي دال لام ويبعد خطّ كاف لام حسبنا بحسب ما يلزم من ذلك مثل ما فعلنا في سائر الكواكب الفضول التي يكون بين هذه الأبعاد وبين الأبعاد التي ترى في فلك البروج على أنّ هذه هي النسب بالتقريب إن نقل مسير فلك التدوير إلى الفلك الخارج المركز الذي وصفناه الذي به يكون الاختلاف الذي يلزم من قبل فلك البروج وذلك أنّا نضع الصورة في نظير هذا المعنى من التبيين في الحال الأولى على أنّ الكوكب موضوع في الشكل أمام نقطة لام وهي البعد الأبعد فلأنّ زاوية نون زاي سين وهي زاوية المسير المستوي في الطول أعني زاوية دال زاي حاء أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فقد تبيّن أنّها خمسة وخمسون جزءًا واثنتان وخمسون دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فإنّها مائة وأحد عشر جزءًا وأربع وأربعون دقيقةً تكون القوس أيضًا التي على خطّ دال حاء مائةً وأحد عشر جزءًا وأربعًا وأربعين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال زاي حاء القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ زاي حاء ما يبقى لتمام نصف دائرة وهو ثمانية وستّون جزءًا وستّ عشرة دقيقةً فخطّ دال حاء إذن من الخطّين اللذين يوترانهما تسعة وتسعون جزءًا وعشرون دقيقةً بالأجزاء التي بها موتر دال نون مائة وعشرون جزءًا وخطّ زاي حاء بهذه الأجزاء سبعة وستّون جزءًا وعشرون دقيقةً فيجب لذلك أن تكون الأجزاء التي بها أمّا خطّ دال زاي وهو الذي بين المركزين ثلاثة أجزاء وأربع وثلاثون دقيقةً وأمّا خطّ دال ألف وهو الذي من مركز الفلك الخارج المركز ستّون جزءًا فيها
خطّ دال حاء جزءان وسبع وخمسون دقيقةً وخطّ زاي حاء على ذلك المثال جزءان ولأنّ المربّع الذي من خطّ دال حاء إذا نقص من المربّع الذي من خطّ دال ألف كان منه المربّع الذي من خطّ ألف حاء يحصل لنا خطّ ألف حاء بهذه الأجزاء تسعةً وخمسين جزءًا وستًّا وخمسين دقيقةً وعلى هذا المثال لأنّ خطّ زاي حاء مساوٍ لخطّ طاء حاء وخطّ طاء هاء ضعف خطّ جيم دال يكون خطّ ألف طاء بأسره أحدًا وستّين جزءًا وستًّا وخمسين دقيقةً بالأجزاء التي بها خطّ هاء طاء خمسة أجزاء وأربع وخمسون دقيقةً ومن أجل ذلك يكون موتر ألف هاء بهذه الأجزاء اثنين وستّين جزءًا وثلاث عشرة دقيقةً فيجب لذلك أن تكون الأجزاء التي بها موتر ألف هاء مائة وعشرون جزءًا فإنّ خطّ هاء طاء بها أحد عشر جزءًا وإحدى وعشرين دقيقةً والقوس التي عليه عشرة أجزاء وإحدى وخمسون دقيقةً بالتقريب بالأجزاء التي بها الدائرة التي ترسم حول مثلّث ألف هاء طاء القائم الزاوية ثلاث مائة وستّون جزءًا فزاوية هاء ألف طاء إذن عشرة أجزاء وإحدى وخمسون دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة ستّون جزءًا وأيضًا لأنّ الأجزاء التي بها خطّ هاء طاء خمسة أجزاء وأربع وخمسون دقيقةً فخطّ راء سين بها وهو من مركز الفلك الخارج المركز ستّون جزءًا وخطّ نون طاء أربعة أجزاء ومن البيّن أنّ خطّ طاء سين بأسره يكون أربعة وستّين جزءًا يحصل لنا موتر هاء سين بهذه الأجزاء أربعة وستّين جزءًا وستّ عشرة دقيقةً فالأجزاء إذن التي بها موتر هاء سين مائة وعشرون جزءًا يكون بها خطّ طاء هاء أحد عشر جزءًا ودقيقتين وتكون القوس التي عليه عشرة أجزاء وثلاثًا وثلاثين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث هاء طاء سين ثلاث مائة وستّون جزءًا فيجب لذلك أن تكون زاوية هاء سين طاء أيضًا عشرة أجزاء وثلاثًا وثلاثين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وبهذه الأجزاء يبيّن أنّ زاوية
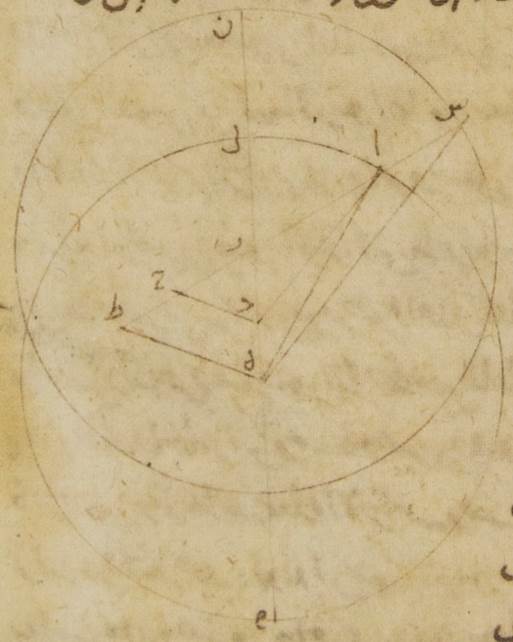 هاء ألف طاء عشرة أجزاء وإحدى وخمسون دقيقةً فزاوية ألف هاء سين إذن الباقية وهي زاوية الفضل المطلوب أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فإنّها ثمان عشرة دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فإنّها تسع دقائق لكنّ هذا الكوكب كان يرى في الحال الأولى على خطّ ألف هاء وحاصله على جزء واحد وثلاث عشر دقيقةً من الميزان فمن البيّن أنّ مركز فلك التدوير لو لم يكن يدور على دائرة ألف لام لكن على دائرة نون سين لكان من هذه الدائرة على نقطة سين وكان الكوكب يرى على خطّ هاء سين متقدّمًا لوضعه على نقطة ألف بالتسع الدقائق وكان حاصله يكون على جزء واحد وأربع دقائق من الميزان يه: ثمّ نضع أيضًا صورة الحال الثانية في مثل هذا المعنى من التبيين على أنّ الكوكب في الصورة متأخّر عن البعد الأبعد فلأنّ قوس نون سين من الفلك الخارج المركز قد تبيّن أنّها تسعة عشر جزءًا وإحدى وخمسون دقيقةً تكون زاوية نون زاي سين والزاوية أيضًا التي على رأسها
هاء ألف طاء عشرة أجزاء وإحدى وخمسون دقيقةً فزاوية ألف هاء سين إذن الباقية وهي زاوية الفضل المطلوب أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فإنّها ثمان عشرة دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فإنّها تسع دقائق لكنّ هذا الكوكب كان يرى في الحال الأولى على خطّ ألف هاء وحاصله على جزء واحد وثلاث عشر دقيقةً من الميزان فمن البيّن أنّ مركز فلك التدوير لو لم يكن يدور على دائرة ألف لام لكن على دائرة نون سين لكان من هذه الدائرة على نقطة سين وكان الكوكب يرى على خطّ هاء سين متقدّمًا لوضعه على نقطة ألف بالتسع الدقائق وكان حاصله يكون على جزء واحد وأربع دقائق من الميزان يه: ثمّ نضع أيضًا صورة الحال الثانية في مثل هذا المعنى من التبيين على أنّ الكوكب في الصورة متأخّر عن البعد الأبعد فلأنّ قوس نون سين من الفلك الخارج المركز قد تبيّن أنّها تسعة عشر جزءًا وإحدى وخمسون دقيقةً تكون زاوية نون زاي سين والزاوية أيضًا التي على رأسها
وهي زاوية دال زاي حاء أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فتسعة عشر جزءًا وإحدى وخمسون دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فتسعة وثلاثون جزءًا واثنتان وأربعون دقيقةً فيجب لذلك أن تكون القوس التي على خطّ دال حاء تسعةً وثلاثين جزءًا واثنتين وأربعين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال زاي حاء القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ زاي حاء الأجزاء الباقية لتمام نصف دائرة وهي مائة وأربعون جزءًا وثمان عشرة دقيقةً فخطّ دال حاء إذن من الخطّين اللذين يوترانهما أربعون جزءًا وخمس وأربعون دقيقةً بالأجزاء التي بها موتر دال زاي مائة وعشرون جزءًا وخطّ زاي حاء بهذه الأجزاء مائة واثنا عشر جزءًا واثنتان وخمسون دقيقةً فيجب لذلك أن تكون الأجزاء التي بها خطّ دال زاي ثلاثة أجزاء وأربع وثلاثون دقيقةً وخطّ دال باء الذي من مركز الفلك الخارج المركز ستّون جزءًا فإنّ خطّ دال حاء بها جزء واحد وثلاث عشرة دقيقةً وخطّ زاي حاء على ذلك المثال ثلاثة أجزاء وإحدى وعشرون دقيقةً ولأنّ المربّع الذي من خطّ دال حاء إذا نقص من المربّع الذي من خطّ دال باء كان من ذلك المربّع الذي من خطّ باء حاء فإنّ خطّ باء حاء يكون بهذه الأجزاء تسعةً وخمسين جزءًا وتسعًا وخمسين دقيقةً بالتقريب وعلى ذلك المثال لأنّ خطّ زاي حاء مساوٍ لخطّ حاء طاء وخطّ هاء طاء ضعف خطّ دال حاء يحصل لنا خطّ باء طاء بأسره ثلاثةً وستّين جزءًا وعشرين دقيقةً بالأجزاء التي بها خطّ هاء طاء جزءان وستّ وعشرون دقيقةً ولذلك يكون موتر هاء باء بهذه الأجزاء ثلاثةً وستّين جزءًا وثلاثًا وعشرين دقيقةً فالأجزاء إذن التي بها موتر باء هاء مائة وعشرون جزءًا يكون بها خطّ هاء طاء أربعة أجزاء وستًّا وثلاثين دقيقةً وتكون القوس التي عليها أربعة أجزاء وأربعًا وعشرين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء هاء طاء القائم الزاوية ثلاث مائة وستّون جزءًا فيجب لذلك أن تكون زاوية هاء باء طاء أيضًا أربعة أجزاء وأربعًا وعشرين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وكذلك أيضًا لأنّ الأجزاء التي بها خطّ زاي سين الذي من مركز الفلك الخارج المركز ستّون جزءًا فإنّ خطّ زاي طاء يحصل به ستّة أجزاء واثنتين وأربعين دقيقةً يكون لنا خطّ سين طاء بأسره ستّةً وستّين جزءًا واثنتين وأربعين دقيقةً بالأجزاء التي بها
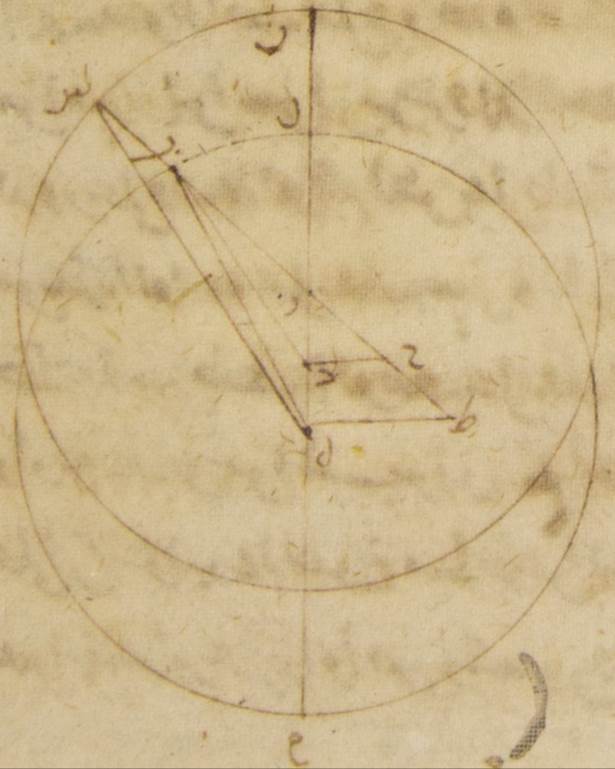 وضع خطّ هاء طاء جزأين وستًّا وعشرين دقيقةً ومن أجل ذلك يكون موتر هاء سين بهذه الأجزاء ستّةً وستّين جزءًا وخمسًا وأربعين دقيقةً فيجب لذلك أن تكون الأجزاء التي بها موتر هاء سين مائة وعشرون جزءًا فخطّ هاء طاء بها أربعة أجزاء وثلاث وعشرون دقيقةً والقوس التي عليه أربعة أجزاء واثنتا عشرة دقيقةً بالأجزاء التي بها الدائرة الت ترسم حول مثلّث هاء طاء سين القائم الزاوية ثلاث مائة وستّون جزءًا فزاوية هاء سين طاء إذن هي أيضًا أربعة أجزاء واثنتا عشرة
وضع خطّ هاء طاء جزأين وستًّا وعشرين دقيقةً ومن أجل ذلك يكون موتر هاء سين بهذه الأجزاء ستّةً وستّين جزءًا وخمسًا وأربعين دقيقةً فيجب لذلك أن تكون الأجزاء التي بها موتر هاء سين مائة وعشرون جزءًا فخطّ هاء طاء بها أربعة أجزاء وثلاث وعشرون دقيقةً والقوس التي عليه أربعة أجزاء واثنتا عشرة دقيقةً بالأجزاء التي بها الدائرة الت ترسم حول مثلّث هاء طاء سين القائم الزاوية ثلاث مائة وستّون جزءًا فزاوية هاء سين طاء إذن هي أيضًا أربعة أجزاء واثنتا عشرة
دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وقد كان تبيّن أنّ زاوية هاء باء طاء بهذه الأجزاء أربعة أجزاء وأربع وعشرون دقيقةً فزاوية باء هاء سين الباقية إذن تكون أمّا بهذه الأجزاء فاثنتي عشرة دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فتكون ستّ دقائق فمن البيّن هاهنا أيضًا أنّ الكوكب لمّا كان في الحال الثانية إذ كان يرى على خطّ هاء باء كان حاصله على تسعة أجزاء وأربعين دقيقةً من الرامي فإنّه لو كان رئي أيضًا على خطّ هاء سين لكان حاصله على تسعة أجزاء وستّ وأربعين دقيقةً من الرامي وقد كان تبيّن أنّ حاصله كان في الحال الأولى على هذا المثال على جزء واحد وأربع دقائق من الميزان فظاهر أنّ البعد الذي يرى بين الحال الأولى وبين الحال الثانية يحصل لو كان الكوكب رئي في فلك نون سين الخارج المركز ثمانية وستّين جزءًا واثنتين وأربعين دقيقةً من فلك البروج يو: وكذلك أيضًا يوضع رسم الحال الثالثة على مثل الصورة التي وضعت في الحال الثانية فلأنّ قوس نون سين قد تبيّن أنّها سبعة وخمسون جزءًا وثلاث وأربعون دقيقةً تكون زاوية نون زاي سين أعني زاوية دال زاي حاء أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فسبعة وخمسون جزءًا وثلاث وأربعون دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا ه - صح: فسبعة وخمسون جزءًا وثلاث وأربعون دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فمائة وخمسة عشر جزءًا وستّ وعشرون دقيقةً فيجب لذلك أن تكون القوس التي على خطّ دال حاء مائة وخمسة عشر جزءًا وستًّا وعشرين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال زاي حاء القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ زاي حاء الأجزاء الباقية لتمام نصف دائرة وهي أربعة وستّون جزءًا وأربع وثلاثون دقيقةً فخطّ دال حاء إذن من الخطّين اللذين يوترانهما مائة جزء وجزء واحد وسبع وعشرون دقيقةً بالأجزاء التي بها موتر دال زاي مائة وعشرون جزءًا وخطّ زاي حاء بهذه الأجزاء أربعة وستّون جزءًا وستّ دقائق فيجب لذلك أن تكون الأجزاء التي بها خطّ دال زاي ثلاثة أجزاء وأربع وثلاثون دقيقةً وخطّ دال جيم الذي من مركز الفلك الخارج المركز ستّون جزءًا فإنّ خطّ دال حاء ثلاثة أجزاء ودقيقة واحدة وخطّ زاي حاء على ذلك المثال جزء واحد وأربع وخمسون دقيقةً⊙ وأيضًا لأنّ المربّع الذي من خطّ دال حاء إذا نقص من المربّع الذي من خطّ دال جيم يكون من ذلك المربّع الذي من خطّ جيم حاء فإنّ خطّ جيم حاء أيضًا يحصل لنا بهذه الأجزاء تسعةً وخمسين جزءًا وستًّا وخمسين دقيقة وعلى ذلك المثال لأنّ خطّ زاي حاء مساوٍ لخطّ طاء حاء وخطّ هاء طاء ضعف خطّ دال حاء يحصل لنا خطّ حاء طاء بأسره أحدًا وستّين جزءًا وخمسين دقيقةً بالأجزاء التي بها يكون خطّ هاء طاء ستّة أجزاء ودقيقتين ولذلك يكون موتر هاء جيم بهذه الأجزاء اثنين وستّين جزءًا وثمان دقائق فالأجزاء إذن التي بها موتر جيم هاء مائة وعشرون جزءًا يكون بها خطّ هاء طاء أحد عشر جزءًا وتسعًا وثلاثين دقيقةً وتكون القوس التي عليه أحد عشر جزءًا وتسع دقائق بالتقريب بالأجزاء التي بها الدائرة التي ترسم حول مثلّث جيم هاء طاء القائم الزاوية ثلاث مائة وستّون جزءًا فيجب لذلك أن تكون زاوية جيم هاء طاء أيضًا أحد عشر جزءًا وتسع دقائق بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وكذلك لأنّ الأجزاء التي بها خطّ زاي سين الذي من مركز الفلك الخارج المركز ستّون جزءًا فإنّ خطّ زاي طاء يحصل لنا بها ثلاثة أجزاء وستًّا
وأربعين دقيقةً فإنّ خطّ سين طاء بأسره يحصل لنا ثلاثةً وستّين جزءًا وثمانيًا وأربعين دقيقةً بالأجزاء التي بها كان خطّ هاء طاء ستّة أجزاء ودقيقتين ومن قبل ذلك يكون موتر هاء سين بهذه الأجزاء أربعةً وستّين جزءًا وخمس دقائق فالأجزاء إذن التي بها موتر هاء سين مائة وعشرون جزءًا يكون بها خطّ هاء طاء أحد عشر جزءًا وثمان عشرة دقيقةً وتكون القوس التي عليه عشرة أجزاء وتسعًا وأربعين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث هاء طاء سين القائم الزاوية ثلاث مائة وستّون جزءًا فيجب لذلك أن تكون زاوية هاء سين طاء أيضًا عشرة أجزاء وتسعًا وأربعين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وبهذه الأجزاء تبيّن أنّ زاوية هاء جيم طاء أحد عشر جزءًا وتسع دقائق فزاوية جيم هاء سين الباقية تكون أمّا بهذه الأجزاء فعشرين دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا
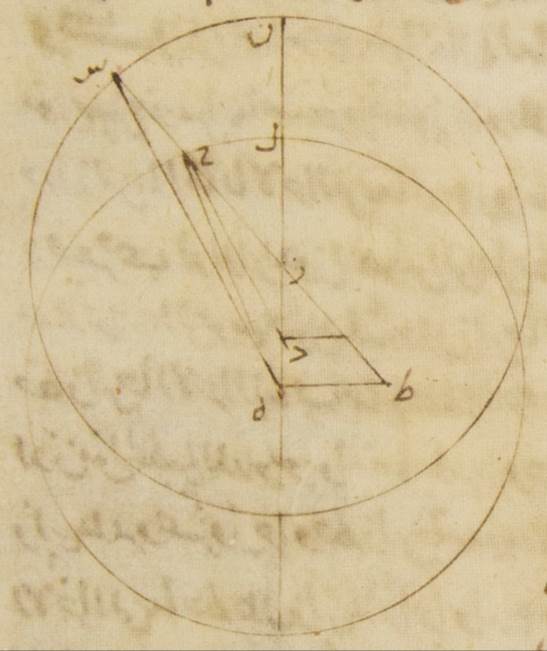 فعشر دقائق فيجب لذلك من قبل أنّ الكوكب في الحال الثالثة إذ كان يرى على خطّ هاء جيم كان حاصله على أربعة عشر جزءًا وأربع عشرة دقيقةً من الجدي فظاهر أنّه لو اتّفق أن كان على خطّ هاء سين لكان حاصله على أربعة عشر جزءًا وأربع وعشرين دقيقةً من الجدي فكان أيضًا البعد الذي يرى بين الحال الثانية وبين الحال الثالثة الذي يوجد في فلك نون سين الخارج المركز سيكون أربعةً وثلاثين جزءًا وثمانيًا وثلاثين دقيقةً فإذ قد اقتفينا ما يدلّ عليه هذان البعدان في هذا المعنى بعينه وجدنا البعد فيما بين مركز فلك البروج وبين مركز الفلك الخارج المركز الذي يشتمل على حركة فلك التدوير المستوية أعني الخطّ المساوي لخطّ هاء زاي ستّة أجزاء وخمسون دقيقةً بالتقريب بالأجزاء التي بها قطر الفلك الخارج المركز مائة وعشرون جزءًا ووجدنا القسيّ من هذا الفلك الخارج المركز أمّا القوس التي من الحال الأولى إلى البعد الأبعد فسبعة وخمسون جزءًا وخمس دقائق وأمّا القوس التي من البعد الأبعد إلى الحال الثانية فثمانية عشر جزءًا وثمان وثلاثون دقيقةً وأمّا القوس التي من البعد الأبعد إلى الحال الثالثة فستّة وخمسون جزءًا وثلاثون دقيقةً وهذه الأقدار الموصوفة قد أخذت هاهنا أيضًا على الحقيقة من قبل أنّ فضول قسيّ فلك البروج يحصل لنا بهذه أيضًا مثل تلك التي تقدّمت على التقريب وأنّ أبعاد الكوكب الذي يرى ويوجد تؤخذ موافقةً للأبعاد التي وجدت بالرصد على ما سيتبيّن لنا بمثل تلك الأعمال⊙ يز: فليوضع شكل الحال الأولى في الفلك الخارج المركز وحدّه الحامل لمركز فلك التدوير فلأنّ زاوية ألف زاي لام إذ توتر من الفلك الخارج المركز سبعةً وخمسين جزءًا وخمس دقائق فإنّها أمّا
فعشر دقائق فيجب لذلك من قبل أنّ الكوكب في الحال الثالثة إذ كان يرى على خطّ هاء جيم كان حاصله على أربعة عشر جزءًا وأربع عشرة دقيقةً من الجدي فظاهر أنّه لو اتّفق أن كان على خطّ هاء سين لكان حاصله على أربعة عشر جزءًا وأربع وعشرين دقيقةً من الجدي فكان أيضًا البعد الذي يرى بين الحال الثانية وبين الحال الثالثة الذي يوجد في فلك نون سين الخارج المركز سيكون أربعةً وثلاثين جزءًا وثمانيًا وثلاثين دقيقةً فإذ قد اقتفينا ما يدلّ عليه هذان البعدان في هذا المعنى بعينه وجدنا البعد فيما بين مركز فلك البروج وبين مركز الفلك الخارج المركز الذي يشتمل على حركة فلك التدوير المستوية أعني الخطّ المساوي لخطّ هاء زاي ستّة أجزاء وخمسون دقيقةً بالتقريب بالأجزاء التي بها قطر الفلك الخارج المركز مائة وعشرون جزءًا ووجدنا القسيّ من هذا الفلك الخارج المركز أمّا القوس التي من الحال الأولى إلى البعد الأبعد فسبعة وخمسون جزءًا وخمس دقائق وأمّا القوس التي من البعد الأبعد إلى الحال الثانية فثمانية عشر جزءًا وثمان وثلاثون دقيقةً وأمّا القوس التي من البعد الأبعد إلى الحال الثالثة فستّة وخمسون جزءًا وثلاثون دقيقةً وهذه الأقدار الموصوفة قد أخذت هاهنا أيضًا على الحقيقة من قبل أنّ فضول قسيّ فلك البروج يحصل لنا بهذه أيضًا مثل تلك التي تقدّمت على التقريب وأنّ أبعاد الكوكب الذي يرى ويوجد تؤخذ موافقةً للأبعاد التي وجدت بالرصد على ما سيتبيّن لنا بمثل تلك الأعمال⊙ يز: فليوضع شكل الحال الأولى في الفلك الخارج المركز وحدّه الحامل لمركز فلك التدوير فلأنّ زاوية ألف زاي لام إذ توتر من الفلك الخارج المركز سبعةً وخمسين جزءًا وخمس دقائق فإنّها أمّا
بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فسبعة وخمسون جزءًا وخمس دقائق وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فهي والزاوية التي على رأسها أعني زاوية دال زاي حاء مائة وأربعة عشر جزءًا وعشر دقائق تكون القوس التي على خطّ دال حاء مائة وأربعة عشر جزءًا وعشر دقائق بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال زاي حاء القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ زاي حاء الأجزاء التي تبقى لتمام نصف دائرة وهي خمسة وستّون جزءًا وخمسون دقيقةً فخطّ دال حاء إذن من الخطّين اللذين يوترانهما مائة جزء وأربع وأربعون دقيقةً بالأجزاء التي بها موتر دال زاي مائة وعشرون جزءًا وخطّ زاي حاء بهذه الأجزاء خمسة وستّون جزءًا وثلاث عشرة دقيقةً فيجب لذلك أن تكون الأجزاء التي بها خطّ دال زاي وهو الذي بين المركزين ثلاثة أجزاء وخمس وعشرون دقيقةً وخطّ دال ألف الذي من مركز الفلك الخارج المركز ستّون جزءًا فإنّ خطّ دال حاء بها جزءان واثنتان وخمسون دقيقةً وخطّ زاي حاء على ذلك المثال جزء واحد وإحدى وخمسون دقيقةً⊙ وأيضًا لأنّ المربّع الذي من خطّ زاي حاء إذا نقص من المربّع الذي من خطّ ألف دال كان من ذلك المربّع الذي من خطّ ألف حاء فإنّ خطّ ألف حاء يحصل لنا بهذه الأجزاء تسعةً وخمسين جزءًا وستًّا وخمسين دقيقةً وعلى ذلك المثال لأنّ خطّ زاي حاء مساوٍ لخطّ حاء طاء وخطّ هاء طاء ضعف خطّ دال حاء فإنّ خطّ ألف طاء بأسره يحصل لنا أحدًا وستّين جزءًا وسبعًا وأربعين دقيقةً بالأجزاء التي بها يحصل خطّ هاء طاء خمسة أجزاء وأربعًا وأربعين دقيقةً ومن قبل ذلك يكون موتر ألف هاء بهذه الأجزاء اثنين وستّين جزءًا وثلاث دقائق
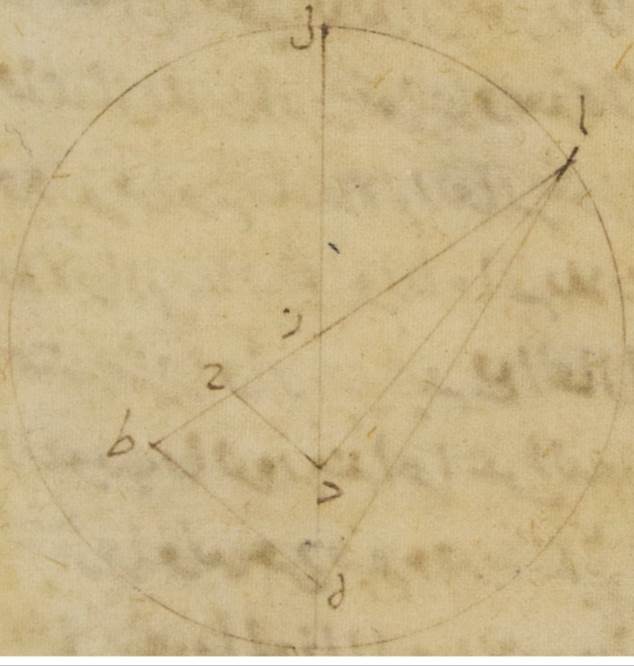 فالأجزاء إذن التي بها موتر ألف هاء مائة وعشرون جزءًا يكون بها خطّ هاء طاء أحد عشر جزءًا وخمس دقائق وتكون القوس التي عليه عشرة أجزاء وستًّا وثلاثين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث ألف هاء طاء القائم الزاوية ثلاث مائة وستّون جزءًا فيجب لذلك أن تكون زاوية هاء ألف زاي عشرة أجزاء وستًّا وثلاثين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وبهذه الأجزاء وضعت زاوية ألف زاي لام مائة وأربعة عشر جزءًا وعشر دقائق فزاوية ألف هاء لام الباقية تكون أمّا بهذه الأجزاء فمائة وثلاثة أجزاء وأربع وثلاثون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فتكون أحدًا وخمسين جزءًا وسبعًا وأربعين دقيقةً فبهذه الأجزاء إذن كان الكوكب في الحال الأولى متقدّمًا للبعد الأبعد يح: وليوضع أيضًا في مثل هذه الصورة رسم الحال الثانية فلأنّ زاوية باء زاي لام أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فقد تبيّن أنّها ثمانية عشر جزءًا وثمان وثلاثون دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فإنّها والزاوية التي على رأسها وهي زاوية دال زاي حاء سبعة وثلاثون جزءًا وستّ عشرة دقيقةً تكون القوس أيضًا التي على خطّ دال حاء سبعةً
فالأجزاء إذن التي بها موتر ألف هاء مائة وعشرون جزءًا يكون بها خطّ هاء طاء أحد عشر جزءًا وخمس دقائق وتكون القوس التي عليه عشرة أجزاء وستًّا وثلاثين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث ألف هاء طاء القائم الزاوية ثلاث مائة وستّون جزءًا فيجب لذلك أن تكون زاوية هاء ألف زاي عشرة أجزاء وستًّا وثلاثين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وبهذه الأجزاء وضعت زاوية ألف زاي لام مائة وأربعة عشر جزءًا وعشر دقائق فزاوية ألف هاء لام الباقية تكون أمّا بهذه الأجزاء فمائة وثلاثة أجزاء وأربع وثلاثون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فتكون أحدًا وخمسين جزءًا وسبعًا وأربعين دقيقةً فبهذه الأجزاء إذن كان الكوكب في الحال الأولى متقدّمًا للبعد الأبعد يح: وليوضع أيضًا في مثل هذه الصورة رسم الحال الثانية فلأنّ زاوية باء زاي لام أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فقد تبيّن أنّها ثمانية عشر جزءًا وثمان وثلاثون دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فإنّها والزاوية التي على رأسها وهي زاوية دال زاي حاء سبعة وثلاثون جزءًا وستّ عشرة دقيقةً تكون القوس أيضًا التي على خطّ دال حاء سبعةً
وثلاثين جزءًا وستّ عشرة دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال زاي حاء القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ زاي حاء الأجزاء الباقية إلى تمام نصف دائرة وهي مائة واثنان وأربعون جزءًا وأربع وأربعون دقيقةً فخطّ زاي حاء من الخطّين اللذين يوترانهما ثمانية وثلاثون جزءًا وعشرون دقيقةً بالأجزاء التي بها موتر دال زاي مائة وعشرون جزءًا وخطّ زاي حاء بهذه الأجزاء مائة وثلاثة عشر جزءًا وثلاث وأربعون دقيقةً فيجب لذلك أن تكون الأجزاء التي بها خطّ دال زاي ثلاثة أجزاء وخمسًا وعشرين دقيقةً وخطّ دال باء الذي من مركز الفلك الخارج المركز تسعون جزءًا فإنّ خطّ دال حاء بها جزء واحد وخمس دقائق وخطّ زاي حاء على ذلك المثال ثلاثة أجزاء وأربع عشرة دقيقةً ولأنّ المربّع الذي من خطّ دال حاء إذا نقص من المربّع الذي من خطّ دال باء يكون منه المربّع الذي من خطّ باء حاء فإنّ خطّ باء حاء يحصل لنا بهذه الأجزاء تسعةً وخمسين جزءًا وتسعًا وخمسين دقيقةً وعلى ذلك المثال لأنّ خطّ زاي حاء مساوٍ لخطّ حاء طاء وخطّ هاء طاء ضعف قوس حاء طاء يحصل لنا خطّ باء طاء بأسره ثلاثةً وستّين جزءًا وثلاث عشرة دقيقةً بالأجزاء التي بها يحصل خطّ هاء طاء جزأين وعشر دقائق ومن أجل ذلك يكون موتر هاء باء بهذه الأجزاء ثلاثةً وستّين جزءًا وخمس عشرة دقيقةً فالأجزاء إذن التي بها موتر هاء باء مائة وعشرون جزءًا يكون بها خطّ طاء هاء أربعة أجزاء وسبع دقائق وتكون القوس التي عليه ثلاثة أجزاء وستًّا وخمسين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء هاء طاء القائم الزاوية ثلاث مائة وستّون جزءًا فيجب لذلك أن تكون زاوية هاء باء زاي ثلاثة أجزاء وستًّا وخمسين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وبهذه الأجزاء وضعت زاوية باء زاي لام سبعةً وثلاثين جزءًا وستّ عشرة دقيقةً فزاوية باء هاء لام القائمة ه – خ: الباقية تكون بهذه الأجزاء ثلاثةً وثلاثين جزءًا وعشرين دقيقةً وتكون
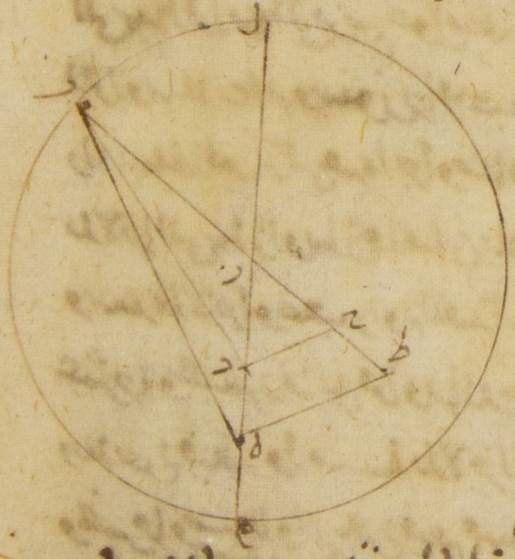 بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا ستّة عشر جزءًا وأربعين دقيقةً ففي الحال الثانية إذن ه: إذن كان الكوكب بالرؤية متأخّرًا عن البعد الأبعد بستّة عشر جزءًا وأربعين دقيقةً وقد تبيّن أنّه في الحال الأولى كان متقدّمًا لهذا البعد الأبعد بأحد وخمسين جزءًا وسبع وأربعين دقيقةً فيجتمع إذن البعد الذي يرى بين الحال الأولى وبين الحال الثانية من الأجزاء الآخذة في جهة واحدة ثمانيةً وستّين جزءًا وسبعًا وعشرين دقيقةً وذلك موافق لما استخرج منه بالأرصاد يط: وليوضع رسم الحال الثالثة أيضًا فلأنّ زاوية جيم زاي لام أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فقد تبيّن أنّها ستّة وخمسون جزءًا وثلاثون دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فإنّها والزاوية التي على رأسها
بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا ستّة عشر جزءًا وأربعين دقيقةً ففي الحال الثانية إذن ه: إذن كان الكوكب بالرؤية متأخّرًا عن البعد الأبعد بستّة عشر جزءًا وأربعين دقيقةً وقد تبيّن أنّه في الحال الأولى كان متقدّمًا لهذا البعد الأبعد بأحد وخمسين جزءًا وسبع وأربعين دقيقةً فيجتمع إذن البعد الذي يرى بين الحال الأولى وبين الحال الثانية من الأجزاء الآخذة في جهة واحدة ثمانيةً وستّين جزءًا وسبعًا وعشرين دقيقةً وذلك موافق لما استخرج منه بالأرصاد يط: وليوضع رسم الحال الثالثة أيضًا فلأنّ زاوية جيم زاي لام أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فقد تبيّن أنّها ستّة وخمسون جزءًا وثلاثون دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فإنّها والزاوية التي على رأسها
وهي زاوية دال زاي حاء مائة وثلاثة عشر جزءًا تكون القوس أيضًا التي على خطّ دال حاء مائةً ثلاثة عشر جزءًا بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال زاي حاء القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ زاي حاء الأجزاء الباقية لتمام نصف دائرة وهي سبعة وستّون جزءًا فخطّ دال حاء إذن من الخطّين اللذين يوترانهما مائة وأربع دقائق بالأجزاء التي بها موتر دال زاي مائة وعشرون جزءًا وخطّ زاي حاء بهذه الأجزاء ستّة وستّون جزءًا وأربع عشرة دقيقةً فيجب لذلك أن تكون الأجزاء التي بها خطّ دال زاي ثلاثة أجزاء وخمس وعشرون دقيقةً وخطّ دال جيم الذي من مركز الفلك الخارج المركز ستّون جزءًا فخطّ دال حاء بها جزءان وإحدى وخمسون دقيقةً وخطّ زاي حاء على ذلك المثال جزء واحد وثلاث وخمسون دقيقةً وأيضًا لأنّ المربّع الذي من خطّ دال حاء إذا نقص من المربّع الذي من خطّ دال جيم يكون منه المربّع الذي من خطّ جيم حاء يحصل لنا خطّ جيم طاء جيم حاء بهذه الأجزاء تسعةً وخمسين جزءًا وستًّا وخمسين دقيقةً وعلى ذلك المثال لأنّ خطّ زاي حاء مساوٍ لخطّ حاء طاء وخطّ هاء طاء ضعف خطّ دال حاء فلأنّ خطّ حاء طاء بأسره يحصل لنا أحدًا وستّين جزءًا وتسعًا وأربعين دقيقةً بالأجزاء التي بها يحصل خطّ هاء طاء خمسة أجزاء واثنتين وأربعين دقيقةً ومن قبل ذلك يكون موتر هاء جيم بهذه الأجزاء اثنين وستّين جزءًا وخمس دقائق فالأجزاء إذن التي بها موتر جيم هاء مائة وعشرون جزءًا يكون بها خطّ هاء طاء أحد عشر جزءًا ودقيقةً واحدةً وتكون القوس التي عليه عشرة أجزاء واثنتين وثلاثين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث جيم هاء طاء القائم الزاوية ثلاث مائة وستّون جزءًا فيجب لذلك أن تكون زاوية هاء جيم طاء أيضًا عشرة أجزاء واثنتين وثلاثين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وبهذه الأجزاء وضعت زاوية جيم زاي لام مائةً وثلاثة عشر جزءًا فزاوية جيم هاء لام الباقية إذن تكون أمّا بهذه الأجزاء فمائة جزء وجزءان
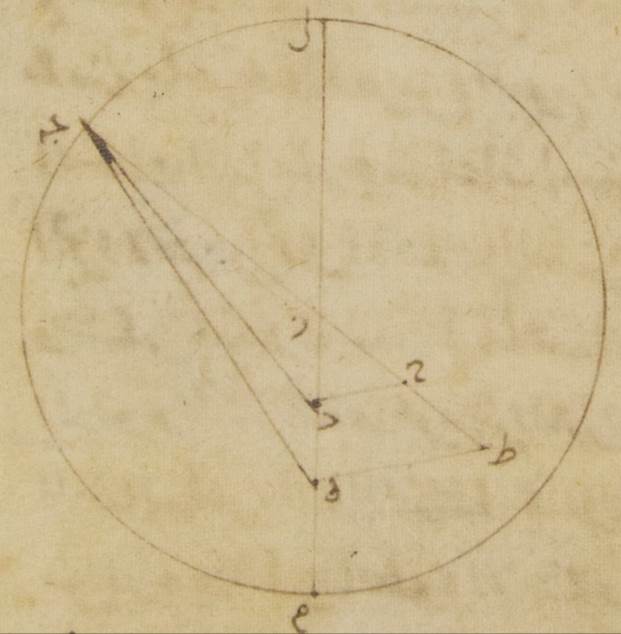 وثمان وعشرون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فتكون إحدى وخمسين دقيقةً وأربع عشرة ثانيةً فبهذا إذن كان مبلغ الأجزاء التي بها كان الكوكب في الحال الثالثة يرى مختلفًا عن البعد الأبعد وقد كان بيّن أنّه كان في الحال الثانية متخلّفًا عن هذا البعد الأبعد بستّة عشر جزءًا وأربعين دقيقةً فيجب لذلك أن يكون ما يحصل من البعد الذي بين الحال الثانية وبين الحال الثالثة هو الفضل بين العددين وذلك أربعة وثلاثون جزءًا وأربع وثلاثون دقيقةً وذلك موافق أيضًا لما استخرج منه بالأرصاد⊙ ومن البيّن من ذلك أنّ الكوكب إذا كان حاصله في الحال الثالثة كان على أربعة عشر جزءًا وأربع عشرة دقيقةً من الجدي وكان متخلّفًا على ما تبيّن عن البعد الأبعد أحدًا وخمسين جزءًا وأربع عشرة دقيقةً فإنّ البعد الأبعد في فلكه الخارج المركز كان
وثمان وعشرون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فتكون إحدى وخمسين دقيقةً وأربع عشرة ثانيةً فبهذا إذن كان مبلغ الأجزاء التي بها كان الكوكب في الحال الثالثة يرى مختلفًا عن البعد الأبعد وقد كان بيّن أنّه كان في الحال الثانية متخلّفًا عن هذا البعد الأبعد بستّة عشر جزءًا وأربعين دقيقةً فيجب لذلك أن يكون ما يحصل من البعد الذي بين الحال الثانية وبين الحال الثالثة هو الفضل بين العددين وذلك أربعة وثلاثون جزءًا وأربع وثلاثون دقيقةً وذلك موافق أيضًا لما استخرج منه بالأرصاد⊙ ومن البيّن من ذلك أنّ الكوكب إذا كان حاصله في الحال الثالثة كان على أربعة عشر جزءًا وأربع عشرة دقيقةً من الجدي وكان متخلّفًا على ما تبيّن عن البعد الأبعد أحدًا وخمسين جزءًا وأربع عشرة دقيقةً فإنّ البعد الأبعد في فلكه الخارج المركز كان
حاصله حينئذ على ثلاثة وعشرين جزءًا من العقرب والبعد الأقرب على الجزء المقابل لهذا الجزء وهو ثلاثة وعشرون جزءًا من الثور ک: وكذلك أيضًا إن نحن رسمنا حول مركز جيم فلك تدوير حاء طاء كاف حصل لنا من ذلك المسير الوسط في الطول لفلك التدوير من البعد الأبعد في الفلك الخارج المركز الآخر التي بيّن من ذلك مبلغها وهي ستّة وخمسون جزءًا وثلاثون دقيقةً وحصلت قوس طاء كاف من فلك التدوير خمسة أجزاء وستّ عشرة دقيقةً من قبل أنّ زاوية هاء جيم زاي أيضًا قد تبيّن أنّها عشرة أجزاء واثنتان وثلاثون دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فيجب أن تكون قوس حاء طاء الباقية وهي التي من البعد الأبعد في فلك التدوير إلى الكوكب يحصل لنا مائةً وأربعةً وسبعين جزءًا وأربعًا وأربعين دقيقةً ففي وقت الحال الثالثة إذن أعني في سنة عشرين من سني أذريانوس في شهر ماسوري عند المصريّين في اليوم الرابع والعشرين منه في انتصاف النهار كان كوكب زحل إذا نظر في أمره بحسب المسير الوسط بعده في الطول من البعد الأبعد في الفلك الخارج المركز ستّةً وخمسين جزءًا وثلاثين دقيقةً على أنّ منزله كان على تسعة عشر جزءًا وثلاثين دقيقةً من الجدي فكان بعده في الاختلاف من البعد الأبعد في فلك التدوير مائة وأربعة وتسعون جزءًا وأربع وأربعون دقيقةً وهذه الأشياء قصدنا لوجودها⊙
〈XI.6〉 و: في تبيين قدر فلك تدوير كوكب زحل
ثمّ من بعد ذلك أخذنا لتبيين قدر فلك تدويره رصدًا تولّيناه نحن ه: نحـ{ـن} في السنة الثانية من سني أنطونيس في شهر ماخير عند المصريّين في اليوم السادس منه في الليلة التي يتلوها اليوم السابع قبل انتصاف الليل بأربع ساعات استوائيّة وذلك أنّه ه - صح: أنه كان المتوسّط للسماء في آلة القياس الجزء الأخير من الحمل إذ حاصل الشمس كان على ثمانية وعشرين جزءًا وإحدى وأربعين دقيقةً من الرامي وكان حينئذ كوكب زحل لمّا قسناه بالدبران يرى حاصله على تسعة أجزاء وجزء من خمسة عشر من الدلو وكان متخلّفًا عن مركز القمر بنصف جزء بالتقريب وذلك أنّ هذا كان قدر بعده من قربته الشمالية لكنّ حاصل القمر كان في تلك الساعة بمسيره الوسط على ستّة أجزاء وخمس وخمسين دقيقةً من الدلو وكان حاصله في الاختلاف على مائة وأربعة وسبعين جزءًا وخمس عشرة دقيقةً من البعد الأبعد في فلك التدوير ومن أجل ذلك وجب أن يكون مسيره الحقيقي كان حاصله على تسعة أجزاء وأربعين دقيقةً من الدلو ومسيره الذي يرى بإسكندريّة على ثمانية أجزاء وأربع وثلاثين دقيقةً فمن هذا الوجه أيضًا وجب في كوكب زحل إذ كان قد كان متخلّفًا عن مركز القمر بنصف جزء بالتقريب أن يكون حاصله كان على تسعة أجزاء وجزء من خمسة عشر من جزء من الدلو أن يكون بعده كان من البعد الأبعد
في فلكه الخارج المركز إذ ليس يقع له من الانتقال في هذا المقدار من الزمان ما يعتدّ به ستّةً وسبعين جزءًا وأربع دقائق وإذ كان الزمان الذي من الحال الثالثة إلى وقت هذا الرصد هو سنتان مصريّتان ومائة وسبعة وستّون يومًا وثمان ساعات وكان أيضًا كوكب زحل يتحرّك على الجليل من الحساب في هذا المقدار من الزمان أمّا في الطول فجزءًا واحدًا وثلاث دقائق وأمّا في الاختلاف فمائة وأربعة وثلاثون جزءًا وأربع وعشرون دقيقةً فإنّا متى زدنا على هذين الحاصلين الحاصلين اللذين وضعنا في الحال الثالثة صار لنا في وقت هذا الرصد أيضًا الذي قدّمنا ذكره حاصل كوكب زحل أمّا في الطول فعلى ستّة وثمانين جزءًا وثلاث وثلاثين دقيقةً من البعد الأبعد في الفلك الخارج المركز وأمّا في الاختلاف فعلى ثلاث مائة وتسعة أجزاء وثمان دقائق من البعد الأبعد في فلك التدوير. فإذ قد وطّئ هذان المعنيان كا: فليوضع أيضًا الرسم الذي وضع لنظير هذا المعنى من التبيين على أن وضع فيه فلك التدوير تاليًا للبعد الأبعد في الفلك الخارج المركز ووضع الكوكب نفسه متقدّمًا للبعد الأبعد في فلك التدوير على ما يوافق ما فرض من المسير فلأنّ زاوية ألف زاي باء أعني زاوية دال زاي ميم أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فإنّها وضعت ستّةً وثمانين جزءًا وثلاثًا وثلاثين دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فمائة وثلاثة وسبعون جزءًا وستّ دقائق تكون أيضًا القوس التي على خطّ دال ميم مائةً وثلاثةً وسبعين جزءًا وستّ دقائق بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال زاي ميم القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ زاي ميم الأجزاء الباقية لتمام نصف دائرة وهي ستّة أجزاء وأربع وخمسون دقيقةً فخطّ دال ميم إذن من الخطّين اللذين يوترانهما يكون مائةً وتسعة عشر جزءًا وسبعًا وأربعين دقيقةً بالأجزاء التي بها موتر دال زاي مائة وعشرون جزءًا ويكون خطّ زاي ميم بهذه الأجزاء سبعة أجزاء وثلاث عشرة دقيقةً فيجب لذلك أن تكون الأجزاء التي بها خطّ دال زاي وهو الذي بين المركزين ثلاثة أجزاء وخمس وعشرون دقيقةً وخطّ دال باء الذي من مركز الفلك الخارج المركز ستّون جزءًا فإنّ خطّ دال ميم بها قريب من ثلاثة أجزاء وخمس وعشرين دقيقةً وخطّ زاي ميم على ذلك المثال اثنتا عشرة دقيقةً ولأنّ المربّع الذي من خطّ دال ميم إذا نقص من المربّع الذي من خطّ دال باء يكون من ذلك المربّع الذي من خطّ باء ميم يحصل لنا خطّ باء ميم أيضًا بهذه الأجزاء تسعةً وخمسين جزءًا وأربعًا وخمسين دقيقةً وعلى ذلك المثال لأنّ خطّ زاي ميم مساوٍ لخطّ ميم لام وخطّ هاء لام ضعف خطّ دال ميم يحصل لنا خطّ باء لام بأسره أيضًا ستّين جزءًا وستّ دقائق بالأجزاء التي بها يجتمع خطّ هاء لام ستّة أجزاء وخمسين دقيقةً ومن أجل ذلك يكون موتر هاء باء بهذه الأجزاء ثمانين جزءًا وتسعًا وعشرين دقيقةً فالأجزاء إذن التي بها موتر ها باء مائة وعشرون جزءًا يكون بها خطّ هاء لام ثلاثة عشر جزءًا وثلاثًا وثلاثين دقيقةً وتكون القوس التي عليه اثنا عشر جزءًا وثمانيًا وخمسين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء هاء لام القائم الزاوية ثلاث مائة وستّون جزءًا فيجب لذلك أن تكون زاوية هاء باء زاي أيضًا اثنا عشر جزءًا وثمانيًا وخمسين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وبهذه الأجزاء وضعت زاوية ألف زاي باء مائةً وثلاثةً وسبعين جزءًا وستّ دقائق فزاوية ألف هاء باء إذن الباقية تكون بهذه الأجزاء مائةً وستّين جزءًا وثمان دقائق لكنّ زاوية ألف هاء لام إذ تشتمل على البعد الذي يرى بين الكوكب وبين البعد الأبعد فإنّها وضعت أمّا بالأجزاء
التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فستّة وسبعون جزءًا وأربع دقائق وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فمائة واثنان وخمسون جزءًا وثمان دقائق فزاوية كاف هاء باء إذن الباقية يحصل لنا بهذه الأجزاء ثمانية أجزاء فيجب لذلك أن تكون القوس أيضًا التي على خطّ باء زاي ثمانية أجزاء بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء هاء زاي القائم الزاوية ثلاث مائة وستّون جزءًا ويكون خطّ باء زاي ثمانية أجزاء واثنتين وعشرين دقيقةً بالأجزاء التي بها موتر هاء باء مائة وعشرون جزءًا فالأجزاء إذن التي بها أمّا خطّ هاء باء فستّون جزءًا وتسع وعشرون دقيقةً وأمّا الخطّ الذي من مركز الفلك الخارج المركز فستّون جزءًا فإنّ خطّ باء زاي يكون بها أربعة أجزاء وثلاثًا وعشرين دقيقةً⊙ وأيضًا لأنّه كان بعد الكوكب من نقطة حاء وهي البعد الأبعد في فلك التدوير ثلاث مائة وتسعة أجزاء وثمان دقائق تكون أيضًا قوس حاء كاف الباقية خمسين جزءًا واثنتين وخمسين دقيقةً فزاوية حاء باء كاف إذن هي أيضًا أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فخمسون جزءًا واثنتان وخمسون دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فمائة جزء وجزء واحد وأربع وأربعون دقيقةً وبهذه الأجزاء كانت زاوية هاء باء زاي أعني زاوية حاء باء طاء اثني عشر جزءًا وثمانيًا وخمسين دقيقةً فزاوية طاء باء كاف الباقية إذن ه: إذن تكون ثمانيةً وثمانين جزءًا وستًّا وأربعين دقيقةً بالأجزاء التي بها تبيّن أنّ زاوية كاف هاء باء بها ه: بها ثمانية أجزاء فتكون إذن زاوية باء كاف نون الباقية بهذه الأجزاء ثمانين جزءًا
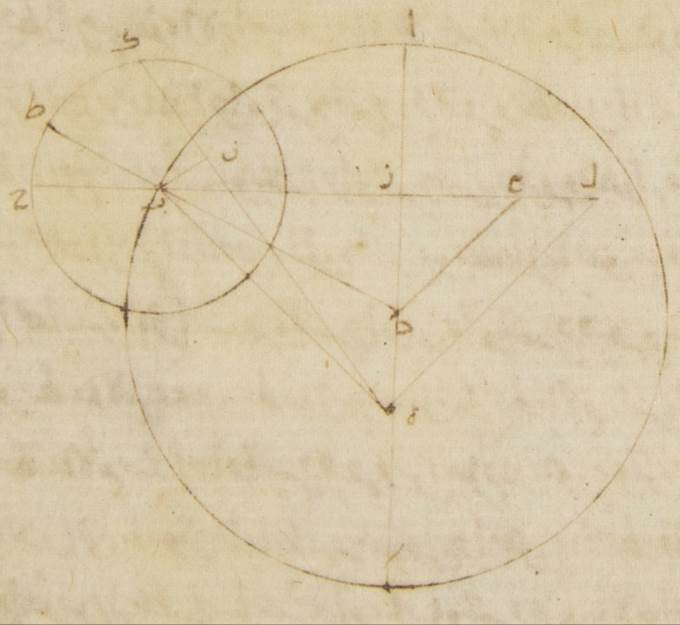 وستًّا وأربعين دقيقةً فيجب لذلك أن تكون أيضًا القوس التي على خطّ باء زاي ثمانين جزءًا وستًّا وأربعين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء كاف نون القائم الزاوية ثلاث مائة وستّون جزءًا ويكون خطّ ميم لام سبعةً وسبعين جزءًا وخمسًا وأربعين دقيقةً بالأجزاء التي بها موتر كاف باء مائة وعشرون جزءًا فالأجزاء إذن التي بها تبيّن أنّ خطّ زاي أربعة أجزاء وثلاث عشرة دقيقةً والخطّ الذي من مركز الفلك الخارج المركز ستّون جزءًا فإنّ خطّ باء كاف الذي من مركز فلك التدوير يحصل بها ستّة أجزاء ونصف جزء بالتقريب فقد حصل لنا أنّ البعد الأبعد لكوكب زحل حاصله في ابتداء ملك أنطونيس على ثلاثة وعشرين جزءًا من العقرب وأنّ الأجزاء التي بها الخطّ الذي من مركز الفلك الحامل لفلك التدوير ستّون جزءًا فإنّ الخطّ الذي
وستًّا وأربعين دقيقةً فيجب لذلك أن تكون أيضًا القوس التي على خطّ باء زاي ثمانين جزءًا وستًّا وأربعين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء كاف نون القائم الزاوية ثلاث مائة وستّون جزءًا ويكون خطّ ميم لام سبعةً وسبعين جزءًا وخمسًا وأربعين دقيقةً بالأجزاء التي بها موتر كاف باء مائة وعشرون جزءًا فالأجزاء إذن التي بها تبيّن أنّ خطّ زاي أربعة أجزاء وثلاث عشرة دقيقةً والخطّ الذي من مركز الفلك الخارج المركز ستّون جزءًا فإنّ خطّ باء كاف الذي من مركز فلك التدوير يحصل بها ستّة أجزاء ونصف جزء بالتقريب فقد حصل لنا أنّ البعد الأبعد لكوكب زحل حاصله في ابتداء ملك أنطونيس على ثلاثة وعشرين جزءًا من العقرب وأنّ الأجزاء التي بها الخطّ الذي من مركز الفلك الحامل لفلك التدوير ستّون جزءًا فإنّ الخطّ الذي
فيما بين المركزين أعني بين مركز فلك البروج وبين مركز الفلك الخارج المركز الذي يفعل الحركة المستوية اجتمع منها ستّة أجزاء وثمانيًا وخمسين دقيقةً والخطّ الذي من مركز فلك التدوير بهذه الأجزاء ستّة أجزاء وثلاثين دقيقةً وهذه الأشياء قصدنا لوجودها⊙
〈XI.7〉 ز: في تصحيح حركات زحل الدوريّة
وإذ قد بقي أن نبيّن كيف نصحّح حركاته الدوريّة فإنّا أخذنا لذلك أيضًا رصدًا من الأرصاد القديمة التي انبنت على الصحّة التي لا شكّ فيها قيل فيه نصًّا إنّ في سنة اثنتين وثمانين من سني الكلدانيّين في الشهر من شهورهم المسمّى كسندقس في اليوم الخامس منه بالعشيّ كان كوكب زحل من دون المنكب الجنوبيّ من العذراء بإصبعين وهذا الوقت كان في سنة خمس مائة وتسع عشرة من عهد بختنصّر في شهر طوبي عند المصريّين بالعشيّ في هذا الوقت نجد حاصل الشمس لسيرها الوسط على ستّة أجزاء وعشر دقائق من الحوت لكنّ الكوكب الثابت الذي على المنكب الجنوبيّ من العذراء كان حاصله أمّا في وقت رصدنا نحن فعلى ثلاثة عشر جزءًا وسدس جزء من العذراء وأمّا في وقت هذا الرصد الذي وضعناه من قبل أنّه يصيب الثلاث المائة والستّ والستّين السنة التي فيما بين الرصدين من حركة الكواكب الثابتة ثلاثة أجزاء وثلثي جزء بالتقريب فمن البيّن أنّ حاصله كان على تسعة أجزاء ونصف من العذراء وذلك كان حاصل كوكب زحل أيضًا إذ كان أميل إلى الجنوب من ذلك الكوكب الثابت بإصبعين وكذلك أيضًا لأنّ بعده الأبعد تبيّن أنّه كان في زماننا في ثلاثة وعشرين جزءًا من العقرب فواجب أن يكون حاصله كان في ذلك الرصد الموصوف على تسعة عشر جزءًا وثلث جزء من العقرب فيجتمع لذلك أنّ في الوقت الموصوف كان الكوكب بالرؤية بعده من البعد الأبعد كان في ذلك الوقت في فلك البروج مائتي جزء وتسعين جزءًا وعشر دقائق وكان وسط الشمس بعده من ذلك البعد الأبعد مائةً وستّة أجزاء وخمسين دقيقةً وإذ قد وطّئ هذان المعنيان كب: فليوضع أيضًا الرسم الذي وضع في نظير هذا المعنى من التبيين على أنّ وضع فلك التدوير فيه متقدّم للبعد الأبعد ووضع الشمس متقدّمًا للبعد الأقرب والخطّ الذي من مركز فلك التدوير إلى الكوكب مواز للخطّ الذي من مركز فلك البروج إلى الشمس فلأنّ كوكب زحل رئي ه: رئي متقدّمًا للبعد الأبعد بالأجزاء الباقية لتمام دائرة واحدة وهي تسعة وستّون جزءًا وخمسون دقيقةً تكون زاوية ألف هاء طاء إذ هي عند مركز فلك البروج أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فتسعة وستّون جزءًا وخمسون دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فمائة وتسعة وثلاثون جزءًا وأربعون دقيقةً وقد وضعت زاوية ألف هاء لام وهي زاوية بعد الشمس أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فمائة وستّة أجزاء وخمسون دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فمائتين وثلاثة عشر جزءًا وأربعون دقيقةً فزاوية طاء هاء لام إذن بأسرها أعني زاوية باء طاء هاء إذ كان خطّا باء طاء هاء لام متوازيين ثلاث مائة وثلاثة وخمسون جزءًا وعشرون دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة
وستّون جزءًا وزاوية باء طاء نون الباقية بهذه الأجزاء ستّة أجزاء وأربعون دقيقةً فيجب لذلك أن تكون أيضًا القوس التي على خطّ باء نون ستّة أجزاء وأربعين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء طاء نون القائم الزاوية ثلاث مائة وستّون جزءًا ويكون خطّ باء نون ستّة أجزاء وثمانيًا وخمسين دقيقةً بالأجزاء التي بها موتر باء طاء مائة وعشرون جزءًا فالأجزاء إذن التي بها خطّ باء طاء الذي من مركز فلك التدوير ستّة أجزاء وثلاثون دقيقةً يكون بها خطّ باء نون ثلاثًا وعشرين دقيقةً وعلى ذلك المثال لا زاوية ألف هاء طاء مائة وتسعة وثلاثون جزءًا وأربعون دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وزاوية هاء دال ميم بهذه الأجزاء أربعون جزءًا وعشرون دقيقةً تكون أيضًا القوس التي على خطّ دال ميم مائةً وتسعةً وثلاثين جزءًا وأربعين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال هاء ميم القائم الزاوية ثلاث مائة وستّون جزءًا ويكون خطّ دال ميم نفسه مائة واثني عشر جزءًا وتسعًا وثلاثين دقيقةً بالأجزاء التي بها موتر هاء دال مائة وعشرون جزءًا فالأجزاء إذن التي بها خطّ هاء دال الذي فيما بين المركزين ثلاثة أجزاء وخمس وعشرون دقيقةً وخطّ دال باء الذي من مركز الفلك الخارج المركز ستّون جزءًا فإن خطّ دال ميم أعني خطّ باء سين يكون بها ثلاثة أجزاء واثنتي عشرة دقيقةً ويكون خطّ باء نون سين بأسره ثلاثة أجزاء وخمسًا وثلاثين دقيقةً بالأجزاء التي بها موتر دال باء ستّون جزءًا فالأجزاء إذن التي بها خطّ دال باء مائة وعشرون جزءًا يكون بها خطّ نون سين سبعة أجزاء وعشر دقائق وتكون القوس التي عليه ستّة أجزاء واثنتين وخمسين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء دال سين القائم الزاوية ثلاث مائة وستّون جزءًا فيجب من ذلك أن تكون زاوية باء دال سين ستّة أجزاء واثنتين وخمسين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وتكون زاوية باء دال ميم الباقية بهذه الأجزاء مائة وثلاثة وسبعون جزءًا وثمان دقائق وتكون زاوية باء دال هاء بأسرها على ذلك المثال مائتي جزء وثلاثة عشر جزءًا وثمانيًا وعشرين دقيقةً وتكون زاوية باء دال ألف الباقية بهذه الأجزاء مائةً وستّةً وأربعين جزءًا واثنتين وثلاثين دقيقةً فيجب لذلك أن تكون القوس التي على خطّ زاي كاف مائةً وستّةً وأربعين جزءًا واثنتين وثلاثين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال زاي كاف القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ دال كاف الأجزاء الباقية لتمام نصف دائرة وهي ثلاثة وثلاثون جزءًا وثمان وعشرون دقيقةً فخطّ زاي كاف إذن من الخطّين اللذين يوترانها يكون مائةً وأربعة عشر جزءًا وخمسًا وخمسين دقيقةً بالأجزاء التي بها موتر دال زاي مائة وعشرين جزءًا ويكون خطّ دال كاف بهذه الأجزاء أربعةً وثلاثين جزءًا وثلاثًا وثلاثين دقيقةً فالأجزاء إذن التي بها مّا خطّ دال زاي الذي بين المركزين فثلاثة أجزاء وخمس وعشرون دقيقةً وأمّا خطّ دال باء الذي من مركز الفلك الخارج المركز فستّون جزءًا يكون بها أمّا خطّ زاي كاف فثلاثة أجزاء وسبع عشرة دقيقةً وأمّا خطّ دال كاف فعلى ذلك المثال تسعًا وخمسين دقيقةً ويكون خطّ كاف باء الباقي تسعةً وخمسين جزءًا ودقيقةً واحدةً بالأجزاء التي بها كان خطّ زاي كاف ثلاثة أجزاء وسبع عشرة دقيقةً ومن أجل ذلك يكون موتر زاي باء بهذه الأجزاء تسعةً وخمسين جزءًا وستّ دقائق فيجب لذلك أن تكون الأجزاء التي بها موتر زاي باء مائة وعشرون جزءًا فإنّ خطّ زاي كاف بها ستّة أجزاء وأربعون دقيقةً والقوس التي عليه ستّة أجزاء واثنتان وعشرون دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء زاي كاف القائم الزاوية ثلاث مائة وستّون جزءًا
فزاوية زاي باء كاف إذن ستّة أجزاء واثنتان وعشرون دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وبهذه الأجزاء كانت زاوية ألف دال باء مائةً وستّةً وأربعين جزءًا واثنتين وثلاثين دقيقةً فزاوية ألف زاي باء بأسرها إذًا ه: إذًا وهي التي تشتمل على المسير المستوي في الطول يحصل لنا أمّا بهذه الأجزاء فمائة واثنان وخمسون جزءًا وأربع وخمسون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فستّة وسبعون جزءًا وسبع وعشرون دقيقةً فكان إذن بعد كوكب زحل في وقت ذلك الرصد الموصوف من البعد الأبعد بالمسير الوسط
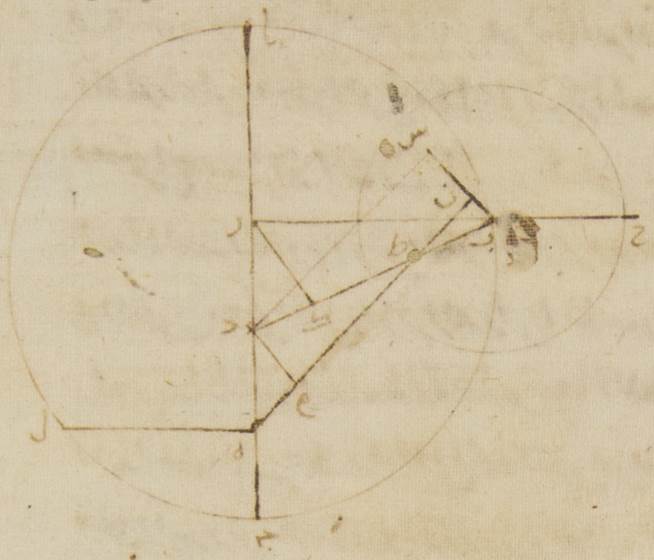 في الطول مائتين وثلاثة وثمانين جزءًا وثلاثًا وثلاثين دقيقةً أعني أنّ حاصله كان على جزأين وثلاث وخمسين دقيقةً من العذراء ولأنّ مسير الشمس الوسط أيضًا قد كان وضع مائةً وستّة أجزاء وخمس دقائق فإنّا إن زدنا على ذلك أجزاء دائرة واحدة وهي ثلاث مائة وستّون جزءًا ونقصنا مما يجتمع وهو أربع مائة وستّة وستّون جزءًا وخمسون دقيقةً أجزاء الطول وهي مائتان وثلاثة وثمانون جزءً وثلاث وثلاثون دقيقةً حصل لنا بعده في ذلك الوقت بعينه في الاختلاف أيضًا من البعد الأبعد في فلك التدوير مائةً وثلاثةً وثمانين جزءًا وسبع عشرة دقيقةً فلأنّ في وقت هذا الرصد الذي قصدنا له وكان في سنة مائة وتسع عشرة من عهد بختنصّر في شهر طوبي في اليوم الرابع عشر منه بالعشيّ تبيّن أنّ بعده كان من البعد الأبعد في فلك التدوير مائة وثلاثة وثمانون جزءًا وسبع عشرة دقيقةً وفي وقت الحال الثالثة كان في سنة ثمان مائة وثلاث وثمانين من عهد بختنصّر في شهر ماسوري في اليوم الرابع والعشرين منه في انتصاف النهار كان بعده منه مائةً وأربعةً وسبعين جزءًا وأربعًا وأربعين دقيقةً فظاهر أنّ في الزمان الذي بين الرصدين وهو يحيط بثلاث مائة وأربع وستّين سنةً مصريّةً ومائتين وتسعة عشر يومًا ونصف وربع يوم تحرّك كوكب زحل بعد الأدوار الثامنة في الاختلاف ثلاث مائة وأحدًا وخمسين جزءًا وسبعًا وعشرين دقيقةً ويكاد أن يكون هذا أيضًا مبلغ ما يجتمع له من أجزاء الفضل في الجداول التي تقدّمنا فوضعناها للحركات الوسطى إذ كان أيضًا المسير الوسط في اليوم إنّما بهذه أنفسها قويّةً بأن قسمت الأجزاء التي تجتمع من عدّة الأدوار ومن الفضلة على عدّة الأيّام التي تجتمع من الزمان الذي فيما بين الرصدين⊙
في الطول مائتين وثلاثة وثمانين جزءًا وثلاثًا وثلاثين دقيقةً أعني أنّ حاصله كان على جزأين وثلاث وخمسين دقيقةً من العذراء ولأنّ مسير الشمس الوسط أيضًا قد كان وضع مائةً وستّة أجزاء وخمس دقائق فإنّا إن زدنا على ذلك أجزاء دائرة واحدة وهي ثلاث مائة وستّون جزءًا ونقصنا مما يجتمع وهو أربع مائة وستّة وستّون جزءًا وخمسون دقيقةً أجزاء الطول وهي مائتان وثلاثة وثمانون جزءً وثلاث وثلاثون دقيقةً حصل لنا بعده في ذلك الوقت بعينه في الاختلاف أيضًا من البعد الأبعد في فلك التدوير مائةً وثلاثةً وثمانين جزءًا وسبع عشرة دقيقةً فلأنّ في وقت هذا الرصد الذي قصدنا له وكان في سنة مائة وتسع عشرة من عهد بختنصّر في شهر طوبي في اليوم الرابع عشر منه بالعشيّ تبيّن أنّ بعده كان من البعد الأبعد في فلك التدوير مائة وثلاثة وثمانون جزءًا وسبع عشرة دقيقةً وفي وقت الحال الثالثة كان في سنة ثمان مائة وثلاث وثمانين من عهد بختنصّر في شهر ماسوري في اليوم الرابع والعشرين منه في انتصاف النهار كان بعده منه مائةً وأربعةً وسبعين جزءًا وأربعًا وأربعين دقيقةً فظاهر أنّ في الزمان الذي بين الرصدين وهو يحيط بثلاث مائة وأربع وستّين سنةً مصريّةً ومائتين وتسعة عشر يومًا ونصف وربع يوم تحرّك كوكب زحل بعد الأدوار الثامنة في الاختلاف ثلاث مائة وأحدًا وخمسين جزءًا وسبعًا وعشرين دقيقةً ويكاد أن يكون هذا أيضًا مبلغ ما يجتمع له من أجزاء الفضل في الجداول التي تقدّمنا فوضعناها للحركات الوسطى إذ كان أيضًا المسير الوسط في اليوم إنّما بهذه أنفسها قويّةً بأن قسمت الأجزاء التي تجتمع من عدّة الأدوار ومن الفضلة على عدّة الأيّام التي تجتمع من الزمان الذي فيما بين الرصدين⊙
〈XI.8〉 ح: في حاصل حركات زحل الدوريّة
ولأنّ الزمان الذي من الحركة الأولى من سني بختنصّر من اليوم الأوّل من شهر توث منها في انتصاف نهاره إلى وقت هذا الرصد القديم الموصوف خمس مائة سنة وثمان عشرة سنةً مصريّةً ومائة وثلاثة وثلاثون يومًا وربع يوم وهذا الزمان يفضل فيه من الأجزاء أمّا في الطول فمائتان وستّة عشر جزءًا وعشر دقائق وأمّا في الاختلاف فمائة وتسعة وأربعون جزءًا وخمس عشرة دقيقةً. فأمّا إن نقصناها بين الفضلتين من الحاصلين الموصوفين في الرصد صار لنا أيضًا في ذلك الوقت المفروض للتحصيلات حاصل كوكب زحل بالحركة
الوسطى في الطول على ستّة وعشرين جزءًا وثلاث وأربعين دقيقةً من الجدي. وفي الاختلاف على اثنين وثلاثين جزءًا ودقيقتين من البعد الأبعد في فلك تدويره. ولذلك بعينه يكون البعد الأبعد في فلك الخارج المركز كان في أربعة عشر جزءًا وعشر دقائق من العقرب وهذه الأشياء ه: يعني الهندسة كان قصدنا وجودها⊙ ه: {...}حل وسط زحل لأوّل يوم من السنة {...} ملك فيمبا بختنصّر كو مجـ د و ح دقائق من الجدي⊙ وفي الاختلاف بميل لب ب د ر ح دقائق من البعد الأبعد من التدوير
〈XI.9〉 ط: كيف تستخرج من قبل الحركات الدوريّة المسيراتُ الحقيقيّة بطريق الخطوط
وبهذه الأشياء ه: يعني الهندسة بأعيانها تبيّن لنا أنّه إذا عكس الأمر فكانت قوسا الدورين أعني القوس من الفلك الخارج المركز الذي يشتمل على الحركة المستوية والقوس من فلك التدوير معطاتين فقد تهيّأ استخراج مسيرات الكوكب بالرؤية بأهون سعي بطريق الخطوط كجـ: وذلك أنّا إذا رسمنا صورةً بسيطةً فيها الفلك الخارج المركز وفلك التدوير ووصلنا فيها خطّي زاي طاء هاء باء حاء فإنّه إذا كان المسير الوسط في الطول معطى أعني زاوية ألف زاي باء كانت زاوية ألف هاء باء معطاة وكانت زاوية هاء باء زاي أعني زاوية هاء باء طاء معطاةً في الأصلين جميعًا اللذين يعمل عليهما من قبل الأشياء التي تقدّم بيانها وكذلك
 أيضًا تكون نسبة خطّ هاء باء إلى الخطّ الذي من مركز فلك التدوير معطاة وإذا أنزل الكوكب مثلًا على نقطة لام من فلك التدوير ووصل خطّا هاء كاف باء كاف وكانت قوس طاء كاف معطاة فإنّا إن لم نخرج كما أخرجنا في عكس هذا المعنى من البرهان من مركز فلك التدوير وهو نقطة باء عمودًا على خطّ هاء كاف بل أخرجنا من النقطة التي على الكوكب وهي نقطة لام عمودًا على خطّ هاء باء كإخراجنا هاهنا عمود كاف لام فإنّ زاوية حاء باء كاف بأسرها تكون معطاةً ومن أجل ذلك تكون نسبة خطّي كاف لام لام باء إلى باء لام وإلى هاء باء معطاةً وذلك بيّن ويلزم ذلك أن تكون أيضًا نسبة خطّ هاء باء لام بأسره إلى خطّ لام كاف معطاةً فيجب لذلك إذا كانت زاوية لام هاء كاف تكون معطاةً أن تجتمع لنا زاوية ألف هاء كاف بأسرها أيضًا معطاةً وهي المشتملة على البعد الذي يرى من البعد الأبعد للكوكب⊙
أيضًا تكون نسبة خطّ هاء باء إلى الخطّ الذي من مركز فلك التدوير معطاة وإذا أنزل الكوكب مثلًا على نقطة لام من فلك التدوير ووصل خطّا هاء كاف باء كاف وكانت قوس طاء كاف معطاة فإنّا إن لم نخرج كما أخرجنا في عكس هذا المعنى من البرهان من مركز فلك التدوير وهو نقطة باء عمودًا على خطّ هاء كاف بل أخرجنا من النقطة التي على الكوكب وهي نقطة لام عمودًا على خطّ هاء باء كإخراجنا هاهنا عمود كاف لام فإنّ زاوية حاء باء كاف بأسرها تكون معطاةً ومن أجل ذلك تكون نسبة خطّي كاف لام لام باء إلى باء لام وإلى هاء باء معطاةً وذلك بيّن ويلزم ذلك أن تكون أيضًا نسبة خطّ هاء باء لام بأسره إلى خطّ لام كاف معطاةً فيجب لذلك إذا كانت زاوية لام هاء كاف تكون معطاةً أن تجتمع لنا زاوية ألف هاء كاف بأسرها أيضًا معطاةً وهي المشتملة على البعد الذي يرى من البعد الأبعد للكوكب⊙
〈XI.10〉 يے: في صفة عمل جداول للاختلافات
ولكيلا يحتاج في كل وقت إلى أن يحسب المسيرات الذي يرى بطريق الخطوط وإن كان بهذا الوجه وحده يصحّ المطلوب من ذلك إلّا أنّ استعمالنا له أصعب وأبعد مأخذًا عند الحاجة إلى تناول ما هو من ذلك محسوب ميسّرًا تكلّفنا عمل جدول لكلّ واحد من الكواكب الخمسة بأسهل ما قدرنا عليه مأخذًا وأقربه مع ذلك من الاستقصاء والتدقيق على اختلافاتها الجزئيّة المعدّلة له كيما يكون إذا فرض لنا حركاتها الدوريّة من البعد الأبعد لواحد واحد منها أمكنّا أن نحسب
بذلك بسهولة مسيراتها التي ترى في وقت وقت فرتّبنا كلّ واحد من هذه الجداول في خمسة وأربعين سطرًا طلبًا أيضًا لحسن التقدير وفي صفوف ثمانية فالصفّان الأوّلان ه - صح: لان من هذه الصفوف يشتملان على أعداد المسيرات الوسطى كما فعل في الشمس وفي القمر إلّا أنّه رتّب في الأوّل منهما المائة والثمانون الجزء من البعد الأبعد من أعلاه فنازلًا ورتّب في الثاني المائة والثمانون الجزء الباقية التي لنصف الدائرة التي من أسفله فصاعدًا حتّى إنّ عدد المائة والثمانين موضوع في الصفر جميعًا في الشطر الأخير وجعل التفاضل فيهما أمّا في الخمسة العشر السطر التي من أعلاهما فستّة أجزاء وأمّا في الثلاثين السطر الباقية التي من دونها فثلاثة أجزاء ثلاثة أجزاء من قبل أنّ الزيادات لأقسام الاختلاف أيضًا أمّا ممّا يلي البعد الأبعد فقلّ ما يخالف بعضها بعضًا وأمّا ممّا يلي البعد الأقرب فإنّ تغييرها يزيد سرعةً. وأمّا الصفّان اللذان يتلوان هذين فإنّ الثالث منهما يشتمل على الزيادات والنقصانات التي تكون بحسب الأعداد التي تكون في سطور كلّ واحد من الكواكب للمسير الوسط في الطول من قبل الفلك الخارج المركز الأعظم خروجًا عن المركز إلّا أنّها مأخوذة على الأمر البسيط كما لو كان مركز فلك التدوير يتحرّك على الفلك نفسه الخارج المركز الذي يشتمل على الحركة المستوية. والرابع من هذين الصفّين يشتمل على الفصول التي تجتمع من الزيادات والنقصانات من قبل أنّ مركز فلك التدوير ليس على هذا الفلك الذي تقدّم ذكره يدور لكن على فلك آخر⊙. وأمّا الوجه الذي به يستخرج كلّ واحد من هذين الأمرين معًا وفرادى بطريق الخطوط فقد يسهل الوقوف عليه بأشكال كثيرة فقد تقدّمنا فوصفناها⊙ . وفي هذا الموضع إذ كان قصدنا إثبات هذين المعنيين في كتاب فالأولى بنا أن نو{...} على هذا التقويم للاختلاف المنسوب إلى فلك البروج عيانًا ولذلك وضعناه في صفّين وأمّا عند الحاجة إلى استعماله والعمل به فقد كان يكتفى بصفّ واحد وهو الحاصل من الزيادة والنقصان الموجودين في هذين الصفّين. وأمّا الثلاثة الصفوف التي تتلو هذين فإنّ كلّ واحد منهما يشتمل على الزيادات والنقصانات التي تكون من قبل فلك التدوير وهذه أيضًا مأخوذة على الأمر البسيط وعلى أنّ ه: أن البعد الأبعد والبعد الأقرب في كلّ واحدة منها إنّما يعمل منهما على حسب البعد من أبصارنا وعلى أنّ الوجه في تبيين ذلك أيضًا قد يسهّل الوقوف عليه فالأشكال التي تقدّمنا فوضعناها. فالصفّ الأوسط من هذه الصفوف الثلاثة وهو الصفّ السادس من الصفّ الأوّل يشتمل على الزيادات والنقصانات التي تجتمع بحسب نسب الأبعاد الوسطى . وأمّا الصفّ الخامس فيشتمل على مبلغ التفاضل الذي يكون في مثل تلك الأقسام بأعيانها بين الزيادات والنقصانات في أعظم البعد وبينها في البعد الوسط⊙. وأمّا الصفّ السابع فيشتمل على مبلغ التفاضل الذي يكون بين الزيادات والنقصانات في أقلّ البعد وبينها
في البعد الوسط⊙ فإذ قد بيّنّا أنّ الأجزاء التي بها الخطّ الذي من مركز فلك التدوير الذي لكوكب زحل فإنّ الأجود الآن أن نبتدئ من فوق فستّة أجزاء وثلاثون دقيقةً⊙ وأمّا الذي لكوكب المشتري فأحد عشر جزءًا وثلاثون دقيقةً⊙ وأمّا الذي لكوكب المرّيخ فتسعة وثلاثون جزءًا وثلاثون دقيقةً⊙ وأمّا الذي لكوكب الزهرة فثلاثة وأربعون جزءًا وعشر دقائق⊙ وأمّا الذي لكوكب عطارد فاثنان وعشرون جزءًا وثلاثون دقيقةً فإنّ البعد الوسط كلّها بتلك الأجزاء ستّون جزءًا أعني البعد الذي يوجد بالقياس إلى الخطّ الخارج من مركز الفلك الخارج المركز الحامل لفلك التدوير وإنّ أعظم البعد لها بحسب مركز فلك البروج⊙ أمّا في كوكب زحل فثلاثة وستّون جزءًا وخمس وعشرون دقيقةً وأمّا في كوكب المشتري فاثنان وستّون جزءًا وخمس وأربعون دقيقةً⊙ وأمّا في كوكب المرّيخ فستّة وستّون جزءًا⊙ وأمّا في كوكب الزهرة فأحد وستّون جزءًا وخمس عشرة دقيقةً⊙ وأمّا في كوكب عطارد فستّة وستّون جزءًا⊙ وإنّ أقلّ البعد على ذلك المثال أمّا في كوكب زحل فستّة وخمسون جزءًا وخمس وثلاثون دقيقةً⊙ وأمّا في كوكب المشتري فسبعة وخمسون جزءًا وخمس عشرة دقيقةً⊙ وأمّا في كوكب المرّيخ فأربعة وخمسون جزءًا⊙ وأمّا في كوكب الزهرة فثمانية وخمسون جزءًا وخمس وأربعون دقيقةً⊙ وأمّا في كوكب عطارد فخمسة وخمسون جزءًا وأربع وثلاثون دقيقةً⊙ وأمّا الصفّ الباقي وهو الثامن فإنّا رتّبناه لأن توجد منه الأجزاء التي فضلت من التفاضل الذي وصفناه إذا لم تتّفق أفلاك تداوير الكواكب في نفس الأبعاد الوسطى أو العظمى أو الصغرى بل اتفقت في المسيرات التي فيما بين ذلك وما حسبناه من هذا التصحيح وأثبتناه في الجداول فإنّما أثبتنا منه أعظم ما يكون فقط من الزيادات والنقصانات في كل واحد من الأبعاد التي فيما بين ذلك التي تحدث عن الخطوط المستقيمة التي تخرج من أبصارنا فيما بين فلك التدوير بين ما يصيب هذه الفصول في الأقسام الجزئيّة من فلك التدوير وبين ما يصيبها في أكثر ما يكون من الزيادات والنقصانات اختلاف له قدر يعتدّ به وكيما يزداد ما وصفناه من ذلك بيانًا ويوقف على الباب نفسه في استخراج هذه الحصص كد: فلنضع خطًّا يمرّ بمركز فلك
 البروج وبمركز الفلك الذي يشتمل على حركة فلك التدوير المستوية وليكن خطّ ألف باء جيم دال ولننزل أنّ مركز فلك البروج نقطة دال ومركز الحركة المستوية لفلك التدوير نقطة باء ولنخرج خطّ باء هاء زاي ولنرسم حول نقطة هاء فلك تدوير زاي حاء ولنخرج من نقطة دال خطّي جيم حاء يماسّه ولنوصل خطّ جيم هاء وعمود
البروج وبمركز الفلك الذي يشتمل على حركة فلك التدوير المستوية وليكن خطّ ألف باء جيم دال ولننزل أنّ مركز فلك البروج نقطة دال ومركز الحركة المستوية لفلك التدوير نقطة باء ولنخرج خطّ باء هاء زاي ولنرسم حول نقطة هاء فلك تدوير زاي حاء ولنخرج من نقطة دال خطّي جيم حاء يماسّه ولنوصل خطّ جيم هاء وعمود
هاء حاء ولننزل على طريق المثال في كلّ واحد من الكواكب الخمسة أنّ مركز فلك التدوير بعده على الاستواء من البعد الأبعد في الفلك الخارج المركز ثلاثون جزءًا فنقول كي لا نكرّر البرهان فيطول بذلك الحساب إنّه لمّا كان قد تبيّن بأشكال كثيرة فيما تقدّم في الأصل الذي يعمل عليه في كوكب عطارد وفي الأصل الذي يعمل عليه في سائر الكواكب أنّ زاوية ألف باء هاء إذا كانت معطاةً كانت نسبة خطّ جيم هاء إلى الخطّ الذي من مركز فلك التدوير أعني خطّ هاء حاء معطاةً وهذه النسبة تحصل بالحساب في واحد واحد من الكواكب الخمسة إذا وضعت زاوية ألف باء هاء ثلاثين جزءًا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا أمّا في كوكب زحل فنسبة ثلاثة وستّين جزءًا ودقيقتين إلى ستّة أجزاء وثلاثين دقيقةً⊙ وأمّا في كوكب المشتري فنسبة اثنين وستّين جزءًا وستّ وعشرين دقيقةً إلى أحد عشر جزءًا وثلاثين دقيقةً وأمّا في كوكب المرّيخ فنسبة خمسة وستّين جزءًا وأربع وعشرين دقيقةً إلى تسعة وخمسين جزءًا ودقيقة⊙ وأمّا في كوكب الزهرة فنسبة أحد وستّين جزءًا وستّ دقائق إلى ثلاثة وأربعين جزءًا وعشر دقائق⊙ وأمّا في كوكب عطارد فنسبة ستّة وستّين جزءًا وخمس وثلاثين دقيقةً إلى اثنين وعشرين جزءًا وثلاثين دقيقةً فإنّ زاوية هاء جيم حاء التي تشتمل حينئذ على أعظم ما يكون من الزيادة والنقصان من قبل فلك التدوير يحصل لنا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا أمّا في كوكب زحل فخمسة أجزاء وخمسًا وخمسين دقيقةً ونصف دقيقةً⊙ وأمّا في كوكب المشتري فعشرة أجزاء وستًّا وثلاثين دقيقةً ونصف دقيقة⊙ وأمّا في كوكب المرّيخ فسبعة وثلاثين جزءًا وتسع دقائق⊙ وأمّا في كوكب الزهرة فأربعة وأربعين جزءًا وستًّا وخمسين دقيقةً ونصف دقيقة⊙ وأمّا في كوكب عطارد فتسعة عشر جزءًا وخمسًا وأربعين دقيقةً والذي يحصل من أعظم ما يكون من الزيادات والنقصانات على حسب النسب الذي وضعناها قبيل أمّا في الأبعاد الوسطى على النسق الذي جرينا عليه الكواكب كيلا نكرّر⊙ ستّة أجزاء وثلاث عشرة دقيقةً⊙ وأحد عشر جزءًا وثلاث دقائق⊙ وأحدًا وأربعون جزءًا وعشر دقائق وستّة وأربعون جزءًا⊙ واثنان وعشرون جزءًا ودقيقتان⊙ وأمّا في أعظم ما يكون من الأبعاد فخمسة أجزاء وثلاث وخمسون دقيقةً⊙ وعشرة أجزاء وأربع وثلاثون دقيقةً وستّة وثلاثون جزءًا وخمس وأربعون دقيقةً⊙ وأربعة وأربعون جزءًا وثمان وأربعون دقيقةً وتسعة عشر جزءًا ودقيقتان⊙ وأمّا في أقل ما يكون من الأبعاد فستّة أجزاء وستّ وثلاثون دقيقةً⊙ وأحد عشر جزءًا وخمس وثلاثون دقيقةً⊙ وسبعة وأربعون جزءًا ودقيقة واحدة⊙ وسبعة وأربعون جزءًا وسبع عشرة دقيقةً⊙ وثلاثة وعشرون جزءًا وثلاث وخمسون دقيقةً⊙ فيكون الخلاف بين الزيادات والنقصانات في الأبعاد الوسطى وبينها في الأبعاد العظمى بعشرين دقيقةً⊙ وتسع وعشرين دقيقةً⊙ وأربعة أجزاء وخمس وعشرين دقيقةً⊙ وجزء واحد واثنتي عشرة دقيقةً⊙ وثلاثة أجزاء⊙
ويكون الخلاف بينهما في الأبعاد الوسطى وبينها في الأبعاد الصغرى ثلاثًا وعشرين دقيقةً⊙ واثنتين وثلاثين دقيقةً⊙ وخمسة أجزاء وإحدى وخمسين دقيقةً⊙ وجزء واحد وسبع عشرة دقيقةً⊙ وجزءًا واحدًا وإحدى وخمسين دقيقةً⊙ فلأنّ الزيادات والنقصانات التي للأبعاد المطلوبة أقلّ منها في الأبعاد الوسطى والخلاف بينها وبينها تسع عشرة دقيقةً ونصف⊙ وستّ وعشرون دقيقةً ونصف⊙ وأربعة أجزاء ودقيقة واحدة⊙ وجزء واحد وثلاث دقائق ونصف⊙ وجزءان وسبع عشرة دقيقةً⊙ وهذه تكون من جمل التفاضل بأسره الذي وضعناه بين الأبعاد الوسطى وبين الأبعاد العظمى أمّا في كوكب زحل فاثنتان وخمسون دقيقةً وثلاثون ثانيةً وأمّا في كوكب المشتري فأربع وخمسون دقيقةً وخمسون ثانيةً⊙ وأمّا في كوكب المرّيخ فأربع وخمسون دقيقةً وأربع وثلاثون ثانيةً⊙ وأمّا في كوكب الزهرة فاثنتان وخمسون دقيقةً وخمس وخمسون ثانيةً⊙ وأمّا في كوكب عطارد فخمس وأربعون دقيقةً وأربعون ثانيةً فإنّا أثبتنا هذه الدقائق في الصفّ الثامن في كلّ جدول بإزاء السطر الذي فيه عدد الثلاثين الجزء من الدور في الطول⊙ فأمّا الأبعاد التي الزيادات والنقصانات فيها أكثر من الزيادات والنقصانات فيها وبين الزيادات والنقصانات في الأبعاد الوسطى فإنّا رددنا أيضًا على ذلك المثال التفاضل الذي كون بينهما إلى أجزاء من ستّين إلّا أنّا إنّما فعلنا ذلك بأخذنا جمل التفاضل بين الزيادات والنقصانات فيها وبين الزيادات والنقصانات في الأبعاد الصغرى لا في الأبعاد العظمى كما فعلنا قبل وبهذا الوجه في سائر التحصيلات حسبنا الدقائق التي تكون من جمل التفاضل بستّة أجزاء ستّة أجزاء من الطول الوسط ووضعناها بإزاء الأعداد التي هي لها وبنينا الأمر على أنّ ما يلحق من الخلاف يكون موافقًا لذلك في الحسّ كما قلنا وإن لم تكن مسيرات الكواكب في نفس أعظم ما يكون من الزيادات والنقصانات من فلك التدوير بل كانت في سائر نواحيه⊙ وهكذا رسم الجداول الخمسة في الطول⊙
〈XI.11〉 يا: جداول لتعديل الكواكب الخمسة في الطول
جدول تعديل الكواكب الخمسة في الطول |
|||||||||||||
الأعداد المشتركة |
تعديل زحل في الطول |
||||||||||||
الزيادة أو النقصان في الطول |
فصول الزيادة أو النقصان |
فصول الزيادة أو النقصان في البعد الأعظم |
الزیادة أو النقصان في البعدين الوسطين |
فصول الزيادة أو النقصان في البعد الأصغر |
دقائق فصول الزيادة أو النقصان |
||||||||
ا |
ب |
ج |
د |
ه |
و |
ز |
ح |
||||||
| أجزاء | أجزاء | أجزاء | دقائق | أجزاء | دقائق | أجزاء | دقائق | أجزاء | دقائق | أجزاء | دقائق | دقائق | ثواني |
| و | شند | | لز | | ب | | ب | | لو | | ب | س | |
| يب | شمح | ا | يج | | د | | د | ا | يا | | د | نح | ل |
| يح | شمب | ا | مط | | و | | ه | ا | مه | | ز | نز | |
| كد | شلو | ب | كج | | ح | | ز | ب | يح | | ط | نه | ل |
| ل | شل | ب | نز | | ط | | ح | ب | ن | | يا | نب | ل |
| لو | شكد | ج | كط | | ي | | ي | ج | ك | | يج | مط | ل |
| مب | شيح | ج | نط | | يا | | يا | ج | مط | | يه | مو | ل |
| مح | شيب | د | كح | | يا | | يب | د | يز | | يز | مج | ل |
| ند | شو | د | نه | | ي | | يد | د | مب | | يط | لط | |
| س | ش | ه | ك | | ط | | يه | ه | د | | ك | لد | ل |
| سو | رصد | ه | مب | | ح | | يز | ه | كه | | ك | ل | |
| عب | رفح | و | | | ز | | يح | ه | مب | | كا | كد | |
| عح | رفب | و | يد | | ه | | يح | ه | نه | | كا | يح | |
| فد | رعو | و | كد | | ج | | يط | و | ه | | كب | يب | |
| ص | رع | و | ل | | ا | | يط | و | يب | | كب | د | ل |
| صج | رسز | و | لا | | | | ك | و | يب | | كج | | مه |
| صو | رسد | و | لب | | ب | | ك | و | يج | | كج | ب | لب |
| صط | رسا | و | لا | | ج | | ك | و | يب | | كد | ه | نا |
| قب | رنح | و | ل | | د | | كا | و | يب | | كد | ط | ح |
| قه | رنه | و | كز | | ه | | كا | و | ط | | كد | يا | مه |
| قح | رنب | و | كج | | و | | ك | و | ه | | كه | يد | كا |
| قيا | رمط | و | يط | | ز | | ك | و | | | كه | يو | نح |
| قيد | رمو | و | يد | | ح | | ك | ه | نه | | كد | يط | لا |
| قيز | رمج | و | ز | | ط | | يط | ه | مح | | كد | كب | يا |
| قك | رم | ه | نط | | ي | | يط | ه | م | | كج | كد | مز |
| قكج | رلز | ه | ن | | ي | | يط | ه | لا | | كج | كز | كد |
| قكو | رلد | ه | لط | | يا | | يح | ه | كا | | كب | ل | |
| قكط | رلا | ه | كز | | يا | | يح | ه | ي | | كب | لب | لز |
| قلب | ركح | ه | يد | | يب | | يز | د | نح | | كا | له | يج |
| قله | ركه | ه | | | يب | | يز | د | مه | | ك | لز | ن |
| قلح | ركب | د | مه | | يب | | يو | د | لا | | يط | م | كو |
| قما | ريط | د | كط | | يب | | يه | د | يو | | يح | مج | ج |
| قمد | ريو | د | يب | | يب | | يد | د | | | يز | مه | لط |
| قمز | ريج | ج | ند | | يب | | يد | ج | مج | | يه | مز | لز |
| قن | ري | ج | له | | يا | | يب | ج | كه | | يد | مط | لد |
| قنج | رز | ج | يو | | يا | | يا | ج | ز | | يج | نا | لب |
| قنو | رد | ب | نو | | ي | | ي | ب | مح | | يب | نج | كط |
| قنط | را | ب | لو | | ط | | ط | ب | كط | | يا | ند | مط |
| قسب | قصح | ب | يه | | ح | | ز | ب | ط | | ي | نو | و |
| قسه | قصه | ا | نج | | ز | | و | ا | مح | | ح | نز | كد |
| قسح | قصب | ا | لا | | و | | ه | ا | كز | | ز | نح | مب |
| قعا | قفط | ا | ط | | ه | | ه | ا | و | | ه | نط | كا |
| قعد | قفو | | مز | | ج | | د | | مه | | د | س | |
| قعز | قفج | | كد | | ب | | ب | | كج | | ب | س | |
| قف | قف | | | | | | | | | | | س | |
جدول تعديل الكواكب الخمسة في لاطول |
|||||||||||||
الأعداد المشتركة |
تعديل المشتري في الطول |
||||||||||||
الزيادة أو النقصان في الطول |
فصول الزيادة أو النقصان |
فصول الزيادة أو النقصان في البعد الأعظم |
الزیادة أو النقصان في البعدين الوسطين |
فصول الزيادة أو النقصان في البعد الأصغر |
دقائق فصول الزيادة أو النقصان |
||||||||
ا |
ب |
ج |
د |
ه |
و |
ز |
ح |
||||||
| أجزاء | أجزاء | أجزاء | دقائق | أجزاء | دقائق | أجزاء | دقائق | أجزاء | دقائق | أجزاء | دقائق | دقائق | ثواني |
| و | شند | | ل | | ا | | ب | | نح | | ب | س | |
| يب | شمح | ا | | | ب | | ه | ا | نو | | ه | نح | نح |
| يح | شمب | ا | ل | | ج | | ز | ب | نب | | ز | نز | نو |
| كد | شلو | ا | نح | | د | | ط | ج | مح | | ط | نو | ند |
| ل | شل | ب | كو | | ه | | يا | د | مب | | يا | ند | ن |
| لو | شكد | ب | نب | | و | | يج | ه | لد | | يج | نا | مج |
| مب | شيح | ج | يز | | ز | | يه | و | كه | | يه | مز | له |
| مح | شيب | ج | م | | ز | | يز | ز | يب | | يح | مج | كز |
| ند | شو | د | ا | | ز | | يط | ز | نز | | ك | لط | يط |
| س | ش | د | ك | | و | | كا | ح | لز | | كب | له | ح |
| سو | رصد | د | لز | | ه | | كج | ط | يد | | كد | كح | نح |
| عب | رفح | د | نا | | د | | كد | ط | مو | | كو | كب | مه |
| عح | رفب | ه | ب | | ج | | كه | ي | يج | | كح | يز | له |
| فد | رعو | ه | ط | | ب | | كو | ي | له | | ل | يا | كج |
| ص | رع | ه | يد | | ا | | كو | ي | نا | | لا | د | م |
| صج | رسز | ه | يه | | | | كز | ي | نز | | لا | ا | ح |
| صو | رسد | ه | يو | | ا | | كز | يا | | | لب | ا | نب |
| صط | رسا | ه | يه | | ا | | كز | يا | ب | | لب | ه | ط |
| قب | رنح | ه | يد | | ب | | كح | يا | ج | | لب | ح | كو |
| قه | رنه | ه | يب | | ب | | كح | يا | ا | | لج | يا | مج |
| قح | رنب | ه | ط | | ج | | كط | ي | نط | | لج | يه | |
| قيا | رمط | ه | ه | | د | | كط | ي | نج | | لج | يز | مط |
| قيد | رمو | ه | | | ه | | ل | ي | مه | | لد | ك | لز |
| قيز | رمج | د | ند | | ه | | ل | ي | له | | لد | كج | كو |
| قك | رم | د | مز | | و | | ل | ي | كد | | لد | كو | يه |
| قكج | رلز | د | لط | | و | | كط | ي | ي | | لج | كط | د |
| قكو | رلد | د | ل | | ز | | كط | ط | ند | | لج | لا | نب |
| قكط | رلا | د | ك | | ز | | كح | ط | لو | | لب | لد | ما |
| قلب | ركح | د | ط | | ح | | كح | ط | يو | | لب | لز | ل |
| قله | ركه | ج | نح | | ح | | كز | ح | ند | | لا | م | يط |
| قلح | ركب | ج | مو | | ح | | كو | ح | ل | | ل | مج | ز |
| قما | ريط | ج | لج | | ح | | كه | ح | د | | كح | مه | كح |
| قمد | ريو | ج | ك | | ز | | كج | ز | لو | | كو | مز | مط |
| قمز | ريج | ج | و | | ز | | كب | ز | و | | كه | مط | مب |
| قن | ري | ب | نا | | و | | كا | و | لد | | كج | نا | لا |
| قنج | رز | ب | لو | | و | | يط | و | | | كا | نب | نح |
| قنو | رد | ب | ك | | ه | | يز | ه | كد | | يط | ند | كب |
| قنط | را | ب | د | | ه | | يه | د | مز | | يز | نه | مز |
| قسب | قصح | ا | مز | | د | | يج | د | ط | | يه | نز | يا |
| قسه | قصه | ا | ل | | ج | | يا | ج | كط | | يج | نز | م |
| قسح | قصب | ا | يج | | ب | | ط | ب | مط | | ي | نح | يج |
| قعا | قفط | | نه | | ب | | ز | ب | ز | | ح | نح | م |
| قعد | قفو | | لز | | ا | | ه | ا | كه | | ه | نط | د |
| قعز | قفج | | يح | | ا | | ج | | مج | | ج | نط | لب |
| قف | قف | | | | | | | | | | | س | |
جدول تعديل الكواكب الخمسة في الطول |
|||||||||||||
الأعداد المشتركة |
تعديل المرّيخ في الطول |
||||||||||||
الزيادة أو النقصان في الطول |
فصول الزيادة أو النقصان |
فصول الزيادة أو النقصان في البعد الأعظم |
الزیادة أو النقصان في البعدين الوسطين |
فصول الزيادة أو النقصان في البعد الأصغر |
دقائق فصول الزيادة أو النقصان |
||||||||
ا |
ب |
ج |
د |
ه |
و |
ز |
ح |
||||||
| أجزاء | أجزاء | أجزاء | دقائق | أجزاء | دقائق | أجزاء | دقائق | أجزاء | دقائق | أجزاء | دقائق | دقائق | ثواني |
| و | شند | ا | | | ه | | ح | ب | كد | | ط | نط | نج |
| يب | شمح | ب | | | ي | | يو | د | مو | | يح | نح | نط |
| يح | شمب | ب | نح | | يه | | كد | ز | ح | | كح | نز | نا |
| كد | شلو | ج | نو | | ك | | لج | ط | ل | | لز | نو | لو |
| ل | شل | د | نب | | كد | | مب | يا | نا | | مو | ند | لد |
| لو | شكد | ه | مو | | كز | | نا | يد | يا | | نو | نب | يا |
| مب | شيح | و | لط | | كح | ا | | يو | كط | ا | و | مط | كح |
| مح | شيب | ز | كح | | كط | ا | ط | يح | مو | ا | يو | مو | يز |
| ند | شو | ح | يد | | كح | ا | يح | كا | | ا | كح | مب | لح |
| س | ش | ح | نز | | كز | ا | كز | كج | يج | ا | م | لح | ح |
| سو | رصد | ط | لو | | كد | ا | لز | كه | كب | ا | نج | لج | كو |
| عب | رفح | ي | ط | | ك | ا | مط | كز | كط | ب | و | كح | ك |
| عح | رفب | ي | لح | | يه | ب | ا | كط | لب | ب | يط | كب | مز |
| فد | رعو | يا | ب | | ي | ب | يد | لا | ل | ب | لج | يو | لج |
| ص | رع | يا | يط | | د | ب | كح | لج | كب | ب | مه | ي | ه |
| صج | رسز | يا | كه | | | ب | له | لد | يه | ب | نز | و | لد |
| صو | رسد | يا | كط | | د | ب | مب | له | و | ج | و | ج | ج |
| صط | رسا | يا | لب | | ح | ب | مط | له | نو | ج | يه | | ه |
| قب | رنح | يا | لب | | يب | ب | نو | لو | مج | ج | كه | ج | يج |
| قه | رنه | يا | لا | | يو | ج | د | لز | كز | ج | لو | و | ا |
| قح | رنب | يا | كح | | يط | ج | يج | لح | ط | ج | مز | ح | مط |
| قيا | رمط | يا | كب | | كب | ج | كب | لح | مح | ج | نح | يا | مد |
| قيد | رمو | يا | يد | | كه | ج | لب | لط | كد | د | ط | يد | لح |
| قيز | رمج | يا | ه | | كح | ج | مج | لط | نو | د | كا | يز | لج |
| قك | رم | ي | نج | | لا | ج | ند | م | كج | د | له | ك | كز |
| قكج | رلز | ي | لط | | لج | د | د | م | مد | د | ن | كج | له |
| قكو | رلد | ي | كج | | له | د | يد | م | نط | ه | ه | كو | مب |
| قكط | رلا | ي | د | | لز | د | كد | ما | ز | ه | كا | كط | لا |
| قلب | ركح | ط | مد | | لط | د | له | ما | ط | ه | لز | لب | ك |
| قله | ركه | ط | كا | | م | د | مه | ما | ب | ه | نه | له | ط |
| قلح | ركب | ح | نه | | ما | د | نو | م | مه | و | يد | لز | نح |
| قما | ريط | ح | كز | | ما | ه | ز | م | يو | و | لد | م | له |
| قمد | ريو | ز | نط | | ما | ه | يح | لط | لز | و | نج | مج | يب |
| قمز | ريج | ز | كز | | ما | ه | كح | لح | م | ز | يب | مه | كو |
| قن | ري | و | ند | | لح | ه | لد | لز | كه | ز | ل | مز | لط |
| قنج | رز | و | يط | | لو | ه | لح | له | نب | ز | مه | مط | ن |
| قنو | رد | ه | ما | | لج | ه | لح | لج | نج | ز | نح | نب | ا |
| قنط | را | ه | ج | | ل | ه | لد | لا | ل | ح | ج | نج | مز |
| قسب | قصح | د | كب | | كز | ه | يح | كح | له | ز | نح | نه | لب |
| قسه | قصه | ج | ما | | كج | د | نب | كه | ج | ز | مز | نو | مد |
| قسح | قصب | ب | نح | | يط | د | يح | كا | | ز | و | نز | نه |
| قعا | قفط | ب | يد | | يه | ج | لب | يو | كه | ه | نط | نح | مط |
| قعد | قفو | ا | ل | | ي | ب | كز | يا | يه | د | كو | نط | مج |
| قعز | قفج | | مه | | ه | ا | يو | ه | مه | ب | ك | نط | نب |
| قف | قف | | | | | | | | | | | س | |
جدول تعديل الکواکب الخمسة في الطول |
|||||||||||||||||||||||||||
الأعداد المشتركة |
تعديل الزهرة في الطول |
||||||||||||||||||||||||||
الزيادة أو النقصان في الطول |
فصول الزيادة أو النقصان |
فصول الزيادة أو النقصان في البعد الأعظم |
الزیادة أو النقصان في البعدين الوسطين |
فصول الزيادة أو النقصان في البعد الأصغر |
دقائق فصول الزيادة أو النقصان |
||||||||||||||||||||||
ا |
ب |
ج |
د |
ه |
و |
ز |
ح |
||||||||||||||||||||
| أجزاء | أجزاء | أجزاء | دقائق | أجزاء | دقائق | أجزاء | دقائق | أجزاء | دقائق | أجزاء | دقائق | دقائق | ثواني | ||||||||||||||
| و | شند | | يد | | ا | | ا | ب | لا | | ب | نط | ي | ||||||||||||||
| يب | شمح | | كح | | ا | | ج | ه | ا | | د | نز | نه | ||||||||||||||
| يح | شمب | | مب | | ا | | ه | ز | لا | | و | نو | م | ||||||||||||||
| كد | شلو | | نو | | ب | | ز | ي | ا | | ح | نه | | ||||||||||||||
| ل | شل | ا | ط | | ب | | ط | يب | ل | | ي | نب | نه | ||||||||||||||
| لو | شكد | ا | كا | | ب | | يا | يد | نح | | يب | مط | له | ||||||||||||||
| مب | شيح | ا | لب | | ج | | يج | يز | كه | | يد | مه | ن | ||||||||||||||
| مح | شيب | ا | مج | | ج | | يه | يط | نا | | يو | مب | ه | ||||||||||||||
| ند | شو | ا | نج | | ج | | يح | كب | يه | | يح | لز | ه | ||||||||||||||
| س | ش | ب | ا | | ب | | ك | كد | لح | | ك | لا | م | ||||||||||||||
| سو | رصد | ب | ح | | ب | | كب | كو | نز | | كج | كو | يه | ||||||||||||||
| عب | رفح | ب | يد | | ب | | كد | كط | يد | | كه | ك | كه | ||||||||||||||
| عح | رفب | ب | يح | | ا | | كز | لا | كز | | كح | يد | له | ||||||||||||||
| فد | رعو | ب | كا | | ا | | كط | لج | لح | | ل | ح | ك | ||||||||||||||
| ص | رع | ب | كج | | ا | | لا | له | مد | | لج | ا | م | ||||||||||||||
| صج | رسز | ب | كج | | | | لج | لو | م | | لو | ا | لا | ||||||||||||||
| صو | رسد | ب | كج | | ا | | له | لز | مج | | لح | د | مب | ||||||||||||||
| صط | رسا | ب | كب | | ا | | لح | لح | م | | م | ز | لط | ||||||||||||||
| قب | رنح | ب | كا | | ا | | م | لط | له | | مج | ي | له | ||||||||||||||
| قه | رنه | ب | ك | | ا | | مب | م | كط | | مه | يج | لب | ||||||||||||||
| قح | رنب | ب | يح | | ا | | مه | ما | ك | | مز | يو | كح | ||||||||||||||
| قيا | رمط | ب | يو | | ا | | مز | مب | ط | | ن | يط | كه | ||||||||||||||
| قيد | رمو | ب | يج | | ب | | مط | مب | ند | | نب | كب | كا | ||||||||||||||
| قيز | رمج | ب | ي | | ب | | نب | مج | له | | نه | كه | يح | ||||||||||||||
| قك | رم | ب | و | | ب | | ند | مد | يب | | نح | كح | يد | ||||||||||||||
| قكج | رلز | ب | ب | | ب | | نز | مد | مه | ا | ا | لا | | ||||||||||||||
| قكو | رلد | ا | نح | | ب | ا | | مه | يد | ا | د | لج | مد | ||||||||||||||
| قكط | رلا | ا | ند | | ب | ا | ج | مه | لو | ا | ح | لو | يح | ||||||||||||||
| قلب | ركح | ا | مط | | ج | ا | و | مه | نا | ا | يا | لح | ن | ||||||||||||||
| قله | ركه | ا | مد | | ج | ا | ي | مه | نط | ا | يد | ما | يا | ||||||||||||||
| قلح | ركب | ا | لط | | ج | ا | يد | مه | نز | ا | يح | مج | لب | ||||||||||||||
| قما | ريط | ا | لج | | ج | ا | يط | مه | مه | ا | كب | مه | مب | ||||||||||||||
| قمد | ريو | ا | كز | | ب | ا | كد | مه | ك | ا | كز | مز | نا | ||||||||||||||
| قمز | ريج | ا | كا | | ب | ا | كط | مد | م | ا | لب | مط | لز | ||||||||||||||
| قن | ري | ا | يد | | ب | ا | لج | مج | لط | ا | لح | نا | كج | ||||||||||||||
| قنج | رز | ا | ز | | ب | ا | لز | مب | يح | ا | مج | نب | مو | ||||||||||||||
| قنو | رد | ا | | | ب | ا | لط | م | كح | ا | مح | ند | ح | ||||||||||||||
| قنط | را | | نج | | ب | ا | ما | لح | ز | ا | نا | نه | يح | ||||||||||||||
| قسب | قصح | | مو | | ا | ا | مب | له | ز | ا | نب | نو | كو | ||||||||||||||
| قسه | قصه | | لط | | ا | ا | لح | لا | كد | ا | ن | نز | كح | ||||||||||||||
| قسح | قصب | | لب | | ا | ا | لا | كو | مو | ا | مج | نح | كو | ||||||||||||||
| قعا | قفط | | كد | | ا | ا | يط | كا | يه | ا | كز | نط | ا | ||||||||||||||
| قعد | قفو | | يو | | ا | | نح | يد | مز | ا | ه | نط | لو | ||||||||||||||
| قعز | قفج | | ح | | ا | | لا | ز | لح | | له | نط | نح | ||||||||||||||
| قف | قف | | | | | | | | | | | س | | ||||||||||||||
جدول تعديل الکواکب الخمسة في الطول |
|||||||||||||||||||||||||||
| الأعداد المشتركة | تعديل عطارد في الطول |
||||||||||||||||||||||||||
الزيادة أو النقصان في الطول |
فصول الزيادة أو النقصان |
فصول الزيادة أو النقصان في البعد الأعظم |
الزیادة أو النقصان في البعدين الوسطين |
فصول الزيادة أو النقصان في البعد الأصغر |
دقائق فصول الزيادة أو النقصان |
||||||||||||||||||||||
ا |
ب |
ج |
د |
ه |
و |
ز |
ح |
||||||||||||||||||||
| أجزاء | أجزاء | أجزاء | دقائق | أجزاء | دقائق | أجزاء | دقائق | أجزاء | دقائق | أجزاء | دقائق | دقائق | ثواني | ||||||||||||||
| و | شند | | يح | | ا | | ي | ا | لح | | ه | نط | ك | ||||||||||||||
| يب | شمح | | لد | | ب | | ك | ج | يو | | يا | نز | ك | ||||||||||||||
| يح | شمب | | نا | | د | | كط | د | نج | | يز | ند | م | ||||||||||||||
| كد | شلو | ا | ز | | ه | | لط | و | كط | | كج | ن | م | ||||||||||||||
| ل | شل | ا | كب | | ه | | مط | ح | د | | كح | مه | م | ||||||||||||||
| لو | شكد | ا | لز | | د | | نط | ط | لو | | لد | لط | م | ||||||||||||||
| مب | شيح | ا | نا | | د | ا | ح | يا | و | | م | لج | | ||||||||||||||
| مح | شيب | ب | د | | ج | ا | يح | يب | لج | | مه | كه | م | ||||||||||||||
| ند | شو | ب | يه | | ا | ا | كح | يج | نح | | ن | يح | | ||||||||||||||
| س | ش | ب | كه | | | ا | لط | يه | يح | | نو | ي | ك | ||||||||||||||
| سو | رصد | ب | لد | | ب | ا | مط | يو | لج | ا | د | ب | ك | ||||||||||||||
| عب | رفح | ب | ما | | د | ا | نط | يز | مج | ا | يا | ط | يد | ||||||||||||||
| عح | رفب | ب | مو | | و | ب | ط | يح | مز | ا | يز | ك | | ||||||||||||||
| فد | رعو | ب | ن | | ز | ب | يط | يط | مد | ا | كج | كط | مد | ||||||||||||||
| ص | رع | ب | نب | | ط | ب | كط | ك | لج | ا | كط | لط | كح | ||||||||||||||
| صج | رسز | ب | نب | | ي | ب | لد | ك | ند | ا | لب | مج | لا | ||||||||||||||
| صو | رسد | ب | نب | | ي | ب | لط | كا | يد | ا | له | مز | لد | ||||||||||||||
| صط | رسا | ب | نا | | يا | ب | مد | كا | كط | ا | لح | ن | | ||||||||||||||
| قب | رنح | ب | ن | | ي | ب | مح | كا | مب | ا | ما | نب | كو | ||||||||||||||
| قه | رنه | ب | مح | | ي | ب | نج | كا | نب | ا | مد | ند | نب | ||||||||||||||
| قح | رنب | ب | مو | | ي | ب | نح | كا | نط | ا | مو | نز | يح | ||||||||||||||
| قيا | رمط | ب | مد | | ط | ج | ب | كب | ب | ا | مط | نح | كج | ||||||||||||||
| قيد | رمو | ب | ما | | ط | ج | د | كب | ا | ا | نب | نط | كح | ||||||||||||||
| قيز | رمج | ب | لز | | ط | ج | و | كا | نو | ا | نه | نط | مد | ||||||||||||||
| قك | رم | ب | لج | | ح | ج | ح | كا | مز | ا | نز | س | | ||||||||||||||
| قكج | رلز | ب | كح | | ز | ج | ط | كا | لج | ا | نط | نط | مد | ||||||||||||||
| قكو | رلد | ب | كج | | ز | ج | ي | كا | يه | ب | | نط | كج | ||||||||||||||
| قكط | رلا | ب | يح | | و | ج | يب | ك | نج | ب | | نح | لط | ||||||||||||||
| قلب | ركح | ب | يب | | و | ج | يب | ك | كه | ب | ا | نز | ن | ||||||||||||||
| قله | ركه | ب | و | | ه | ج | ط | يط | ن | ب | ا | نو | مو | ||||||||||||||
| قلح | ركب | ب | | | د | ج | و | يط | ي | ب | | نه | ما | ||||||||||||||
| قما | ريط | ا | نج | | د | ج | ب | يح | كد | ب | | ند | ج | ||||||||||||||
| قمد | ريو | ا | مو | | ج | ب | نز | يز | لب | ا | نح | نب | كو | ||||||||||||||
| قمز | ريج | ا | لح | | ج | ب | نا | يو | له | ا | نج | ن | مح | ||||||||||||||
| قن | ري | ا | ل | | ب | ب | مب | يه | لا | ا | مز | مط | يا | ||||||||||||||
| قنج | رز | ا | كب | | ب | ب | لب | يد | ك | ا | ما | مز | لد | ||||||||||||||
| قنو | رد | ا | يج | | ب | ب | كا | يج | ج | ا | لد | مه | نز | ||||||||||||||
| قنط | را | ا | ه | | ا | ب | ط | يا | ما | ا | كو | مد | لو | ||||||||||||||
| قسب | قصح | | نو | | ا | ا | نه | ي | يج | ا | يز | مج | يه | ||||||||||||||
| قسه | قصه | | مو | | ا | ا | لح | ح | م | ا | ز | مب | كو | ||||||||||||||
| قسح | قصب | | لح | | | ا | يط | ز | ا | | نو | ما | لز | ||||||||||||||
| قعا | قفط | | كح | | | ا | ا | ه | يط | | مج | م | مح | ||||||||||||||
| قعد | قفو | | يط | | | | مب | ج | له | | كح | م | | ||||||||||||||
| قعز | قفج | | ط | | | | كا | ا | مح | | يد | لط | مد | ||||||||||||||
| قف | قف | | | | | | | | | | | لط | كح | ||||||||||||||
〈XI.12〉 يب: في حساب نقلة الكواكب الخمسة المتحيّرة في الطول
فمتى آثرنا أن نعرف بهذه الجداول التي عملناها من قبل الحركات الدوريّة في الطول وفي الاختلاف المسيرات التي ترى لواحد واحد من هذه الكواكب جعلنا حسابنا لتنقّلها وهو واحد بعينه في الكواكب الخمسة بهذا الوجه الذي أنا واصفه⊙ نجمع من جداول الحركة الوسطى التحصيلات المستوية التي تكون في الوقت المطلوب ذلك فيه بعد الأدوار التامّة في الطول وفي الاختلاف ثم نعمد إلى الأجزاء بين البعد الأبعد في ذلك الوقت في الفلك الخارج المركز وبين المسير ه: يعني موضع المسير الوسط في الطول أوّلًا فندخلها إلى جدول الاختلاف الذي لذلك الكوكب المقصود له ممّا كان بإزاء ذلك العدد في الصفّ الثالث من التعديل ه: يعني مقدار تزاد عليها هذه الدقائق أو تنقص منها في الطول مع زيادة أو نقصان الدقائق التي حصلت في الصفّ الرابع نظرنا فإن كان العدد الذ وضع للطول في الصفّ الأوّل نقصناها من أجزاء الطول وزدناها على أجزاء الاختلاف وإن كان في الصفّ الثاني زدناها على أجزاء الطول ونقصناها من أجزاء الاختلاف كيما يحصل لنا المسيرات جميعًا معدّلين. ثمّ نعمد إلى العدد المعدّل من البعد الأبعد للاختلاف فندخله أيضًا إلى الصفّين الأوّلين فما كان بإزائه من الزيادة أو النقصان في الصفّ السادس التي للبعد الوسط ه: يعني البعد الوسط من الجهتين جميعًا عن البعد الأبعد أثبتناه وكذلك أيضًا نعمد إلى عدد الطول المستوي الذي كنّا تقدّمنا فأدخلناه بدئًا فندخله في هذين ه: يعني إلى الصفّين الأوّلين العددين بأعيانهما فإن وجدناه في السطور الأول ه: يريد بقوله السطور الأول التي هي أبعد {...} للأبعاد التي هي أبعد من الأوسط وكذلك في الأقرب التي هي أبعد من البعد الوسط وذلك يتبيّن من الدقائق التي في الصفّ الثامن. ثمّ نظرنا ما بإزائه من الدقائق في نفس الصفّ الثامن فكم كانت أخذنا بقدر عدّتها من الفضل الذي بالحذاء في السطر الذي فيه الزيادة والنقصان الوسط الذي أخذ فأثبت في الصفّ الخامس الذي لأعظم البعد فما حصل نقصناه ممّا أخذناه فأثبتناه وإن وجدنا عدد الطول الذي ذكرناه في السطور الأسفل التي هي أقرب من البعد الوسط نظرنا ما بإزائه على ذلك المثال من الدقائق ف الصفّ الثامن فكم كانت أخذنا بقدر عدّتها من الفضل الذي حيال الزيادة والنقصان الوسط الذي أخذ فأثبت في الصفّ السابع الذي لأقلّ البعد فما حصل زدناه على ما كنّا أخذناه فأثبتناه فما اجتمع من الأجزاء الزيادة أو النقصان المعدّل نظرنا فإن وجدنا عدد الاختلاف المعدّل في الصفّ الأوّل زدناه على أجزاء الطول المعدّل وإن وجدناه في الصفّ الثاني نقصناه منها فما اجتمع من عدد الأجزاء ألقيناه مبتدئين من البعد الأبعد الكوكب في ذلك الوقت فإنّا ننتهي إلى مسيره الذي يرى⊙ تمّت المقالة الحادية عشرة من كتاب بطلميوس المنسوب إلى التعاليم وهي يب قولًا والحمد لله على عونه بسم الله الرحمن الرحيم عونك يا واحد جُمَلُ ما في المقالة الثانية عشرة من كتاب بطلميوس المنسوب إلى التعاليم⊙ الأولى فيما يحتاج إلى تقديمه لتقدّم ه: التقدّم يعني به رجوع الكوكب وذاك أنّ هذه الكواكب لمّا كان سبيلها أن تسير على توالي البروج وكان مسيرها قدمًا أعني على ضدّ توالي البروج رجوعًا الكواكب؛ الثانية في تبيين تقدّم زحل؛ الثالثة في تبيين تقدّم المشتري؛ الرابعة في تبيين تقدّم المرّيخ؛ الخامسة في تبيين تقدّم الزهرة؛ السادسة في تبيين تقدّم عطارد؛ السابعة في عمل جدول للوقوفات؛ الثامنة الجدول المعمول للوقف؛ التاسعة في تبيين الأبعاد العظمى من الشمس للزهرة ولعطارد⊙