/L158/ بسم الله الرحمن الرحيم نقلنا من شرح أبي جعفر محمّد بن الحسن الخازن للمقالة الأولى من المجسطي

قال بطلميوس وإنّ الأشكال المختلفة التي إحاطتها متساوية ما هو منها أكثر زوايا فهو أعظم قدراً ولذلك وجب أن الدائرة أعظم السطوح والكرة أعظم المجسّمات.

يعني أنّ الأشكال المختلفة من ذوات الأضلاع المستقيمة كالمثلّث والمربّع والمخمّس وسائر ذلك إلى ما لا ينتهي إذا كانت أضلاع كلّ واحد منها مساوية لأضلاع الآخر مجموعةً فإنّ أكثرها زوايا أعظمها مساحة، مثل المثلّث والمربّع والخمّس إذا كانت جملة أضلاع كلّ واحد منها عشرة كان المربّع أعظم مساحة من المثلّث والمخمّس أعظم مساحة من المربّع ثمّ كذلك إلى ما لا نهاية له في الأشكال الكثيرة الأضلاع، ثمّ الدائرة التي محيطها عشرة أعظمها كلّها، واعتبار ذلك بالحساب يسير وأمّا بيانه بالهندسة فإنّا نقدّم ما يحتاج إليه من المقدّمات فنقول إنّ كلّ شكلين من الأشكال ذوات الأضلاع المستقيمة المتساوية العدد والإحاطة وأحدهما متساوي الأضلاع والزوايا فإنّه أعظم من الآخر، ومن مقدمّات ذلك:

ا مثلّث ا ب ج متساوي الأضلاع ومثلّث ا د ه متساوي الساقين، أقول إنّ فضل ا ب على ا د أصغر من فضل ا د على ب ه وإنّ كلي الفضلين مثل فضل ا ب على ب ه وهو 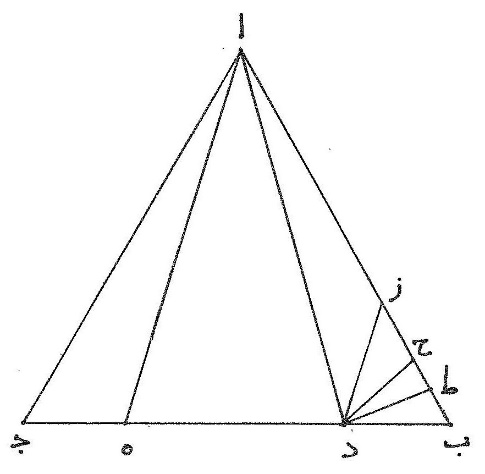ب د، برهان ذلك أنّ نخرج د ز يوازي ا ج ونلقي عمود د ح فمثلّث ب ز د متساوي الأضلاع فب ح مثل ز ح واح أصغر من ا د ونأخذ ا ط مثل ا د فيكون ب ط أصغر من ط ز ولكن ب ط فضل اب على ا د وط ز فضل ا د على ب ه لأنّ ز ا مثل د ج ود ج مثل ب ه وجميع ب ط ط ز مثل ب د فإذن فضل ضعف ا ب على ب ه ا د وهو ب د ب ط أصغر من فضل ا ب ا د على ضعف ب ه وهو ب د ط ز ونجعل ا ب مشتركاً بين ضعف ا ب وبين ب ه ا د وب ه مشتركاً بين ا ب ا د وبين ضعف ب ه فيكون فضل ثلاثة /L160/ أمثال ا ب على جميع ا ب ب ه ا د أعني ه ا أصغر من فضل جميع ا ب ب ه ه ا على ثلاثة أمثال ب ه ويكون ضرب ثلاثة أمثال ب ه في ثلاثة أمثال ا ب الذي هو ضرب ب ه فى تسعة أمثال ا ب أصغر من مربّع جميع ا ب ب ه ه ا لأنّ نسبة الأوّل إلى الثاني أصغر من نسبة الثاني إلى الثالث من قبل أنّ الفضل المنقوص من الأوّل وهو ب د ب ط حتّى بقي الثاني أصغر من الفضل المنقوص من الثاني وهو ب د ط ز حتّى بقي الثالث.

ب مثلّث ا ب ج متساوي الأضلاع ومثلّث ا د ه متساوي الساقين، أقول إنّ نسبة مربّع محيط ا د ه إلى مربّع محيط ا ب ج أعظم من نسبة مثلّث ا د ه إلى مثلّث ا ب ج، برهان ذلك أنّ مربّع محيط ا ب ه أعظم من ضرب ب ه في تسعة أمثال ب ج وأيضاً مربّع محيط ا د ج أعظم من ضرب د ج في تسعة أمثال ب ج وذلك مثل ضرب ب ج في تسعة أمثال ب ج وضرب د ه في تسعة أمثال ب ج، إلّا أنّ ضرب ب ج في تسعة أمثاله مثل ⟨مربّع⟩ محيط ا ب ج فمربّعا محيطي ا ب ه ا د ج أعظم من مربّع محيط ا ب ج وضرب د ه في تسعة أمثال ب ج، ولكن الخطّ المساوي لمحيطي ا ب ج ا د ه قد /L162/ انقسم بقسمين متساويين وهما ا ب ه ا د ج وبقسمين مختلفين وهما ا ب ج ا د ه فمربّعا محيطي ا ب ج ا د ه أعظم من مربّعي محيطي ا ب ه ا د ج، وقد تبين أنّ مربّعي ا ب ه ا د ج أعظم من مربّع محيط ا ب ج وضرب د ه في تسعة أمثال ب ج فمربّعا محيطي 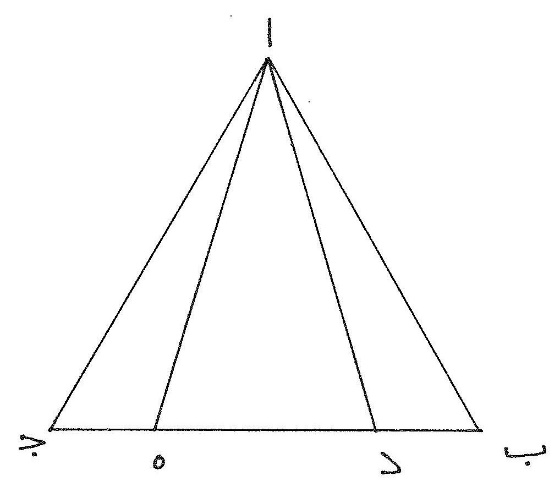ا ب ج ا د ه أعظم كثيراً من مربّع محيط ا ب ج وضرب د ه في تسعة أمثال ب ج ويلقي مربّع محيط ا ب ج المشترك فيبقى مربّع محيط ا د ه أعظم من ضرب د ه في تسعة أمثال ب ج فنسبة مربّع محيط ا د ه إلى مربّع محيط ا ب ج أعظم من نسبة ضرب د ه في تسعة أمثال ب ج إلى مربّع محيط ا ب ج ولكن ضرب د ه في تسعة أمثال ب ج مثل ضرب ثلاثة أمثال د ه في ثلاثة أمثال ب ج ونسبة ضرب ثلاثة أمثال د ه في ثلاثة أمثال ب ج إلى مربّع محيط ا ب ج كنسبة ثلاثة أمثال د ه إلى ثلاثة أمثال ب ج وكنسبة د ه إلى ب ج وكنسبة مثلّث ا د ه إلى مثلّث ا ب ج فنسبة مربّع محيط ا د ه إلى مربّع محيط ا ب ج أعظم من نسبة مثلّث ا د ه إلى مثلّث ا ب ج.

ج مثلّث ا ب ج متساوي الساقين وقد جاز على نقطة ا خط د ه يوازي ب ج 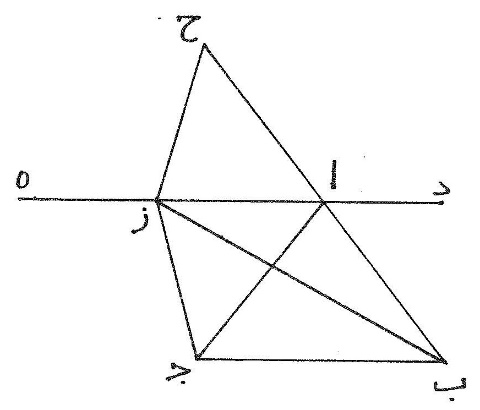وخرج إليه من نقطتي ب ج خطّان فالتقيا على ز، أقول إنّ مجموع ب ز ز ج أطول من مجموع ا ب ا ج، برهان ذلك أن نزيد في ا ب مثله وهو ا ح ونصل ز ح /L164/ فزاوية د ا ب مثل زاوية ز ا ح وزاوية د ا ب مثل زاوية ا ب ج التي تساوي زاوية ا ج ب وزاوية ا ج ب مثل زاوية ز ا ج فزاوية ز ا ج مثل زاوية ز ا ج وا ح مثل ا ج وا ز مشترك في مثلّتي ا ز ج ا ز ح فضلع ز ح مثل ز ج ومجموع ز ب ز ح أطول من ب ح فمجموع ب ز ز ج أطول من مجموع ا ب ا ج.

د مثلّث ا ب ج متساوي الأضلاع ومثلّث د ه ز متساوي الساقين وهما د ه د ز ومحيطاهما متساويان، أقول إن مثلّث ا ب ج أعظم من مثلّث د ه ز، برهان ذلك أنّا نعمل مثلّث د ح ط متساوي الأضلاع فتكون نسبة مربّع محيط د ه ز إلى مربّع 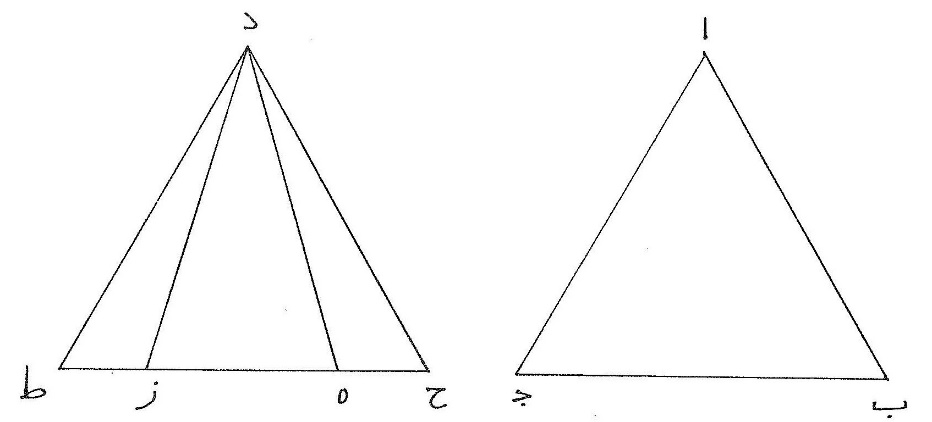محيط د ح ط أعظم من نسبة مثلّث د ه ز إلى مثلّث د ح ط ولكن مربّع محيط د ه ز مساوٍ /L166/ لمربّع محيط ا ب ج فنسبة مربّع محيط ا ب ج إلى مربّع محيط د ح ط أعظم من نسبة مثلّث د ه ز إلى مثلّث د ح ط ولكن نسبة مربّع محيط ا ب ج إلى مربّع ⟨محيط⟩ د ح ط كنسبة مثلّث ا ب ج إلى مثلّث د ح ط فنسبة مثلّث ا ب ج إلى مثلّث د ح ط أعظم من نسبة مثلّث د ه ز إلى مثلّث د ح ط فمثلّث ا ب ج أعظم من مثلّث د ه ز.

ه مثلّث ا ب ج متساوي الأضلاع ومثلّث د ه ز مختلف الأضلاع ومحيطاها متساويان، 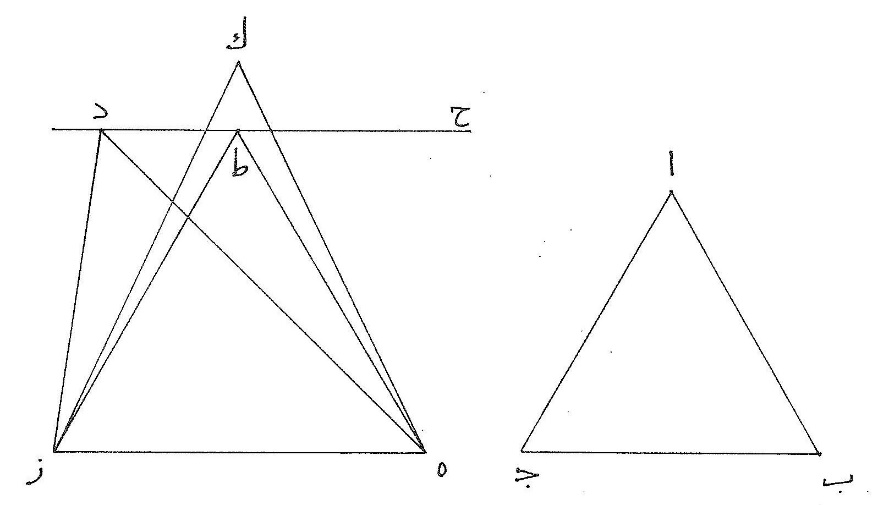أقول إنّ مثلّث ا ب ج أعظم من مثلّث د ه ز، برهان ذلك أنّا نجيز على نقطة د خطّ د ح غير محدود يوازي ه ز ونخرج إليه من نقطتي ه ز خطّي ه ط ز ط متساويين فمجموع ط ه ط ز أصغر من مجموع د ه د ز ونخرج من نقطتي ه ز خطّي ه ك ز ك متساويين ومساويين لخطّي د ه د ز فمثلّث ه ك ز أعظم من مثلّث ه ط ز ومثلّث ه ط ز مثل مثلّث ه د ز لأنّهما على قاعدة واحدة وبين خطّين متوازيين فمثلّث ه ك ز أعظم من مثلّث ه د ز ومثلّث د ك ز كما قد بيّنّا ليس بأعظم من مثلّث ا ب ج لأنّ محيطيهما متساويان فمثلّث ا ب ج أعظم من مثلّث د ه ز وقد تبيّن من ذلك أنّ المثلّث المتساوي الساقين أعظم من المثلّث المختلف الأضلاع إذا كان محيطاهما متساويين.

/L168/ و ونعيد مثلّثي ا ب ج د ه ز ونضعفهما بخطوط ا ح ج ح ز ط د ط فيكون معيّن ب ح 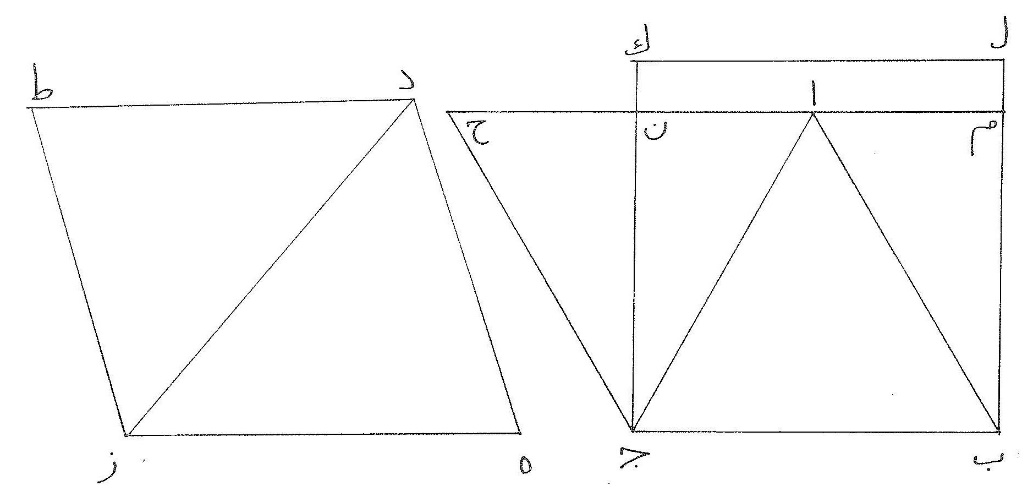أعظم من معيّن ه ط المستطيل وأحدهما متساوي الأضلاع والآخر مختلفها وإن كان محيطاهما متساويين، ونخرج ج ك على زاوية قائمة من ب ج يساوي اج وك ل يساوي ويوازي ب ج ونصل ل ب ونخرج ا ح إلى م فمثلّث ا م ب مثل مثلّث ج ن ح ومربّع ب م ن ج مثل معيّن ب ح فمربّع ب ك أعظم من معيّن ب ح فهو أعظم كثيراً من معيّن ه ط وأحدهما متساوي الأضلاع والزوايا والآخر مختلف الأضلاع والزوايا، وهذه حال كلّ شكلين من الأشكال ذوات الأضلاع الكثيرة المستقيمة المتساوية العدد والإحاطة إنّ المتساوي الأضلاع والزوايا منهما أعظم من المختلف الأضلاع والزوايا.

ز مثال ذلك أن يكون مخمّس ا ب ج د ه متساوي الأضلاع والزوايا، ونصل خطّ 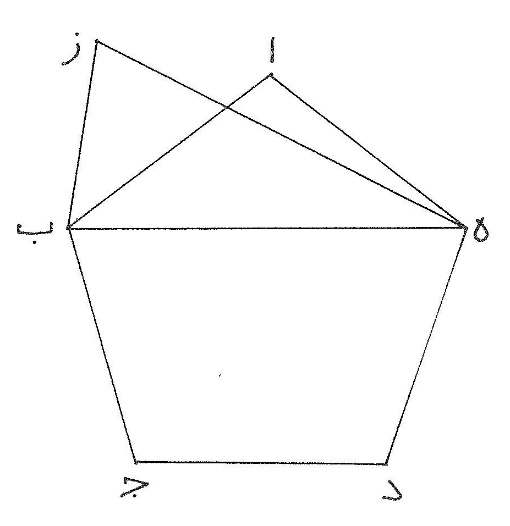ه ب ونخرج من نقطتي ه ب خطّين يلتقيان على ز ويكون مجموعهما مثل مجموع ا ه ا ب /L170/ فيكون مثلّث ا ه ب أعظم من مثلّث ه ز ب ونجعل سطح ه ب ج د مشتركاً فيكون مخمّس ا ب ج د ه أعظم من مخمّس ز ب ج د ه وإن عُمل مثل ذلك على سائر الأضلاع فيكون مخمّس ا ب ج د ه أعظم كثيراً من المختلف الأضلاع وأيضاً زاوية ه ا ب مثل كلّ واحدة من زوايا ا ب ج ب ج د ج د ه د ه ا وزاوية ه ز ب مخالفة لزاوية ه ا ب ويكون مخمّس ا ب ج د ه المتساوي الزوايا أعظم من مخمّس ز ب ج د ه المختلف الزوايا.

ح كلّ شكل ذي أضلاع مستقيمة يحيط بدائرة فإنّ ضرب نصف قطر الدائرة في نصف جملة الأضلاع مساحة الشكل، فليكن الشكل ا ب ج والدائرة التي يحيط بها د ه ز ومركزها ط ونخرج ط د ط ه ط ز فتكون أعمدة على الأضلاع ونصل خطوط ا ط ب ط ج ط فضرب ط د في نصف ا ج مثلّث ا ط ج وضرب ط ه في نصف 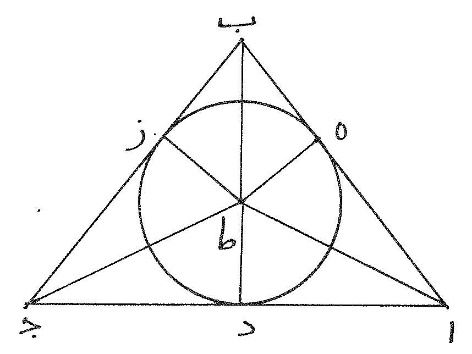/L172/ ا ب مثلّث ا ب ط وضرب ط ز في نصف ب ج مثلّث ب ط ج فضرب نصف قطر الدائرة في نصف جملة الأضلاع مساحة مثلّث ا ب ج، وإن كان الشكل ذا أربعة أضلاع انقسم بأربع مثلّثات وإن كان كثير الأضلاع انقسم بمثلّثات على عدّة الأضلاع وكان ضرب نصف قطر الدائرة التي يحيط بها الشكل في نصف كلّ واحد من الأضلاع مساحة واحدٍ واحدٍ من المثلّثات وجملة المثلّثات هي مساحة الشكل ومساحة الشكل أعظم من مساحة الدائرة لأنّ ضرب نصف قطرها في نصف محيطها مساحتها ونصف محيطها أصغر من نصف جملة أضلاع الشكل لأنّ الشكل محيط بها ولذلك يكون ضرب نصف قطر الدائرة التي تحيط بالشكل في نصف جملة أضلاعه أعظم من مساحة الشكل وضربه في نصف محيط الدائرة مساحة الدائرة فمساحتها أعظم من مساحة الشكل الذي تحيط هي به.

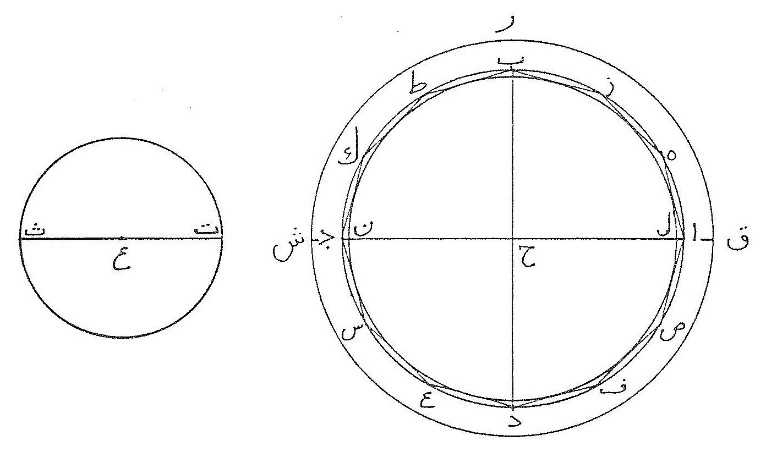
ط كلّ شكلين من الأشكال ذوات الأضلاع المستقيمة المتساوية الإحاطة متساويي الأضلاع والزوايا من نوعين مختلفين فإنّ أكثرهما زوايا هو أعظم، مثال ذلك أن يكون مثلّث ا ب ج ومربّع د ه ز ح متساويي الأضلاع والزوايا وتكون إحاطتاهما متساويتين فيكون المربّع أعظم من المثّلث، برهان ذلك أن نفرض نقطتي ط ك مركزي الدائرتين اللتين يحيط بهما الشكلان فنصل ا ط ب ط ج ط ح ك دك ه ك زك فجملة الزوايا الثلاث عند نقطة ط مثل جملة الزوايا الأربع عند نقطة ك لأنّ كلّ واحدة /L174/ من الجملتين مثل أربع زوايا قائمة فزاوية ا ط ج ثلث أربع زوايا قائمة وزاوية د ك ح ربع أربع زوايا قائمة وا ج ثلث محيط ا ب ج ود ح ربع محيط مربّع د ه ز ح والمحيطان متساويان فنسبة زاوية ا ط ج إلى زاوية د ك ح كنسبة ا ج إلى د ح وزاوية ا ط ج أعظم من زاوية د ك ح وا ج أعظم من د ح، ونلقي عمودي ط ل ك م فتنقسم كلّ واحدة من زاويتي ا ط ج د ك ح وكلّ واحد من ضلعي ا ج د ح نصفين نصفين فنسبة زاوية ا ط ل إلى زاوية د ك م كنسبة ا ل إلى د م وزاوية ا ط ل أعظم من زاوية د ك م وا ل أعظم من د م فنأخذ ن ل مثل د م ونصل ن ط، ونرسم على نقطة ط وببعد ط ن قوس س ن ع ونخرج ط ل إلى س فنسبة زاوية ا ط ن إلى زاوية ن ط ل كنسبة قطاع ط ن ع إلى قطاع ط ن س ونسبة قطاع ط ن ع إلى قطاع ط ن س أصغر من نسبة مثلّث ا ط ن إلى مثلّت ن ط ل ونسبة مثلّث ا ط ن إلى مثلّث ن ط ل كنسبة ا ن إلى ن ل، فنسبة زاوية ا ط ن إلى زاوية ن ط ل أصغر من نسبة ان إلى ن ل، وفي التركيب نسبة زاوية ا ط ل إلى زاوية ن ط ل أصغر من نسبة ال إلى ن ل ون ل مثل د م فنسبة زاوية ا ط ل إلى زاوية ن ط ل أصغر من نسبة ا ل إلى د م ولكن نسبة زاوية ا ط ل إلى زاوية د ك م كنسبة ا ل إلى د م فنسبة زاوية ا ط ل إلى زاوية ن ط ل أصغر من نسبة زاوية ا ط ل إلى زاوية د ك م 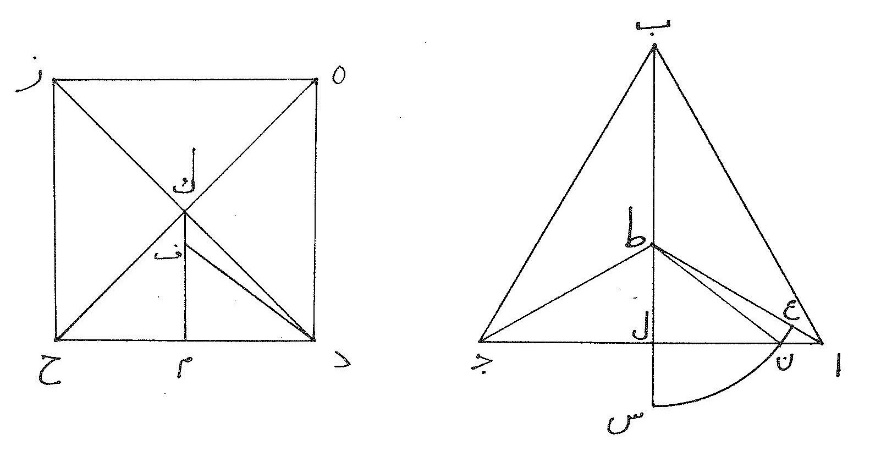/L176/ وزاويتا ا ل ط د م ك قائمتان فتبقى زاوية ط ن ل من مثلّث ط ل ن أصغر من زاوية ك د م من مثلّث ك م د، فنعمل زاوية م د ف مثل زاوية ط ن ل ومثلّث م د ف يشبه مثلّث ل ن ط ولكن د م مثل ن ل فم ف مثل ل ط فضرب نصف محيط مربّع د ه ز ح في ك م أعظم من ضربه في ف م ولكن ضربه في ك م مساحة مربّع د ه ز ح وضربه في ف م مساحة مثلّث ا ب ج، وبمثل هذا التدبير تبين في شكلين متساويي الأضلاع والزوايا من الاشكال ذوات الأضلاع المستقيمة أنّ أكثرهما زوايا أعظمهما مساحة.

ى ونعيد مثلّث ا ب ج دون القطاع ونرسم معه دائرة د ه ز على مركز ك وليكن محيطاهما متساويين فنقول إنّ الدائرة أعظم من المثلّث، برهان ذلك أن نخطّ مثلّث م ن س متساوي الأضلاع يحيط بالدائرة ونصل ك م ك س فنسبة محيط مثلّث م ن س إلى محيط مثلّث ا ب ج كنسبة ضلع م س إلى ضلع ا ج ومحيط مثلّث م ن س 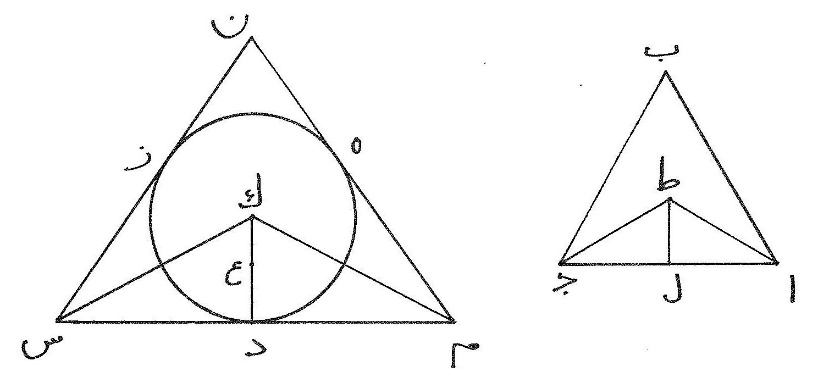أعظم من محيط مثلّث ا ب ج لأنّه أعظم من محيط دائرة د ه ز فضلع م س أعظم من ضلع ا ج فيكون م د أعظم من ا ل وزاوية م ك س مثل زاوية ا ط ج لأنّ كلّ واحدة منهما ثلث أربع زوايا قائمات وزاوية م ك د نصف زاوية م ك س وزاوية ا ط ل نصف زاوية ا ط ج فزاوية م ك د مثل زاوية ا ط ل وزاوية م د ك قائمة مثل زاوية ا ل ط فمثلّث م ك د يشبه مثلّث ا ط ل ولكن م د أعظم من ا ل فد ك أعظم من ل ط فنأخذ منه د ع مثل ل ط /L178/ وضرب نصف محيط دائرة د ه ز في د ك مساحة الدائرة وضربه في د ع مساحة مثلّث ا ب ج فالدائرة أعظم من المثلّث.

ونقيس أيضاً هذه الدائرة إلى مربّع د ه ز ح من الشكل المتقدّم بأن نعيد المربّع مكان مثلّث ا ب ج ونتوهّم جملة أضلاعه مساوية لمحيط دائرة د ه ز ونعمل على الدائرة مربّعاً مكان مثلّث م ن س وتبين بمثل البرهان الأوّل أنّ مساحتها أعظم من مساحة مربّع د ه ز ح، وكذلك نقيسها إلى مخمّس متساوي الأضلاع والزوايا جملة أضلاعه مساوية لمحيطها وإلى شكل شكل من الأشكال المتساوية الأضلاع والزوايا بعد المخمّس بالغة ما بلغت ليتبيّن أنّ الدائرة أعظم الأشكال ذوات الأضلاع المستقيمة المتساوية الإحاطة، وقد يمكن أن نبيّن ما بيّنّا بشكلين مختلفي الأضلاع بعد أن يكونا متشابهين بمثل ما دبرنا سواءً وذلك أن نجعل بدل مثلّثي ا ب ج م ن س شكلين من ذوات الأضلاع الأربعة أو من ذوات الأضلاع الكثيرة مختلفي الأضلاع متشابهين إلّا أنّا آثرنا بيان ذلك بشكلين متساويي الأضلاع والزوايا لأنّ كلّ واحد منهما أعظم من نظيره الذي تختلف أضلاعه ويساويه في الإحاطة كما بيّنّا فيما تقدّم.

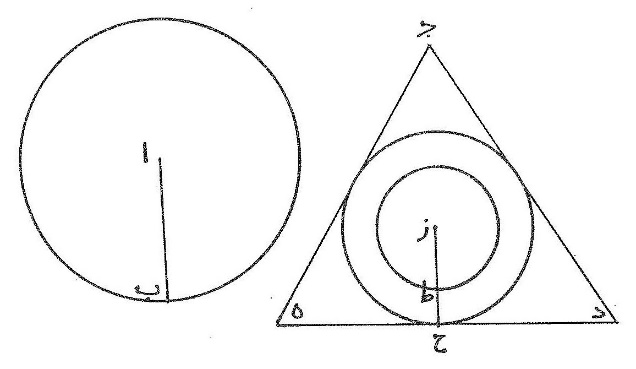
ومن بعد ذلك فإنّا نبيّن أنّ الكرة أعظم الأشكال المجسّمة المتساوية الإحاطات كانت إحاطاتها سطوحاً مستوية كالمكعّب والمنشور والمخروط الذي قاعدته مستقيمة الأضلاع أو كانت سطوحاً مقوّسة كالكرة والأسطوانة ومخروط الأسطوانة، ونبتدئ بالمخروط الذي قاعدته مثلّثة ذات أضلاع مستقيمة متساوية فإنّ المخروط مبدأ هذه الأشكال كما أنّ المثلّث مبدأ الأشكال المسطّحة ذوات الأضلاع ونرسمه على هذه الصورة ونتوهّم قاعدته وهي مثلّث ا ب ج المتساوي الأضلاع موضوعة في سطح موازٍ للأفق ونقطة د وهي رأسه في الهواء مع مثلّثات ا ب د ا د ج ب د ج وكلّ واحد منها متساوي الساقين /L180/ وخطّ د ه عمود على سطح القاعدة فإن كانت أضلاع كلّ واحد منها متساوية ومساوية لأضلاع قاعدة ا ب ج كان المخروط أوّل الأشكال الخمسة المذكورة في آخر كتاب الأصول ويسمّى الشكل الناريّ لشبهه بشكل لهيب النار مثل ضوء السراج وما أشبهه من أضواء النيّران غير أنّ انخراطه مائل إلى التدوير وإن كانت قاعدته مستقيمة الأضلاع وذلك أنّ هذا الاسم يقع على كلّ مخروط تكون قاعدته ذات أضلاع مستقيمة متساوية ثلاثةً كانت الأضلاع أو أربعةً أو أكثر من ذلك بالغة ما بلغت وسائر سطوحه مثلّثات متساوية السوق والحكم في هذا النوع من المخروطات ما نذكره في هذا المخروط

⟨11⟩ وهو أنّ مساحة سطحه دون مساحة سطح قاعدته أن نضرب العمود الذي يلقى من نقطة د إلى ضلع من أضلاع ا ب ب ج ا ج وهو يقسمه بنصفين في نصف جملة الأضلاع لأنّ ضرب هذا العمود في نصف الضلع مساحة المثلّث الواحد وفي ثلاثة أنصاف الأضلاع مساحة جملة المثلّثات الثلاث التي هي ظاهر سمك المخروط ولأنّ نصف قطر الدائرة التي يحيط بها مثلّث ا ب ج في نصف جملة أضلاعه هو مساحة المثلّث يكون ضرب مجموع العمود ونصف قطر الدائرة في نصف جملة أضلاع ا ب ب ج ا ج هو مساحة سطح كلّ المخروط، ولأنّ المنشور الذي قاعدته مثلّث ا ب ج وعموده ه د ينقسم بثلاث 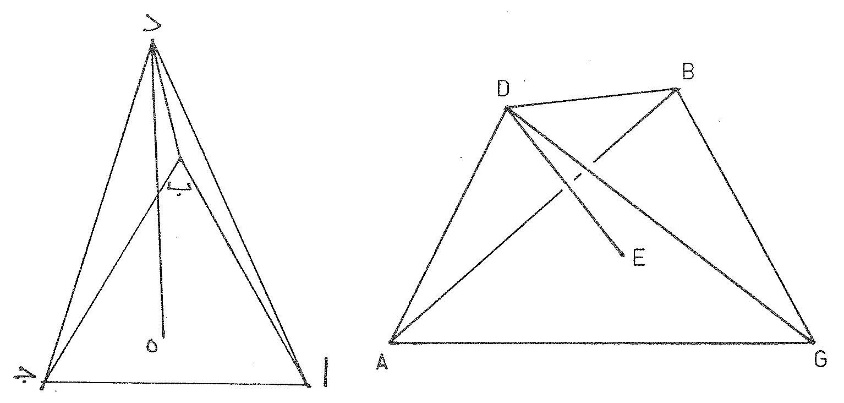مخروطات متساويات كما بُيّن في الشكل السادس من القول الثاني عشر من كتاب الأصول /L182/ يكون مخروط ا ب ج د ثلث المنشور ولكن ضرب عمود د ه في سطح ا ب ج جسم المنشور فضربه في ثلث سطح ا ب ج جسم المخروط.

ويتبيّن من ذلك أنّ نسبة سطح المخروط الذي قاعدته شكل مستقيم الأضلاع إلى سطح القاعدة كنسبة العمود الواقع على ضلع من أضلاعه إلى نصف قطر القاعدة لأنّ ضرب نصف جملة أضلاع القاعدة في هذا العمود سطح المخروط وضربه في نصف قطر القاعدة سطح القاعدة ومن أجل ذلك يكون ضرب نصف قطر الكرة التي يحيط بها المخروط ذو القواعد المسطوحة في ثُلث قواعده جسمه لأنّه ينقسم إلى مخروطات تجتمع رؤوسها عند مركز الكرة وتكون قواعدها قواعد المخروط والكرة تماسّ كلّ واحدة من القواعد ويقوم نصف قطرها عموداً على موضع التماسّ ويكون ضربه في ثلث كلّ قاعدة مخروط من تلك المخروطات لأنّه ثلث المنشور الذي قاعدته قاعدته وارتفاعه ارتفاعه وضرب الارتفاع في القاعدة هو جسم المنشور تساوت أضلاع القاعدة أو اختلفت وكما بيّنّا أيضاً أنّ ضرب نصف قطر الدائرة التي يحيط بها الشكل ذو الأضلاع في نصف جملة أضلاعه تساوت أو اختلفت هو سطح الشكل كذلك ضرب نصف قطر الكرة التي يحيط بها هذا المخروط في ثلث جملة قواعده تساوت أو اختلفت هو جسم المخروط.

الأسطوانة المستديرة شكل مجسّم تحيط به دائرتان متوازيتان وسطح يقوم بينهما ذو تقويس وكلّ واحدة من الدائرتين تسمّى قاعدة الأسطوانة وكلّ خطّ مستقيم يصل ما بين محيطي القاعدتين ويقوم عليهما على زوايا قائمة يسمّى ضلع الأسطوانة والخطّ الذي يصل ما بين مركزي القاعدتين يسمّى سهم الأسطوانة فإن كان قيام السهم على سطحي القاعدتين على غير زوايا قائمة سمّيت الأسطوانة مائلة وإن كان قيامه عليهما على زوايا قائمة سمّيت قائمة وحدوثها من سطح متوازي الأضلاع يثبت أحد ضلعيه المحيطين بالزاوية /L184/ القائمة ويُدار السطح حتّى يعود إلى حيث منه بدأ، ومخروط الأسطوانة القائمة شكل مجسّم يأخذ في الانخراط من محيط إحدى قاعدتي الأسطوانة حتّى يفنى عند مركز القاعدة الأخرى وذلك المركز هو رأس المخروط ويسمّى ايضاً الشكل الصنوبريّ لشبهه بثمرة الصنوبر وسهم الأسطوانة هو عمود ويسمّى ايضاً الارتفاع وكلّ خطّ مستقيم يخرج من رأسه إلى محيط قاعدته على زوايا قائمة يُسمّى ضلع المخروط

⟨12⟩ ونصوّره على هذا المثال ونتوهّم قاعدته وهي دائرة ا ب ج د ومركزها نقطة ه موضوعة على سطح موازٍ للأفق ونقطة ز في الهواء بحيث إذا وُصِل بينها وبين ه بخطّ مستقيم قام على سطح الدائرة على زوايا قائمة ونخرج قطر ا ج ونصل خطّي ز ا ز ج ونقول إنّ ضرب ا ز في قوس ا ب ج التي هي نصف دائرة ا ب ج د سطح مخروط ا ب ج د ز دون سطح قاعدته برهان ذلك أنّه لا يمكن غيره فإن أمكن فليكن ضرب ا ز في قوس أعظم من قوس ا ب ج سطح مخروط ا ب ج د ز ونجعلها قوس ط ك ل التي هي نصف محيط دائرة ط ك ل ح ونعمل على محيط ا ب ج د شكلاً ذا أضلاع مستقيمة متساوية يحيط بالدائرة وهو مسدّس ا م ج ن ونتوهّم خطوطاً مستقيمة تنزل من نقطة ز إلى أطراف المسدّس فتُحدث مخروطاً قاعدته ذات أضلاع مستقيمة متساوية ويكون أعظم من مخروط ا ب ج د ز لأنّه محيط به ونصل خطّي ز ط ز ك فيحدث مخروط ط ك ل ح ز ونضرب ا ز في قوس ط ك ل فيخرج سطح مخروط ا ب ج د ز ونضربه في نصف جملة أضلاع المسدّس فيخرج سطح مخروط ا م ج ن ز فنسبة قوس ط ك ل إلى نصف جملة أضلاع المسدّس كنسبة سطح مخروط ا ب ج د ز إلى سطح مخروط ا م ج ن ز وقوس ط ك ل أعظم من نصف جملة أضلاع المسدّس فسطح مخروط ا ب ج د ز أعظم من سطح مخروط ا م ج ن ز ولكنّه أصغر منه وهذا خلف، وإن كان ضرب ا ز في أقلّ من قوس ا ب ج سطح /L186/ مخروط ا ب ج د ز فضربه في قوس ا ب ج سطح مخروط هو أعظم من سطح مخروط ا ب ج د ز فليكن سطح مخروط ط ك ل ح ز فيكون من ضرب ا ز في قوس ا ب ج سطح مخروط ط ك ل ح ز ومن ضربه في نصف جملة أضلاع المسدّس سطح مخروط ا م ج ن ز فنسبة قوس ا ب ج إلى نصف جملة أضلاع المسدّس كنسبة سطح مخروط ط ك ل ح ز إلى 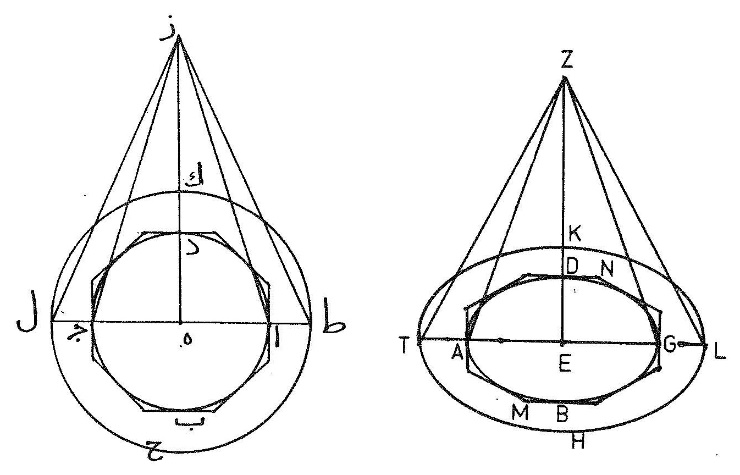سطح مخروط ا م ج ن ز وقوس ا ب ج أصغر من نصف جملة أضلاع الشكل المسدّس فسطح مخروط ط ك ل ح ز أصغر من سطح مخروط ا م ج ن ز ولكنّه أعظم منه وهذا خلف لا يمكن فليس ما يجتمع من ضرب ا ز في قوس أعظم من قوس ا ب ج ولا في قوس أصغر منها سطح مخروط ا ب ج د ز فإذن ضربه في قوس ا ب ج سطح مخروط ا ب ج د ز ثمّ نخرج عمود ه ز ونضربه في ثلث سطح قاعدة ا ب ج د فيجتمع جسم مخروط ا ب ج د ز لأنّ ضرب عمود ه ز في سطح قاعدة ا ب ج د هو جسم الأسطوانة القائمة ومخروط الأسطوانة ثلثها كما بيّن أوقليدس في شكل ط من مقالة يب من كتاب الأصول وأيضاً عمود ه ز في ثلث سطح الشكل المسدّس هو مخروط ا م ج ن ز لأنّه ثلث الأسطوانة التي قاعدتها سطح الشكل المسدّس وارتفاعها عمود ه ز كما ذكر في هذا الشكل من كتاب الأصول.

/L188/ ⟨13⟩ دائرة ا ب ج د وقدرا ه ز ح مفروضان وه ز أعظم من ح، نريد أن نعمل في الدائرة وعليها شكلين كثيري الزوايا متشابهين تكون نسبة المعمول منهما على الدائرة إلى المعمول فيها أقلّ من نسبة ه ز إلى ح، فنفرض خطّين مستقيمين مختلفين تكون نسبة الأعظم منهما إلى الأصغر أقلّ من نسبة ه ز إلى ح ووجود ذلك أن نأخذ ز ط مثل ح ونضعّف ه ط حتّى تزيد أمثاله على ح وليكن ه ك ونفرض ل م كيف اتّفق ونقسمه بعدّة ما في ه ك من أمثال ه ط وليكن م ن مثل أحد أقسام ل م فتكون نسبة م ن إلى ل م كنسبة ه ط ألى ه ك وه ك أعظم من ح أعني من ز ط فنسبة ه ط إلى ه ك أقلّ من نسبة ه ط إلى ز ط ونسبة ه ط إلى ه ك كنسبة م ن إلى ل م فنسبة م ن إلى ل م أقلّ من نسبة ه ط إلى ز ط وفي التركيب نسبة ن إلى ل م أقلّ من نسبة ه ز إلى ح، وإن كان قدرا ه ز وح سطحين أو جسمين فقد يمكن أن نستخرج خطّي ل ن ل م حتّى تكون نسبة ز إلى ح أقلّ من نسبة ل ن إلى ل لأنّ العمل بالأضعاف وبالقسمة مفرد بما في جنس جنس، وبعد وجود ل ن ل م نضعهما مفردين على هذا الوضع ونخرج خطّ م س على زاوية قائمة من خطّ ل م إخراجاً إذا وصلنا خطّ ل س كان مثل ل ن وذلك ممكن لأنّ ل ن أعظم من ل م ونخرج في الدائرة قطري ا ج ب د يتقاطعان على زوايا قائمة ونقسم زاوية ا و ب بنصفين ونصفها بنصفين ولا نزال نفعل ذلك حتّى تبقى زاوية أصغر من ضعف زاوية م ل س وهي زاوية ا و ع ونصل خطّ ا ع فيكون أحد أضلاع الشكل المعمول في الدائرة وننصّف زاوية ا و ع بخطّ و ف ونجيز على ف خطّ ص ق يماسّ الدائرة ونخرج و ا و ع إلى نقطتي ص ق فيكون ص ق أحد أضلاع الشكل المعمول على الدائرة الشبيه بالمعمول فيها فزاوية ا و ع وهي ضعف زاوية ا و ز أقلّ من ضعف زاوية م ل س فزاوية ا و ز أقلّ من زاوية م ل س وزاوية م قائمة مثل زاوية ز فزاوية س أصغر من زاوية ا وإذا أخرج من خطّ م س خطّ مستقيم على مثل زاوية ا يساوي ل س ويلاقي ل م لاقاه فوق نقطة ل فليكن ت ث فتكون نسبته إلى /L190/ ث م أصغر من نسبة ل س إلى ل م ونسبة ت ث إلى ث م كنسبة ا و أعني ف و إلى ز و فنسبة ف و إلى ز و أصغر من نسبة ل س إلى ل م ونسبة ف و إلى ز و كنسبة ص و إلى ا و وكنسبة ص ق إلى ا ع فنسبة ص ق إلى ا ع أقلّ من نسبة ه ز إلى ح بكثير ونتمّم الشكلين بسائر الأضلاع وتبين من ذلك أنّا إذا أردنا أن تكون نسبة الشكل إلى 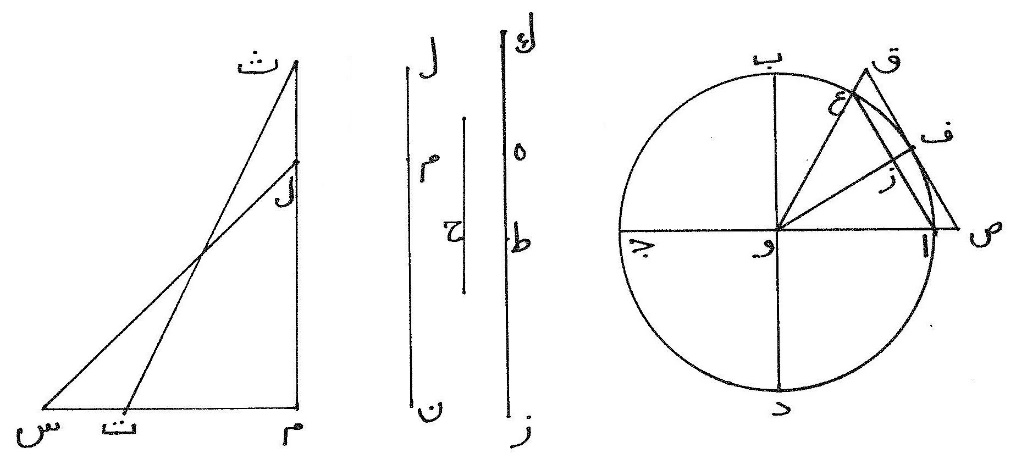الشكل أقلّ من نسبة ل ن إلى ل م استخرجنا خطاً يتوسّطهما في النسبة ثمّ نعمل بخطّ ل ن وبه في استخراج ضلعي الشكل ما عملنا بخطّي ل ن ل م فتصير نسبة الضلع إلى الضلع أقلّ من نسبة ل ن إلى الخطّ المتوسّط ولكن نسبة الضلع إلى الضلع مثنّاة بالتكرير أقلّ من نسبة ل ن إلى الخطّ المتوسّط مثنّاة بالتكرير ونسبة الضلع إلى الضلع مثنّاة بالتكرير كنسبة الشكل إلى الشكل كما بُيّن في يط من قول و من كتاب الأصول ونسبة ل ن إلى الخطّ المتوسّط مثنّاة بالتكرير كنسبة ل ن إلى ل م فنسبة الشكل إلى الشكل أقلّ من نسبة ل ن إلى ل م. ⟨14⟩ شكل ا ب ج د ز مخروط أسطوانة قائمة ونصف قطر دائرة ط ك ل ح وهو ط م وسط في النسبة بين ضلع المخروط وهو ا ز وبين نصف قطر قاعدته وهو ا ه، أقول إنّ دائرة /L192/ ط ك ل ح أعني سطحها مثل سطح المخروط سوى قاعدته، فإن لم يكن كذلك فليكن أصغر منه فيكون سطح المخروط ودائرة ط ك ل ح قدرين مختلفين وأعظمهما بسيط المخروط فنعمل في الدائرة وعليها شكلين كثيري الزوايا متساويي الأضلاع متشابهين تكون نسبة المعمول عليها إلى المعمول فيها أقلّ من نسبة سطح المخروط إلى دائرة ط ك ل ح وذلك بما قدّمناه سهل وليكونا مسدّس ط ن ل س ع ك ف ح فتكون نسبة مسدّس ط ن ل س إلى مسدّس ع ف ك ح أقلّ من نسبة سطح المخروط إلى الدائرة ولتعلم أنّا إذا نسبنا شكلاً إلى شكل من دائرة أو من ⟨ذى⟩ أضلاع فإنّما يعني ذلك سطحي الشكلين ونعمل على دائرة ا ب ج د مسدّس ا ص ج ق فتكون نسبته إلى مسدّس ط ن ل س كنسبة مربّع ا ه إلى مربّع ط م كما بُيّن في قول يب من كتاب الأصول ونسبة مربّع ا ه إلى مربّع ط م كنسبة ا ه إلى ا ز ونسبة ا ه إلى ا ز كنسبة مسدّس ا ص ج ق إلى سطح مخروط ا ص ج ق ز كما بيّنّا في شكل يا من هذه الأشكال فنسبة مسدّس ا ص ج ق إلى مسدّس ط ن ل س كنسبة مسدّس ا ص ج ق إلى سطح مخروط ا ص ج ق ز فسطح المخروط مثل مسدّس ط ن ل س ولكن نسبة مسدّس ط ن ل س إلى مسدّس ع ك ف ح أقلّ من نسبة سطح مخروط ا ب ج د ز إلى دائرة ط ك ل ح وإذا بدلنا تكون نسبة سطح مخروط ا ص ج ق ز إلى مسدّس ع ك ف ح أقلّ من نسبة سطح مخروط ا ب ج د ز إلى دائرة ط ك ل ح وإذا بدلنا تكون نسبة سطح مخروط ا ص ج ق ز إلى سطح مخروط ا ب ج د ز أقلّ من نسبة مسدّس ع ك ف ح إلى دائرة ط ك ل ح وهذا خلف لأنّ سطح مخروط ا ص ج ق ز أعظم من سطح مخروط ا ب ج د ز ومسدّس ع ك ف ح أصغر من دائرة ط ك ل ح فليست دائرة ط ك ل ح بأصغر من سطح مخروط ا ب ج د ز، وأقول إنّها ليست بأعظم منه، وإن أمكن ذلك فلتكن نسبة مسدّس ط ن ل س إلى مسدّس ع ك ف ح أقلّ من نسبة دائرة ط ك ل ح إلى سطح مخروط ا ب ج د ز ونعمل في دائرة ا ب ج د مسدّس ش ب ي د يشبه مسدّس /L194/ ع ك ف ح ونصل ز ي ز ش فتكون نسبة مسدّس ش ب ي د إلى مسدّس ع ك ف ح كنسبة مربّع ش ه إلى مربّع ع م ونسبة مربّع ش ه إلى مربّع ع م كنسبة مربّع ا ه إلى مربّع ط م ونسبة مربّع ا ه إلى مربّع ط م كنسبة ا ه إلى ا ز ونسبة ا ه إلى ا ز أعظم من نسبة ش ه إلى ش ز لأنّا نخرج ش ر يوازي ا ز فتكون نسبة ش ه إلى ش ز أصغر من نسبة ش ه إلى ش ر ولكن نسبة ش ه إلى ش ر كنسبة ا ه إلى أ ز فنسبة ش ه إلى ش ز أصغر من نسبة ا ه إلى ا ز وفي العكس نسبة ا ه إلى ا ز أعظم من نسبة ش ه إلى ش ز ونسبة ش ه إلى ش ز كنسبة مسدّس ش ب ي د إلى سطح مخروط ش ب ي د ز فنسبة ا ه إلى ا ز أعظم من نسبة مسدّس ش ب ي د إلى سطح مخروط ش ب ي د ز فنسبة مسدّس ش ب ي د إلى سطح مخروط ش ب ي د ز ⟨...⟩ فسطح مخروط ش ب ي د ز أعظم من مسدّس ع ك ف ح ونسبة مسدّس ط ن ل س إلى مسدّس ع ك ف ح كما فرضنا أقلّ من نسبة دائرة ط ك ل ح إلى سطح مخروط ا ب ج د ز فنسبة مسدّس ط ن ل س إلى سطح مخروط ش ب ي د ز أقلّ كثيراً من نسبة دائرة ط ك ل ح إلى سطح مخروط ا ب ج د ز، وهذا /L196/ خلف لأنّ مسدّس ط ن ل س أعظم من دائرة ط ك ل ح وسطح مخروط ش ب ي د ز أقلّ من سطح مخروط ا ب ج د ز وقد تبيّن أنّها ليست بأصغر منه فهي مثله.

⟨15⟩ مثلّث ا ب ج سطح قاطع لمخروط أسطوانة قائمة على سهمه وهو ب د ومثلّثا ه ط ز 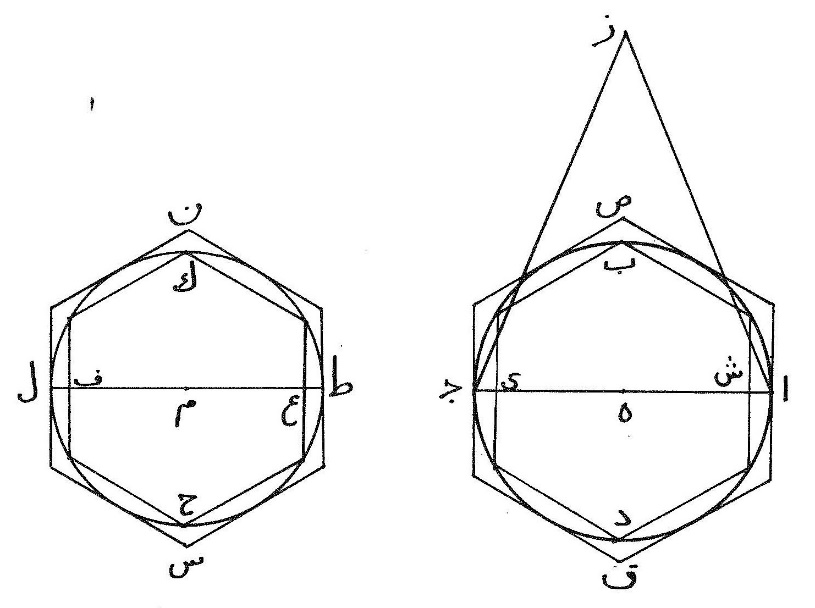ك ل ن سطحان قاطعان لمخروطي أسطوانتين قائمتين على سهميهما وهما ط م ل س والسهام الثلاثة متّصلة على استقامة وأقطار قواعد المخروطات وهي خطوط ا ج ه ز ك ن متوازية ومن قبل توازيها تصير قاعدتا المخروطين الأعليين دائرتين مثل قاعدة المخروط الأسفل لأنّه إذا أثبت خطّ د ل وأديرت مثلّثات ا ب ج ه ط ز ك ل ن حتّى تعود إلى مواضعها الأولى لزم خطّ ا ج في دورانه محيط القاعدة ورسم لذلك ه ز ك ن دائرتين على سطحي المخروطين الأسفل والأوسط ويخرج أيضاً خطّ ق ر يوازي ك ن فيكون قاعدة المخروط الذي عليه مثلّث ق ل ر، وأقول إنّ الخطّ الذي يتوسّط في النسبة بين ا ه وبين مجموع ا د ه م نصف قطر الدائرة المساوية لسطح القطعة التي عليها ا ه ز ج من المخروط الأسفل،

برهان ذلك أنّا نخرج ه ح يوازي ب د ونفرض خطّ ع يقوى على ضرب ا ه في مجموع ا د ه م وخطّ ف يقوى على ضرب ب ا في ا د وخطّ ص يقوى على ضرب ب ه في ه م فيكون خطّ ف نصف قطر الدائرة المساوية لسطح المخروط الأسفل وخطّ ص نصف قطر الدائرة المساوية لسطح المخروط الذي عليه مثلّث ه ب ز كما بُيّن فيما تقدّم وضرب ب ا في ا د مثل ضرب ب ه في ا د وه ا في ا د ولكن ضرب ب ه في ا د مثل ضربه في ه م وفي ا ح وضربه في ا ح مثل ضرب ه ا في ه م لأنّ مثلّثي ب ه م ا ه ح متشابهان فضرب ب ا في ا د مثل ضرب ب ه في ه م وه ا في ه م وفي ا د وننقص منه ما يجتمع من ضرب ب ه في ه م الذي يقوى عليه خطّ ف فيبقى ما يجتمع من ضرب ه ا في ه م وفي ا د الذي يقوى عليه خطّ ع، وبمثل ذلك تبين أنّ الخطّ الذي يقوى على ضرب ك ه في مجموع ك س ه م نصف /L198/ قطر الدائرة المساوية لسطح قطعة المخروط الذي عليها 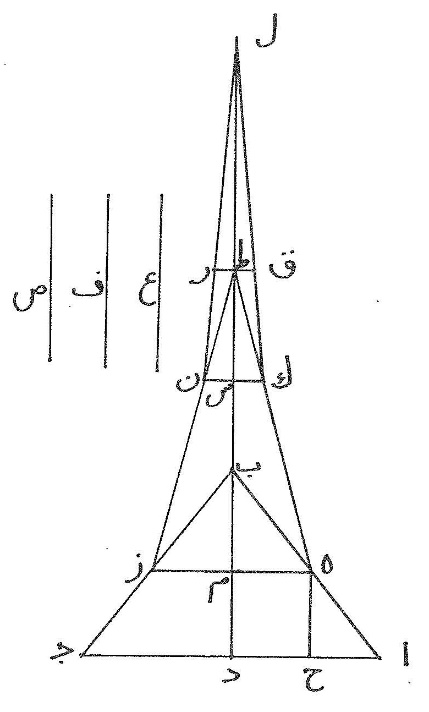منحرف ه ك ن ز وأنّ الخطّ الذي يقوى على ضرب ق ك في مجموع ق ط ك س نصف قطر الدائرة المساوية لسطح القطعة التي عليها ك ق ر ن وتبيّن من ذلك أنّ كلّ مجسّم مركّب من قطع مخروطات الأساطين القائمة تتوازي قواعدها وتتّصل كلّ قطعتين منها على قاعدة مشتركة بينهما والخطوط المستقيمة التي تمرّ سطوحها وتصل بين أطراف قواعدها مثل ا ه ه ك ك ق متساوية فإنّ ضرب أحدها في نصف قطر القاعدة السفلي وفي قطر كلّ قاعدة مشتركة في نصف قطر القاعدة العليا هو مربّع نصف قطر الدائرة المساوية لسطح المجسّم دون قاعدته وإن كان رأس المجسّم مخروطاً كما في هذا المثال فإن ضرب أحدها في نصف قطر القاعدة السفلي وفي أقطار سائر القواعد هو مربّع نصف قطر الدائرة المساوية لسطح المجسّم دون قاعدته والحكم في مخروط واحد إذا قُطع بمثل هذه القطع وفي المجسّم المركّب منها كما في المثال واحد.

/L200/ ⟨16⟩ دائرة ا ب ج د أعظم دائرة تقع على كرة وأعظم دائرة تقع على الكرة هي التي تقطعها بنصفين وقد تقاطع قطرا ا ج ب د على زوايا قائمة وفيه شكل كثير الزوايا متساوي الأضلاع يعدّ أضلاعه عدد زوج وليكن نصف شكل ا ه ز ب ط ك ج وسواء يعدّ أضلاعه عدد زوج أو يعدّها عدد فرد إلّا أنّ العمل بما يعدّ أضلاعه عدد زوج أسهل ثمّ إذا ظهر فيه ما يُرام من البرهان أمكن أن يجري في غيره من الأشكال الكثيرة الأضلاع التي يعدّها عدد فرد كالمخمّس والمسبّع وما عداها إلى ما لا ينتهي، ونصل خطّي د ك ز ط فيتوازيان وتوازي ا ج ونرسم دائرة ل م ن يحيط بها الشكل ونتوهّم نقطتي ب د قطبي الكرة فيكون محورها قطر ب د فإذا دارت الكرة حتّى تعود إلى موضعها الأول رسم ضلعا ا ه ه ز قطعتي مخروطي أسطوانتين قائمتين قطرا قاعدتيهما ا ج ه ك ورسم ضلع ز ب مخروط أسطوانة قائمة قطر قاعدته ز ط والقواعد متوازية لأنّ أقطارها متوازية فأقول إنّ سطح المجسّم المركّب من قطع مخروطات الأساطين دون قاعدته أقلّ من ضعف سطح ⟨...⟩ نصف الكرة التي تحيط بالمجسّم وأعظم من ضعف سطح ⟨...⟩ نصف الكرة الذي يحدث من دوران نصف دائرة ل م ن ويحيط به المجسّم

برهان ذلك أن نضع نقطة س على تماسّ ضلع ز ب ودائرة ل م ن وهي أيضاً تنصّف ضلع ز ب ونصل خطوط س ح ط ه ك ا فتتوازي ط ه ك ا ويوازيان ز ب وتتشابه مثلّثات ز ب ع ط ص ع ه ف ص ك ق ف ا ق ح وتكون نسبة ز ع إلى ع ب كنسبة ط ع إلى ع ص وكنسبة ه ف إلى ف ص وكنسبة ك ف إلى ف ق وكنسبة ا ح إلى ق ح ونسبة واحد من المقدّمات إلى واحد من التوالي كنسبة الجميع إلى الجميع فنسبة ز ع إلى ع ب كنسبة مجموع ز ط ه ك ا ح إلى ب ح ونسبة ز ع إلى ع ب كنسبة س ح إلى س ب لتشابه المثلّثين فنسبة س ح إلى س ب كنسبة مجموع ز ط ه ك ا ح إلى ب ح فضرب س ب في مجموع ز ط ه ك ا ح مثل ضرب س ح في ب ح وضرب س ح في ب ح أقلّ من ضرب /L202/ ب ح في نفسه وأعظم من ضرب س ح في نفسه ولكن ضرب ز ب وهو ضعف س ب في مجموع ز ط ه ك ا ح كما قدّمناه مربّع نصف قطر الدائرة المساوية لسطح المجسّم 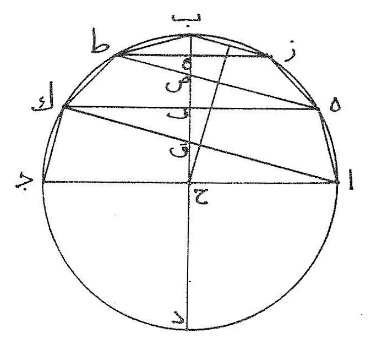المركّب ونسبة مربّع نصف قطر كلّ دائرة إلى مربّع نصف قطر دائرة أخرى كنسبة الدائرة إلى الدائرة فسطح المجسّم أقلّ من مثلي دائرة ا ب ج د وهي أعظم دائرة تقع على الكرة التي تحيط بالمجسّم وأعظم من مثلي دائرة ل م ن التي هي أعظم دائرة تقع على الكرة التي يحيط بها المجسّم.

⟨17⟩ ونعيد رسم الشكل إلّا خطوط ز ط ه ط ه ك ا ك س ح ونتمّم أضلاع الشكل الكثير الزوايا ونقول إنّ أربعة أمثال دائرة ا ب ج د أعني سطح الدائرة مثل سطح الكرة التي هذه الدائرة أعظم دائرة تقع عليها فإن لم يكن كذلك فلتكن أصغر منه ولتساو سطح كرة أصغر من الكرة التي عليها دائرة ا ب ج د وهي الكرة التي عليها دائرة ل م ن ودائرة ل م ن أعظم دائرة تقع على هذه الكرة فسطح هذه الكرة أصغر من سطح المجسّم المركّب من قطع مخروطات شبيهة بالمجسّم الأول مماسّ للكرة التي عليها دائرة ا ب ج د لأنّه محيط بها وقد تبيّن أنّ سطح المجسّم أصغر من أربعة أضعاف دائرة ا ب ج د فسطح الكرة التي عليها دائرة ل م ن أصغر من أربعة أضعاف دائرة ا ب ج د بكثير وقد فرض مثله وهذا خلف، ثمّ /L204/ لتكن أربعة أمثال دائرة ا ب ج د أعظم من سطح الكرة التي عليها دائرة ا ب ج د ولتساو سطح الكرة التي عليها دائرة ق ر ش وهذه الدائرة أعظم دائرة تقع على هذه الكرة ونتوهّم الكرة تحيط بمجسّم مركّب من قطع مخروطات الأساطين فيكون سطحه أعظم من أربعة أمثال دائرة ا ب ج د ولكن سطح الكرة التي عليها دائرة ق ر ش أعظم من سطح هذا المجسّم لأنّها محيطة به فإذن سطح هذه الكرة أعظم من أربعة أمثال دائرة ا ب ج د 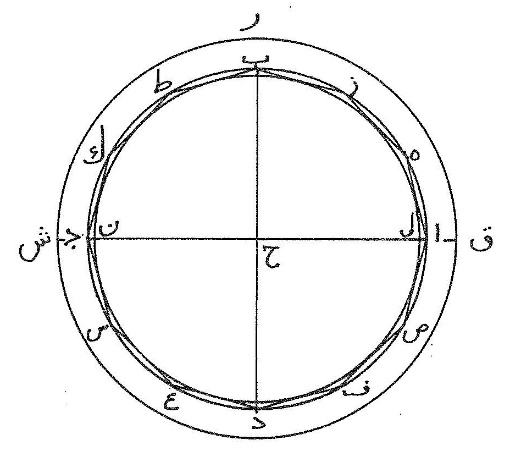وقد فُرض مثله وهذا خلف، فإذن سطح كلّ كرة أربعة أضعاف أعظم دائرة تقع عليها ولأنّ الدائرة هي من ضرب قطرها في جميع محيطها يكون سطح الكرة من ضرب قطر أعظم دائرة تقع عليها في محيطها،

⟨18⟩ ونعيد الشكل كما هو ونقول إنّ ضرب ب ح وهو نصف قطر دائرة ا ب ج د في ثلث سطح الكرة التي عليها دائرة ا ب ج د جسم الكرة وإلّا فليكن جسم كرة أصغر منها وهي الكرة التي عليها دائرة ل م ن ونتوهّم دائرة تمرّ بنقطتي ب د وتقاطع دائرة ا ب ج د على زوايا قائمات ودائرة تجوز عليها على زوايا قائمة وتمرّ بنقطتي ا ج حتّى تقسمها الأرباع /L206/ ودائرتين فيما بين كلّ ربعين من الدائرة الثانية تمرّان بنقطتي ب د فيقسم كلّ ربع من أرباع الدائرة بثلاثة أثلاث ونتوهّم كلّ دائرة من الدوائر الخمس تحيط بشكل كثير الزوايا مثل الشكل الذي في دائرة ا ب ج د ونصل طرفي كلّ ضلعين نظيرين من كلّ شكلين فيما بين دائرتين متواليتين فيحدث مجسّم ذو قواعد مسطوحة أمّا قواعده التي تلي كلّ واحد من قطبي ب د فمثلّثات وأمّا ما سواها فمنحرفات وهي قواعد لمخروطات ينقسم إليها المجسّم وتجتمع رؤوسها على مركز الكرة وهو نقطة ح، والكرة التي عليها دائرة ل م ن تماسّ كلّ واحد من القواعد ونصف قطرها يكون عموداً على موضع التماسّ فضربه في ثلث جملة القواعد جملة المخروطات التي هي جملة المجسّم وجملة قواعدها سطح المجسّم فضرب م ح وهو نصف قطر الكرة التي عليها دائرة ل م ن في ثلث سطح المجسّم كمّيّة المجسّم ولكن ضربه في ثلث سطح المجسّم أعظم من ضربه في ثلث سطح الكرة التي عليها دائرة ل م ن لأنّه محيط بها فضرب ب ح في ثلث سطح الكرة التي عليها دائرة ا ب ج د أعظم من جسم الكرة التي عليها دائرة ل م ن بكثير وقد فُرض مثلها هذا خلف، ثمّ لنفرض ضرب ب ح في ثلث سطح كرة أعظم من الكرة التي عليها دائرة ا ب ج د جسم الكرة ولتكن الكرة التي دائرة ق ر ش أعظم دائرة تقع عليها ونتوهّمها تحيط بمجسّم ذى قواعد شبيه بالمجسّم الأول مماسّ للكرة التي عليها دائرة ا ب ج د فيكون ضرب ب ح في ثلث سطح المجسّم أعظم من الكرة التي عليها دائرة ا ب ج د وليكن ضرب ب ح كما فُرض في ثلث سطح هذه الكرة هو جسم الكرة التي عليها دائرة ق ر ش وهذه الكرة أعظم من /L208/ المجسّم لأنّها محيطة به فثلث سطحها أعظم من ثلث سطحه فضرب ب ح في ثلث سطحها أعظم من جسم الكرة التي عليها دائرة ا ب ج د بكثير وقد فُرض مثلها وهذا خلف، فليس ضرب نصف قطر الكرة التي عليها دائرة ا ب ج د في ثلث سطح كرة أصغر ولا أعظم منها بجسمها فإذن ضربه في ثلث سطحها هو جسمها وقد تبيّن أن سطح أعظم دائرة تقع على الكرة ربع سطح الكرة وسطح الدائرة مع ثلثه ثلث سطح الكرة فضرب نصف قطر الكرة في مثل وثلث سطح أعظم دائرة تقع عليها هو جسم الكرة فضرب نصف قطر الكرة في مثلي أعظم دائرة تقع عليها مثل ونصف الكرة ولكن الأسطوانة التي تحيط بالكرة ضرب سهمها وهو قطر الكرة في قاعدتها وهي أعظم دائرة تقع على الكرة هو الأسطوانة وكذلك ضرب نصف قطر الكرة في مثلي أعظم دائرة تقع عليها فالأسطوانة التي تحيط بالكرة مثل ونصف الكرة ولأنّ مخروط الأسطوانة ثلثها يكون المخروط الذي قاعدته مثل أعظم دائرة تقع على الكرة وسهمه مثل نصف قطر الكرة ربع الكرة فالكرة أربعة أمثال المخروط ولكن نسبة مخروط أسطوانة إلى مخروط أسطوانة أخرى كنسبة القاعدة إلى القاعدة إذا كانا في ارتفاع واحد كما تبيّن في شكل يا من قول يب من كتاب الأصول فالمخروط الذي قاعدته مثل أربعة أمثال أعظم دائرة تقع على الكرة وسهمه مثل نصف قطر الكرة أربعة أمثال المخروط الذي قاعدته مثل أعظم دائرة تقع على الكرة وسهمه مثل نصف قطر الكرة فهذا المخروط مثل الكرة،

⟨19⟩ ثمّ لنرسم دائرة ت ث على مركز ع ولتكن أعظم دائرة تقع على الكرة ونخرج قطر ت ث وليساو سطح هذه الكرة سطح المجسّم المحيط بالكرة التي عليها دائرة ل م ن فتكون الكرة أعظم من المجسّم لأنّ م ح وهو نصف قطر الكرة التي عليها دائرة ل م ن إن كان مثل /L210/ ت ع كانت الكرة مثل الكرة ولكن سطح الكرة التي عليها دائرة ل م ن أصغر من سطح المجسّم وسطح المجسّم مثل سطح الكرة التي عليها دائرة ت ث فسطح الكرة التي عليها دائرة ل م ن أصغر من سطح الكرة التي عليها دائرة ت ث والكرة التي عليها دائرة ل م ن أصغر من الكرة الأخرى فنصف قطرها وهو م ح أقصر من ت ع ولكن ضرب م ح في ثلث سطح الكرة ⟨...⟩ جسم الكرة التي عليها دائرة ت ث أعظم من المجسّم فإذن الكرة أعظم المجسّمات المتساوية الإحاطة.

/L212/ بسم الله الرحمن الرحيم

مقالة في أنّ سطح كلّ دائرة أوسع من كلّ سطح مستقيم الأضلاع متساويها متساوي الزوايا مساوية إحاطته لإحاطتها،

نريد أن نبيّن أنّ سطح كلّ دائرة أوسع من كلّ سطح مستقيم الأضلاع متساويها متساوي الزوايا مساوية إحاطته لإحاطتها، فلتكن دائرة مركزها ا ونصف قطرها ا ب وإحاطتها مساوية لإحاطة شكل ج د ه المتساوي الأضلاع والزوايا فأقول إنّ سطح دائرة ا ب أوسع من سطح ج د ه برهان ذلك أنّا ندير في سطح ج د ه دائرة يحيط بها وليكن مركزها ز ونخرج نصف قطرها إلى ح وهو موضع التماسّ فإن كان ز ح مثل ا ب فدائرة ا ب مساوية لدائرة ز ح ومسطّح ز ح في نصف محيط دائرة ز ح هو سطح دائرة ز ح ومسطّح ز ح في نصف إحاطة شكل ج د ه هو مساحة سطح ج د ه فدائرة ز ح إذن مساوية لسطح ج د ه الأصغر للأعظم هذا خلف، وليس اب أيضاً ناقصاً من ز ح لأنّه إن كان كذلك فصلنا من ز ح مثل ا ب وليكن ز ط فدائرة ز ط مساوية لدائرة ا ب فمحيط دائرة ز ح أطول من محيط دائرة ز ط ومحيط شكل ج د ه أعظم من محيط دائرة ز ح فمحيط شكل ج د ه أعظم كثيراً من محيط دائرة ا ب وقد كان فُرض مساويا له هذا خلف فليس ز ح بمساوي ا ب ولا أطول منه فهو أقصر منه /L214/ وز ح في نصف محيط شكل ج د ه هو مساحة سطح ج د ه وا ب الأطول في نصف محيط دائرة ا ب المساوي لمحيط شكل ج د ه أعظم من ز ح الأقصر في نصف محيط شكل ج د ه المساوي لمحيط دائرة ا ب فدائرة ا ب أعظم من شكل ج د ه وذلك ما أردنا أن نبيّن.

آخر المقالة ولله الحمد.