بسم الله الرحمان الرحيم

حلّ شكوك في كتاب المجسطي يشكّك فيها بعض أهل العلم

الشكّ الأوّل وهو قول بطلميوس في الفصل الثالث الذي ترجمته في أنّ السماء كرية وحركتها أيضًا كرية والذي يرى من الزيادة في عظمها يعني Correction mg. النجوم إذا كانت في الآفاق فليس إنّما يراها كذلك لقربها وقلّة بعدها عند الأفق ولكنّ بخارًا رطبًا وهو الذي يحيط بالأرض بصر فيما بين البصر وبينها فيرى كذلك كما أنّ ما يلقى في الماء يرى أعظم وكلّما رسب إلى أسفل كان أربد في عظمه.

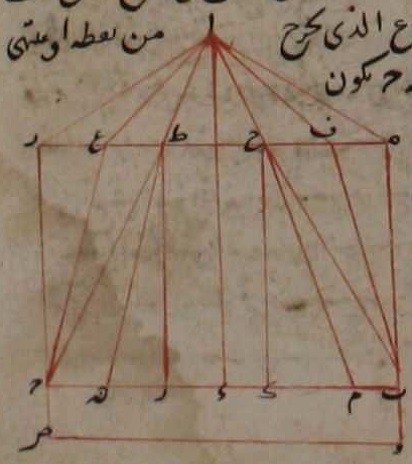
الجواب قد بيّن بطلميوس في المقالة االخامسة من كتابه في المناظر أنّ المبصر إذا كان في الماء فإنّ مقداره يرى أعظم من مقداره إذا رؤي وهو في الهواء. برهانه على ذلك هو كما نصف ولسنا نتحرّي لفظ بطلميوس بعينه بل نزيد البرهان شرحًا ولا نتعدّي الطريق الذي اعتمده فليكن مركز البصر نقطة ا وايكن قطر المبصر بج وليكن مواجهًا للبصر والمبصر المواجه للبصر هو الذي يكون العمود الخارج من مركز البصر القائم على المبصر واقعًا على وسط المبصر ونخرج من نقطة ا عمودًا على بج وليكن اد فتكون نقطة د وسط بج ونصل اب اج فإذا كان بج في الهواء فإنّ بصر ا يدرك مقدار بج بزاوية باج ثمّ ليصر هذا المبصر في الماء وهو على ما عو عليه من البعد والوضع وزاية باج على ما هي عليه وليكن سطح الماء هز وليعرض خطّ هز مستقيمًا وذد بيّن بطلميوس أنّ المبصرات التي ترى في الماء ليس تدرك بشعاعات مستقيمة بل شعاعات البصر إذا انتهت إلى سطح الماء وكانت مائلة على سطح الماء انعطفت وامتدّت بعد انعطافها على استقامة ويكون انعطافها إلى جهة العمود القائم على سطح الماء الخارج من النقطة التي عليها لقي الشعاع

سطح الماء وإذا انعطف الشعاع قرب من العمود ولم ينته إليه وإذا كان المبصر في الماء وكان مواجهًا للبصر فسطح الماء أيضًا مواجه للبصر وإذا فرض سطح الماء مسطحًا وهو مواجه للبصر فهو موازي لخطّ بج وإذا كان موازيًا لخطّ بج كان اد عمودًا على سطح الماء وإذا كان اد عمودًا على سطح الماء فشعاعا اب اج مائلين على سطح الماء وليقطع شعاعات اج سطح الماء على نقطتي ح ط فتكون زاويتا احط اطح حادّتين ونخرج من نقطتي ح ط عمودين على سطح الماء وليكونا حك طل فشعاع اب ينعطف من نقطة ح ولا ينتهي إلى نقطة ك فليكن مثل خطّ احم وكذلك شعاع اج يكون مثل خطّ اطن فشعاع اح اط أنّها تدركان من مقدار بج مقدار من فقط ونخرج من نقطتي ب ج عمودين على سطح الماء وليكونا به جز فيكون زه مساويًا لبج فيكون اد مارًّا بوسطه ز ونصل اه از فشعاعا اه از إذا انعطفا كانا من وراء نقطتي ب ج ولم يصلا إلى نقطتي ب ج لأنّ هب زج عمودان على سطح الماء والشعاع إذا انعطف لم ينته إلى العمود الخارج من موضع الانعطاف فشعاعا اه از ليس ينتهيان إلى نقطتي ب ج فهما يحيطان بمقدار أعظم من مقدار بج فالشعاع الذي يخرج من نقطة ا وينتهي إلى سطح الماء وينعطف إلى نقطة ب يكون فيما بين خطّي اه اح فليكن ذلك الشعاع افب وكذلك الشعاع الذي يخرج من نقطة ا وينتهي إلى سطح الماء وينعطف إلى نقطة ج يكون فيما بين خطّي از اط فليكن ذلك الشعاع اعج فمقدار بج يدرك بزاوية فاع وزاوية فاع أعظم من زاوية باج فهذا الطريق بيّن بطلميوس أنّ الزاوية التي يرى بها

المبصر إذا كان في الماء تكون أعظم من الزاوية التي يرى بها إذا كان في الهواء فلنثبت الصورة على حالها ثمّ نتوهّم خطّ بج قد رسب إلى أسفل هو على وضعه حتّى صار مثل خطّ وص فإذا كان وضع خطّ وص هو وضع خطّ بج فإنّ خطّ اد ينتهي إلى وسط خطّ وص وإذا كان اد ينتهي إلى وسط خطّ وص فإنّ خطّي هب زج ينتهيان إلى نقطتي و ص لأنّ وص موازي لبج ونخرج خطّي هب زج حتّى ينتهيان إلى نقطتي و ص فخطّ نب إذا امتدّ على استقامة في جهة ب فليس ينتهي إلى نقطة و بل يقع من ورائها لأنّه يقطع خطّ هبو وكذلك خطّ عج إذا امتدّ في جهة ج فليس ينتهي إلى نقطة ص بل يقع من ورائها فليس يدرك بصر ا مقدار وص بشعاعي اف اع ولا بشعاعين أبعد منهما عن خطّ اد بل إنّما يدرك البصر مقدار وص بشعاعين أقرب إلى خطّ اد من شعاعي اب اع وإذا كان ذلك كذلك فبصر ا إنّما يدرك وص بزاوية أصغر من زاوية فاع والذي يعتقد أنّ مقدار المبصر إنّما يدركه البصر بحسب مقدار الزاوية فقط يعرض له الشكّ في قول بطلميوس أنّ المبصر كلّما رسب رسب إلى أسفل كان أزيد في عظمه وليس يكون هذا القول مشكوكًا فيه إلّا إذا اعتمد المتشكّك في مقدار العظم على مقدار الزاوية فقط والذي يعتمد في مقدار العظم على مقدار الزاوية فقط هو غالط فيما اعتمد عليه وذلك أنّ بطلميوس قد بيّن في كتابه في المناظر عند كلامه في العظم أنّ مقدار العظم ليس يدرك بحسب مقدار الزاوية فقط بل بحسب مقدار الزاوية ومقدار البعد وبحسب كيفية الوضع في الميل والمواجهة وهو يقول عند كلامه في العظم في الشكل لكان من أشكال العظم أنّ المبصرين إذا أدركا بزاوية واحدة وكان أحدهما أبعد من الآخر فإنّ الأقرب ليس يظهر في وقت من الأوقات أعظم لكنّه يرى إمّا أصغر وذلك إذا كان بعد أحدهما من الآخر بعدًا له مقدار في الحسّ وإمّا

أن يظهر مساويًا وذلك إذا لم يكن مقدار اختلاف البعد محسوسًا فلو كان مقدار العظم يدرك بحسب مقدار الزاوية فقط لكان المبصر أنّ اللذان يريان بزاوية واحدة أو زاويتين متساويتين يريان أبدًا متشاويين وإن كان أبعدهما في غاية البعد وأقربهما في غاية القرب وليس يريد الأمر كذلك وقد بيّنّا نحن في كتابنا في المناظر عند كلامنا في العظم أنّ العظم إنّما يدركه البصر بحسب مقدار الزاوية وبحسب مقدار البعد وبقياس ed. Sabra; ىتىاىن in the witness الزاية إلى البعد لا بحسب مقدار الزاوية add. mg. فقط ونحن نبيّن في هذا الموضع بيانًا يقنع Correction mg. معه اليقين أنّ عظم المبصر ليس يدرك بحسب مقدار الزاوية فقط وذلك أنّ الناظر إذا نظر إلى عمود قائم على وجه الأرض طوله على طريق المثال عشرون ذراعًا وكان بعده عن البصر بمقدار عشرين دراعًا ونظر في الحال إلى شخص إنسان قائم بقربه وكان بين الناظر وبين ذلك الإنسان قدر ذراعين وكان الناظر مضطجعًا وبصره عند سطح الأرض الذي العمود قائم عليه والإنسان أيضًا قائم عليه فليس يري ارتفاع العمود أصغر من ارتفاع قامة الإنسان بوجه من الوجوه بل يري العمود أطول من الإنسان والزاوية التي يري فيها العمود على الصفة التي ذكرناها تكون نصف قائمة والزاوية التي يري بها الإنسان إذا كان بعده عند قدر ذراعين يكون أعظم من نصف قائمة فالزاوية التي يري بها العمود تكون أصغر من الزاوية التي يري بها الإنسان وهو مع ذلك يري العمود أعظم من قامة وإن تباعد الناظر أيضًا عن موضعه حتّى يصير بعده عن العمود أكثر من البعد الأوّل ولا يكون بعده عنه متفاوتًا بل يكون بحيث تتحقّق صورة العمود وقرب ذلك الإنسان أيضًا منه حتّى يصير بينه وبينه أقلّ من البعد الأوّل فإنّه يري العمود أيضًا أطول من قامة الإنسان والزاوية التي يدرك بها العمود عند تباعده عنه تكون أصغر من الزاوية الأولى

التي أدركه بها والزاوية التي تدرك بها شخص الإنسان عند قربه منه تكون أعظم من الزاوية الأولى التي أدركه بها وكلّ مبصر من المبصرات إذا أدركه البصر وهو قريب منه ثمّ تباعد عنه تباعدًا ليس بالمتفاوت فليس يدرك مقداره أصغر ممّا كان أدركه في الأوّل ومثال ذلك شخص الإنسان إذا أدركه الناظر وبينه وبينه ثلاثة أذرع بالمثال ثمّ صار بينه وبينه خمسة أذرع فليس يرى مقداره أصغر من مقداره الأوّل والمبصر إذا بعد عن البصر أدنى بعد صغرت الزاوية التي يدركه بها فجميع المبصرات التي يدركها البصر من الأبعاد المعتدلة ليس تختلف مقاديرها عند البصر ومع ذلك فالزوايا التي يدركها بها من الأبعاد المختلفة تكون مختلفة فيتبيّن ممّا ذكرناه بيانًا واصحًا تسقط معه الشهاب أنّ مقدار المبصر ليس يدرك بحسب مقدار الزاوية فقط. وبطلميوس عند تبيينه لعظم ما يرى في الماء في الشكل السابع عشر من المقالة الخامسة فقد فرض لمبصر الذي في الماء خطّ زح إذا بيّن عظم الزاية التي يرى بها خطّ زح يقول قولًا هذه حكايته فيرى زج بزاوية أعظم وبعده باق على حاله ووضعه وإذا كان كذلك فإنّه أبدًا يرى أعظم فيجب من ذلك أن يكون للأشياء التي ترى في الماء تكون أعظم منها لو كانت على ذلك البعد بعينه وعلى ذلك الوضع ونظر إليها على استقامة. فلم يعتمد بطلميوس في تبيين عظم المبصر الذي في الماء على عظم الزاوية فقط حتّى ضمّ إليه تساوي البعد والوضع والمبصر الذي يرى في الماء إذا رسب غلى أسفل ورأى بزاوية أصغر فإنّ بعده يكون أعظم وإذا كان بعده أعظم فليس يلزم من أجل صغر زاويته أن يرى أصغر لأنّه إنّما يجب أن يرى أصغر إذا صغرت زاويته وكان بعده مع ذلك مثل بعده الأوّل فأمّا إذا كان بعده أعظم فليس يلزم أن يرى من أجل صغر الزاوية أصغر لأنّ زيادة بعده يوجب له العظم وذلك أنّه قد تبيّن أنّ المبصرين اللذين يدركان بزاوية واحدة إذا كان مختلفي البعد فالأبعد يرى أعظم فظهر من

ذلك أنّ زيادة البعد يوجب العظم فعلى حسب الأصول التي فرّرها بطلميوس من علم المناظر ليس يلزم من صغر المبصر من أجل صغر الزاوية فقط ومن أجل ما بيّنّاه نحن بالأمثلة في المبصرات المختلفة الأبعاد المختلفة الزوايا التي يرى الصغير الزاوية منها أوظم يظهر ظهورًا بيّنًا أنّ صغر الزاوية ليس يوجب صغر المبصر وقد يمكن المشكّك أن يعرض بهذا القول أعني زيادة بعد المبصر الذي ازداد رسوبًا في الماء. فيقول أنّ المبصر الذي يرى في الماء ليس يرى في موضعه وإنّما يرى في موضع الخيال وقد بيّن ذلك بطلميوس فالمبصر الذي قد رسب إلى أسفل إنّما يرى في موضع خياله فبعده إنّما هو بعد خياله لأنّ البعد الذي يقيس به البصر إنّما هو بعد الصورة التي يراها وإذا كان ذلك كذلك فبعد الممبصر الذي فد رسب إلى أسفل يكون أقرب من موضعه الذي ه فيه. فنقول في جواب هذا القول إنّ البصر إن كان يعتبر من المبصر بعد رسوبه بعد خياله لأبعده نفسه فهو يعتبر منه قبل رسوبه بعد خياله أيضًا لأبعده نفسه وخياله بعد رسوبه يكون أبعد من خياله قبل رسوبه إذا كانت الزاوية التي يرى بها بعد رسوبه أصغر من الزاوية التي يرى بها قبل رسوبه فيعود القياس إلى ما كان عليه فالمبصر الذي يرى في الماء إذا add. mg. ازداد رسوبًا في الماء إنّما يرى أعظم لأنّ بعده يصير أعظم من بعده قبل رسوبه ولأنّ بعد خياله أعظم من بعد خياله قبل رسوبه ولأنّ ما يوجبه له زيادة البعد من العظم أكثر ممّا يوجبه صغر الزاوية من الصغر فقد تبيّن ممّا بيّنّاه أنّه يلزم بحسب الأصول التي قرّرها بطلميوس وبحسب ما بيّنّاه بالأمثلة من الأمور الموجودة أنّ المبصر الذي يرى في الماء إذا رسب إلى أسفل يجب أن يرى أعظم ومع ذلك فإنّ بطلميوس لم يشبّه عظم الكواكب في الآفاق بعظم ما يلقي في الماء من أجل ما بيّنه في كتاب المناظر وإنّما شبّهها بما يلقي في الماء لأنّ الوجود لهذه الصفة أعني أنّ كلّ مبصر يلقي في الماء فإنّه يرى أعظم ممّا كان يرى وهو في الهواء وكلّما ازداد رسوبًا في الماء ازدادت

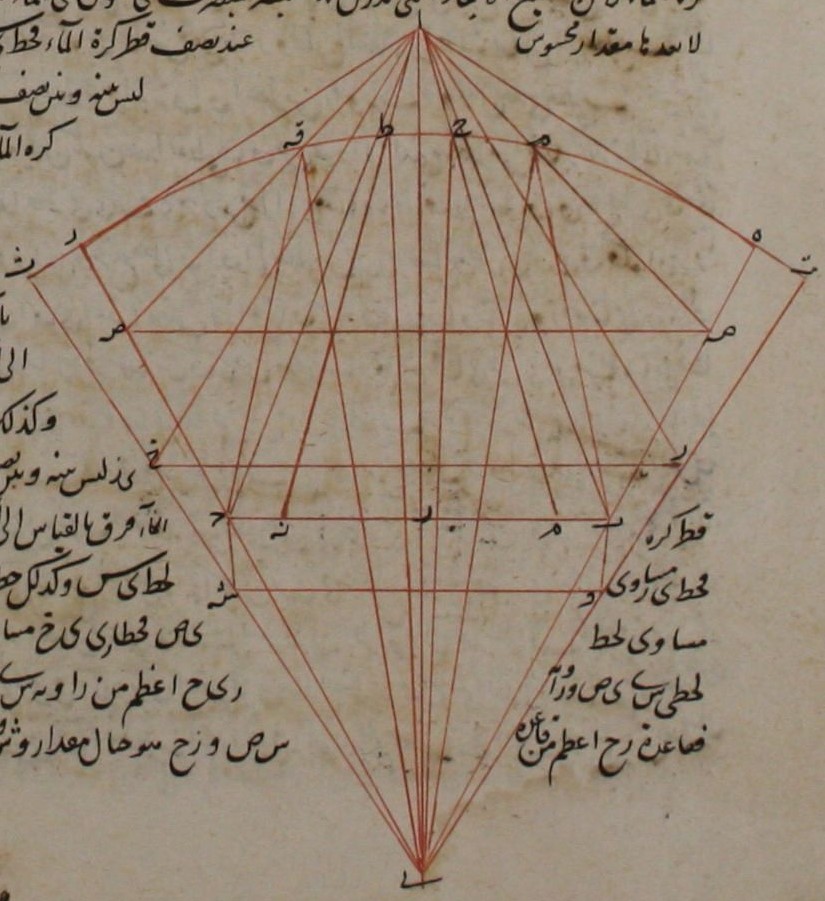
صورته عظمًا وأنّما ذكر الناس هذا المعنى في كتب المناظر وعلّلوه أعني عظم المبصر الذي يرى في الماء لما وجدوه بالمشاهدة كذلك وإذا كان الوجود على هذه الصفة وكان بطلميوس قد استدلّ بمعنى يشهد به الوجود وكانت الكواكب إنّما ترى في الآفاق من وراء البخار الرطب لم يتطرّق على قوله شكّ فإذا قيس هذا القول بما ذكره في كتاب المناظر ولزم منه شكّ كان الشكّ إنّما هو فيما ذكره في كتاب المناظر لا فيما ذكره في المجسطي فقد تبيّن من جميع ما بيّنّاه أنّ قول بطلميوس الذي ذكره في المجسطي هو قول صادق لا شبهة فيه ولا يتطرّق عليه شكّ فإنّ الشكّ الذي يكر إنّما يتطرّق فيما ذكره من كتاب المناظر. وقد انحلّ هذا الشكّ فيما ذكره في المناظر بزيادة بعد ما يزداد رسوبًا في الماء وإذ قد تبيّن جميع ذلك فإنّا نقول أنّ البيان الذي بيّنه بطلميوس في كتاب المناظر في عظم ما يرى في الماء هو بيان على التقريب لا على التحقيق وذك إنّه جعل سطح الماء مسطحًا وليس هو كذلك بل سطح الماء كري مركزه مركز العالم وإذ الأمر كذلك فقد بقي أن يحقّق العلّة التي من أجلها يرى المبصر في الماء أعظم. وكلّما ازداد رسوبًا ازداد عظمًا ونحن نبيّن ذلك ولا نتعدّي الأصول التي قرّرها بطلميوس. فلنعدّ المبصر والبصر على الوضع الذي كانا عليه ونجعل سطح الماء كريًا مركزه مركز العالم لأنّه كذلك على الحقيقة. فلأنّ بج مواحه للبصر وهو في قعر الماء يكون بج موازيًا للأفق واد عمود على بج فاد عمود على سطح الأفق فهو قطر من أقطار العالم. فخطّ اد إذا امتدّ على استقامة في جهة د انتهى إلى مركز العالم فليكن مركز العالم نقطة ي ولينته خطّ اد إلى نقطة ي ونخرج السطح الذي فيه خطًا ادي بدج فهو يقطع سطح الماء ونحدث فيه قوسًا من دائرة فلتكن القوس التي تحدث في سطح الماء قوس هز ونصل خطّي يب يج ونخرجهما على استقامة حتّى يلقيا قوس هز فليلقياها على نقطتي ه ز وإذا كان بج

في داخل الماء وبصر ا خارج الماء فإنّ خطّي اب اج يقطعان قوس هز فليقطعاها على نقطتي ح ط ونصل يح يط فيكونان عمودين على سطح الماء فشعاعا اح اط إذا انتهيا إلى نقطتي ح ط انعطفا ولم يخرجا على استقامتهما لأنّهما مائلان على سطح الماء وإذا انعطفا فليس ينتهيان إلى عمودي يح يط فلينعطف شعاعا اح اط على خطّي حم طن فشعاعا احم اطن إنّما يدركان من مقدار بح مقدار من فقط ونصل اه از فشعاعا اه از ينعطفان عند نقطتي ه ز ولا ينتهيان إلى عمودي يه يز فليس نيتهيان إذا انعطفا إلى نقطتي ب ج فالشعاع الذي ينعطف إلى نقطة ب يكون فيما بين خطّي اه اح والشعاع الذي ينعطف إلى نقطة ج يكون فيما بين خطّي اط از وليكن الشعاعان المنعطفان إلى نقطتي ب ج شعاعي افب اقج فزاوية فاق أعظم من زاوية باج ولأنّ بعدي نقطتي ب ج عن عمود اد متساويان يكون بعدا نقطتي ف ق عن عمود اد الذي هو قطر من أقطار كرة الماء ومتساويين وبعدا قطري يبه يجز عن قطر ادي متساويان فبعدا نقطتي ف ق عن قطري يه يز متساويان ونخرج خطّي اف اق إلى نقطتي س ص ونصل سص يف يق فتكون ظاويتا فيا قيا متساويتين وزاويتا فيه قيز متساويتين وزاويتا ياف ياق متساويتان فزاويتا سفي صقي متساويتان فخطّا يس يص متساويان وخطّا يب يج متساويان فخطّ سص مواز لخطّ بج وزاوية ساص قد تبيّن أنّها أعظم من زاوية باج فخطّ سص أقرب إلى البصر من خطّ بج فسص أعظم من بج وسص هو خيال خطّ بج وقد بيّن بطلميوس في كتابه في المناظر أنّ المبصر الذي يرى في الماء يرى في موضع الخيال وإذا كان يرى في موضع الخيال فهو يرى بمقدار الخيال كانت زاوية الخيال أعظم أو كانت أصغر لأنّ أطرافه ترى عند أطراف الخيال فمقدار بج إذا رأى في الماء يرى أعظم لأنّ خياله أعظم منه فهذه هي العلّة الحقيقية التي من أجلها نري المبصر في الماء أعظم منه إذ رأى في الهواء. ثمّ فلينحطّ مقدار بج إلى أنّ بصر مثل

مقدار وس ونثبت وضعه على ما كان عليه ونصل يو يس وننفذهما حتّى يلتقيا قوس هز ويلقياهما على نقطتي ت ث ونخرج الشعاعين اللذين ينعطفان إلى نقطتي و س وننفذهما على استقامة حتّى يلقيا خطّي يت يث وليلقياهما على نقطتي ز خ ونصل زخ فنبيّن كما نبيّن من قبل أنّ زخ موازي لوش فهو موازي لسص ولأنّ خطّ يه نصف قطر كرة الماء والبعد الذي بين نقطة ه وبين نقطة س ليس له قدر محسوس عند مقدار نصف قطر كرة الماء لأنّ جميع الأبعاد التي يدرك منها البصر المبصرات التي تكون في الماء ليس لأبعدها مقدار محسوس عند نصف قطر كرة الماء. فخطّ يس ليس بينه وبين نصف قطر كرة الماء فرق بالقياس إلى الحسّ. وكذلك خطّ يز ليس بينه وبين نصف قطر كرة الماء فرق بالقياس إلى الحسّ. فخطّ يز مساوي لخطّ يس وكذلك خطّ يخ مساوي لخطّ يص. فخطّا زي يخ مساويان لخطّي سي يص وزاوية زيح أعظم من زاوية سيص فقاعدة زح أعظم من قاعدة سص وزح هو خيال مقدار وش وسص

هو خيال مقدار بج فالمبصر الذي يرى في الماء إذا رسب إلى أسفل كان خياله أعظم وإذا كان خياله أعظم كان مقداره في رأي العين أعظم. وذلك ماأردنا أن نبيّن.

الشكّ الثاني وهو قول بطلميوس في الفصل الثالث أيضًا من المقالة الأولى. وإنّ لأشكال المختلفة التي إحاطاتها متساوية ما هو أكثر زوايا هو أعظم قدرًا ولذلك وجب أنّ الدائرة أعظم السطوح والكرة أعظم المجسّمات والسماء أعظم ممّا سواها من الأجسام.

الجواب قد عملنا في هذا المعنى مقالة مستقصاة بيّنّا فيها بالبراهين المحقّقة أنّ الكرة أعظم الأشكال الجسّمة المتشابهة الإحاطة التي إحاطاتها متساوية وأنّ الدائرة أعظم الأشكال المسطحة المتشابهة الإحاطة التي إحاطاتها متساوية وأنّ ما كان أقرب إلى الاستدارة من الأشكال المجسّمة فهو أعظم ممّا كان أبعد عن الاستدارة من الأشكال المجسّمة المتشابهة الإحاطة التي أحاطتها متساوية وأنّ ما كان أقرب إلى الاستدارة من الأشكال المسطحة فهو أعظم ممّا كان أبعد عن الاستدارة من الأشكال المسطحة المتشابهة الإحاطة التي إحاطاتها متساوية وإذا غن لنا الفراغ حرّرنا منها نسخة وأنفذناها لتقف عليها.

الشكّ الثالث وهو قول بطلميوس في الفصل الرابع من المقالة الأولى ويجد أبدًا الساعات التي أثبتها من قاس من المشرقيين أكثر تأخرًا عن نصف النهار مّما أثبت دكره المغربيون.

الجواب إنّما يعرض الشكّ في هذا القول إذا قيس وقت الكسوف بدائرة نصف النهار ولم يقس بطلميوس وقت الكسوف بدائرة نصف النهار وإنّما قاس وقت الكسوف بنصف نهار اليوم الذي في عشية كان الكسوف وإذا كان الأمر على ذلك كان القول الذي ذكره قولًا صحيحًا

ويمثّله في ذلك مثالًا وهو إنّا نعرض أن كسوفً قمريًا كان وسطه على خمس ساعات مستوية من الليل عند بعض المواضع المشرقية وكان وسطه على ثلاث ساعات مستوية من الليل عند موضع غربي عن ذلك الموضع وكان في الموضع المشرقي بين وقت وسط الكسوف وبين دائرة نصف النهار بساعة واحدة مستوية على طريق المثال وإذا كان بين وقت وسط الكسوف وبين دائرة نصف النهار الشرقي ساعة واحدة فبين وقت وسط الكسوف وبين دائرة نصف نهار الموضع الغربي أكثر من ساعة واحدة فليكن على طريق المثال ثلاث ساعات وإذا كان ذلك كذلك فبين وقت وسط الكسوف الذي هو وسط مخروط الظلّ وبين نصف ليل الموضع الشرقي ساعة واحدة وإذا كان بين وقت وسط الكسوف وبين نصف الليل ساعة واحدة فبين وقت وسط الكسوف وبين نصف نهار اليوم الذ في عشية كان الكسوف أحد عشر ساعة وكذلك إذا كان بين وقت وسط الكسوف وبين نصف ليل الموضع الغربي ثلاث ساعات فبين وقت وسط الكسوف وبين نصف نهار اليوم الذي في عشية كان الكسوف تسع ساعات فتكون بين وقت وسط الكسوف وبين نصف نهار الموضع الشرفي أحد عشر ساعة وبين وقت وسط الكسوف وبين نصف ذلك اليوم في الموضع الغربي تسع ساعات فساعات الموضع الشرقي أكثر تأخرًا عن نصف النهار من ساعات الموضع الغربي وهذا هو الذي ذكره بطلميوس ومعنى قول بطلميوس أكثر تأخرًا أيّ أبطأ ومعنى أبطأ أكثر زمانًا والأمر كذلك فقد انحلّ الشكّ هذا المثال وظهر أنّ قول بطلميوس في ذلك قول صحيح لا شبهة فيه.

الشكّ الرابع وهو قول بطلميوس في الفصل العشر من المقالة الأولى فمن البيّن أنّ ركبنا مع الأوتار المعلومة كلّها وتر جزء ونصف وحسبنا الأوتار التي نصل فإنّا نرسم بالجملة كلّ قوس إذا أضعفت كان لها ثلاث.

الجواب يريد

بطلميوس بهذا القول أنّه إذا ركب مع كلّ قوس معلومة وتر جزء ونصف فقد وجد أوتار الأجزاء المتزيّدة بثلاثة أجزاء ثلاثة أجزاء لأنّه قد بيّن أنّه إذا وجد وتر قوس فقد وجد وتر نصفها ولزم من ذلك أنّه إذا وجد وتر قوس فقد وجد وتر ضعفها فهو يعني أنّه إذا وجد أوتار القسي المتزيدة بجزء ونصف جزء نقص فقد وجد أوتار القسي المتزيّدة بثلاثة أجزاء ثلاثة أجزاء لأنّ القسي المتزيّدة بثلاثة أجزاء ثلاثة أجزاء هي أضعاف القسي المتزيّدة بجزء ونصف جزء ونصف فتزيّد بقوله كلّ قوس معلومة القسي التي هي أضعاف الجزء ونصف وإذا وجد ذلك وكان غرضه أن يجد أوتار القسي المتزيّدة بنصف جزء فليس يبقي عليه إلّا أن يجد وتر نصف جزء ولذلك قال من بعد هذا القول القسي التي إذا أضعفت فهذا الذي ذكرناه هو غرض بطلميوس في قوله القسي التي إذا أضعفت كان لها ثلاث.

الشكّ الخامس وهو قول لبطلميوس في الفصل الحادي عشر من المقالة الأولى فهذا الرصد سيّما ما امتحناه منه في الانقلابين أنفسهما في أدوار كثيرة في الأجزاء التي هو واحدة بعينها من دائرة نصف النهار.

الجواب إنّ بطلميوس رصد الشمس وكان رصده لها في كلّ يوم رصدها فيه عند حصولها على دائرة نصف النهار فوجد الشمس تقرب إلى سمت الرأس حتّى تنتهي إلى نقطة من دائرة نصف النهار بعدها عن سمت الرأس أجزاء ما ثمّ ترجع من بعد ذلك فتبعد عن سمت الرأس فيثبت الأجزاء التي انتهت إليها ويحصّلها ثمّ رصدها حتّى تنتهي في البعد عن سمت الرأس إلى غاية ما ويصير بعدها عن سمت الرأس أجزاء ما ثمّ ترجع فتقرب من سمت الرأيس فيثبت أيضًا الأجزاء التي كانت غاية بعدها عن سمت الرأس ثمّ تعود في السنة الثانية عند قربها من سمت الرأس فرصدها فيجدها تنتهي إلى الجزء بعينه الذي كانت انتهت إليه ثمّ يجدها

تعود فتبعد ولا تتجاوز ذلك الجزء الذي كان أثبته وحصّله ثمّ يرصدها أيضًا عند غاية بعدها فيجدها تنتهي إلى الجزء الذي كانت انتهت إليه ثمّ ترجع وقوله سيّما ما امتحناه في الانقلابين أنفسهما في أدوار كثيرة في الأجزاء التي هي واحدة بعينها من دائرة نصف النهار يعني أنّه كان يمتحن الشمس سنين كثيرة في كلّ سنة إذا انتهت إلى الجزء الذي هو أقرب جزء انتهت إليه والجزء الذي هو أبعد جزء انتهت إليه فيعتبر ممّا عند وصولها إلى ذلك الجزء فيجدها تنتهي إلى ذلك الجزء بعينه ولا تتجاوزه فالأجزاء الواحدة بعينها من دائرة نصف النهار التي ذكرها وذكر أنّه امتحن الشمس فيها هي الدرجة والدقيقة والثانية التي انتهت إليها في غاية قربها والدرجة والدقيقة والثانية التي انتهت إليها في غاية بعدها والدليل على ذلك قوله سيّما ما امتحناه في الانقلابين أنفسهما يريد أنّه كان يعتبرها في كلّ سنة عند حصولها في الانقلابين وكان اعتباره لها في جميع أرصاده لها عند حصولها على دائرة نصف النهار لأنّه كذلك قال في هذا الفصل وإذا كان اعتباره لها في دائرة نصف النهار وكان اعتباره لها في وقت حصولها في الانقلابين فليس بعتربها إلّا في تلك الأجزاء بعينها من دائرة نصف النهار التي هي غاية قربها وغاية بعدها فقد اتّضح المعنى الذي أشار إليه بطلميوس في هذا الفصل وصحّ وزالت الشبهة.

المسئلة الأولى. وهذه حكايتها في رؤية الكواكب عند الأفق إذا كانت الأشياء ترى في الماء أعظم وكلّما رسبت ازدادت عظمًا كما هو موجود وكان السبب في ذلك الانعطاف الذي يعرض لشعاع البصر عند سطح الماء لأنّه يلقي جسمًا أكثف من جسم الهواء الذي نفذ فيه وكانت الكواكب ترى عند الآفاق Correction mg. عظيمة لأجل الرطوبة المحيطة بالأرض وإنّ الانعطاف يعرض فيها كما يعرض في الماء فأين يعرض هذا الانعطاف والرطوبة مبثوثة حولنا محيطة بنا لا تخصّ

موضعًا دون غيره ولا لها سطح معلوم ممّا يلينا وإنّما البصر لا يفهم منها ما كان فريبًا ويفهم ما بعد إذا أمعن في الذهاب ويكون إحساسه شيئًا فشيئًا كما يعرض للبصر في اليوم العصب والمواضع القريبة من البخار وفي أيّ الموضعين تكون رؤية الكواكب أقرب إلى الحقيقة أرؤيتها عند الأفق أم رؤيتها في وسط السماء.

الجواب البخار الغليظ والسحاب شكل كلّ واحد منهما شكل كري لأنّه يرتفع من سطح كري محدّب إلى سطح كري مقعّر فإذا كان البخار أوالسحاب متّصلًا فهو كري وإذا كان منقطعًا فهو قطعة من كرة فالبخار الغليظ الذي يرى في الآفاق هو قطعة من كرة مقعّرها يلي الأرض ومحدّبها يلي السماء وسطحها الذي يلي البصر سطح مستوي إمّا صحيح الاستواء وذلك قد يعرض بالاتّفاق وإمّا متشعّثًا غير محقّق الاستواء وذلك في أكر الأوقات إلّا أنّ البخار الغليظ وإن كان متّصلًا فالهواء اللطيف الذي يلي أبصارنا فليس يمتدّ من الأفق إلى البصر على تدريج حتّى يكون ألطفه يلي البصر وأغلظه يلي الأفق ولا يكون تضاعيفه موضع تتباين فيه أجزاؤه ولكنّ البخار الغليظ يجري مجرى السحاب وهو متناه وإن لم تكن نهايته سطحًا واحدًا ولكنّه جسم غليظ أغلظ من الهواء المتّصل بالبصر وإن كانت أجزاؤه مختلفة الوضع وإذا كان ذلك كذلك فكلّ جزء من البخار الغليظ إذا انتهى إليه شعاع البصر انعطف عنه ولم يمتدّ على استقامة وإذا كانت الشعاعات تنعطف عند أجزاء البخار الغليظ فليس يدرك البصر للكواكب من وراء البخار إلّا بالانعطاف وإذا كان ذلك كذلك فكلّ قطر من أقطار الكواكب إنّما يدرك البصر طرفيه بشعاعين منعطفين ويدرك ما بين الطرفين بشعاعات أخر منعطفة إمّا شبيهة الوضع بوضع الشعاعات Correction mg. الأول وإمّا بأوضاع مختلفة وإذا كان يدرك طرفيه بشعاعين منعطفين فهو يدرك مقداره أعظم من مقداره لو أدركه على استقامة لأنّ الزاوية التي تحيط بها بالشعاعان المنعطفان تكون أعظم. فإن لم يكن سطح البخار مستويًا لأنّه قد يمكن أن يمرّ بسطحي الجزئين

من البخار خطّ مستقيم وإن لم يكن جميع ذلك الخطّ في سطح مستوي من البخار بل قد يقنع في الانعطاف أن يمرّ بسطح كلّ واحد من الجزئين خطّ مستقيم في غاية الصغر وإن لم يكن أحدهما على استقامة الآخر بعد أن يكون وضعهما وضعًا متشابهًا وليس يخلوا البخار مع كثرة أجزائه وتكاثفها أن يكون فيها أجزاء متفرّقة متشابهة الوضع أعني أن يكون وضعها عند البصر وضعًا واحدًا وإن كان أحدهما أقرب والآخر أبعد فقد تبيّن من هذا البيان أنّ الكواكب إذا كانت من وراء البخار الغليظ الذي في الآفاق فإنّها ترى أعظم من أجل غلظ البخار وإن لم يكن هناك سطح محقّق يكون عنده الانعطاف. ولهذا المعنى نظير في الوجود وهو قوس قزح وذلك أنّ القوس ليس يصحّ أن تكون إلّا في سطح مستدير مقعّر يلي البصر وتكون القوس هي إنّما يظهر في السحاب الرقيق أو في الهواء الغليظ وكثيرًا ما تظهر القوس في الهواء والسماء صحيحة لا سحاب فيها وذلك يكون لغلظ الهواء والهواء الغليظ الذي تظهر فيه القوس متّصل بالهواء الذي يلي البصر وليس في تضاعيف هذا الهواء سطح محدود يفصل بين غليظه ولطيفه وكذلك السحاب أيضًا الذي هو أغلظ كثيرًا في الهواء الذي يلي البصر ليس سطحه سطح كري صحيح الاستدارة بل متشعّثًا تشتّتًا في أكثر الأحوال ومع ذلك فإنّ القوس تظهر في الهواء الغليظ وفي السحاب تظهر صحيحة التقويس وعلّة ذلك أنّ القوس تدرك بالانعكاس والانعكاس الذي تدرك به القوس هو انعكاس من الرذاذ الصغار التي هي أجزاء الهواء الغليظ أو السحاب ينعكس الشعاع من كلّ واحد منها إلى الشمس كانت الشمس فوق الأفق أو تحت ذلك الأفق ]من[ وقريبة منه وقد بيّنت ذلك في مقالتي في قوس قزح. وهذا الرذاذ الذي ينعكس منه الشعاع يكون كثيرًا مكاثفًا فإذا اتّفق أن يكون في تضاعيف الهواء رذاذ ينتظم من أوضاعه سطح مستدير وانعكس الشعاع من ذلك الرذاذ إلى الشمس تمّت القوس. ولذلك تظهر القوس في كلّ وقت يوجد فيه هواء غليظ

أو سحاب وفي وقت انعكاس الشعاع عن الرذاذ المنتظم المقوّس قد تنعكس شعاعات كثيرة عن كثير من الرذاذ المتفرّق المختلف الوضع الذي هو أقرب إلى البصر من الرذاذ المنتظم وأبعد منه إلّا أنّه إذا تمّت القوس كان ما يدرك بالشعاعات الباقية تدرك الصورة بها منضمّة إلى الصورة المدركة بالشعاعات المنتظمة ولا تتميّز add. mg. منها في الحسّ لبعد المسافة ولهذه العلّة صارت صورة القوس قوية بيّنة لأنّه لو كانت صورة القوس إنّما هي الصورة التي تحدث من الانعكاس عن الرذاذ المنتظم لكانت خفية جدًّا لأنّه ليس يكون الرذاذ المنتظم على التقويس إلّا يسيرًا نادرًا فكما أنّ القوس تدرك الشعاعات متفرّقة متشتّتة ومع ذلك فإنّه يدرك من جملتها صورة منتظمة كذلك الكوكب الذي يرى من وراء البخار يدرك محيطه شعاعات منعطفة زاويتها أعظم من الزاوية التي تمتدّ إليه من البصر على استقامة وتكون الشعاعات التي تنعطف من الأجزاء المتفرّقة المختلفة الوضع من أجزاء البخار التي تنتهي إلى وسط الكوكب وجميع أجزائه التي بين محيطه يدرك بها أجزاء الكواكب منضمّة إلى محيطه. فقد تبيّن من هذا القول كيف تدرك الكواكب عند الآفاق بالانعطاف ولمن يري من وراء البخار أعظم فأمّا في أيّ الموضعين تكون رؤية الكواكب أقرب إلى الحقيقة أرؤيتها عند الأفق أم رؤيتها في وسط السماء. فالجواب عن ذلك هو أنّه ليس شيء من الكواكب يرى على add. mg. الحقيقته لأنّ شعاعات البصر الذي تمتدّ إليه تمتدّ على استقامة لأنّها تكون أعمدة على مقعّر السماء وقريبًا جدًّا من الأعمدة وأمّا الكواكب التي في جميع المواضع من السماء سوى سمت الرأس فليس يدرك إلّا بالانعطاف وليس يدرك على حقيقتها إلّا أنّه كلّما كان منها أقرب إلى وسط السماء وإلى سمت الرأس كان أقرب إلى الحقيقة لأنّ الشعاعات التي تنعطف إليه يكون انعطافها يسيرًا

وكلّما كان أبعد عن وسط السماء كان أبعد عن الحقيقة لأنّ الشعاعات التي تنعطف إليه يكون انعطافها كثيرًا. وهذا الذي ذكرناه كاف في جواب هذه المسئلة.

المسئلة الثانية وهذه حكايتها ما الذي يتحصّل من كلام بطلميوس في الجملة الأولى من المقادير الثالثة وفي المقالة add. mg. السابعة من قول أبرخس في انتقال نقطتي الانقلابين هل قال إنّ أبرخس كان يري ذلك أو قال إنّه لا يراه وما الذي بيّن من رأي بطلميوس فيه.

الجواب الذي تبيّن من كلام بطلميوس في الفصل الأوّل من المقالة الثالثة وفي كلّ موضع يتكلّم فيه في حركة الشمس أنّ نقطتي الانقلابين ثابتتان غير منقلبين لأنّه في الجملة الأولى تحصّل زمان سنة الشمس بالقياس إلى كلّ واحدة من نقطتي الانقلابين والاستوائين ثمّ أنّه في المقالة السابعة في الفصل الثاني يبيّن أنّ الكواكب الثابتة تتحرّك في كلّ مائة سنة جزء واحد فتقرب وتبعد من كلّ واحدة من هذه النقط وبيّن في الفصل الثالث من هذه المقالة أنّ هذه الحركة هي على قطبي دائرة البروج وهذان المعنيان ظاهران في كتاب المجسطي لا تتداخلهما شبهة. فلو كان يعتقد أنّ لنقطتي الانقلابين حركة لكانت تلك الحركة إمّا على قطبي دائرة البروج وإمّا على قطبين غيرهما فإن كانا تتحرّكان على قطبي دائرة البروج لكان يختلف بعدهما عن دائرة معدّل النهار ويختلف ميلهما وهو ظاهر من كلامه في الميل أنّ الميل لا يختلف فليس تتحرّك نقطتا الانقلابين عنده على قطبي دائرة البروج لا حركة مساوية لحركة الكواكب الثابتة ولا مخالفة بها ولو كانت نقطتا الانقلابين تتحرّكان على قطبين غير قطبي دائرة البروج وغير قطبي معدّل النهار لكان ميلهما عن دائرة معدّل النهار أيضًا يختلف وإن كانت هاتان النقطتان تتحرّكان على قطبي معدّل النهار لكانت حركتهما مخالفة لحركة الكواكب الثابتة إذ كانت حركة الكواكب

عنده على قطبي دائرة البروج وكان يلزم من ذلك أن تختلف عروض الكواكب الثابتة بالقياس إلى دائرة البروج وعروض الكواكب الثابتة بالقياس إلى دائرة البروج عنده لا تختلف وذلك يتبيّن من المقالة السابعة والثامنة عند تقريره لعروض الكواكب ومن الجداول التي في هاتين المقالتين التي أثبتت فيها ما أسبقه من عروض الكواكب فقد تبيّن من هذا الذي بيّنّاه أن رأى بطلميوس في نقطتي الانقلابين ونقطتي الاستوائين أنّها ثابتة لا حركة لها غير الحركة السريعة. فأمّا ما حكاه من قول أبرخس في المقالة السابعة في آخر الفصل الثاني منها وهو قوله حين قال يعني أبرخس فأنّه لو كان من قبل هذا السبب نقطتا الانقلابين ونقطتا الاستوائين تنتقلان قدمًا للبروج في السنة اليس بأقلّ من جزء من مائة جزء لقد كان يجب أن يكون في الثلاثمائة سنة إنّما انتقلت ليس بأقلّ من ثلاثة أجزاء فهو أنّ أبرخس كان لا يتحقّق حركة الكواكب الثابتة ولا كان ظهر من قبل أبرخس حركة للكواكب الثابتة وإنّما كان قد رصدت وقرّرت مواضع الكواكب في الطول والعرض من قبل أبرخس فلمّا رصدها أبرخس وجد مواضعها مخالفة لما كان قرّر وأثبت فبيّن له أنّ هناك حركة والذي يبيّن له هو أنّ الكواكب التي قبل الانقلاب الصيفي قد قربت من الانقلاب الصيفي وأنّ الكواكب التي بعد الانقلاب الصيفي قد بعدت عن الانقلاب الصيفي وكذلك الكواكب التي عن جنبتي الانقلاب الشتوي وعن جنبتي كلّ واحدة من نقطتي الاستوائين. وهذا المعنى يحتمل أن تكون حركة الكواكب على توالي البروج ويحتمل أن تكون الحركة نقطتي الانقلابين ونقطتي الاستوائين إلى خلاف توالي البروج فلمّا ظهرت لأربخس هذه الحركة جوز أن تكون نقطتا الانقلابين وتقطتا الاسوائين تحرّكت على خلاف توالي البروج وهو قوله قدمًا للبروج فكلّما يسمّيه بطلميوس قدمًا للبروج فإنّما يريد به على خلاف توالي البروج فحركة الكواكب الثابتة وكيفية حركتها لم تكن تحقّقت في أيّام أبرخس ولا تحرّرت فلمّا رصدها بطلميوس

†وانعمر† النظر فيها تحقّقت وقرّرت حركاتها وتبيّن من كلامه أنّ الحركة التي ظهرت لأبرخس وتحقّقت له هو إنّما هو حركة الكواكب الثابتة لا حركة نقطتي الانقلابين والاستوائين فقد تبيّن من جميع ما ذكرناه أن رأى بطلميوس في نقطتي الانقلابين والاستوائين أنّها ثابتة غير محرّكة بضرب من ضروب الحركات وأنّ أبرخس كان مشكّكًا في كيفية هذه الحركة.

المسئلة الثالثة وهذه حكايتها في هذه الجملة يحكي عن أبرخس أنّ في كتابه في الشهور والأيّام الكبيسة لما تقدّم وقال إنّ زمان السنة أمّا على رأي ال ميطن وأقطيمن فثلاثمائة وخمسة وستّون يومًا ومع ذلك ربع يوم وجزء من ستّة وسبعين جزءًا من يوم وأمّا على رأي قيلبس فثلاثمائة وخمسة وستّين يومًا وربع يوم فقط اتّبع ذلك بأن قال بألفاظه †نصا† هذا القول وأمّا نحن فإنّا نجد شهورًا أيّامها محصورة في التسع عشر سنة عدتها مثل عدّتها عندهم. فأمّا السنة فنجدها أقلّ أيضًا من الربع بجزء من ثلاثمائة جزء من يوم بغاية التقريب لمبلغه حتّى يكون في ثلاثمائة سنة ينقص إمّا على رأي ماطن فخمسة أيّام وإمّا على رأي قيلبس فيومًا واحدًا. ما معنى هذا الكلام كلّه وكيف يجوز أن يجتمع أن يكون أبرخس قلّد هذين الرأيين المختلفين أعني الذي على رأي ماطن والذي على رأيه؟

الجواب أنّ وجود زمان سنة Correction mg. الشمس صعب متعسّر وهذا الزمان ما يحصله مقداره إلى وقتنا هذا وهو من أصعب المعاني التي في السماء وهو أنّه أيّ وقت رصدت فيه الشمس وجدت الزيادة التي تزيدها السنة على ثلاثمائة وخمس وستّين يومًا مختلف مقداره ولا توجد هذه الزيادة في رصدين مختلفين متساويي المقدار على التحرير بل توجد أبدًا مختلفًا إلّا أنّ الاختلاف الذي يوجد في مقدار هذه الزيادة هو يسير. فأمّا قول أبرخس إنّ زمان السنة أمّا على رأي add. mg. ميطن وأقطيمن فثلاثمائة وخمسة وستّين يومًا

ومع ذلك ربع يوم وجزء من ستّة وسبعين جزءًا من يوم وأمّا على رأي قيلبس فثلاثمائة وخمسة وستّين يومًا وربع يوم فقط وأمّا نحن فإنّا نجد شهورًا أيّامها محصورة في التسعة عشر سنة عدتها مثل عدّتها عندهم فأمّا السنة فنجدها أقلّ أيضًا من الربع جزء من ثلاثمائة جزء من يوم بغاية التقريب فإنّه يجتمع هذا القول إنّ زمان سنة add. mg. الشمس هو ثلاثمائة وخمسة وستّين يومًا وقريبًا جدًّا من ربع يوم وإنّه وإن خالف الربع فبمقدار يسير جدًّا وذكر الزمانين اللذين وجدهما من كان قبله اللذين أحدهما الربع add. mg. والآخر ربع وجزء من ستّة وسبعين جزءًا ليكونا شاهدين له على أنّ الزيادة على الأيّام التامّة ليس يخالف الربع بمقدار يعتدّ به ولمّا وجد هذه الزيادة برصده وبرصد من تقدّمه وجدها فريبه من الربع وكان يعتقد أنّ رصده أشدّ تحصيلًا وتحريرًا من رصد من تقدّمه حكم برصد وجعل رصدي من تقدّمه شاهدين لصحّة رصده وأشار إلى أنّ الاختلاف الذي يخالف به رصداهم رصده إنّما هو لقلّة تحريرهم وكذلك آلاتهم. فإنّ رصده إنّما خالف رصدهم لشدّة تحريره فرأي أبرخس ورأي بطلميوس الذي يعتمد أنّه هو أنّ زمان سنة الشمس هو ثلاثمائة وخمسة وستّين يومًا وقريب جدًّا من ربع يوم ولا يتحقّقان مقدار الاختلاف الذي به يخالف هذه الزيادة الربع وما أصعب تحرير هذه الزيادة وقد كنت ألّفت مقالة في التنبيه على مواضع الغلط في كيفية الرصد تبيّن فيها أنّه لا طريق إلى إدراك المعاني السمائية على غاية التحقيق الذي لا يقع فيه شيء من التقريب وإذا كان ذلك كذلك فلا طريق إلى إدراك مقدار سنة add. mg. الشمس على غاية التحقيق فالتفاوت الذي في مقدار الزيادة وتختلاف ما أخرجته الأرصاد من هذه الزيادة إنّما هو الزلل الذي لا يحلوا الأرصاد منه فقد تبيّن ممّا شرحناه ما †منه† اعتقاد أبرخس في سنة الشمس.

المسئلة الرابعة هذه حكايتها

قال في الجملة العاشرة وأمّا الفصل الذي عند دائرة نصف النهار فإنّه واحد بعينه في كلّ مسكن وليس يريد ولا على أزمان الفصل الذي يجتمع من قبل الاختلاف الذي يلحق الشمس فقد تبيّن أنّ أكثر فصل اختلاف الشمس أربعة أجزاء ونصف وربع وأكثر اختلاف ممرّ البروج في وسط السماء أربعة أجزاء ونصف هذا إذا أخذ الفصل بين برجين عن جنبتي نقطة واحدة من نقطة الاستواء وبرجين عن جنبتي نقطة واحدة من نقطة الانقلاب فأمّا أن أخذ الفصل بين أكثر من برجين كان أكثر من خمسة أجزاء مثل القوس التي من نصف الدلو إلى نصف الثور والقوس التي من نصف العقرب إلى نصف الدلو.

الجواب أنّ بطلميوس لمّا تكلّم في اختلاف الأيّام بلياليها ابتداء بالاختلاف الذي يعرض من أجل تعديل الشمس فذكر الاختلاف الذي يعرض بين نصفي دائرة البروج اللذين أحدهما يلي البعد الأبعد من فلك الشمس والآخر يلي البعد الأقرب وهو أكثر الاختلاف بين كلّ نصفين من أنصاف دائرة البروج. ثمّ ذكر الاختلاف الذي يعرض من أجل المطالع فابتداء بالاختلاف الذي يعرض في مطالع الآفاق المائلة فذكر أنّ أعظم الختلاف الذي يقع بين نصفي دائرة البروج في الآفاق المائلة هو الاختلاف بين نصفي دائرة البروج اللذين تحدّهما نقطتا الانقلابين لأنّ النصف من دائرة البروج الذي يلي الاعتدال الخريفي يكون مطالعه في جميع الآفاق المائلة أبدًا أكثر من نصف دائرة والنصف من دائرة البروج الذي يلي الاعتدال الربيعي يكون مطالعه في جميع الآفاق المائلة أبدًا أقلّ من نصف دائرة والاختلاف بين مطالع هذين النصفين في الآفاق المائلة هو أكثر اختلاف بين مطالع كلّ نصفين من دائرة البروج في الآفاق المائلة. ثمّ ذكر الاختلاف الذي يعرض في مطالع الكرة المنتصبة وليس في دائرة البروج نصفان يكون مطالع أحدهما في الكرة المنتصبة زائدًا ويكون مطالع النصف الآخر ناقصًا بل كلّ نصفين من دائرة البروج فإنّ مطالعهما في الكرة المنتصبة أبدًا متساويان

فاعتمد بطلميوس أن يبيّن أعظم اختلاف بين برجين من دائرة البروج يكون مطالع أحدهما أعظم من مطالع كلّ واحد من البروج الباقية ويكون مطالع البرج الآخر أصغر من مطالع كلّ واحد من البروج الباقية وهذان البرجان هما اللذان أحدهما يلي نقطة الانقلاب والآخر يلي نقطة الاعتدال ولأنّ مطالع كلّ واحد من هذين البرجين مساوي لمطالع البرج الذي يليه في الكرة المنتصبة جعل الاعتبار بمطالع البرجين التّصلين وقاسهما بمطالع البرجين الآخرين المتّصلين. فبيّن ممّا ذكره أعظم الفصل بين مطالع برجين من دائرة البروج فلمّا بيّن ذلك عاد فقسم جميع دائرة البروج بقسمين يكون التفاضل بينهما أعظم التفاضل add. mg. فوجد هذين القسمين ممّا اللذان من نصف الدلو إلى الميزان ومن العقرب إلى نصف الدلو والذي اعتمده بطلميوس في هذا الموضع هو أن بيّن أعظم الفصل بين قسمي دائرة البروج add. mg. وبين برجين من دائرة البروج فقط فأمّا القوسان اللتان إحداهما من نصف الدلو إلى نصف الثور والأخرى من نصف العقرب إلى نصف الدلو وكلّ واحدة منهما هي ثلاثة بروج. فلو ذكر التفاضل الذي لثلاثة بروج للزمه أن يذكر التفاضل الذي لأربع بروج ولخمسة add. mg. بروج ولبرج ونصف ولكلّ قوس من دائرة البروج مع كلّ قوس مساوية لها وهذه الأجزاء هي بال نهاية فلمّا رأى أنّ الأجزاء بلا نهاية وليس واحد منها أولى بأن يذكر تفاضله من غيره من الأجزاء اقتصر من جميع الأجزاء على برجين فقط ثمّ بيّن أعظم التفاضل بين قسمي جميع دائرة البروج لأنّه هو الغرض والتفاضل بين البرجين إنّما أشار به إلى أنّه قد يقع التفاضل بين أجزاء دائرة البروج لئلا يظنّ أنّ التفاضل ليس يكون إلّا من قسمي جميع دائرة البروج فقط. فقد تبيّن ممّا ذكرناه شلامة قول بطلميوس وتبيّن مع ذلك الطريق التي قصدها في ذكر التفاضل.

المسئلة الخامسة وهذه حكايتها في المقالة الرابعة النسب التي ذكرها في الجملة الحادية عشرة غير صحيحة.

الجواب ليس لغلط بطلميوس في النسب فإن كان في نسخته غلط فهو غلط في النسخ

إمّا في نسخته وإمّ في النسخة التي نسخت منها. والنسب التي ذكرها هناك أمّا الأولى منها فقال هي نسبة ثلاثة ألف ومائة وأربعة وأربعين إلى ثلاثمائة وسبعة وعشرين ونصف وهذه النسبة هي نسبة ستّين إلى ستّة وربع وهاتان النسبتان صحيحتان متناسبتان. وأمّا النسبة الثانية فقال هي نسبة ثلاثة ألف ومائة واثنين وعشرين ونصف إلى مائتي وسبعة وأربعين ونصف وهذه النسبة هي نسبة ستّين إلى أربعة أجزاء وستّة وأربعين دقيقة وهاتان النسبتان أيضًا صحيحتان متناسبتان.

المسئلة السادسة وهذه حكايتها في المقالة السادسة قد استعمل في الجملة الخامسة القوس القائمة على فلك البروج مكان القوس القائمة على الفلك المائل للقمر في حدود الكسوفات وفي المدد التي يقع فيها الكسوف وذلك غير واجب وما استخرجه أيضًا محالف ما تقتضيه الجداول وما تقتضيه نسبة جزء واحد إلى أحد عشر جزءًا ونصف.

الجواب إنّما بيّن بطلميوس حدود الكسوف واعتمد القوس القائمة على الدائرة المائلة عند كلامه في كسوف القمر واعتمد في حدود الكسوف على قوس قائمة على دائرة البروج عند كلامه في كسوف الشمس وهو مصيب في الجميع لأنّ حدود الكسوف إنّما يكون عند قوس هي أقصر قوس تكون بين محيط الشيء الكاسف وبين الدائرة التي يتحرّك عليها مركز الجرم من المنكسف والشيء الكاسف للقمر هو الظلّ فحدود كسوف القمر يكون عند القوس التي تمرّ بمركز الظلّ وتكون قائمة على الدائرة المائلة التي يتحرّك عليها مركز القمر والشيء الكاسف للشمس هو القمر فحدود كسوف الشمس يكون عند القوس التي تمرّ بمركز القمر وتكون قائمة على الدائرة التي يتحرّك عليها مركز الشمس فحدود كسوف القمر هو قوس تفصلها القوس القائمة على دائرة البروج فهذه هي الفلك التي من أجلها اعتمد بطلميوس في حدود الكسوف مرّة من الدائرة القائمة على فلك القمر ومرّة من الدائرة القائمة على فلك الشمس فأمّا قوله وما استخرجه أيضًا مخالف لما يقتضيه الجداول وما يقتضيه

نسبة واحدة إلى أحد عشر جزءًا ونصف فما عرفت الموضع الذي أشار إليه.

المسئلة السابعة وهذه حكايتها في المقالة التاسعة. قال في الجملة الثانية ولا على أنّه قد يكون لكلّ واحد منها رجوعان ما الرجوعان؟

الجواب الرجوع هو التعديل الناقص وللكواكب الخمسة تعديلان ناقصان أحدهما من جهة الفلك الخارج المركز الحامل والآخر من جهة فلك التدوير وقد يحتمل أيضًا أن يكون التعديل الذي من جهة فلك التدوير هو من جهة فلك آخر خارج المركز لأنّ ذلك قد بيّنه بطلميوس فلكلّ واحد من الكواكب الخمسة تعديلان وإذا كان التعديل ناقصًا فهو رجوع لأنّ حركة الكوكب المستوية يوجب له أن يكون في موضع في موضع من دائرة البروج فإذا عدّل بالنقصان صار موضعه من دائرة البروج قبل ذلك الموضع فيكون راجعًا بالحركة المحتلفة إلّا أنّ أحد هذين الرجوعين يدرك بالحسّ وبالقياس إلى الكواكب الثابتة وهو الرجوع الذي يوجبه فلك التدوير أو فلك خارج المركز يقوم مقام فلك التدوير والرجوع الآخر الذي بحسب الفلك الحامل ليس يدرك بالحسّ والعلّة في ذلك أنّ التعديل الناقص الذي يدرك من أجله الرجوع بالحسّ مقداره أكثر من مقدار القوس من دائرة البروج التي يقطعها مركز فلك التدوير ومركز الكوكب في الزمان الذي يقطع فيه الكوكب قوس التعديل فيكون الكوكب إذا يحرّك فقطع قوس التعديل متوجّهًا إلى خلاف توالي البروج يكون الفلك الحامل قد نقله على توالي البروج أقلّ من تلك القوس فيرى بالحسّ ممتأخّرًا عن موضعه بمقدار التفاضل بين القوسين والتعديل الناقص الذي لما يدرك من أجله الرجوع بالحسّ مقداره أقلّ من مقدار القوس من دائرة البروج التي يقطعها مركز فلك التدوير ومركز الكوكب في الزمان الذي يقطع فيه مركز فلك التدوير ومركز الكوكب قوس للتعديل فيكون الكوكب إذا قطع قوس التعديل متوجّهًا إلى خلاف توالي البروج يكون الفلك الحامل من أجل خروج مركزه فذروة على توالي البروج أكثر من تلك القوس فلا يرى بالحسّ متأخّرًا عن موضعه بل

توجد حركته أبطأ ممّا كانت في أوقات التعديلات الدائرة فالتعديلان الناقصان هما على الحقيقة رجوعان بالقياس إلى حساب حركة الكوكب إلّا أنّ أحدهما محسوس والآخر غير محسوس. ولذلك سمّي المحسوس منهما رجوعًا ولم يسمّ الآخر رجوعًا لأنّهم اعتمدوا في التسمية على الحسّ ولذلك أيضًا لم يسمّ القمر راجعًا وله تعديلان شبيهان ببعد يليّ الكواكب الخمسة إلّا أنّهما جمعيًا غير محسوسين. فأمّا المتقدّمون من أصحاب التعاليم الذين كانوا قبل أبرخس فلم يكن ظهر لهم للكواكب الخمسة أكثر من اختلاف واحد ولم يكونوا أحسّوا بأنّ هناك اختلافين فلمّا انتهى الزمان إلى أبرخس رصد الكواكب وجد مواضعها وحركاتها مخالفة لما يوجبه حسابها الذي قد كان قرّره المتقدّمون قبله فخطر له أنّ للكواكب اختلافًا آخر غير الاختلاف الذي قرّره المتقدّمون ولكنّه لم يتحقّقه فلم يقدّم على أن يحكم أنّ للكواكب اختلافين. وذلك قول بطلميوس فإنّه يشبه أن يكون كان يرى يعني أبرخس أنّه ليس ينبغي أن يقدّم على الحكم بأنّ كلّ واحد منها له اختلافان ولا على أنّه قد يكون لهما رجوعان يعني تعديلين ناقصين ثمّ قال على أنّ سائر أصحاب التعاليم إنّما بنوا الأمر في براهينهم الخطوطية على أنّ الاختلاف واحد بعينه وكذلك الرجوع. فأمّا قوله بالجدول الذي يسمّى الأبدي إلّا أنّ ذلك قد اجتمع فيه أنّه بغير برهان وأنّه باطل فهو أنّه قد كان للمتقدّمين جدول يقومون منه الكواكب فكان ذلك الجدول زيجًا من الزيجات فالزيجات ليس يكون فيها براهين. فقوله بغير برهان فلأنّه لم يكن برهانه مقترنًا به ولا بيّن فيه كيف يعرف ذلك الجدول كما يكون الجداول التي في سائر الزيجات؟ وأمّا قوله وأنّه باطل فلأنّه كان إذا قوم الكوكب بذلك الجدول واعتبر موضع الكوكب بالرصد وجد موضعه مخالفًا لما أوجبه تقويمه بذلك الجدول.

المسئلة الثامنة وهذه حكايتها. قال في الجملة السابعة في رصد عطارد في العكس وكان يري لطيفًا جدًّا خفّيًا ما يفيد هذا القول وعطارد †مهما† في بعده الأوسط لأنّه في أبعد بعده من الشمس.

الجواب أنّ أبعد البعد الصباحي الذي يرى ليس يكون أبدً متساويًا وكذلك أبعد البعد المسائي وإذا اعتبرت

هذه الأبعاد من الأرصاد التي في المجسطي وجدت كذلك والعلّة في ذلك أنّ فلك عطارد المائل ليس يثبت على ميله بل يتحرّك منطبق تارة على دائرة البروج وتارة يفارقها فمركز فلك التدوير يكون تارة في سطح فلك البروج وتارة خارجًا عنها تختلف أبعادها أيضًا عن دائرة البروج والكوكب أيضًا نفسه قد يكون تارة على نصف دائرة البروج وتارة خارجًا عنها وقد يكون مركز الكوكب على دائرة البروج ومركز فلك التدوير خارجًا عن دائرة البروج وأبعد بعد الكوكب عن الشمس هو أن يكون على الخطّ الخارج من البصر المماسّ لمحيط فلك التدوير وإذا كان مركز فلك التدوير يختلف وضعه من دائرة البروج فموضع المماسّة ليس يكون بعده من الشمس أبدًا متساويًا بل يكون بعده مختلفًا وأقرب ما يكون هذا الموضع من الشمس هو إذا كان مركز فلك التدوير في سطح دائرة البروج فأبعد ما يكون من الشمس إذا كان فلك التدوير في عاية ميله عن سطح دائرة البروج وللانحراف أيضًا في هذا الموضع تأثير وأقرب ما يكون الكوكب من الشمس غذا كان مركزه في سطح دائرة البروج وموضع الكوكب في الوقت الذي يكره بطلميوس كان على ثمانية عشر جزءًا ونصف وربع من الثور وبعده الأبعد كان في عشر درجات من الحمل فكان بعده من البعد الأبعد ثمانية وثلاثين جزءًا ونصف وربع. فيحتمل أن يكون الكوكب كان في ذلك الوقت في سطح دائرة البروج أو قريبًا منه أو ليس في غاية بعده من الشمس بل كان على الحقيقة كذلك لأنّ بعده كان من الشمس أحد وعشرين جزءًا وربع وهذا القدر ليس هو أبعد الأبعاد الصباحية لأنّ أبعد الأبعاد الصباحية قد يكون أكثر من ذلك ويوجد في المجسطي أبعاد صباحية هي أكثر من هذا القدر. فقول بطلميوس وكان يرى لطيفًا جدًّا خفّيًا أيّ لم يكن في عاية بعده عن الشمس يشير إلى أنّه كان في سطح دائرة البروج أو قريبًا منه لأنّ الكوكب إذا كان قريبًا من الشمس ظهر صغيرًا خفّيًا فهذه هو فائدة قول بطلميوس وكان يرى لطيفًا جدًّا خفّيًا.

المسئلة التاسعة وهذه حكايتها في المقالة الثالثة عشر. قال في الجملة الرابعة في الانحراف من قبل أنّا لو خلطناها معه لكان سنحتاج في ذلك من الجداول إلى أكثرهما وضعناه وكان

الحساب فيها سيكون أصعب من قبل أنّ المسيرات المسائية والمسيرات الصباحية من شأنها أن تكون غير متساوية فأن لا تكون لا محالة في جهة واحدة بعينها من فلك البروج ومع ذلك فإنّ ميل فلكيهما الخارجين لمّا كان ليس يبقي add. mg. على حال واحدة فإن فضلات التنقّص عن الميول العظمى كانت سيخالف فضلات التنقّص عن الانحرافات العظمى فلمّا أفردنا الفضل صار تناول شيء شيء منها أسهل علينا كما سيبيّن من نفس ما يتلوا هذا القول.

الجواب أنّ بطلميوس استخرج انحرافات فلك التدوير لكوكبي الزهرة وعطارد لجزء جزء من فلك التدوير على أنّ مركز فلك التدوير على البعد الأبعد والبعد الأقرب من الفلك الخارج المركز ثمّ استخرج بالجدول الأخير الذي سمّاه الدقائق مقادير هذه الانحرافات عند كون مركز فلك التدوير على نقطة نقطة من محيط الفلك الخارج المركز بقسط الدقائق التي في هذا الجدول من مقادير الانحرافات التي استخرجها فلأنّ مركز فلكي تدوير هذين الكوكبين يتحركّان على محيطي الفلكين انحرافي المركزين يلزم أن يكون انحراف تلك تدوير كلّ واحد من هذين الكوكبين عن سطح فلك البروج مركّبًا من انحراف فلك التدوير الذي توجبه حركة فلك التدوير على الدائرة الصغرة التي ذكرها ومن ميل الفلك الخارج المركز عن سطح فلك البروج فلو خلط الانحراف مع ميل الفلك الخارج المركز لصعب تقويم انحراف الكوكب لأنّ ميل الفلك الخارج المركز ليس يثبت على حال واحدة بل هو متحرّك متغيّر وكان يحتاج في تقويم الانحراف إلى زيادة جدول يستخرج به قسط الدقدائق من الانحراف بحسب حركة ميل الفلك الخارج المركز وميل الفلك الخارج المركز يحتاج أن يقوّم ويحصّل مقداره في كلّ وقت فكان يحتاج في تقويم الانحراف إلى زيادة جدول يستخرج به قسط الدقائق من الانحراف بحسب حركة ميل الفلك الخارج المركز وإذا استخرج الانحراف مفردًا وميل الفلك الخارج المركز مفردًا استغنى عن زيادة الجدول الذي يحتاج أن يقوّم به مقدار الانحراف بحسب ميل الفلك المائل للخارج المركز. فأمّا قول بطلميوس من قبل أنّ المسيرات المسائية والمسيرات الصباحية من شأنها أن تكون غير متساوية

وأن لا تكون لا محالة في جهة واحدة بعينها من فلك البروج فلأنّ أعظم الانحرافات التي تظهر لهذين الكوكبين إنّما يكون عند كون الخطّ الخارج من مركز البصر إلى الكوكب مماسًّا لفلك التدوير وهذه المماسّة وأعظم الانحرافات إنّما توجد عند أعظم البعد الصباحي وأعظم البعد المسائي لأنّ هذين الكوكبين يكونان أبدًا قريبين من الشمس فليس يتمكّن من رصدهما إلّا عند الصباح وعند المساء هذه الانحرافات قد تكون مرّة شمالية عن سطح فلك البروج ومرّة جنوبية عنه والشمالية من هذه الانحرافات مخالفة للجنوبية. وذلك أنّ الانحراف يكون في أحد جنبتي فلك البروج مركّبًا من الانحراف ومن ميل الفلك المائل ويكون في الجهة الأخرى من فلك البروج تاقصًا مقدار ميل الفلك المائل. فلو خلط الانحراف بميل الفلك المائل add. mg. لكان يحتاج إلى عدّة جداول يقوّم بها هذا الانحراف من أجل اختلاف ميل الفلك المائل ومن أجل اختلاف جهة الميل والانحراف ولمّا فرد الانحراف وأضاف إليه مقدار ميل الفلك الخارج المركز المائل لم يختج إلى أكثر من جدول الدقائق فقط. فهذا الذي ذكرناه هو تفسير قول بطلميوس لو خلطناها وما تبعه من الكلام.

وهذا آخر ما ذكره من المسائل.

الشكّ الأوّل. من المعلوم أنّ كلّ موضع من الأرض موافق لما بعده منه ربع دائرة وأنّ العارض في رؤية الكواكب يعرض في كلّ موضع من الأرض فالبخار الرطب إذن يعمّ جميع الأرض فشعاع البصر منذ يخرج من العين يمرّ في البخار عرضًا إلى الأفق وعلوًّا إلى سمت الرأس لا ينفكّ منه وإذا كان ذلك فليس للبخار سطح ممّا يلينا يلقاه شعاع البصر ولا يكون يتناول شعاع البصر في قوامين مختلفين لطيف وكثيف بل هو سالك في هذا البخار وحده إلى أن يفارقه خارجًا منه فيجب أن تكون رؤية الكوكب في الأفق وفي وسط السماء بمقدار واحد وليس الأمر كذلك.

الجواب. قد استعمل في هذا القول مقدّمتين أحدهما أنّ البخار الذي يكون في الأفق يجب أن يكون متّصلًا يعمّ جميع آفاق الأرض وهذا محال والمقدّمة الأخرى هي أنّ هذا العارض في رؤية الكواكب يعرض في كلّ موضع من الأرض وليس

الأمر كذلك وإنّما يعرض في المواضع المسكونة من المعمورة الشمالية وما سوى هذه المعمورة تختلف أحوالها. فأمّا بطلان المقدّمة الأولى فيتبيّن يما نصف وهو أنّ الشمس إذا كانت في الآفاق فإنّ البصر يمكنه أن يدركها ويحقّق النظر إليها ويديم تأمّلها ولا يتألّم لذلك ولا يعجز عنه وإذا ارتفعت عن الأفق أو صارت في وسط السماء فإنّ البصر لا يستطيع النظر إليها ولا يمكنه تأمّلها وهذا دليل واضح لا تعرضه شبهة على أنّ البخار غير متّصل بالبصر ولا محيطًا بالأرض. وأمّا بطلان المقدّمة الأخرى فهو أنّ المواضع المجيطة بالمساكن الشمالية هو مستحرّة والماء يشملها فيرتقي منها البخار الغليظ والمواضع المسكونة ليست مستحرّة فلا يرتقي منها بخار غليظ والمواضع الذي تحت ذلك البخار التي هي المواضع المستحرّة التي المساكن الشمالية في آفاقها لا يصحّ أن ترى فيها الكواكب كما يراها أهل المساكن الشمالية لأنّه ليس في وسط سماء أهل المساكن الشمالية بخار ولو كان في وسط سماء أهل المساكن الشمالية بخار لكان البصر يدرك الشمس في وسط السماء كما يدركها في الآفاق ويمكنه تأمّلها وأطاله النظر إليها وليس يوجد الأمر كذلك. وإنّما ليس في المواضع الشمالية المسكونة بخار غليظ لأنّها غير مستحرّة. فهاتان المقدّمتان باطلتان وعلى هاتين المقدّمتين بنى الشكّ في الجواب وإذا كانت هاتان المقدّمتان باطلتين فالجواب هو الجواب الذي يكرناه لم يتغيّر ولم ينتقض. وأيضًا فإنّ الشكّ الذي ذكره في المسائل الأولى هو شكّ في جواب تشكّكه في قول بطلميوس أنّ علّة عظم الكواكب في الآفاق هو البخار لأنّه كالشيء الذي يرى في الماء فجعل البخار علّة لعظمها وهو مصيب في هذا القول والشكّ الذي اعترضه في هذا القول قد انحلّ. فالجواب الذي كنت أنفذته في العام الماضي وتشكّكه في ذلك الجواب وهو الشكّ الذي أنفذه قبل هذا الشكّ قد انحلّ بالجواب الذي أنفذته قبل هذا الجواب وهذا الشكّ الآخر الذي هو شكّ في الجواب الثاني add. mg. قد انحلّ بهذا الجواب فجواب الشكّ الأوّل الأصلي الذي هو شكّ في قول لطبميوس هو الجواب الأوّل القديم وهو على هيئته لم يتغيّر منه شيء. وإذ قد تبيّن ذلك فإنّي أقول أنّ جميع ما ذكرته إلى الآن هو جوابات مسائله وتشكّكه لأجل جميع الشكوك التي في

المعاني التي يشكّك فيها فإنّ المواضع التي يشكّك فيها شكوك أخر أصعب من الشكوك التي ذكرها وفي جميع المجسطي شكوك أكثر من أن يحصى وإنّما أجيب عمّا يسئل عنه لا غير لأنّ الجواب لا يجوز أن يكون إلّا على نفس جواب السؤال. فمن الشكوك التي في عظم الكواكب في الآفاق هو أنّ الكواكب في السماء فالسماء ألطف من الهواء إذا كان المبصر في الجسم الألطف والبصر في الجسم الأغلظ أدبك البصر المبصر أصغر ممّا هو وإذا ازداد الجسم الذي يلي البصر غلظًا ازداد المبصر صغرًا الهواء في الآفاق أغلظ منه في وسط السماء فقد كان يجب أن يرى الكواكب في الآفاق أصغر ممّا يرى في وسط السماء وليس يوجد الأمر كذلك. وهذا المعنى قد بيّنت في كتابي في المناظر عند الكلام في الانعطاف وبيّنت هناك أنّ لعظم الكواكب في الآفاق علّة كلّية غير البخار هي التي من أجلها يرى الكواكب وأبعاد ما بين الكواكب في الآفاق أعظم منها في وسط السماء وما ارتفع عن الآفاق وبيّنت مع ذلك أنّ البخار الذي يزيد في الأفىق يزيد في عظمها على العظم الذي يوجبه لها العلّة الكلّية إلّا أنّي لم أذكر هذا له لأنّه ليس من شكوكه ولا الجواب عنه جواب عن مسائله.

فأمّا الشكّ الثاني وهو قوله موضع السؤال.

الشكّ الثاني في موضع سؤال هو قول أبرخس وأمّا نحن فإنّا نجد شهورًا أيّامها محصورة في التسع عشرة سنة عدّتها مثل عدّتها عندهم. ما هذه الشهور التامّة وما التسع عشر سنة؟ كيف رصدها؟

الجواب أنّ بطلميوس عند كلامه في سنة الشمس في الجملة الأولى من المقالة الثالثة يحكي عن أبرخس أنّه قال بألفاظه كلامًا أوّله فأمّا تحسب هذه الأرصاد. ثمّ قال لكن قد يمكن أن يتبيّن اختلاف أزمان السنة من قبل الأرصاد التي وقعت بحلقة النحاس. ثمّ قال فيقول إنّ الاستواء الخريفي كان في السنة السابعة عشر من الدور الثالث من أدوار قيلبس. ثمّ قال وكان بعد ثلاث سنين. ثمّ قال وكان بعد سنة واحدة. ثمّ قال وكان بعد ثلاث سنين وهذه السنين المتفرّقة هي تسعة عشر سنة وهي التي أشار إليها أبرخس في قوله وأمّا نحن فإنّا نجد شهور أيّامه محصورة في التسع عشر سنة عدّتها مثل عدّتها

عندهم وأمّا السنة فنجدها أقلّ أيضّا من الربع بجزء من ثلاثمائة جزء. يزيد بهذا القول الأخير أنّه لمّا رصد الأرصاد في السنين التي تقدّم ذكرها في التفصيل وجد في زمان رصده زمان عدّة من الشهور موافقًا لزمان تلك الشهور في رصد من تقدّمه ووجد زمان جملة السنة مخالفًا لزمان جملة السنة عندهم فأمّا أيّ الشهور هي الشهور التي وجدها تامّة فإنّ أبرخس لم يعيّن عليها وأنا فلا أعلم شيءًا من الغيب وإنّما لم أشرح هذا الفصل في الجواب الذي ذكرته لأنّه لا فائدة فيه غير ما يفهم من ظاهر اللفظ فقط لأنّ الغرض في جميع الكلام الذي ذكر في الجملة الأولى من المقالة الثالثة إنّما هو مقدار زمان سنة add. mg. الشمس فقط وقد ذكر الجواب عنه وأمّا قوله موضع السؤال هو قول أبرخس يعني هذا الفصل فما هذا الفصل موضع السؤال لأنّ موضع السؤال في جميع هذه الجملة هو مقدار سمة الشمس لا غير.

الشكّ الثالث. كان الجواب تضمّن أنّ حدود الكسوف إنّما تكون عند قوس هي أقصر قوس تكون بين مركز الشيء الكاسف وبين الدائرة التي يتحرّك عليها مركز الجسم المتكسّف وأنّ الشيء الكاسف للقمر هو الظلّ فحدود كسوف القمر تكون عند القوس التي تمرّ بمركز الظلّ وتكون قائمة على الدائرة المائلة التي يتحرّك عليها مركز القمر والشيء الكاسف للشمس هو القمر فحدود كسوف الشمس تكون عند القوس التي تمرّ بمركز القمر وتكون قائمة على الدائرة التي يتحرّك عليها مركز الشمس وهذا القول يكون صحيحًا لو كانت حركة القمر على دائرته عند كسوف الشمس أبطأ من حركة الشمس. فأمّا حركة القمر أسرع على كلّ حال فإنّ أقصر قوس تقع بين المركزين في وقت الكسوف لا تكون إلّا من الدائرة القائمة على الدائرة المائلة.

الجواب. هذا الشكّ قد بني على مقدّمة باطلة وهو أنّ سرعة حركة القمر تغيّر حدود الكسوف وهذا محال. والجواب أنّ الذي ذكرته الذي شكّ فيه جواب صحيح إلّا أنّه إشارة إلى الحدّ وتلويح لأنّي ظننت أنّ الإشارة مقنعة. وإذ قد شكّ في هذه الإشارة فإنّ أشرح هذا المعنى شرحًا مستقصى وأبيّن بالبرهان الذي لا شكّ فيه أنّ حدّ كسوف الشمس لا يكون إلّا من قوس قائمة على دائرة البروج ولا يصحّ أن يكون من قوس قائمة على دائرة القمر فنقول إنّ حدّ الكسوف هو حدّ

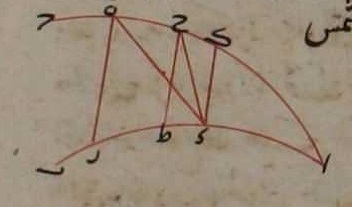
ابتداء الكسوف وابتداء الكسوف هو أن يكون الكاسف والمتكسّف متماسّين وإذا كانا متماسّين فإنّ القوس الذي يصل بين مركزيهما هي التي توترها نصف قطر الكاسف ونصف قطر المتكسّف وحدّ ابتداء الكسوف يتقوّم من قوسين إحدىهما قوس من دائرة الكاسف فيما بين النقطة التي تحدّ ابتداء الكسوف وبين العقدة التي هي نقطة التقاطع بين دائرتي الكاسف والمتكسّف وهذه القوس هي حدّ الكسوف في الطول فحدّ الكسوف في الطول هي أعظم من add. mg. قوس دائرة الكاسف يصحّ أن تقع بين النقطة التي تحدّ ابتداء الكسوف وبين العقدة والقوس الأخرى التي منها يتقوّم أيضًا ابتداء الكسوف القوس التي تصل بين مركزي الكاسف والمتكسّف ويكون وترها مساويًا لنصفي قطري الكاسف والمتكسّف وهذا المعنى أعني حدّ الكسوف وإذ قد تقرّر ذلك فإنّا نقول إنّ حدّ كسوف الشمس في العرض لا يصحّ أن يكون إلّا من قوس قائمة على دائرة البروج ولا يصحّ أن يكون من قوس قائمة على دائرة القمر برهان ذلك أنّا نجعل دائرة البروج اب ودائرة القمر اج ولتكن قوس هد قائمة على دائرة اب ولتكن مساوية للقوس التي توترها نصفًا قطري الشمس والقمر فهي بيّن أنّ مركز القمر إذا كان على نقطة ه وكان مركز الشمس على نقطة د فإنّ الشمس والقمر يكونان متماسّين فقوس هد هي حدّ في العرض لكسوف الشمس وقوس ها هي حدّ في الطول لكسوف الشمس وأيضًا فإنّ قوس اه أعظم من قوس اد لأنّ دائرة اد قائمة على دائرة ده وقوس اد أقلّ من ربع دائرة فالخطّ المستقيم الذي نخرج من نقطة ا إلى نقطة د هو أقصر الخطوط التي تخرج من نقطة ا إلى دائرة ده كما تبيّن ذلك في كتاب الأكر فقوس اه أعظم من قوس اد فنفصل اح مثل اد ونجعل اط مثل اه ونجيز على نقطتي حط قوسًا من دائرة عظيمة فتكون مساوية لقوس ده وتكون قائمة على دائرة اج على زوايا قائمة لأنّ قوس اط مثل قوس اه وقوس اح مثل قوس اد فالخطّ المستقيم الذي نخرج من نقطة ط إلى نقطة ح مساوي للخطّ الذي نخرج من نقطة ه إلى نقطة د فالخطّ المستقيم الذي نخرج من نقطة ط إلى نقطة ح هو أقصر الخطوط التي نخرج من نقطة ط إلى دائرة اج

فقوس طح قائم على دائرة اج وهي مساوية لقوس هد ونجيز على نقطة د قوسًا تكون قائمة على دائرة اج أيضًا ولتكن دك فتكون نقطة ك أقرب إلى نقطة ا من نقطة ح لأنّ قوسي كد حط لا تلتقيان إلّا على قطب دائرة اج وقوس كد حط كلّ واحدة منهما أقلّ من ربع دائرة وتمرّ على نقطة ه أيضًا قوسًا قائمة على دائرة اج ولتكن هز فتكون نقطة ز أبعد عن نقطة ا من نقطة ط فتكون قوس زه أعظم من قوس طح وطح أعظم من قوس دك لأنّ هذه القسي هي ميول قسي زاط ادا فقوس هز أعظم من قوس هد لأنّ هد مثل حط ونجيز أيضًا على نقطتي حد قوسًا من دائرة عظيمة فلأنّ دائرة كد قائمة على دائرة اج وقوس دك أقلّ من ربع دائرة يكون الخطّ الواصل بين نقطتي دك أقصر الخطوط التي تخرج من نقطة د إلى دائرة اج وما قرب منه أقصر ممّا بعد فقوس دح أصغر من قوس ده فقوس هز أعظم من قوس هد وقوس هد أعظم من قوس دح فإذا كان مركز القمر على نقطة ه وكان مركز الشمس على نقطة د كان الشمس والقمر متماسّين. ثمّ إذا تحرّك القمر إلى جهة نقطة ا قصر الخطّ الذي بين مركزه وبين مركز الشمس فحينئذ يكسف الشمس وإذا انتهى القمر إلى نقطة ك كان غاية كسوفه الذي يوجبه جرم القمر ما سوى اختلاف المنظر. ثمّ إذا تجاوز القمر نقطة ك إلى جهة ا كان ابتداء الانجلاء. فقد تبيّن من هذا البيان أنّ قوس هد هي حدّ في العرض لكسوف الشمس وأنّ قوس ها هي حدّ في الطول الكسوف الشمس وأيضًا فإنّه إذا كان مركز القمر على نقطة ه وكان مركز الشمس على نقطة ز فليس يكون القمر مماسًّا للشمس لأنّ قوس هز أعظم من القوس التي توترها نصفًا قطري الشمس والقمر فقوس هز ليس حدًّا في العرض لكسوف الشمس وأيضًا فإنّه إذا كان مركز القمر على نقطة ح وكان مركز الشمس على نقطة ط فإنّ الشمس والقمر يكونان متماسّين. فإذا تحرّك القمر متوجهًا إلى نقطة ا بعدت المسافة بينه وبين الشمس لأنّ الخطّ الذي يصل بين نقطتي ط ح هو أقصر الخطوط التي تخرج من نقطة ط إلى محيط دائرة اج. فإذا جاوز القمر نقطة ح فليس يكسف الشمس وكلّما تحرّك بعد عن

الشمس وكلّ الخطوط الخارجة من نقطة ط إلى قوس حج هي أعظم من الخطّ الذي يصل بين نقطتي طح فإذا تحرّك القمر على دائرة اج ومركز الشمس على نقطة ط فليس يكسف الشمس يوجب من الوجوه فليس قوس حط حدًّا في الطول لكسوف الشمس وأيضًا فإنّ قوس حا أصغر من قوس اه فليس قوس add. mg. حا أعظم قوس تتماسّ عند ط فيها الشمس والقمر لأنّهما قد تتماسّان عند نقطة ه فليس قوس حا حدًّا في الطول لكسوف الشمس وكلّ قوس أعظم من قوس حط فليس تتماسّ عليها الشمس والقمر وكلّ قوس أصغر من قوس حط فليس يكون حدًّا لابتداء الكسوف وليس يقع فيما بين دائرتي اب اج قوس أخرى مساوية لقوس حط وتكون قريبة من نقطة ا فليس يمكن أن يكون حدّ كسوف الشمس مأخوذًا من قوس قائمة على دائرة القمر وقد تبيّن أنّ القوس القائمة على دائرة البروج قد تكون حدّ الكسوف الشمس. فالقوس التي توترها نصفا قطري الشمس والقمر غذا كانت قائمة على دائرة البروج فقد يصحّ أن يكون حدًّا في العرض لابتداء الكسوف وإذا كانت قائمة على دائرة القمر فليس يصحّ أن يكون حدًّا في العرض لابتداء الكسوف وذلك ما أردنا أن نبيّن.

فقد تبيّن من هذا البرهان بيانًا واضحًا أنّ حدّ كسوف الشمس في العرض ال يصحّ أن يكون إلّا من القوس القائمة على دائرة البروج لا غير. فأمّا قوله إنّ ثابتًا Correction mg. ذكر في تعليق الحاشية أنّ هذا على طريق التساهل في بطلميوس فلعلّه إنّما أراد بالتساهل في مقدار هذه القوس أو في شيء آخر غير †ماىىه† هذه القوس لا تجوز أن تكون إلّا قائمة على دائرة البروج. فقد تبيّن بالبرهان أنّه لا يجوز غير ذلك وهذا المعنى

ما بيّنه أحدّ قطّ بالبرهان ولا بيّنه بطلميوس بالبرهان فقد كان هذا المعنى يحتمل التشكّك قبل هذا البرهان. فأمّا بعد هذا البرهان فقد انكسف وسقط كلّ شكّ يعرض فيه ولم استعمل في هذا البرهان شيءًا من التقريب ولا استعملت الخطوط المستقيمة بدل لقسي فهو برهان على غاية التحقيق.

الشكّ الرابع وهو قوله. كان ذكر في الجواب أنّ أبعاد عطارد الصباحية والمسائية لا تكون متساوية أبدًا وأنّ العلّة في ذلك أنّ فلكه المائل غير ثابت الميل لأنّه ينطبق على دائرة البروج تارة وتفارقة أخرى فمركز فلك التدوير لأجل ذلك يكون تارة في سطح دائرة البروج وتارة حارجًا عنه والكوكب أيضًا قد يعرض له ذلك وإن لم يكن مركز فلك التدوير على دائرة البروج لأجل ميل فلك التدوير وانحرافه وإن أقرب ما يكون موضع البعد الأعظم وهو موضع المماسّة من الشمس إذا كان مركز فلك التدوير في سطح دائرة البروج وهذا الجواب يوجب أنّ مركز فلك التدوير إذا كان في موضع واحد بعينه فإنّ أعظم البعدين الصباحي والمسائي متساو وليس يوجد الأمر كذلك لأنّه فد تبيّن في أرصاد كثرة اختلاف البعدين.

الجواب. جميع ما ذكرته في الأبعاد الصباحية والمسائية هو ما ذكرته لا تختلف ولا تتغيّر إلّا أنّه قد بقي معنى واحد لم أذكره لأنّي ما ظننت أنّه يخفى عليه وأنا أذكره لأنّ وهو أنّ أبعد البعد الصباحي عن المسير الوسط الذي هو موضع مركز فلك التدوير هو الزاوية التي يحيط بها الخطّ الخارج من البصر المماسّ لفلك التدوير والخطّ الخارج من البصر إلى مركز فلك التدوير وهذه الزاوية تختلف مقدارها لأنّ مركز فلك التدوير تختلف أبعاده عن البصر من جنبتين أحديهما اختلاف موضهه من فلكه الحامل والثانية اختلاف بعد مركز الفلك الحامل عن البصر يتحرّك الفلك المدير المركز الفلك الحامل هذه هي علّة كلّية لاختلاف مقدار أببعد البعد الصباحي عن المسير الوسط وكذلك حال أبعد البعد المسائي وهذه أيضًا هي علّة لمخالفة البعد

الصباحي للبعد المسائي. وذلك أنّ البعد الصباحي والبعد المسائي ليس يكونان في وقت واحد ولكن يكون البعد الصباحي في وقت ويكون البعد المسائي في وقت آخر ومركز فلك التدوير قد يمكن أن يكون في الوقتين المختلفين في موضعين مختلفين من الفلك الحامل وقد يمكن أن يكون في الوقتين المختلفين في موضع واحد من الفلك الحامل. فإن كان مركز فلك التدوير في الوقتين المختلفين في موضعين مختلفين من الفلك الحامل فالاختلاف بين Correction mg. البعد الصباحي والبعد المسائي قد يمكن أن يكون من الجنبتين اللتين يقدّم مركزهما وإن كان مركز فلك التدوير في الوقتين المختلفين في موضع واحد من الفلك الحامل أو في موضعين متشابهين منه فقد يمكن أن يكون الاختلاف من جهة الفلك التدوير وأن كان مركز فلك التدوير في الوبتين وضعه من الفلك الحامل وضع واحد ووضعه من الفلك المدير أيضًا وضع واحد فليس يخالف البعد المسائي البعد الصباحي إلّا للأسباب الجزئية التي تقدّم ذكرها في الجواب الأوّل. أن كان تلك توجب في ذلك الوقت اختلافًا فقد ثبتت العلّة في اختلاف الأبعاد الصباحية والأبعاد المسائية وفي مخالفة الأبعاد الصباحية للأبعاد المسائية. فأمّا حركة ميل فلكي الزهرة وعطارد الحركتين المتضادّتين فقد ذكر بطلميوس العلّة التي من أجلها جعلهما متحرّكين حركتين متضادّتين. فأمّا ]لم[ لم تجعل حركتهما على دوائر صغار كما جعله في فلك التدوير فإن كان ذلك لأنّه لو تحرّك الفلك المائل على دائرة صغيرة لتغيّر موضع مركز فلك التدوير الذي هي موضع الحركة الوسطى من دائرة البروج لأنّ حركة البعد الأبعد على الدائرة الضغيرة بميل البعد الأبعد وكلّ نقطة على محيط الفلك الحامل تارة إلى المشرق وتارة إلى المغرب. فأمّا لم استجاز أن نجعل للفلك المائل حركتين متضادّتين فهو كما استجاز أن جعل في السماء حركتين متضادّتين أحديهما من المشرق إلى المغرب والأخرى

من المغرب إلى المشرق وجميع الأجرام السماوية من جوهر واحد بسيط وطبيعة واحدة والجوهر الواحد البسيط لا يجوز أن يكون له حركتان متضادّان ولحركة الفلك المائل لكوكبي عطارد والزهرة †ىطائر† في الحركات السماوية وهي حركة قطر فلك تدوير القمر إلى مسامتة نقطة المحاذاة. فأنّ هذا القطر يتحرّك حركتين متضادّتين وليس يتحرّك القطر المتوهّم إلّا بجسم حركة وكذلك أقطار أفلاك تداوير الكواكب الخمسة تتحرّك إلى مسامتة مركز معدّل المسير حركتين متضادّتين. فأن كان ذلك ممكن في أقطار أفلاك التداوير فبيس بممتنع أن يكون في فلكي الزهرة وعطارد المائلين. وأنا أري أنّ كوكبي الزهرة وعطارد ليس دائرتاهما اللتيان يتحرّك عليهما مركز أفلكي تدويرهما عظيمتين بل صغيرتين أحدهما أقرب إلى الشمال وهي دائرة الزهرة والآخر أقرب إلى الجنوب وهي دائرة عطارد. وكذلك توجد الزهرة في أبعد بعدها وفي أقرب قربها أبدًا في جهة الشمال ويوجد عطارد في أبعد بعده وفي أقرب قربه أبدًا في جهة الجنوب. ثمّ الأعراض الباقية التي تعرض في عروضها تمكن أن تعرض لها دوائر وأفلاك تحرّكها حركات توجب لها تلك الأعراض بدل ما فرض لفلكي تدويرهما. وإذا كانت هاتان الدائرتان صغيرتين سقطت الحركتان المتضادّتان واساغنى عنها ونقص أيضًا من جملة الحركات حركتين وهي حركة الفلكين المائلين Correction mg.. فهذا الذي ذكرته هو جواب ما تشكّك فيه.

جواب شكّ في اختلاف منظر القمر من شكوك أبي القاسم بن معدان. وقفت على ما أنبيه مولاي الشيخ أنار الله برهانه في اختلاف منظر القمر وعلى شكّ الذي في آخر الكلام وهو موضع شكّ إلّا أنّ بطلميوس قصد في متلافات منظر القمر الجزئية التقريب دون التحقيق. وكذلك جميع ما دكره بطلميوس في المجسطي من الأعمال الجزئية اعتمد فيه التقريب. وأوّل ذلك الأوتار فإنّه زيّد القسي بنصف جزء نصف جزء وستخرج أوتارها ثمّ في الأوتار التي تزيد بالدقائق زيدها بالتساوي وليست

زياداتها متساوية وإنّما قصد فيها التقريب لتسهيل العمل وكذلك فعل في جزئيات اختلاف المنظر إنّما قصد فيها التقريب لتسهيل العمل في تقويم اختلاف منظر القمر. ولو اعتمد التحقيق في جزئيات اختلاف المنظر لكان يحتاج أن يستخرج زوايا اختلاف المنظر عند كلّ جزء من أجزاء فلك التدوير التي بين الحدّ الأوّل وبين الحدّ الثاني وهي مائة وثلاثون جزءًا ويكون ذلك ومركز فلك التدوير عند البعد الأبعد من الفلك الخارج المركز. ثمّ يستخرج الزوايا عند كلّ واحد من أجزاء فلك التدوير عند كون مركز فلك التدوير عند جزء جزء من أجزاء الفلك الخارج المركز وهي مائة وثمانون جزءًا فكان يكون مجموع الزوايا هو ما يجتمع من ضرب مائة وثمانين في مائة وثماينين add. mg. وهو اثنين وثلاثين ألفًا وأربعمائة ويكون جميع هذه الزوايا هي زوايا اختلاف المنظر عند جزء واحد بعينه من أجزاء ربع للدائرة السمتيّة فيحتاج أن يستخرج ميل جميع هذه الزوايا عند جزء جزء من أجزاء ربع الدائرة السمتيّة التي هي تسعون جزءًا فيكون جميع الزوايا التي يحتاج أن يستخرجها هي اثنين وثلاثين ألفًا وأربعمائة مضروبة في تسعين فيجتمع من ذلك ألف ألف وتسع مائة ألف وستّة عشر ألف زاوية فيحتاج لذلك إلى جداول تشتمل على ألفي ألف سطر وتسع مائة ألف سطر وستّة عشر ألف سطرًا. ولو تمّ له ذلك لكان لا ينظر أحد في كتاب المجسطي ولا يقوّم أحد اختلاف منظر القمر لأنّه لا يمكنه أن يستقري جميع تلك السطور ومع ذلك لو همّ بطلميوس باستخراج ذلك لكان يعني عمره قبل أن يستوفي عمل جميع هذه الزوايا. فاعتمد بطلميوس التقريب في اختلاف المنظر الجزئية لصعوبة الطريق إلى تحقيقها ولصغر قدر التفاوت بين التقريب والتحقيق في الجزئيات ومع جميع ذلك فإنّ بطلميوس لم يحرف في التقريب الذي اعتمده في الجزئيات بل اعتمد على مقدّمة اقناعية وهو علّة اختلاف منظر القمر التي هي العلّة الأولى وذلك أنّ علّة اختلاف منظر القمر إنّما هي قرب القمر

من الأرض وكلّما قرب من الأرض زاد اختلاف منظره وكلّما بعد نقص اختلاف منظره فزيادة قربه من الأرض ونقصان قربه منها هي العلّة الأولى في زيادات اختلاف منظره نقصانها وهي العلّة الذاتية الكلّية. وإن لم تكن نسب الأبعاد بعضها إلى بعض هي نسب الزوايا بعضها إلى بعض إلّا أن تغيّر مقدار البعد تغيّر مقدار الزاوية وتغيّر البعد الذي هي تغيّر زيادة توجب نقصان الزاوية وتغيّر البعد الذي هي نقصان يوجب زيادة الزاوية. وهذا المعنى يطرد في أبعاد القمر فهو العلّة الأولى في زيادات الزوايا ونقصانها فجعل بطلميوس العلّة الأولى في اختلاف الزوايا هي العلّة القريبة التي توجب مقادير الزوايا على مقادير الأبعاد على علم منه بأنّه قياس اقناعي لا قياس برهاني وأنّه مع ذلك قياس نتيجته قريبة من التحقيق وليس بينها وبين التحقيق تفاوت مسير ف. وهذا القول هو غاية ما يمكن أن يعتذر به لبطلميوس في استعماله التقريب في جزئيات اختلاف منظر القمر دون التحقيق وذلك ما أردنا أن نبيّن.

تمّت الشكوك في المجسطي وحلّها والحمد لله ربّ العالمين والصلوة على رسوله محمّد وآله أجمعين.