〈Praefatio translatoris〉

St〈ephanus〉 Gracilis Io〈anni〉 Magnenio medico longe praestantissimo et mathematicae scientiae regio apud Lutetiam professori salutem dat.

Magna certe tua laus est, Magneni doctissime, qui summum semper studium cum in omnibus bonarum rerum disciplinis, tum in scriptis veterum mathematicorum illustrandis collocasti. Nam, ut superiores annos taceam, quibus tu de tua industria et docendi constantia nihil unquam remisisti, postquam e vita cessit Orontius Finaeus, cuius ne posteritas quidem omnium seculorum immemor erit, tuque in eius locum suffectus, in augustissimum regiae professionis collegium summa cum gratulatione huius academiae et laetitia cooptatus es, omnem tuum laborem, diligentiam, operam ad magnam Ptolemaei Syntaxin, magnum opus omnino et arduum, contulisti. Quam facili, sed erudita interpretatione dum palam explicare cogitas, idque unum studes, ut quam plurimorum commodis rationibusque servias, primum totius operis librum ab Erasmo Reinholto latine redditum (non enim graece sciunt omnes) aggressus, multa in eo interprete sane quam doctissimo iure desiderasti, quae Ptolemaei verba animique sensa exprimerent. Sed quum ista emendandae aliorum interpretationis et invidia vacare et molestia defungi velles, frequenti horatatione mecum egisti, ut perspecto etiam atque etiam altero eius commentationis libro, quem tu diligenter enodatum propediem exponeres, Latinam Georgi Trapezuntii interpretationem (nam primum duntaxat librum Erasmus Latinum fecit) cum Graecis Ptolemaei scriptis studiose conferrem, et, si quid vel praetermissum, vel non satis expressum, vel perperam (pace tanti viri dixerim) redditum videretur, adscriptis e regione Graecis Ptolemaei ipsius verbis, admonerem. Ad ea siquidem, quae obscurius prodidit, eruenda, magno id quam plurimis usui fore. Ego vero cum tuae voluntati morem gerendum statuerem, neque recusandum quominus in eo me curriculo, quod mihi circunscriptum velles, exercerem, fide subsidioque tuo fretus plus oneris sustuli, quam ferre me posse intelligerem. Proinde istud conanti multa ante oculos obversabantur, quae laborem alio transferendum mihi suaderent, onere deposito. Nam ut alia omittam, quae me ab instituto dehortabantur, tam multiplices variique errores inspicientibus nobis omnique acie ingenii contemplantibus ostendebant se et occurrebant, ut restituendae et corrigendae editionis tam depravatae nulla spes esse, eaque ratione cogitabam adductum, cuius paulo ante mentionem feci, Reinholtum primum operis librum latine de integro vertisse, ut suo scilicet exemplo, id in aliis libris tentarent caeteri, quod ipse in primo perfecisset, neque praeiudicata cuiusquam industria quenquam ab opere deterreret. Hic mihi quisquam: ‘Tune Georgium Trapezuntium et Graecum hominem et philosophum percelebrem ἀμαθίας insimulare audes?’ Equidem Georgium omni laude ingenii clarissimum fuisse agnosco, quemque disputationis huius insolentia, atque harum rerum inscitia, tam saepe lapsum mihi religio sit dicere, nedum alienae culpae reum facere. Ita non suo hominis praestantissimi vitio, sed partim inveterata librariorum incuria, partim densissima rerum mathematicarum caligine, quicquid id est erroris creatum arbitror, et Georgium a culpa libenter eximo. Huius ergo interpretationis passim mendosae, tu iam olim optime tibi conscius, Magneni, de molesto et inviso forte nonnullis labore, quem in restituendis nostra sententia locis consumerem, querenti apud te mihi, novi ipse consilii suasor et autor esse coepisti. Hortatus es scilicet, ut praetermissa aliorum interpretatione, hunc librum qua possem fide et accuratione latinitate donarem, eiusque rei perspiciendae studio ita me incendisti, ut relictis aliquantisper negotiis, intentum ad id muneris animum sempe habuerim. Tuae ergo petitioni nunc demum parui, quod certe vix facturus eram, si per gravissima medicinae, quam multos iam annos Lutetiae foeliciter exerces, officia, quae te respirare vix sinunt, aliquid relinqui temporis vacui, quod huic studio dares, cognovissem. Sed quid non extorqueat tam propensa in rempublicam literariam hominis de nobis optime meriti voluntas? Caeterum quum multa in hoc praesertim scientiarum genere incidant, quae apte et commode latine dici nequeunt, coactus sum equidem Graeca interdum nomina usurpare, ubi propria Latinos deficiunt, interdum circuitione, verborum et orationis anfractu ea dilucidius exponere, quae vel unico vel paucioribus Graeci nominibus significant. Quinetiam trita quaedam in scholis nomina nonnunquam mutanda censui, ut cum inclinatam sphaeram verti, quae obliqua vulgo nominatur. Sic enim melius et ad explicandam rei naturam aptius dici posse existimavi Graeci sermonis imitatione et geometrarum more, qui inclinationem plani, ἐγκεκλιμένη σφαῖρα ἐπιπέδου κλίσις Euclidis lib. 11 Elemento i. m. P unde ducta videtur sphaere inclinatio, non raro appellare solent. Quos si quibus forte locis non plane consentire cum Graecis codicibus, qui sunt in manibus omnium, nostra videbitur interpretatio, id Graeco exemplari, quod ex regia tibi bibliotheca de promptum nobis libenter impertitus es, adscribendum scito ut tute legens cognosces. Habes igitur qualequnque nostri laboris pensum, ut, cum ad exquisitam sapientiae trutinam singula revocaris, de re tota arbitratu iudicioque tuo statuas. Vale. Lutetiae, idibus Aprilis 1556.

Argumentum huius libri in sua capita distinctum

〈1〉 De universo situ terrae quae a nobis incolitur

〈2〉 Quomodo, data maximi diei magnitudine, dantur horizontis peripheriae aequinoctiali

et obliquo circulo comprehensae

〈3〉 Quomodo, iisdem suppositis, datur poli elevatio et contra

〈4〉 Quemadmodum ratiocinari deceat quibus, et quando, et quoties Sol in vertice consistat

〈5〉 Quemadmodum ex iis quae exposita sunt gnomonum rationes ad aequinoctiales et solstitiales meridianis temporibus umbras deprehendantur

〈6〉 Expositio proprietatum, quae singulis conveniunt parallelis

〈7〉 De communibus zodiaci et aequinoctialis circuli in sphaera inclinata ascensionibus

〈8〉 Tabellae quibus exponuntur per decadas in qualibet inclinatione ascensiones

〈9〉 De iis quae ascensiones particulatim consequuntur

〈10〉 De angulis qui a zodiaco et meridiano fiunt circulo

〈11〉 De angulis qui ab eodem obliquo circulo et horizonte fiunt

〈12〉 De angulis et peripheriis quae cum eodem circulo ab eo fiunt qui per horizontis polos describitur

〈13〉 Expositio praedictorum angulorum et peripheriarum in singulis climatibus

〈II〉 Claudii Ptolemaei Mathematicae constructionis liber secundus

〈II.1〉 CAPUT 1: De universo situ terrae quae a nobis incolitur

His primo constructionis huius libro expositis, quae de universi habitudine summatim anticipanda erant et quae ad rectam cum pertineant sphaeram rerum propositarum contemplationi utilia videbantur, dabimus operam ut quae inclinatae conveniunt sphaerae eorum rursus potissima quaeque quam facillima poterit ratione hoc libro deinceps explicemus. Atque hic quidem illud omnino primum sumere decet, terra ab aequinoctiali et altero, qui per aequinoctialis polos describitur, circulo in quatuor divisa partes, magnitudinem eius quam nos habitamus altera septentrionum parte fere contineri. Id vero in latitudine quidem, hoc est progressu a meridie in boream, ex eo maxime perspici potest, quod meridianae gnomonum umbrae aequinoctialibus ubique diebus ad septentriones semper vergunt, numquam ad meridiem, in longitudine vero, id est ab ortu ad occasum transitu, quod, quoties eaedem eclipses in primisque lunares eodem ab iis conspiciuntur tempore, qui extremas in nostra aquilonari orbis parte, tum ad orientem, tum ad occidentem terras colunt, non maior reperitur nec minor quam duodecim horarum aequinoctialium differentia, notato apud utrosque defectionis tempore. μὴ πλέον δώδεκα προτερεῖν ἢ ὑστρεῖν ὡρῶν ἰσημερινῶν i. m. P Nam ipsa quae in longitudinem patet quarta terrae pars, quoniam uno aequinoctialis definitur semicirculo, duodecim horarum intervallum continet. Verum Propositio huius libri i. m. P ex iis quae particulatim inspicienda sunt ad hanc tractationem in primis pertinere videntur praecipuae proprietates quae per singulos aequinoctiali circulo parallelos ad boream declinantes subiectis accidunt habitationibus. Eius generis sunt haec: quantum primae lationis poli ab horizonte distent, aut quantum ab aequatore in meridiano circulo absit verticis punctum, quibus, quando, et quoties Sol in vertice consistat, quae sint meridiano tempore rationes aequinoctialium et solstitialium ad gnomonas umbrarum, quantique sint maximorum aut minimorum dierum, si cum aequinoctialibus conferantur, excessus, caeteraque omnia quae circa accretiones et diminutiones dierum atque noctium, ἀυξομειώσις τῶν νυχθημέρων συνανατολὰς καὶ συγκαταδύσεις i. m. P ad haec circa communes ortus et occasus aequinoctialis et obliqui circuli, quaeque circa proprietates et magnitudines angulorum qui a praecipuis maximisque fiunt circulis particulatim accidere, conspiciuntur.

〈II.2〉 CAPUT 2: Quo modo, data maximi diei magnitudine, dantur horizontis peripheriae aequinoctiali et obliquo circulo interceptae

Proponatur itaque generaliter descriptus verbi causa per Rhodum circulus aequinoctiali parallelus, ubi elevatio quidem poli partium est 36, dies vero maximus aequinoctialium horarum 14 scrupulo 30, 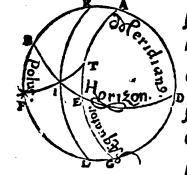sitque meridianus quidem circulus ABGD, horizontis autem orientalis semicirculus BED, et item aequinoctialis semicirculus AEG, cuius australis polus F, et concedatur hybernum solstitiale punctum eius circuli qui per medium signorum est oriri per punctum I, et per puncta F, I describatur FIT maximi circuli quadrans, sed data prius maximi diei magnitudine, proponaturque EI inveniendus horizontis arcus. Cum igitur sphaerae conversio circa aequinoctialis perspiciatur ἀποτελεῖται i. m. P polos, manifestum est I et T puncta eodem tempore in ABGD meridiano fore, tempusque ab ortu I puncti ad coeli, quod supra terram eminet, medium, aequinoctialis circuli arcu TA definiri, tempus vero a coeli, quod sub terra latet, medio, ad ortum, arcu GT contineri. Consequens est autem, ut diei quidem tempus duplum sit eius quod arcu TA, noctis vero tempus duplum sit eius quod GT arcu comprehenditur, quandoquidem omnium circulorum a〈e〉quinoctiali Aquinoctiali i. m. P parallelorum segmenta, et quae super terram extant, et quae sub terra latent, a meridiano in partes aequales seorsim dividuntur, ob eamque causam ET arcus, cum differentiae minimi aut maximi diei ad aequinoctialem sit dimidium, in proposito parallelo unius quidem est horae cum quadrante, temporum vero 18 45′, reliquus autem quadrantis circuli arcus TA, eorundem temporum 71 15′. Quoniam igitur ex iis quae supra demonstrata sunt in duobus maximorum circulorum arcubus AE, et AF, duo descripti sunt EB, FT, se vicissim secantes in puncto I, ratio subtensae dupli arcus TA ad subtensam dupli arcus AE composita est ex ratione subtensae dupli arcus TF ad subtensam dupli arcus FI et ratione subtensae dupli arcus IB ad subtensam dupli arcus BE. Atqui duplum arcus TA partium est 142 30′, eique subtensa recta partium 113 37′ 54′′, duplum vero AE arcus partium 180, eique subtensa recta partium 120, rursusque duplum arcus TF partium 180, eique subtensa recta partium 120, duplum vero FI partium 132 17′ 20′′, eique subtensa recta partium 109 44′ 53′′. Si igitur a ratione 113 37′ 54′′ ad 120 subducamus rationem 120 ad 109 44′ 53′′, relinquetur nobis ratio subtensae dupli arcus IB ad subtensam dupli BE partium 103 55′ 26′′ ad 120. Est autem subtensa dupli arcus BE (cum BE sit circuli quadrans) partium 120, unde subtensa dupli arcus IB earundem est partium 103 55′ 26′′. Quamobrem duplum BI peripheriae partium erit 120 proxime, ipsa vero BI peripheria earundem partium 60. Reliqua igitur IE talium restat 30 partium, qualium horizon 360. Quod erat demonstrandum.

〈II.3〉 CAPUT 3: Quomodo iisdem suppositis, datur poli elevatio, et contra.

Hoc autem dato, proponatur rursus exquirenda poli altitudo, hoc est BF meridiani peripheria. Est igitur in eadem descriptione ratio subtensae dupli arcus ET ad subtensam dupli arcus TA composita et ex ratione subtensae dupli arcus EI ad subtensam dupli arcus IB et ratione subtensae dupli arcus BF ad subtensam dupli arcus FA. Sed duplum quidem arcus ET partium est 7 30′, quaeque ei subtenditur recta partium 38 34′ 22′′, duplum vero arcus TA partium est 142 30′, quaeque ei subtenditur recta partium 113 37′ 54′′, ac rursus duplum arcus EI partium est 60, quaeque ei subtenditur recta partium 60, duplum vero arcus IB partium est 120, quaeque ei subtenditur recta partium 103 55′ 23′′. Si igitur a ratione 38 34′ 22′′ ad 113 37′ 54′′ subtrahamus rationem 60 ad 103 55′ 23′′, relinquetur ratio subtensae dupli BF ad subtensam dupli FA, 70 33′ proxime ad 120. Atque rursus est subtensa dupli arcus FA partium 120. Quare subtensa dupli arcus BF earundem erit partium 70 33′. Itaque duplum arcus BF erit partium 72 1′, ipse autem BF arcus earundem partium 36 proxime. Rursus in eadem descriptione e converso Aνάπαλιν i. m. P BF quidem arcus elevationis poli detur, quae observata sit partium 36. Sit autem nobis invenienda differentia minimi aut maximi diei ab aequinoctiali, hoc est duplum arcus ET. Est igitur ob easdem causas ratio subtensae dupli arcus FB ad subtensam dupli arcus BA composita et ex ratione subtensae dupli arcus FI ad subtensam dupli arcus IT et ex ratione subtensae dupli arcus TE ad subtensam dupli arcus EA. Sed duplum quidem arcus FB partium est 72, eique subtensa 70 32′ 3′′. Duplum vero arcus BA partium est 108, eique subtensa partium 97 4′ 56′′. Atque rursus duplum quidem arcus FI partium est 132 17′ 20′′, eique subtensa partium 109 44′ 53′′, duplum vero arcus IT partium 47 42′ 40′′, eique subtensa partium 48 31′ 55′′. Si igitur a ratione partium 70 32′ 3′′ ad 97 4′ 56′′ subducamus rationem 109 44′ 53′′ ad 48 31′ 55′′, relinquetur nobis ratio subtensae dupli arcus TE ad subtensam dupli arcus EA, partium 31 11′ 23′′ ad 97 4′ 56′′, quumque eadem fere ratio sit 38 34′ ad 120, subtensa vero dupli arcus EA partium sit 120, concluditur subtensam quoque dupli arcus ET earundem esse partium 38 34′. Quare duplum etiam arcus ET partium quidem erit 37 30′ proxime, horarum autem aequinoctialium 2 cum semisse. Quod erat demonstrandum. Ex eisdem vero causis dabitur etiam EI horizontis peripheria De invenienda rursus horizontis peripheria, quam latitudinem ortus eclipticae vocant i. m. P. Nam et data ratio subtensae dupli arcus FA ad subtensam dupli arcus AB composita est ex ratione subtensae dupli arcus ET ad subtensam dupli arcus TI, quae et ipsa data est et ratione subtensae dupli arcus IE ad subtensam dupli arcus EB, ita ut, cum data sit EB, relinquatur etiam ipsius EI magnitudo. Perspicuum est autem, De aliis zodiaci segmentis i. m. P etiam si hybernae conversionis punctum I non sumas, sed aliam quamlibet circuli portionem, iisdem rationibus datum etiam iri utramque ET, et EI peripheriam. Iam enim per obliquationis tabellam expositae sunt nobis meridiani peripheriae quae a singulis eius circuli qui per medium signorum est partibus et circulo aequinoctiali intercipiuntur, hoc est quae arcui IT sunt similes. Unde etiam consequetur ut partes zodiaci quae ab iisdem designantur parallelis, hoc est quae aequaliter distant ab eodem tropico puncto, easdem horizontis sectiones et ad easdem aequatoris partes, noctium item et dierum similium magnitudines utrasque utrisque aequales efficiant. Huc accedit quod eae quoque zodiaci portiones quae ab aequalibus fiunt parallelis, hoc est quae aequaliter ab aequinoctiali absunt puncto, non modo horizontis peripherias aequales ex utraque aequinoctialis parte definire demonstrantur, sed etiam noctium dierumque dissimilium aequales ἐναλλὰξ magnitudines facere. Si enim in proposita descriptione, supposito ipso quoque C puncto quo aequalis et parallelus descripto per I circulo secat BED horizontis semicirculum, compleamus IL et CM parallelorum segmenta, quae videlicet ἐναλλαξ se habent et invicem aequalia sunt, ac per C et aquilonarem polum quadrantem NCX describamus, aequalis quidem erit TA peripheria peripheriae XG, quod utraque utrique ipsarum LI et MC sit similis. Erit autem etiam ET reliqua reliquae EX aequalis, fientque duorum quoque trilaterorum similium EIT et ECX duo quidem latera duobus aequalia, ET quidem ipsi EX, IT vero ipsi CX. 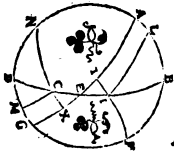Atqui angulorum qui ad T et X, uterque rectus est. Quare basis EI basi CE est aequalis.

〈II.4〉 CAPUT 4: Quemadmodum ratiocinari deceat quibus, et quando, et quoties Sol in verticis puncto consistit

His autem constitutis, facile est ratiocinatione complecti quibus, quando, et quoties Sol in vertice consistat. Cum enim per se sit manifestum nunquam ad eorum verticem Solem pervenire, qui sub parallelis habitant amplius ab aequatore distantibus spatio 23 51′ 20′′ proxime (quanta est solstitialis puncti integra declinatio), semel autem aestivo nimirum solstitio verticem eorum attingere, qui sub parallelis hoc ipso distantibus intervallo versantur, απόστασις i. m. P atque bis in eorum vertice consistere, qui sub parallelis agunt minore quam propositarum partium numero disiunctis, ex obliquationis certe tabella, quo id tempore fiat, facile intelligi potest. Nam totidem in secunda tabulae pagella inventis partibus, quot ab aequinoctiali distat oblatus quivis parallelus inter aestivum tropicum et aequatorem situs, adiacentes ipsis in prima tabulae columna, ex quadrante zodiaci partes habebimus, quibus ab utroque aequinoctialium punctorum ad aestivum tropicum Sol remotus in eorum vertice consistit, qui sub illo habitant parallelo.

〈II.5〉 CAPUT 5: Quemadmodum ex iis quae explicata sunt gnomonum rationes ad aequinoctiales et solstitiales meridianis temporibus umbras deprehendantur

Quod vero, semel datis arcubus qui partim inter tropicos, partim inter horizontem et polos comprehenduntur, propositae ad gnomonas umbrarum rationes planius cognoscantur, ad hunc sane modum perspicuum erit. Sit enim meridianus circulus ABGD circa centrum E, et posito verticis puncto A, protrahatur diameter AEG, cui ad rectos angulos in meridiani plano ducatur linea GCFN, communi scilicet horizontis cum meridiano sectioni parallela. Atque quoniam puncti centrique rationem, si sensum consulas, tota terra obtinet cum Solis orbe collata, ut inter centrum E et gnomonis apicem nihil sit discriminis, intelligatur gnomo quidem GE, linea vero GCFN recta, in quam meridianis temporibus umbrarum extrema cadant, et per punctum E ducantur radii quos in aequinoctio et tropicis punctis Sol meridie fundit, sitque aequinoctialis quidem radius BEDF, aestivus vero IETC, hybernus autem LEMN, ut GC quidem aestiva sit umbra, GF aequinoctialis, brumalis vero GN. 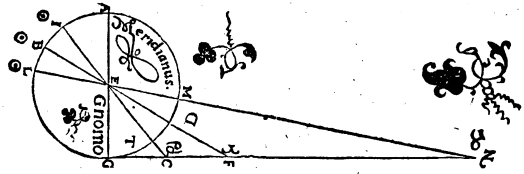Cum igitur GD peripheria, cui aequalis est ea, qua in proposito climate polus aquilonaris super horizontem attollitur, talium sit 36 partium, qualium ABG meridianus 360, utraque autem TD et DM earundem 23 51′ 20′′, patet reliquam quoque GT peripheriam partium fore 12 8′ 40′′, totam vero GM peripheriam earundem 59 51′ 20′′. Quamobrem ex angulis etiam qui sub illis comprehenduntur, qualium quatuor recti sunt 360 partium, talium sub CEG quidem angulus est 12 8′ 40′′, qui vero sub FEG earundem 36, et qui sub NEG similiter 59 51′ 20′′, qualium autem duo recti sunt 360, talium sub CEG quidem angulus 24 17′ 20′′, qui autem sub FEG, earundem est 72, et qui sub NEG similiter 119 42′ 40′′, et descriptis igitur circulis circa CEG, FEG et NEG triangulos orthogonios, peripheria quidem super GC rectam, partium est 24 17′ 20′′, et quae super linea GE reliqua semicirculi peripheria earundem est 155 42′ 40′′, quae vero super GF rectam partium 72, et quae super GE earundem similiter partium est 108, quae vero super GN rectam, partium est 119 42′ 40′′, et quae super GE earum est rursus quae ad semicirculum complendum supersunt partium 60 17′ 20′′. Quare et subtensarum ipsis rectarum linea GE talium concluditur 117 18′ 51′′, qualium GC est 25 14′ 43′′, qualium autem GF rursus est 70 32′ 4′′, talium 97 4′ 56′′, et qualium GN similiter 103 46′ 16′′, talium 60 15′ 42′′. Qualium igitur gnomo GE partium est 60, talium et GC quidem aestiva umbra colligetur 12 55′, GF vero aequinoctialis 43 36′, atque GN brumalis 103 20′ proxime. Hinc vero compertum est quod et vice versa, Ἀνάπαλiν i. m. P si duae tantum ex tribus propositis qualescumque ipsius GE gnomonis ad umbras datae sint rationes, datur et poli elevatio et comprehensa inter tropicos peripheria. Nam duobus qui ad E angulis quibuslibet datis, datur et reliquus, cum aequales sint TD et DM peripheriae, quanquam, quod ad exactas observationes attinet, illa quidem citra dubitationem eo quem praescripsimus modo explicari possunt, sed memoratarum ad gnomonas umbrarum rationes non item, propterea quod aequinoctialium quidem tempus per se quodammodo indefinitum est, brumalium vero extremitates aegre distingui possunt.

〈II.6〉 CAPUT 6: Expositio proprietatum quae singulis conveniunt parallelis

Eadem sane, quam in illis demonstrandis secuti sumus, ratione in caeteris quoque parallelis universas, quae traditae sunt, complexi proprietates, quarta horae unius aequinoctialis parte (quod satis esse videtur) adaucto inclinationum excessu, eas nos generatim exponemus, priusquam ad alias quae particulatim conveniunt accedamus ab eo qui aequinoctiali subest exorsi parallelo. Is meridianam plagam a quarta, quam nos fere totam habitamus, orbis parte distinguit, solusque dies omnes cum noctibus exequat. Nam eo tantum loco omnes, qui in sphaera sunt, paralleli in aequales duas portiones ab horizonte secantur, ut quae super terram extant ipsorum segmenta et inter se similia et iis quae sub terra latent singula singulis sint aequalia, quod in nulla cernitur inclinatione, sed solus quidem aequinoctialis rursus ab horizonte, qui et ipse in maximis est circulis, aequaliter ubique in duo divisus, aequales, si sensus iudicium adhibeas, suos noctibus dies facit. Reliqui vero cum inaequaliter dividantur, et secundum nostri orbis inclinationem, partim magis australes, partim sint magis aquilonares, illi quidem et minores super terram sectiones et breviores noctibus dies, hi vero maiores contra super terram sectiones et longiores diebus noctes efficiunt. Est autem et amphiscius hic parallelus. Amphiscii Paralleli 6 quorum hic primus est i. m. P Sol enim, quibus locis aequinoctialis obliquusque circulus se invicem secant, hominum in subiecta regione habitantium vertici bis recta imminet, ut tunc solum nullae meridiano tempore gnomonum sint umbrae, cumque per aquilonarem semicirculum fertur, umbras ad austrum, cum vero per australem, eas ad aquilonem mittat. Atque hic, qualium gnomo est partium 60, talium utraque tum aestiva tum brumalis umbra partium est 26, 30 proxime. Umbras autem eas in universum dicimus, quae meridie fiunt, quasi nulla re memorabili ab aequinoctialibus et solstitialibus differentes, siquidem meridianis ipsis temporibus aequinoctia et solstitia non omnino perficiuntur. διὰ τὸ μὴ πάντως ἀποπελεῖσθαι i. m. P Quaecunque autem astra in ipso convertuntur aequinoctiali circulo, ad verticem perveniunt subiectarum aequinoctiali regionum, omniaque et oriri et occidere conspiciuntur, cum sphaerae poli in ipso sint horizonte, nullumque describant circulum, nec parallelum semper conspicuum, semperve latentem, nec meridianum colurum. κόλουρον i. m. P Caeterum habitabilem esse sub aequinoctiali regionem, ut quae valde temperata sit, ferunt. Solem enim ob celerem circa aequinoctiales sectiones in latitudinem discessum, nec verticis diu insistere punctis, unde temperata sequatur aestas, nec brumis solstitiisque multum a vertice distare, ut rigidam et asperam minime reddat hyemem. Sed quaenam istae sint habitationes certo affirmare et pronunciare non possumus. Nam in hunc diem nostri orbis homines ad eas sedes minime penetrarunt, ut quae de ipsis narrantur coniecturae similia magis quam historiae videantur. Hactenus proprietates paralleli qui aequinoctiali subest breviter exposuimus. De reliquis autem quibus etiam habitationes quidam cir〈cum〉scribi cirumcscribi P putant illa in commune adiiciemus, quae alioquin in singulis iterum atque iterum repetenda essent: quod quaecumque stellae pari, qua propositus quivis parallelus, peripheria circuli per aequinoctialis polos ducti ab aequinoctiali distant, in singulorum qui sub eo habitant parallelo vertice deinceps consistunt, quodque descriptus aquilonari quidem aequinoctialis polo, elevationis autem poli intervallo circulus cum iis, quas complectitur, stellis perpetuo cernitur, contra vero nunquam sub aspectum venit descriptus australi polo, eodemque elevationis poli intervallo circulus, necnon quicquid stellarum suo concludit ambitu, semper occultum latet.

Alter est parallelus, Amphis. 2 i. m. P in quo maximus dies horarum aequinoctialiu est 12 15′, hic ab aequinoctiali abest partibus 4 15′, et per Taprobanen insulam describitur. Est autem hic quoque amphiscius. Sol enim rursus in subiectae regionis vertice bis consistit, et gnomonibus meridiano tempore umbram adimit, cum a solstitio aestivo utrinque distat partibus 79 30′. Ita dum per 159 hasce partes commeat, gnomonum umbrae ad austrum declinant, dum vero per reliquas 201 partes, ad boream. Atque hic, qualium gnomo est partium 60, talium aequinoctialis quidem umbra 4 25′, aestiva vero 21 20′, brumalis 32.

Tertius est parallelus, Amphis. 3 i. m. P ubi dies maximus horarum est aequinoctialium 12 cum semisse. Hic autem ab aequatore distat partibus 8 25′, et per Aualitum describitur sinum, estque ex amphisciorum numero, cum Sol subiectae regionis verticem bis teneat, et gnomonas meridianis

temporibus umbra spoliet, quoties ab aestivo solstitio utrinque distat partibus 69, ita quandiu per has 138 partes commeat, gnomonum umbrae ad meridiem tendunt, cum vero per reliquas 22 2′ ad septentriones. Atque hoc quidem loco, qualium gnomo partium est 60, talium aequinoctialis quidem umbras 8 50′, aestiva autem 16 50′, brumalis vero 37 54′.

Quartus est parallelus, Amphis. 4 i. m. P ubi dies maximus horis aequinoctialibus constat 12 45′. Hic ab aequatore distat partibus 12 30′, et per Aduliticum sinum describitur, ac inter amphiscios numeratur, quandoquidem sub eo degentibus Sol in vertice bis consistit, atque in meridiani traiectione gnomonibus umbras adimit, quoties ab aestiva conversione utrinque abest partibus

57 50′, ita ut, quandiu istas 115 partes 40′ conficit, gnomonum umbrae ad austrum declinent, dum vero reliquas 244 20′, ad boream. Atque in hoc situ, qualium est gnomo 60 partium, talium aequinoctialis quidem umbra 13 20′, aestiva autem 12, hyberna vero 44 30′.

Quintus parallelus Amphis. 5 i. m. P diem habet maximum horarum aequinoctialium 13, abestque ab aequatore partibus 16 27′, et per Meroen insulam ducitur, necnon inter amphiscios collocatur, quod nimirum sub eo habitantibus Sol in vertice bis consistat et gnomonas meridianis temporibus umbrae expertes reddat, quoties ab aestivo utrinque tropico distat partibus 45, ita ut, quandiu istas 90 partes Sol perlustrat, gnomonum umbrae ad austrum, dum vero reliquas 270, ad septentriones deflectant. Atque hoc quidem in loco, qualium gnomo est 60 partium, talium aequinoctialis umbra 17 45′, aestiva 7 45′, brumalis 51.

Sextus Amphis. 6 i. m. P diem habet maximum horarum aequinoctialium 13 15′ et ab aequatore disiunctus est partibus 20 14′, describiturque per Napata, et in amphisciorum numerum adscribitur, Sole videlicet per eorum verticem, qui sub illo habitant, bis transeunte et gnomonibus meridiano tempore umbram detrahente, quoties ab aestivo utrinque solstitio distat partibus 31, ita ut, quandiu 72 hasce partes emetitur, gnomonum umbrae ad meridiem, dum vero reliquas 298, ad aquilonem spectent. Atque hic, qualium gnomo partium est 60, talium aequinoctialis quidem umbra est 22 30′, aestiva vero 3 45′, brumalis autem 58 30′.

Septimus maximum continet diem horarum aequinoctialium 13 30′, abestque ab aequatore partibus 23 51′, et per Syenem describitur. Hic primus Heterosciorum 26 parallelorum primus i. m. P est eorum qui heteroscii nominantur. Nunquam enim apud illos qui in hoc versantur parallelo gnomones ad austrum meridiano tempore umbram iaciunt, sed in ipso tantum solstitio eorum vertici Sol recta imminet, nullaque a gnomonibus umbra fieri cernitur. Tantum enim illi ab aequatore distant, quantum ipsum quoque solstitii punctum. Universo autem reliquo tempore gnomonum umbrae ad arctos tendunt. Atque hic, qualium gnomo partium est 60, talium aequinoctialis quidem umbra 26 30′, brumalis vero 65 50′. Nam aestivam gnomones nullam iaciunt umbram. Caeterum omnes paralleli qui ad boream hoc propius accedunt usque ad eum qui nobis habitatam orbis terrae partem distinguit in heterosciis numerantur. Nunquam enim meridiano apud eos tempore, aut expertes sunt umbrae gnomones, aut ad austrum umbram iaciunt, sed ad boream semper, quod eorum verticem Sol nunquam attingat.

Octavus est parallelus, Heterosc. 2 i. m. P ubi dies maximus aequinoctialibus constat horis 13 45′, abestque ab aequatore partibus 27 12′, et per Ptolemaida Thebaidis cui Ἑρμείου nomen est describitur. Atque hic, qualium gnomo partium est 60, talium aestiva quidem umbra 3 30′, aequinoctialis vero 36 50′, brumalis vero 74 30′.

Nonus Heterosc. 3 i. m. P maximum diem habet horarum aequinoctialium 14, et ab aequatore distat partibus 30 22′, ac per inferiorem Aegypti regionem describitur. Atque hic, qualium gnomo partium est 60, talium aestiva quidem umbra 6 50′, aequinoctialis vero 35 12′, brumalis 83 12′.

Decimus Heteros. 4 i. m. P diem maximum continet horarum aequinoctialium 14 15′, abest autem hic ab aequatore partibus 33 18′, et per mediam Phoeniciam describitur. Atque hoc loco, qualium gnomo 60 partium, talium aestiva quidem umbra 10, aequinoctialis autem 39 30′, brumalis vero 93 5′.

Undecimus est parallelus, Heteros. 5 i. m. P ubi maximus dies horis aequinoctialibus absolvitur 14 30′, abestque ab aequatore partibus 36, et per Rhodum describitur. Atque hic, qualium gnomo partium est 60, talium aestiva quidem umbra 12 56′, aequinoctialis autem 43 50′, brumalis vero 103 20′.

Duodecimus est parallelus, Heteros. 6 i. m. P ubi dies maximus horarum aequinoctialium est 14 45′, distat autem hic ab aequatore partibus 38 35′, et per Smyrnen describitur. Atque in hoc situ, qualium partium gnomo est 60, talium aestiva quidem umbra 15 20′, aequinoctialis vero 47 50′, brumalis vero 114 55′.

Tertius et decimus Heteros. 7 i. m. P diem maximum habet horarum aequinoctialium 15, abestque ab aequatore partibus 40 56′, et per Hellespontum describitur. Atque hic, qualium gnomo est 60 partium, talium solstitialis quidem umbra 18 30′, aequinoctialis vero 52 30′, brumalis autem 127 50′.

Quartus et decimus Heteros. 8 i. m. P diem habet maximum horarum aequinoctialium 15 15′, distat autem ab aequatore partibus 43 15′, et per Massiliam describitur. Atque hic, qualium gnomo partium est 60, talium solstitialis quidem umbra 20 50′, aequinoctialis vero 55 55′, brumalis vero 144.

Quintus et decimus Heteros. 9 i. m. P diem habet maximum horarum aequinoctialium 15 30′, abestque ab aequatore partibus 45 1′, et per medium Pontum describitur. Hic autem, qualium gnomo 60 est partium, talium aestiva quidem umbra 23 15′, aequinoctialis vero 60, brumalis 155 5′.

Sextus et decimus Heteros. 10 i. m. P diem habet maximum horarum aequinoctialium 15 45′, distatque ab aequatore partibus 46 51′, et per fontes Istri fluvii describitur. Est autem hoc in loco, qualium gnomo 60 partium, talium solstitialis quidem umbra 25 30′, aequinoctialis vero 63 55′, brumalis autem 171 30′.

Septimus et decimus Heteros. 11 i. m. P diem habet maximum horarum aequinoctialium 16, abest vero ab aequatore partibus 48 32′, et per ostia Borysthenis describitur. Qualium vero gnomo hic partium est 60, talium aestiva quidem umbra 27 30′, aequinoctialis autem 67 50′, brumalis vero 188 35′.

Octavus et decimus Heter. 12 i. m. P diem habet maximum horarum aequinoctialium 16 15′, distat autem ab aequatore partibus 50 15′, et per media Meotida paludem describitur. Qualium autem gnomo partium hic est 60, talium aestiva quidem umbra 29 55′, aequinoctialis autem 71 20′, brumalis autem 208 20′.

Nonus et decimus Heter. 13 i. m. P maximum diem habet horarum aequinoctialium 16 30′, abest autem ab aequatore partibus 51 40′, et per maxime australes Britanniae terras describitur. Atque hic qualium gnomo partium est 60, talium aestiva quidem umbra 31 25′, aequinoctialis vero 75 35′, hyberna vero 229 20′.

Vigesimus Heter. 14 i. m. P est parallelus ubi dies maximus horis aequinoctialibus 16 45′ continetur, abest autem ab aequatore partibus 52 50′, atque per Rheni ostia describitur. Qualium vero hic partium 60 gnomo, talium aestiva quidem umbra est 33 20′, aequinoctialis vero 79 5′, brumalis autem 253 30′.

Primus et vigesimus Heter. 15 i. m. P diem maximum habet aequinoctialibus definitum horis 17, distatque ab aequatore partibus 54 15′, et per Tanaidis ostia describitur. Hic vero, qualium gnomo partium est 60, talium aestiva quidem umbra 34 55′, aequinoctialis vero 82 35′, brumalis autem 278 45′.

Secundus et vigesimus Heter. 16 i. m. P maximum diem habet horarum aequinoctialium 17 15′, distatque ab aequatore partibus 55, et per Brigantium magnae Britanniae describitur. Hic vero, qualium gnomo partium est 60, talium aestiva quidem umbra 36 15′, aequinoctialis vero 85 20′, brumalis autem 304 30′.

Tertius et vigesimus Heter. 17 i. m. P maximum diem habet horis aequinoctialibus 17 30′ descriptum, abest autem ab aequatore partibus 56, et per magnae Britanniae medium ducitur. Atque hic qualium gnomo 60 est partium, talium aestiva quidem umbra 37 20′, aequinoctialis vero 88 50′, brumalis vero 335 15′.

Quartus et vigesimus Heter. 18 i. m. P diem habet maximum horarum aequinoctialium 17 45′, distatque ab aequatore partibus 57, et per Britanniae Caturactonium describitur. Qualium vero gnomo partium hic est 60, talium aestiva quidem umbra 39 20′, aequinoctialis vero 92 25′, hyberna autem 372 5′.

Quintus et vigesimus Heter. 19 i. m. P diem habet maximum horarum aequinoctialium 18, abest autem ab aequatore partibus 58, et per australes parvae Britaniae plagas describitur. Atque qualium hic partium gnomo est 60, talium solstitialis quidem umbra 40 20′, aequinoctialis autem 96, brumalis vero 419 5′.

Sextus et vigesimus Heter. 20 i. m. P maximum diem habet horarum aequinoctialium 18 30′, distatque ab aequatore partibus 59 30′ et per medium parvae Britanniae describitur. Caeterum hoc loco non usi sumus quadrantis horarum incremento, tum quod crebri frequentesque iam sunt paralleli, elevationumque differentia non amplius integrae partis unius colligitur, tum quod in regionibus

ad boream propius iam spectantibus non tam accurate scrutanda sunt nobis omnia. Quare umbrarum etiam ad gnomonas rationes, ut in locis longe disiunctis, supervacaneum existimavimus apponere. Atque ubi quidem maximus dies horarum est aequinoctialium 19, ille parallelus Heter. 21 i. m. P ab aequatore distat partibus 61, et per aquilonares parvae Britanniae partes describitur.

Ubi autem maximus dies horis aequinoctialibus 19 30′ definitur, parallelus ille Heter. 22 i. m. P ab aequatore distat partibus 62, et per insulas quas Ebudas nominant describitur.

Ubi vero maximus dies horarum est aequinoctialium 20, parallelus ille Heter. 23 i. m. P ab aequatore distat partibus 63, et per Thulem insulam describitur.

Ubi autem dies maximus horarum est aequinoctialium 21, parallelus ille Heter. 24 i. m. P ab aequatore distat partibus 64 30′, et per ignotas gentes Scythicas describitur.

Ubi autem dies maximus horis aequinoctialibus 22 continetur, parallelus Heter. 25 i. m. P ab aequatore distat partibus 65 30′.

Ubi autem maximus dies horarum est aequinoctialium 23, parallelus Heter. 26 i. m. P ille ab aequatore abest 66 partibus.

Ubi autem maximus dies horarum est aequi noctialium 24, parallelus ille ab aequatore distat partibus 66 8′ 40′′. Primus autem est hic perisciorum. Perisciorum 7 parallelorum primus i. m. P

Nam aestivo tantum solstitio non occidente illic Sole, gnomonum umbrae in omnes circumaguntur horizontis partes. Atque hic aestivus quidem tropicus parallelus semper conspicitur, brumalis nunquam, propterea quod ambo ἐναλλάξ horizonta contingunt. Obliquus vero, quique per medium signorum est circulus, cum verni aequinoctii signum oritur, idem cum horizonte efficitur. Quos si quis aliter contemplationis studio magis universa exquirat inclinationum ad boream propius vergentium accidentia, is reperiet, quo loco polus aquilonaris 67 fere partibus eminet, Peris. 2 i. m. P ibi nullo pacto occidere orbis signorum partes 15 quae ad utrunque aestivi Solstitii latus consistunt, ita ut dies maximus et umbrarum in omnes horizontis partes conversio menstrua fere sit. Haec enim facile intelligi possunt ex proposita obliquationis tabella. Nam quot partibus distantem ab aequatore parallelum inveniemus, ut eum verbi gratia qui ex utroque puncti solstitii latere partes 15 intercipit, quique tum semper vel extat, vel latet, cum intercepta sectione circuli qui per medium signorum ducitur, tot profecto partibus elevatio aquilonaris poli deficiet a 90 unius quadrantis portionibus.

Atque ubi quidem partibus 69 30′, Peris. 3 i. m. P polus attollitur, ibi ex utroque aestivi solstii latere partes 30 ommino non occidere comperias, ut in duos fere menses et maximus producatur dies et gnomonum umbrae circumvehantur.

Ubi autem polus attollitur partibus 73 20′, Peris. 4 i. m. P illic ex utroque aestivi solstitii latere 45 partes non occidere reperias, ut et maximus dies et circumductae gnomonum umbrae ad tres fere menses producantur.

Ubi vero partibus 78 20′ polus elevatur, Peris. 5 i. m. P ibi ex utroque eiusdem puncti solstitialis latere 60 partes non occidere deprehendas, ut et quatuor fere mensium sit dies maximus, et tanto tempore gnomonum umbrae circumagantur.

Ubi vero partibus 84 polus eminet, Peris. 6 i. m. P ibi ex utroque aestivae conversionis latere partes 75 non occidere animadvertas, ut quinque fere mensium maximus rursus sit dies, tantoque tempore gnomones quaqua versum umbras suas iaciant.

Ubi vero 90 totius quadrantis partibus australis polus supra horizontem erectus cernitur, Peris. 7 i. m. P ibi totus zodiaci semicirculus qui ab aequatore ad boream declinat nunquam sub terram demergitur, qui vero ad austrum spectat nunquam emergit, ita ut uno quidem die unaque nocte, quorum utrumque sex fere sit mensium, annuum quodlibet definiatur spatium, gnomones vero umbram semper in omnem partem iaciant. Huic inclinationi haec proprie conveniunt, ut aquilonaris polus verticem teneat, aequinoctialis vero circulus partim semper, partim nunquam conspicui, nec non horizontis situm habeat, totumque aquilonare hemisphaerium super terram quidem, sub terra vero brumale semper contineat.

〈II.7〉 CAPUT 7: De communibus zodiaci et aequinoctialis in sphaera inclinata ascensionibus συναναφορῶν i. m. P

Postquam ea explanavimus quae circa inclinationes in genere spectanda sunt, sequitur ut demonstremus quomodo in qualibet inclinatione aequinoctialis tempora cognoscantur quae cum zodiaci arcubus simul ascendunt, ex quibus caetera quoque omnia quae particulatim accidunt nobis postea artificiose tractabuntur.

Abutemur autem signorum Ζωδίων i. m. P nominibus ad indicandas obliqui circuli partes duodecimas, δωδεκατημόρια i. m. P et quasi ipsorum initia a tropicis aequinoctialibusque punctis ducantur, primam quidem duodecimam, quae ab aequinoctio verno in consequentia motionis universi protenditur, Arietem, alteram vero Taurum appellabimus, similique in sequentibus ratione, pro 12 signorum tradito nobis ordine. Primum Lemmation 1 i. m. P autem probabimus zodiaci peripherias paribus intervallis ab eodem aequinoctiali puncto distantes cum aequalibus aequinoctialis circuli arcubus una subvehi. Sit enim meridianus circulus ABGD, horizontis autem semicirculus BED, aequatoris vero AEG, duoque obliqui circuli segmenta FI et TC, ita ut utrunque F et T vernum aequinoctii punctum esse, 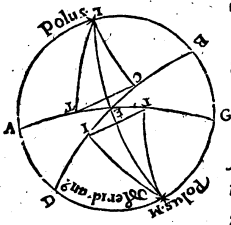aequales vero ex utraque ipsius parte interceptas peripherias FI et TC per puncta C et I o〈r〉iri oiri P supponantur. Aio utrasque etiam aequinoctialis peripherias FE et TE quae una oriuntur aequales esse. Sint enim polorum aequatoris puncta L et M, et per ipsa describantur maximorum circulorum portiones LEM et LT, itemque LC, FM, et MI. Cum igitur FI sit aequalis ipsi TG, quique per C et I describuntur paralleli aequaliter ab aequatore utrinque distent, ut ob eam causam LC quidem peripheria peripheriae MI, EC autem ipsi EI sit aequalis. Aequilatera igitur sunt LCT quidem ipsi MIF, LEC vero ipsi MEI, unde angulus qui sub CLE angulo qui sub IME aequalis est, quique sub CLT totus toti qui sub IMF aequalis, ita ut reliquus etiam qui sub ELT reliquo qui sub EMF aequalis futurus sit: Quamobrem basis ET basi EF est aequalis. Quod erat demonstrandum. Rursus Lemmation 2 i. m. P autem demonstrabimus aequinoctialis peripherias quae cum zodiaci arcubus aequalibus et aequaliter ab eodem tropico distantibus puncto ascendunt binas binis συναμροτέρας συναμροτέραις i. m. P quae in sphaera recta ascensionibus aequales esse. Sit enim ABGD meridianus, et ex semicirculis BED quidem horizontis, AEG vero aequinoctialis, describanturque duae aequales et aequaliter a brumali puncto distantes obliqui circuli peripheriae FI et TI, positis T quidem verno, F autem autumnali punctis, ita ut punctum I commune sit ortui ipsarum cum horizonte, cum ab eodem circulo aequatori parallelo comprehendantur FI et TI peripheriae, simulque ipsa quidem TE cum TI, EF vero cum FI oriatur. Hinc igitur manifestum est totam TED peripheriam aequalem esse ipsarum FI et TI peripheriarum in recta sphaera ascensionibus. Si enim, posito C puncto australi aequatoris polo, per eum et punctum I describamus maximi circuli quadrantem CIL, qui horizontis recti l〈o〉cum lecum P obtinet, ipsa rursus TL peripheria una cum TI in recta sphaera subvehitur, LF vero peripheria simul cum FI pariter attollitur, ita ut binae TLFI binis TEF aequales sint atque in una eademque TF peripheria contineantur. Quod erat demonstrandum. Atque Usus superiorum lemmatiῶn i. m. P ex his perspicuum nobis evasit quod, si in uno tantum quadrante particulares cuiusque inclinatio〈n〉is inclinatiouis P συνανατολὰς Coortus i. m. P supputaverimus, manifestae insuper nobis erunt reliquorum quoque trium quadrantum συνανατολαί. His ita constitutis, ponatur rursus Rhodum traiiciens parallelus, Apodoxis de propositis ascensionibus i. m. P ubi maximus quidem dies horarum est aequinoctialium 14 30′, aquilonaris vero polus supra horizontem extat partibus 36, sitque meridianus circulus ABGD, et horizontis similiter quidem semicirculus BED, aequatoris vero AEG, eiusque qui per medium signorum est FIT, sic collocatus, ut I vernum supponatur punctum, atque assumpto in C aquilonari aequinoctialis polo, per eum et zodiaci cum horizonte sectionem L De ascensione Arietis in quarto climate i. m. P describatur maximi circuli quadrans CLM. Proponatur vero, data IL peripheria, aequinoctialis peripheriae EI, scilicet quae cum illa subvehitur inventio. Ac primum quidem IL peripheria duodecimam circuli partem, Arietem verbi gratia, comprehendat. Quoniam igitur in duobus maximorum circulorum, qui descripti sunt, arcubus EG, et GC deliniati sunt ED et CM se invicem secantes puncto L, ratio subtensae dupli arcus CD ad rationem subtensae dupli arcus DG composita est tum ex ratione subtensae dupli arcus CL ad subtensam dupli arcus LM, tum ex ratione subtensae dupli arcus ME ad subtensam dupli arcus EG. Sed duplicatus ED arcus partium est 72, quaeque eam subtendit recta partium 70 32′ 4′′, duplicatus vero GD arcus partium 108, et quae ei subtenditur recta 97, 4, 56. Ac rursus duplum quidem arcus CL partium est 156, 41 et quae subtus ducitur recta 117 31′ 15′′. Duplum autem arcus LM partium est 23 19′ 59′′, quaeque ei subiicitur recta 24 15′ 57′′. Si igitur a ratione partium 70 32′ 4′′ ad 97 4′ 56′′ detrahamus rationem partium 117 31′ 15′′ ad 24 15′ 57′′, restabit subtensae dupli arcus ME ratio ad subtensam dupli arcus EG, partium scilicet 18 0′ 5′′ ad 120. Atqui subtensa dupli arcus EG partium est 120. Quare subtensa dupli arcus ME earumdem est partium 18 0′ 5′′. Itaque duplicatus etiam ME arcus partium erit 17 16′ proxime, ipse vero ME partium earumdem 8 38′′, sed totus IM arcus, quoniam una cum IL in recta sphaera simul ascendit, Ascensio Piscium i. m. P partium est quae supra demonstratae sunt 27 50′, ob idque reliquus EI arcus partium est 19 12′ atque una demon[mon]stratum demonmonstratum P est Pisces, duodecimam scilicet partem, iisdem simul emergere temporibus 19 12′, utrunque autem et Virginis et Librae Ascensio Virginis et Librae i. m. P signum temporibus 36 28′, quae ad complendum duplicatam Arietis in sphaera recta ascensionem restant. Quod erat demonstrandum. Rursus IL peripheria contineat duarum duodecimarum, Arietis inquam et Tauri, De ascensione Arietis et Tauri i. m. P partes 60. Manentibus igitur aliis, duplicatus quidem CL arcus per ea quae exposita sunt partium est 138 59′ 42′′, quae que ei subtenditur recta partium 112 23′ 56′′. Duplicatus autem LM arcus partium 41 9′ 18′′, et quae ei subtenditur recta partium 42 1′ 48′′. Si ergo rursus a ratione partium 70 32′ 4′′ ad 97 4′ 56′′ auferamus rationem 112 23′ 56′′ ad 42 1′ 48′′, supererit ratio subtensae dupli arcus ME ad subtensam dupli arcus EG, partium scilicet 32 36′ 4′′ ad 120. Atqui subtensa dupli arcus EG partium 120. Quare subtensa dupli arcus ME earundem est 32 36′ 4′′. Itaque duplicatus ME arcus partium est 31 32′ proxime. Ipsa autem ME peripheria earundem partium 15 46′, sed totus MI arcus iisdem de causis supra demonstratus est partium 57 44′, reliquus igitur IE arcus partium est 41 58′. Quamobrem Aries et Taurus ascendunt ambo simul temporibus 41 58′, quorum Aries una cum temporibus 19 12′ ascendere probatus est. Sola igitur pars duodecima quae Taurum continet simul emergit cum temporibus 22 46′. Ex iisdem vero causis duodecima rursus pars quae Aquarium Ascensio Aquarii i. m. P comprehendit cum aequalibus temporibus 22 46′ simul attolletur, utrumque autem et Leonis et Scorpii Ascensio Leonis et Scorpii i. m. P signum temporibus 37 2′, quae ad duplicatam in recta sphaera ascensionem restant. Cum autem maximus etiam dies horarum aequinoctialium sit 14 30′, minimus autem 9 30′, manifestum est ipsum quoque a Cancro ad Sagitarium semicirculum una ascensurum cum aequinoctialis temporibus 217 30′, a Capricorno autem ad Geminos Ascensio semicirculi a Cancro ad Sagitarium i. m. P semicirculum temporibus 142 30′. Quamobrem uterque quidem qui ex utraque est verni puncti parte zodiaci quadrans simul emerget cum temporibus ex utraque 71 15′, Ascensio quadrantum ex utraque tum verni puncti tum autumnalis parte i. m. P uterque vero qui punctum autumnale u〈t〉rinque urinque P circumstat temporibus 108 45′. Reliquum igitur tum Geminorum, tum Capricorni Ascensio Geminorum et Capricorni i. m. P signum attolletur cum temporibus 29 17′, quae ad quadrantis tempora 71 15′ restant. Reliqu〈u〉m reliqum P item tum Cancri tum Sagitarii Ascensio Cancri et Sagiatrii i. m. P signum temporibus 35 15′, quae ad huius etiam quadrantis tempora 108 45′ reliqua manent. Patet item eadem, quam hic secuti sumus, ratione nobis percipi posse minorum etiam portionum eius qui per medium signo〈r〉um signotum P est circuli συνανατολὰς. Iam vero commodiore et apertiore via ipsas colligere possumus ad hunc etiam modum. Alia ratio inveniendarum ascensionum propositarum i. m. P Sit enim primum meridianus circulus ABGD, et horizontis quidem semicirculus BED, aequatoris autem AEG, eius vero qui per medium signorum est FEI, in verno puncto posita e sectione, Lemmation i. m. P 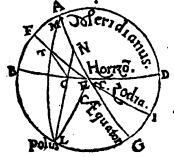et desecta in eo quavis ET peripheria, describatur per punctum T segmentum circuli paribus intervallis ab aequatore distantis, nempe TC, sumptoque L aequinoctialis polo, per eum describantur maximorum circulorum quadrantes LTM, LCN, atque LE. Hinc igitur constat quod EI segmentum eius, qui per medium signorum est, circuli in sphaera quidem recta cum EM peripheria aequinoctialis simul oritur, in inclinata vero cum ea quae sit aequalis ipsi NM, quando quidem CT paralleli peripheria cum qua simul segmentum ET subvehitur similis est ipsi NM aequatoris peripheriae.

Similes autem parallelorum peripheriae aequalibus ubique oriuntur temporibus. Unde segmenti

ET ascensio in sphaera inclinata maior est quam in recta, spatio scilicet EN peripheriae. Atque ita demonstratum est (quod etiam in universum genus patet), si quae maximorum circulorum peripheriae sic describantur, ut LTM, LCN, segmentum EN continebit excessum quo in recta et inclinata sphaera discrepant ascensiones peripheriarum obliqui circuli quae puncto E et descripto per C parallelo intercipiuntur. Quod erat demonstrandum. 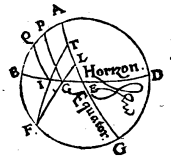Hoc ante percepto, proponatur Apodixis altera de ascensionibus propositis i. m. P sola semicirculorum tum meridiani tum horizontis et aequinoctialis descriptio, atque per F australem aequatoris polum describantur duo maximorum circulorum quadrantes FIT et FCL, supponatur autem punctum quidem I commune horizonti cum parallelo per brumalis solstitii punctum descripto, C vero commune eidem horizonti cum descripto per initium Piscium verbi gratia aut per aliam quamlibet datam quadrantis sectionem parallelo. In duobus igitur maximorum rursus circulorum arcubus FT et ET descripti sunt tum FCL, tum ECI seinvicem secantes in puncto C, estque subtensae dupli arcus TI ad subtensam dupli FI ratio c〈o〉mposita cemposita P ex ratione subtensae dupli arcus TE ad subtensam dupli EL et ex ratione subtensae dupli CL ad subtensam dupli CF. Sed in omnibus inclinationibus et duplicata TI peripheria eadem data est, cum sit inter tropicos media, et ob id geminata etiam quae reliqua est IF peripheria et similiter in iisdem zodiaci segmentis, ipsa quoque LC duplicata peripheria per omnes inclinationes est eadem, daturque per obliquationis tabellam, necnon ob eam causam reliqua rursus duplicata ipsius CF peripheria. Quamobrem etiam ratio subtensae dupli arcus TE, ad subtensam dupli EL relinquitur eadem per omnes inclinationes in iisdem quadrantis segmentis. Quos si, cum ita haec se habeant, differentiam CL peripheriae adaugeamus partibus 10 quadrantis qui a verno aequinoctio ad brumale porrigitur punctum (quandoquidem ad usum futura est satis, quae per tantos arcus progreditur divisio) semper habebimus duplum ipsius quidem TI peripheriae partium 47 42′ 40′′, quaeque ei subtenditur rectam partium 48 31′ 55′′, duplum vero IF peripheriae partium 132 17′ 20′′, eique subtensam partium 109 44′ 53′′. Eodemque modo in peripheria quae decem partibus a verno puncto versus brumale tropicum distat duplum quidem ipsius CL partium 8 3′ 16′′, eique subtensam re[r]ctam rerctam P partium 8 25′ 39′′, duplum vero arcus CF partium 171 56′ 44′′, quaeque ei subtenditur rectam partium 119 42′ 14′′; in peripheria autem quae 20 partibus similiter distat duplicatam quidem CL peripheriam partium 15 54′ 6′′, eique subtensam partium 16 35′ 56′′, duplum autem arcus CF partium 164 5′ 54′′, et rectam ei subtensam partium 118 50′ 47′′; in peripheria autem quae 30 abest partibus duplum quidem arcus LC partium 23 19′ 58′′, et rectam ei subtensam partium 24 15′ 56′′, duplum autem arcus CF partium 156 41′, rectamque ei subtensam partium 117 31′ 15′′, in peripheria quae 40 distat partibus duplicatum quidem LC arcum partium 30 8′ 8′, et rectam quae ei subest partium 31 11′ 43′′, geminatum vero CF arcum partium 149 51′ 52′′, eique subtensam partium 115 52′ 19′′; in peripheria autem quae partibus 50 abest duplum quidem LC arcus partium 36 5′ 46′′, et rectam quae ei subiicitur partium 37 10′ 39′′, duplum vero CF partium 143 54′ 14′′, eique subtensam partium 114 5′ 44′′; in peripheria item quae 60 distat partibus duplicatum quidem LC arcum partium 41 0′ 16′′, eique subtensam rectam partium 42 1′ 46′′, duplum vero CF partium 138 59′ 42′′, et subtensam ei rectam partium 112 23′ 57′′; in peripheria autem quae 70 distat partibus duplum quidem arcus LC partium 44 40′ 22′′, eique subtensam rectam partium 45 36′ 18′′, duplicatum vero CF arcum partium 135 19′ 38′′, eique subtensam rectam partium 110 59′ 47′′; in peripheria vero quae 80 abest partibus duplum quidem arcus LC partium 46 56′ 32′′, quaeque ei subtenditur rectam partium 47 47′ 40′′, duplicatum autem CF arcum partium 133 3′ 28′′, eique subtensam rectam 114 16′. Atque per ea quae ante posita sunt, si ratione subtensae dupli arcus TI ad subtensam dupli arcus IF, hoc est a ratione partium 48 31′ 55′′, ad 109 44′ 53′′, subducamus quamlibet propositarum per decadas rationum subtensae dupli arcus LC ad subtensam dupli arcus CF, relinquetur nobis ratio subtensae dupli arcus TE ad subtensam dupli arcus EL in omnibus inclinationibus eadem rationi 60 in peripheria quidem quae, ut diximus, 10 partibus distat ad 9 33′, in ea vero quae 20 abest partibus ad 18 57′, in ea quae 30 ad 28 1′, in ea vero quae 40 ad 36 33′, in ea quae 50 ad 44 12′, in ea quae 60 ad 50 44′, in ea quae 70 ad 55 45′, in ea vero quae 80 ad 58 55′. Hinc autem perspicuum est quod in singulis inclinationibus, dato duplo arcus TE (quandoquidem partium est totidem, quot temporibus aequinoctialis dies minimum superat), dataque recta quae duplicatum ipsum subtendit arcum, et data ratione huius rectae ad subtensam dupli arcus EL, ipsam quoque datam habebimus, necnon arcus EL duplum, cuius dimidio, hoc est ipso EL arcu qui supra memoratum continet excessum subtracto a propositae in recta sphaera zodiaci peripheriae ascensionibus, ipsius peripheriae in dato quovis climate ascensionem reperiemus. Sit enim exempli gratia Exemplum superioris Apodixeos i. m. P inclinatio rursus eius qui per Rhodum ducitur paralleli, in quo duplum quidem arcus ET partium est 37 30′, quae vero ei subest recta partium 38 34′ proxime. Cum igitur eadem sit ratio 60 ad 38 34′, quae 9 33′ ad 6 8′, quaeque 18 57′ ad 12 11′, et que 28 1′ ad 18 0′, quae item 36 33′ ad 23 29′, et quae 44 12′ ad 28 25′, quae etiam 50 44′ ad 32 37′, quaeque 55 45′ ad 35 52′, et quae 58 55′ ad 37 52′, fit ut subtensa quidem dupli arcus EL in singulis decadibus excessum contineat qui expositis segmentis congruat, dimidium vero eius peripheriae quae illi subtensae incumbit, hoc est ipsa EL, in prima quidem decade partium 2 56′, in secunda vero, partium 5 50′, in tertia autem 8 38′, in quarta 11 17′, in quinta 13 42′, in sexta 15 46′, in septima 17 28′, in octava 18 24′, in nona vero ipsarum 18 45′. Quamobrem, cum in sphaera etiam recta peripheria quidem quae ad primam usque decada protenditur simul oriatur cum temporibus 9 10′, quae vero usque ad secundam cum 18 25′, quae usque ad tertiam cum 27 50′, quae usque ad quartam cum 37 30′, quae ad quintam cum 47 28′, quae ad sextam cum 57 44′, quae usque ad septimam cum 68 18′, quae vero ad octavam cum 79 5′, quae vero ad nonam cum totius quadrantis 90 temporibus, patet quod, si a singulis propositarum in sphaera recta ascensionum propriam quantitatem excessus qui secundum EL peripheriam spectatur auferamus, eorundem arcuum in proposito climate ascensiones habebimus. Atque peripheria quidem quae ad primam porrigitur decada una emerget cum reliquis temporibus 6 14′, quae vero ad secundam cum 12 35′, quae ad tertiam cum 19 12′, quae ad quartam cum 26 13′, quae ad quintam cum 33 46′, quae ad sextam cum 41 58′, quae ad septimam cum 50 50′, quae ad octavam cum 60 41′, quae vero ad nonam, hoc est totum quadrantem, cum temporibus 71 15′ collectis ex dimidio magnitudinis diei. Ipsarum igitur decadum prima quidem simul attolletur cum temporibus 6 14′, secunda vero cum 6 21′, tertia cum 6 37′, quarta cum 7 1′, quinta cum 7 33′, sexta cum 8 12′, septima cum 8 56′, octava cum 9 48′, nona cum 10 34′.

Arcus EL qui per decadas variatur quantitas

Quibus demonstratis, per se rursus ex iis que ante percepta sunt una demonstratae fuerunt reliquorum quoque quadrantum consequenter ascensiones. Eadem sane ratione supputatis in qualibet decade aliorum parallelorum ascensionibus, ad quos usus frequenter pertinere potest, eas, ut ad reliqua viam muniant, in tabula exponemus διὰ το μὴ ἀξιολογον γίνεσθαι τὴν τῶν μεταξὺ ποῦ ημιωρίου παρὰ τὰ ὁμαλὰ διαρορόν i. m. P. Atque ab eo, qui aequatori subiectus est exorsi, circulo, ad eum perveniemus, ubi horarum 17 dies maximus evasit, facta ad ipsas semissis horae accessione, propterea quod non habetur ratio differentiae eorum, quae sunt inter horae semissem, si aequabiliter augeantur.

Praepositis itaque 36 circuli decadibus, singulis deinceps adiiciemus sua climatis ascensionis tempora, temporumque collectionem ad hunc modum.

〈II.8〉 〈CAPUT 8: Tabellae quibus exponuntur per decadas in qualibet inclinatione ascensiones〉

〈II.9〉 CAPUT 9: De iis quae ascensiones particulatim consequuntur

Quod autem, ascensionum temporibus a nobis ad hunc modum declaratis, reliqua facile percipi possunt quae ad hanc partem attinent, ac neque linearibus ad singula eorum probanda nobis opus futurum demonstrationibus, neque supervacanea tabularum descriptione ex ipsis rerum quae postea tractabuntur argumentis perspici poterit. Primum De invenienda dies vel noctis magnitudine i. m. P enim dati diei vel noctis cognoscitur magnitudo, numeratis scilicet proprii climatis temporibus, interdiu quidem a loco Solis ad eum qui ex diametro in consequentia signorum Soli adversatur, noctu vero ab ea, quae

Soli ex adverso est, parte ad ipsum Solis locum. Nam collectorum temporum sumpta quidem parte decimaquinta, comperiemus quot sit horarum aequinoctialium propositum diei vel noctis intervallum, duodecima vero, quot temporum sit eiusdem intervalli hora temporalis, cognoscitur. Invenitur De invenienda hora unius temporalis magnitudine. ἡ καιρκὴ ὥρα i. m. P autem etiam facilius horae unius magnitudo, de prompto scilicet ex praescripta ascensionum tabella, collectionum excessu, quae, si diei horam investigas, loco Solis adiaceant, sin noctis, parti ex diametro obiectae adhaereant, idque tum in eo, qui aequinoctiali subest, tum in eo, qui propositi est climatis, parallelo. Nam inventi excessus sexta parte detracta, quam unius aequinoctialis horae quindecim temporibus, si in aquilonari quidem semicirculo oblatus erit Solis locus, adiicias, si vero in australi semicirculo, ab ipsis quindecim temporibus subtrahas, multitudo aggerabitur temporum, ex quibus hora temporalis proposita constet. Post haec Analysis horarum temporalium in aequinoctiales i. m. P autem datas quidem temporales horas ad aequinoctiales revocabimus, si in horae unius tempora quae eodem illo die in proprio notata erunt climate diurnas, in nocturna vero nocturnas temporales horas ducamus. Nam procreati numeri collecta pars quinta et decima horarum aequinoctialium multitudinem nobis reddet. Contra Ἀνάπαλιν i. m. P vero datas aequinoctiales horas in temporales commutabimus, si natum ex illarum ductu in 15 numerum per oblatas sui intervalli temporales horas partiamur.

Rursus De investiganda oriente zodiaci parte i. m. P dato nobis tempore et hora qualibet temporali, primum quidem exorientem tunc obliqui circuli partem capiemus, ducto in propria horae unius tempora horarum numero, quae interdiu quidem ab ortu Solis, noctu vero ab occasu numerentur. Nam collectum ex ea multiplicatione numerum producemus, διεκβαλοῦμεν, quod vulgo dirigemus i. m. P interdiu quidem a loco solari, noctu vero a parte ex diametro obversa in signorum consequentia, secundum propositi climatis ascensiones, eamque, cui numerus occurret, partem tum oriri pronunciabimus. Quod si eam partem quae supra terram in meridiano consistit circulo deprehendere libet, temporales omnino horas quae a praeterito meridie ad datam elapsae sunt horam in propria horae unius tempora multiplicantes numerum procreatum producemus ἐκβαλοῦμεν, quod etiam dirigemus dicere solent i. m. P a loco Solis in consequentia secundum eas quae in sphaera recta sunt ascensiones, et in quam numerus inciderit partem, illa tum temporis in meridiano versabitur circulo. Similiter De invenienda zodiaci parte, quae in meridiano super terram consistit circulo i. m. P autem ex parte oriente eam capiemus, quae in meridiano super terram consistit circulo, inspecto scilicet in proprii climatis tabella collectionis numero qui orienti adiacet parti. Demptis enim omnino quadrantis ab eo temporibus 90, comperiemus ex collectione quae in sphaerae rectae tabella notatur partem e regione numeri positam in meridiano tum temporis versari circulo. Contra Ἀνάπαλιν i. m. P vero ab ea quae coeli super terram medium tenet orientem rursus deprehendemus partem, observato in sphaerae rectae tabella collectionis numero qui parti adscriptus est coeli medium occupanti. Illi enim additis omnino iisdem rursus 90 temporibus, considerabimus ex oblati climatis collectione quaenam pars numero adiaceat, eamque tunc orientem reperiemus. Manifestum etiam est quod sub eodem degentibus meridiano Sol pari horarum aequinoctialium intervallo a diei noctisque medio distat, qui vero sub eodem meridiano non versantur, apud eos tantum est aequinoctialium temporum discrimen,

quot partibus meridianus horum ab illorum meridiano distat.

〈II.10〉 CAPUT 10: De angulis qui a signifero et meridiano fiunt circulo

Sed cum ad propositam initio huius libri contemplationem reliquum sit, ut de angulis sermonem faciamus qui cum obliquo fiunt circulo, illud Definitio quae ad sequentem disputationem confert i. m. P primo loco sumendum arbitor rectum angulum a maximis circulis (nostra interpretatione) contineri, quum polo quidem, communi scilicet circulorum sectione, et quolibet intervallo descripti circuli peripheria Anguli ratio ex circuli peripheria i. m. P segmentis angulum complectentibus intercepta sui circuli quadrantem explet, atque in universum angulum sub planorum inclinatione comprehensum, eam habere ad 4 rectos rationem, quam intercepta peripheria ad descriptum eo quem prodidimus modo circulum.

Quamobrem cum perimetrum supponamus partium 360, quot invenietur partium intercepta peripheria, totidem erit quem illa subtendet angulus, qualium rectus unus est 90. Angulorum porro, Quae hoc libro explicandis restant i. m. P qui cum obliquo fiunt circulo, illi maximum adferent propositae contemplationi adiumentum quos mutuae ipsius cum meridiano vel cum horizonte sectiones in quolibet situ complectuntur, quos item mutua ipsius et maximi circuli per polos horizontis descripti sectio comprehendit, si cum eiusmodi angulis una quoque explicentur huius circuli peripheriae quae ipsa sectione et horizontis polo, hoc est verticis puncto, continentur. Nam horum singula demonstratione illustrata et ad ipsam contemplationem sunt accommodatissima, et ad ea quae circa Lunae parallaxes quaeruntur conducunt quam plurimum, utpote quarum nulla sit prorsus, nisi illis ante perceptis, comprehensio. Caeterum quum anguli quatuor contineantur duorum circulorum sectione eius nimirum qui per medium signorum est et alicuius eorum qui cum illo conserti haerent, nosque de uno, qui secundum situm similis est, verba facturi simus, illud ante definiendum est ex duobus in universum angulis qui sunt circum zodiaci peripheriam quae communem sequitur circulorum sectionem alterum qui ab aquilone consistit intelligi oportere, ita ut accidentia quaeque demonstrabuntur quantitates ad eius generis angulos pertineant. Quoniam autem simplicior est demonstratio angulorum zodiaci quos cum meridiano efficit circulo, ab iis incipiemus, ac primum Lemmation 1 i. m. P docebimus illos angulos a zodiaci punctis quae ab eodem aequinoctiali puncto aequaliter distant aequales inter se fieri. 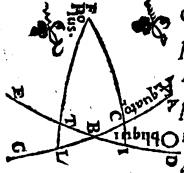Sit enim aequinoctialis quidem peripheria ABG, zodiaci vero DBE, polus vero aequinoctialis punctum F, et interceptis aequalibus peripheriis BI et BT ex utraque puncti aequinoctialis B parte, describantur per polum F et puncta I, T meridianorum circulorum peripheriae FCI et FTL. Aio aequalem esse qui sub CIB angulum ei qui sub FTE, quod hinc manifestum est. Etenim trilaterum BIC aequiangulum est trilatero BTL, quandoquidem et tria latera tribus lateribus aequalia habet singula singulis, latus nimirum IB lateri BT, latus vero IC lateri TL, et latus BC lateri BL. Demonstrata sunt enim prius haec omnia. Quare et angulus qui sub CIB aequalis est angulo qui sub BTL, id est ei qui sub FTE. Quod erat demonstrandum. Rursus Lemmation 2 i. m. P probare oportet angulos qui a zodiaci punctis aequaliter ab eodem tropico puncto distantibus cum meridiano fiunt ambos simul duobus rectis aequales esse. 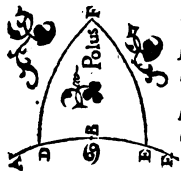Sit enim zodiaci peripheria ABG, posito B tropico puncto, et interceptis ex utraque ipsius parte aequalibus peripheriis, BD scilicet et BE, describantur per D et E puncta ac per F aequinoctialis polum meridianorum circulorum periphaeriae FD et EF. Aio angulum qui sub FDB, et sub FEG utrumque simul duobus rectis exaequari. Est autem etiam hoc inde manifestum quod, cum puncta D et E pari intervallo distent ab eodem puncto tropico, aequalis est ipsa quoque DF peripheria peripheriae FE, unde angulus quoque qui sub FDB ei qui sub FEB aequalis est. Atqui anguli FEB et FEG duobus sunt rectis aequales. Quare angulus etiam qui sub FDB cum eo qui sub FEG duobus rectis sunt aequales. Quod erat demonstrandum. His ante perspectis, sit Apodixis de angulis propositis i. m. P meridianus quidem circulus ABGD, zodiaci vero semicirculus AEG, posito in a hyberno puncto tropico, atque polo A, intervallo autem quadrati latere describatur BED semicirculus. Quoniam igitur ABGD meridianus et per semicirculi AEG et per semicirculi BED polos descriptus est, quadrantem continet ED peripheria. Rectus ergo est qui sub DAE angulus, rectus autem ex iis quae supra demonstravimus is etiam est angulus, qui ab aestivo fit tropico puncto. Quod demonstrare oportebat. Sit rursus meridianus quidem circulus ABGD, aequinoctialis autem semicirculus AEG, describaturque zodiaci semicirculus AFG, ita ut punctum A autumnalis aequinoctii punctum sit, atque polo A et intervallo latere quadrati describatur BFED semicirculus. Ob easdem ergo caus[s]as, caussas P cum ABGD descriptus sit per polos ipsorum AEG et BED, quadrantem complectitur utraque AF et ED peripheria. Quamobrem ipsum quidem F brumalis conversionis punctum erit, peripheria vero FE partium quae demonstratae sunt 23 51′ proxime. Tota ergo FEB peripheria partium est 113 51′, qui vero sub GAF angulus talium est 113 51′, qualium rectus unus est 90. Usus lemmatii 2 i. m. P Ex his autem quae supra docuimus angulus rursus qui a verno fit aequinoctiali puncto earum etiam quae ad complendum duos rectos angulos restant partium erit 66 9′. 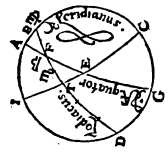Sit item meridianus quidem circulus ABGD, atque aequinoctialis semicirculus AEG, zodiaci vero BFD, ita ut ipsum quidem F autumnale supponatur punctum, BF autem peripheria sit primum unius duodecimae partis, ut pote Virginis, atque B punctum, initium scilicet Virginis. Polo rursus B, intervallo autem latere quadrati describatur semicirculus ITEC, sitque investigandus qui sub CBT angulus. Cum itaque ABGD meridianus tum per AEG, tum per IEC polos descriptus sit, quadrantis est quaelibet harum BI, BT et EI peripheria. Ob descriptionem autem ratio subtensae dupli arcus BA ad subtensam dupli arcus IA composita est tum ex ratione subtensae dupli arcus BF ad subtensam dupli TF et ratione subtensae dupli arcus TE ad subtensam dupli EI. Atqui ex iis quae supra demonstravimus duplicatus arcus BA partium est 23 20′, quaeque ei subtenditur recta partium 24 16′, geminatus vero AI arcus partium est 150 40′, eique subtensa recta partium 117 31′. Ac rursus duplicata FB peripheria partium est 60, quaeque ei subest recta partium 60, geminatus vero FT arcus partium 120, eique subtensa recta partium 103 55′ 23′′. Si rursum igitur a ratione 24 16′ ad 117 31′ subducamus rationem 60 ad 103 55′ 23′′, restabit ratio subtensae dupli arcus TE ad subtensam dupli EI partium 42 58′ proxime ad 120, estque subtensa dupli arcus EI partium 120. Quare subtensa dupli TE earundem est 42 58′. Itaque et duplicatus TE arcus partium est 42 proxime. Ipsa autem TE peripheria earundem 21. Tota igitur TEC tum ipsa, tum qui sub CBI angulus partium est 111. Ex iis Usus lemmatii 1 i. m. P autem quae ante probata sunt, angulus etiam qui ab initio Scorpii efficitur, aequalium erit partium 111. Uterque Usus Lemmatii 2 i. m. P autem et qui ab initio Tauri et qui ab initio Piscium constituitur partium est 69, quae ad complendum duos rectos supersunt, quod demonstrandum erat. Rursus in eadem descriptione FB peripheria supponatur altera zodiaci pars duodecima, ita ut B punctum sit Leonis initium, iisdemque suppositis, duplum quidem peripheriae AB partium sit 41, quaeque ei subest recta partium 42 2′, geminata vero AI peripheria partium 139, eique subtensa partium 112 24′. Atque rursus duplum quidem ipsius BF partium 120, rectaque ei subtensa partium 103 55′ 23′′, duplum vero FT partium 60, et subtensa ei recta partium 60. Si rursus igitur a ratione 42 2′, ad 120 24′ subtrahas rationem 103 55′ 23′′ ad 60, relinquetur ratio subtensae dupli TE ad subtensam dupli EC partium 25 53′ ad 120. Quae ergo subtenditur geminatae TE peripheriae earundem est partium 25 53′. Quamobrem duplicata TE peripheria partium erit 25 proxime. Ipsa vero TE earundem 12 30′. Tota igitur TEI et ipsa, et qui sub IBT angulus partium 102 6′. Iisdem sane de causis Lemmatίωn usus i. m. P angulus etiam qui sub Sagittarii initio continetur aequalium est partium 102 30′, uterque vero et qui sub initio Geminorum et qui sub initio Aquarii continetur partium est 77 6′, quae ad duorum rectorum complementum restant. Atque haec nobis demonstrata sunt quae proposita erant. Nam ad exiliores item obliqui circuli portiones eadem sane quam in maioribus secuti sumus patebit via, πραγμαπείας tractationis i. m. P quae et ad ipsum artis usum et ad exponendas sigillatim duodecimas zodiaci partes futura est satis.

〈II.11〉 CAPUT 11: De angulis qui ab eodem obliquo circulo et horizonte fiunt

Deinceps vero docebimus quemadmodum in quovis climate angulos cognoscamus, quos etiam cum horizonte obliquus facit circulus, quod et illi simpliciore quam reliqui ratione percipiantur. Manifestum est ergo angulos qui cum meridiano fiunt eorum nequaquam dissimiles esse, qui in sphaera recta cum horizonte fiunt.

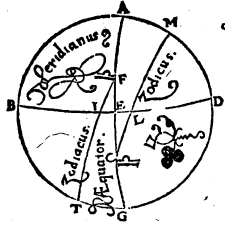Ut Lemmation 1 i. m. P autem in sphera quoque inclinata capiantur, illud rursus primo loco demonstrandum est angulos ab obliqui circuli punctis quae ab eodem aequinoctiali puncto aequaliter distant cum eodem horizonte inter se aequales effici. Sit enim meridianus circulus ABGD, et aequinoctialis quidem semicirculus AEG, horizontis vero BED, describanturque obliqui circuli duo segmenta FIT et CLM, quae ita habeant, ut utrumque F et C fingatur autumnalis aequinoctii punctum, peripheria vero FI peripheriae CL aequalis. Aio angulum qui sub EIT, aequalem esse angulo qui sub DLC, idque inde perspicuum est. Nam aequiangulum rursus est EFI trilaterum trilatero ECL, quum ex his quae supra demonstravimus tria latera tribus lateribus singula singulis habeant aequalia, latus quidem FI lateri CL, latus vero IE, sectionis scilicet horizontis, lateri EL latus item EF, ascensionis scilicet, lateri EC. Aequalis est igitur angulus qui sub EIF angulo qui sub ELC, reliquus ergo qui sub EIT reliquo qui sub DLC est aequalis. Quod demonstrare oportuit. Aio Lemmation 2 i. m. P item orientalem angulum alterius punctorum ex diametro adversorum cum alterius occidentali angulo duobus rectis aequales esse. Si enim horizonta quidem describamus circulum ABGD, zodiacum vero AEGF, se invicem secantes in punctis A et G, ambo quidem simul tum qui sub FAD, tum qui sub DAE duobus sunt rectis aequales. Aequalis est autem qui sub FAD ei qui sub FGD. Quare ambo simul et qui sub FGD et qui sub DAE duos rectos efficiunt angulos. Quod erat demonstrandum. Haec cum ita habeant, probatumque sit angulos qui a punctis aequaliter ab eodem aequinoctiali puncto distantibus cum horizonte fieri cernuntur Lemmation 3 ex duobus proximis collectum i. m. P inter se aequales esse, hoc etiam consequetur orientalem angulum alterius punctorum aequaliter ab eodem conversionis puncto distantium cum occidentali alterius angulo utrosque simul duobus rectis aequales esse. Ob eam itaque causam, si orientales invenerimus angulos qui ab Ariete ad Libram usque efficiuntur, una demonstrati fuerint alterius quoque semicirculi orientales et insuper duorum semicirculorum occidentales anguli. Sed qua id ratione colligatur, paucis exponemus eodem rursus exempli gratia usi parallelo, ubi scilicet aquilonaris polus partibus 36, supra horizontem sublatus conspicitur. Anguli autem qui ab aequinoctialibus zodiaci punctis cum horizonte fiunt citra ullum negotium cognosci possunt. Si enim meridianum quidem describamus circulum ABGD, propositi vero horizontis orientalem semicirculum AED, atque aequinoctialis quadrantem EF, obliqui circuli duos quadrantes EB et EG, qui ita habeant, ut punctum E, si ad EB quadrantem referatur, autumnale, sin ad EG, vernum intelligatur, et B quidem hybernum, G vero aestivum sit conversionis punctum, colligitur, posita DF peripheria partium 54, utraque vero BF et FG aequalium 23 51′ proxime, ipsam quoque GD peripheriam partium esse 30 9′, BD autem earundem 77 51′. Quamobrem cum E sit polus meridiani ABG, angulus quoque sub DEG, qui ab Arietis fit initio, talium est 30 9′, qualium unus rectus 90, angulus vero sub DEB, qui a Librae efficitur principio, earundem 77 51′. Verum ut ad reliquos via quoque muniatur, sit verbi causa inveniendus orientalis angulus qui a Tauri initio et horizonte efficitur, sitque meridianus circulus ABGD, propositi vero horizontis orientalis semicirculus BED, et describatur zodiaci semicirculus AEG, ita ut punctum E sit Tauri initium. 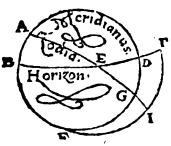Quoniam vero in hoc climate, emergente Tauri initio, in meridiano sub terra consistunt Tauri partes, 17 41′ (docuimus etenim per expositas nobis ascensiones ea ista facile perspici posse), minor quadrante est EG peripheria. Describatur sane polo E, et intervallo latere quadrati, maximi circuli segmentum TIF, et compleantur EGI et EDT quadrantes. Est autem et DGF et FIT utraque quadrantis peripheria, quod BET horizon per polos transit tum FGD meridiani tum FIT maximi circuli. Rursus quoniam Cancri partes quidem 17 41′ ab aequinoctiali ad arctos distant in maximo, qui per eius polos ducitur, circulo partibus 22 40′ (nam et haec nobis exposita sunt), aequinoctialis vero distat ab F polo horizontis in eadem FGD peripheria partibus 36, colligitur ipsa quoque FG peripheria partium 58 40′. His igitur datis, consequens est ex descriptione rationem subtensae dupli arcus GD ad subtensam dupli DF compositam et ex ratione subtensae dupli arcus GE ad subtensam dupli EI et ratione subtensae dupli arcus IT ad subtensam dupli FT. Sed per ea que ante tradidimus duplicata GD peripheria partium est 62 40, quaeque ei subest recta partium 62 24′, geminata vero DF peripheria partium est 180, eiusque subtensa 120, itemque duplicata GE peripheria partium est 155 24′, quaeque ei subest recta partium 117 14′, geminata vero ei partium 180, eiusque subtensa 120. Si igitur a ratione partium 62 24′ ad 120 subtrahamus rationem partium 117 14′ ad 120, relinquetur nobis ratio subtensae dupli arcus TI ad subtensam dupli FT, partium 63 52′ ad 120. Quare subtensa dupli arcus IT earundem est partium 63 52′, unde consequens est duplicatam IT peripheriam partium esse 64, 20′, ipsam vero IT, quique sub IET continetur, angulum earundem 32 10′. Quod oportebat demonstrasse. Eadem vero ratio, ne in singulis idem inculcantes huius constructionis commentationem longius producamus, in reliquis etiam 12 signis et climatibus deprehendetur.

〈II.12〉 CAPUT 12: De angulis et peripheriis quae cum eodem circulo ab eo fiunt qui per horizontis polos describitur

Quoniam autem ea nobis ratio explicanda restat, per quam angulos etiam cognoscamus qui in qualibet inclinatione atque situ a zodiaco et altero qui per horizontis polos ducitur circulo fiunt, addita semper, ut monuimus, demonstratione quae interceptam verticis puncto et circuli per horizontis polos descripti cum zodiaco sectione ipsius circuli peripheriam colligat, illa rursus exponemus, quae ad hanc partem praeponenda videntur. Atque primum Lemmation 1 i. m. P docebimus, si puncta zodiaci circuli aequaliter ab eodem puncto tropico distent, quorum alterum ab ortu, alterum ab occasu aequalia ex utraque meridiani parte tempora comprehendat, non modo maximorum circulorum peripherias a verticis puncto ad illa productas inter se aequales esse, sed etiam angulos qui cum illis fiunt eo, quem definivimus, modo duobus rectis exaequari. Sit enim meridiani segmentum ABG, in eoque supponatur verticis quidem punctum B, aequinoctialis vero polus G. 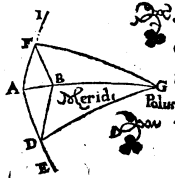Atque describantur duo zodiaci segmenta ADE, et AFI, quae ita habeant, ut D et F puncta ab eodem tropico aequaliter distent et aequales ex utraque ABG meridiani parte intercipiant peripherias paralleli per ipsa descripti. Ducantur autem ab ipso G polo aequinoctialis per D et F puncta maximorum etiam circulorum peripheriae GD et GF, a verticis autem puncto B ducantur BD et BF. Aio ipsam BD peripheriam BF peripheriae aequalem esse, angulum vero qui sub BDE cum eo qui sub BFA duobus rectis aequari. Cum enim puncta D et F a meridiano ABG distent aequalibus peripheriis descripti per ipsa paralleli, angulus qui sub BGD aequalis est ei qui sub BGF. Duo igitur sunt trilatera, BGD nimirum et BGF, quorum duo latera duobus lateribus sunt aequalia alterum alteri, latus quidem GD lateri GF, commune autem GB, angulus quoque BGD angulo BGF sub aequalibus lateribus contento aequalis, unde basis BD basi BF, et angulus sub BFG angulo sub BDG aequalis colligitur. Sed cum paulo ante probatum sit punctorum aequaliter ab eodem conversionis puncto distantium angulos qui cum circulo per polos aequinoctialis transeunte fiunt ambos simul duobus rectis aequales esse, consequens est ambos simul et qui sub GDE et qui sub GFA duobus rectis exaequari. Demonstratum est autem a〈n〉gulum augulum P quoque qui sub BDG, angulo sub BFG aequalem esse. Quare ambo simul et qui sub BDE et qui sub BFA duobus rectis sunt aequales. Quod erat demonstrandum. Rursus Lemmation 2 cuius duae sunt partes i. m. P vero probandum est, si eadem zodiaci puncta aequalibus utrinque temporibus a meridiano distent, et descriptas a verticis puncto ad illa maximorum circulorum peripherias inter se aequales esse, et ambos simul angulos qui cum illis tum ad ortum tum ad occasum fiunt duobus quos cum eodem zodiaci puncto meridianus efficit aequales esse, cum in utroque situ ambo quae meridianum occupant puncta vel ad austrum vel ad boream propius quam verticis punctum accedunt. Ubi puncta A, B quae meridianum traiiciunt, austro sunt propiores quam G verticis punctum i. m. P Primum autem fingamus magis australia esse ambo illa puncta, sitque meridiani segmentum ABGD, in eo autem verticis quidem punctum G, aequinoctialis autem polus D, describanturque duo zodiaci segmenta AEF et BIT, ita ut punctum E et punctum I, quod idem sumitur, aequali peripheria ex utraque paralleli per eum ducti parte a meridiano ABGD distet, et per illa describantur rursus a puncto G maximorum circulorum segmenta GE et GI, a puncto autem D describantur DE et DI. Ob easdem profecto, quas supra commemoravimus, causas, cum puncta E, I eundem efficientia parallelum aequales eius ex utraque parte meridiani faciant peripherias, trilaterum GDE et aequilaterum et aequiangulum est trilatero GDI, ita ut latus GE lateri GI sit aequale. Dico autem utrosque etiam simul angulos, tum qui sub GEF, tum qui sub GIB duobus qui sub DEF, et sub DIB aequales esse. Quoniam enim qui sub DEF idem est cum eo qui sub DIB, qui vero sub GED aequalis est ei qui sub DIG, ambo itaque simul tum qui sub GED tum qui sub GIB aequales sunt ei qui sub DEF. Quare et ambo simul tum qui sub GEF totus tum qui sub GIB duobus qui sub DEF et sub DIB sunt aequales. Quod erat demonstrandum. Describantur rursus Ubi puncta A, B in meridiani traiectione septentriones propius spectant quam G verticis punctum i. m. P eadem propositorum circulorum segmenta, ita ut A et B puncta magis aquilonaria sint quam punctum G. 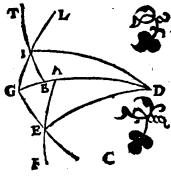Aio idem hac etiam ratione consecuturum, hoc est ambos simul angulos tum qui sub CEF tum qui sub LIB duobus qui sub DEF et DIB aequales esse. Cum enim angulus quidem sub DEF idem sit atque is qui sub DIB, aequalis autem qui sub DEC ei qui sub DIL, totus igitur qui sub LIB aequalis est ambobus simul et ei qui sub DEF et ei qui sub DEC. Quare et ambo simul tum qui sub LIB tum qui sub CEF duobus qui sub DEF et DIB sunt aequales. 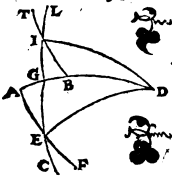Proponatur Lemmation 3, ubi punctorum A et B quae in meridiano versantur, illud propius est austro, B vero aquiloni quam G verticis punctum i. m. P autem rursus similis descriptio, ita ut orientalis quidem segmenti punctum A, scilicet quod in meridiano consistit circulo, australis sit puncto verticis G, occidentalis vero segmenti punctum B, quod in meridiano consistit circulo, ad aquilonem magis spectet quam ipsum G. Aio ambos angulos tum eum qui sub GEF tum qui sub LIB duobus qui sub DEF, et sub DIB maiores esse duorum rectorum excessu. Quoniam enim angulus quidem qui sub DIG aequalis est ei qui sub DEG, ambo vero simul tum qui sub DIG tum qui sub DIL duobus sunt rectis aequales, ambo ergo simul tum qui sub DEG tum qui sub DIL duobus rectis sunt aequales. Est autem etiam qui sub DEF angulus idem cum DIB. Quare et ambo simul tum qui sub GEF tum qui sub LIB ambobus simul, tum eo qui sub DEF, tum qui sub DIB, hoc est bis eo qui sub DEF maiores sunt excessu amborum simul, tum eius qui sub DEG tum eius qui sub DIL, qui quidem duobus sunt rectis aequales. Quod erat demonstrandum. 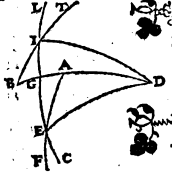Proponatur Lemmation 4, ubi punctorum A et B, quae meridianum tenent, illud boream, hoc vero austrum propius spectat quam G verticis punctum i. m. P autem, quod superest, in simili descriptione segmenti quidem orientalis punctum A in meridiano situm circulo, quod ad septentrionem propius accedat quam G, segmenti autem occidentalis punctum B in meridiano consistens, quod austrum propius spectet. Aio ambos simul angulos tum qui sub CEF tum qui sub GIB duobus qui sub DEF et DIB minores esse pro duorum rectorum quantitate. Ex iisdem enim rursus causis ambo quidem simul tum qui sub CEF tum qui sub GIB ambobus simul, eo nempe qui sub DEF et qui sub DIB, hoc est duobus qui sub DEF minores sunt pro quantitate duorum simul, eorum scilicet qui sub DEC et sub DIG. At hi duobus sunt rectis aequales, propterea quod ambo etiam simul qui sub DEC et sub DEG duobus rectis sunt aequales, aequalis autem is quoque qui sub DEG ei qui sub DIG, quod erat demonstrandum. Quod Theorema de propositis hoc capitulo tum angulis tum peripheriis, quae in meridiano et horizonte fiunt i. m. P autem ea, quam praescripsimus, ratione facile deprehendi possint quantitates tum angulorum tum peripheriarum quae ab obliquo circulo cum eo qui per verticis punctum maximus ducitur, quaeque in meridiano et horizonte fiunt, hinc manifestum erit. 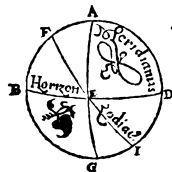Si enim describamus meridianum circulum ABGD, et horizontis semicirculum BED, zodiaci autem alterum semicirculum FEI, qui, quomodocunque se habeat, atque ipso F puncto meridianum occupante, intelligamus circulum maximum per A punctum verticis descriptum, idem efficietur cum ipso ABGD meridiano, eritque angulus sub DFE nobis idcirco datus (quoniam et punctum F et puncti angulus qui cum meridiano efficitur datus est), et ipsa a F peripheria, cum perspectum habeamus quot partibus in meridiano circulo et punctum F ab aequinoctiali et aequinoctialis ab ipso A verticis puncto distent. Quod si per exoriens ipsum E punctum intelligamus maximum circulum per A descriptum, qualis est AEG, hinc ad eundem modum perspicuum est AE omnino fore quadrantis peripheriam, propterea quod punctum A polus est horizontis BED. Sed quum (recto semper ob eandem causam qui sub AED angulo) datus sit is quem obliquus circulus cum horizonte efficit, hoc est qui sub DEI continetur, dabitur etiam totus qui sub AEI angulus. Quod erat demonstrandum. Haec igitur quum ita se habeant, manifestum est, Usus lemmatii 2 i. m. P si eorum tantum signorum quae ab initio Cancri ad Capricorni initium eos solum angulos et peripherias quae meridianum antecedunt in qualibet inclinatione colligamus, una quoque demonstratum iri ipsorum et angulos et peripherias quae meridianum sequuntur, reliquorum Usus Lemmatii 1 i. m. P autem signorum et angulos et peripherias quae meridianum tum antecedunt tum sequuntur. Ut autem in quolibet situ ad haec quoque pateat aditus, exempli rursus causa demonstrationem unico theoremate afferemus, Theorema ad propositas orientales peripherias in praedicto semicirculo investigandas i. m. P quae ad genus universum manet, supposito in eadem inclinatione, ubi aquilonaris polus supra horizontem partibus 36 eminet, Cancri initio, quod verbi gratia versus ortum una aequinoctiali hora distet a meridiano, quo certe situ Geminorum partes 16 12′ in proposito parallelo meridianum traiiciunt, oriuntur autem Virginis partes 17 37′. Sit autem meridianus circulus ABGD, et horizontis quidem semicirculus BED, zodiaci vero FITC ita ut punctum quidem 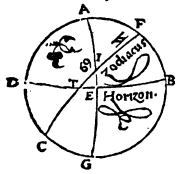I Cancri sit initium, F autem Geminorum partes 16 12′ comprehendat, T vero Virginis partes 17 37′. Atque per verticis punctum A et per Cancri initium I describatur maximi circuli segmentum AIEG. Sit autem invenienda primum AI peripheria. Constat sane peripheriam quidem FT partium esse 91 25′, IT vero partium 77 37′. Similiter autem, quum meridiani partes 23 7′ ab aequatore ad boream Geminorum quidem partibus 16 12′ comprehendantur, aequinoctialis vero a puncto verticis A distet partibus 36, erit ipsa quidem AF peripheria partium 12 53′, FB autem reliquarum ad explendum quadrantem partium 77. His datis, est rursus propter descriptionem ratio subtensae dupli arcus FB ad subtensam dupli BA composita tum ex ratione subtensae dupli arcus FT ad subtensam dupli TI tum ex ratione subtensae dupli arcus IE ad subtensam dupli arcus EA. Sed duplum peripheriae FB partium est 154 14′, quaeque ei subtenditur recta partium 16 59′, duplum vero peripheriae BA partium 180, eique subtensa partium 120. Ac rursus duplum quidem peripheriae FT partium 182 50′, quaeque ei subtenditur recta partium 119 58′, duplum autem peripheriae TI partium 155 14′, eiusque subtensa partium 117 12′. Si igitur a ratione partium 116 59′ ad 120 subducamus rationem partium 119 58′, ad 117 12′, relinquetur nobis ratio subtensae dupli arcus EI ad subtensam dupli EA, partium scilicet 114, 16 proxime ad 120, estque subtensa dupli arcus EA partium 120, quae ergo subtenditur duplicatae EI peripheriae earundem est partium 114 16′. Quamobrem duplicata quidem EI peripheria partium est 144 26′ proxime, ipsa vero IE earundem 72 13′. Reliqua igitur AI reliquarum ad complendum quadrantem partium 17 47′. Quod erat demonstrandum. Deinceps De propositis orientalibus angulis in eodem semicirculo investigandis autem etiam eum, qui sub AIT continetur, angulum hoc pacto reperiemus. 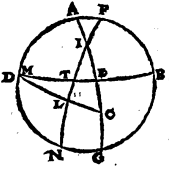Proponatur enim eadem descriptio, atque polo I, intervallo autem latere quadrati describatur maximi circuli segmentum CLM ita ut, quoniam AIE circulus per polos tum ipsius ETM tum ipsius CLM descriptus est, utraque EM et CM quadrantis sit peripheria. Rursus ergo propter descriptionem erit ratio subtensae dupli arcus IE ad subtensam dupli arcus EC composita et ex ratione subtensae dupli arcus IT ad subtensam dupli arcus TL et ex ratione subtensae dupli arcus LM ad subtensam dupli arcus CM. Atqui duplicatus IE arcus partium est 144 26′, quaeque ei subtenditur recta partium 114 16′, duplicatus vero EC arcus partium 35 34′, et quae ei subtenditur recta partium 36 38′, rursusque duplicatus TI arcus partium est 155 14′, eiusque subtensa partium 117 12′, duplicatus vero TL arcus partium 24 46′, eique subtensa partium 25 44′. Quare si a ratione partium 114 16′ ad 38 subtrahamus rationem partium 17 12′ ad 25 44′, relinquetur nobis ratio subtensae dupli arcus LM ad subtensam dupli MC, partium scilicet 72 11′ proxime ad 120, estque subtensa dupli arcus MC partium 120, unde subtensa dupli arcus LM earundem est 82 11′. Quare duplicatus quidem LM arcus partium est 86 26′, ipse vero LM earundem 43, 14. Reliquus igitur LC arcus, tum ipse, tum qui sub LIC angulus partium est 46 46′. Quamobrem etiam qui sub AIT angulus reliquarum erit ad explendum duos rectos partium 133 14′. Quod erat demonstrandum. Eadem igitur et in caeteris ratio ad ea quae proposita sunt investiganda colligitur. Nos autem ut alios quoque et angulos et arcus in promptu expositos habeamus, quorum in particularibus inquisitionibus usum fore consentaneum est, eos etiam lineari demonstratione collegimus ab eo qui per Meroen ducitur exorsi parallelo, ubi dies maximus horarum est aequinoctialum 13, ad eumque progressi qui ultra Pontum per Borysthenis ostia describitur, ubi maximus quidem dies horarum est aequinoctialium 16. Caeterum incremento in singulis usi sumus in climatibus quidem semissis rursus horae, quemadmodum et in ascensionibus, in zodiaci autem segmentis unius signi, in meridiani vero tum ad ortum tum ad occasum situ unius aequinoctialis horae. Haec autem per singula et climata et signa exponemus in tabula, cuius primae quidem partes numerum continebunt aequinoctialium horarum quibus intervallum ex utraque meridiani parte post ipsius situm notatur, secundae vero partes comprehendent quantitates peripheriarum quae a verticis puncto ad propositi signi, ut diximus, initium ducuntur, in tertiis vero et quartis partibus collocabuntur quantitates angulorum qui sub proposita sectione eo, quem definivimus, modo continentur, in tertiis quidem anguli qui ad orientalem meridiani partem situm obtinent, in quartis autem qui ad occidentalem, ut et initio distinximus. Meminisse etia decet ex duobus, qui sequente zodiaci segmento continentur, angulis eum nos semper assumpsisse qui a septentrionali eiusdem segmenti stat parte, attributa singulis quantitate, quae in uno recto partium est 90. Atque haec quidem est tabellarum descriptio.

〈II.13〉 〈CAPUT 13: Expositio praedictorum angulorum et peripheriarum in singulis climatibus〉

Tabularis angulorum et arcuum in singulis climatibus expositio. Primi Climatis per Meroen, horarum 13, latitudinis 16 27′

Secundi Climatis per Syenen, horarum 13 30′, latitudinis 23 51′