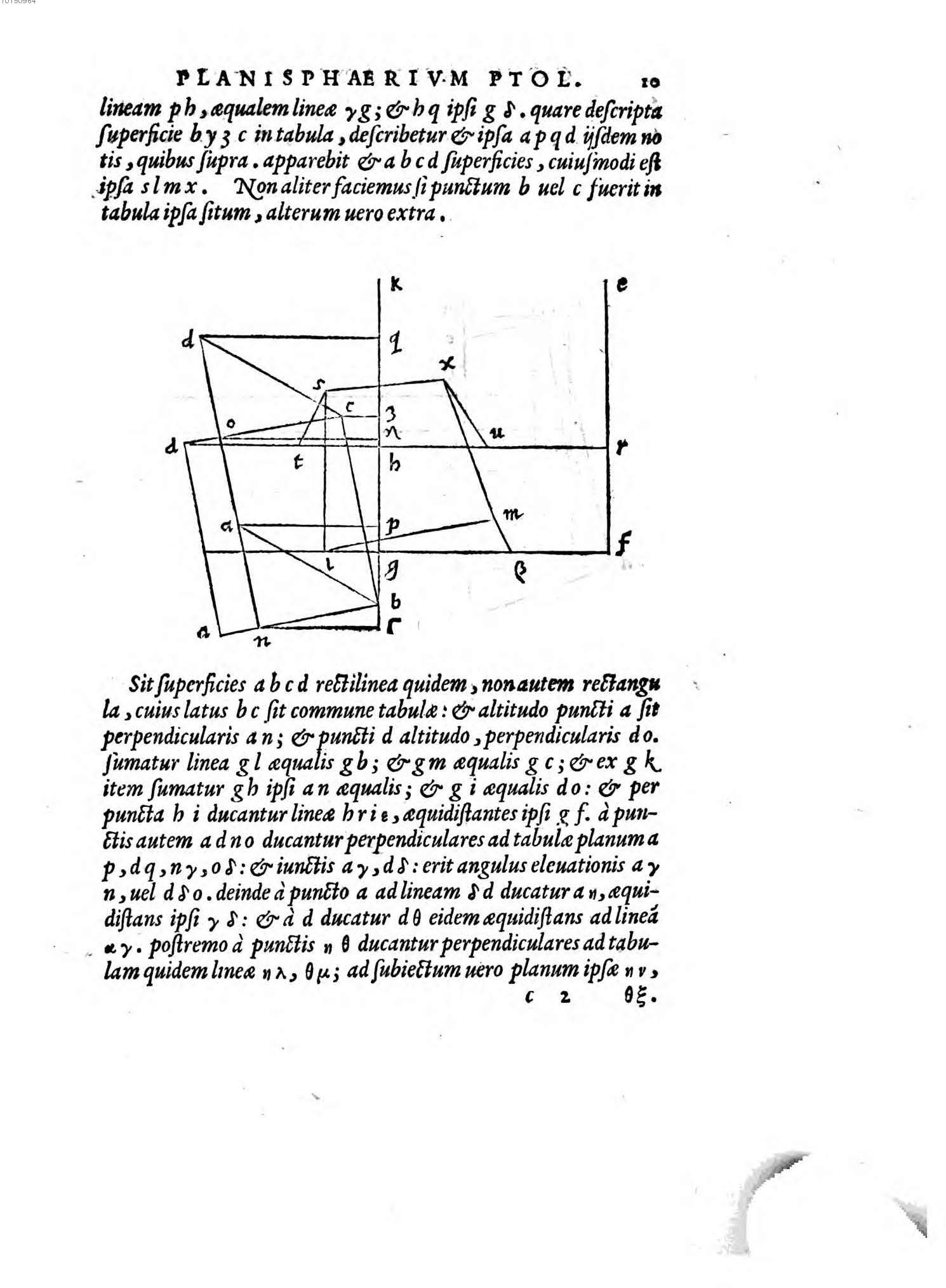
lineam PH aequalem lineae γG et HQ ipsi Gδ; quare descripta superficie BYʒC in tabula describetur et ipsa APQD iisdem notis quibus supra apparebit, et ABCD superficies cuiusmodi est ipsa SLMX. Non aliter faciemus, si punctum B vel C fuerit in tabula ipsa situm, alterum vero extra.

Sit superficies ABCD, rectilinea quidem, non autem rectangula, cuius latus BC sit commune tabulae, et altitudo puncti A sit perpendicularis AN, et puncti D altitudo perpendicularis DO. Sumatur linea GL aequalis GB et GM aequalis GC, et ex GK item sumatur GH ipsi AN aequalis et GI aequalis DO, et per puncta H I ducantur lineae HRIε aequidistantes ipsi GF. A punctis autem A D N O ducantur perpendiculares ad tabulae planum AP, AP] read αP DQ, Nγ, Oδ, et iunctis Aγ, Aγ] read αγ Dδ erit angulus elevationis AγN AγN] read αγN vel DδO. Deinde a puncto A A] read α ad lineam δD ducatur AN AN] read αN aequidistans ipsi γδ, et a D ducatur Dθ Dθ] read Dδ eidem aequidistans ad lineam αγ. Postremo a punctis N θ ducantur perpendiculares ad tabulam; quidem lineae ηλ, θμ ad subiectum vero planum ipsae ην,