Federici Commandini Urbinatis in Planisphaerium Ptolemaei commentarius

In hoc libro rationem tradit Ptolemaeus, qua circulos omnes sphaerae caelestis in plano describere possimus, ex quorum descriptione ipsius etiam caeli imago repraesentatur. Sed cum id simpliciter faciat nec demonstrationes adhibeat magna ex parte, ego antequam ad verborum interpraetationem accesserim, generatim atque universe de hoc toto genere mihi scribendum esse iudicavi. Qua in re quantum fieri potuit, brevitatem secutus sum. Addidi necessarias mathematicorum demonstrationes, ne quis omnino scrupulus relinquatur qui studiosos solicitet. Quamvis non ignorem fieri posse ut ego, qui primus hanc viam et obscuram et difficilem sum ingressus, aliquid offenderim, tamen hoc periculum subire malui quam studiosis non prodesse. Fortassis enim alii a me invitati, quae in praesentia quodammodo inchoata sunt, ea facilius perficient et absolvent.

Figuram visam, quemadmodum appareat in proposito plano describere. Quod quidem nihil aliud est nisi describere communem sectionem plani propositi et conorum vel pyramidum visualium, quibus figura ipsa spectatur.

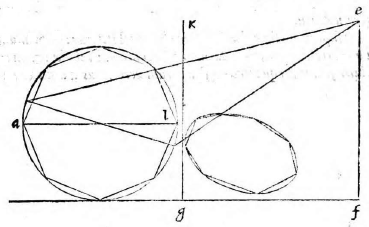
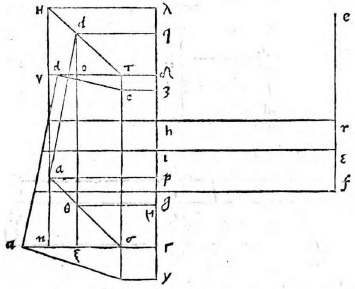
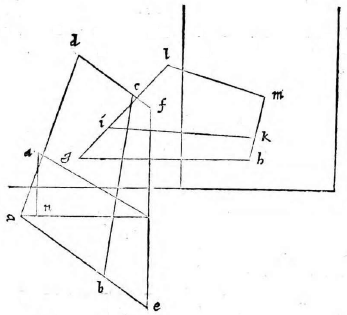
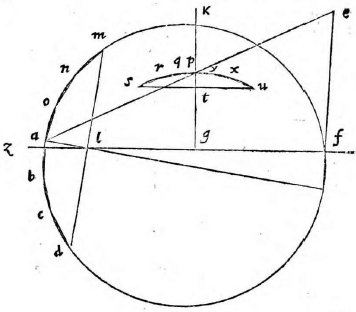
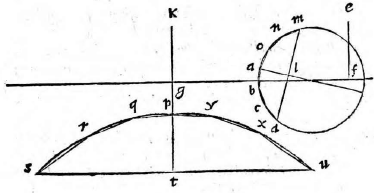
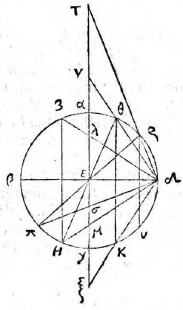
Planum propositum, in quo figuram describi oportet (quod vulgo parietem nos non inepte tabulam dicemus), sit perpendiculariter erectum super horizontem. Figura autem vel erit superficies vel corpus; si superficies, vel rectilinea vel curvilinea, vel ex his mixta, et vel horizonti aequidistans vel super horizontem elevata; praeterea vel erit ultra propositum planum, vel citra, vel partim ultra, partim citra. Sit primum ea superficies ultra propositum planum, hoc est ultra tabulam constituta,

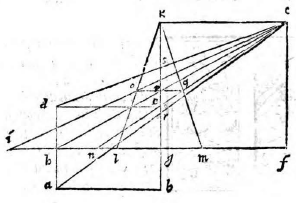
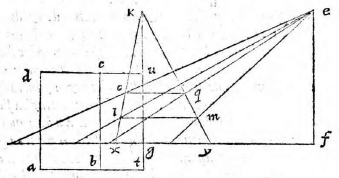
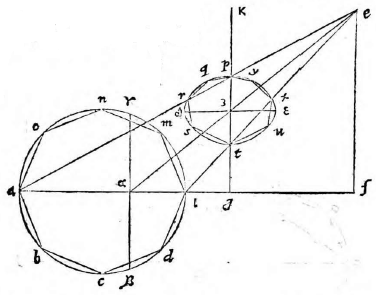
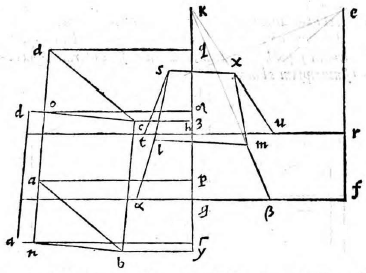
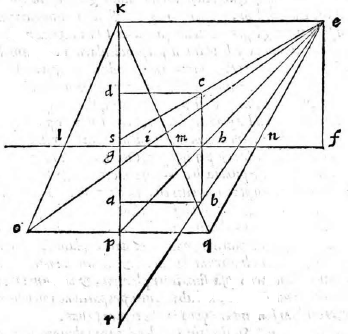
sitque horizonti aequidistans et rectangula, ut ABCD, cuius unum latus BC sit in tabula ipsa situm. Et siquidem oculus ponatur esse in eodem plano, in quo figura visa apparebit, ea linea una, quae videlicet communis sectio est plani in quo est figura et ipsius tabulae. Si vero ponatur extra illud planum, ut in E, sit altitudo eius a plano linea EF, et a puncto F ad lineam BC vel ad ipsam protractam ducatur perpendicularis, producaturque ut secet BC in G et AD in H. Deinde a puncto G elevetur GK perpendicularis ad GH, quae sit aequalis ipsi FE. Erunt igitur FE, GK inter se aequidistantes, cum utraeque sint super idem planum perpendiculariter erectae (6, undecimi). (6, undecimi)] Euclid, Elements XI.6 Itaque intelligatur figura quidem ABCD sita in eo plano, cuius recta linea est FG; tabula autem in plano, cuius recta linea GK, ita ut plani per lineas EF, FG ducti, et tabulae communis sectio sit linea GK; at vero tabulae et plani in quo superficies ABCD, communis sectio sit linea BC. Oportet iam figuram ABCD describere in tabula GK, quemadmodum oculo in E posito appareat, cuius altitudo a plano linea EF, ut dictum est, distantia autem a tabula linea FG. Sumatur in ipsa FG a puncto G linea GL, aequalis ipsi GB, et GM aequalis GC; sumatur quoque LI aequalis BA et MN aequalis CD et ducantur LK, KM, HE, IE, NE. Secet autem IE lineam LK in puncto O, et HE secet GK in P, et NE ipsam MK in Q, et iungantur puncta O P Q, quae erunt in linea una aequidistanti lineae LM, ut monstrabitur (33, primi). (33, primi)] Euclid, Elements I.33 Dico figuram ABCD in tabula talem apparere qualis est ipsa OLMQ. Ductis enim lineis AE, DE et ducta KE, quae aequidistabit ipsi GF, fiet triangulum OIL simile triangulo OEK, nam angulus IOL est aequalis angulo EOK et angulus OLI aequalis ipsi OKE, reliquus igitur angulus reliquo aequalis. Et eodem modo monstrabitur triangulum PHG simile triangulo PEK et QNM ipsi QEK; quare, ut EK ad KO, ita IL ad LO. Et permutando, ut EK ad IL, ita KO ad OL. Et similiter monstrabitur, ut EK ad GH, ita KP ad PG et ut EK ad MN, ita KQ ad QM. Sed EK ad LI eandem habet proportionem quam ad GH et item eandem quam ad MN, cum aequales sint lineae LI, GB, GB] read GH MN, ergo KO ad OL eandem habet quam KP ad PG et quam KQ ad QM. Unde sequitur ex secunda sexti puncta O P Q in eadem esse linea ipsi LM aequidistanti. Constat praeterea punctum H in tabula apparere, ubi est P et G in eodemmet puncto. Verum cum linea GL sit aequalis lineae GB et GM ipsi GC, si manente linea GK triangulum KLM intelligatur circumferri quousque linea GL perveniat ad GB, cadet punctum L in B et M in C et erunt puncta B C communia utrique figurae, quare ex iisdem locis ad oculum pertingent.

Intelligatur quoque planum ex AD perpendiculariter erectum super horizontem, hoc est super planum in quo est ABCD, ut sit ipsius et trianguli EAD communis sectio linea AD, erit illud tabulae aequidistans, trianguli vero EAD et tabulae communis sectio sit RS, quare lineae AD, RS inter se aequidistantes erunt; sed sunt aequidistantes et ipsae AD, BC, ergo R S in qua est etiam punctum P ipsi BC aequidistabit. Itaque cum linea LM applicuerit lineae BC et linea OQ applicabit se ipsi RS et fiet una atque eadem linea, nam quatuor puncta O Q R S sunt in eodem plano in quo est P, aequidistanti ipsi plano figurae visae. Cadet etiam punctum O in R et Q in S, quoniam linea PO est aequalis lineae PR et PQ ipsi PS. Est enim propter similitudinem triangulorum EHA, EPR, ut EH ad HA, ita EP ad PR. Et permutando, ut EH ad EP, ita HA ad PR. Rursus eadem ratione, ut KG ad GL, ita KP ad PO. Et permutando, ut KG ad KP, ita GL ad PO. Est etiam propter similitudinem triangulorum HPG, EPK, ut EP ad PK, ita HP ad PG. Et permutando, ut EP ad PH, ita KP ad PG. Componendoque et per conversionem rationis, ut EH ad EP, ita KG ad KP. Erat autem, ut EH ad EP, ita HA ad PR, et ut KG ad KP, ita GL ad PO. Ut ergo HA ad PR, ita GL ad PO. Et permutando, ut HA ad GL, ita PR ad PO. Quod cum sit aequalis GL ipsi HA, quoniam utraeque sunt aequales, eidem GB erit et PO ipsi PR aequalis, et ita demonstrabitur PQ aequalis ipsi PS. Cum igitur puncta B C videantur in punctis L M figurae descriptae et puncta A D in ipsis OQ, videbitur et tota linea BC in tota LM, et AD linea in linea OQ. Et idcirco BA in LO et CD in MQ, quare tota figura ABCD apparebit in tabula ea forma qua descripsimus ipsam OLMQ.

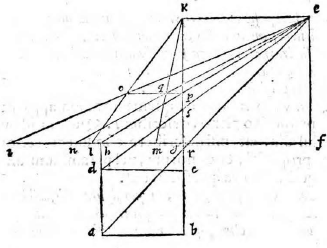
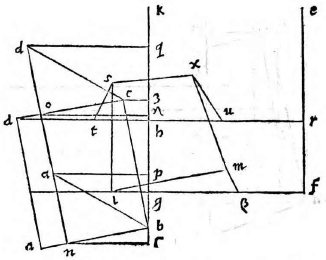
Aliter. Sit ut in superioribus superficies ABCD quam describere oporteat oculi altitudo EF et tabula cuius recta linea GK. Ducantur autem lineae FA, FD, ita ut FA secet ipsam BC in puncto I et FD secet eandem in N. Et rursus linea FG secet AD in H, in qua sumatur a puncto G linea GL aequalis ipsi GB et GM aequalis GC. Sumatur quoque ex parte L linea GT aequalis ipsi GI et ex altera parte GU aequalis GN et ducta HE, quae secet GK in P. Per P ducatur linea OQ aequidistans ipsi LM. Deinde per puncta T U ducantur lineae ad LM perpendiculares, ita ut per T ducta secet lineam OQ in O et ducta per U secet in Q. Aequidistabunt lineae TO, UQ inter sese et ipsi GP (6, undecimi). (6, undecimi)] Euclid, Elements XI.6 Quare TP, PU parallelogramma erunt et linea OP aequalis erit lineae TG et PQ ipsi GU (34, primi). (34, primi)] Euclid, Elements I.34 Postremo iungantur LO, MQ. Dico figuram ABCD in tabula GK apparere qualis est ipsa OLMQ. Ducantur enim rursus AE, DE, intelligaturque ex AD planum perpendiculariter erectum super planum, in quo superficies ABCD, quod erit tabulae aequidistans, et intelligatur triangulum EAD secans utrunque, ut sit ipsius et plani per AD communis sectio. Linea AD, eiusdem vero et tabulae communis sectio RS erunt eadem ratione lineae AD, RS aequidistantes et propterea aequidistantes ipsae RS 〈et〉 BC (16 et 9, undecimi). (16, 9 undecimi)] Euclid, Elements XI.16 and XI.9 Quod cum triangula EAF, EDF sint

perpendiculariter erecta super idem planum. Transeunt enim per lineam perpendicularem EF, erunt ipsorum ipsorum] ipsornm V et tabulae communes sectiones IR, NS perpendiculares ad IN et aequidistantes lineae GP (18 et 19, undecimi). (18, 19, undecimi)] Euclid, Elements XI.18 and XI.19 Et idcirco parallelogramma erunt ipsa IP, PN et linea RP aequalis lineae IG et PS ipsi GN. Demonstratum autem est lineam OP aequalem lineae TG et PQ ipsi GU. Facta est praeterea TG aequalis ipsi IG et GU aequalis GN, erit ergo linea OP aequalis RP et PQ ipsi PS. Itaque si manente linea GP superficies OLMQ circumferatur adeo, ut linea GL applicet lineae GB, applicabit et PO ipsi PR, et parallelogramma item TP, PU parallelogrammis IP, PN. Quare cadet punctum L in B, M in C, O in R et denique Q in S. Cum igitur puncta B C videantur in punctis L M et AD in ipsis OQ, videbitur et tota superficies ABCD in tota OLMQ atque erit in tabula GK descripta figura qualis est ipsa OLMQ, ut oportebat.

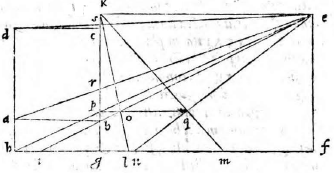
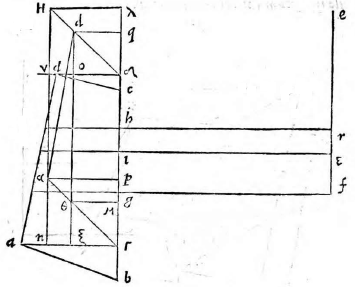
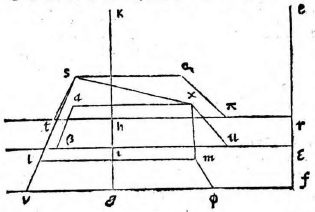
Si vero latus BC vel aliud quodvis non sit commune tabulae, sed tamen ei aequidistet, ut in subiecta figura, producemus latera

ABCD usque ad tabulam in puncta T U et ex iis quae proxime dicta sunt describemus superficiem rectangulam BTUC, quae sit LXYM. Rursus describemus superficiem ATUD, quae sit OXYQ. Cum igitur puncta A B C D videantur in ipsis OLMQ, erit ipsa OLMQ figura quam describere oportebat. Eodem modo procedemus in reliquis huiusmodi.

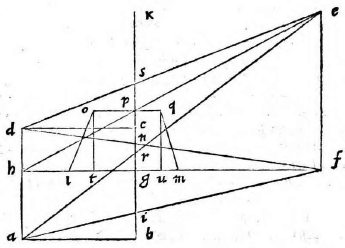
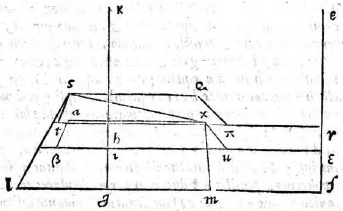
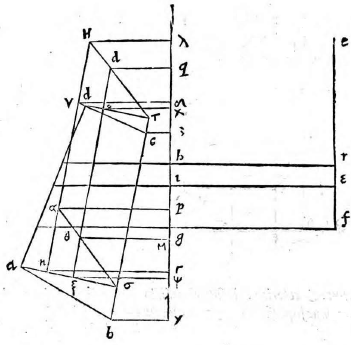
Sit superficies ABCD rectilinea quidem, non autem

rectangula, cuius latus BC sit commune tabulae. Maneant etiam eadem quae in superioribus, et a punctis A D ad lineam BC perpendiculares ducantur AN, DO. Sumantur quoque GP aequalis ipsi GN, GQ aequalis GO, PR aequalis NA et QS aequalis OD et ducantur PK, KQ. Ducaturque RE secans PK in T et S〈E〉 secans QK in U. Iungantur demum LT, TU, UM. Dico figuram ABCD apparere ea forma qua descripta est LTUM. Ducatur enim ab A puncto ad lineam DO ipsa AX aequidistans BC et a puncto D ad NA ducatur DY eidem aequidistans, atque ex iis quae tradita sunt describatur in proposito plano figura rectangula ANOX, quae sit TPQʒ et rursus describatur alia YNOD, sitque ωPQU. Quoniam igitur puncta B C apparent in LM, punctum vero A apparet in T et D in U, apparebit linea AB in ipsa TL, BC in LM, CD in MU et DA in UT. Quare tota figura ABCD in ipsa TLMU apparebit.

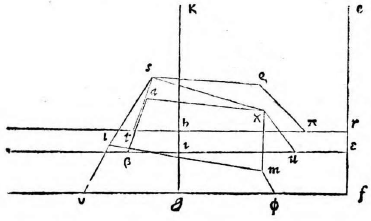
At cum superficies ABCD a tabula distans quomodocunque sit posita, a punctis A B C D ducemus lineas AL, BM, CN, DO

perpendiculares ad lineam GK, videlicet ad ipsam tabulam, et describemus figuras ABML, DCNO ex iis quae proxime diximus, quae sint PQSR, UTYʒ ita ut PQSR respondeat ipsi ABML et UTYʒ ipsi DCNO et iungemus PU, QT; erit figura PQTU quam describere oportebat. Similiter faciemus in aliis figuris quibuscunque.

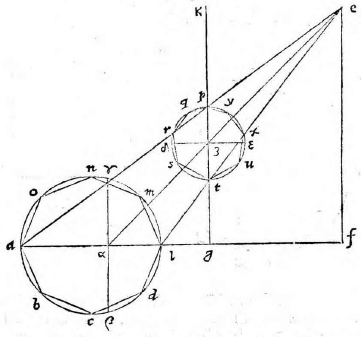
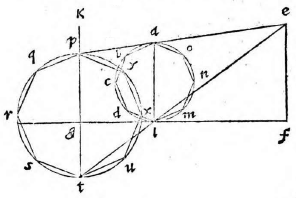
Sit circulus et in eo descripta figura, quae multis lateribus contineatur ABCDLMNO, et sit AL circuli diameter in eadem recta linea ipsi GF. Itaque figuram ABCDLMNO in tabula

describemus, quemadmodum superius traditum est, quae sit PQRSTUXY. In medio autem lineae PT, quae refert AL circuli diametrum, sumatur punctum ʒ; ductaque Eʒ producatur ad planum in quo circulus est, occurrens lineae AL in α et per α ad angulos rectos ipsi AL, ducatur βαγ, quae secet circulum in punctis β γ et ipsi βαγ respondens in tabula ducatur δʒε. Apparebit circulus ABCDLMNO, vel circulus vel ellipsis, cuius centrum ʒ et ipsae PT, δε diametri erunt. Intelligatur enim conus basim habens circulum ABCDLMNO, verticem vero punctum E, et quoniam is secatur plano coeunte cum utroque latere trianguli per axim, ita ut plani in quo est basis et plani secantis, ipsius scilicet tabulae communis, sectio sit recta linea perpendicularis ad basim trianguli per axim, vel ad eam quae est in eadem ipsi recta linea, si quidem planum secans subcontrarie ponatur plano in quo est basis coni. Hoc est, si triangula EAL, ETP similia

sint ut in prima figura, sectio circulus erit ex quinta primi conicorum; sin minus, erit ellipsis ex decimatertia eiusdem ut in secunda. Quare descripto circulo vel ellipsi, ut opus fuerit, circa diametros PT, δε cadent in ipsis puncta P Q R S T U X Y et quodcunque aliud punctum in circumferentia circuli ABCDLMNO sumptum sit similiter atque in superioribus cadere demonstrabitur in communi eorum sectione, hoc est in ipsa circuli circumferentia vel ellipsi. Circulus ergo ABCDLMNO tali forma apparebit in proposita tabula qualis est ea quae a nobis descripta fuerit.

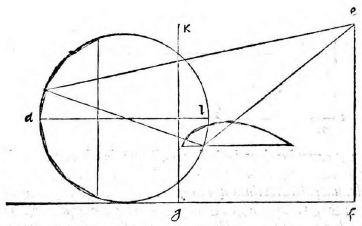
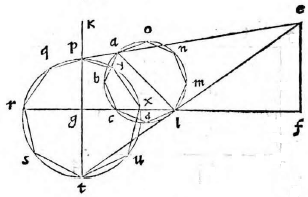
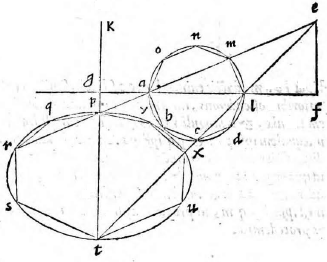
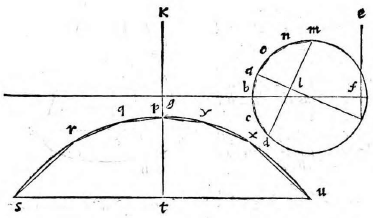
Sit circuli portio et in ea figura multorum laterum ABCDLMNO, cuius basis DM et diameter AL. Sitque AL similiter in ea

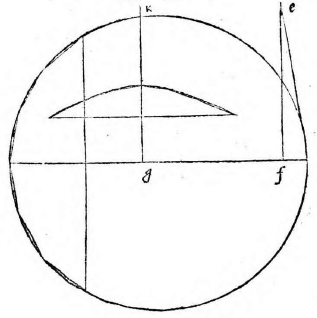
dem recta linea ipsi GF. Rursus figuram describemus, quae sit PQRSTUXY, ita ut PT linea respondeat ipsi AL diametro et SU ipsi basi DM. Itaque completo circulo, si planum tabulae circulum non secet, erit communis sectio transiens per puncta figurae descriptae, vel circuli portio, vel ellipsis, quod superius est demonstratum. Si vero secet circulum, rursus intelligatur conus, basim habens circulum dictum, et verticem punctum E. Vel ergo diameter sectionis coni factae a plano aequidistans est alteri lateri trianguli per axim, vel non est aequidistans. Et si non est aequidistans, vel coit cum eo ad partes verticis, hoc est extra verticem coni, vel ad partes basis. Si sit aequidistans, ut in prima figura, erit ea sectio parabole, cuius diameter PT ex undecima primi conicorum.

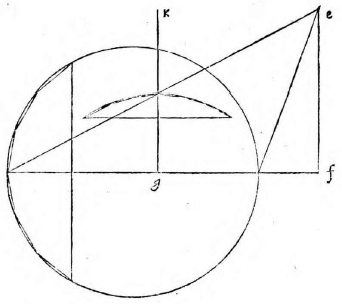
Quod si non sit aequidistans et coeat cum eo ad partes verticis, ut in secunda figura, erit hyperbole ex duodecima eiusdem. Si denique coeat ad partes basis, erit portio circuli vel ellipsis, nam

 producto cono et plane secante complebitur, et circulus vel ellipsis ex quinta et decimatertia primi conicorum.

At vero, cum circuli ABCDLMNO diameter AL non sit in eadem recta linea, ipsi GF communes sectiones non erunt, neque circuli neque ellipses, quoniam plani, in quo est coni basis et tabulae ipsius, communis sectio non erit recta linea perpendicularis

ad basim trianguli per axim, vel ad eam, quae in eadem ipsi recta linea constituitur, et pariter continget cum portionis circuli ABCDLMNO diameter AL non sit in eadem recta linea, ipsi GF, nam sectiones non erunt, neque paraboles, neque hyperboles, neque circuli vel ellipsis portiones. Quare, quo pluribus lateribus constabunt figurae in circulo vel circuli portione descriptae, eo aptius formae in tabula delineabuntur ductis, scilicet, lineis curvis, quae earum angulos apposite coniungant, quemadmodum res ipsa exigere videatur.

Si superficies super horizontem elevata statuatur, sit primum ABCD rectangula, cuius latus BC sit commune tabulae et in eo plano situm, in quo linea GF. Alterum vero latus AD ita

elevetur, ut angulus elevationis sit aequalis angulo ABN; quare altitudo eius erit perpendicularis a puncto A vel D ducta ad ipsum planum, videlicet, linea AN vel DO. Sumatur igitur GL aequalis GB et GM aequalis GC, et ex GK sumpta, GH aequali ipsi NA per H ducatur HR aequidistans GF, quae secet EF in R. Iungantur autem NB, NO, OC et a punctis A D ad tabulae planum perpendiculares ducantur AP, DQ. Erit iam superficies APQD in eodem plano, in quo linea HR, atque erit aequalis et similis superficiei NBCO. Quoniam enim lineae AN, PB perpendiculares sunt super idem planum, aequidistant inter sese (6, undecimi); (6, undecimi)] Euclid, Elements XI.6 sunt autem et aequales, ergo sequitur, ut lineae NB, AP aequales sint, et aequidistantes; eadem quoque ratione demonstrabuntur aequales et aequidistantes lineae OC, DQ et ipsae NO, AD et BC, PQ (33, primi). (33, primi)] Euclid, Elements I.33 Sed cum lineae APQ continentes angulum P aequidistent lineis NBC, quae continent ipsum B angulum, erunt anguli B, P aequales, et pariter aequales anguli C, Q et ipsi O, D et N, A (10, undecimi). (10, undecimi)] Euclid, Elements XI.10 Quare, et superficies APQD aequalis et similis erit superficiei NBCO. Praeterea, cum lineae BP, GH inter se aequidistantes aequales sint, [et] lineae PH, BG erunt aequales et eadem ratione aequales ipsae HQ, GC. Itaque sumpta linea HT aequali ipsi GB et HU aequali GC, superficiem APQD describemus in tabula GK, quemadmodum apparet oculo in E posito, cuius altitudo a plano est linea ER, sitque STUX; et quoniam puncta B C videntur in punctis L M et puncta A D in ipsis S X iunctis LS, MX, apparebit ABCD superficies elevata super horizontem ut dictum est ea forma, qua descripsimus ipsam SLMX.

Sed cum latus BC non sit tabulae commune, quanquam in eodem plano situm, in quo linea GF sit primo ipsi aequidistans, ut in secunda figura, et latus AD a plano similiter elevatum, quanta est linea AN vel DO. Iungantur NB, NO, OC et producatur NB usque ad tabulam in punctum Y, et OC producatur in Z. Erit ex proxime demonstratis superficies APQD in eo plano sita, in quo linea HR aequalis et similis superficiei NYZO, et linea item PH aequalis lineae YG et HQ ipsi GZ. Itaque primum superficiem BYZO BYZO] read NYZO in tabula describemus, quae sit LαβM; deinde describemus ipsam APQD et sit STUX. Puncta ergo B C videbuntur in punctis B M et puncta A D in ipsis S X; quare, iunctis LS, MX, apparebit tota figura ABCD in tabula, qualis est ipsa SLMX.

Sit deinde latus BC non aequidistans tabulae et maneant eadem prioribus. A punctis autem N B C O ducantur

perpendiculares ad tabulam Nγ, BY, Cʒ, Oδ. Similiter demonstrabimus superficiem APQD aequalem et similem esse superficiei NγδO et lineam PH aequalem lineae γG et HQ ipsi Gδ; quare descripta superficie BYʒC in tabula describetur et ipsa APQD iisdem notis quibus supra apparebit, et ABCD superficies cuiusmodi est ipsa SLMX. Non aliter faciemus, si punctum B vel C fuerit in tabula ipsa situm, alterum vero extra.

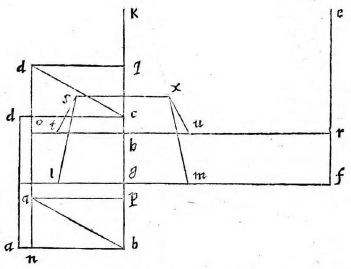
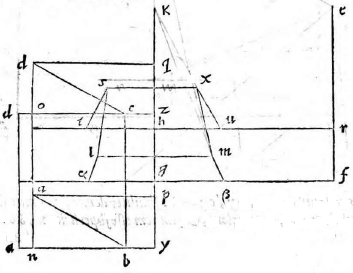
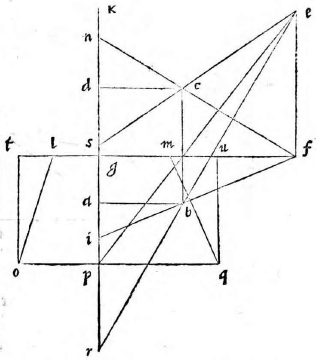
Sit superficies ABCD, rectilinea quidem, non autem rectangula, cuius latus BC sit commune tabulae, et altitudo puncti A sit perpendicularis AN, et puncti D altitudo perpendicularis DO. Sumatur linea GL aequalis GB et GM aequalis GC, et ex GK item sumatur GH ipsi AN aequalis et GI aequalis DO, et per puncta H I ducantur lineae HRIε aequidistantes ipsi GF. A punctis autem A D N O ducantur perpendiculares ad tabulae planum AP, AP] read αP DQ, Nγ, Oδ, et iunctis Aγ, Aγ] read αγ Dδ erit angulus elevationis AγN AγN] read αγN vel DδO. Deinde a puncto A A] read α ad lineam δD ducatur AN AN] read αN aequidistans ipsi γδ, et a D ducatur Dθ Dθ] read Dδ eidem aequidistans ad lineam αγ. Postremo a punctis N θ ducantur perpendiculares ad tabulam; quidem lineae ηλ, θμ ad subiectum vero planum ipsae ην, θξ. Erit ex iis quae demonstrata sunt, superficies APλη APλη] read αPλη aequalis et similis superficiei Nγδν et in eo plano sita, in quo linea HR

et superficies θμQD aequalis et similis ipsi ξγδO et in eo plano, in quo Iε. Superficiem ergo αPλη describemus in tabula, quae sit STπρ, et describemus ipsam θμQD, quae sit αβUX, et ductis LS, MX, XS erit ipsa SLMX superficies, quam describere oportebat. In figura autem huius et in duabus sequentibus, ne nimia linearum inculcatio confusionem pareret, visum est seorsum ponere et ad superficiem describendam ABCD et ipsam figuram in tabula descriptam.

Si vero latus BC aequidistet tabulae, secet linea Nγ perpendicularis ad tabulam ducta ipsam BC in σ et Oδ secet eandem in τ, iunctisque Aσ, Dτ, angulus elevationis erit AσN vel DτO. Compleantur rursus Aστη, θστD superficies aequidistantium

laterum et ceteris modo superius dicto manentibus. Primum describemus superficiem BγʒC, BγʒC] read BYʒC quae sit LυφM, deinde ipsas APλη, θμQD, quae sint STπρ, AβUX et iunctis LS, MX, XS, sequitur superficiem SLMX eam esse, quam describere volebamus.

Quod si non aequidistet cetera, sint eadem superioribus, ducatur autem ab O puncto ad tabulam perpendicularis Oχ, et a puncto ξ ducatur perpendicularis ξψ, erit superficies θμQD aequalis et similis superficiei ξψχO, et alia similiter eodem modo.

Sit superficies ABCD a plano quomodocunque elevata et intelligatur producta ad subiectum planum ita ut communis eorum sectio sit recta linea EF; altitudo puncti A linea AN, et describantur in proposita tabula superficies BEFC, AEFD, ut superius dictum est, quae sint IGHK, LGHM. Erit ipsa LIKM superficies, quam describere oportebat. Simili modo faciemus in omnibus aliis superficiebus rectilineis, quaecunque super horizontem fuerint elevatae.

Sit circulus ABCDLMNO super horizontem elevatus, et diametri ipsius AL; punctum L sit in plano, in quo linea FG, punctum vero A ab eo elevatum ut angulum faciat ALZ, et descripta figura in tabula KG, quae sit PQRSTUXY, ducantur lineae AE, EL. Itaque si planum, in quo circulus ABCDLMNO sit, tabulae aequidistans, erit figura PQRSTUXY circulus ex quarta primi conicorum; nam conus EAL secabitur plano aequidistanti basi. Si vero non sit aequidistans et communis eorum sectio sit recta linea perpendicularis ad basim trianguli per axim, vel ad ipsam productam, talis figura vel circulus erit, vel ellipsis; circulus quidem cum tabulae planum plano basis subcontrarie ponatur ex quinta primi conicorum. Ellipsis vero cum aliter quomodocunque, ex decimatertia eiusdem, alioqui neque circulus erit, neque ellipsis, sed alia quaedam irregularis figura.

Rursus sit circuli portio super horizontem elevata ABCDLMNO et sit eius basis DM in plano, in quo linea FG; diameter vero AL ad idem planum angulum faciat qualis ALZ, et describatur figura. Erit ipsa quandoque vel circuli portio, vel ellipsis, vel paraboles, vel hyperboles; quandoque neutra earum secundum planorum inter sese positionem, ut superius est demonstratum.

Sit superficies ABCD citra datum planum, hoc est citra tabulam constituta et horizonti aequidistans, cuius latus AD sit commune tabulae. Sitque tabulae ipsius recta linea GK, oculi altitudo

EF et distantia FG ut in superioribus secet. Autem FG ipsam BC lineam in H sumatur; rursus GL ipsi GA aequalis et GM aequalis GD; et a puncto L versus F sumatur LI aequalis AB et MN aequalis ipsi DC; ducanturque LK, KM, IE, HE, EN ita ut EI secet KL productam in O et EH secet KG item productam in P; et EN ipsam KM in Q et iungantur OP, quae erunt in linea una ipsi LM aequidistanti. Dico superficiem ABCD in tabula apparere ea forma qua est ipsa LOQM; nam ductis KE, BE, EC demonstrabitur ex iis quae superius dicta sunt lineam KO ad OL eandem habere proportionem quam KP ad PG et quam KQ ad QM. Quare, dividendo KL ad LO, habebit eandem quam KG ad GP et KM ad MQ; et idcirco aequidistabit LM ipsi OQ. Itaque punctum H in tabula apparet in P et G in eodemmet puncto. Et cum linea GL sumpta sit aequalis lineae GA et GM ipsi GD, si triangulum KLM manente KG eousque circumvolvatur quousque linea GL perveniat ad GA, cadet L in A et M in D. Intelligatur autem ex CB planum perpendiculariter erectum super horizontem et triangulum EBC producatur usque ad tabulam ut sit eorum communis sectio linea RS. Demonstrabitur similiter ipsam RS in qua est P aequidistare ipsi AD; quare linea LGM applicata ad AGD applicabitur et OPQ ad RPS; cadetque O in R et Q in S, nam eadem ratione demonstrabitur lineam PO ipsi PR aequalem esse et PQ ipsi PS. Cum igitur puncta A D videantur in LM et puncta B C in OQ, videbitur et tota figura ABCD in proposito plano qualis est ipsa LOQM. Eadem ratione describentur et aliae superficies, sive horizonti aequidistantes fuerint sive ab eo elevatae; nihil enim differt harum descriptio a descriptione illarum quae ultra datum planum statuuntur, nisi sumptione linearum LI, MN et similium. Nam quemadmodum superficies ipsae sunt inter planum et oculum, ita et hae lineae a punctis L M vel ab iis quae proportione respondent versus oculum sumuntur, quod in illis contra fiebat.

Aliter. Sit superficies ABCD citra tabulam GK, altitudo oculi EF et distantia FG secet autem FG ipsam BC in H et ducantur FB, FC et producantur usque ad lineam GK in puncta I N. Rursus sumatur GL aequalis ipsi GA et GT aequalis GI, atque ex altera parte sumatur GM aequalis GD et GU aequalis GM; GM] read GN ductaque EH et producta usque ad lineam GK in punctum P, per P ducatur OPQ aequidistans ipsi T〈G〉U et a punctis T U ducantur ipsae TO, UQ perpendiculares ad eandem et postremo iungantur LO, MQ. Dico superficiem ABCD in tabula apparere

velut est ipsa LOQM. Ductis enim EBR, ECS lineis similiter atque in superioribus, ostendemus lineam RS communem, videlicet sectionem tabulae et trianguli RES, aequidistantem esse lineae AD et OP, aequalem ipsi PR et PQ, ipsi PS. Quare, si manente linea GP superficies LOQM circumducatur quousque linea GL transeat ad ipsam GA, transibit et L punctum ad punctum A, M ad D, O ad R et Q ad S, et videbitur superficies ABCD in tabula qualis est ipsa LOQM ut proponebatur. Et eodem modo in aliis procedemus.

Sit circulus ABCDLMNO citra datum planum, qui in eo describatur ut dictum est, et siquidem circulus dato plano aequidistet aut subcontrarie ponatur figura descripta, circulus erit quod inferius demonstrabitur; sin minus, vel erit ellipsis vel aliud quidpiam ad eius formam accedens.

Circuli autem portio descripta vel erit circuli vel ellipsis portio vel paraboles vel hyperboles vel alia figura similis. Horum autem omnium ratio patet ex antedictis.

Sit conus cuius vertex punctum A, basis circulus BC, intelligaturque conus produci et secari plano ipsi BC circulo aequidistanti, ut sit sectio in superficie coni linea DE. Dico ipsam DE circulum esse, qui centrum habet in axi. Sit enim F centrum circuli BC, et ducta AF producatur usque ad secans planum in G; erit AG coni axis. Itaque secetur conus plano per axem ducto, et sint plani secantis et aliorum planorum communes sectiones rectae lineae BC, DE. Sumatur praeterea in linea DE quodvis punctum H, et iuncta GH rursus per ipsam et per axem ducatur aliud planum secans circulum BC in linea KF; erunt rectae lineae BC, DE et KF, HG aequidistantes, quoniam plana aequidistantia esse posuimus. Quare et ipsa ABF, ADG,

AFC, AGE, AKF, AHG triangula erunt similia; ergo ut AF ad AG, ita FB ad GD, FC ad GE et FK ad GH. Quod cum tres lineae FB, FC, FK sint aequales, et ipsae GD, GE, GH aequales erunt et eadem ratione demonstrabuntur aequales lineae omnes a puncto G ad ipsam DE ductae; circulus igitur est linea DE centrum habens in axi cuius diameter est recta linea DE, communis videlicet sectio planorum.

Sit conus cuius vertex A, basis circulus BC, seceturque plano per axem perpendiculariter erecto ad circulum BC, et sit sectio triangulum ABC. Et producatur conus et planum secans per axim, seceturque alio plano basi subcontrario posito, quod faciat sectionem in superficie coni lineam DE, ita ut AED angulus sit aequalis angulo ABC. Dico sectionem DE circulum esse; sumantur enim in lineis BC, DE puncta quaevis F G, et ab ipsis ad planum per triangulum ABC perpendiculares ducantur FH, GK. Cadent profecto HAE in communes planorum sectiones atque inter se aequidistantes erunt. Itaque per K ducta linea LKM ipsi BHC aequidistanti erit planum ductum per GK, LM aequidistans circulo BC, qui est basis coni; quare sectio circulus erit, cuius diameter LM et rectangulum LKM aequale quadrato QK. QK] read GK Sed cum linea LM aequidistans sit ipsi BC, erit angulus ALM aequalis angulo ABC; hoc est ipsi AED suntque anguli ad K aequales. Simile est igitur triangulum LKD triangulo EKM, et ut LK ad KD, ita EK ad KM; quare rectangulum LKM aequale est rectangulo DKE. Est autem quadrato GK aequale rectangulum LKM ut ostensum est; ergo et rectangulum DKE quadrato GK aequale erit.

Similiter demonstrabimus quadrata perpendicularium omnium, quae a DGE linea ad ipsam DE ducuntur, aequalia esse rectangulis ex partibus DE; unde sequitur sectionem DGE circulum esse, cuius diameter DE.

Sit conus ABC ut dictum est et producatur, seceturque plano per axem. Secetur autem et alio plano non aequidistanti basi neque ei subcontrarie posito, quod faciat sectionem DE, ita ut communis sectio planorum sit recta linea perpendicularis ad basim trianguli per axim vel ad ipsam productam. Dico lineam DE ellipsim esse. Secetur enim rursus alio plano quod coni basi BC aequidistet; et sit sectio NO. Erit NO circulus, ut proxime demonstratum est. Et quoniam conus ANO secatur plano DE neque basi aequidistanti neque subcontrarie posito, sectio ellipsis erit, quod monstravit Apollonius in decimatertia primi conicorum. Eodem modo fiet demonstratio et in circuli portione, quod nos brevitatis caussa omisimus.

Sit circulus ABCDLMNO, cuius pars NOABC sit ultra

datum planum constituta, pars vero CDLMN citra; et describantur figurae quae sint XYPQR et RSTUX. Et siquidem figurae descriptae sint portiones circuli, erunt unius et eiusdem circuli portiones ipsum totum absolventes; quod sic patet. Producatur enim conus EAL et secetur plano basi aequidistanti TZ; erit sectio TZ circulus, ut monstratum est. Quare conus ETZ secabitur plano basi subcontrarie posito atque erit talis sectio circulus, cuius diameter PT ex quinta primi conicorum. Quod si figurae descriptae sint ellipsis, portiones simul iunctae perficient totam ellipsim. Secabitur nanque conus ETZ plano neque basi aequidistanti neque subcontrarie posito ex decimatertia eiusdem. Similiter si portio circuli describatur, cuius pars sit ultra datum planum, pars vero citra, erit tota figura descripta; quandoque vel circuli portio, vel ellipsis, vel paraboles, vel hyperboles, quod ex iam dictis satis superque cuilibet patere potest. Ex quibus constat circulum in plano dato descriptum maiorem quidem esse eo a quo describitur, si fuerit citra datum planum, minorem vero si fuerit ultra.

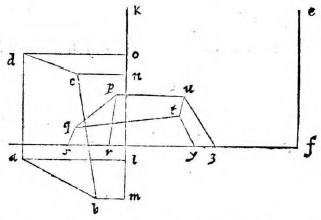
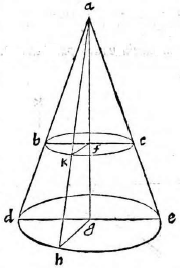
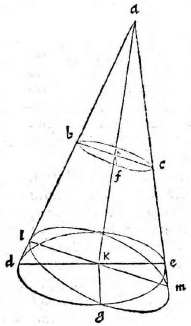
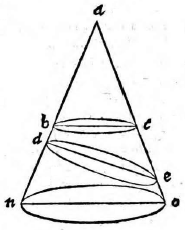
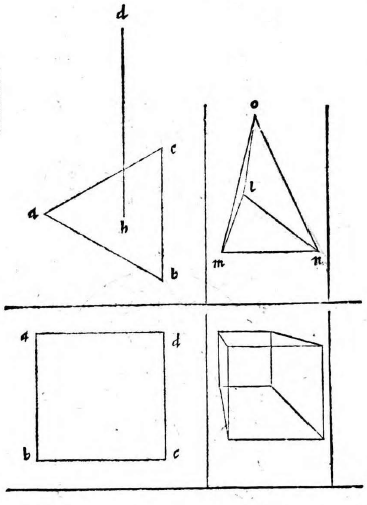
Sit pyramis basim habens ABC verticem D, cuius altitudo linea DH. Sit autem dicta pyramis vel ultra datum planum, vel citra, vel partim ultra, partim citra. Itaque describantur

superficies ABC, DAB, DBC, DCA, quae sint LMN, OLM, OMN, ONL; et tum demum descripta erit figura sicut oportebat.

Eodem modo describetur et cubus, cuius basis ABCD et aliud quodvis corpus.

〈A.〉 Cum sit possibile o Syre etc.］

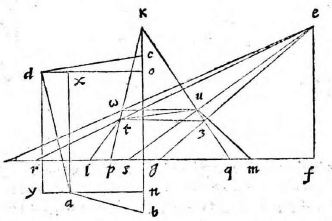
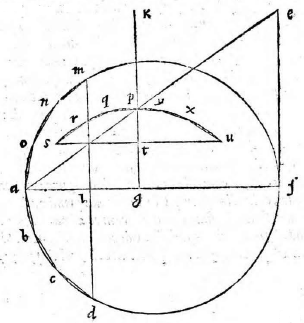
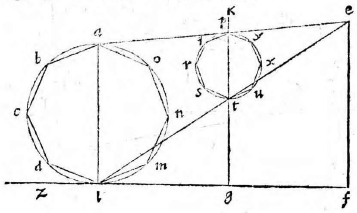
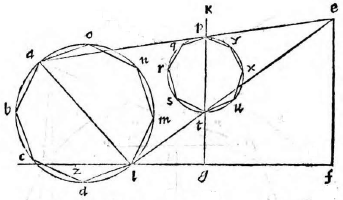
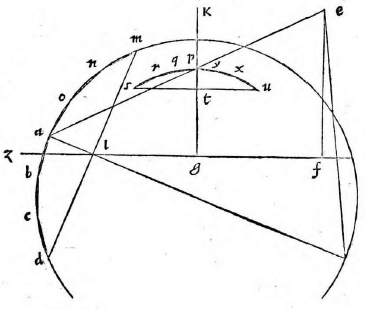
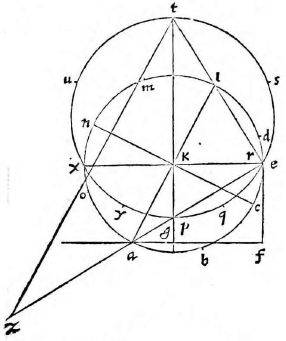
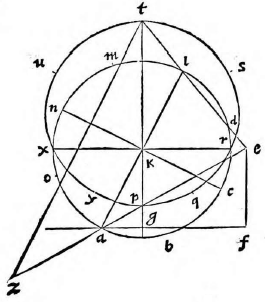
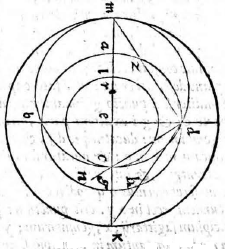
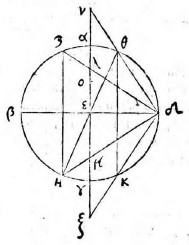
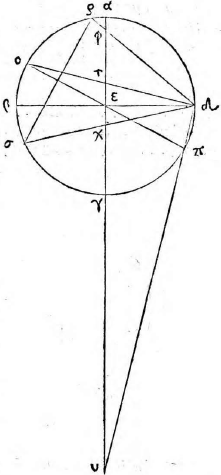
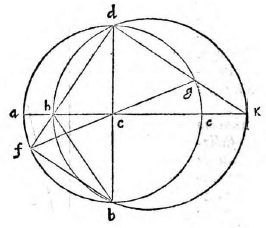
Primum docet Ptolemaeus dato aequinoctiali circulo in plano proposito describere et alios circulos qui sunt in solida sphaera, videlicet meridianum zodiacum, circulos aequinoctiali aequidistantes; atque inter hos praecipue duos tropicos qui zodiacum intra sese concludunt. Docet autem hoc pacto: Describatur aequinoctialis circulus qui sit ABGD circa centrum E et ducantur diametri sese invicem secantes ad angulos rectos AG, BD. Erit altera diameter, videlicet AG pro circulo meridiano et punctum E pro polo mundi arctico. Producatur deinde AG et ex utraque parte puncti G circuli ABGD aequales arcus abscindantur GN, GH ut sit GH versus D, idque secundum quantitatem distantiae circulorum aequidistantium, quos describere oporteat. Sumantur autem primo arcus GN, GH ita ut contineant partes viginti tres et minuta 51 earum partium, quarum totus circulus continet 360, quae scilicet est distantia duorum tropicorum ab aequinoctiali et maxima zodiaci declinatio tempore Ptolemaei. Et ducta DH producatur ut secet lineam AG in K et ducatur DN secans eandem in C, et centro quidem E intervallis autem EK, EC circuli describantur KM, CL et rursus sumpto in linea CM puncto medio quod sit R; ex eo describatur alius circulus circa CM. Erit iam circulus CL tropicus Cancri, KM tropicus Capricorni et CM zodiacus inter hos inter medius qui aequinoctialem bifariam in punctis B D oppositis secabit. Ducta enim DM secante aequinoctialem in Z, erit arcus AZ aequalis arcui GH, hoc est ipsi GN; quare ZDN erit dimidii circuli circumferentia et angulus ZDN rectus. Itaque quoniam trianguli MDC angulus ad D rectus est, punctum D cadet in circumferentia circuli CM. Non aliter demonstrabimus cadere punctum B in circumferentia eiusdem, patet ergo zodiacum secare aequinoctialem in punctis B D. Quod si eadem ratione alii aequidistantes circuli pro cuiusque signi declinatione describantur, quo loco hi zodiacum secent, initia statuentur signorum et ita singulae etiam signorum partes invenientur. Quae quidem omnia ita esse ex antedictis facile demonstrari possunt; propositum nanque est Ptolemaeo describere in plano circulos solidae sphaerae, quemadmodum oculo in antarctico polo existente appareant. Planum autem sumit, ut opinor, illud in quo est aequinoctialis circulus, solus enim is in eadem permanet quantitate cum alii vel augeantur vel minuantur; quod non accideret si in alio plano videretur. Sit sphaera αβγδ cuius centrum ε seceturque plano per axem ducto et per meridianum circulum cui colurus solstitiorum coniungatur; et sit sectio circulus αβγδ polus arcticus β, antarcticus δ; eius autem plani et circuli aequinoctialis communis sectio sit recta linea αγ coluri

aequinoctiorum, recta βδ tropici aestivi ζη hyemalis θκ et zodiaci ηθ. Itaque describere oportet circulos αγ, αβγδ, βδ, ζη, θκ, ηθ in plano in quo est aequinoctialis, oculo ipso in δ constituto quorum circulorum αγ est in dato plano et propterea idem manet, ζη ultra datum planum, θκ citra; sed αβγδ, βδ, ηθ partim ultra, partim citra. Ducantur δζ, δη et secet δζ ipsam αγ in λ; δη vero secet in μ et producta utrinque αγ, ducatur δθ et producatur ut coeat cum αγ in ν et ducta δκ item producatur ad eandem in ξ et describantur figurae in plano ut dictum est. Erunt circuli αβγδ, βδ descripti rectae lineae cum oculus sit in eodemmet plano et sese ad angulos rectos secabunt quoniam et plana sed ipse ζη erit circulus minor intra aequinoctialem contentus, cuius diameter λμ, centrum ε in quo scilicet videtur polus arcticus β et θκ circulus maior aequinoctialem ambiens, ambiens] ambieus V cuius idem centrum et diameter νξ cum plana ζη, θκ aequidistantia sint plano αγ. At vero ηθ et ipse circulus erit circa diametrum λμ, cuius centrum O; quod planum ηθ plano αγ subcontrarie ponatur. Est enim angulus δνμ aequalis angulo δθκ propter linearum aequidistantiam et angulus δηθ aequalis eidem δθκ quoniam arcus θδ, δκ sunt aequales (29, primi). (29, primi)] Euclid, Elements I.29 Angulus ergo δνμ aequalis est angulo δηθ et reliquus δμν reliquo δθη (21, tertii), (21, tertii)] Euclid, Elements III.21 quare sequitur ut plana ηθ, νμ subcontrarie ponantur. Eadem ratione monstrabuntur et plana circulorum omnium in sphaera descriptorum qui aequinoctiali non aequidistent, sive maiores sint sive minores, eius plano subcontrarie collocari, quare omnes in ipso circuli apparebunt. apparebunt] apparebuut V Et quoniam aequinoctialis circulus ABGD et meridianus αβγδ, cum sint eiusdem sphaerae maiores circuli aequales, sunt, et earum quartae DG, δγ erunt aequales, et arcus item maximarum declinationum GH, γκ, GN, γη, αζ, αθ, quare et ipsi DH, δκ, BN, βη, DZ, δθ, BH, βκ, BZ, βθ aequales angulus, ergo EDC aequalis est angulo εδμ. Sed cum

angulus ad E aequalis sit ei qui ad ε, quod uterque rectus erit et reliquus reliquo aequalis, et triangulum EDC triangulo εδμ aequiangulum. Ut igitur DE ad EC, ita δε ad εμ. Et permutando ut DE ad δε, ita EC ad εμ; sunt autem DE, δε aequales quare et EC, εμ aequales erunt, et ita demonstrabuntur aequales EK, εξ, ME, νε, unde colligitur MC aequalem esse ipsi νμ. Itaque cum aequinoctialis circulus sit ABGD, erit tropicus Cancri circulus CL, tropicus Capricorni

KM, zodiacus CM, meridianus seu colurus solstitiorum recta linea KM. Colurus aequinoctiorum recta BD et punctum C principium Cancri, M Capricorni, B Arietis et D Librae, in quibus quidem BD punctis zodiacum secare aequinoctialem manifestissime constat. Recte igitur omnes iam dicti circuli in proposito plano descripti erunt, quod facere oportebat.

Similiter si a puncto G sumantur alii duo arcus aequales GF ex parte D et GI ex altera parte, quanta est declinatio principii Geminorum, ducaturque DF et producatur quousque secet lineam MK in O, et ducatur DI secans eandem in P. Et rursus centro E et intervallis EO, EP circuli describantur OQ, PS, ut secet circulus OQ zodiacum in punctis T U, et circulus PS eundem secet in XY. Erit punctum T principium Aquarii U principium Sagittarii, X Geminorum, Y Leonis et in aliis eodem modo, non tantum in principiis signorum, sed et in singulis eorum partibus. Demonstratio autem eadem erit.

Ex superius demonstratis facile apparere potest quae caussa sit cur Ptolemaeus sphaerae circulos in plano describere volens oculum in superficie ipsius potissimum statuerit. Ex eo enim loco spectanti quotquot in sphaera circuli imaginari possunt, omnes vel per rectas lineas vel per circulos repraesentantur. Alioquin, oculo alibi constituto, quandoque repraesentarentur per ellipses, quandoque etiam per alias curvas lineas, quarum descriptionem difficillimam esse nullus est qui nesciat. Ex punctis vero quae in sphaerae superficie sunt polum australem delegit et ut septentrionalis caeli regio quae nobis semper versatur ante oculos in planisphaerio collocaretur et punctum immobile alterum referens polum circa quem ea circumfertur centri locum teneret.

B. Hac itaque ratione etc.］

Meridianos circulos rectis lineis per centrum aequinoctialis, hoc est, per polum transeuntibus repraesentari oportere iam dictum est; et cum sphaerae circuli maiores sese bifariam secent in partibus oppositis, et rectae lineae omnes quae meridianos referunt zodiacum in partibus oppositis secabunt.

C. Designabitur deinde omnis horizon etc.］

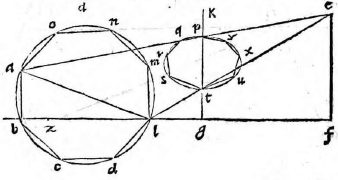
Transit Ptolemaeus ad descriptionem horizontis, qui cum ab aequinoctiali circulo declinet, quemadmodum zodiacus et ipse per circulos aequinoctiali aequidistantes describendus est secundum aliam atque aliam declinationem pro loci cuiusque situ. Et cum sit unus

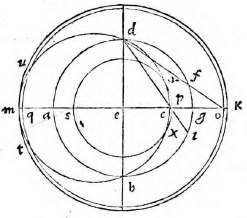
ex circulis maioribus aequinoctialem et zodiacum bifariam secat, sit enim aequinoctialis circulus ABGD, cuius centrum E, et diametri sese secantes ad angulos rectos AG, BD et ex utraque parte G sumantur arcus aequales GN, GH. Secundum declinationem horizontis, modoque superius dicto, circuli aequidistantes describantur KM, CL, et in medio lineae CM sumpto centro R, describatur alius circulus CM. Erit ipse CM pro horizonte, quod ita demonstrabitur. Sit rursus sphaera αβγδ et alia, ut in superiori figura, sitque plani ducti per meridianum αβγδ et horizontis communis sectio πρ, et ducatur πδ, quae secet αγ in σ et δρ. Producatur ad eandem in τ et describatur circulus πρ in plano per αγ oculo in δ posito. Erit descripta figura circulus circa diametrum στ; planum enim πρ plano αγ subcontrarie ponitur, quod facile demonstrabimus, ducta ρυ aequidistanti ipsi αγ. Sicuti superius demonstratum est, planum ηθ eidem plano αγ subcontrarie

poni. Rursus, cum aequinoctialis circulus ABGD meridiano αβγδ aequalis sit, similiter demonstrabimus lineam EC lineae εσ et EM ipsi ετ aequalem esse, et idcirco CM ipsi στ erit; igitur circulus circa CM in plano descriptus loco horizontis, et eadem ratione secabit circulum aequinoctialem et zodiacum semper bifariam in oppositis punctis, ut contingit in solida sphaera.

D. Describatur enim circulus aequinoctialis, etc.］

Quod dixerat superius nunc demonstratione confirmat, videlicet omnes rectas lineas quae per polum transeunt, instar meridianorum, ad partes zodiaci oppositas pertingere, et quoniam partes zodiaci oppositae ab aequinoctiali aequaliter declinant, per circulos ipsi aequidistantes designantur. Quare si demonstrabitur lineas illas terminari ad puncta per quae describuntur circuli aequidistantes, perspicuum iam erit quod oportebat demonstrare. Potest autem haec demonstratio et ad horizontem accommodari.

E. Designabimus deinde circulum alium declivem］

Ostendit horizontem cum aequinoctalem bifariam secet et zodiacum ita secare in partibus oppositis, hoc est eorum sectionum puncta rectis lineis per polum transeuntibus coniungi, ut inde constet hos circulos in plano ita descriptos esse, sicut oportebat.

F. Quoniam enim in circulo HATG lineae duae se invicem secant, etc.］

Quoniam in circulo HATG rectae lineae AG, HT se invicem secant, erit rectangulum HET aequale rectangulo AEG, hoc est ipsi BED. Quare duas lineas HET, BED in eodem circulo esse necesse est; erit ergo punctum T et in zodiaco.

G. His ita constitutis, nunc metienda est proportio semidiametrorum, etc.］

Inquirit quantitatem semidiametrorum circulorum aequinoctiali aequidistantium, per quos in planisphaerio describuntur et zodiacus et horizon, et zodiaci item signa distinguuntur, videlicet quot partes quaelibet earum contineat, quarum semidiameter aequinoctialis continet LX, ut inde monstretur signorum omnium ortum consentire ei qui in solida sphaera apparet, tam recta quam obliqua. Sunt autem omnia quae hoc loco dicuntur adeo manifesta ut interpraetationis lumen minime desiderent, quanquam notae quibus et gradus et graduum particulae significantur mendo non careant; non enim respondent exacto calculo, sed tamen corrigere non placuit, nisi quae insigniter depravata erant.

H. Unde angulos BDT et BDK recto aequales esse consequens est］

Sumatur enim ex altera parte B arcus BL aequalis arcui BH. Erit LT semicirculus, quare angulus LTD rectus est; sed anguli BDT, BDK aequales sunt angulis BDT, BDL, qui quidem recto LDT sunt aequales. Angulos ergo BDT, BDK recto aequales esse necessarium est.

I. Sunt autem anguli EDK atque EKD recto aequales, sunt ergo similes］

Cum recto aequales sint anguli EDT, EDK et anguli item EDK, EKD, sublato utrinque communi angulo EDK, relinquetur angulus EKD aequalis ipsi EDT. Est autem angulus DEK communis utrique triangulo; reliquus igitur angulus EDK reliquo EZD aequalis erit, et triangulum EDK triangulo EZD simile.

K. Manifestum est enim etc.］

Quae enim proportio est anguli BDT ad angulum DBT, eadem est arcus BT ad arcum TD. Triangulum vero EZD simile est triangulo TBD, nam angulus DEZ rectus recto DTB est aequalis, et EDZ communis utrique. Reliquus igitur EZD, reliquo TBD aequalis erit. Quare descripto circulo circa triangulum EDZ, quae est proportio anguli EDZ ad angulum EZD, ea erit arcus EZ ad arcum ED. Sed proportio anguli EDZ ad angulum EZD eadem est ei quae anguli BDT ad angulum DBT, hoc est quae arcus BT ad arcum TD. Quae ergo proportio est anguli EDZ, hoc est anguli BDT ad angulum EZD, ea est arcus BT ad arcum TD et arcus EZ ad arcum ED. Ex quo sequitur ut et eorum arcuum chordae eandem habeat proportionem, ut igitur recta linea EZ ad rectam ED et ut recta ED ad ipsam EK, ita recta BT ad TD, hoc est ad BH.

L. Si ergo comparemus ad lineam KE tetragonum KT etc.］

Abscindatur a linea FK ipsa FO, aequalis lineae FE. Quadratum TK excedet quadratum TE rectangulo contento linea KE et linea KO, hoc est excessu quo linea KF ipsam EF excedit, ut monstrabitur. At cum quadratum TK excedat ipsum TE quadrato EB, quod angulus TEB sit rectus et linea TB aequalis lineae TK, erit quadratum EB aequale rectangulo EKO (penultima, primi). (penultima, primi)] Euclid, Elements I.47 Quare si quadratum EB apposuerimus ad lineam EK, hoc est si diviserimus quadratum EB per lineam EK, proveniet ipsa HO. At vero quadratum KT excedere quadratum TE rectangulo EKO, ita monstrabimus. Quoniam enim quadratum KT aequale est duobus quadratis TF, FK, et quadratum item TE aequale duobus TF, FE, dempto utrinque communi quadrato TF, reliquum quadratum KF excedet reliquum FE eodem illo excessu quo quadratum KT excedit ipsum TE. Sed quadratum KF aequale est rectangulo EKO una cum quadrato OF, hoc est quadrato FE. Ergo quadratum KF excedit quadratum CF rectangulo CKO, et propterea quadratum KT eodem excessu excedit quadratum TE, quod demonstrare oportebat (6, secundi). (6, secundi)] Euclid, Elements II.6

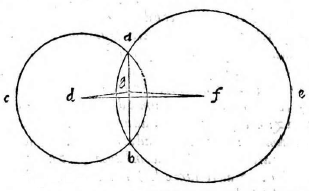
M. Quoniam ergo quoties duo circuli se invicem secant, etc.］

Sint duo circuli ABC, cuius centrum D, et ABE, cuius centrum F. Secent autem sese in punctis A B et iungantur AB, DF. Dico lineam DF secare lineam AB bifariam et ad

angulos rectos. Si enim fieri potest non secet bifariam, sumaturque in ipsa AB punctum medium quod sit G, et ducantur DG, FG; erunt ipsae perpendiculares ad lineam AB et anguli DGB, BGF recti (3, tertii). (3, tertii)] Euclid, Elements III.3 Quare DG, GF lineae in eadem linea recta erunt, est autem et DF recta, ergo duae rectae lineae superficiem intra sese concludunt, quod fieri non potest (14, primi). (14, primi)] Euclid, Elements I.14 Secat igitur linea DF ipsam AB bifariam atque idcirco ad angulos rectos, quod demonstrandum fuerat (3, tertii). (3, tertii)] Euclid, Elements III.3

N. Superioris tractatus particula de circulis aequidistantibus recto, etc.］

Superius tradidit Ptolemaeus rationem describendi in plano circulos solidae sphaerae dato aequinoctiali circulo. Nunc ad planisphaerii fabricam proprius accedens, cuius magnitudo a circulo Capricorni determinatur, docet dato primum eo circulo, qui omnes alios ambit, aequinoctialem describere. De circulo autem Cancri nihil hoc loco dixit, quoniam quemadmodum describatur intra aequinoctialem ex superioribus satis apparet.

O. Producimus deinde lineam a puncto G aequidistantem lineae ED terminatam notis GH］

Hic locus mendo non caret. Corrigetur autem si in hanc sententiam verba addantur: Ducemus lineam a puncto D ad Z et producemus, et a G ducemus GH aequidistantem ipsi ED, quae secet lineam DZ in H.

P. Est enim quanta DE ad lineam EG, tanta DT ad lineam TK］

Hoc est quam proportionem habet linea DE ad EG, eandem habet DT ad TK.

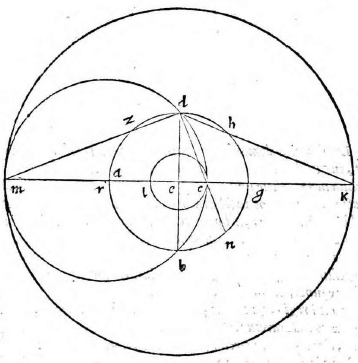
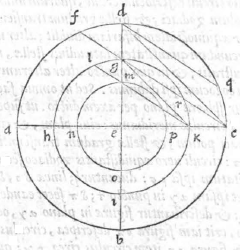
Possumus autem et alia via et fortasse expeditiori intra Capricorni circulum describere aequinoctialem et circulum Cancri. Sit enim ABCD circulus Capricorni, cuius centrum E. Ducanturque diametri sese ad angulos rectos secantes AC, BD, et a puncto D versus a sumatur arcus DF secundum distantiam qua distat a circulo aequinoctiali, aequinoctiali] aerquinoctiali V et ducta CF, quae secet lineam DE in G. Centro quidem E, distantia autem EG circulus describatur GHIK; deinde a puncto G sumatur arcus GL secundum eandem distantiam, ductaque KL secante DE in M,

describatur alius circulus ex eodem centro et distantia EM, qui sit MNOP. Dico circulum GHIK esse aequinoctialem, ipsum vero MNOP circulum Cancri. Ducatur enim a puncto D ad circumferentiam linea DQ aequidistans lineae FC, et iungantur GK; erunt anguli EDQ, EGC aequales et item aequales CDQ, DCF. Quare arcus BCQ similis erit arcui IKR, et arcus QD qui semicirculum complet similis ipsi RG; ergo et QC reliquus de quadrante reliquo RK similis. Et quoniam arcus CQ aequalis est ipsi FD, quod anguli CDQ, FCD sint aequales, sequitur ut arcus KR sit secundum distantiam circuli Capricorni ab aequinoctiali; et similiter arcus LG qui eadem ratione est aequalis ipsi KR. Quare si circulus GHIK ponatur aequinoctialis, erit ex iis quae demonstravimus ABCD circulus Capricorni et MNOP Cancri, nam ex utraque parte aequinoctialis descripti sunt circuli aequidistantes secundum distantiam qua is ab utroque tropicorum distat.

〈Q.〉 Deinceps convenit propositum insequi］

Stellarum fixarum loca ex longitudine et earum latitudine habentur ut apparet apud Ptolemaeum Ptolemaeum] Ptolemaenm V in septimo libro magnae compositionis. Quare si stellas ipsas in planisphaerio collocare oporteat, primum duo circuli describendi erunt, quorum unus cum maximus sit per polum zodiaci et stellae gradum transiens et zodiacum ipsum et aequinoctialem bifariam dividit; alter vero zodiaco aequidistat secundum quantitatem latitudinis stellae, vel septentrionalis vel australis, et in quo puncto alter alterum secat, ex parte stellae, in eo locum ipsi dabimus. Sed ut omnia facile percipiantur, secetur sphaera plano per axem ducto ut superius, et sit sectio αβγδ, circulus meridianus eius plani et circuli maximi per zodiaci polum et stellae gradum transeuntis. Communis sectio sit Oπ, circuli vero aequidistantis zodiaco secundum latitudinis quantitatum, ipsa ρσ ducanturque lineae δO, δπ, δρ, δσ, ut δO secet ipsam αγ in puncto τ, δπ secet eandem in υ, δρ in φ, δσ in χ, et describantur figurae in plano αγ. Oculo ipso in δ constituto, erit iam figura Oπ descripta, circulus circa diametrum τυ, et figura ρσ item, circulus circa φχ, quoniam plana Oπ, ρσ plano αγ subcontrarie posita sunt, ut monstravimus, et punctum τ pro zodiaci polo erit. Sit igitur aequinoctialis circulus in plano descriptus, ut in Ptolemaei figura ABGD circa centrum E et zodiacus LBHD, et quoniam aequinoctialis ABGD et meridianus αβγδ aequales sunt, erit arcus BT, quae est distantia poli zodiaci ab aequinoctialis polo, aequalis ipsi βO, et idcirco recta linea EK, aequalis demonstrabitur ipsi ετ, quare punctum κ zodiaci polum repraesentabit. Duobus igitur circulis in planisphaerio descriptis, ipsius stellae locus facile invenietur, et ita fiet in reliquis pro cuiusque stellae longitudine et latitudine, circulos describendo.

Est etiam alius modus inveniendi stellarum fixarum loca in planisphaerio, cognita earum declinatione et gradu zodiaci, cum quo ad meridiem veniunt. Descripto nanque circulo aequinoctiali aequidistante secundum stellae declinationem, et

ducta recta linea instar meridiani per zodiaci gradum, cum quo ad meridiem venit et per mundi polum transeunte, in quo puncto sese secant ex parte stellae, ipsi locum assignabimus.

R. Nunc aequidistantium zodiaco in planisphaerio descriptio notanda］

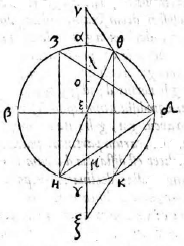
Docet describere circulos qui zodiaco aequidistant, simulque demonstrat eos in plano descriptos circulos esse. Mirum autem est cur non et zodiacum et horizontem circulos esse demonstravit demonstravit] demonstrarit V Ptolemaeus, et insuper duos tropicos et alios aequinoctiali aequidistantes, quanquam de his minus dubitari contingat. Quorum omnium demonstrationes nos superius attulimus, possumus tamen et simili ratione illud ipsum ostendere in zodiaco. Sit circulus meridianus per utrunque polum transiens ABCD, cuius centrum E, et ducantur diametri AC, BD ut sit BD axis polus australis, punctum D et linea AC

diameter aequinoctialis. Sit autem FG diameter zodiaci, quem in planisphaerio describere oporteat. Ducatur DF secans AC in H et DG secans eandem productam in K. Dico circulum, cuius diameter FG, designari posse circa diametrum HK et aequinoctialem bifariam secare. Iunctis enim BF, BH, quoniam anguli DFB, BEH recti sunt, erunt quatuor puncta B F H E in circumferentia circuli cuius diameter BH. Quare angulus BHE aequalis est angulo BFE; est autem BFE aequalis angulo BDG. Angulus ergo BHK ipsi BDK erit aequalis, et idcirco quatuor puncta B H D K in circumferentia circuli sita erunt. Finge nunc circulum ABCD, qui antea pro meridiano habebatur, aequinoctialem esse (nihil enim prohibet) et circa diametrum HK circulus describatur; transibit is per puncta B D. Itaque quoniam BD sunt in aequinoctiali, circulus BHDK, qui repraesentat zodiacum, aequinoctialem bifariam secabit, quod fuerat demonstrandum. Eadem erit demonstratio et in ipso horizonte.

〈S.〉 Quoniam enim arcus ZT aequalis arcui KH etc.］

Cum enim hi circuli zodiaco aequidistantes ponantur, et inter se aequidistantes sunt et linea ZH lineae TK aequidistans, quare arcus ZT, HK qui inter eas interiiciuntur sunt aequales. Ex quinquagesima tertia primi Vitellionis, angulus igitur ZDT aequalis est angulo KDH, hoc est YDN ipsi CDF, et arcus YN arcui CF; ideoque ex quinquagesima secunda primi eiusdem Vitellionis, linea LM aequidistans est lineae FY et DL. Ad LY eam proportionem habet quam DM ad MF.

〈T.〉 At vero quae proportio lineae DL ad lineam LY etc.］

Hoc est quae proportio est lineae DL ad lineam LY; ea est quadrati DL ad rectangulum DLY et quae lineae DM ad MF; ea quadrati DM ad rectangulum DMF. Sequitur autem hoc ex lemmate vicesimaetertiae decimi Euclidis.

〈V.〉 Quoniam itaque loco circuli etc.］

Ducatur a puncto L linea contingens circulum; erit quadrato eius aequale rectangulum DLY et rectangulum item CLN. Quare rectangulum DLY aequale est rectangulo CLN et eadem ratione monstrabitur aequale rectangulum DMF ipsi NMC. Ergo quae proportio est quadrati DL ad rectangulum CLN, ea est quadrati DM ad rectangulum NMC. Et permutando, quae quadrati DL ad quadratum DM, ea rectanguli CLN ad rectangulum NMC.

X. Est autem tetragonis tetragonis] tetragonns V DM maior tetragono DL prout etc.］

Circuli zodiaco aequidistantes obliquum habent situ respectu aequinoctialis; quare ex altera parte ad mundi polum magis accedunt et recta lineae a puncto D ad eorum diametrorum extremitates ductae inaequales angulos faciunt cum linea axis. Itaque cum in hoc situ maior sit angulus BDH, angulo BDZ maior erit linea EM ipsa EL, et quadratum EM una cum quadrato ED maius quam quadratum EL una cum eodem quadrato ED. At vero quadratum DM aequale est duobus quadratis DE, EM et quadratum DL aequale quadratis DE, EL. Maius igitur est quadratum DM ipso DL quadrato, ex quibus sequitur et rectangulum NMC maius esse rectangulo CLN; sed rectangulum NMC est aequ〈a〉le rectangulo NCM et quadrato CM. Et rectangulum CLN aequale rectangulo CNL et quadrato NL (1, secundi). (1, secundi)] Euclid, Elements II.1 Quare rectangulum NCM una cum quadrato CM maius est rectangulo CNL una cum quadrato NL, quorum eaedem altitudines basis; ergo CM maior erit ipsa NL.

Y. Deinceps, quoniam aequidistans zodiaco nec in planisphaerio descriptus etc.］

Docet in plano describere etiam circulos qui in planisphaerio non cadunt; modus autem tum describendi tum demonstrandi idem est cum antedictis. Sit enim meridianus ABGD circa centrum E, et ductis diametris AG, BD secantibus sese ad angulos rectos, sit axis BD, polus australis punctum D, et AG aequinoctialis diameter. Sit praeterea ZH diameter circuli aequidistantis aequinoctiali et TL aequidistantis zodiaco, quos describere oporteat in plano in quo est aequinoctialis. Producatur AG ex utraque parte, et ad ipsam ducantur DZ, DH, DT, DL in puncta Q, N, O, C et figurae describantur. Ut dictum est, erit ZH in plano descriptus circulus cuius centrum E, diameter QN et TL; item circulus cuius diameter OC, quoniam plano AC planum quidem ZH aequidistans est, ipsum vero TL subcontrarie ponitur et propterea punctum Y, in quo hi circuli in plano descripti sese secant, respondebit puncto sectionis circulorum ZH, TL in solida sphaera. At vero Ptolemaeus demonstrat circulum OC secare ipsum QN in arcus similes iis qui fiunt circulo TL, ipsum ZH secante, cuius demonstratio talis erit: Intelligantur circuli circa diametros QN, OC descripti in plano perpendiculariter erecto ad planum in quo est circulus ABGD, et similiter circa centrum F et diametrum ZH; intelligatur descriptus semicirculus ZMH in plano ad idem planum perpendiculariter erecto, instar illius qui est in solida sphaera. Itaque, quoniam circulus aequidistans zodiaco cuius diameter TL circulum ZMH secat et sunt ambo ad idem planum perpendiculariter erecti, communis eorum sectio, recta linea, est perpendicularis ad dictum dictum] ditum V planum; sit autem communis sectio quae cadit in semicirculo ZMH, ipsa KM erit MKF angulus rectus (19, undecimi). (19, undecimi)] Euclid, Elements XI.19 Iungatur FM et ad E fiat angulus NEY aequalis angulo KFM, ut sit punctum Y in circumferentia circuli QN; erit Y et in circumferentia circuli OC, hoc est in communi circulorum sectione, ut postea apparebit. Ex quibus sequitur circulum CYO secare ipsum NYQ in arcus NY, YQ similes arcubus HM, MZ qui contingunt in solida sphaera. Ducatur enim linea DK usque ad ipsam ON in R, iungaturque RY et producatur HZ usque ad TO in P. Deinde TX ducatur aequidistans lineae ON et DLC secet ipsam PH in S; erit iam linea ON divisa in partes proportionales iis quae sunt in linea ipsi aequidistante PH. Quoniam igitur angulus DTX aequalis est angulo DLT et angulo DPH cum arcus DX sit aequalis arcui DT et linea TX aequidistet ipsi PTH, erit angulus DLT angulo DPH, hoc est angulus TLS ipsi TPS aequalis et quatuor puncta L S T P in circumferentia eiusdem circuli sita erunt. Quare rectangulum PKS aequale est rectangulo TKL, sed rectangulum TKL est aequale ipsi ZKH; rectangulum ergo PKS rectangulo ZKH et propterea rectangulum ORC rectangulo QRN aequale erit. Et quoniam triangula DEN, DFH similia sunt, et triangula item DER, DFK similia, habebit NE ad ED proportionem eandem quam HF ad FD et ED ad ER eandem quam FD ad FK; ex aequali igitur NE, hoc est EY ad ER, habebit eandem quam HF, hoc est FM ad FK. Estque angulus REY aequalis angulo KFM. Quare triangula REY, KFM aequiangula erunt et linea YR ad ON perpendicularis; quadratum ergo ipsius YR aequale est rectangulo QRN et cum rectangulum QRN aequale sit rectangulo ORC, erit et quadratum YR ipsi ORC rectangulo aequale, et ideo punctum Y in circumferentia quoque circuli OC cadet, ex quibus constat quod oportebat demonstrare.

Z. Similis descriptionis exemplo etc.］

Si circulus zodiaco aequidistans per polum mundi australem transeat, in quo ponitur oculus, apparebit linea una, quae videlicet communis sectio est plani eius circuli et plani aequinoctialis, in quo describitur, ut superius dictum est. Si ergo describendus sit eiusmodi circulus, cuius diameter DL, et circulus aequinoctiali aequidistans, cuius diameter ZH, producatur DL usque ad lineam AG in C punctum, ductaque DH producatur ad eandem in N, et figurae describantur, erit circulus DL recta linea, quae sit BCY perpendicularis ad planum, in quo est meridianus ABGD, quoniam et ipse circulus DL et aequinoctialis perpendiculariter erecti sunt ad idem planum, et idcirco ad lineam AN perpendicularis existet (19, undecimi). (19, undecimi)] Euclid, Elements XI.19 Sed ZH circulus erit circa centrum E et diametrum QN, quam recta linea BCY secet in Y; ergo punctum Y repraesentabit in plano locum sectionis eorum circulorum in solida sphaera. At vero arcus circuli descripti NY, YQ proportionales esse arcubus ZH liquido apparet ex demonstratione, quam affert Maslem in commentariis.

Y. Quae linea in planisphaerio locum obtinet circuli cuius diameter DLZ etc.］

Ex his verbis et ex superioribus apertissime colligitur Ptolemaeum sphaerae circulos describere in plano in quo est ipse aequinoctialis, quod nos supra monuimus, non autem in plano quod sphaeram in septentrionali polo contingit, ut imaginatus est Iordanus.

Φ. Quae ratio cogit septentrionales semper esse minores etc.］

Quoniam visus in australi polo constituitur, fit ut et polus septentrionalis in plano centri locum obtineat respectu aequinoctialis circulorumque ipsi aequidistantium; et septentrionales circuli, quo magis ad eorum polum accedant, eo sint minores, quemadmodum contingit in sphaera. Australes vero, contra, quam in sphaera, eo maiores evadant; fit etiam ut meridiani circuli rectis lineis describantur.

X. Quibus id evenit quod unus etc.］

Circulorum enim zodiaco aequidistantium, qui per mundi polum transit, in plano recta linea designatur, ut proxime diximus.

Ψ. In circulis vero magnis per hunc polum transeuntibus aliter］

Circuli magni per zodiaci polos transeuntes, si in plano describantur, circuli sunt, uno duntaxat excepto qui et per mundi polos transit; quoniam cum in meridianorum numero habeatur, recta linea est, in qua centra circulorum zodiaco aequidistantium sumuntur.

Ω. Unde in assignationibus stellarum etc.］

Dictum est superius stellarum fixarum loca in planisphaerio duobus modis inveniri posse, sive ratione habita ad zodiacum, sive ad aequinoctialem. In utroque autem et zodiacum et aequinoctialem dividimus, et sicut circulis magnis, qui per zodiaci polos permeant, similiter dividimus et zodiacum et circulos zodiaco aequidistantes. Ita rectis lineis meridianos referentibus et aequinoctialem ipsum et aequinoctiali aequidistantes circulos pariter secamus, unde stellarum loca certissima ratione deprehenduntur.