Ptolemy
Almagesti (tr. Erasmus Reinhold)
Wittenberg, Johannes Lufft, 1549
transcribed by Colette Dufossé
How to cite this transcription?
This transcription has been made from ed. Wittenberg, Johannes Lufft 1549 (W), prepared by Erasmus Reinhold. It follows the projectʼs guidelines. Marginal notes of the edition have been added in footnotes with the mention ‘i. m. W’. Typos have been corrected (in which case the original reading is given in a footnote), but the accents of Greek words have been kept as they appear in the edition. Reinholdʼs commentary is reproduced in italics, as it is in the edition.
Table of contents and links to chapters
〈I〉 Primus liber Magnae constructionis Ptolemaei
ΠΤΟΛΕΜΑΙΟΣ
Οἶδʼ ὅτι θνητὸς ἔφυν, καὶ ἐφάμερος, ἀλλʼ ὅτʼ ἂν ἄστρων
ἰχνεύω κατὰ νοῦν ἀμφιδρόμους ἕλικας,
οὐκέτʼ ἐπιψαύω γαίης ποσίν, ἀλλα παρʼ ἀυτῷ
ζηνί διοτρεφέος πίμπλαμαι ἀμβροσίης.
Οptime mihi videntur hi qui dextre philosophati sunt separasse speculativam philosophiae partem ab activa. Philosophiae duae sunt partes, speculativa et activa i. m. W Etsi enim accidit activae ut ipsam quoque antecedat speculatio, nihilominus aliae magnae differentiae sunt, non solum haec quod morales virtutes aliquae natura inesse nonnullis possunt etiam sine doctrina, sed artes speculativas nemo sine doctrina integras assequi potest, sed etiam aliud est discrimen, quod activa magnam utilitatem adfert in assiduis actionibus vitae, at speculativa hanc utilitatem adfert, quod proficiendo uberior et locupletior scientia contingit. Nam activae artes monent ut animi impetus in actionibus ad certam normam moderemur, ne in communi consuetudine omittamus diligentiam, quae decus et ordinem in moribus efficit. Sed in vita interiori vacemus plurimum speculativae doctrinae, quae et multiplex est, et pulcherrima, praesertim ea, quae proprie vocatur mathematica.
Nam et Aristoteles speculativam partem valde concinne in tria prima genera distribuit, Tria genera partis speculativae i. m. W physicum, mathematicum, et theologicum. Cum enim omnia ex materia, forma, et motu constent, etsi haec seorsim in subiecto percipi sensu non possunt, tamen seorsim intelligi possunt, si quis igitur sine caeteris primam causam primi et universalis motus secundum simplicem naturam cogitet, ratiocinabitur eam causam esse Deum invisibilem et motu vacantem, ideoque doctrinae genus theologicum dicitur, Theologicum genus i. m. W quod hanc causam inquirit, quia haec vis mundi sublimia transcendens tantum mente cogitatur, et prorsus a sensibilibus seiuncta est. Alterum Physicum i. m. W vero genus scrutatur materiales qualitates, quae semper sunt mutabiles, ut unde oriatur album, calidum, dulce, molle, et similia. Haec doctrina vocatur physica, quae continet substantias obnoxias corruptioni magna ex parte, et agitatas sub orbe lunari. Tertium genus Mathematicum i. m. W disserit de formis et motu locali et qualitate, ac ostendit figuras, multitudinem, et magnitudines, locum, tempus, et similia. Haec doctrina vocatur mathematica, cuius res velut mediae sunt inter alia duo genera, non solum eo quod partim sensu, partim sine sensu comprehenduntur, sed eo etiam quia utrisque accidunt mortalibus et immortalibus. Mortalia enim semper obnoxia sunt mutationi propter formam separabilem, quae simul mutatur, immortalia vero et aethereae naturae conservant suae formae incommutabilitatem immobilem.
Cum Collatio horum trium generum i. m. W vero duo speculativae partis genera magis sint coniecturae, quam certa scientia, quia theologicum prorsus remotum est a nostro conspectu, et incomprehensibile, physicum vero propter materiae instabilitatem ita ambiguum est, ut non arbitremur philosophos de eo unquam consensuros esse, solum vero mathematicum, si quis id recta via inquirat et tractet, firmam et immutabilem scientiam discenti adferat, quia demonstrationibus arithmeticis et geometricis constat, quarum viae nequaquam dubiae sunt, praecipue visum est hanc partem pro viribus illustrare, quae peculiariter de coelestibus corporibus et motibus disserit, cumque sola consideret res perpetuas et semper eodem modo se habentes, est et ipsa comprehensibilis, certa, sine confusione, et semper eodem modo se habens, quod proprium est scientiae.
Caeterum nonnihil ad reliquas artes haec doctrina conducet. Mathematica doctrina conducit et ad reliquas artes i. m. W Maxime enim praeparat viam ad theologicam partem, quia de immobili et separata vi aeterna magis potest coniecturam capere ex vicinitate accidentium, videlicet ex perpetuis motibus, ordine et vicibus, quae accidunt sensibilibus et incorruptibilibus orbibus, que perpetuo motu volvuntur.
Conducet et physico generi, quia universaliter deprehenditur proprietas substantiae materialis ex motu locali, ut corruptibile et incorruptibile agnoscuntur, quia alterius motus est rectus, alterius circularis, et grave et leve, seu passivum et activum discernuntur penes hoc quod vel
ad medium vel a medio corpus fertur.
Postremo plurimum prodest moribus. Quia enim monstrat in rebus divinis perpetuam similitudinem, optimum ordinem, concinnitatem, et obsequium sine contumacia, perspicaciores nos reddit, ac amorem exuscitat imitandae huius divinae pulchritudinis, ac inflammatos animos
adsuefacit ad actiones iusto ordine moderandas.
Nos quoque incensi amore huius doctrinae de rebus perpetuis assidue eam augere conamur. Verecunde dicit de se et toto hoc opere i. m. W Ac ea quidem quae antea inventa sunt ab optimis artificibus didicimus, quae vero interea usque ad meam aetatem deprehensa sunt, adiiciemus, et quae in lucem prolata sunt, quanta fieri poterit brevitate, ita ut has res assequi possint hi qui non sunt omnino rudes, sed aliquantulum promoverunt, complectemur. Et ut sit integra doctrina, omnia ad cognitionem coelestium motuum utilia apto ordine trademus, et vitandae prolixitatis causa tantum recitabo ea quae a veteribus satis explicata sunt, caetera vero quae aut non fuerunt comperta, aut non satis commode tradita, latius pro viribus exponemus.
〈I.1〉 CAPUT I: De ordine huius doctrinae
Initium autem erit huius operis haec consideratio, quomodo se tota terra universaliter habeat ad totum coelum. Particularium vero deinceps hoc erit primum dicere de situ obliqui circuli et de terra habitata, quales sint differentiae inclinationum in singulis horizontibus inter se collatis. Nam haec initia praebent aditum faciliorem ad reliqua. Deinde dicetur de motu Solis et Lunae et de iis quae utrique accidunt. Nisi enim haec prius fuerint cognita, non potest doctrina de reliquis stellis percipi. Tandem cum de stellis dicendum erit, Principia astronomiae sunt φαινόμενα καὶ τηρήσεις inde Geometria et arithmetica artem extruunt i. m. W conveniet prius de orbe stellarum fixarum disseri, postea de iis quae vocantur erraticae. Singula autem monstrare conabimur utentes principiis et quasi fundamentis ad inquisitionem, partim evidentibus adparentiis, partim indubitatis veterum et nostri temporis observationibus. Haec deinceps accommodata ad demonstrationes lineares certa via prosequemur.
Sunt autem hae primae sententiae de consideratione universi, Primae sententiae i. m. W quod coelum sit figurae sphaericae et circumagatur motu circulari, quod terrae figura, quo ad universales partes secundum sensum sumpta, sit et ipsa figurae sphaericae, situ vero in medio mundi centro similis collocata sit, magnitudine vero et distantia ad fixarum stellarum orbem habeat se, ut punctum, nec motu locali agitetur. Haec breviter admonendi lectoris causa percurrenda sunt.
〈I.2〉 CAPUT II: Quod coelum sit sphaericum et globi modo circumvolvatur
Consentaneum est igitur priscos homines ad primas cogitationes ex tali observatione deductos esse. Prima ratio a stellis orientibus et occidentibus i. m. W Videbant enim Solem et Lunam et alias stellas ab ortu versus occasum semper in circulis inter se aequidistantibus ferri, ita ut initio sursum ex inferiore loco velut a terra paulatim in altum conscendant, deinde rursus pro proportione circumvectae descendant, donec prorsus velut delabentes in terram occultentur, postea vero tempore interiecto videbant occultatas ab alio intio exoriri et occidere. Haec autem tempora et loca ortuum et occasuum certo ordine similiter in universum redire.
Maxime vero movit eos, ut agnoscerent coelum esse figurae sphaericae, circumvolutio stellarum semper adparentium, Altera ratio a stellis semper adparentibus i. m. W quae cernuntur semper circa unum et idem centrum circumagi. Necessario enim fit polus punctum illud coelestis globi, circa quod propiores stellae conficiunt minores circulos, remotae vero efficiunt maiores ambitus pro proportione, donec pervenitur ad eas stellas quae adeo procul distant a polo, ut occultentur, quarum hae quae propiores sunt, exiguo tempore latent, remotae vero pro proportione diutius.
Initio ab hac sola consideratione ad eas cogitationes deducti sunt, reliquam vero doctrinam deinceps ex his quae congruunt cum his extruxerunt. Nam omnes adparentiae repugnant diversum sentientibus.
Si quis enim ponat stellas in directum moveri in infinitum, Quod coeli motus non sit rectilineus i. m. W ut quibusdam visum est, quomodo possent quottidie ab iisdem initiis exoriri, quomodo enim regredi possent, si in infinitum evagarentur, aut qui fieret ne redeuntes conspicerentur, aut quomodo non evanescerent sensim diminuta magnitudine? Nunc autem econtra maiores videntur in occasu, ubi truncatae occultantur, quasi terra obiecta subinde partes aliquas praecidat.
Accendi vero stellas a terra, et rursus extinctas in terra ruere absurdissime dicitur. Confutat Epicureum deliramentum, videlicet, quod stellea non accendantur et extinguantur i. m. W Primum enim quomodo posset manere idem ordo, eadem magnitudo, multitudo, distantiae locorum, series temporum, si temere et casu sic accenderetur materia? Iam quomodo alia pars terrae naturam habet inflammantem, alia extinguentem, aut eademne pars alias inflammat, alias extinguit, aut eaedemne stellae aliis accensae vel extinctae sunt, aliis nondum? Ut maxime haec quamvis ridicula non inquirantur, quid de semper adparentibus dicent, quae nec oriuntur nec occidunt? Aut quam ob caussam non fit ut stellae quae accenduntur et extinguuntur ubique oriantur, et occidant, econtra vero quae non sunt obnoxiae huic passioni semper sint supra terram? Non enim eaedem stellae aliis accenduntur et extinguuntur, aliis vero nihil horum patiuntur, cum prorsus manifestum sit stellas easdem quibusdam regionibus oriri et occidere, aliis semper apparere.
Denique ut breviter dicam, quaecunque figura alia coeli esse ponitur praeter sphaericam, Quod nulla alia figura coeli sit, praeter sphaericam i. m. W necesse erit inaequales distantias a terra ad partes superiorum corporum fieri, ubicunque et qualiscunque erit terrae situs. Quare oporteret magnitudines et distantias stellarum iisdem inaequales videri in quolibet circuitu, quasi alibi magis distarent, alibi minus. Id autem non accidit.
Nam quod iuxta horizontes stellae videntur maiores, Cur stellae appareant maiores iuxta horizontem i. m. W id non fit propter distantiam breviorem, sed propter vapores in aere qui inter nostrum visum et stellas existunt, sicut et maiores videntur res in aquam mersae, et quo profundius merguntur, eo maiores apparent.
Testatur et haec ratio coelum esse sphaericum, Alia ratio sumpta ab instrumentis i. m. W quod si alia figura esset ulla, non possent congruere cum motu coelestium ulla instrumenta indicantia motus, sed ad solam sphaericam conveniunt.
Accedit et haec ratio, quod coelum celerrime et facilime circumvolvitur, minimeque impeditur eius motus. A velocitate motus i. m. W Figurarum autem omnium celerrime circumaguntur hae in superficiebus circularis, in solidis corporibus sphaerica.
Praeterea cum inter diversas figuras aequalem ambitum habentes hae sint capaciores quae habent plures angulos, A capacitate i. m. W circulus quidem in planis capacior est, sphaera autem in solidis. Est autem coelum omnium corporum capacissimum.
Ad hanc sententiam congruunt et physicae rationes, Physicae rationes i. m. W quod inter omnia corpora aether est maxime subtilium et similium partium. Superficies autem eorum quae similes habent partes est et ipsa similium partium. Solae autem superficies in planis circularis, in solidis sphaerica similes habent partes. Cum autem aether sit solidus, sphaericum esse sequitur.
Praeterea terrestria et corruptibilia corpora natura constituit ex rotundis, sed dissimilium partium, aetherea vero et divina ex figuris similium partium et sphaerica.
Nam si stellae planae aut disci similes essent, Alia ratio a figura stellarum i. m. W non possent omnibus in terra diversis locis eodem tempore contuentibus videri figurae circularis. Ideo consentaneum est et aethera, ἐπίλογος i. m. W qui ambit eas, esse similis naturae et sphaericum, et cum sit similium partium, ferri circulari et aequali motu.
〈I.3〉 CAPUT III: Quod terra sit sphaerica ad sensum secundum universas partes
Quod autem et terra secundum universas partes accepta sphaerica sit ad sensum, sic maxime deprehenditur. Terram esse rotundam in longitudinem he versus ortum et occasum testatur observatio eclipsium i. m. W
Non eodem tempore oriuntur et occidunt omnibus regionibus Sol, Luna, et caeterae stellae, sed semper prius orientalibus, postea vero occidentalibus. Nam eclipses quae eodem tempore fiunt, ac maxime lunares, constat non iisdem horis, hoc est aequaliter a meridie distantibus, apud omnes spectari, sed semper horae ab orientalibus annotatae posteriores sunt quam horae ab occidentalibus annotatae, cumque horarum differentiae quadrent ad distantias regionum pro proportione, non absurde terram esse sphaericam adfirmari potest. Nam si terrae attribuimus rotunditatem secundum universas partes aequabilem, Confutatio de caeteris figuris i. m. W sequitur occultationes non ubique simul fieri, sed continua serie iuxta proportionem, quod accidere non posset, si alia quam sphaerica figura esset.
Id hinc etiam adparet: si cava esset terra, 1. κοίλη i. m. W stellae in ortu prius conspicerentur ab occidentalibus, si plana esset, 2. ἐπίπεδος i. m. W eodem tempore omnibus orirentur et occiderent, si triangularis aut quadrangularis aut aliam haberet figuram plurium angulorum, 3. πυραμίς, κύβος, πολυεδρὸν i. m. W orirentur et occiderent pariter omnibus in eadem recta linea habitantibus, quod nusquam videtur accidere.
Quod vero nec cylindri figuram habeat, 4. κύλινδρος i. m. W ita ut rotunda superficies ad ortum et occasum versa sit, basium vero planarum latera ad mundi polos, ut aliqui suspicati sunt, inde perspicuum est quod nullae stellae ab iis qui habitarent in convexa superficie semper conspici possent, sed omnes orirentur et occiderent, praeter stellas circa utrunque polum, quae semper laterent. II. Quod terra rotunda sit in latitudinem i. m. W Nunc vero, quo ad Arctum propius accedimus, eo plures in Austro occultantur, et plures in Arcto conspici possunt, ut hinc etiam appareat quod, cum rotunditas terrae ad partes laterales quoque iuxta proportionem impediat prospectum, undique sphaerica sit terrae figura.
Postremo cum a quovis ad quemvis angulum navigamus versus littora ac montes arduos, Testimonia navigationum i. m. W paulatim earum magnitudo crescere videtur, quasi e mari emergant, cum antea propter globositatem aequoris latuissent.
σχόλιον. Vult Ptolemaeus non solum hoc demonstrare quod terra sit globosa, verumetiam quod haec duo elementa, aqua et terra, pariter in unum eundemque globum coeant. ldeo et argumentum ad huius rei demonstrationem adsumit a navigationum perpetua experientia. Voluit autem Deus ob res nascentes et propter vitam ac salutem animantium terram non esse totam aquis immersam, sed multis suis partibus hinc illinc extare et eminere extra aquas. Etsi autem terra aquis tota undique obtegeretur, ut a superiori elemento, sicut et aer undique circumdat corpora inferiora, tamen adhuc aquae extremitas esset figurae sphaericae, idque ratiocinari nos docet duplex experientia inmutabilis et ubique obvia, quarum prior haec est.
Videmus aquam omnem deorsum ferri, et occupare humilima quaeque, ac propter nativam humidi molliciem diffluere ac dispergi tantisper, donec ab altiori termino tanquam repagulo quodam coherceatur. Hinc etiam in aquis nulla existit cavitas seu hiatus, qualis est inter duos montes, quia aqua in medio confluit in sese residens, et exaequat omnia, unde et maria aequoris nomen acceperunt.
Altera experientia in navigationibus maxime illustris est, quae docet aquae superficiem non esse planam, id quod priorem experientiam sequi videtur, sed in spacio non ita magno velut intumescere, et in gibbositatem seu curvaturam quandam attoli, quia navigantibus illa a quibus recedunt paulatim disparent, velut in aquam immersa, econtra sensim quasi ex aquis emergunt ea ad quae cursum dirigunt.
Hae duae experientiae, quarum altera testatur aquam sua natura appetere quandam extremitatis aequabilitatem et quasi libramentum, altera vero etiam κυρτότητα, gignunt ex sese hanc conclusionem, quod aqua sit aequabiliter convexa, ac ob id naturaliter appetat et conservet globi figuram, ut quae sola constet perpetua curvaturae seu convexitatis aequabilitate, quemadmodum ex definitione sphaerae manifestum est.
Idem etiam ex longo tractu fluminis iudicari potest supposita terrae totius rotunditate. Ut Danubius inter Ulmam vicinam fontibus ipsius et inter Byzantium Thraciae, iuxta cuius longitudinem seu meridianum fere in Pontum Euxinum exoneratur, ingentem terrae convexitatem superat et transcendit, quae a recta linea tanquam subtendente circumferentiam in extremitate terrae inter illa duo loca interceptam attolitur fere 13 milliaribus germanicis, hoc est plus vicesima quarta parte totius itineris inter Ulmam et Byzantium. Ideo aquae motus naturaliter, et universaliter appetit figuram sphaericam, eamque una cum globo terrae conservat.
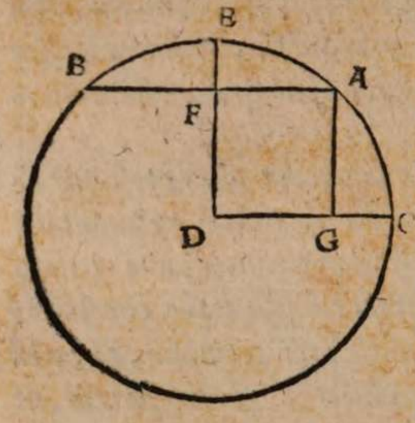 Esto enim maximus circulus in superficie terrae ABC centro terrae D descriptus per fontes Danubii in signo A, et per ostia eiusdem in signo B, circumferentiam autem AEB inventam partium 2 0, qualium tota ponitur 360, subtendat recta AB, cui ex centro D occurrat recta DF in signo F πρὸς ὄρθας, eaque protracta incidat in circumferentiam in signo E. Erit igitur EF summa altitudo convexitatis et terrae et fluminis inter fontes et ostia eius, quae altitudo invenienda est; agatur ex signo A recta AG, ut sit parallela rectae ED. Erit igitur circumferentia AEB secta in duas aequales in signo E per 3 et 30 tertii Elementorum et recta FD per 34 primi aequalis rectae AG, quae per eadem est semissis rectae subtendentis duplum circumferentia AC, cicrumferentia denique AEC quadrans est totius circunferentiae circuli ob angulum EDC rectum. Et quoniam circumferentia AEB datur partium 20, erit dimidiata eius AE partium earundem 10 et reliqua ad quadrantem circumferentia AC partium 80. Ideo ex Canone subtensarum Ptolemaei, qui paulo post sequetur, erit AG erecta, hoc est DF, segmentorum 59 scrupulorum 5 secundorum 18, qualium segmentorum ea quae ex centro terrae, scilicet recta DE, 60 ponitur. Qualium ergo eadem DE supponitur 859 milliarium germanicorum, talium DF colligitur 846. Reliqua igitur FE summa altitudo, quam in toto suo cursu transcendit Danubii flumen, milliarium est germanicorum 13 fere, ut posuimus, vel qualium semidiameter terrae DE sumitur 28636 stadiorum ex Ptolemaei sententia, qui singulis partibus maximi circuli adscribit 500, talium DF 28201, ac reliqua FE 435 stadiorum, cum totum intervallum itineris constet fere una myriade stadiorum.
Esto enim maximus circulus in superficie terrae ABC centro terrae D descriptus per fontes Danubii in signo A, et per ostia eiusdem in signo B, circumferentiam autem AEB inventam partium 2 0, qualium tota ponitur 360, subtendat recta AB, cui ex centro D occurrat recta DF in signo F πρὸς ὄρθας, eaque protracta incidat in circumferentiam in signo E. Erit igitur EF summa altitudo convexitatis et terrae et fluminis inter fontes et ostia eius, quae altitudo invenienda est; agatur ex signo A recta AG, ut sit parallela rectae ED. Erit igitur circumferentia AEB secta in duas aequales in signo E per 3 et 30 tertii Elementorum et recta FD per 34 primi aequalis rectae AG, quae per eadem est semissis rectae subtendentis duplum circumferentia AC, cicrumferentia denique AEC quadrans est totius circunferentiae circuli ob angulum EDC rectum. Et quoniam circumferentia AEB datur partium 20, erit dimidiata eius AE partium earundem 10 et reliqua ad quadrantem circumferentia AC partium 80. Ideo ex Canone subtensarum Ptolemaei, qui paulo post sequetur, erit AG erecta, hoc est DF, segmentorum 59 scrupulorum 5 secundorum 18, qualium segmentorum ea quae ex centro terrae, scilicet recta DE, 60 ponitur. Qualium ergo eadem DE supponitur 859 milliarium germanicorum, talium DF colligitur 846. Reliqua igitur FE summa altitudo, quam in toto suo cursu transcendit Danubii flumen, milliarium est germanicorum 13 fere, ut posuimus, vel qualium semidiameter terrae DE sumitur 28636 stadiorum ex Ptolemaei sententia, qui singulis partibus maximi circuli adscribit 500, talium DF 28201, ac reliqua FE 435 stadiorum, cum totum intervallum itineris constet fere una myriade stadiorum.
〈I.4〉 CAPUT IIII: Quod terra in medio coeli sita sit
Considerata figura, si quis deinceps locum inquirat, deprehendet ea quae de adparentiis stellarum diximus ita tantum posse accidere, si collocemus terram in medio coeli tanquam centrum. Nam si alio loco esset, Distributio situum terrae i. m. W aut esset extra axem distans aequaliter ab utroque polo, aut esset in axe, sed recederet propius ad alterum polorum, aut neque in axe esset, neque distaret aequaliter a polis.
Cum primo situ haec maxime pugnant, I. Quae phaenomena repugnent, quo minus terra sita sit extra axem aequaliter distans ab utroque polo, id est, in plano aequinoctialis circuli i. m. W nam si sursum aut deorsum terra collocata esset, sequeretur hunc positum, quod in recta quidem sphaera nunquam fieri posset aequinoctium, eo quod horizon semper in duas inaequales portiones coelum divideret, alteram supra terram, alteram infra.
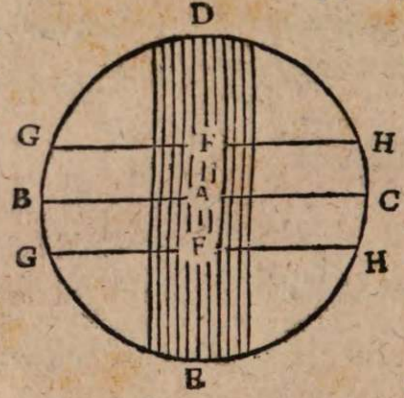 σχόλιον. Esto centrum mundi A, poli eiusdem B C, per quos descriptus sit meridianus circulus BDCE. in hoc sumatur D signum verticale distans aequaliter, hoc est quadrante circuli ab utroque polo B C, per quod signum transeat planum aequinoctialis circuli DAE secans πρὸς ὄρθας planum meridiani circuli. Iam si terra in plano quidem aequinoctialis collocata est, sed extra axem mundi BC, ut in F, sit horizontis planum GFH, ad quod erectum est planum aequinoctialis circulio DFE. Erit igitur communis sectio duorum planorum meridiani quidem BDCE, et horizontis GFH, recta linea GFH. Eiusdem vero meridiani et aequinoctialis DAE communis sectio recta linea DAE, quae cum utraque recta DFH et BAC rectos facit angulos, eo quod planum aequinoctialis et ad mundi axem BC et ad planum recti horizontis GFH erigitur. Quare rectae GH et BC invicem parallelae sint, quia sunt in eodem plano. Meridiani igitur circuli arcus GB et BC quibus distant poli ab horizonte sunt invicem aequales. Ex his manifestum est, primum quod segmenta meridiani circuli GDH et HEG, ac propterea etiam segmenta sphaerae supra et infra terram sint inter se inaequalia, deinde quod uterque polus aequaliter aut extet supra horizontem, aut deprimatur infra. Ex quo rursus sequitur quod in hoc situ terre horizon secaret omnes parallelos perpetua mundi vertigine descriptos per inaequalia, eo quod totus axis secundum aequidistantiam aut esset sublatus supra horizontem, aut infra demersus.
σχόλιον. Esto centrum mundi A, poli eiusdem B C, per quos descriptus sit meridianus circulus BDCE. in hoc sumatur D signum verticale distans aequaliter, hoc est quadrante circuli ab utroque polo B C, per quod signum transeat planum aequinoctialis circuli DAE secans πρὸς ὄρθας planum meridiani circuli. Iam si terra in plano quidem aequinoctialis collocata est, sed extra axem mundi BC, ut in F, sit horizontis planum GFH, ad quod erectum est planum aequinoctialis circulio DFE. Erit igitur communis sectio duorum planorum meridiani quidem BDCE, et horizontis GFH, recta linea GFH. Eiusdem vero meridiani et aequinoctialis DAE communis sectio recta linea DAE, quae cum utraque recta DFH et BAC rectos facit angulos, eo quod planum aequinoctialis et ad mundi axem BC et ad planum recti horizontis GFH erigitur. Quare rectae GH et BC invicem parallelae sint, quia sunt in eodem plano. Meridiani igitur circuli arcus GB et BC quibus distant poli ab horizonte sunt invicem aequales. Ex his manifestum est, primum quod segmenta meridiani circuli GDH et HEG, ac propterea etiam segmenta sphaerae supra et infra terram sint inter se inaequalia, deinde quod uterque polus aequaliter aut extet supra horizontem, aut deprimatur infra. Ex quo rursus sequitur quod in hoc situ terre horizon secaret omnes parallelos perpetua mundi vertigine descriptos per inaequalia, eo quod totus axis secundum aequidistantiam aut esset sublatus supra horizontem, aut infra demersus.
In obliqua vero sphaera, aut rurus nullum omnino fieret aequinoctium, aut non in medio transitu inter aestivum et hibernum solstitium. Nam haec spacia necessario fierent inaequalia. Non enim secaret horizon amplius in duo aequalia circulum aequinoctialem, ac maximum eorum parallelorum, qui perpetua mundi conversione describuntur, sed alium seu magis borealem, seu magis australem parallelum. Constat autem haec spacia utrinque aequalia esse ubique, vel eo argumento quod, quanto dies longissimus in aestivo solstitio maior est quam dies aequinoctialis, tanto vicissim brevissimus dies minor est in solstitio hiberno
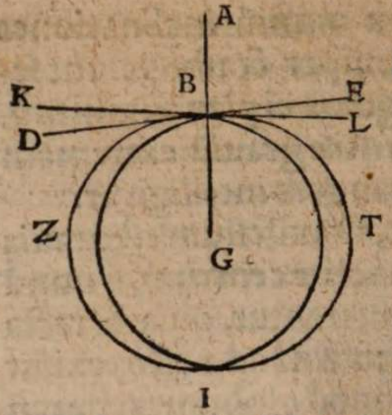
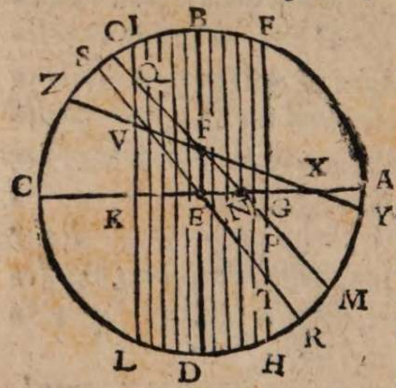 σχόλιον. Esto enim axis mundi AEC, centro mundi E, et polis A, C, per quos sit descriptus meridianus circulus ABCD, in quo sit BED aequinoctialis seu maximus omnium parallelorm et medius inter utrunque polum, tropici autem paralleli, hoc est extremi eorum, per quos sol transit annuo motu per obliquum, sint FH et IL secantes axem in signis G, K πρὸς ὄρθας. Iam si terra est extra axem aequaliter distans a polis, ut in F, ille tantum horizon, cui alter polus verticalis est, secabit sphaeram in duo equalia, ita ut aequinoctialis circulus omnino cum eo congruat, ut in linea BFKD alias semper in obliqua sphaera secabit horizon coelum in duo inaequalia segmenta, quorum alterum supra terram est, alterum infra, nec fiet ullum aequinoctium, aut non in medio transitu inter aestivum solstitium et hibernum, ut, si sumatur A signum polus semper adparens, secabit planum horizontis dimidiatum axem mundi AGE vel inter duo signa A, G, vel inter reliqua duo G, E. Secet primum inter duo signa GE, ut in N, ut sit horizon MNFO secans extremos parallelos tropicos in signis P, Q. Fiet igitur equinoctium non in medio parallelo BED, sed in eo qui describitur per signum N propior tropico FH quam tropico IL. Planum enim horizontis MNO secat hunc parallelum per N descriptum in aequalia, cum omnium parallelorum centra in axe mundi consistant. Quare etiam GP excessus diei maximi super diem aequinoctialem non erit aequalis defectui KQ, quo brevissimus dies hibernus minor est eodem die aequinoctiali, id quod manifeste repugnat omnium locorum experientiae. Quod si horizon secet axem in arcu AG, ut in signo X, nullum fieri potest aequinoctium, eo quod horizon non transeat per ullius paralleli centrum, sed omnium parallelorum centra una cum ea parte axis aut lateant demersa infra horizontem, aut emineant sublata supra horizontem.
σχόλιον. Esto enim axis mundi AEC, centro mundi E, et polis A, C, per quos sit descriptus meridianus circulus ABCD, in quo sit BED aequinoctialis seu maximus omnium parallelorm et medius inter utrunque polum, tropici autem paralleli, hoc est extremi eorum, per quos sol transit annuo motu per obliquum, sint FH et IL secantes axem in signis G, K πρὸς ὄρθας. Iam si terra est extra axem aequaliter distans a polis, ut in F, ille tantum horizon, cui alter polus verticalis est, secabit sphaeram in duo equalia, ita ut aequinoctialis circulus omnino cum eo congruat, ut in linea BFKD alias semper in obliqua sphaera secabit horizon coelum in duo inaequalia segmenta, quorum alterum supra terram est, alterum infra, nec fiet ullum aequinoctium, aut non in medio transitu inter aestivum solstitium et hibernum, ut, si sumatur A signum polus semper adparens, secabit planum horizontis dimidiatum axem mundi AGE vel inter duo signa A, G, vel inter reliqua duo G, E. Secet primum inter duo signa GE, ut in N, ut sit horizon MNFO secans extremos parallelos tropicos in signis P, Q. Fiet igitur equinoctium non in medio parallelo BED, sed in eo qui describitur per signum N propior tropico FH quam tropico IL. Planum enim horizontis MNO secat hunc parallelum per N descriptum in aequalia, cum omnium parallelorum centra in axe mundi consistant. Quare etiam GP excessus diei maximi super diem aequinoctialem non erit aequalis defectui KQ, quo brevissimus dies hibernus minor est eodem die aequinoctiali, id quod manifeste repugnat omnium locorum experientiae. Quod si horizon secet axem in arcu AG, ut in signo X, nullum fieri potest aequinoctium, eo quod horizon non transeat per ullius paralleli centrum, sed omnium parallelorum centra una cum ea parte axis aut lateant demersa infra horizontem, aut emineant sublata supra horizontem.
Sed si terram collocemus in centro mundi, ut sit E, ut sit horizon obliquae sphaerae RS secans tropicos paralelos in signis T, V, tunc demum omnia rite respondebunt, nempe ut aequinoctium fiat sole transeunte per medium et maximum parallelum BED, et aequale invicem sint excessus et defectus, videlicet GT et VK etc.
Si vero terra fingatur recedere propius ad orientem, aut ad occidentem, accidet, ut nec stellarum magnitudines et distantiae videantur eaedem in horizonte mane et vesperi, nec tempus sit aequale ab ortu ad meridiem, et a meridie ad occasum. Haec autem manifeste pugnant cum adparentia.
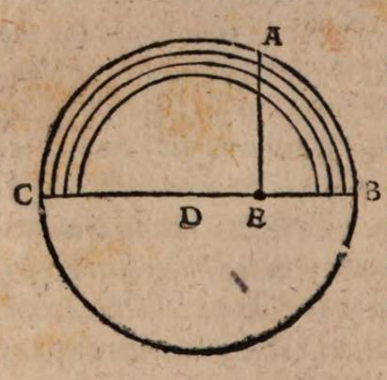 σχόλιον. Esto enim centrum mundi D, et planum horizontis CDB, ita ut duorum punctorum BC alterum sit orientis stellae, alterum occidentis, si iam terra non est in medio collocata, ut in D, sed extra versus ortum aut occasum, ut in E, sit verticale puctum, per quod transeat meridianus circulus AE secans planum horizontis CDB πρὸς ὄρθας, parallelum autem motu stellae descriptum secet supra horizontem in signo A. Esto autem centrum mundi D inter signa C et E. Manifestum est igitur stellam in C longius distare ab E terra, ac propterea minorem apparere, et minus distare in B atque apparere maiorem, similiter et paralleli arcum CA ab horizonte ad meridianum maiorem esse arcu eiusdem AB a meridiano ad horizontem, ac tempora eodem modo inaequalia.
σχόλιον. Esto enim centrum mundi D, et planum horizontis CDB, ita ut duorum punctorum BC alterum sit orientis stellae, alterum occidentis, si iam terra non est in medio collocata, ut in D, sed extra versus ortum aut occasum, ut in E, sit verticale puctum, per quod transeat meridianus circulus AE secans planum horizontis CDB πρὸς ὄρθας, parallelum autem motu stellae descriptum secet supra horizontem in signo A. Esto autem centrum mundi D inter signa C et E. Manifestum est igitur stellam in C longius distare ab E terra, ac propterea minorem apparere, et minus distare in B atque apparere maiorem, similiter et paralleli arcum CA ab horizonte ad meridianum maiorem esse arcu eiusdem AB a meridiano ad horizontem, ac tempora eodem modo inaequalia.
Secunda opinio, II. De secundo situ, si terra collocaretur extra planum aequinoctialis in axe tamen mundi i. m. W qua terra in axe fingitur ita posita, ut ad alterum polorum propius accedat, ita refutatur. Si sic haberet res, superficies horizontis in quocunque climate secaret coelum in duas inaequales portiones, alteram supra terram, alteram infra, nec eodem modo ubique, sed aliter in aliis climatibus. Nam in sola recta sphaera secari coelum ab horizonte in duo aequalia posset. In obliqua vero, in qua propior polus esset semper conspicuus, semper minor portio esset supra terram, maior infra. Unde accideret, ut superficies horizontis non secaret aequaliter zodiacum, qui ex maximis circulis est, quod secus esse palam cernimus. Semper enim et omnibus apparent sex signa supra terram, reliquis mersis sub terram, et rursus cum haec supra terram cernuntur, contraria occultantur. Manifestum est igitur ab horizonte in duo aequalia zodiacum secari, quia iidem semicirculi modo supra terram, modo sub terra integri sunt.
 σχόλιον. Centro enim mundi D, polis A, C sumptis, sit meridianus ABC, et in axe mundi AC sumatur situs terrae in E propior polo A quam C. Et sit declivis horizon BEH, et alius horizon FEG, ad cuius planum erectus sit axis mundi AC. Erit igitur AEC horizon sphaerae rectae, secans coelum in duo aequalia hemispheria ABC et CGA. At horizon BEH non secat coelum in duo hemisphaeria, sed in segmenta inaequalia, quorum maius est BCH propter comprehensum in eo centrum, minus autem reliquum HAB. Similiter horizon FEG secat coelum in segmenta inaequalia, quorum maius est FCG, minus autem GAF. Maius tamen est segmentum FCG, quam BCH, propterea quod planum horizontis FEG longius recedit a centro sphaerae D quam planum horizontis FEG. Quod facilime patet a centro sphaerae D, normali linea DI demissa. Erit enim in orthogonio triangulo DIE, cuius angulus ad I rectus, latus DE rectum subtendens maior utroque latere DI, et IE.
σχόλιον. Centro enim mundi D, polis A, C sumptis, sit meridianus ABC, et in axe mundi AC sumatur situs terrae in E propior polo A quam C. Et sit declivis horizon BEH, et alius horizon FEG, ad cuius planum erectus sit axis mundi AC. Erit igitur AEC horizon sphaerae rectae, secans coelum in duo aequalia hemispheria ABC et CGA. At horizon BEH non secat coelum in duo hemisphaeria, sed in segmenta inaequalia, quorum maius est BCH propter comprehensum in eo centrum, minus autem reliquum HAB. Similiter horizon FEG secat coelum in segmenta inaequalia, quorum maius est FCG, minus autem GAF. Maius tamen est segmentum FCG, quam BCH, propterea quod planum horizontis FEG longius recedit a centro sphaerae D quam planum horizontis FEG. Quod facilime patet a centro sphaerae D, normali linea DI demissa. Erit enim in orthogonio triangulo DIE, cuius angulus ad I rectus, latus DE rectum subtendens maior utroque latere DI, et IE.
 Caeterum et hunc positum terrae consequuntur priora absurda, videlicet, quod in obliqua sphaera aut nullum omnino fieret aequinoctium, aut non in medio transitu inter duo solititia, ut si repetita superiori diagrammate terra cogitetur in X, vel in N. In recta autem sphaera, etsi foret perpetuum aequinoctium, tamen Sol nunquam fieret verticalis, aut non in medio parallelo, sed in alio quodam, qui alteri extremorum tropicorum esset propior.
Caeterum et hunc positum terrae consequuntur priora absurda, videlicet, quod in obliqua sphaera aut nullum omnino fieret aequinoctium, aut non in medio transitu inter duo solititia, ut si repetita superiori diagrammate terra cogitetur in X, vel in N. In recta autem sphaera, etsi foret perpetuum aequinoctium, tamen Sol nunquam fieret verticalis, aut non in medio parallelo, sed in alio quodam, qui alteri extremorum tropicorum esset propior.
Praeterea, nisi terra sub ipso aequinoctiali sita esset, Umbrarum ratio i. m. W sed ad Arctum aut meridiem ad alterum polorum propius accederet, omnino eveniret ut ne ad sensum quidem in aequinoctialibus diebus gnomonum umbrae orientales et occidentales in eandem rectam lineam congruerent super aequidistantes superficies horizonti. At ubique cernitur hoc ita fieri.
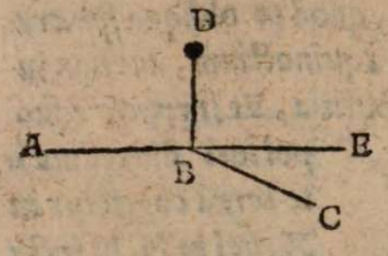 σχόλιον. Sit enim planum horizontis ABC, ad quod sit erectus gnomon BD, cuius vertex D, et sit A signum orientis Solis, D occidentis, porro die aequinoctii dum Sol mane ex A emergit, umbram iaciat gnomon secundum rectam lineam BE versus occasum, vesperi autem dum in E demergitur, secundum rectam BA versus ortum. Testatur itaque perpetua experientia omnium locorum, quod hae ambae lineae AB et BE. Si quis accurate examinet, prorsus in unam eandemque rectam lineam congruant. ld fieri nequaquam posset nisi terrae centrum ἀκριβῶς intra planum aequinoctialis circuli collocatum esset, quia umbrae hae alias non coirent ἐπʼ ἐυθείας, sed ad angulum velut CB, BE rectae angulum comprehendmt CBE in plano horizontis.
σχόλιον. Sit enim planum horizontis ABC, ad quod sit erectus gnomon BD, cuius vertex D, et sit A signum orientis Solis, D occidentis, porro die aequinoctii dum Sol mane ex A emergit, umbram iaciat gnomon secundum rectam lineam BE versus occasum, vesperi autem dum in E demergitur, secundum rectam BA versus ortum. Testatur itaque perpetua experientia omnium locorum, quod hae ambae lineae AB et BE. Si quis accurate examinet, prorsus in unam eandemque rectam lineam congruant. ld fieri nequaquam posset nisi terrae centrum ἀκριβῶς intra planum aequinoctialis circuli collocatum esset, quia umbrae hae alias non coirent ἐπʼ ἐυθείας, sed ad angulum velut CB, BE rectae angulum comprehendmt CBE in plano horizontis.
Hinc et tertia opinio refutari poterit, III. Tertia ratio positus terrae i. m. W cum eadem absurda inde sequantur, quae /58r/ prioribus opinionibus repugnant.
Ac ut summatim dicam, nisi terra in medio esset, A serie incrementi et decrementi dierum ac noctium i. m. W universa series in decrementis et incrementis dierum et noctium penitus confunderetur.
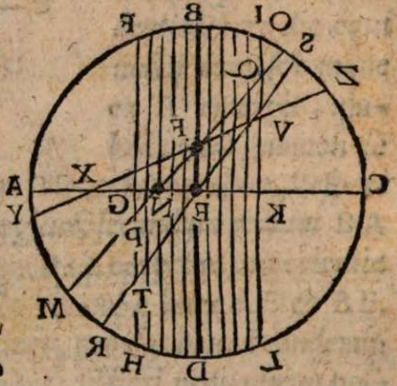
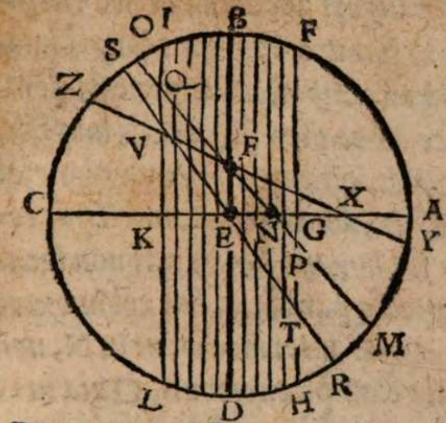 σχόλιον. Supra tantum ratiocinatus est Ptolemaeus ab aequali differentia maximi et minimi diei ad diem aequinoctialem. Nunc universam seriem incrementi et decrementi dierum ac noctium iubet considerare. Rursum autem proponat sibi lector διάγραμμα, quo supra in primo situ terrae usi sumus. Si enim planum horizontis secat axem mundi extra parallelos qui intra ambos tropicos comprehenduntur, ut in signo X versus polum A, quia in altero hemisphaerio mundi intercipiuntur segmenta parallelorum minora semicirculis, ut in YBZ, in altero autem maiora, ut in ZDY, manifestum est, non posse existere hanc seriem, quae ubique extra rectam sphaeram apparet in decrementis et incrementis dierum atque noctium, quia in hoc horizonte nullum fieret aequinoctium, ac semper prolixiores essent dies noctibus vel e contra. At manifesta experientia ostendit bis in anno fieri aequinoctium, et ab altero horum paulatim crescere dies supra noctes usque ad medium, reliquo tempore decrescere iterum dies, donec existat alterum aequinoctium, hinc minui diurna spacia convenienter, et augeri nocturna, donec rursus circa medium tempus fiat nox brumalis longissima, quae quidem tantum excedit diem aequinoctialem, quantum prius excedebat dies solstitialis longissimus, inde contrahi noctes iterum pro proportione, et aliquid accedere diebus, donec prius anni tempus revertatur. Similiter, si planum horizontis non secaret axem mundi in medio parallelo, sed vel in extremo, ut in G, vel in aliquo intermedio, ut in N, non evenirent congruentia cum phaenomenis, quia in G semel tantum foret aequinoctium. Alias vero per totum annum, vel noctes essent prolixiores diebus, vel econtra. lta etiam in N, et si fieret aequinoctium bis per annum, et utrinque crescerent, ac decrescerent dierum noctiumque spacia, tamen dierum incrementa et decrementa nec numero nec magnitudine essent aequalia incrementis noctium, id quod vel oculi iudicare possunt collatis duobus triangulis GNP et KNQ, quia et plura et maiora segmenta parallelorum comprehendit triangulum KNQ quam triangulum GNP. Duntaxat igitur secante plano horizontis medium parallelum BD in axe mundi, ut in signo E, perpetua illa series aequabiliter crescentium et decrescentium dierum atque noctium constare et conservari potest, quia triangula GET et VEK non solum similia sunt, sed et aequalia, et intercipiunt aequalia parallelorum a medio aequaliter distantium segmenta, ut GT et VR, et reliqua deinceps similiter.
σχόλιον. Supra tantum ratiocinatus est Ptolemaeus ab aequali differentia maximi et minimi diei ad diem aequinoctialem. Nunc universam seriem incrementi et decrementi dierum ac noctium iubet considerare. Rursum autem proponat sibi lector διάγραμμα, quo supra in primo situ terrae usi sumus. Si enim planum horizontis secat axem mundi extra parallelos qui intra ambos tropicos comprehenduntur, ut in signo X versus polum A, quia in altero hemisphaerio mundi intercipiuntur segmenta parallelorum minora semicirculis, ut in YBZ, in altero autem maiora, ut in ZDY, manifestum est, non posse existere hanc seriem, quae ubique extra rectam sphaeram apparet in decrementis et incrementis dierum atque noctium, quia in hoc horizonte nullum fieret aequinoctium, ac semper prolixiores essent dies noctibus vel e contra. At manifesta experientia ostendit bis in anno fieri aequinoctium, et ab altero horum paulatim crescere dies supra noctes usque ad medium, reliquo tempore decrescere iterum dies, donec existat alterum aequinoctium, hinc minui diurna spacia convenienter, et augeri nocturna, donec rursus circa medium tempus fiat nox brumalis longissima, quae quidem tantum excedit diem aequinoctialem, quantum prius excedebat dies solstitialis longissimus, inde contrahi noctes iterum pro proportione, et aliquid accedere diebus, donec prius anni tempus revertatur. Similiter, si planum horizontis non secaret axem mundi in medio parallelo, sed vel in extremo, ut in G, vel in aliquo intermedio, ut in N, non evenirent congruentia cum phaenomenis, quia in G semel tantum foret aequinoctium. Alias vero per totum annum, vel noctes essent prolixiores diebus, vel econtra. lta etiam in N, et si fieret aequinoctium bis per annum, et utrinque crescerent, ac decrescerent dierum noctiumque spacia, tamen dierum incrementa et decrementa nec numero nec magnitudine essent aequalia incrementis noctium, id quod vel oculi iudicare possunt collatis duobus triangulis GNP et KNQ, quia et plura et maiora segmenta parallelorum comprehendit triangulum KNQ quam triangulum GNP. Duntaxat igitur secante plano horizontis medium parallelum BD in axe mundi, ut in signo E, perpetua illa series aequabiliter crescentium et decrescentium dierum atque noctium constare et conservari potest, quia triangula GET et VEK non solum similia sunt, sed et aequalia, et intercipiunt aequalia parallelorum a medio aequaliter distantium segmenta, ut GT et VR, et reliqua deinceps similiter.
Accedit hoc etiam Alia ratio sumpta a defectibus Lunae i. m. W quod Lunae eclipses non iuxta quamlibet caeli partem fieri possent in opposito loco Solis, cum saepe terra inter haec duo lumina non in diametrali ipsorum positu, sed in spaciis minoribus semicirculo media interveniret.
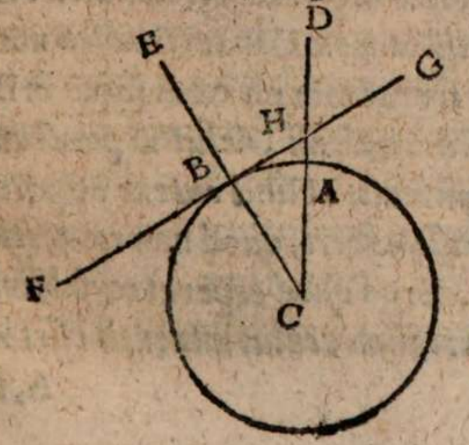
 σχόλιον. Esto enim centrum mundi A, et super eo descriptus circulus per media signa BCDEF, in cuius plano Luna deficiens Soli obiiciatur. Si terra igitur non possidet medium locum mundi A, sed extra sedem habet, ut in G, non semper deficiet Luna in diametrali positu Solis. Acta enim per G linea BE, minime transiens per A centrum universi, si Soli in B obiiciatur Luna e regione in eadem recta linea circa E, deficiet quidem Luna, sed non in diametrali positu Solis, quia circumferentia BEF minor est semicirculo. Ac breviter Lunae defectus tantum fieri potest in oppositis per semicirculum locis, cum Sol fuerit in recta transeunte per utrunque centrum, terre inquam et universi, ut in recta CAGF.
σχόλιον. Esto enim centrum mundi A, et super eo descriptus circulus per media signa BCDEF, in cuius plano Luna deficiens Soli obiiciatur. Si terra igitur non possidet medium locum mundi A, sed extra sedem habet, ut in G, non semper deficiet Luna in diametrali positu Solis. Acta enim per G linea BE, minime transiens per A centrum universi, si Soli in B obiiciatur Luna e regione in eadem recta linea circa E, deficiet quidem Luna, sed non in diametrali positu Solis, quia circumferentia BEF minor est semicirculo. Ac breviter Lunae defectus tantum fieri potest in oppositis per semicirculum locis, cum Sol fuerit in recta transeunte per utrunque centrum, terre inquam et universi, ut in recta CAGF.
I. Si terra sita esset in plano circuli aequinoctialis extra mundi axem.
Pugnarent haec cum phaenomenis.
1. In sphaera recta nullum prosus fieret aequinoctium.
2. Alicubi etiam magnitudines stellarum in ortu et occasu non essent aequales.
3. Nec antemeridianum tempus aequale postmeridiano.
II. Si terra in axe mundi sita esset extra planum aequinoctialis.
1. In sphaera recta, etsi esset aequinoctium, tamen subiectis locis Sol aut non fieret verticalis, aut non in medio transitu inter tropicos.
2. Etsi tempus antemeridianum aequale esset postmeridiano, tamen stellarum distantiae et magnitudines non essent semper et ubique aequales.
3. Umbrae orientales et occidentales die aequinoctii non congruerent ἐπʼ ἐυθείας
III. Si terra nec in axe mundi collocata esset, nec in plano aequinoctialis circuli.
1. In recta sphaera nullum eveniret aequinoctium.
2. Reliqua pugnantia cum phaenomenis in utroque priori situ hic pariter concurrerunt.
Communia omnibus tribus sitibus terrae.
1. In obliqua sphaera, aut non fieret aequinoctium, aut non in medio transitu.
2. In obliqua sphaera ille tantum horizon secaret sphaeram per aequalia, qui transiret per centrum mundi.
3. In neutra sphaera semper apparerent sex signa.
4. Confunderetur universa series in decrementis et incrementis dierum.
5. Eclipses, ut plurimum evenirent, cum Sol et Luna non versarentur in locis, quae per semicirculum invicem opponerentur.
〈I.5〉 CAPUT V: Quod terra velut punctum sit ad coelum collata
Quod vero puncti rationem, Prima ratio, eadem magnitudine conspiciuntur stellae ubique i. m. W quod ad sensum attinet, terra habeat ad distantiam orbis stellarum fixarum, hoc illustre argumentum est, quod ab omnibus terrae partibus magnitudines et distantiae stellarum iisdem temporibus aequales, similesque cernuntur ubique, quemadmodum earundem stellarum observationes factae in diversis climatibus ostendunt, quae ne quidem in minima re discrepant.
σχόλιον. Ut Martis stellae etiam si longe alia magnitudine apparet apogaeus in eccentro quam perigaeus, tamen eodem tempore ubique terrarum conspicitur eadem magnitudine.
Accedit et hoc, Altera ratio ab eruditis observationibus quae fiunt per instrumenta astronomica i. m. W quod gnomones et centra armillarum sphaericarum in quacunque parte terrae ponantur, tantundem valent, quantum in vero centro terrae, et conservant considerationes et circumductiones umbrarum adeo regulares et consentientes hypothesi adparentiarum, ac si reipsa in medio terrae puncto collocarentur.
σχόλιον. Confirmat Ptolemaeus testimoniis valde illustribus tum adparentiarum, tum aliarum eruditarum observationum has, ut ipse vocat, primas sententias. Hinc etiam umbrarum rationem iis saltem temporibus toto terrarum orbe celeberrimam atque usitatissimam allegat, quae nunc vix eruditis nota est. Olim enim partes diei, adeoque horae, quas καιρικὰς dixerunt, ubique gentium discernebantur penes umbrarum magnitudines, incrementa, ac decrementa. Et vocabatur haec doctrina γνωμονική, quia erectus gnomon horarum indicium in plano faciebat, in quo earum variae lineae circa gnomonem designatae erant. Sed ingeniosi homines, quos pro generositate naturae movebat communis utilitas totius generis humani, varia in hunc usum instrumenta foeliciter excogitarunt, quorum alia vasa horoscopa vocabantur, alia horologia scioterica, aliis denique erant alia nomina. Ac celebratur in sacris literis horologium Achas regis Iuda patris Ezechiae. Nec dubium est sapientes Reges, qui primos obeliscos in Aegypto statuerunt solis numini sacratos, et ingentes moles Pyramidum extruxerunt, his astronomicis et veris utilitatibus praecipue invitatos esse, etsi accessit postea ut fit stulta et prodiga aemulatio. Fuisse autem ubique gentium in usu, ut dixi, hanc umbrarum doctrinam et accuratam considerationem, vel secundus liber huius operis abunde testatur, in quo discernit Ptolemaeus climata ac parallelos omnes, tum penes longissimorum dierum, tum penes umbrarum spacia, quod harum rerum observatio facillima esset, et maxime obvia, nam veteres etiam geographi, ut ex Strabone apparet, contenti fuerunt insignium locorum in diversis regionibus latitudines penes umbras quas gnomones die aequinoctii medio iactabant descripsisse, cuius rei pauca quaedam exempla Plinius recenset cap. 72, libri 2. ltaque haec suavis et erudita γνωμονική, ac naturae proxima ad aliquam partem etiam μετεωροσκοπικῆς conducebat, quia ex umbrarum ratione altitudo poli in uno quolibet loco et expedite et liquido iudicari potest. Verum desiit multis iam saeculis ubique fere usus gnomonices, postquam praeclara illa ἀυτόματα horologia nostra inventa sunt, quae rotulis quibusdam mira arte coniunctis ita librantur ponderibus, ut totum diem civilem seu νυχθήμερον distribuant in 24 horas aequales seu ἰσημερινὰς, quae nunc rectius vulgares dici possunt quam illae inaequales καιρικαί, quia, cum ueteres dividerent pariter ommes dies totius anni in duodecim spacia aequalia, erat necessario solstitialis hora diurna maior quam hora aequinoctialis, et haec vicissim maior quam brumalis hora. Etsi autem valde consentaneum est, non extitisse communem usum horarum aequinoctialium antequam fabrica horum nobilium ἀυτομάτων publicaretur, quibus quidem humana vita in his tam rigentibus et nebulosis climatis aegre caritura esset, tamen ex Albategnii astronomico satis adparet, quod eius aetate in Asia horae καιρικαὶ adhuc vulgo usurpatae fuerint. Floruit autem Albategnius 100 fere annis, postquam per Carolum Magnum imperium a Graecis translatum esset ad Germanos.
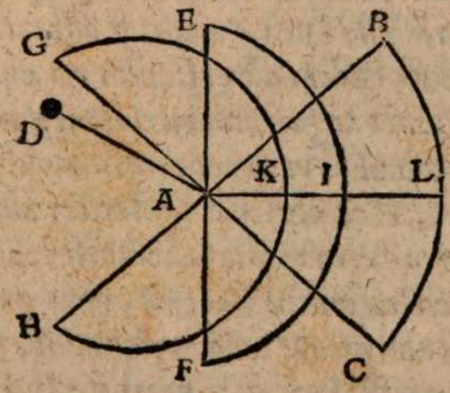 Sed ut in hoc Ptolemaei loco rudem lectorem nonnihil iuvemus, esto ad planum horizontis ABC in signo A erectus gnomon AD, cuius vertex A. Et inventam lineam meridianam secet πρὸς ὄρθας linea aequinoctialis EAF, in quam congruunt die aequinoctii, ut supra dictum est, umbrae orientales et occidentales, verum similiter ex eadem recta linea cernuntur tum solstitialis exortus et brumalis occasus, tum etiam brumalis ortu et solititialis occasus, ut, si sit sostitialis exortus in recta AG, erit in AC ἐπʼ ἐυθείας brumalis occasus, et si brumalis exortus in AB recta, solstitialis occasus similiter in AH. Descripserit autem vertex gnomonis in aestivo solstitio lineam quandam GKH, et in aequinoctio utroque EIF, in bruma denique BLC, in signis KIL per meridianam lineam transeuntes. Similes igitur sint quolibet die harum linearum portiones antemeridianae versus occasum portionibus postmeridianis versus ortum, ut portio GK similis portioni KH, et portiones EI, et BL portionibus IF et LC, imo et singularum horarum a meridiana linea aequaliter distantium interceptae portiones eodem die et similes et aequales, postremo similiter et anguli antemeridiani aequales angulis postmeridianis, ut verbi gratia angulus BKL angulo LKC. Haec fieri ita regulariter nullo modo possent, si terra extra medium universi collocata esset, nec puncti rationem haberet, quia gnomonum umbrae alias non forent indices altitudinis poli.
Sed ut in hoc Ptolemaei loco rudem lectorem nonnihil iuvemus, esto ad planum horizontis ABC in signo A erectus gnomon AD, cuius vertex A. Et inventam lineam meridianam secet πρὸς ὄρθας linea aequinoctialis EAF, in quam congruunt die aequinoctii, ut supra dictum est, umbrae orientales et occidentales, verum similiter ex eadem recta linea cernuntur tum solstitialis exortus et brumalis occasus, tum etiam brumalis ortu et solititialis occasus, ut, si sit sostitialis exortus in recta AG, erit in AC ἐπʼ ἐυθείας brumalis occasus, et si brumalis exortus in AB recta, solstitialis occasus similiter in AH. Descripserit autem vertex gnomonis in aestivo solstitio lineam quandam GKH, et in aequinoctio utroque EIF, in bruma denique BLC, in signis KIL per meridianam lineam transeuntes. Similes igitur sint quolibet die harum linearum portiones antemeridianae versus occasum portionibus postmeridianis versus ortum, ut portio GK similis portioni KH, et portiones EI, et BL portionibus IF et LC, imo et singularum horarum a meridiana linea aequaliter distantium interceptae portiones eodem die et similes et aequales, postremo similiter et anguli antemeridiani aequales angulis postmeridianis, ut verbi gratia angulus BKL angulo LKC. Haec fieri ita regulariter nullo modo possent, si terra extra medium universi collocata esset, nec puncti rationem haberet, quia gnomonum umbrae alias non forent indices altitudinis poli.
Indicium et hoc est rem ita habere, TERTIA ratio ab horizontibus, ubique apparet coeli hemisphaerium i. m. W quod ubique superficies excurrentes, quatenus visus noster se profert, quas vocant horizontes, secant totum coelum in duo aequalia, quod non accideret, si terrae magnitudo sensibilis esset collata ad coeli distantiam. Sola enim superficies quae exit a centro terrae posset circumdatum orbem aequaliter dividere, a quacunque vero planicie terrae duceretur, necesse esset subterraneas portiones maiores fieri.
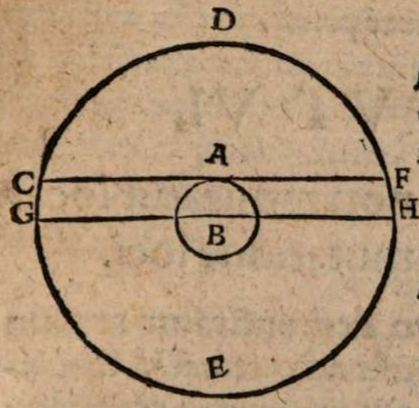 σχόλιον. Esto enim A locus in superficie terrae, eius qui sibi planum horizontis circumscribit CAF, cui plano sit aliud planum GBH, aequidistans per ipsum B centrum terrae cogitatione deductum. Iam etsi terra collocetur in medio, sicut alia φαινόμενα perspicue flagitant, tamen coelum ipsum nondum divideret horizon aequaliter, nisi eadem terra puncti quoque rationem haberet ad orbem stellarum inerrantium, quia semper portio coeli CDF supra terram pro proportione sensibiliter maior esset portione subterranea FEC, quia sola GDH et HED vera hemisphaeria essent invicem aequalia. Quum autem portiones coeli CDF et FEH, quas sensus oculorum discernit, insensibiliter differant a veris hemisphaeriis GDH et HEG, necesse est arcus DG et FH oppositos et aequales circuli maximi per verticem capitis descripti ita exiguos esse, ut sensu non percipiantur, ac propterea rectam quoque quae duplum circumferentiae vel CG vel FH subtendit, hoc est diametrum terre, incomparabilem esse ad totius coeli diametrum. Quare et corporum ipsorum coeli ac terrae magnitudo comparare invicem ad sensum minime potest.
σχόλιον. Esto enim A locus in superficie terrae, eius qui sibi planum horizontis circumscribit CAF, cui plano sit aliud planum GBH, aequidistans per ipsum B centrum terrae cogitatione deductum. Iam etsi terra collocetur in medio, sicut alia φαινόμενα perspicue flagitant, tamen coelum ipsum nondum divideret horizon aequaliter, nisi eadem terra puncti quoque rationem haberet ad orbem stellarum inerrantium, quia semper portio coeli CDF supra terram pro proportione sensibiliter maior esset portione subterranea FEC, quia sola GDH et HED vera hemisphaeria essent invicem aequalia. Quum autem portiones coeli CDF et FEH, quas sensus oculorum discernit, insensibiliter differant a veris hemisphaeriis GDH et HEG, necesse est arcus DG et FH oppositos et aequales circuli maximi per verticem capitis descripti ita exiguos esse, ut sensu non percipiantur, ac propterea rectam quoque quae duplum circumferentiae vel CG vel FH subtendit, hoc est diametrum terre, incomparabilem esse ad totius coeli diametrum. Quare et corporum ipsorum coeli ac terrae magnitudo comparare invicem ad sensum minime potest.
〈I.6〉 CAPUT VI: Quod terra non moveatur locali motu, seu mutatione loci
Per Confirmatio sumpta ex superioribus i. m. W eadem vero demonstratur terram nullo modo posse ad praedictas laterales partes moveri, aut unquam a centri loco recedere. Eadem enim acciderent quae diximus eventura, si alius esset terrae situs, nisi in medio.
Quare De quaestione, cur gravia moveantur ad medium i. m. W supervacaneum est causam quaerere, cur gravia moveantur ad medium, cum ex adparentibus manifestum sit, quod et terra medium locum teneat, et ponderosa omnia ad ipsam ferantur.
Est Ratiocinatur ex casu gravium ex sublimi, quod terras non moveatur i. m. W et hoc argumentum in promptu ad hanc sententiam confirmandam, quod, cum terra sit sphaerica et in medio, ut diximus, gravium corporum omnium inclinationes et proprii motus semper et ubique fiunt secundum rectos angulos ei plano immoto quod in loco incidentiae gravium extremam terrae superficiem tangere intelligitur.
Quod Gravia ipsum terrae centrum terrae petitura esse, nisi terrae soliditas obstaret i. m. W cum ita sit, manifestum est gravia petitura esse ipsum terrae centrum, si non a superficie terrae sustinerentur, quia et recta linea ad centrum tendens ad rectos existit angulos ei plano quod globum terrae tangit in puncto quo linea eadem secat terrae convexitatem.
σχόλιον. Nihil opus est, inquit et Ptolemaeus, quaerere, cur gravia moveantur ad medium, quia universaliter sic condita est natura, ut proprio et nativo impetu ea quae sint cognatae naturae appetant eundem locum. Sunt autem cognatae naturae terra, ac caetera gravia, estque ex aliis phaenomenis manifestum quod terra medium locum teneat. Ergo et caetera gravia ad medium feruntur, et sedem ibi nacta per se quiescunt. Imo, inquit Ptolemeus, hic ipse aequabilis casus gravium seu ponderosorum aperte convincit terram immotam quiescere in medio. Quod antequam declaremus, ex Theone prius integra demostratio recitanda est, quod gravia ipsum terrae centrum petitura essent, nisi soliditas eius obstaret.
 Intelligatur ergo globus terrae, ad quem grave quiddam proprio motu et absque ulla deflexione delatum designet in sublimi quidem rectam AB, Recta AB, ut turris aliqua aeditior i. m. W sed in terrae extremitate punctum B, et intelligatur per B punctum planum ad rectam AB immobile tangens globum terrae, cuius centrum sumatur G, et connectatur recta BG, per quam actum planum sectione sua efficiet in extremitate quidem globi circulum per 1 Theodosii, at in plano illo ad AB rectam immobili efficiet rectam lineam per 3 undecimi Elementorum. Sit ergo hic circulus in globo BZI, in plano autem recta linea DBE. Et quoniam planum non secat globum, nec recta in eo secat circulum. Tangit igitur recta DBE circulum ZBI, quare recta BG rectae DE existit ad rectos angulos. Rursus aliud planum per rectam BG actum efficiat in extremitate globi circulum BIT, et in plano ad rectam AB immobili rectam lineam KBL. Erit per eadem, ut prius, recta GB ad rectos angulos rectae lineae KBL. Quoniam igitur recta GB duabus rectis DE et KL secantibus se existit ad rectos angulos super communi ipsarum sectione B, ideo et ad planum per ipsas actum erecta est, quod quidem planum est illud ipsum, quod ad AB rectam immobile est. Ideo GB recta ad idem planum erecta est. A signo igitur B in utranque partem eidem plano ad rectos angulos insistunt rectae AB et BG. Ideo ABG est una eademque recta linea. Proinde, nisi grave illud in signo B prohiberetur a soliditate terrae, tenderet recto ac continuo impetu ad ipsius centrum, ut locum suum maxime proprium occuparet.
Intelligatur ergo globus terrae, ad quem grave quiddam proprio motu et absque ulla deflexione delatum designet in sublimi quidem rectam AB, Recta AB, ut turris aliqua aeditior i. m. W sed in terrae extremitate punctum B, et intelligatur per B punctum planum ad rectam AB immobile tangens globum terrae, cuius centrum sumatur G, et connectatur recta BG, per quam actum planum sectione sua efficiet in extremitate quidem globi circulum per 1 Theodosii, at in plano illo ad AB rectam immobili efficiet rectam lineam per 3 undecimi Elementorum. Sit ergo hic circulus in globo BZI, in plano autem recta linea DBE. Et quoniam planum non secat globum, nec recta in eo secat circulum. Tangit igitur recta DBE circulum ZBI, quare recta BG rectae DE existit ad rectos angulos. Rursus aliud planum per rectam BG actum efficiat in extremitate globi circulum BIT, et in plano ad rectam AB immobili rectam lineam KBL. Erit per eadem, ut prius, recta GB ad rectos angulos rectae lineae KBL. Quoniam igitur recta GB duabus rectis DE et KL secantibus se existit ad rectos angulos super communi ipsarum sectione B, ideo et ad planum per ipsas actum erecta est, quod quidem planum est illud ipsum, quod ad AB rectam immobile est. Ideo GB recta ad idem planum erecta est. A signo igitur B in utranque partem eidem plano ad rectos angulos insistunt rectae AB et BG. Ideo ABG est una eademque recta linea. Proinde, nisi grave illud in signo B prohiberetur a soliditate terrae, tenderet recto ac continuo impetu ad ipsius centrum, ut locum suum maxime proprium occuparet.
Ex quo etiam manifestum est, Porisma i. m. W haec tria puncta verticale, centrum horizontis, et centrum terrae semper in eandem rectam lineam congruere.
His ita explicatis considerandum nunc est Ptolemaei argumentum, cuius haec est sententia. Perpetua et universalis experientia omnium temporum et locorum testatur gravia ex sublimi ferri suopte nutu et pondere in terram ac mare ad rectos angulos. Necesse est igitur tum planum horizontis, cui grave illud ad rectos angulos illabitur, tum vero terram ipsam esse immotam.
 Si enim moveretur terra circa centrum et axem suum, superis omnibus stantibus, ut Nicias Syracusius arbitrabatur. Esto globus terrae AB, qui circa centrum suum convertatur spacio 24 horarum, et iuncta recta CA producatur sursum in D. Per praecedens igitur porisma, dum A locus est circumspicientis, sive centrum horizontis, erit D signum super verticem, et DA linea erecta ad planum horizontis, quod terrae convexitatem in signo tangit. Moveatur igitur terra ex A in B interea, dum grave quiddam (ut imber grando, seu aliud etiam sursum proiectum) delabitur ex signo D. Et ducta ex C centro recta linea CB in E, erit rursum E punctum verticale, dum horizontis centrum B. Aut igitur aer terrae proximus, et contenta in eo simul cum terra circumaguntur, aut quiescit vicinus aer, dum eadem ab occasu in ortum summa convertitur celeritate. Primum, si proximus aer in eoque comprehensa una volvuntur, nihil quod est in aere usquam moveri, sed omnia semper immota in eodem haerere loco existimabuntur, id quod minime apparet. Non igitur una rapitur aer vicinus. Sed quiescat nunc aer terra in gyrum circumacta. Et quia, dum grave quiddam ex D in terram seu mare delabitur, interea terra mota est ex A signo in B, facto igitur E puncto verticali, desiit D punctum imminere vertici aspicientis. Nihil autem apparet directo pondere deorsum ferri, quod non ex verticali signo delabitur. Ergo quod ceperat ex sublimi signo D deorsum ferri, dum oculus intuentis esset in A, id non amplius secundum rectos angulos, sed oblique videtur in terram decidere oculo ad locum B ex A traducto, signoque E facto nunc verticali. Cogitetur enim per E, D verticalia signa descriptus maximus circulus, et per B similiter planum horizontis tangens convexitatem terrae in signo B. Erit igitur communis sectio horum duorum planorum recta linea, quae sit FBHG secans rectam DC in signo H. Et quoniam angulus CBH rectus est, erit angulus BHC minor recto, ac propterea contiguus ei BHD maior recto, ad quem angulum videtur aspicienti grave ex signo D declinare in terram. Sed hoc repugnat universali experientiae, quia omnia gravia, quae incipiunt aspicientibus ex verticali suo signo decidere, ferri in terram secundum rectos angulos apparent. Necesse est igitur planum horizontis, hoc est ipsam terram manere immotam.
Si enim moveretur terra circa centrum et axem suum, superis omnibus stantibus, ut Nicias Syracusius arbitrabatur. Esto globus terrae AB, qui circa centrum suum convertatur spacio 24 horarum, et iuncta recta CA producatur sursum in D. Per praecedens igitur porisma, dum A locus est circumspicientis, sive centrum horizontis, erit D signum super verticem, et DA linea erecta ad planum horizontis, quod terrae convexitatem in signo tangit. Moveatur igitur terra ex A in B interea, dum grave quiddam (ut imber grando, seu aliud etiam sursum proiectum) delabitur ex signo D. Et ducta ex C centro recta linea CB in E, erit rursum E punctum verticale, dum horizontis centrum B. Aut igitur aer terrae proximus, et contenta in eo simul cum terra circumaguntur, aut quiescit vicinus aer, dum eadem ab occasu in ortum summa convertitur celeritate. Primum, si proximus aer in eoque comprehensa una volvuntur, nihil quod est in aere usquam moveri, sed omnia semper immota in eodem haerere loco existimabuntur, id quod minime apparet. Non igitur una rapitur aer vicinus. Sed quiescat nunc aer terra in gyrum circumacta. Et quia, dum grave quiddam ex D in terram seu mare delabitur, interea terra mota est ex A signo in B, facto igitur E puncto verticali, desiit D punctum imminere vertici aspicientis. Nihil autem apparet directo pondere deorsum ferri, quod non ex verticali signo delabitur. Ergo quod ceperat ex sublimi signo D deorsum ferri, dum oculus intuentis esset in A, id non amplius secundum rectos angulos, sed oblique videtur in terram decidere oculo ad locum B ex A traducto, signoque E facto nunc verticali. Cogitetur enim per E, D verticalia signa descriptus maximus circulus, et per B similiter planum horizontis tangens convexitatem terrae in signo B. Erit igitur communis sectio horum duorum planorum recta linea, quae sit FBHG secans rectam DC in signo H. Et quoniam angulus CBH rectus est, erit angulus BHC minor recto, ac propterea contiguus ei BHD maior recto, ad quem angulum videtur aspicienti grave ex signo D declinare in terram. Sed hoc repugnat universali experientiae, quia omnia gravia, quae incipiunt aspicientibus ex verticali suo signo decidere, ferri in terram secundum rectos angulos apparent. Necesse est igitur planum horizontis, hoc est ipsam terram manere immotam.
Qui Terram librari in mundi medio, quia est instar puncti i. m. W autem mirantur tantam molem terrae, nec suspensam esse alicunde, nec provehi, hi, cum ad aliorum parvorum corporum accidentia, non ad universi naturam respiciant, in hac collatione falluntur. Nam haec res non videretur eis mira, si scirent totam terrae magnitudinem collatam ad totum coeli ambitum instar puncti esse. lta enim possibile videretur id quod proportione minimum est ab alio vere maximo, quod constat ex partibus similibus sustineri aequali conpulsu undique sine aliqua deflexione, cum quod ad ambitum ipsum attinet, nulla pars vere sit sursum aut deorsum, sicut haec neque sphaerae tribuuntur.
Caeterum Dissimilitudo levium et gravium i. m. W corpora inclusa terrae differunt proprietate naturali et motu. Levia enim, et ex subtilibus partibus conflata tendunt ad exteriora, et quasi ad circumferentiam erumpunt, Vapores i. m. W quae quidem ad superiora levari ideo dicuntur, quia omnia quae sunt supra caput et appellantur superiora tendunt et ipsa ad superficiem quae eas res ambit. Pluviae i. m. W Gravia vero et ex crassis partibus constantia omnia ad medium tanquam ad centrum feruntur, ideoque dicuntur deorsum labi, quae quia sub pedibus sunt et appellantur inferiora tendunt ad centrum terrae, ibique sedem circa medium accipiunt propter mutuam et aequalem partium collisionem et compressionem. Quare convenienter universa moles terrae magna est et stabilis, ut parva corpora, quae ad eam minimo pondere feruntur, irruentia excipiat.
Quod Congeries absurdorum, si terra moveretur i. m. W si et ipsa tota moveretur, sicut caetera gravia corpora, celerius agitata propter ponderis magnitudinem anteverteret omnia, ac destitueret animantia et alias res impositas, ac relinqueret pendentes in aere ac celerrime etiam per ipsum caelum rueret. Hoc vero etiam cogitare ridiculum est. Haec sententia adeo perspicua est, ut nemo non adsentiatur.
Sed De ea opinione, quae fingit coelum immobile i. m. W sunt, qui arbitrantur nihil obsistere, si verbi gratia supponant coelum immobile esse, terram vero in axe ab occasu in ortum singulis diebus una pene revolutione circumagi, aut si utrunque moveatur coelum et terra, moveri tamen circa eundem axem et congruentibus inter se conversionibus.
Etsi Confutatio sumpta ex collatione corporum coelestium et elementarium, quod ad motum attinet i. m. W autem fortassis adparentiae stellarum non impedirent hanc sententiam secundum crassiorem considerationem, tamen absurditas conspicitur ex iis quae acciderent circa nos et in aere. Quanquam enim donemus eis, quod praeter naturam est, res levissimas et subtilissimarum partium, aut prorsus non moveri, aut non aliter moveri quam contrarias naturas, cum palam videamus res aereas et minus subtiles citius moveri quam terrenas. Econtra vero gravissima et ex spissis partibus constantia celerem et aequalem motum deorsum habere, terrena vero multa vix impelli aut trahi ab aliis moventibus posse, tamen illud negare non possent, Quae sequuntur ex hac opinione pugnant cum phaenomenis i. m. W cum esset terrae velocissima conversio (ut quae in tam brevi spacio tantum circuitum absolveret) et caetera quae in ipsa non sunt in contrarium ferri viderentur, fore ut nec nubes, nec volitantia, aut proiecta in aere ad ortum tendere videretur. Terra enim propter celeritatem res illas omnes ad ortum praecurreret, et relinquere eas ad occasum videretur.
Quod si dicerent aerem una circumagi simili velocitate, tamen adhuc res illas in aere praecurreret et terra et simul circumactus aer. Aut si et res illae iunctae aeri simul raperentur, tamen nec praecedere nec sequi videri possent, sed semper stare existimarentur, nec conspiceremus volantia aut proiecta usquam provehi aut progredi. Hi vero motus palam conspiciuntur. Quare si terra non staret, nec velocitas, nec tarditas motuum diiudicari posset.
〈I.7〉 CAPUT VII: Quod primi motus in coelo sint duplices
Has hypotheses profuturas deinceps in particulari doctrina et sequenti, satis sit hactenus summatim tradidisse, quae quidem testimonia habebunt ex perpetuo consensu eorum ad adparentias quae deinceps demonstrabuntur.
Prodest autem et hoc initio inter communia praecepta tradere, quod primi motus in coelo sint duplices. Unus est, I. Communis motus totius coeli i. m. W quo omnia feruntur ab ortu ad occasum semper eodem modo et simili celeritate in circulis parallelis, qui circa polos sphaerae omnia aequaliter circumducentis describuntur. Inter hos circulos maximus est aequinoctialis, Aequinoctialis circulus i. m. Wquia solus in duo aequalia dividitur ab horizonte, qui et ipse maximus est, et fit aequinoctium adparens ubique, cum Sol in eo convertitur. Alter autem motus est, II. Alter proprius inferiorum orbium i. m. W quo orbes stellarum contra priorem motum vehuntur circa alios polos, non circa eosdem circa quos prior circumductio fit.
/68v/ Haec Phaenomena, quae testantur hunc duplicem motum i. m. W ita esse supponimus ideo, quia videmus quotidie omnia quae sunt in coelo in locis similibus et aequidistantibus aequinoctiali sensibiliter oriri, ascendere in medium coeli, et occidere. Ac talis quidem est primus motus.
Sed alia observatio assidua ostendit stellas quidem fixas intervalla inter se et loca primo motui congruentia fere eadem retinere, Solem vero et Lunam ac stellas errantes facere varias progressiones et inter se inaequales, omnes tamen adversus primum motum ad ortum ac ad partes a quibus discesserunt fixae stellae ab una sphaera circumactae.
Iam Quod secundus motus non sit ὑπόλειψις ἢ ὑστέρησις i. m. W si haec progressio errantium stellarum fieret in circulis aequidistantibus aequinoctiali, hoc est circa polos primi motus, videretur una et eadem esse omnium circumvolutio et primam comitans. Esset enim consentaneum hanc progressionem accidere tantum propter tarditatem inferiorum orbium, non propter contrarium motum. Sed non solum progrediuntur ad ortum, sed etiam evagantur ad septentrionem et meridiem. Et huius discessus spacia adeo inaequalia sunt, ut quidam arbitrati sint, planetas vi aliqua propelli. Verum haec sunt quidem inaequalia, quod ad rudem imaginationem attinet, sed tamen ordinata sunt, quod ad circulum eum attinet qui obliquus est ad aequinoctialem.
Est Zodiacus i. m. W igitur unus et idem ac proprius errantium circulus, qui exactissime describitur motu Solis, peragratur vero a Luna et ab errantibus undique quae in eo versantur, nec excidunt temere a metis utrinque definitis.
Cum igitur et hic circulus maximus sit, quia in eo et Sol aequaliter ab aequinoctiali ad septentrionem et meridiem digreditur, et omnes planetae suos motus versus orientem conficiunt, necesse fuit alterum hunc motum diversum ab universali constituere circa polos huius obliqui circuli sic deprehensi tendentem contra primum motum.
σχόλιον ex Theone. Si stella super aliquem circulum delatus aequali circunferentia maximi circuli digreditur in boream et austrum, circulus super quem defertur maximus est.
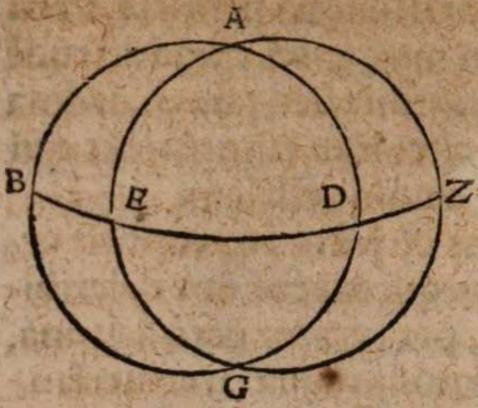 Esto enim aequinoctialis et maximus circulus ABGD. Obliquus autem per media signa ductus, super quem Sol defertur, AEGZ recedens ab aequinoctiali in boream et austrum aequali circumferentia maximi circuli per utrosque polos descripti, qui circulus sit BEDZ. Sint autem boreae partes ad Z, australes ad E. Et Sol sive stella maxime borealis existat in Z, maxime vero australis in E, ita ut aequalis sit ZD circumferentia circumferentiae EB. Dico quod maximus est circulus AEGZ. Quia enim aequalis est BE circumferentia circumferentiae DZ, communis autem ED, tota igitur BED aequalis est toti EDZ. Est autem maximi circuli semicirculus BED (per 15 primi Theodosii), ideo et EDZ eiusdem circuli semicirculus est. Et quia AEGZ zodiacus circulus maximum BEDZ circulum secat in duo aequalia, ipse quoque maximus est (per 16 primi Theodosii). Quod erat demonstrandum.
Esto enim aequinoctialis et maximus circulus ABGD. Obliquus autem per media signa ductus, super quem Sol defertur, AEGZ recedens ab aequinoctiali in boream et austrum aequali circumferentia maximi circuli per utrosque polos descripti, qui circulus sit BEDZ. Sint autem boreae partes ad Z, australes ad E. Et Sol sive stella maxime borealis existat in Z, maxime vero australis in E, ita ut aequalis sit ZD circumferentia circumferentiae EB. Dico quod maximus est circulus AEGZ. Quia enim aequalis est BE circumferentia circumferentiae DZ, communis autem ED, tota igitur BED aequalis est toti EDZ. Est autem maximi circuli semicirculus BED (per 15 primi Theodosii), ideo et EDZ eiusdem circuli semicirculus est. Et quia AEGZ zodiacus circulus maximum BEDZ circulum secat in duo aequalia, ipse quoque maximus est (per 16 primi Theodosii). Quod erat demonstrandum.
Iam si cogitemus per utriusque circuli polos duci maximum circulum, hic necessario et aequinoctialem et obliquum in duo aequalia secundum angulos rectos secabit, eruntque quatuor obliqui circuli puncta, Quatuor puncta i. m. W duo in contactu aequinoctialis, Duo aequinoctialia i. m. W opposita inter se, quorum alterum, a quo a meridie versus septentrionem ascenditur, nominatur vernum, oppositum vero autumnale. Fiunt et a circulo qui per utriusque circuli polos ducitur alia duo puncta opposita, quae vocantur solstitialia, Duo solstitialia i. m. W quorum id quod ad meridiem est, vocatur hibernum, septentrionale vero nominatur aestivum.
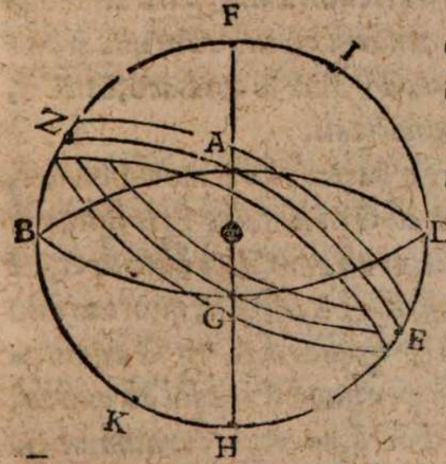 σχόλιον. Sit aequinoctialis circulus ABGD, cuius poli F H, obliquus autem, qui per media signa describitur AEGZ, secans aequinoctialem in duobus signi A et G. Huius obliqui circuli poli sint I K. Esto autem per utrosque polos, scilicet I, F, K, H, descriptus maximus circulus ZBED. Et quoniam duo maximi circuli ABGD et AZGE secant se in signis A, G, ideo per primi Theodosii semicirculi sunt ABG, et GDA, item AZG et GEA, ac puncta sectionum AG ex diametro opposita. Ac propterea etiam duo puncta Z E ex diametro opposita sunt, eo quod in iisdem secent se invicem duo maximi circuli AZGE et IZKE. Rursus quoniam maximus circulus ZBED transit per polos I, F, H, K, duorum maximorum circulorum ABGD et AZGE sese invicem secantium, dividit utraque segmenta utriusque eorum in duo aequalia per 12 secundi Theodosii. Aequalia igitur sunt segmenta AZ, ZG, et GE, EA, et AB, BG, et GD, DA. Et quoniam tota segmenta sint invicem aequalia, erunt et dimidiata invicem aequalia. Sunt autem tota segmenta semicirculi maximorum circulorum. Quare dimidiata segmenta erunt eorundem circulorum quadrantes, videlicet AZ, ZG, GE, EA in zodiaco, et AB, BG, GD, DA in aequinoctiali.
σχόλιον. Sit aequinoctialis circulus ABGD, cuius poli F H, obliquus autem, qui per media signa describitur AEGZ, secans aequinoctialem in duobus signi A et G. Huius obliqui circuli poli sint I K. Esto autem per utrosque polos, scilicet I, F, K, H, descriptus maximus circulus ZBED. Et quoniam duo maximi circuli ABGD et AZGE secant se in signis A, G, ideo per primi Theodosii semicirculi sunt ABG, et GDA, item AZG et GEA, ac puncta sectionum AG ex diametro opposita. Ac propterea etiam duo puncta Z E ex diametro opposita sunt, eo quod in iisdem secent se invicem duo maximi circuli AZGE et IZKE. Rursus quoniam maximus circulus ZBED transit per polos I, F, H, K, duorum maximorum circulorum ABGD et AZGE sese invicem secantium, dividit utraque segmenta utriusque eorum in duo aequalia per 12 secundi Theodosii. Aequalia igitur sunt segmenta AZ, ZG, et GE, EA, et AB, BG, et GD, DA. Et quoniam tota segmenta sint invicem aequalia, erunt et dimidiata invicem aequalia. Sunt autem tota segmenta semicirculi maximorum circulorum. Quare dimidiata segmenta erunt eorundem circulorum quadrantes, videlicet AZ, ZG, GE, EA in zodiaco, et AB, BG, GD, DA in aequinoctiali.
Sint iam ad Z Boreae partes, ad E meridionales, ad A occidentales, et ad G orientales. Erit igitur series signorum zodiaci, ut ab A in Z, et hinc in G, et quatuor illa puncta zodiaci A, Z, G, E, quorum duo sub ipso aequinoctiali et zodiaco A et G aequinoctialia, horum alterum, per quod transit Sol ab austro, ut ab E digrediens in boream, vocetur vernum, ut G. Oppositum vero ex diametro seu a borea in austrum, hoc est a Z, in consequentia vocetur autummale, ut G. Reliqua vero duo sub zodiaco et eo circulo, qui per polos ducitur, sunt et ipsa ex diametro opposita, et tropica appellata, ut E Z. Horum alterum ab aequinoctiali in meridiem, ut E, vocetur hibernum, alterum vero oppositum in boream, ut Z, aestivum.
Cogitetur Conclusio i. m. W autem unus ille et primus motus ambiens reliquos omnes circumscriptus, et quasi determinatus a circulo maximo per utrunque polum ducto. Qui quidem circulus et ipse circumagitur et reliqua omnia secum circunducit ab ortu ad occasum circa polos aequinoctialis fixos in eo circulo, qui vocatur meridianus. Hic eo tantum differt a praedicto, quod non semper transit per polos obliqui circuli et continue rectos angulos ad horizontem facit.
Vocatur autem Meridianus, Meridianus i. m. W qui,a cum situs ipsius utrunque hemisphaerium subterraneum et superius in duo aequalia secet, efficit medietates dierum et noctium.
Secundus autem et varius motus, qui ambitur a priore, et ambit omnium errantium orbes, etsi vehitur a priore, tamen contra ipsum circumvolvitur circa polos obliqui circuli, qui cum et ipsi in eo circulo qui primam facit conversionem, hoc est qui transit per utrunque polum, fixi sint, una cum eodem convenienter circumaguntur, et tamen interea iuxta motum secundae circumductionis, quae fit in contrarium prioris, semper conservant eundem situm maximi circuli descripti ab eadem circumductione et obliqui ad aequinoctialem.
σχόλιον. Circulus qui per utrunque polum ducitur usitata appellatione vocatur colurus solstitiorum, quia in zodiaco designat duo puncta solstitialia, ut dictum est, sed coluri Coluri i. m. W vocantur omnes circuli per polos descripti, quia cum reliqui circuli in mundi conversione integri cernantur, colurorum certae partes, aliae quidem in aliis climatis, emergunt nunquam, sed semper latent infra horizontem, ac similiter certae quaedam et prioribus oppositae circa polum conspicuum nunquam occidunt, sed semper apparent. Differt autem meridianus circulus a coluro solstitiorum, quod hic per utrosque polos transit, ille vero per polos tantum aequinoctialis et verticem horizontis. Unde et immobilis est et ad rectos angulos plano horizontis, nec unus tantum ubique, sed varius et cuilibet loco versus ortum et occasum proprius.
Porro et si poli zodiaci in mundi conversione una circumducuntur describentes eos circulos, quorum adparens arcticus vulgo vocatur, non adparens antarcticus, tamen sicut aequinoctialis circulus medius existit inter ambos mundi polos, ita et zodiacus medium semper locum inter suos polos conservat, tametsi oblique interea et tortuose volvatur.
〈I.8〉 CAPUT VIII: De particularium scientia
Quae Propositio sequentium i. m. W vero praemittenda erant de initiis huius doctrinae praecipuis et universalibus, ea sic exposuimus summatim. Nunc vero tradituri sumus demonstrationes de singulis partibus, quarum primam arbitramur esse eam, qua circumferentia inter praedictos polos media circuli maximi per eos descripti quanta sit, conprehenditur. Ad hanc necessarium est prius exponere doctrinam de quantitate rectarum in circulo, praesertim cum omnia lineari demonstratione ostensuri simus.
〈I.9〉 CAPUT IX: De quantitate rectarum linearum in circulo
Ergo De partibus circumferentiae et diametri i. m. W ad faciliorem usum postea tabulas quantitatis earum construemus, et totum ambitum in trecentas sexaginta partes dividemus, et addemus cuique circumferentiae iuxta incrementa semissium subtensas rectas, id est quot sint portionum, nempe diametro in centum viginti partes divisa, quia computatio per istos numeros commodior est.
Prius autem ostendemus, quomodo per pauca, quantum fieri potest, et per brevia theoremata compendiariam et facilem intelligentiam quantitatis rectarum assequamur, ut non tantum nudae tabulae extent, in quibus sint magnitudines rectarum, sed etiam lineari demonstratione facile possimus errata deprehendere.
Universaliter Numerus sexagenarius i. m. W autem utemur numeris iuxta sexagenarii rationem, ne fractionum difficultates sint nobis impedimento.
In multiplicationibus vero et divisionibus id quod proxime ad veritatem accedit, sumemus, ita ut quod reliquum est non differat sensibiliter ab eo quod sensus exacte percipit.
σχόλιον de ordine sequentis doctrinae. Admiranda facilitate ac brevitate complexus est Ptolemaeus universam doctrinam rectarum in circulo, quum ante ipsum Hipparchus eam XII, et Menelaus VI libris tractaverint. Etsi autem res ipsa ab autore, ut excellenti artifice ita perspicue ac diserte explicatur, ut excultus geometriae studio non valde desideret interpretem aut praeceptorem, tamen studiosum lectorem breviter de ordine sequentis huius tractationis admonebimus.
Complexus est Ptolemaeus totam hanc doctrinam quatuor theorematis et uno problemate, quibus tamen praemittit necessaria lemmatia, hoc est propositiones, quae non extant in Elementis Euclideis, et tamen hic requiruntur.
Primum autem uno theoremate quam brevissime complectitur ea omnia, quae in hunc usum demonstrata extant in Elementis geometriae, videlicet quantum sit latus decagoni, pentagoni hexagoni, tetragoni, et trigoni in eodem circulo descriptorum, cuius quidem circuli diameter supponitur partium 120. Posita autem circunferentia circuli 360 partium erit circunferentia, quam decagoni latus subtendit partium 36, pentagoni partium 72, hexagoni 60, quadrati 90, trigoni 120. Harum igitur circumferentiarum subtensae per hoc primum theorema exhibentur.
Subiungit deinde velut porisma, quod prompte hinc etiam reliquarum ad semicirculum circumferentiarum subtensae dentur, eo quod ambo quadrata, eius inquam cuius sumitur reliqua et ipsius reliquae, coacervata faciant quadratum diametri, per 30 tertii et penultinam primi Elementorum. Per hoc porisma prioribus 5 rectis adhuc duae adiunguntur, scilicet ea quae partes 144 et quae partes 108 subtendit. Haec igitur prima fundamenta iacta sint ex praeceptis Euclideis.
Reliqua tria theoremata, per quae caeterarum deinceps circumferentiarum omnium in semicirculo subtensae colliguntur, sunt ab ipso Ptolemaeo sagacissime inventa, quorum primi haec est sententia. Si inaequalium circumferentiarum in semicirculo rectae subtensae fuerint datae, datur et subtensa eius, quo maior minorem excedit. Ad quod tamen demonstrandum praemittit lemma hoc, quod inter Euclidea theoremata non extat: in omni quadrilatero, quod circulo utcunque inscribitur, rectangulum sub diagoniis comprehensum aequale est ambobus rectangulis quae sub oppositis lateribus continentur. Per hoc theorema κατὰ τὴν ὑπεροχὴν proxime inveniuntur aliae et rectae has circumferentias subtendentes, videlicet eam quae partium 12, et quae partium 18, et quae partium 24, et quae partium 30, et quae partium 48, et quae partium 54, denique eam quae partium 84.
Secundum theorema. Data subtendente quamlibet circumferentiam, datur et ea quae dimidiatam circumferentiam subtendit. Per hoc theorema τῆς διχοτομίας ut Theon nominat, colliguntur aliae 12 subtensae, ex proximis quidem subtensa partium 6, et hinc 3, et rursum partis unius cum semisse, denique dodrantis unius partis, item subtensa 9 partium et 4 cum semisse, item subtensa 15 partium et 7 cum semisse unius partis, item subtensa 27 partium et 13 cum semisse, ex subtensa autem 90 partium subtensa 45 partium et 22 cum semisse.
Tertium theorema κατὰ σύνθεσιν. Datis subtensis duarum circumferentiarum datur et subtensa compositae ex iis circumferentiae. Per hoc theorema investigantur omnes aliae rectae, quae bis sumptae tertiam partem habent, ita ut canon construatur per intervalla sesquipartis, ac in singulis duo tantum desiderentur, quo minus continue per semisses partium assurgat canon.
Cum autem per lineares demonstrationes haud detur recta subtendens tertiam partem totius circumferentiae cuius subtensa datur, tandem quasi problema instituens docet collatione quadam coniectare proxime subtensam unius partis et inde semissis. Huic problemati praemittit iterum lemma gubernans eam collationem, videlicet quod si in circulo actae fuerint duae rectae inaequales, minor sit ratio maioris ad minorem quam circumferentiae supra rectam maiorem ad circumferentiam supra minorem. Postquam igitur certa coniectura deprehendit quam proxime subtentensam semissis unius partis, replet deinceps vacua intervalla, ita ut canon continua serie accrescat per semisses graduum. Et ad eam perfectionem, ac quasi exaedificationem alternis utitur duobus illis prioribus theorematis, quorum alterum est κατὰ σύνθεσιν, alterum κατὰ ὑπεροχὴν, ob eam causam, ut semper ad inveniendam aliam subtensam altera duarum, ex quibus alia eruitur, sit exacte inventa. Nam si alterum tantum horum theorematum adhiberetur, necessario in singulis intervallis accideret, ut utraque duarum esset παχυμερέστερον sumpta, nec altera ἀκριβῶς inventa. Unde et canon minus absolutus existeret, id quod Theonis commentarius declarat prolixius. Haec admonendi lectoris gratia praefari libuit.
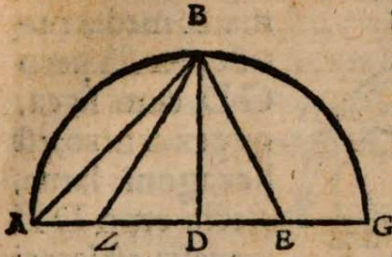 Sit Primum theorema de latere decagoni, pentagoni, hexagoni, quadrati et trigoni i. m. W ergo semicirculus ABG super diametrum ADG circa centrum D, et ex centro D ducatur ad rectos angulos diametro AG recta linea BD, et dividatur DG recta in duo aequalia in puncto E, et connectatur recta EB, et ponatur ei aequalis recta EZ, et coniungatur recta ZB. Dico rectam ZD esse latus decagoni, rectam ante BZ pentagoni. Nam quoniam DG recta linea divisa est in duo aequalia in puncto E, et adiecta est ei in rectum linea DZ, rectangulum quod continetur
Sit Primum theorema de latere decagoni, pentagoni, hexagoni, quadrati et trigoni i. m. W ergo semicirculus ABG super diametrum ADG circa centrum D, et ex centro D ducatur ad rectos angulos diametro AG recta linea BD, et dividatur DG recta in duo aequalia in puncto E, et connectatur recta EB, et ponatur ei aequalis recta EZ, et coniungatur recta ZB. Dico rectam ZD esse latus decagoni, rectam ante BZ pentagoni. Nam quoniam DG recta linea divisa est in duo aequalia in puncto E, et adiecta est ei in rectum linea DZ, rectangulum quod continetur 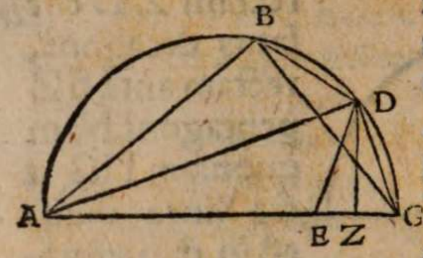 sub GZ, et ZD una cum quadrato lineae ED aequale est quadrato lineae EZ, hoc est quadrato quod fit ex BE, quia recta EB aequalis est rectae ZE. Sed quadrato quod fit ex EB aequalia sunt quadrata quae fiunt ex ED, et DB. Ergo rectangulum quod continetur sub GZ et ZD una cum quadrato quod fit ex DE aequale est quadratis quae fiunt ex ED et DB. Et ablato communi quadrato quod fit ex ED, reliquum rectangulum quod continetur sub GZ et ZD aequale est quadrato quod fit ex DB, hoc est quadrato quod fit ex DG. Ergo recta linea ZD secta est in puncto D extrema et media ratione. Quoniam igitur cum hexagoni latus et decagoni latus in eodem circulo descriptorum sunt in una recta linea, ea linea secta est extrema et media ratione, recta vero GD, cum sit ea quae ex centro, est hexagoni latus. Recta ergo DZ aequalis est lateri decagoni. Similiter autem, quoniam pentagoni latus tantum potest, quantum hexagoni et decagoni in eodem circulo descriptorum, trianguli vero rectanguli BDZ quadratum quod fit ex BZ aequale est ei quod fit ex BD, scilicet hexagoni lateri, et illi quod fit ex DZ, scilicet decagoni lateri, recta ergo linea BZ est aequalis lateri pentagoni.
sub GZ, et ZD una cum quadrato lineae ED aequale est quadrato lineae EZ, hoc est quadrato quod fit ex BE, quia recta EB aequalis est rectae ZE. Sed quadrato quod fit ex EB aequalia sunt quadrata quae fiunt ex ED, et DB. Ergo rectangulum quod continetur sub GZ et ZD una cum quadrato quod fit ex DE aequale est quadratis quae fiunt ex ED et DB. Et ablato communi quadrato quod fit ex ED, reliquum rectangulum quod continetur sub GZ et ZD aequale est quadrato quod fit ex DB, hoc est quadrato quod fit ex DG. Ergo recta linea ZD secta est in puncto D extrema et media ratione. Quoniam igitur cum hexagoni latus et decagoni latus in eodem circulo descriptorum sunt in una recta linea, ea linea secta est extrema et media ratione, recta vero GD, cum sit ea quae ex centro, est hexagoni latus. Recta ergo DZ aequalis est lateri decagoni. Similiter autem, quoniam pentagoni latus tantum potest, quantum hexagoni et decagoni in eodem circulo descriptorum, trianguli vero rectanguli BDZ quadratum quod fit ex BZ aequale est ei quod fit ex BD, scilicet hexagoni lateri, et illi quod fit ex DZ, scilicet decagoni lateri, recta ergo linea BZ est aequalis lateri pentagoni.
Quoniam ἐπιλόγισμος vel computatio i. m. W ergo, ut diximus, circuli diametrum posuimus esse partium 120, fiet propter suppositionem linea DE, quae est semissis eius, quae ex centro, partium 30, et quadratum, quod fit ex ea, 900. BD autem, cum sit ea quae ex centro, erit partium 60, et quadratum quod fit ex ea, 3600. Quadratum vero quod fit ex linea EB, hoc est ex linea EZ, earundem 4500. Erit igitur longitudo lineae EZ partium 67, scrupulorum 4, secundorum 55 proxime, et reliqua DZ earundem 37, scrupuloum 4, secundorum 55. Ergo decagoni latus subtendens circumferentiam talium 36 partium, Latus decagoni i. m. W qualium est circulus 360, erit talium 37, scrupulorum 4, secundorum 55, qualium diameter est 120.
Rursus, quoniam linea DZ est partium 37, scrupulorum 4, secundorum 55, quadratum quod fit ex ea erit 1375 partium, scrupulorum 4, secundorum 15. Est autem et quadratum quod fit ex DB earundem 3600, que coacervata constituunt quadratum quod fit ex BZ, 4975, scrupulorum 4, secundorum 15. Erit igitur longitudo lineae BZ partium 70, scrupulorum 32, secundorum 3 proxime. Quare et pentagoni latus, Pentagoni i. m. W quod subtenditur partibus 72, qualium circulus est 360, talium est partium 70, scrupulorum 32, secundorum 3, qualium diameter est 120.
Patet autem per se latus hexagoni, Hexagoni i. m. W quod 60 partibus subtenditur, et aequale est ei quae ex centro, partium, videlicet 60.
Similiter quoniam quadrati latus quod subtenditur 90 partibus, potentia duplum est ei quae ex centro, latus vero trigoni, quod subtenditur partibus 120, potentia triplum est eius quae ex centro, quadratum vero, quod fit ex ea, quae ex centro, partium est 3600, colligetur quadrati lateris Quadrati i. m. W quadratum 7200, lateris vero trianguli 10800. Trigoni i. m. W Quare longitudo rectae lineae quae subtenditur nonaginta partibus, talium est 84, scrupulorum 51, secundorum 10 proxime, qualium diameter est 120. Quae vero subtenditur partibus circumferentiae 120 earundem fit 103, scrupulorum 55, secundorum 23.
Porro Porisma de subtensa circumferentiae reliquae ad semicirculum i. m. W hae subtensae, de quibus dixi, sint hoc modo sumptae faciliter ex his demonstrationibus, eritque perspicuum inde, datis rectis, facile etiam dari subtensas residuae circumferentiae in semicirculo, cum quadrata earum coacervata diametri quadratum constituant. Ut, quoniam recta subtensa partibus 36 demonstrata est esse partium 37, scrupulorum 4, secundorum 55, et quadratum eius 1375, scrupulorum 4, secundorum 15, diametri vero quadratum partium 14400, fiet rectae lineae, qua residuae partes in semicirculo subtenduntur, videlicet 144, quadratum partium 13024, scrupulorum 55, secundorum 45. Ac est longitudo eius earundem 114, scrupulorum 7, secundorum 37 proxime, in reliquis quoque similiter.
 Sed Lemma i. m. W quomodo ab istis reliquae subtensae pro singulis circumferentis partibus dentur, ostendemus deinceps. Prius autem tradendum est lemma valde utile ad praesens negocium.
Sed Lemma i. m. W quomodo ab istis reliquae subtensae pro singulis circumferentis partibus dentur, ostendemus deinceps. Prius autem tradendum est lemma valde utile ad praesens negocium.
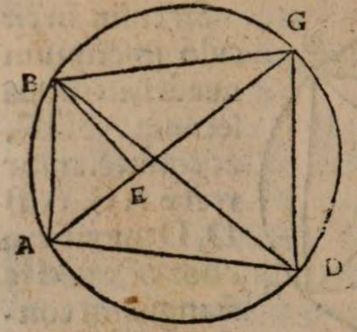 Sit enim in circulo inscriptum quadrilaterum qualecunque ABGD, ac connectantur rectae AG et BD, Demonstrandum est quod rectangulum contentum sub lineis AG et BD aequale est utrisque simul sumptis quae continentur sub AB et GD et sub AD et BG rectis. Ponatur enim angulo sub DBG angulus aequalis sub ABE. Iam si addamus communem angulum sub EBD, erit aequalis angulus sub ABD angulo sub EBG. Est autem et angulus sub BDA aequalis angulo sub BGE. Idem enim segmentum subtendunt. Triangula igitur ABD et BGE aequiangula sunt. Quare proportionaliter se habent, sicut latus BG ad latus GE, ita BD ad latus DA. Ergo rectangulum sub BG, AD aequale est rectangulo sub BD, EG. Rursus quoniam angulus sub ABE aequalis est angulo sub DBG, est autem et angulus BAE aequalis angulo sub BDG, ergo triangula ABE et BGD sunt aequiangula. Quare proportionaliter se habent, sicut BA ad AE, ita BD ad DG. Ergo rectangulum sub BA, DG aequale est rectangulo sub BD, AE. Demonstratum est autem et rectangulum sub BG, AD aequale esse rectangulo sub BD, GE. Totum igitur rectangulum sub AG, BD aequale est utrisque simul sumptis quae continentur sub AB, DG et sub AD, BG Quod erat demonstrandum.
Sit enim in circulo inscriptum quadrilaterum qualecunque ABGD, ac connectantur rectae AG et BD, Demonstrandum est quod rectangulum contentum sub lineis AG et BD aequale est utrisque simul sumptis quae continentur sub AB et GD et sub AD et BG rectis. Ponatur enim angulo sub DBG angulus aequalis sub ABE. Iam si addamus communem angulum sub EBD, erit aequalis angulus sub ABD angulo sub EBG. Est autem et angulus sub BDA aequalis angulo sub BGE. Idem enim segmentum subtendunt. Triangula igitur ABD et BGE aequiangula sunt. Quare proportionaliter se habent, sicut latus BG ad latus GE, ita BD ad latus DA. Ergo rectangulum sub BG, AD aequale est rectangulo sub BD, EG. Rursus quoniam angulus sub ABE aequalis est angulo sub DBG, est autem et angulus BAE aequalis angulo sub BDG, ergo triangula ABE et BGD sunt aequiangula. Quare proportionaliter se habent, sicut BA ad AE, ita BD ad DG. Ergo rectangulum sub BA, DG aequale est rectangulo sub BD, AE. Demonstratum est autem et rectangulum sub BG, AD aequale esse rectangulo sub BD, GE. Totum igitur rectangulum sub AG, BD aequale est utrisque simul sumptis quae continentur sub AB, DG et sub AD, BG Quod erat demonstrandum.
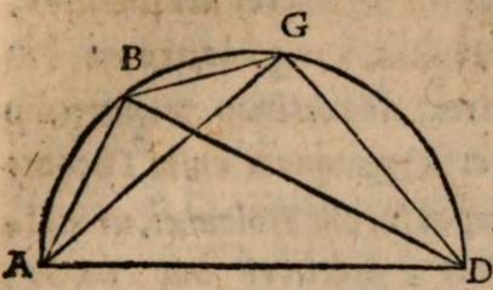 Hoc ita exposito, Alterum theorema τὸ καθʼ ὑπεροχὴν i. m. W sit semicirculus ABGD super diametrum AD, et ab A producantur duae rectae AB et AG, et sit utraque data magnitudine, qualium diameter est data 120, et connectatur recta BG. Dico quod et ipsa detur. Connectantur enim rectae BD et GD, quas videlicet datas esse necesse est, quia sunt subtensae residuarum circumferentiarum in semicirculo. Quoniam igitur in circulo quadrilaterum inscriptum est ABGD, erit rectangulum sub AB, GD cum rectangulo sub AD, BG aequale rectangulo sub AG, BD. Est autem rectangulum sub AG, BD datum, et datum est rectangulum sub AB, GD. Datur igitur et reliquum rectangulum sub AD, BG. Et est AD diameter. Quare et BG recta data est. Hinc manifestum est quod, si dentur duae circumferentiae et rectae eas subtendentes, dabitur et recta subtendens excessum duarum circumferentiarum datarum.
Hoc ita exposito, Alterum theorema τὸ καθʼ ὑπεροχὴν i. m. W sit semicirculus ABGD super diametrum AD, et ab A producantur duae rectae AB et AG, et sit utraque data magnitudine, qualium diameter est data 120, et connectatur recta BG. Dico quod et ipsa detur. Connectantur enim rectae BD et GD, quas videlicet datas esse necesse est, quia sunt subtensae residuarum circumferentiarum in semicirculo. Quoniam igitur in circulo quadrilaterum inscriptum est ABGD, erit rectangulum sub AB, GD cum rectangulo sub AD, BG aequale rectangulo sub AG, BD. Est autem rectangulum sub AG, BD datum, et datum est rectangulum sub AB, GD. Datur igitur et reliquum rectangulum sub AD, BG. Et est AD diameter. Quare et BG recta data est. Hinc manifestum est quod, si dentur duae circumferentiae et rectae eas subtendentes, dabitur et recta subtendens excessum duarum circumferentiarum datarum.
Hinc Usus praecedentis theorematis i. m. W patet quod per hoc theorema alias non paucas rectas inscribemus quae subtendunt excessus duarum circumferentiarum quae secundum easdem datae sunt, ac illam quoque quae subtendit circumferentiam 12 partium, cum habeamus et subtensam 60 partibus et subtensam 72 partibus.
σχόλιον. Arbitror graecum textum hoc loco depravatum ac mutilum esse, atque ita legendum vel similiter, ἄλλας τέ οὐκ ὀλίγας ἐυθείας ἐγγράψομεν τὰς ὑπὸ τὰς τὴν δύο κατʼ ἀυτὰς δεδομένων περιφερεῶν ὑπεροχας καὶ δὴ etc. Quanquam enim Theonis commentarius ita recitat locum Ptolemaei, ut multas dictiones omittat, videlicet hoc modo, ἐγγράψομεν καὶ δὴ, omissis omnibus mediis, quas modo posimus, tamen ipse exponens haec mox subiicit, φανερὸν δὲ φησιν, ὅτι διὰ τούτου τοῦ λημματίου ἄλλάς τε οὐκ ὀλίγας ἐυθείας εἰς τὸν κανόνα ἐγγράψομεν, καὶ δὴ καὶ ὑπὸ τὰς τῶν δεδομένων περιφερειῶν, ὧν ἁι ὑπʼ ἀυτὰς ἐυθεῖαι δέδονται, ὑπεροχὰς ὑποτείνουσας ἐυθείας.
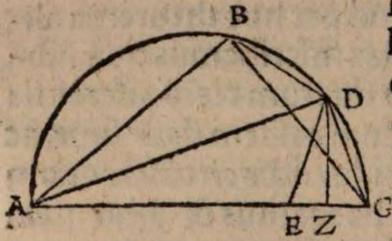 Rursus Tertium theorema τὸ κατὰ διχοτομίαν i. m. W sit propositum, data aliqua recta in circulo, invenire rectam eam quae dimidium subtensae circumferentiae subtendit, et sit semicirculus ABG super diametrum AG, et sit data recta BG, et circumferentia GB in iter. W duo aequalia secetur in puncto D, et connectantur rectae AB, AD, BD, DG, et a puncto D in diametrum AG deducatur perpendicularis DZ. Dico quod recta ZG est medietas excessus rectarum AB et AG. Ponatur enim rectae AB aequalis recta AE, et connectatur recta DE. Quoniam aequalis est AB rectae AE, communis autem AD, duo igitur latera AB, AD duobus lateribus AE, AD sunt aequalia utrunque utrique, et angulus qui sub BAD aequalis est angulo sub EAD. Basis igitur BD aequalis est basi BE. Sed BD recta aequalis est rectae DG. Itaque et DG recta aequalis est rectae DE. Cum igitur triangulum DEG sit isosceles, et a vertice ipsius in basin deducta perpendicularis DZ, aequalis est linea EZ lineae ZG. Sed EG est totus excessus rectarum AB et AG. Recta igitur ZD dimidium est excessus earum. Quare cum, supposita recta subtendente circumferentiam BG, hinc etiam data sit recta AB subtendens residuam circumferentiam ad semicirculum, dabitur etiam recta ZG, quae est dimidium excessus rectarum AG et AB. Verum quia in orthogonio triangulo AGD ab angulo recto qui sub ADG deducta est perpendicularis DZ in basin AG, fit triangulum orhogonium ADG aequiangulum triangulo DGZ, et sicut est recta linea AG ad GD lineam, ita GD ad GZ. Rectangulum igitur quod continetur sub AG GZ aequale est quadrato quod fit ex GD. Quare et GD recta dabitur longitudine, quae subtendit dimidium circumferentiae BG.
Rursus Tertium theorema τὸ κατὰ διχοτομίαν i. m. W sit propositum, data aliqua recta in circulo, invenire rectam eam quae dimidium subtensae circumferentiae subtendit, et sit semicirculus ABG super diametrum AG, et sit data recta BG, et circumferentia GB in iter. W duo aequalia secetur in puncto D, et connectantur rectae AB, AD, BD, DG, et a puncto D in diametrum AG deducatur perpendicularis DZ. Dico quod recta ZG est medietas excessus rectarum AB et AG. Ponatur enim rectae AB aequalis recta AE, et connectatur recta DE. Quoniam aequalis est AB rectae AE, communis autem AD, duo igitur latera AB, AD duobus lateribus AE, AD sunt aequalia utrunque utrique, et angulus qui sub BAD aequalis est angulo sub EAD. Basis igitur BD aequalis est basi BE. Sed BD recta aequalis est rectae DG. Itaque et DG recta aequalis est rectae DE. Cum igitur triangulum DEG sit isosceles, et a vertice ipsius in basin deducta perpendicularis DZ, aequalis est linea EZ lineae ZG. Sed EG est totus excessus rectarum AB et AG. Recta igitur ZD dimidium est excessus earum. Quare cum, supposita recta subtendente circumferentiam BG, hinc etiam data sit recta AB subtendens residuam circumferentiam ad semicirculum, dabitur etiam recta ZG, quae est dimidium excessus rectarum AG et AB. Verum quia in orthogonio triangulo AGD ab angulo recto qui sub ADG deducta est perpendicularis DZ in basin AG, fit triangulum orhogonium ADG aequiangulum triangulo DGZ, et sicut est recta linea AG ad GD lineam, ita GD ad GZ. Rectangulum igitur quod continetur sub AG GZ aequale est quadrato quod fit ex GD. Quare et GD recta dabitur longitudine, quae subtendit dimidium circumferentiae BG.
Per hoc quoque theorema Usus proximi theorematis i. m. W multae aliae rectae in circulo reperiuntur sumendo semisses propositarum circumferentiae, veluti, data recta subtendente duodecim partes circumferentiae, habebimus et subtendentem sex partes, deinde tres, deinde sesquipartem, denique et dodrantem unius partis circumferentiae. Invenimus autem ex hac computatione subtensam sesquiparti talium partium 34, scrupulorum 15, secundorum proxime, qualium diameter est 120, et subtensam dodranti unius partis, earundem 0, scrupulorum 47, secundorum 8.
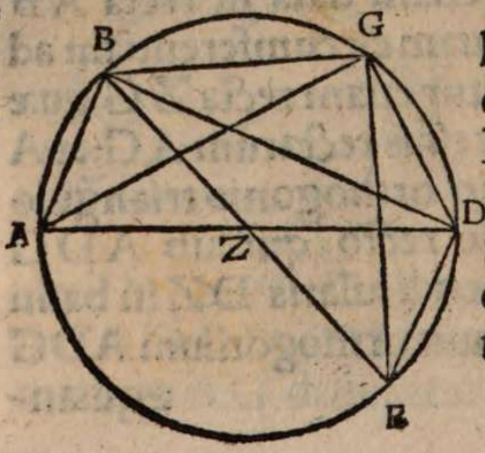 Sit Quartum theorema τὸ κατὰ σύνθεσιν i. m. W rursus circulus ABGD circa diametrum AD, centrum vero Z, et a puncto A sint sumptae duae circunferentiae datae una post aliam circumferentia AB et circumferentia BG, et sub ipsis coniunctae rectae lineae AB et BG datae et ipsae similiter. Dico quod, si iungamus rectam AG, dabitur et ipsa. Ducatur enim ex B diameter circuli BZE, et connectantur lineae BD, DG, GE, DE. Patet autem propter datam BG dari et GE, ac propter AB datam dari et BD, et DE. Et propter eadem, quae praemissa sunt, quoniam in circulo quadrilaterum est BGDE et lineae diagoniae sunt BD et GE, rectangulum quod continetur sub diagoniis aequale est utrisque rectangulis simul sumptis quae continentur sub lateribus oppositis. Quare quoniam datum est rectangulum contentum sub BD, GE, datur vero etiam rectangulum contentum sub BG, DE, datur igitur rectangulum contentum sub BE, GD. Sed data est BE diameter. Reliqua igitur subtendens circumferentiam GD erit data. Quare propter haec et GA subtendens residuum circumferentiae semicirculi erit data. Itaque si dentur duae circunferentiae et rectae eas subtendentes, dabitur per hoc theorema et recta ambas circumferentias coniunctas subtendens.
Sit Quartum theorema τὸ κατὰ σύνθεσιν i. m. W rursus circulus ABGD circa diametrum AD, centrum vero Z, et a puncto A sint sumptae duae circunferentiae datae una post aliam circumferentia AB et circumferentia BG, et sub ipsis coniunctae rectae lineae AB et BG datae et ipsae similiter. Dico quod, si iungamus rectam AG, dabitur et ipsa. Ducatur enim ex B diameter circuli BZE, et connectantur lineae BD, DG, GE, DE. Patet autem propter datam BG dari et GE, ac propter AB datam dari et BD, et DE. Et propter eadem, quae praemissa sunt, quoniam in circulo quadrilaterum est BGDE et lineae diagoniae sunt BD et GE, rectangulum quod continetur sub diagoniis aequale est utrisque rectangulis simul sumptis quae continentur sub lateribus oppositis. Quare quoniam datum est rectangulum contentum sub BD, GE, datur vero etiam rectangulum contentum sub BG, DE, datur igitur rectangulum contentum sub BE, GD. Sed data est BE diameter. Reliqua igitur subtendens circumferentiam GD erit data. Quare propter haec et GA subtendens residuum circumferentiae semicirculi erit data. Itaque si dentur duae circunferentiae et rectae eas subtendentes, dabitur per hoc theorema et recta ambas circumferentias coniunctas subtendens.
Perspicuum est autem Usus quarti theorematis i. m. W quod semper, si cum praedictis lineis coniungimus subtensam sesquipartis, et connexas computemus, inscribemus omnes simpliciter quarum duplicatarum praecise tertia pars sumi potest. Et erunt residuae solae quae sunt intra spacia crescentium per sesquipartem, duae in singulis, quia per semissem partis incrementa in inscriptione facimus. Quare, cum subtensam semissis invenimus, ipsa tum per compositionem, tum per excessum, qui est ad datas rectas lineas comprehendentes intervalla, residuas omnes in mediis spaciis complebit.
Verum quoniam, data aliqua recta linea, ut subtendente sesquipartem, non datur per lineares demonstrationes subtendens huius sesquipartis trientem. Nam si id possibile esset, haberemus inde et subtensam dimidae partis, supponemus igitur lemma, per quod prius subtensam unius partis investigabimus a subtensa sesquipartis, et subtensa dodrantis, quod etsi minime possit cuiuslibet rectae in circulo quantitatem determinare, has tamen minimas ita prope venatur, ut ad determinatas illas nulla animadverti queat differentia.
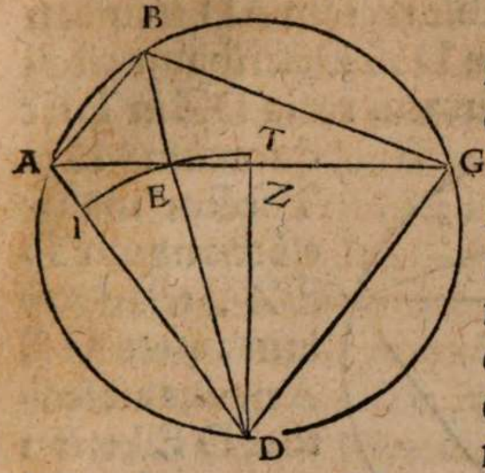 Dico igitur Alterum lemma, quod gubernat sequens problema quod, si in circulo ducantur duae rectae lineae inaequales, maior ad minorem minorem rationem habet quam circumferentia quae est supra maiorem rectam ad circumferentiam quae est supra minorem. Sit enim circulus ABGD, et ducantur in eo duae rectae inaequales, quarum minor sit AB et maior BG. Dico quod recta BG ad rectam BA minorem rationem habet quam BG circumferentia ad BA circumferentiam. Secetur enim angulus qui sub ABG per aequalia per BD rectam, et connectantur rectae AEG, et AD, et GD. Et quoniam angulus ABG per aequalia sectus est recta linea BED, aequalis sane est recta GD rectae AD. Maior est autem recta GE quam EA. Et ex puncto D in lineam AEG agatur perpendicularis DZ. Quoniam
Dico igitur Alterum lemma, quod gubernat sequens problema quod, si in circulo ducantur duae rectae lineae inaequales, maior ad minorem minorem rationem habet quam circumferentia quae est supra maiorem rectam ad circumferentiam quae est supra minorem. Sit enim circulus ABGD, et ducantur in eo duae rectae inaequales, quarum minor sit AB et maior BG. Dico quod recta BG ad rectam BA minorem rationem habet quam BG circumferentia ad BA circumferentiam. Secetur enim angulus qui sub ABG per aequalia per BD rectam, et connectantur rectae AEG, et AD, et GD. Et quoniam angulus ABG per aequalia sectus est recta linea BED, aequalis sane est recta GD rectae AD. Maior est autem recta GE quam EA. Et ex puncto D in lineam AEG agatur perpendicularis DZ. Quoniam 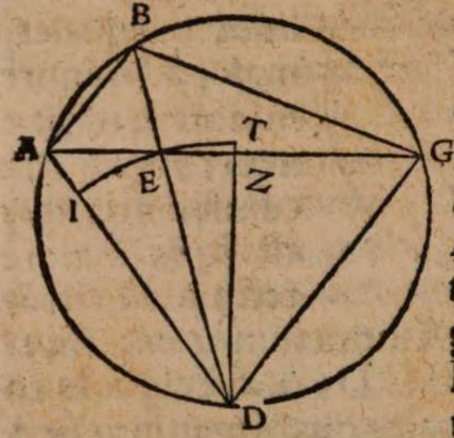 igitur maior est recta linea AD quam ED, atque ED maior quam DZ, descriptus igitur circulus in centro quidem D et intervallo DE secabit rectam AD, transcendet autem rectam DZ. Describatur circulus IET, et producatur recta DZ in T. Et quoniam DET sector maior est triangulo DEZ, triangulum autem DEA maius est sectore DEI, triangulum igitur DEZ ad DEA triangulum minorem rationem habet quam sector DET ad sectorem DEI. Sed sicut est DEZ triangulum ad triangulum DEA, ita EZ recta ad EA rectam. Sicut autem sector DET ad sectorem DEI, ita et angulus qui sub ZDE ad angulum qui sub EDA. Recta igitur ZE minorem rationem habet ad EA, quam angulus ZDE ad angulum EDA. Componendo igitur ZA recta ad rectam EA minorem rationem habet quam angulus ZDA ad angulum ADE, et antecedentium dupla, scilicet recta linea GA ad rectam AE minorem rationem habet quam angulus sub GDA ad angulum qui sub EDA, et dividendo recta GE ad rectam EA minorem rationem habet quam angulus GDE ad angulum EDA. Sed sicut recta GE ad rectam EA, ita GB recta ad rectam BA. Sicut autem angulus GDB ad angulum BDA, ita circumferentia GB ad circumferentiam BA. Quare GB recta ad rectam BA minorem rationem habet, quam GB circumferentia ad circumferentiam BA.
igitur maior est recta linea AD quam ED, atque ED maior quam DZ, descriptus igitur circulus in centro quidem D et intervallo DE secabit rectam AD, transcendet autem rectam DZ. Describatur circulus IET, et producatur recta DZ in T. Et quoniam DET sector maior est triangulo DEZ, triangulum autem DEA maius est sectore DEI, triangulum igitur DEZ ad DEA triangulum minorem rationem habet quam sector DET ad sectorem DEI. Sed sicut est DEZ triangulum ad triangulum DEA, ita EZ recta ad EA rectam. Sicut autem sector DET ad sectorem DEI, ita et angulus qui sub ZDE ad angulum qui sub EDA. Recta igitur ZE minorem rationem habet ad EA, quam angulus ZDE ad angulum EDA. Componendo igitur ZA recta ad rectam EA minorem rationem habet quam angulus ZDA ad angulum ADE, et antecedentium dupla, scilicet recta linea GA ad rectam AE minorem rationem habet quam angulus sub GDA ad angulum qui sub EDA, et dividendo recta GE ad rectam EA minorem rationem habet quam angulus GDE ad angulum EDA. Sed sicut recta GE ad rectam EA, ita GB recta ad rectam BA. Sicut autem angulus GDB ad angulum BDA, ita circumferentia GB ad circumferentiam BA. Quare GB recta ad rectam BA minorem rationem habet, quam GB circumferentia ad circumferentiam BA.
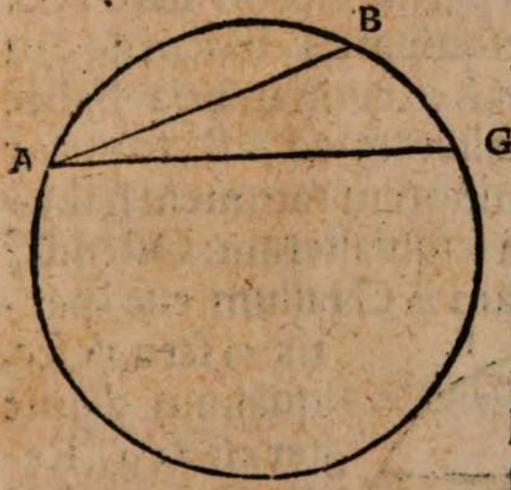 Hoc igitur supposito, Problema quo venatur satis exacte subtensam unius partis ut circulus ABG, et ducantur in eo duae rectae lineae inaequales, scilicet AB et AG. Ponatur autem primum linea AB esse subtensa dodranti unius partis, deinde linea AG esse subtensa uni parti. Quoniam recta AG ad rectam AB minorem rationem habet quam AG circumferentia ad circumferentiam AB, sed ratio AG circumferentiae ad AB circumferentiam est sesquitertia.
Hoc igitur supposito, Problema quo venatur satis exacte subtensam unius partis ut circulus ABG, et ducantur in eo duae rectae lineae inaequales, scilicet AB et AG. Ponatur autem primum linea AB esse subtensa dodranti unius partis, deinde linea AG esse subtensa uni parti. Quoniam recta AG ad rectam AB minorem rationem habet quam AG circumferentia ad circumferentiam AB, sed ratio AG circumferentiae ad AB circumferentiam est sesquitertia.
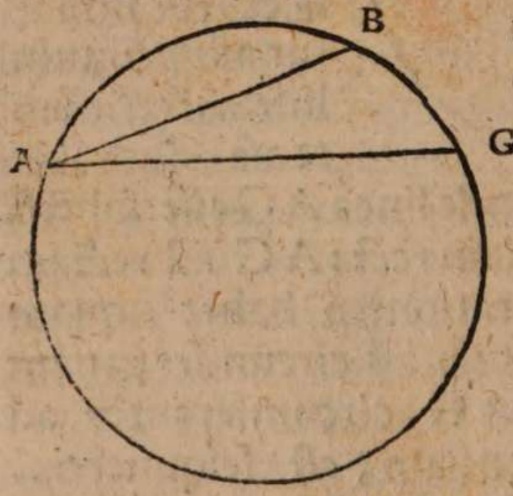 Recta igitur GA ad rectam BA minorem rationem habet quam sesquitertiam. Demonstratum est autem AB rectam talium partium esse 0, scrupulorum 47, secundorum 8, qualium diameter est 120. Recta igitur GA minor est, quam una pars, scrupula 2, et secunda 50 earundem. Hic enim numerus est in sesquitertia ratione proxime ad 0 partes 47 scrupula 8 secunda. Rursus in eadem descriptione supponamus rectam AB esse subtensam unius partis, rectam vero AG subtensam esse sesquipartis, iisdem de causis, quoniam AG circumferentia habet rationem sesquialteram ad AB, sequitur et rectam GA minorem rationem habere ad BA, quam sesquialteram. Ostendimus autem rectam AG talium esse 1 partis, 34 scrupulorum 15 secundorum, qualium diameter est 120. Recta igitur AB maior est quam pars una, scrupula 2, secunda 50 earundem. Nam ad hunc numerum habet sesquialteram rationem superior numerus, pars una, scrupula 34, secunda 15. ltaque quoniam recta unius partis et maior et minor est, hanc scilicet sumemus, ita ut sit partis unius, scrupulorum 2, secundorum 50 proxime talium, qualium est diameter 120. Et per prius demonstrata invenitur subtensa dimidiae partis earundem 0, scrupulorum 31, secundorum 25 proxime.
Recta igitur GA ad rectam BA minorem rationem habet quam sesquitertiam. Demonstratum est autem AB rectam talium partium esse 0, scrupulorum 47, secundorum 8, qualium diameter est 120. Recta igitur GA minor est, quam una pars, scrupula 2, et secunda 50 earundem. Hic enim numerus est in sesquitertia ratione proxime ad 0 partes 47 scrupula 8 secunda. Rursus in eadem descriptione supponamus rectam AB esse subtensam unius partis, rectam vero AG subtensam esse sesquipartis, iisdem de causis, quoniam AG circumferentia habet rationem sesquialteram ad AB, sequitur et rectam GA minorem rationem habere ad BA, quam sesquialteram. Ostendimus autem rectam AG talium esse 1 partis, 34 scrupulorum 15 secundorum, qualium diameter est 120. Recta igitur AB maior est quam pars una, scrupula 2, secunda 50 earundem. Nam ad hunc numerum habet sesquialteram rationem superior numerus, pars una, scrupula 34, secunda 15. ltaque quoniam recta unius partis et maior et minor est, hanc scilicet sumemus, ita ut sit partis unius, scrupulorum 2, secundorum 50 proxime talium, qualium est diameter 120. Et per prius demonstrata invenitur subtensa dimidiae partis earundem 0, scrupulorum 31, secundorum 25 proxime.
Hoc modo reliqua spacia, De replendis reliquis spaciis i. m. W ut dixi, replebuntur. Nam exempli gratia in primo intervallo demonstramus subtensam duarum partium ex compositione subtensae semissis et sesquipartis. Per excessum vero subtensae trium partium invenimus subtensam duarum partium et semissis. Sic et in caeteris.
σχόλιον ex Theone. Cum exposita sit hactenus doctrina rectarum in circulo, duximus haec quoque adiungenda esse, videlicet quod minorum rectarum quantitates crescunt maioribus differentiis, et contra maiorum quantitates minoribus, cum incrementa circumferentiarum continua sint aequalia, item quod rectae, quae subtendunt circumferentias minores 60 partibus, maiores sunt suis circumferentiis, quo ad numerum, contra vero post 60 partes, minores existunt, etc.
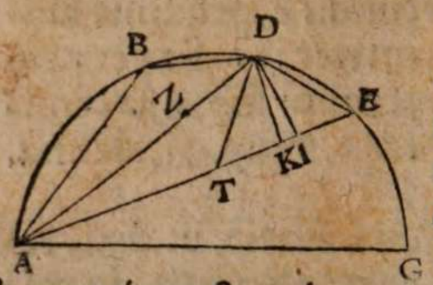 Demonstrabimus autem per lineas primum quod minorum rectarum quantitates crescant maioribus differentiis, cum interea circumferentiarum incrementa semper sint aequalia. Esto enim semicirculus ABG, et avulsa sit circumferentia AB verbi gratia partium 10, circumferentia autem AD partium 10 cum semisse, et AE circumferentia partium 11, et iungantur sub ipsas rectae, scilicet AB, et AE, et ponatur rectae quidem AB aequalis recta AZ, rectae vero AD aequalis recta AI. Dico quod excessus rectae AD ad rectam AB, hoc est ZD, maior est, quam excessus rectae AE ad AD, hoc est quam IE. Ponatur enim rectae AB aequalis AT, et connectantur rectae BD, DE, DI, DT. Quoniam igitur aequalis est recta AB rectae AT, communis autem AD, duae BA, AD duabus TA, AD aequales sunt utraque utrique, et angulus sub BAD aequalis angulo sub EAD, quia et circumferentia BD aequalis est circumferentiae DE, basis igitur BD basi DT est aequalis, sed et BD recta rectae DE aequalis est, igitur aequales sunt rectae DT, DE, ac propterea isosceles existit triangulum DET. Acuti igitur sunt anguli ad T, E. Et quoniam AD aequalis est rectae AI, quarum recta AZ aequalis rectae AT, reliqua igitur DZ reliquae TI aequalis est. Rursus quoniam aequales sunt rectae AD et AI, angulus igitur sub ADI aequalis est angulo sub AID. Acutus igitur uterque, et quia acutus est angulus qui sub AID, sed et qui ad T, perpendicularis igitur a signo D acta in rectam TE cadit inter ambo signa T, I. Acta sit D K. Et quia in isoscele triangulo DTE a vertice ad basin acta est perpendicularis, secat basin per aequalia. Aequales sint igitur TK, et KE. Maior igitur TI, hoc est ZD, quam IE. Et est ZD quidem excessus rectae AD ad AB, sed IE excessus rectae AE ad AD. Minorum igitur rectarum maiores sunt excessus, circumferentiis aequali spacio crescentibus.
Demonstrabimus autem per lineas primum quod minorum rectarum quantitates crescant maioribus differentiis, cum interea circumferentiarum incrementa semper sint aequalia. Esto enim semicirculus ABG, et avulsa sit circumferentia AB verbi gratia partium 10, circumferentia autem AD partium 10 cum semisse, et AE circumferentia partium 11, et iungantur sub ipsas rectae, scilicet AB, et AE, et ponatur rectae quidem AB aequalis recta AZ, rectae vero AD aequalis recta AI. Dico quod excessus rectae AD ad rectam AB, hoc est ZD, maior est, quam excessus rectae AE ad AD, hoc est quam IE. Ponatur enim rectae AB aequalis AT, et connectantur rectae BD, DE, DI, DT. Quoniam igitur aequalis est recta AB rectae AT, communis autem AD, duae BA, AD duabus TA, AD aequales sunt utraque utrique, et angulus sub BAD aequalis angulo sub EAD, quia et circumferentia BD aequalis est circumferentiae DE, basis igitur BD basi DT est aequalis, sed et BD recta rectae DE aequalis est, igitur aequales sunt rectae DT, DE, ac propterea isosceles existit triangulum DET. Acuti igitur sunt anguli ad T, E. Et quoniam AD aequalis est rectae AI, quarum recta AZ aequalis rectae AT, reliqua igitur DZ reliquae TI aequalis est. Rursus quoniam aequales sunt rectae AD et AI, angulus igitur sub ADI aequalis est angulo sub AID. Acutus igitur uterque, et quia acutus est angulus qui sub AID, sed et qui ad T, perpendicularis igitur a signo D acta in rectam TE cadit inter ambo signa T, I. Acta sit D K. Et quia in isoscele triangulo DTE a vertice ad basin acta est perpendicularis, secat basin per aequalia. Aequales sint igitur TK, et KE. Maior igitur TI, hoc est ZD, quam IE. Et est ZD quidem excessus rectae AD ad AB, sed IE excessus rectae AE ad AD. Minorum igitur rectarum maiores sunt excessus, circumferentiis aequali spacio crescentibus.
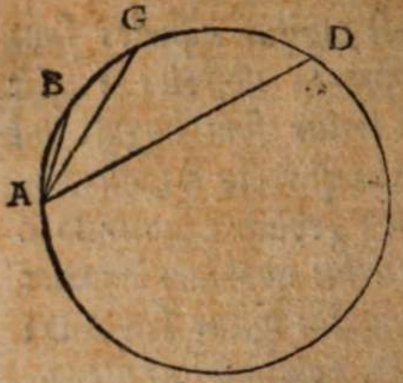 Demonstrabimus porro, quod rectae quae circumferentias minores 60 partibus subtendunt, maiores sunt, quo ad numerum, suis circumferentiis, quae vero maiores circumferentias, minores.
Demonstrabimus porro, quod rectae quae circumferentias minores 60 partibus subtendunt, maiores sunt, quo ad numerum, suis circumferentiis, quae vero maiores circumferentias, minores.  Est autem hoc notum ex theoremate quod ab ipso Ptolemaeo paulo ante demonstratum est. Esto enim circulus ABG, et actae sint in ipso duae rectae, ut AB subtendens circumferentiam 30 partium, et AG subtendens circumferentiam 60 partium Et quoniam AG recta ad AB rectam habet minorem rationem, quam AG circumferentia ad circumferentiam AB, est autem ABG circumferentia dupla circunferentiae AB, recta igitur AG minor est, quam dupla rectae AB. Est autem AG recta partium sexaginta. Igitur AG recta maior est quam 30 partium. Quare AB recta maior est, quo ad numerum, circumferentia quae supra ipsam incumbit. Rursus sit acta AD subtendens partes 120. Et quia recta AD ad AG minorem habet rationem quam AD circumferentia ad AG circumferentiam, est autem AGD circumferentia dupla circumferentiae ABG, ideo recta AD minor est quam dupla rectae AG. Sed AG recta est partium 60. Igitur AD recta minor est quam partium 120, cum ipsa circumferentia AD sit partium 120.
Est autem hoc notum ex theoremate quod ab ipso Ptolemaeo paulo ante demonstratum est. Esto enim circulus ABG, et actae sint in ipso duae rectae, ut AB subtendens circumferentiam 30 partium, et AG subtendens circumferentiam 60 partium Et quoniam AG recta ad AB rectam habet minorem rationem, quam AG circumferentia ad circumferentiam AB, est autem ABG circumferentia dupla circunferentiae AB, recta igitur AG minor est, quam dupla rectae AB. Est autem AG recta partium sexaginta. Igitur AG recta maior est quam 30 partium. Quare AB recta maior est, quo ad numerum, circumferentia quae supra ipsam incumbit. Rursus sit acta AD subtendens partes 120. Et quia recta AD ad AG minorem habet rationem quam AD circumferentia ad AG circumferentiam, est autem AGD circumferentia dupla circumferentiae ABG, ideo recta AD minor est quam dupla rectae AG. Sed AG recta est partium 60. Igitur AD recta minor est quam partium 120, cum ipsa circumferentia AD sit partium 120.
Verum licet et hoc modo colligere, quod cum rectae et maiores inventae sint, quo ad numerum, circumferentiis quae supra ipsas sunt, et minores, conveniat et mediam quandam aequinumeram reperiri, ita scilicet, ut, quanquam circumferentia semper maior sit quam recta ei subtensa, tamen utraque existat partium 60.
Quod autem hoc propositum theorema nequaquam determinet magnitudines rectarum quae subtensae sunt maioribus circunferentiis, sicut supra venatus est Ptolemaeus subtensam uni parti ex subtensa uni parti cum quadrante, et subtensa dodranti, ostendemus sic. Supponatur enim rursus AB circumferentia partium 30, et subtensa ipsi data partium 31, scrupulorum 4, secundorum 30, circumferentia autem ABD partium 120, et subtensa ipsi partium 103, scrupulorum 55, secundorum 23. Libeat ex his invenire subtensam partibus 60. Quoniam igitur circumferentia AG circumferentiae AB dupla est, ideo AG erecta minor est, quam dupla rectae AB. Et est AB partium 31, scrupulorum 3, secundorum 30. Igitur AG recta minor est quam partium 62, scrupulorum 7. Rursus iisdem de causis AD recta minor est quam dupla rectae AG, estque AD partium 103, scrupulorum 55, secundorum 23. Igitur AG recta maior est quam partium 51, scrupulorum 57, secundorum 42 proxime. Demontrata est autem et minor quam partium 62, scrupulorum 7. Manifestum est igitur, quod magnitudinem eius non liceat proxime determinare, propterea quod differentia existat partium 10 et scrupulorum fere totidem.
Ac Descriptio canonis sequentis i. m. W rectarum in circulo doctrina hoc modo facilime tractari poterit. Verum, ut paratas linearum quantitates cum opus fuerit, in promptu habeamus, canonem addemus quadragenorum quinonorum versuum commoditatis causa, ubi primus ordo continebit quantitates circumferentiarum crescentes semisse, secundus ordo continebit quantitates subtensarum respondentium circumferentiis, prout diameter est segmentorum 120, tertius ordo tricesimas rectarum, quae adiectae sunt singulis circumferentiis crescentibus per semisses, ut habentes unius sexagesimae partem proportionalem mediam non notabiliter discrepantem a praecisione, quo ad sensum, possimus competentes quantitates inter dimidias partes prompte invenire.
Ac si forte in scribendo error De erratis deprehendendis et corrigendis i. m. W circa aliquam rectarum in canone acciderit, facile et hoc intelligi poterit, tum ex his, tum ex supradictis, quomodo is deprehendi et emendari queat, scilicet vel ex duplo eius circumferentiae, cuius subtensam quaerimus, vel ab excessu, ad alias quascunque datas, vel ex recta subtendente circunferentiam residuam de semicirculo.
Et series canonis haec est.
Circumferentiarum |
Rectarum subtensarum |
Trigesimarum |
|||||
grad. |
scru. |
grad. |
scru. |
sec. |
scru. |
sec. |
ter. |
0 |
30 |
0 |
31 |
25 |
1 |
2 |
50 |
1 |
0 |
1 |
2 |
50 |
1 |
2 |
50 |
1 |
30 |
1 |
34 |
15 |
1 |
2 |
50 |
2 |
0 |
2 |
5 |
40 |
1 |
2 |
50 |
2 |
30 |
2 |
37 |
4 |
1 |
2 |
48 |
3 |
0 |
3 |
8 |
28 |
1 |
2 |
48 |
3 |
30 |
3 |
39 |
52 |
1 |
2 |
48 |
4 |
0 |
4 |
11 |
16 |
1 |
2 |
47 |
4 |
30 |
4 |
42 |
40 |
1 |
2 |
47 |
5 |
0 |
5 |
14 |
4 |
1 |
2 |
46 |
5 |
30 |
5 |
45 |
27 |
1 |
2 |
45 |
6 |
0 |
6 |
16 |
49 |
1 |
2 |
44 |
6 |
30 |
6 |
48 |
11 |
1 |
2 |
43 |
7 |
0 |
7 |
19 |
3 |
1 |
2 |
42 |
7 |
30 |
7 |
50 |
54 |
1 |
2 |
41 |
8 |
0 |
8 |
22 |
15 |
1 |
2 |
40 |
8 |
30 |
8 |
53 |
35 |
1 |
2 |
39 |
9 |
0 |
9 |
24 |
54 |
1 |
2 |
38 |
9 |
30 |
9 |
56 |
13 |
1 |
2 |
37 |
10 |
0 |
10 |
27 |
32 |
1 |
2 |
35 |
10 |
30 |
10 |
58 |
49 |
1 |
2 |
33 |
11 |
0 |
11 |
30 |
5 |
1 |
2 |
32 |
11 |
30 |
12 |
1 |
21 |
1 |
2 |
30 |
Circumferentiarum |
Rectarum subtensarum |
Trigesimarum |
|||||
grad. |
scru. |
grad. |
grad. |
scru. |
grad. |
grad. |
scru. |
12 |
0 |
12 |
32 |
36 |
1 |
2 |
28 |
12 |
30 |
13 |
3 |
50 |
1 |
2 |
27 |
13 |
0 |
13 |
35 |
4 |
1 |
2 |
25 |
13 |
30 |
14 |
6 |
16 |
1 |
2 |
23 |
14 |
0 |
14 |
37 |
27 |
1 |
2 |
21 |
14 |
30 |
15 |
8 |
38 |
1 |
2 |
19 |
15 |
0 |
15 |
39 |
47 |
1 |
2 |
17 |
15 |
30 |
16 |
10 |
56 |
1 |
2 |
15 |
16 |
0 |
16 |
42 |
3 |
1 |
2 |
13 |
16 |
30 |
17 |
13 |
9 |
1 |
2 |
10 |
17 |
0 |
17 |
44 |
14 |
1 |
2 |
7 |
17 |
30 |
18 |
15 |
17 |
1 |
2 |
5 |
18 |
0 |
18 |
46 |
19 |
1 |
2 |
2 |
18 |
30 |
19 |
17 |
21 |
1 |
2 |
0 |
19 |
0 |
19 |
48 |
21 |
1 |
1 |
57 |
19 |
30 |
20 |
19 |
19 |
1 |
1 |
54 |
20 |
0 |
20 |
50 |
16 |
1 |
1 |
51 |
20 |
30 |
21 |
21 |
11 |
1 |
1 |
48 |
21 |
0 |
21 |
52 |
6 |
1 |
1 |
45 |
21 |
30 |
22 |
22 |
58 |
1 |
1 |
42 |
22 |
0 |
22 |
53 |
49 |
1 |
1 |
39 |
22 |
30 |
23 |
24 |
39 |
1 |
1 |
36 |
Circumferentiarum |
Rectarum subtensarum |
Trigesimarum |
|||||
grad. |
scru. |
grad. |
grad. |
scru. |
grad. |
grad. |
scru. |
23 |
0 |
23 |
55 |
27 |
1 |
1 |
33 |
23 |
30 |
24 |
26 |
13 |
1 |
1 |
30 |
24 |
0 |
24 |
56 |
58 |
1 |
1 |
26 |
24 |
30 |
25 |
27 |
41 |
1 |
1 |
22 |
25 |
0 |
25 |
58 |
22 |
1 |
1 |
19 |
25 |
30 |
26 |
29 |
1 |
1 |
1 |
15 |
26 |
0 |
26 |
59 |
38 |
1 |
1 |
11 |
26 |
30 |
27 |
30 |
14 |
1 |
1 |
8 |
27 |
0 |
28 |
0 |
48 |
1 |
1 |
4 |
27 |
30 |
28 |
31 |
20 |
1 |
1 |
0 |
28 |
0 |
29 |
1 |
50 |
1 |
0 |
56 |
28 |
30 |
29 |
32 |
18 |
1 |
0 |
52 |
29 |
0 |
30 |
2 |
44 |
1 |
0 |
48 |
29 |
30 |
30 |
33 |
8 |
1 |
0 |
44 |
30 |
0 |
31 |
3 |
30 |
1 |
0 |
40 |
30 |
30 |
31 |
33 |
50 |
1 |
0 |
35 |
31 |
0 |
32 |
4 |
7 |
1 |
0 |
31 |
31 |
30 |
32 |
34 |
22 |
1 |
0 |
27 |
32 |
0 |
33 |
4 |
35 |
1 |
0 |
22 |
32 |
30 |
33 |
34 |
46 |
1 |
0 |
17 |
33 |
0 |
34 |
4 |
55 |
1 |
0 |
12 |
33 |
30 |
34 |
35 |
1 |
1 |
0 |
8 |
Circumferentiarum |
Rectarum subtensarum |
Trigesimarum |
|||||
grad. |
scru. |
grad. |
grad. |
scru. |
grad. |
grad. |
scru. |
34 |
0 |
35 |
5 |
5 |
1 |
0 |
3 |
34 |
30 |
35 |
35 |
6 |
0 |
59 |
57 |
35 |
0 |
36 |
5 |
5 |
0 |
59 |
52 |
35 |
30 |
36 |
35 |
1 |
0 |
59 |
48 |
36 |
0 |
37 |
4 |
55 |
0 |
59 |
43 |
36 |
30 |
37 |
34 |
47 |
0 |
59 |
38 |
37 |
0 |
38 |
4 |
36 |
0 |
59 |
32 |
37 |
30 |
38 |
34 |
22 |
0 |
59 |
27 |
38 |
0 |
39 |
4 |
5 |
0 |
59 |
22 |
38 |
30 |
39 |
33 |
46 |
0 |
59 |
16 |
39 |
0 |
40 |
3 |
24 |
0 |
59 |
11 |
39 |
30 |
40 |
33 |
0 |
0 |
59 |
5 |
40 |
0 |
41 |
2 |
33 |
0 |
59 |
0 |
40 |
30 |
41 |
32 |
3 |
0 |
58 |
54 |
41 |
0 |
42 |
1 |
30 |
0 |
58 |
48 |
41 |
30 |
42 |
30 |
54 |
0 |
58 |
42 |
42 |
0 |
43 |
0 |
15 |
0 |
58 |
36 |
42 |
30 |
43 |
29 |
33 |
0 |
58 |
31 |
43 |
0 |
43 |
58 |
49 |
0 |
58 |
25 |
43 |
30 |
44 |
28 |
1 |
0 |
58 |
18 |
44 |
0 |
44 |
57 |
10 |
0 |
58 |
12 |
44 |
30 |
45 |
26 |
16 |
0 |
58 |
6 |
45 |
0 |
45 |
55 |
19 |
0 |
58 |
0 |
Circumferentiarum |
Rectarum subtensarum |
Trigesimarum |
|||||
grad. |
scru. |
grad. |
grad. |
scru. |
grad. |
grad. |
scru. |
45 |
30 |
46 |
24 |
19 |
0 |
57 |
54 |
46 |
0 |
46 |
53 |
16 |
0 |
57 |
47 |
46 |
30 |
47 |
22 |
9 |
0 |
57 |
47 |
47 |
0 |
47 |
51 |
0 |
0 |
57 |
34 |
47 |
30 |
48 |
19 |
47 |
0 |
57 |
27 |
48 |
0 |
48 |
48 |
30 |
0 |
57 |
21 |
48 |
30 |
49 |
17 |
11 |
0 |
57 |
14 |
49 |
0 |
49 |
45 |
48 |
0 |
57 |
7 |
49 |
30 |
50 |
14 |
21 |
0 |
57 |
0 |
50 |
0 |
50 |
42 |
51 |
0 |
56 |
53 |
50 |
30 |
51 |
11 |
18 |
0 |
56 |
46 |
51 |
0 |
51 |
39 |
42 |
0 |
56 |
39 |
51 |
30 |
52 |
8 |
0 |
0 |
56 |
32 |
52 |
0 |
52 |
36 |
16 |
0 |
56 |
25 |
52 |
30 |
53 |
4 |
29 |
0 |
56 |
18 |
53 |
0 |
53 |
32 |
38 |
0 |
56 |
10 |
53 |
30 |
54 |
0 |
43 |
0 |
56 |
3 |
54 |
0 |
54 |
28 |
44 |
0 |
55 |
55 |
54 |
30 |
54 |
56 |
42 |
0 |
55 |
48 |
55 |
0 |
55 |
24 |
36 |
0 |
55 |
40 |
55 |
30 |
55 |
52 |
26 |
0 |
55 |
33 |
56 |
0 |
56 |
20 |
12 |
0 |
55 |
25 |
56 |
30 |
56 |
47 |
54 |
0 |
55 |
17 |
Circumferentiarum |
Rectarum subtensarum |
Trigesimarum |
|||||
grad. |
scru. |
grad. |
grad. |
scru. |
grad. |
grad. |
scru. |
57 |
0 |
57 |
15 |
33 |
0 |
55 |
9 |
57 |
30 |
57 |
43 |
7 |
0 |
55 |
1 |
58 |
0 |
58 |
10 |
38 |
0 |
54 |
53 |
58 |
30 |
58 |
38 |
5 |
0 |
54 |
45 |
59 |
0 |
59 |
5 |
27 |
0 |
54 |
37 |
59 |
30 |
59 |
32 |
45 |
0 |
54 |
29 |
60 |
0 |
60 |
0 |
0 |
0 |
54 |
21 |
60 |
30 |
60 |
27 |
11 |
0 |
54 |
12 |
61 |
0 |
60 |
54 |
17 |
0 |
54 |
4 |
61 |
30 |
61 |
21 |
19 |
0 |
53 |
56 |
62 |
0 |
61 |
48 |
17 |
0 |
53 |
47 |
62 |
30 |
62 |
15 |
10 |
0 |
53 |
39 |
63 |
0 |
62 |
42 |
0 |
0 |
53 |
30 |
63 |
30 |
63 |
8 |
45 |
0 |
53 |
22 |
64 |
0 |
63 |
35 |
26 |
0 |
53 |
13 |
64 |
30 |
64 |
2 |
1 |
0 |
53 |
4 |
65 |
0 |
64 |
28 |
34 |
0 |
52 |
55 |
65 |
30 |
64 |
55 |
1 |
0 |
52 |
46 |
66 |
0 |
65 |
21 |
24 |
0 |
52 |
37 |
66 |
30 |
65 |
47 |
43 |
0 |
52 |
28 |
67 |
0 |
66 |
13 |
57 |
0 |
52 |
19 |
67 |
30 |
66 |
40 |
7 |
0 |
52 |
10 |
Circumferentiarum |
Rectarum subtensarum |
Trigesimarum |
|||||
grad. |
scru. |
grad. |
grad. |
scru. |
grad. |
grad. |
scru. |
68 |
0 |
67 |
6 |
12 |
0 |
52 |
0 |
68 |
30 |
67 |
32 |
12 |
0 |
51 |
52 |
69 |
0 |
67 |
58 |
8 |
0 |
51 |
43 |
69 |
30 |
68 |
23 |
59 |
0 |
51 |
33 |
70 |
0 |
68 |
49 |
45 |
0 |
51 |
23 |
70 |
30 |
69 |
15 |
27 |
0 |
51 |
14 |
71 |
0 |
69 |
41 |
4 |
0 |
51 |
4 |
71 |
30 |
70 |
6 |
36 |
0 |
50 |
55 |
72 |
0 |
70 |
32 |
3 |
0 |
50 |
45 |
72 |
30 |
70 |
57 |
26 |
0 |
50 |
35 |
73 |
0 |
71 |
22 |
44 |
0 |
50 |
26 |
73 |
30 |
71 |
47 |
56 |
0 |
50 |
16 |
74 |
0 |
72 |
13 |
4 |
0 |
50 |
6 |
74 |
30 |
72 |
38 |
7 |
0 |
49 |
56 |
75 |
0 |
73 |
3 |
5 |
0 |
49 |
46 |
75 |
30 |
73 |
27 |
58 |
0 |
49 |
36 |
76 |
0 |
73 |
52 |
46 |
0 |
49 |
26 |
76 |
30 |
74 |
17 |
29 |
0 |
49 |
16 |
77 |
0 |
74 |
42 |
7 |
0 |
49 |
6 |
77 |
30 |
75 |
6 |
39 |
0 |
48 |
55 |
78 |
0 |
75 |
31 |
7 |
0 |
48 |
45 |
78 |
30 |
75 |
55 |
29 |
0 |
48 |
34 |
Circumferentiarum |
Rectarum subtensarum |
Trigesimarum |
|||||
grad. |
scru. |
grad. |
grad. |
scru. |
grad. |
grad. |
scru. |
79 |
0 |
76 |
19 |
46 |
0 |
48 |
24 |
79 |
30 |
76 |
43 |
58 |
0 |
48 |
13 |
80 |
0 |
77 |
8 |
5 |
0 |
48 |
3 |
80 |
30 |
77 |
32 |
6 |
0 |
47 |
52 |
81 |
0 |
77 |
56 |
2 |
0 |
47 |
41 |
81 |
30 |
78 |
19 |
52 |
0 |
47 |
31 |
82 |
0 |
78 |
43 |
38 |
0 |
47 |
20 |
82 |
30 |
79 |
7 |
18 |
0 |
47 |
9 |
83 |
0 |
79 |
30 |
52 |
0 |
46 |
58 |
83 |
30 |
79 |
54 |
21 |
0 |
46 |
47 |
84 |
0 |
80 |
17 |
45 |
0 |
46 |
36 |
84 |
30 |
80 |
41 |
3 |
0 |
46 |
25 |
85 |
0 |
81 |
4 |
15 |
0 |
46 |
14 |
85 |
30 |
81 |
27 |
22 |
0 |
46 |
3 |
86 |
0 |
81 |
50 |
24 |
0 |
45 |
52 |
86 |
30 |
82 |
13 |
19 |
0 |
45 |
40 |
87 |
0 |
82 |
36 |
9 |
0 |
45 |
29 |
87 |
30 |
82 |
58 |
54 |
0 |
45 |
18 |
88 |
0 |
83 |
21 |
33 |
0 |
45 |
6 |
88 |
30 |
83 |
44 |
4 |
0 |
44 |
55 |
89 |
0 |
84 |
6 |
32 |
0 |
44 |
43 |
89 |
30 |
84 |
28 |
54 |
0 |
44 |
31 |
90 |
0 |
84 |
51 |
10 |
0 |
44 |
20 |
Circumferentiarum |
Rectarum subtensarum |
Trigesimarum |
|||||
grad. |
scru. |
grad. |
grad. |
scru. |
grad. |
grad. |
scru. |
90 |
85 |
13 |
20 |
0 |
44 |
8 |
|
91 |
30 |
85 |
35 |
24 |
0 |
43 |
57 |
91 |
0 |
85 |
57 |
23 |
0 |
43 |
45 |
92 |
30 |
86 |
19 |
15 |
0 |
43 |
33 |
92 |
0 |
86 |
41 |
2 |
0 |
43 |
21 |
93 |
30 |
87 |
2 |
42 |
0 |
43 |
9 |
93 |
0 |
87 |
24 |
17 |
0 |
42 |
57 |
94 |
30 |
87 |
45 |
45 |
0 |
42 |
45 |
94 |
0 |
88 |
7 |
7 |
0 |
42 |
33 |
95 |
30 |
88 |
28 |
24 |
0 |
42 |
21 |
95 |
0 |
88 |
49 |
34 |
0 |
42 |
9 |
96 |
30 |
89 |
10 |
39 |
0 |
41 |
57 |
96 |
0 |
89 |
31 |
37 |
0 |
41 |
45 |
97 |
30 |
89 |
52 |
29 |
0 |
41 |
33 |
97 |
0 |
90 |
13 |
15 |
0 |
41 |
21 |
98 |
30 |
90 |
33 |
55 |
0 |
41 |
8 |
98 |
0 |
90 |
54 |
29 |
0 |
40 |
55 |
99 |
30 |
91 |
14 |
56 |
0 |
40 |
42 |
99 |
0 |
91 |
35 |
17 |
0 |
40 |
30 |
100 |
30 |
91 |
55 |
32 |
0 |
40 |
17 |
100 |
0 |
92 |
15 |
40 |
0 |
40 |
4 |
101 |
30 |
92 |
35 |
42 |
0 |
39 |
52 |
101 |
0 |
92 |
55 |
38 |
0 |
39 |
39 |
Circumferentiarum |
Rectarum subtensarum |
Trigesimarum |
|||||
grad. |
scru. |
grad. |
grad. |
scru. |
grad. |
grad. |
scru. |
102 |
0 |
93 |
15 |
27 |
0 |
39 |
26 |
102 |
30 |
93 |
35 |
11 |
0 |
39 |
13 |
103 |
0 |
93 |
54 |
47 |
0 |
39 |
0 |
103 |
30 |
94 |
14 |
17 |
0 |
38 |
47 |
104 |
0 |
94 |
33 |
41 |
0 |
38 |
34 |
104 |
30 |
94 |
52 |
58 |
0 |
38 |
21 |
105 |
0 |
95 |
12 |
9 |
0 |
38 |
8 |
105 |
30 |
95 |
31 |
13 |
0 |
37 |
55 |
106 |
0 |
95 |
50 |
11 |
0 |
37 |
42 |
106 |
30 |
96 |
9 |
2 |
0 |
37 |
29 |
107 |
0 |
96 |
27 |
47 |
0 |
37 |
16 |
107 |
30 |
96 |
46 |
24 |
0 |
37 |
3 |
108 |
0 |
97 |
4 |
55 |
0 |
36 |
50 |
108 |
30 |
97 |
23 |
20 |
0 |
36 |
36 |
109 |
0 |
97 |
41 |
38 |
0 |
36 |
23 |
109 |
30 |
97 |
59 |
49 |
0 |
36 |
9 |
110 |
0 |
98 |
17 |
54 |
0 |
35 |
56 |
110 |
30 |
98 |
35 |
52 |
0 |
35 |
42 |
111 |
0 |
98 |
53 |
43 |
0 |
35 |
29 |
111 |
30 |
99 |
11 |
27 |
0 |
35 |
15 |
112 |
0 |
99 |
29 |
5 |
0 |
35 |
1 |
112 |
30 |
99 |
46 |
35 |
0 |
34 |
48 |
Circumferentiarum |
Rectarum subtensarum |
Trigesimarum |
|||||
grad. |
scru. |
grad. |
grad. |
scru. |
grad. |
grad. |
scru. |
113 |
0 |
100 |
3 |
59 |
0 |
34 |
34 |
113 |
30 |
100 |
21 |
16 |
0 |
34 |
20 |
114 |
0 |
100 |
38 |
26 |
0 |
34 |
6 |
114 |
30 |
100 |
55 |
28 |
0 |
33 |
52 |
115 |
0 |
101 |
12 |
25 |
0 |
33 |
39 |
115 |
30 |
101 |
29 |
15 |
0 |
33 |
25 |
116 |
0 |
101 |
45 |
57 |
0 |
33 |
11 |
116 |
30 |
102 |
2 |
33 |
0 |
32 |
57 |
117 |
0 |
102 |
19 |
1 |
0 |
32 |
43 |
117 |
30 |
102 |
35 |
22 |
0 |
32 |
29 |
118 |
0 |
102 |
51 |
37 |
0 |
32 |
15 |
118 |
30 |
103 |
7 |
44 |
0 |
32 |
0 |
119 |
0 |
103 |
23 |
44 |
0 |
31 |
46 |
119 |
30 |
103 |
39 |
37 |
0 |
31 |
32 |
120 |
0 |
103 |
55 |
23 |
0 |
31 |
18 |
120 |
30 |
104 |
11 |
2 |
0 |
31 |
4 |
121 |
0 |
104 |
26 |
34 |
0 |
30 |
49 |
121 |
30 |
104 |
41 |
59 |
0 |
30 |
35 |
122 |
0 |
104 |
57 |
16 |
0 |
30 |
21 |
122 |
30 |
105 |
12 |
26 |
0 |
30 |
7 |
123 |
0 |
105 |
27 |
30 |
0 |
29 |
52 |
123 |
30 |
105 |
42 |
26 |
0 |
29 |
37 |
Circumferentiarum |
Rectarum subtensarum |
Trigesimarum |
|||||
grad. |
scru. |
grad. |
grad. |
scru. |
grad. |
grad. |
scru. |
124 |
0 |
105 |
57 |
14 |
0 |
29 |
23 |
124 |
30 |
106 |
11 |
55 |
0 |
29 |
8 |
125 |
0 |
106 |
26 |
29 |
0 |
28 |
54 |
125 |
30 |
106 |
40 |
56 |
0 |
28 |
39 |
126 |
0 |
106 |
55 |
15 |
0 |
28 |
24 |
126 |
30 |
107 |
9 |
27 |
0 |
28 |
10 |
127 |
0 |
107 |
23 |
32 |
0 |
27 |
56 |
127 |
30 |
107 |
37 |
30 |
0 |
27 |
40 |
128 |
0 |
107 |
51 |
20 |
0 |
27 |
25 |
128 |
30 |
108 |
5 |
2 |
0 |
27 |
10 |
129 |
0 |
108 |
18 |
37 |
0 |
26 |
56 |
129 |
30 |
108 |
32 |
5 |
0 |
26 |
41 |
130 |
0 |
108 |
45 |
25 |
0 |
26 |
26 |
130 |
30 |
108 |
58 |
38 |
0 |
26 |
11 |
131 |
0 |
109 |
11 |
44 |
0 |
25 |
56 |
131 |
30 |
109 |
24 |
42 |
0 |
25 |
41 |
132 |
0 |
109 |
37 |
32 |
0 |
25 |
26 |
132 |
30 |
109 |
50 |
15 |
0 |
25 |
11 |
133 |
0 |
110 |
2 |
50 |
0 |
24 |
56 |
133 |
30 |
110 |
15 |
18 |
0 |
24 |
41 |
134 |
0 |
110 |
27 |
39 |
0 |
24 |
26 |
134 |
30 |
110 |
39 |
52 |
0 |
24 |
10 |
135 |
0 |
110 |
51 |
57 |
0 |
23 |
55 |
Circumferentiarum |
Rectarum subtensarum |
Trigesimarum |
|||||
grad. |
scru. |
grad. |
grad. |
scru. |
grad. |
grad. |
scru. |
135 |
30 |
111 |
3 |
54 |
0 |
23 |
40 |
136 |
0 |
111 |
15 |
44 |
0 |
23 |
25 |
136 |
30 |
111 |
27 |
26 |
0 |
23 |
9 |
137 |
0 |
111 |
39 |
1 |
0 |
22 |
54 |
137 |
30 |
111 |
50 |
28 |
0 |
22 |
39 |
138 |
0 |
112 |
1 |
47 |
0 |
22 |
24 |
138 |
30 |
112 |
12 |
59 |
0 |
22 |
8 |
139 |
0 |
112 |
24 |
3 |
0 |
21 |
53 |
139 |
30 |
112 |
35 |
0 |
0 |
21 |
37 |
140 |
0 |
112 |
45 |
48 |
0 |
21 |
22 |
140 |
30 |
112 |
56 |
29 |
0 |
21 |
7 |
141 |
0 |
113 |
7 |
2 |
0 |
20 |
51 |
141 |
30 |
113 |
17 |
27 |
0 |
20 |
36 |
142 |
0 |
113 |
27 |
44 |
0 |
20 |
20 |
142 |
30 |
113 |
37 |
54 |
0 |
20 |
4 |
143 |
0 |
113 |
47 |
56 |
0 |
19 |
49 |
143 |
30 |
113 |
57 |
50 |
0 |
19 |
33 |
144 |
0 |
114 |
7 |
37 |
0 |
19 |
17 |
144 |
30 |
114 |
17 |
15 |
0 |
19 |
2 |
145 |
0 |
114 |
26 |
46 |
0 |
18 |
46 |
145 |
30 |
114 |
36 |
9 |
0 |
18 |
30 |
146 |
0 |
114 |
45 |
24 |
0 |
18 |
14 |
146 |
30 |
114 |
54 |
31 |
0 |
17 |
59 |
Circumferentiarum |
Rectarum subtensarum |
Trigesimarum |
|||||
grad. |
scru. |
grad. |
grad. |
scru. |
grad. |
grad. |
scru. |
147 |
0 |
115 |
3 |
30 |
0 |
17 |
43 |
147 |
30 |
115 |
12 |
22 |
0 |
17 |
27 |
148 |
0 |
115 |
21 |
6 |
0 |
17 |
11 |
148 |
30 |
115 |
29 |
41 |
0 |
16 |
55 |
149 |
0 |
115 |
38 |
9 |
0 |
16 |
40 |
149 |
30 |
115 |
46 |
29 |
0 |
16 |
24 |
150 |
0 |
115 |
54 |
40 |
0 |
16 |
8 |
150 |
30 |
116 |
2 |
44 |
0 |
15 |
52 |
151 |
0 |
116 |
10 |
40 |
0 |
15 |
36 |
151 |
30 |
116 |
18 |
28 |
0 |
15 |
20 |
152 |
0 |
116 |
26 |
8 |
0 |
15 |
4 |
152 |
30 |
116 |
33 |
40 |
0 |
14 |
48 |
153 |
0 |
116 |
41 |
41 |
0 |
14 |
32 |
153 |
30 |
116 |
48 |
20 |
0 |
14 |
16 |
154 |
0 |
116 |
55 |
28 |
0 |
14 |
0 |
154 |
30 |
117 |
2 |
28 |
0 |
13 |
44 |
155 |
0 |
117 |
9 |
20 |
0 |
13 |
28 |
155 |
30 |
117 |
16 |
4 |
0 |
13 |
12 |
156 |
0 |
117 |
22 |
40 |
0 |
12 |
56 |
156 |
30 |
117 |
29 |
8 |
0 |
12 |
40 |
157 |
0 |
117 |
35 |
28 |
0 |
12 |
24 |
157 |
30 |
117 |
41 |
40 |
0 |
12 |
7 |
Circumferentiarum |
Rectarum subtensarum |
Trigesimarum |
|||||
grad. |
scru. |
grad. |
grad. |
scru. |
grad. |
grad. |
scru. |
158 |
0 |
117 |
47 |
43 |
0 |
11 |
51 |
158 |
30 |
117 |
53 |
39 |
0 |
11 |
35 |
159 |
0 |
117 |
59 |
27 |
0 |
11 |
19 |
159 |
30 |
118 |
5 |
7 |
0 |
11 |
3 |
160 |
0 |
118 |
10 |
37 |
0 |
10 |
47 |
160 |
30 |
118 |
16 |
1 |
0 |
10 |
31 |
161 |
0 |
118 |
21 |
16 |
0 |
10 |
14 |
161 |
30 |
118 |
26 |
23 |
0 |
9 |
58 |
162 |
0 |
118 |
31 |
22 |
0 |
9 |
42 |
162 |
30 |
118 |
36 |
13 |
0 |
9 |
25 |
163 |
0 |
118 |
40 |
55 |
0 |
9 |
9 |
163 |
30 |
118 |
45 |
30 |
0 |
8 |
53 |
164 |
0 |
118 |
49 |
56 |
0 |
8 |
37 |
164 |
30 |
118 |
54 |
15 |
0 |
8 |
20 |
165 |
0 |
118 |
58 |
25 |
0 |
8 |
4 |
165 |
30 |
119 |
2 |
26 |
0 |
7 |
48 |
166 |
0 |
119 |
6 |
20 |
0 |
7 |
31 |
166 |
30 |
119 |
19 |
6 |
0 |
7 |
15 |
167 |
0 |
119 |
13 |
44 |
0 |
6 |
59 |
167 |
30 |
119 |
17 |
13 |
0 |
6 |
42 |
168 |
0 |
119 |
20 |
34 |
0 |
6 |
26 |
168 |
30 |
119 |
23 |
47 |
0 |
6 |
10 |
Circumferentiarum |
Rectarum subtensarum |
Trigesimarum |
|||||
grad. |
scru. |
grad. |
grad. |
scru. |
grad. |
grad. |
scru. |
169 |
0 |
119 |
26 |
52 |
0 |
5 |
53 |
169 |
30 |
119 |
29 |
49 |
0 |
5 |
37 |
170 |
0 |
119 |
32 |
37 |
0 |
5 |
20 |
170 |
30 |
119 |
35 |
17 |
0 |
5 |
4 |
171 |
0 |
119 |
37 |
49 |
0 |
4 |
48 |
171 |
30 |
119 |
40 |
13 |
0 |
4 |
31 |
172 |
0 |
119 |
42 |
28 |
0 |
4 |
14 |
172 |
30 |
119 |
44 |
36 |
0 |
3 |
58 |
173 |
0 |
119 |
46 |
35 |
0 |
3 |
42 |
173 |
30 |
119 |
48 |
26 |
0 |
3 |
26 |
174 |
0 |
119 |
50 |
8 |
0 |
3 |
9 |
174 |
30 |
119 |
51 |
43 |
0 |
2 |
53 |
175 |
0 |
119 |
53 |
10 |
0 |
2 |
36 |
175 |
30 |
119 |
54 |
27 |
0 |
2 |
20 |
176 |
0 |
119 |
55 |
38 |
0 |
2 |
3 |
176 |
30 |
119 |
56 |
39 |
0 |
1 |
47 |
177 |
0 |
119 |
57 |
32 |
0 |
1 |
30 |
177 |
30 |
119 |
58 |
18 |
0 |
1 |
14 |
178 |
0 |
119 |
58 |
55 |
0 |
0 |
57 |
178 |
30 |
119 |
59 |
24 |
0 |
0 |
41 |
179 |
0 |
119 |
59 |
44 |
0 |
0 |
25 |
179 |
30 |
119 |
59 |
56 |
0 |
0 |
9 |
180 |
0 |
120 |
0 |
0 |
0 |
0 |
0 |
〈I.10〉 CAPUT X: De circumferentia inter tropicos
Exposita quantitate rectarum in circulo, primum iam demonstrandum est, ut diximus, quantum obliquus circulus, qui est per medium signorum, sit inclinatus ad aequinoctialem, hoc est quam rationem habeat circulus maximus per utrosque polos transiens ad interceptam inter eosdem polos circumferentiam cui aequaliter distant puncta tropica ab aequinoctiali.
σχόλιον ex Theone. Mutua aequinoctialis circuli et zodiaci inclinatio intercipit aequalem circumferentiam ei quae est inter polos utriusque circuli.
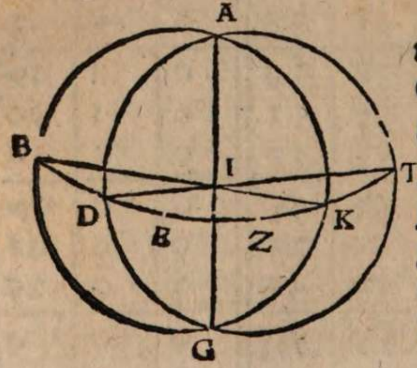 Si enim intelligamus zodiacum ABG, aequinoctialem autem ADG, et A signum in verna eius sectione, B autem signum tropicum aestivum, et accipiamus zodiaci ABG polum in E. Sed AGD aequinoctialis polum in Z, et per ZE maximum scribamus circulum, ut BEZT, existit ZD circumferentia aequalis circumferentiae EB. Sunt enim ex polis maximorum circulorum, et communi ED ablata, relinquitur ZE, quae est inter ambos polos, aequalis circumferentiae inclinationis BD. Quare si hanc circulorum inclinationem invenerimus, in maximo circulo ad hunc modum descripto, inventa erit nobis eadem quoque opera circumferentia inter utrunque polum.
Si enim intelligamus zodiacum ABG, aequinoctialem autem ADG, et A signum in verna eius sectione, B autem signum tropicum aestivum, et accipiamus zodiaci ABG polum in E. Sed AGD aequinoctialis polum in Z, et per ZE maximum scribamus circulum, ut BEZT, existit ZD circumferentia aequalis circumferentiae EB. Sunt enim ex polis maximorum circulorum, et communi ED ablata, relinquitur ZE, quae est inter ambos polos, aequalis circumferentiae inclinationis BD. Quare si hanc circulorum inclinationem invenerimus, in maximo circulo ad hunc modum descripto, inventa erit nobis eadem quoque opera circumferentia inter utrunque polum.
Quod autem BD sit circumferentia inclinationis circulorum, demonstrabimus hoc modo. Si enim coniungemus rectas quae sunt communes circulorum sectiones AG, BK, DT, erit I centrum sphaerae, propterea quod maximi sunt circuli, quorum diametri sunt BK, DT, AG. Et quoniam circulus BDKT erectus est ad circulos ABGK, et ADGT (per 19 primi Theodosii), sunt igitur et ABGK et ADGT circuli erecti ad circulum BDKT. Ideo et communis ipsorum sectio AG erecta est ad circulum BDKT (per 19 undecimi elementorum), ac propterea etiam ad omnes lineas, quae ductae in plano circuli BDKT tangunt eam ipsam communem sectionem AG (per conversionem secundae definitionis XI). Ideo et ad rectos BI et DI erecta est AG, et quia communi sectioni AG circulorum, scilicet zodiaci et aequinoctialis, in utroque planorum ad rectos sint angulos lineae IB et ID, igitur angulus sub BID inclinatio est eorundem planorum, et est ad centrum sphaerae. Quare et BD est circumferentia inclinationis eorundem planorum.
Hoc autem per instrumentum Descriptio primi instrumenti i. m. W simplici fabricatione constructum hoc modo deprehendetur.
Faciemus I. κατασκευὴ structura i. m. W circulum aeneum iusta magnitudine accurate tornatum, ita ut undique quatuor habeat latera, quo utemur tanquam meridiano. Hunc primum dividemus in partes 360, quas maximo circulo tribuimus, deinde etiam in scrupula, quotquot possibile erit. Postea faciendus erit alius circulus minor ita congruens intra maiorem, ut latera quidem ipsorum maneant in una superficie, minor autem intra maiorem in eodem illo plano expedite circumvolvi queat ad septentrionem et meridiem. Addemus autem in duobus oppositis minoris circuli segmentis ex eadem parte duas tabellas aequales, quae et ad se invicem et ad centrum circulorum examinate spectent, apponemusque in medio latitudinis ipsarum indices parvos, qui contingant divisiones maioris circuli.
Hoc instrumento varie uti possumus. Erit autem collocandus θέσις collocatio i. m. W circulus supra mediocrem columnam, cuius basis in pavimento non declinante a plano horizontis sub dio ita constituatur, ut planum circulorum sit erectum ad planum horizontis, et aequidistans meridiano, quorum prius ita deprehendetur, si suspensum perpendiculum ab eo signo quod nobis verticale futurum est, et subiectis fulchris, ubi res postulat, observemus tantisper, donec aequabiliter iuxta commune planum utriusque circuli dependeat, alterum vero, nempe ut meridiano aequidistet, ita assequemur, si exacte notata linea meridiana in pavimento sub columna circumducamus instrumentum in obliquum, donec conspiciatur aequidistare illi lineae.
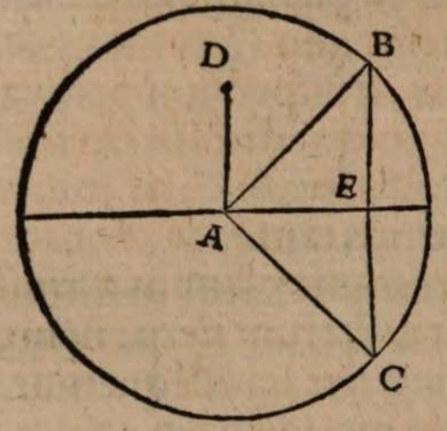 σχόλιον. Meridianam lineam erudite simul ac expedite invenies hoc modo, ut Proclus annotavit. Ad planum quod horizonti parallelum est erecto gnomone, describas circulum circa radicem gnomonis, tanquam circa centrum, intervallo quod maius sit altitudine gnomonis, et observes primum ante meridiem, donec extremum umbrae gnomonis desinat in ipsam circuli circumferentiam. ld signum accurate notabis. Deinde similiter quoque post meridiem facta observatione, notabis aliud signum in circumferentia. Haec duo signa coniunges recta linea, eamque divides per aequalia. Quod si hoc punctum sectionis coniunges cum centro circuli, ut radice gnomonis, inventam habes eius loci lineam meridianam. Ut in plano horizontis ABC sit erectus gnomen AD, et centro A, intervallo AB, quod maius sit quam DA altitudo gnomonis, describatur circulus BC. Sit autem ante meridiem AB umbra illa, quae desinit in circuli circumferentiam in signo B, post meridiem vero similiter in C signo. Coniungatur recta BC, eaque in signo E divisa in duo aequalia coniungatur recta AE. Quae eius est loci meridiana linea. Porro hac gubernatrice licebit quoque in proximis locis eandem multo facilius designare, si videlicet ad splendorem Solis perpendiculo libere demisso eius umbram notaveris in subiecto plano.
σχόλιον. Meridianam lineam erudite simul ac expedite invenies hoc modo, ut Proclus annotavit. Ad planum quod horizonti parallelum est erecto gnomone, describas circulum circa radicem gnomonis, tanquam circa centrum, intervallo quod maius sit altitudine gnomonis, et observes primum ante meridiem, donec extremum umbrae gnomonis desinat in ipsam circuli circumferentiam. ld signum accurate notabis. Deinde similiter quoque post meridiem facta observatione, notabis aliud signum in circumferentia. Haec duo signa coniunges recta linea, eamque divides per aequalia. Quod si hoc punctum sectionis coniunges cum centro circuli, ut radice gnomonis, inventam habes eius loci lineam meridianam. Ut in plano horizontis ABC sit erectus gnomen AD, et centro A, intervallo AB, quod maius sit quam DA altitudo gnomonis, describatur circulus BC. Sit autem ante meridiem AB umbra illa, quae desinit in circuli circumferentiam in signo B, post meridiem vero similiter in C signo. Coniungatur recta BC, eaque in signo E divisa in duo aequalia coniungatur recta AE. Quae eius est loci meridiana linea. Porro hac gubernatrice licebit quoque in proximis locis eandem multo facilius designare, si videlicet ad splendorem Solis perpendiculo libere demisso eius umbram notaveris in subiecto plano.
Hoc III. χρῆσις usus i. m. W modo collocato instrumento observabimus Solis accessum ad septentrionem et meridiem circumvolventes interiorem circulum meridie, donec inferior tabella tota a superiore obumbrata erit. Ita enim extremi indices nobis significabunt, quot partibus Sol in meridie distat a vertice.
Typus prioris instrumenti.
Typi σχόλια. Hoc primum instrumentum et copiose et diligenter descripsit Proclus in eo libello, cui titulum fecit ὑποτυπῶσις τῶν ἀστρονομικῶν ὑποθέσεων. Constat duobus circulis tanquam armillis, quas Graeci κρίκους dicunt, sicut sphaera alia est στέρεα, alia κρικοτὴς.
Prior circulus ABC meridianus, μεσήμβρινος, tetragonus superficie, ita ut binae oppositae parallelae sint, quarum duae invicem oppositae ad latera, quae planae sint, et meridiani circuli planum representant, vocantur a Ptolemaeo πλουραὶ, a Proclo κρόταφοι ‘tempora’, sumpta similitudine a capite hominis. Reliquae vero duae superficies oppositae similiter sursum et deorsum, non sunt planae, sed altera earum, ut exterior, κυρτὴ ‘convexa’ seu ‘curva’, altera ut interior κοίλη ‘concava’.
Alter circulus seu κρίκος DE similis est priori, sed minor, quare et ab autore κυκλίσκος dicitur
Debet autem huius circli κυρτὴ superficies contigua esse superficiei κοίλη exterioris, quantum omnino fieri potest.
Centrum commune utriusque circuli F.
D λεπίδες, laminae binae ex utroque latere seu tempore circulorum oppositae, quae affixae sunt minori orbi, ut minor intra maiorem rite maneat, nusquam ab eo effluens, et tamen possit expedite circumvolvi.
E tabellae, Ptolemeo πρισμάτια, Proclo πηγμάτια, quae sint invicem similes et aequale forma parallelogramma, et erecta ad planum seu latera circulorum, in quibus diagoniorum sectio ostendit locum διαυγίου iuxta Procli sententiam.
His superadditi indices parvi, γνωμόνια λεπτὰ, quae tangunt divisiones maioris circuli, forma sint triangli orthogonii cuius basis dimidium est minoris lateris parallelogrammi, suntque erecta quidem ad πρισμάτια, quibus continue adhaerent, sed contigua superficiei seu κροταφῷ circulorum, simul etiam funguntur officio laminarum,
A, vel G, signa κατὰ κορυφὴν
GH, perpendiculum, καθέτιον, suspensum in signo G ad claviculum.
H, βαρύλλιον μολύβδινον, κωνάριον, ut Theon vocat, a forma coni.
I, canalis excavatus congruenter, ut in eo quasi equitent erecti circuli, a Proclo vocatur σωλκνοειδὴς περιφέρεια τετράγωνος κατὰ τὴν κοιλότητα.
L, columnella, στυλίσκος, quae gestat totam hanc structuram.
MN, pavimentum, seu tabula, aequidistans horizonti forma parallelogramma, ἀκλινές ἔδαφος, ut Ptolemaeus vocat, πλάξ, ut Proclus. Ad hoc erecta est tum columnella, tum reliqua structura, in cuius medio ducta est meridiana linea OP. Huic debet esse aequidistans commune planum circulorum erectum simul ad planum horizontis.
AD, diameter orbium ducta a puncto verticis, in planum horizontis VFX πρὸς ὄρθας. Huic diametro aequidistare debet perpendiculum libere dependens. Id enim vocat hic Ptolemaeus ποιεῖν τὴν πρόσνευσιν κατὰ διάμετρον.
T, fulchra, ὑποθέματα, ἢ ὑποθεμάτια, quae subiiciuntur pavimento seu tabulae, cui infixa est columnella, ut fiat parallelum plano horizontis.
S, Sol, cuius radius incidens in superius πρισμάτιον obumbrat totum inferius, congruentibus interea quoque διαυγιοις, ita ut Solis radius simul transeat per utrunque.
Notetur autem in aestiva Solis conversione signum B in meridiano circulo, et in hiberno signum C, eritque BC circumferentia meridiani circuli intercepta inter duo tropicos, cuius medium signum R in aequinoctialem incidit, a quo signo ducta ad circulorum centrum F recta RF existit communis sectio utrisque circuli aequinoctialis et meridiani.
Est autem BR, vel RC circumferentia inclinationis planorum aequinoctialis et zodiaci, cui aequaliter distant invicem poli utriusque circuli.
Usi sumus Descriptio alterius instrumenti astronomici i. m. W et alia commodiore observatione. Extruximus pro circulis parvum parietem lapideum vel ligneum quadratum et immotum, mediocri latitudine et crassicie, ut latera eius firmius consisterent, I. κατασκευὴ fabricatio seu constructio i. m. W quorum alterum erat aequabile et accurate complanatum, in quo ad unum angulorum sumpto centro depinximus circuli quadrantem, et a centro usque ad depictam circumferentiam rectas lineas deduximus continentes rectum angulum sub quadrante circumferentiae, quam similiter in nonaginta partes et earum scrupula divisimus. Post haec in una rectarum, quae ad horizontis planum erigenda erat et situm habitura versus meridiem, inservimus erectos et aequales undique duos cylindros parvos et similiter tornatos, alterum quidem in ipso centro, alterum vero ad terminum inferiorem rectae lineae.
Collocavimus II. θέσις collocatio i. m. W autem hoc latus parietis iuxta meridianam lineam in subiecto plano designatam, ut idem latus esset aequidistans plano meridiani circuli, ac perpendiculo per cylindros demisso, subiectisque fulchris, ubi usus postulabat, attente exploravimus, ut linea per eosdem cylindros acta esset ad planum horizontis aequabiliter erecta.
Observabamus III. χρῆσις usus i. m. W igitur umbram in meridie, quae fiebat a cylindro qui erat in centro, admoventes tabellam aliquam ad circumferentiam instrumenti, ut certius umbrae locus appareret. Huius umbrae medio signato, accipiebamus segmentum circumferentiae indicans progressum Solis in meridiano circulo iuxta latitudinem.
σχόλιον. Sit paries ACE constans sex lateribus seu superficiebus, quae binae ex opposito sunt invicem parallelae, ita ut paries sit solidum parallelepipedon. Earum autem duae parallelae sint quadratae, quas vocat κροτάφους, quia ampliore sunt caeteris et stant erectae ad subiectum planum. Horum laterum alterum accurate complanatum est ABCD, cuius longitudo AB aequalis latitudini BC. Crassicies igitur seu profunditas huius parietis est AF, vel DE, vel CG, aliquanto minor quam longitudo, sed ita tamen,
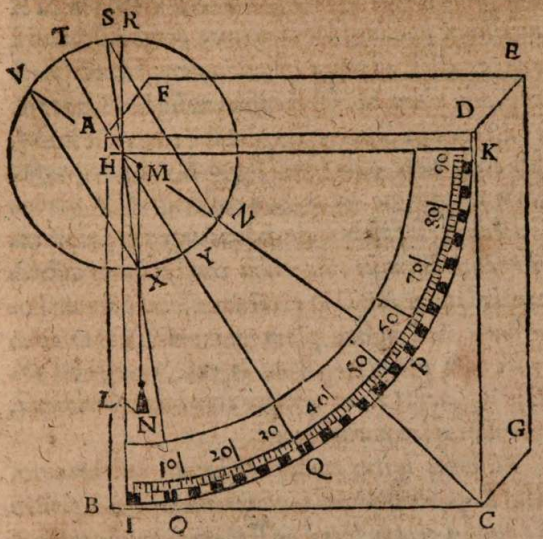 ut paries firmiter consistat. Reliquae quatuor superficies sint parallelogrammae oblongiores aequales et similes inter se.
ut paries firmiter consistat. Reliquae quatuor superficies sint parallelogrammae oblongiores aequales et similes inter se.
In quadrato igitur latere ABCD centro H descriptus est circumferentiae circuli quadrans IK, lineis HI, HK rectum angulum IHK comprehendentibus. Estque hic quadrans divisus in partes 90 et earum scrupula.
Duo cylindri parvi HM et LN aequales, et ad angulos rectos inserti plano ABCD in linea HI, quae linea ut congruat cum linea perpendiculari a vertice capitis ad terrae centrum demissa, necesse est perpendiculum MN suspensum in signo M, hoc est in extremitate superioris cylindrii centro H infixi, apte congruere cum simili signo N cylindrii inferioris. Et ad hanc accuratam collocationem parietis utendum est fulchris, de quibus antea in priori instrumento diximus. Sic enim constat huius instrumenti planum ABCD erectum esse ad planum horizontis. Sed ut hoc ipsum planum ABCD congruat cum plano meridiani circuli, necesse est rectam BC, vel HK, congruere cum linea meridiana, vel collocari ei parallelam.
Ad hunc igitur modum collocato instrumento, erit IK quadrans meridiani circuli descripti centro H, quod a centro terrae ad sensum non differt, eo quod observatio ita prorsus congruit, ac si H centrum descripti quadrantis revera in mundi medio collocatum esset.
Ac verbi gratia Alexandriae fuerit Ptolemaei tempore extremum umbrae exceptum in signo O, dum Sol meridianus versaretur in aestiva conversione, similiter autem in P signo in hiberna conversione, ita ut circumferentia OP fuerit deprehensa partium 47, scrupulorum 42 cum besse unius scrupuli fere. Haec est distantia amborum tropicorum in sphaera, secta autem circumferentia OP per aequalia in signo Q, erit acta linea QH, tum communis sectio aequinoctialis et meridiani, tum umbra cylindrii superioris iacta die aequinoctii. Circumferentia autem OQ, vel QP, est inclinationis aequinoctialis et zodiaci, similiter et circumferentia IOQ distantia aequinoctialis circuli a vertice capitis, seu latitudo Alexandriae, cui aequatur exaltatio poli, ut paulo post dicemus.
Haec ut clarius intelligantur, sit centro H descriptus integer circulus meridianus RSTV in saepe dicto plano ABCD, secans umbram aestivae conversionis in X, aequinoctialem in Y, et hibernae conversionis in Z, et producantur rectae IH, XH, YH, ZH, in signa R, S, T, V, coniunganturque rectae SZ, VX. Erit igitur signum R κατὰ κορυφὴν, SZ diameter circuli aestivi tropici, et VX diameter hiberni tropici, et manifestum est, quod Sol ex S ad HM cylindrium mittat radium SHX in O distans ab R vertice circumferentia RS, hoc est IO, ex V autem radium VZ in P digressus a vertice intervallo circumferentiae RV, hoc est circumferentiae IOP.
Et quoniam talia instrumenta observationum collocanda sunt in pavimento non declinante a plano horizontis, accurate prius explorandum erit librationibus, utrum pavimentum declinet nec. Modos autem librationum, ac praecipue eum, qui fit per chorobaten, diligenter descripsit Vituvius libro 8, capitulo 6.
Ex his observationibus Observatio Ptolemaei i. m. W et maxime iis quae in solsticiis factae sunt multis annis, cum designatio in aestivo et hiberno solsticio a puncto verticis semper interciperet aequales et easdem portiones meridiani circuli, inveniebamus inter maxime borealem terminum et maxime australem semper fuisse circumferentiam, quae est in medio inter duos tropicos, partium 47, et plusculum duabus tertiis et minus medietate et quarta. Per quae eadem fere ratio colligitur, quae apud Eratosthenem est, Eratosthenes i. m. W qua et Hipparchus usus est. Hipparchus i. m. W Nam circumferentia quae est inter solsticialia puncta est partium undecim proxime, qualium meridianus est octoginta trium.
Ex hac observatione Collatio latitudinis loci et exaltationis poli i. m. W etiam inclinationes habitationum, in quibus fiunt observationes, facile deprehendi possunt, si accipiamus medium punctum quod est inter tropicos, quod est in aequinoctiali, et circumferentiam quae est inter hoc punctum et inter verticale punctum, cui aequalis est circumferentia qua distant poli ab horizonte.
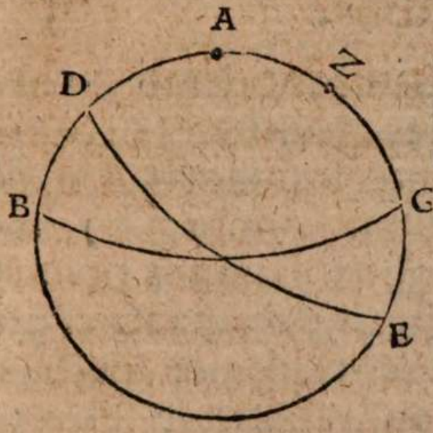 σχόλιον ex Theone. Quod distantia aequinocialis a puncto verticali sit aequalis exaltationi poli eius loci in quo facimus observationes, sic nobis erit manifestum. Sit enim meridianus circulus ABG, et supra ipsum verticale punctum A, horizon autem BG. Quia igitur in omni habitatione polus horizontis est illud verticale signum, ideo AG est quadrans circuli. Esto autem aequinoctialis circulus DE, et polus ipsius signum Z. Igitur et DZ quadrans est eiusdem maximi circli. Aequales igitur sint AG, et DZ circumferentiae. Et communi ablata AZ circumferentia, reliqua AD reliquae ZG aequalis est, estque AD circumferentia a vertice usque ad aequinoctialem, sed GZ ab horizonte ad polum quae est poli exaltatio. Proinde circumferentia a vertice ad aequinoctialem circulum aequalis est poli exaltationi.
σχόλιον ex Theone. Quod distantia aequinocialis a puncto verticali sit aequalis exaltationi poli eius loci in quo facimus observationes, sic nobis erit manifestum. Sit enim meridianus circulus ABG, et supra ipsum verticale punctum A, horizon autem BG. Quia igitur in omni habitatione polus horizontis est illud verticale signum, ideo AG est quadrans circuli. Esto autem aequinoctialis circulus DE, et polus ipsius signum Z. Igitur et DZ quadrans est eiusdem maximi circli. Aequales igitur sint AG, et DZ circumferentiae. Et communi ablata AZ circumferentia, reliqua AD reliquae ZG aequalis est, estque AD circumferentia a vertice usque ad aequinoctialem, sed GZ ab horizonte ad polum quae est poli exaltatio. Proinde circumferentia a vertice ad aequinoctialem circulum aequalis est poli exaltationi.
〈I.11〉 CAPUT XI: Theoremata praemittenda sphaericis demonstrationibus
Nunc cum sequatur ut demonstrentur particulares quantitates circumferentiarum quae inter aequinoctialem et eum qui per medium signorum est intercipiuntur, descriptis maximis circulis per polos aequinoctialis, prius pauca et utilia lemmata breviter trademus, quibus plurimas fere demonstrationes in sphaericis materiis simplicissime et artificiosissime, quantum fieri poterit, faciemus.
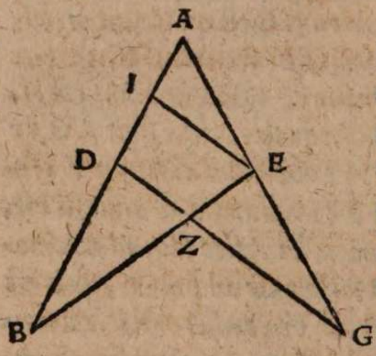 In Primum lemmation ἐυθύγραμμον κατὰ σύνθεσιν i. m. W duas rectas lineas AB et AG deductae duae rectae lineae BE et GD secent se mutuo in puncto Z. Dico quod ratio GA ad AE composita est ex ratione GD ad DZ et ex ratione ZB ad BE. Ducatur enim per punctum E linea EI aequidistans lineae GD. Quoniam igitur lineae GD et EI sunt aequidistantes, ratio lineae GA ad AE eadem est quae est lineae GD ad lineam EI. Adsumatur autem deforis linea ZD. Erit igitur composita ratio lineae GD ad lineam EI ex ratione lineae GD ad lineam DZ et ex ratione lineae DZ ad lineam EI. Quare et ratio lineae GA ad lineam AE composita est ex ratione lineae GD ad lineam DZ et ex ratione lineae DZ ad lineam EI. Est autem et ratio lineae DZ ad EI eadem rationi lineae ZB ad lineam BE, cum aequidistantes sint lineae EI et ZD. Ratio igitur lineae GA ad lineam AE composita est ex ratione lineae GD ad lineam DZ et ex ratione lineae ZB ad lineam BE. Quod erat demonstrandum.
In Primum lemmation ἐυθύγραμμον κατὰ σύνθεσιν i. m. W duas rectas lineas AB et AG deductae duae rectae lineae BE et GD secent se mutuo in puncto Z. Dico quod ratio GA ad AE composita est ex ratione GD ad DZ et ex ratione ZB ad BE. Ducatur enim per punctum E linea EI aequidistans lineae GD. Quoniam igitur lineae GD et EI sunt aequidistantes, ratio lineae GA ad AE eadem est quae est lineae GD ad lineam EI. Adsumatur autem deforis linea ZD. Erit igitur composita ratio lineae GD ad lineam EI ex ratione lineae GD ad lineam DZ et ex ratione lineae DZ ad lineam EI. Quare et ratio lineae GA ad lineam AE composita est ex ratione lineae GD ad lineam DZ et ex ratione lineae DZ ad lineam EI. Est autem et ratio lineae DZ ad EI eadem rationi lineae ZB ad lineam BE, cum aequidistantes sint lineae EI et ZD. Ratio igitur lineae GA ad lineam AE composita est ex ratione lineae GD ad lineam DZ et ex ratione lineae ZB ad lineam BE. Quod erat demonstrandum.
σχόλιον. Demonstrat hoc loco Ptolemaeus regulam, ut vulgo vocant, sex quantitatum profuturam ad sphaericas demonstrationes, ac contentus est duplicem huiusce connexionis se coniugationis modum in genere monstrasse, quorum priorem ipse vocat κατὰ σύνθεσιν, posteriorem autem κατὰ διαίρεσιν. Sed arbitror studiosum lectorem admonendum esse hoc loco paulo accuratius de tota hac doctrina, cuius usus latissime patet. Est igitur huiusce coniugationis quadruplex varietas κατὰ σύνθεσιν, et duplex κατὰ διαίρεσιν, sicut et Theon docet, cuius tamen ordinem non per omnia sequemur, et adiiciemus aliquanto plura quam hactenus traditum est ab aliis. Nam κατὰ σύνθεσιν aut tota exterior linea confertur ad partem suam vel superiorem ad angulum, qui inter duas exteriores lineas comprehenditur, vel ad partem inferiorem, aut similiter tota interior seu διηγμένη confertur ad partem suam vel superiorem vel inferiorem. His quatuor modis κατὰ σύνθεσιν respondent totidem ἀνάπαλιν. Sed κατὰ διαίρεσιν confertur aut exterioris pars inferior ad superiorem, aut similiter interioris pars inferior ad superiorem. Respondent autem et his duobus modis alii duo ἀνάπαλιν. Ac ne quid desideret studiosus lector, cui servire cupimus totum hunc laborem, subiungemus ommium horum modorum demonstrationes, ac primum eorum qui sunt κατὰ σύνθεσιν.
In I. Tota exterior ad partem suam superiorem i. m. W duas igitur rectas lineas AB et AG actae sint duae rectae, BE scilicet et GD, secantes sese in signo Z. Dico quod ratio rectae GA ad rectam AE composita est ex ratione rectae GD ad DZ, et ex ratione rectae ZB ad BE. Atque hic modus inipso textu demonstratus est, et primo loco a Theone recensetur.
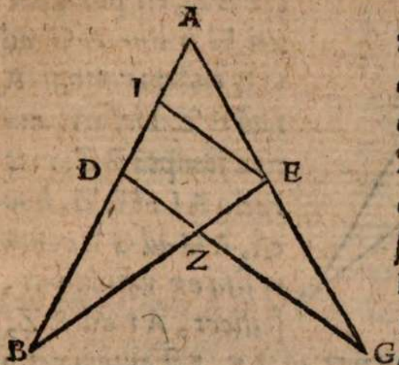 Ἀνάπαλιν. Dico etiam, quod retrorsum ratio EA ad AG composita est ex ratione EB ad BZ, et ex ratione ZD ad DG. Sit enim rursus acta aequidistans EI rectae GD. Et quoniam aequidistantes sunt rectae EI, ZD, est igitur per 4 sexti Elementorum, καὶ ἐναλλαξ ratio EA ad AG eadem rationi EI ad DG. Deforis autem est ZD. Ratio igitur EI ad DG componitur ex ratione EI ad ZD et ex ratione ZD ad DG. Quare et EA ad AG ratio composita est ex rationibus, scilicet EI ad ZD et ZD ad DG. Est autem et ratio EI ad ZD eadem rationi EB ad BZ, eo quod aequidistantes sunt rectae EI et ZD. Ratio igitur EA ad AG composita est ex rationibus, scilicet EB ad BZ et ZD ad DG, quod demonstrasse oportuit.
Ἀνάπαλιν. Dico etiam, quod retrorsum ratio EA ad AG composita est ex ratione EB ad BZ, et ex ratione ZD ad DG. Sit enim rursus acta aequidistans EI rectae GD. Et quoniam aequidistantes sunt rectae EI, ZD, est igitur per 4 sexti Elementorum, καὶ ἐναλλαξ ratio EA ad AG eadem rationi EI ad DG. Deforis autem est ZD. Ratio igitur EI ad DG componitur ex ratione EI ad ZD et ex ratione ZD ad DG. Quare et EA ad AG ratio composita est ex rationibus, scilicet EI ad ZD et ZD ad DG. Est autem et ratio EI ad ZD eadem rationi EB ad BZ, eo quod aequidistantes sunt rectae EI et ZD. Ratio igitur EA ad AG composita est ex rationibus, scilicet EB ad BZ et ZD ad DG, quod demonstrasse oportuit.
Dico rursus II. Tota exterior ad partem suam inferiorem i. m. W quod ratio AG ad GE composita est ex ratione AD ad DB et ex ratione BZ ad ZE. Sit enim acta aequidistans AI rectae EB, et producatur ad ipsam GDI. Quia enim rursus aequidistans est AI recta rectae EZ, est per 4 sexti Elementorum ratio AG ad GE eadem rationi AI ad EZ. Deforis autem sumpta BZ, erit ratio AI ad EZ, hoc est AG ad GE, composita ex rationibus, scilicet AI ad BZ, [scilicet AI ad BZ,] et BZ ad 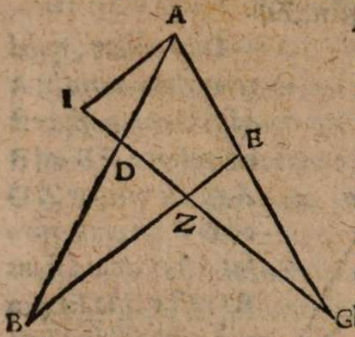 ZE. Est autem ratio AI ad BZ eadem rationi AD ad DB. Quare ratio AG ad GE composita est ex rationibus AD ad DB et BZ ad ZE, quod demonstrandum erat. Haec forma a Theone recensetur sexto loco.
ZE. Est autem ratio AI ad BZ eadem rationi AD ad DB. Quare ratio AG ad GE composita est ex rationibus AD ad DB et BZ ad ZE, quod demonstrandum erat. Haec forma a Theone recensetur sexto loco.
Ανάπαλιν. Dico quod retrorsum etiam EG ad GA ratio composita est ex ratione EZ ad ZB et ex ratione BD ad DA. Manente enim priori constructione, est ratio EG ad GA eadem rationi EZ ad IA, et sumpta deforis recta BZ, ratio EZ ad IA, hoc est EG ad GA, composita est ex duabus, scilicet EZ ad ZB et ZB ad IA. Est autem rationi ZB ad IA eadem ratio BD ad DA. Ratio igitur EG ad GA composita est ex rationibus EZ ad ZB et BD ad DA, quod demonstrandum erat.
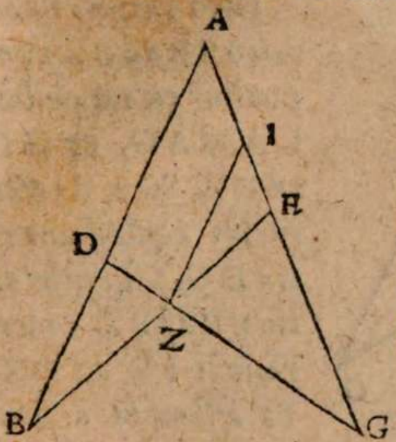 Dico rursus III. Tota interior ad partem suam superiorem i. m. W quod ratio BE ad EZ composita est ex rationibus, scilicet, BA ad AD et DG ad GZ. Nam ex signo Z sit acta ZI aequidistans rectae AB. Et quia AB, ZI rectae aequidistantes sunt, ideo ratio BE ad EZ eadem est rationi AB ad IZ. Sumpta autem deforis AD, componitur ratio AB ad IZ, hoc est BE ad EZ ex duabus, scilicet BA ad AD et AD ad IZ. Est autem ratio AD ad IZ eadem rationi DG ad GZ. Ratio igitur BE ad EZ componitur ex duabus, scilicet BA ad AD et DG ad GZ, quod erat demonstrandum. Hanc formam exponit Theon tertio loco.
Dico rursus III. Tota interior ad partem suam superiorem i. m. W quod ratio BE ad EZ composita est ex rationibus, scilicet, BA ad AD et DG ad GZ. Nam ex signo Z sit acta ZI aequidistans rectae AB. Et quia AB, ZI rectae aequidistantes sunt, ideo ratio BE ad EZ eadem est rationi AB ad IZ. Sumpta autem deforis AD, componitur ratio AB ad IZ, hoc est BE ad EZ ex duabus, scilicet BA ad AD et AD ad IZ. Est autem ratio AD ad IZ eadem rationi DG ad GZ. Ratio igitur BE ad EZ componitur ex duabus, scilicet BA ad AD et DG ad GZ, quod erat demonstrandum. Hanc formam exponit Theon tertio loco.
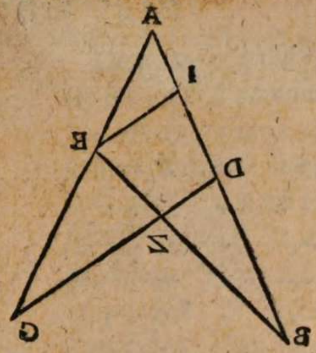 ἀνάπαλιν. Dico etiam quod retrorsum ZE ad EB ratio composita est ex rationibus ZG ad GD et DA ad AB. Manente enim proxima constructione, ratio ZE ad EB eadem est rationi IZ ad AB, et sumpta deforis AD recta, componitur ratio IZ ad AB, hoc est ratio ZE ad EB, ex duabus rationibus, scilicet IZ ad DA et DA ad AB. Est autem ratio IZ ad DA eadem rationi ZG ad GD. Quare ratio ZE ad EB componitur ex dabus, ZG ad GD, et DA ad AB, quod erat demonstrandum.
ἀνάπαλιν. Dico etiam quod retrorsum ZE ad EB ratio composita est ex rationibus ZG ad GD et DA ad AB. Manente enim proxima constructione, ratio ZE ad EB eadem est rationi IZ ad AB, et sumpta deforis AD recta, componitur ratio IZ ad AB, hoc est ratio ZE ad EB, ex duabus rationibus, scilicet IZ ad DA et DA ad AB. Est autem ratio IZ ad DA eadem rationi ZG ad GD. Quare ratio ZE ad EB componitur ex dabus, ZG ad GD, et DA ad AB, quod erat demonstrandum.
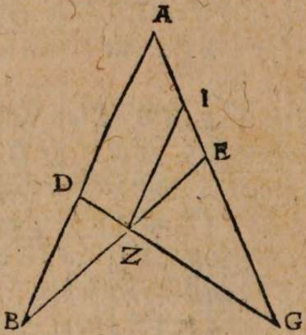 Dico rursus IIII. Tota interior ad partem suam inferiorem i. m. W quod ratio EB ad BZ componitur ex rationibus EA ad AG et GD ad DZ. Sit enim EI acta rursus aequidistans rectae DG. Est igitur ratio EB ad BZ eadem rationi IE ad DZ. Et assumpta deforis recta GD, componitur ratio IE ad DZ, hoc est EB ad BZ ex rationibus IE ad GD, et GD ad DZ. Estque ratio IE ad GD eadem rationi EA ad AG. Quare ratio EB ad BZ componitur ex duabus, scilicet ratione EA ad AG et GD ad DZ.
Dico rursus IIII. Tota interior ad partem suam inferiorem i. m. W quod ratio EB ad BZ componitur ex rationibus EA ad AG et GD ad DZ. Sit enim EI acta rursus aequidistans rectae DG. Est igitur ratio EB ad BZ eadem rationi IE ad DZ. Et assumpta deforis recta GD, componitur ratio IE ad DZ, hoc est EB ad BZ ex rationibus IE ad GD, et GD ad DZ. Estque ratio IE ad GD eadem rationi EA ad AG. Quare ratio EB ad BZ componitur ex duabus, scilicet ratione EA ad AG et GD ad DZ.
 Aliter. Sit acta ZI aequidistans rectae AB. Est igitur ratio EB ad BZ eadem rationi EA ad AI. Et assumpta deforis recta AG, componitur ratio EA ad AI, hoc est EB ad BZ, ex rationibus scilicet EA ad AG et GA ad AI. Est autem GA ad AI ratio eadem rationi GD ad DZ. Quare ratio EB ad BZ composita est ex rationibus EA ad AG et GD ad DZ, quod erat demonstrandum. Haec est Theoni secunda forma.
Aliter. Sit acta ZI aequidistans rectae AB. Est igitur ratio EB ad BZ eadem rationi EA ad AI. Et assumpta deforis recta AG, componitur ratio EA ad AI, hoc est EB ad BZ, ex rationibus scilicet EA ad AG et GA ad AI. Est autem GA ad AI ratio eadem rationi GD ad DZ. Quare ratio EB ad BZ composita est ex rationibus EA ad AG et GD ad DZ, quod erat demonstrandum. Haec est Theoni secunda forma.
Regula. Observes in hisce demonstrationibus contexendis, ut quae assumitur deforis, sit vel aequidistans alteri duarum, quibus interponitur, aut etiam adiungitur, vel pars alterius earundem, vel econtra, ut altera harum sit pars assumptae deforis.
Ανάπαλιν. Dico quod etiam retrorsum ZB ad BE ratio componitur ex ratione ZD ad DG et GA ad AE. Sit enim rursus acta EI aequidistans rectae GD. Ratio igitur ZB ad BE eadem est rationi DZ ad IE. Assumpta autem deforis recta DG, componitur ratio DZ ad IE, hoc est ZB ad BE, ex rationibus ZD ad DG et DG ad IE, estque ratio DG ad IE eadem rationi GA ad AE. Ratio igitur ZB ad BE composita est ex rationibus, scilicet ZD ad DG et GA ad AE, quod erat demonstrandum.
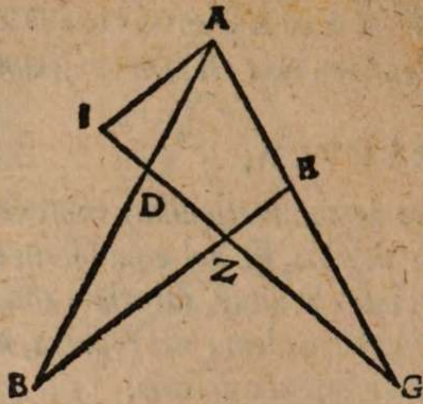 Eodem modo Secundum lemmation, ἐυθύγραμμον, κατὰ διαίρεσιν i. m. W demonstrabitur quod et secundum divisionem ratio lineae GE ad lineam EA componitur ex ratione linee GZ ad ZD, et ex ratione lineae DB ad BA, ducta per A punctum linea Al aequidistante lineae EB, et protracta in eandem GDI. Rursus enim quoniam linea AI aequidistans est lineae EZ, est sicut GE ad EA, sic GZ ad ZI. Adsumpta autem deforis linea ZD, ratio lineae GZ ad ZI componitur ex ratione lineae GZ ad lineam ZD et ex ratione lineae DZ ad lineam ZI. Est autem ratio lineae DZ ad lineam ZI eadem quae est ratio DB ad BA, eo quod in aequidistantes lineas AI et ZB ductae sunt lineae BA et ZI. Quare ratio lineae GZ ad lineam ZI componitur ex ratione lineae GZ ad lineam ZD et ex ratione lineae DB ad lineam BA. Porro ratio lineae GE ad EA eadem est quae est ratio linae GZ ad lineam ZI. Ergo ratio lineae GE ad lineam EA componitur ex ratione lineae GZ ad lineam ZD et ex ratione lineae DB ad lineam BA. Quod demonstrandum erat.
Eodem modo Secundum lemmation, ἐυθύγραμμον, κατὰ διαίρεσιν i. m. W demonstrabitur quod et secundum divisionem ratio lineae GE ad lineam EA componitur ex ratione linee GZ ad ZD, et ex ratione lineae DB ad BA, ducta per A punctum linea Al aequidistante lineae EB, et protracta in eandem GDI. Rursus enim quoniam linea AI aequidistans est lineae EZ, est sicut GE ad EA, sic GZ ad ZI. Adsumpta autem deforis linea ZD, ratio lineae GZ ad ZI componitur ex ratione lineae GZ ad lineam ZD et ex ratione lineae DZ ad lineam ZI. Est autem ratio lineae DZ ad lineam ZI eadem quae est ratio DB ad BA, eo quod in aequidistantes lineas AI et ZB ductae sunt lineae BA et ZI. Quare ratio lineae GZ ad lineam ZI componitur ex ratione lineae GZ ad lineam ZD et ex ratione lineae DB ad lineam BA. Porro ratio lineae GE ad EA eadem est quae est ratio linae GZ ad lineam ZI. Ergo ratio lineae GE ad lineam EA componitur ex ratione lineae GZ ad lineam ZD et ex ratione lineae DB ad lineam BA. Quod demonstrandum erat.
σχόλιον. V. Extrerioris lineae pars inferior ad superiorem i. m. W Hanc fomam κατὰ διαίρεσιν recitat Theon quarto loco. Subiungamus et huius ἀνάπαλιν.
Dico igitur quod retrorsum etiam ratio AE ad EG componitur ex ratione AB ad BD, et DZ ad ZG. Sit enim rursus acta AI aequidistans rectae EB, producta GD in I. Et quia aequidistantes sunt rectae AI, et EB, est igitur per 2 sexti Elementorum ratio AE ad EG eadem rationi IZ ad ZG. Adsumatur deforis DZ. Ratio igitur IZ ad ZG, hoc est AE ad EG, componiur ex rationibus IZ ad ZD et DZ ad ZG. Est autem ratio IZ ad ZD eadem rationi AB ad BD, eo quod in aequidistantes AI et BZ actae sunt AB et ZI. Ergo ratio AE ad EG componitur ex duabus rationibus, scilicet AB ad BD et DZ ad ZG, quod erat demonstrandum.
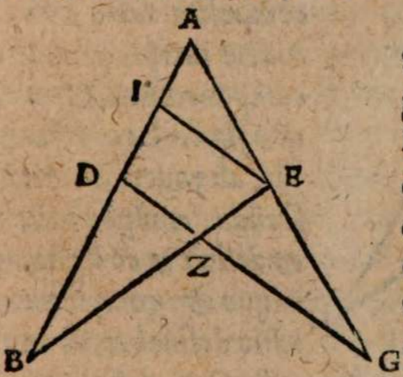 Dico rursum VI. Interioris lineae pars inferior ad superiorem i. m. W quod ratio BZ ad ZE componitur ex ratione BD ad DA, et ex AG ad GE. Sit enim rursus acta EI aequidistans rectae GD. Est igitur ratio BZ ad ZE eadem rationi BD ad DI. Et sumpta deforis DA, componitur ratio BD ad DI, hoc est BZ ad ZE ex ratione BD ad DA et AD ad DI, estque AD ad DI ratio eadem rationi AG ad GE. Ratio igitur BZ ad ZE composita est ex ratione BD ad DA et ex AG ad GE, quod erat demonstrandum. Hanc Theon demonstrat quinto loco.
Dico rursum VI. Interioris lineae pars inferior ad superiorem i. m. W quod ratio BZ ad ZE componitur ex ratione BD ad DA, et ex AG ad GE. Sit enim rursus acta EI aequidistans rectae GD. Est igitur ratio BZ ad ZE eadem rationi BD ad DI. Et sumpta deforis DA, componitur ratio BD ad DI, hoc est BZ ad ZE ex ratione BD ad DA et AD ad DI, estque AD ad DI ratio eadem rationi AG ad GE. Ratio igitur BZ ad ZE composita est ex ratione BD ad DA et ex AG ad GE, quod erat demonstrandum. Hanc Theon demonstrat quinto loco.
Ἀνάπαλιν. Dico quod retrorsum etiam ratio EZ ad ZB componitur ex ratione EG ad GA et ex ratione AD ad DB. Manente enim priori κατασκευῇ, est ratio EZ ad ZB eadem rationi ID ad DB. Et adsumpta deforis DA, componitur ratio ID ad DB, hoc est EZ ad ZB, ex rationibus, scilicet ID ad DA et DA ad AB, estque ratio ID ad DA eadem rationi EG ad GA. Quare ratio EZ ad ZB composita est ex ratione EG ad GA, et ex ratione AD ad DB, quod erat demonstrandum.
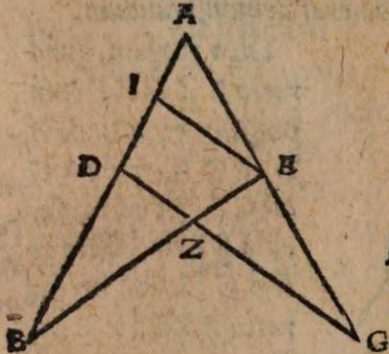 Theonis regula. A quo signo incipit composita ratio, ab eodem incipit prima componentium, et in quo signo haec desinit, ab eodem incipit secunda componentium, et desinit in eo signo in quo et composita ratio desinebat, ut in primo modo Ptolemaei, ratio rectae GA ad AE coepit a signo G et desiit in D. Deinde prima componentium ratio GD ad DZ coepit a signo G, a quo et composita ratio, et desiit in Z. Et postea ZB ad BE ratio coepit a Z, in quo desiit prima componentium, et desiit in E, in quo et composita ratio desinebat.
Theonis regula. A quo signo incipit composita ratio, ab eodem incipit prima componentium, et in quo signo haec desinit, ab eodem incipit secunda componentium, et desinit in eo signo in quo et composita ratio desinebat, ut in primo modo Ptolemaei, ratio rectae GA ad AE coepit a signo G et desiit in D. Deinde prima componentium ratio GD ad DZ coepit a signo G, a quo et composita ratio, et desiit in Z. Et postea ZB ad BE ratio coepit a Z, in quo desiit prima componentium, et desiit in E, in quo et composita ratio desinebat.
Hactenus ea fere commemoravimus, quae apud Theonem sunt in huius loci explicatione. Sed cum recentiores, inter quos praecipue Arab〈u〉s Alchindus nominatur, multiplicem varietatem huiusce συνθέσεως τοῦ λόγου, seu compositionis rationum literis mandarint, commodum videtur eam hic recitare, et quantum a nobis fieri potest, universam complecti, ac velut ob oculos ponere.
Quando ratio aliqua composita dicitur ex aliis duabus rationibus, necessario sex quantitates seu magnitudines intelliguntur, quia una quaelibet ratio inter duas magnitudines quasi terminos versatur. Datis autem sex magnitudinibus, συζυγία ὴ συνδυασμὸς quindecim Quindecim συζυγίαι i. m. W modis variari potest, hoc est binae invicem consociari possint diversis modis quindecin, quemadmodum traditur in numerorum praeceptis de progressione, ut vocant, arithmetica, ut prima magnitudo cum reliquis quinque, secunda cum reliquis quatuor, tertia cum reliquis tribus, quarta cum reliquis duabus, quinta cum sola sexta reliqua coniugatur. Reliquae autem quatuor magnitudines duodenis invicem modis transponi seu commutari possunt, quemadmodum sequens tabella hanc varietatem oculis subiciit in prima συζυγίᾳ.
Ad hunc modum colliguntur per quindecim illas συνζυγίας modi 180, et quia hi omnes ἀνάπαλιν sumi possunt, fiunt in summa modi 360, ex quibus omnibus soli 36 necessarii existunt, 12 impossibiles, reliqua vero turba prorsus inutilis. Investigari autem et diiudicari omnes hi modi aptissime et facilime possunt per sex numeros, quorum primi ad secundum ratio est composita ex ratione tertii ad quartum, et quinti ad sextum, ut sit ratio 8 ad 3 composita ex ratione 2 ad 1, et 4 ad 3, quia multiplicata 2 per 4 faciunt 8, et 1 per 3 multiplicatum facit 3, sicut in praeceptis numerorum traditur. Ab hac ceu radice ac primo modo praecedentis tabellae propagatur tota reliqua varietas, ut in prima hac συζυγίᾳ, in qua primae quantitatis ratio ad secundam componitur ex duabus rationibus reliquarum quatuor quantitatum, deprehenditur per hosce numeros, quod ratio etiam primae quantitatis ad secundam componatur ex ratione tertiae quantitatis ad sextam, et quintae ad quartam, qui modus in praecedenti tabella sextus erat. Reliqui vero modi 10 eiusdem tabellae prorsus sunt inutiles. Hac igitur ratione colliguntur ex 9 syzygiis seu coniugationibus modi tantum 18 necessarii, bini scilicet ex singulis. Ex aliis autem 6 coniugationibus modi 6 impossibiles. His modis utrobique respondent totidem ἀνάπαλιν. Reliqua vero turba prorsus est inutilis, ut diximus. Sed ut hi modi necessarii sint in conspectu, proponamus in tabula.
Tabula xviii. modorum necessarium
Manifeste autem apparet ex hac tabella quod ratio primae magnitudinis ad quartam et sextam non componatur ex reliquis duabus ratonibus, similiter nec ratio secundae ad tertiam et quintam, nec tertiae ad quintam, neque quartae ad sextam, cum reliquae tamen rationes singulae dupliciter componantur.
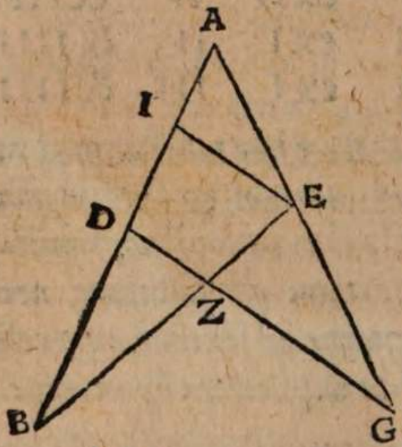 Nec difficile est hanc varietatem simul monstrare γραμμικῶς ex superioribus diagrammatis et in singulis 6 modis, quos supra ex Theonis sententia demonstravimus, constituere 18 hasce formas necessarias, atque inter sese diversas, ut, quia in primo modo demonstrata est ratio rectae GA ad rectam AE componi ex ratione GD ad DZ et ex ratione rectae ZB ad BE, existit GA prima magnitudo, AE secunda, GD tertia, DZ quarta, ZB quinta, BE sexta. Hoc ordine instituto, proxima tabella gubernabit seriem seu collocationem harum sex magnitudinum in reliquis 17 modis. Erit enim hic septimus modus. Ratio AE ad DZ componitur ex ratione AG ad GD et EB ad BZ. Et octavus ratio AE ad DZ componitur ex ratione AG ad BZ et EB ad DG. Ac similiter caeteri facilime constituentur. Lineares autem seu γραμμικὰς demonstrationes facile in promptu habebit is qui superiores recte percepit, ut in septimo et octavo modo sit acta EI aequidistans rectae DG. Et quia rectae IE, DG aequidistantes sint, existit ratio AE ad EI eadem rationi AG ad GD. Duabus autem magnitudinibus AE, EI adsumatur deforis tertia DZ. Componitur ergo ratio AE ad DZ, ex duabus, scilcet AE ad EI, EI ad DZ. Est autem ratio AE ad EI eadem rationi AG ad GD, et EI ad DZ ratio eadem rationi EB ad BZ. Ratio igitur AE ad DZ composita est ex duabus rationibus AG ad GD et EB ad BZ. Ita demonstratus est septimus modus. Rursus quia AE ad EI ratio eadem est rationi AG ad GD, adsumatur deforis DZ secunda, ut sit AE prima magnitudo et EI tertia. Erit igitur ratio AE ad EI, hoc est AG ad GD composita ex duabus, scilicet AE ad DZ et DZ ad EI. Est autem ratio DZ ad EI eadem rationi ZB ad BE. His ergo duabus magnitudinibus ZB, BE similiter interpositis inter duas AG et GD, erit ratio AG ad GD, hoc est AE ad EI, composita ex tribus rationibus, scilicet AG ad ZB et ZB ad BE et BE ad GD. Duae ergo rationes AE ad DZ et DZ ad EI compositae sunt ex tribus, scilicet AG ad ZB et ZB ad BE et BE ad GD. Est autem ratio DZ ad EI eadem rationi ZB ad BE. Reiectis ergo utrobique iisdem rationibus, relinquitur ratio AE ad DZ composita ex duabus, scilicet AG ad ZE et BE ad GD. Ita et octavus modus demonstratus est. Verum nos brevitati consulentes relinquimus haec cuique studioso lectori pertexenda.
Nec difficile est hanc varietatem simul monstrare γραμμικῶς ex superioribus diagrammatis et in singulis 6 modis, quos supra ex Theonis sententia demonstravimus, constituere 18 hasce formas necessarias, atque inter sese diversas, ut, quia in primo modo demonstrata est ratio rectae GA ad rectam AE componi ex ratione GD ad DZ et ex ratione rectae ZB ad BE, existit GA prima magnitudo, AE secunda, GD tertia, DZ quarta, ZB quinta, BE sexta. Hoc ordine instituto, proxima tabella gubernabit seriem seu collocationem harum sex magnitudinum in reliquis 17 modis. Erit enim hic septimus modus. Ratio AE ad DZ componitur ex ratione AG ad GD et EB ad BZ. Et octavus ratio AE ad DZ componitur ex ratione AG ad BZ et EB ad DG. Ac similiter caeteri facilime constituentur. Lineares autem seu γραμμικὰς demonstrationes facile in promptu habebit is qui superiores recte percepit, ut in septimo et octavo modo sit acta EI aequidistans rectae DG. Et quia rectae IE, DG aequidistantes sint, existit ratio AE ad EI eadem rationi AG ad GD. Duabus autem magnitudinibus AE, EI adsumatur deforis tertia DZ. Componitur ergo ratio AE ad DZ, ex duabus, scilcet AE ad EI, EI ad DZ. Est autem ratio AE ad EI eadem rationi AG ad GD, et EI ad DZ ratio eadem rationi EB ad BZ. Ratio igitur AE ad DZ composita est ex duabus rationibus AG ad GD et EB ad BZ. Ita demonstratus est septimus modus. Rursus quia AE ad EI ratio eadem est rationi AG ad GD, adsumatur deforis DZ secunda, ut sit AE prima magnitudo et EI tertia. Erit igitur ratio AE ad EI, hoc est AG ad GD composita ex duabus, scilicet AE ad DZ et DZ ad EI. Est autem ratio DZ ad EI eadem rationi ZB ad BE. His ergo duabus magnitudinibus ZB, BE similiter interpositis inter duas AG et GD, erit ratio AG ad GD, hoc est AE ad EI, composita ex tribus rationibus, scilicet AG ad ZB et ZB ad BE et BE ad GD. Duae ergo rationes AE ad DZ et DZ ad EI compositae sunt ex tribus, scilicet AG ad ZB et ZB ad BE et BE ad GD. Est autem ratio DZ ad EI eadem rationi ZB ad BE. Reiectis ergo utrobique iisdem rationibus, relinquitur ratio AE ad DZ composita ex duabus, scilicet AG ad ZE et BE ad GD. Ita et octavus modus demonstratus est. Verum nos brevitati consulentes relinquimus haec cuique studioso lectori pertexenda.
Summa. Cum Summa omnium modorum i. m. W igitur in uno quolibet superiorum sex modorum, quos non incommode genera appellabimus, reperiantur 18 modi diversi ac necessari et 6 impossibiles, sequitur ex omnibus sex generibus colligi modos necessarios 108 et impossibiles, 36. Sed tamen non omnes hi 108 modi diversi sunt, sed plurimi inter se plane congruunt, seu potius iidem sint. Primum enim alio quidem ordine, sed tamen per omnia conveniunt 18 modi, qui existunt ex primo genere a nobis supra demostrato cum aliis 18 modis, qui existunt similiter ex quarto nostro genere. Similiter per omnia conveniunt 18 modi ex secundo genere cum 18 modis ex sexto genere. Hoc palam ostendit literarum similitudo seu ταυτότης potius, si quis omnes modos 108 ortos ex illis sex generibus, ac iuxta superiora diagrammata collectos in conspectu habeat. Deinde etsi reliqui 72 modi diversi videntur propter literarum dissimilitudinem, tamen rursus inter se congruunt 18 modi ex primo genere cum aliis 18 ex tertio genere, ac similiter 18 modi ex 5 genere cum 18 modis ex sexto. Ac ut breviter et summatim dicam, quae genera, quive modi ex illis derivati revera inter se discrepent aut congruant, ita quam expeditissime iudicari potest, si consideretur, quae lineae, aut quae partes earum cum quibus copulentur ac comparentur. Cum enim sint quatuor rectae totae et singulae sectae in duas partes, existunt membra in universum duodecim. Itaque in primo genere ratio totius exterioris lineae ad partem suam superiorem componitur ex ratione interioris lineae confinis ad partem suam superiorem, et ex ratione partis inferioris lineae interioris transversae ad totam eandem transversam. Haec ipsa sex membra comparent etiam collata seu copulata tam in tertio genere quam in quarto eorum quae supra posuimus. Itaque in unum tantum genus coeunt tria nostra genera, primum, tertium et quartum, Theonis vero primum, secundum et tertium. Similiter cum in secundo genere nostro ratio exterioris lineae totius ad partem suam inferiorem componatur ex ratione partis superioris ad partem inferiorem exterioris transversae et ex ratione partis inferioris interioris lineae transversae ad partem suam superiorem, manifeste comparent et haec sex membra in quinto nostro et sexto genere. Itaque rursus in unum genus coalescunt tria nostra genera, secundum, quintum et sextum, Theonis vero quartum, quintum et sextum. Ex quibus omnibus manifestum est quod ex toto illo numero modorum necessariorum relinquantur adhuc 36, qui inter se non congruunt, sed specie diuersi sunt, et ex duobus nostris generibus primo et secundo propagantur. Hos in eadem tabula spectandas proposuimus. Huc pertinet tabula XVI syzygiarum i. m. W Sicut autem ex 108 modis necessariis tantum tertia pars relinquitur, ita et ex 36 modis impossibilibus 12 tantum reliqui manent caeteris ad hosce congrentibus. ἁπλῶς ἢ ἀνάπαλιν. Porro, ut saepe iam dictum est, reliquis modis tum necessariis tum impossibilibus qui specie differunt, utrobique totidem respondent ἀνάπαλιν.
Sed nunc breviter in summam quandam conferamus, quae hactenus tradita sunt. Duodecim illa membra, hoc est 4 rectae lineae totae, et earum partes 8 efficiunt συνζυγίας seu coniugationes 66 secundum praecepta numerorum, ex quibus coniugationibus relinquuntur 36 specie differentes, quia caeterae 30 cum his congruunt ἢ ἁπλῶς, ἢ ἀνάπαλιν. Et sunt hae: primum tota exterior copulatur cum omnibus reliquis undecim membris, secundo pars superior exterioris lineae copulatur cum novem tantum reliquis membris, quia antea facta est copulatio partis superioris exterioris lineae cum tota exteriori transversa, tertio pars inferior exterioris septem modis copulatur videlicet, aut cum tota interiori confini, aut cum parte superiori, aut inferiori eiusdem, aut cum tota interiori transversa, aut parte superiori, aut inferiori eiusdem, aut denique cum inferiori parte exterio〈r〉is exteriotis W transversae, quarto tota interior seu διηγμένη quinque modis copulatur, scilicet vel cum parte sua superiori vel inferiori, vel cum tota interiori transversa, vel parte eius superiore vel inferiore, quinto pars superior interioris tripliciter copulatur, hoc est vel cum parte inferiore eiusdem, vel cum parte superiori interioris transversae, vel inferiori parte eiusdem. Postremo pars inferior interioris lineae cum parte inferiore interioris lineae transversae copulatur. Ex his 36 coniugationibus necessariae sunt 16, impossibiles 12, inutiles vero seu ineptae 8. Rursum ex necessariis illis sedecim duae componuntur quadrupliciter, reliquae vero quatuordecim tantum dupliciter. Ita redent illi 36 modi, de quibus iam saepe dictum est, in quibus una ratio ex duabus aliis componitur, quemadmodum haec ommia aperte patent ex nostra tabula.
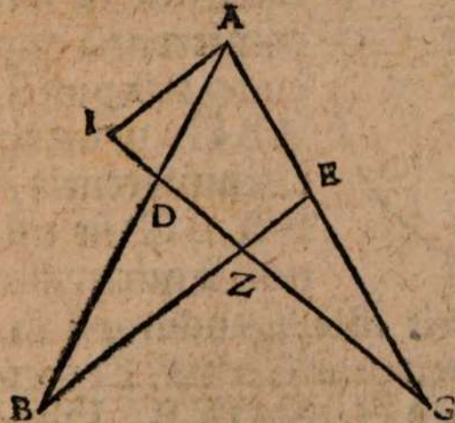 Sed Exemplum numerorum i. m. W antequam hanc tractationem relinquamus, aptum etiam exemplum numerorum subiiciendum est. Ponamus igitur facilitatis gratia angulum ad A rectum, et in triangulo orthogonio ABE, qualium AB 12, talium BE 13, et EA 5. Similiter in orthogonio triangulo ADG, qualium AD 8, talium AG 15, et GD 17. Hinc constant totae exteriores AB et AG cum suis partibus. Similiter constant totae interiores seu διηγμέναι, sed partes ipsarum ratiocinari licet per primum modum secundae nostrae syzygiae in tabula, aut etiam per alios modos. In integris ergo numeris primis seu minimis sic constabit hoc exemplum. Qualium GA 105, talium AE 35, et EG 70, et GD 119, et DZ 17, et ZG 102, et EB 91, et EZ 52, et ZB 39, et AB 84, et AD 56, denique DB 28. Verum post hanc satis longam digressionem lectori studioso utilem, tandem ad textum revertamur.
Sed Exemplum numerorum i. m. W antequam hanc tractationem relinquamus, aptum etiam exemplum numerorum subiiciendum est. Ponamus igitur facilitatis gratia angulum ad A rectum, et in triangulo orthogonio ABE, qualium AB 12, talium BE 13, et EA 5. Similiter in orthogonio triangulo ADG, qualium AD 8, talium AG 15, et GD 17. Hinc constant totae exteriores AB et AG cum suis partibus. Similiter constant totae interiores seu διηγμέναι, sed partes ipsarum ratiocinari licet per primum modum secundae nostrae syzygiae in tabula, aut etiam per alios modos. In integris ergo numeris primis seu minimis sic constabit hoc exemplum. Qualium GA 105, talium AE 35, et EG 70, et GD 119, et DZ 17, et ZG 102, et EB 91, et EZ 52, et ZB 39, et AB 84, et AD 56, denique DB 28. Verum post hanc satis longam digressionem lectori studioso utilem, tandem ad textum revertamur.
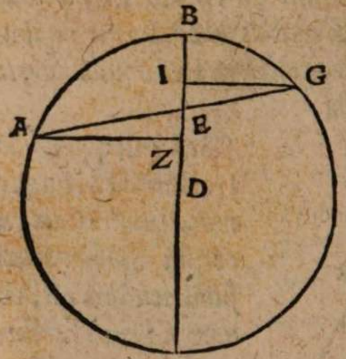 Rursus Primum lemma κυκλικὸν i. m. W sit circulus ABG, cuius centrum D, et accipiantur in circumferentia quaecunque tria puncta A, B, G, ut utraque circumferentia AB et BG sit minor semicirculo, —quod similiter erit intelligendum, si deinceps sumantur circumferentiae—, et coniungantur rectae AG et DEB. Dico quod est recta subtendens duplum circumferentiae AB ad rectam subtensam duplo circumferentiae BG, sicut recta AE ad rectam EG. Deducantur enim ab A et G punctis ad rectam lineam DB perpendiculares, videlicet AZ et GI. Quoniam igitur rectae AZ et GI sunt aequidistantes, et acta est in eas recta AEG, est sicut AZ ad GI, sic AE ad EG. Porro eadem est ratio rectae AZ ad rectam GI quae est subtensae duplo circumferentiae AB ad subtensam duplo circumferentiae BG. Dimidia enim est utraque utriusque. Ergo et ratio rectae AE ad rectam EG eadem est quae est ratio subtensae duplo circumferentiae AB ad subtensam duplo circumferentiae BG. Quod erat demonstrandum.
Rursus Primum lemma κυκλικὸν i. m. W sit circulus ABG, cuius centrum D, et accipiantur in circumferentia quaecunque tria puncta A, B, G, ut utraque circumferentia AB et BG sit minor semicirculo, —quod similiter erit intelligendum, si deinceps sumantur circumferentiae—, et coniungantur rectae AG et DEB. Dico quod est recta subtendens duplum circumferentiae AB ad rectam subtensam duplo circumferentiae BG, sicut recta AE ad rectam EG. Deducantur enim ab A et G punctis ad rectam lineam DB perpendiculares, videlicet AZ et GI. Quoniam igitur rectae AZ et GI sunt aequidistantes, et acta est in eas recta AEG, est sicut AZ ad GI, sic AE ad EG. Porro eadem est ratio rectae AZ ad rectam GI quae est subtensae duplo circumferentiae AB ad subtensam duplo circumferentiae BG. Dimidia enim est utraque utriusque. Ergo et ratio rectae AE ad rectam EG eadem est quae est ratio subtensae duplo circumferentiae AB ad subtensam duplo circumferentiae BG. Quod erat demonstrandum.
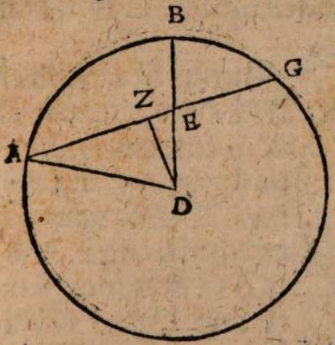 Hinc sequitur Secundum lemmation κυκλικὸν i. m. W quod, si dentur tota circumferentia AG et ratio subtensae duplo circumferentiae AB ad subtensam duplo circumferentiae BG, dabitur etiam utraque circumferentia AB et BG. Manente enim eadem figura connectatur recta AD, et a signo D deducatur perpendicularis DZ in lineam AEG. Quod igitur, circumferentia AG data, detur et angulus qui sub ADZ semissem eiusdem circumferentiae subtendens, et totum triangulum ADZ manifestum est. Deinde, quia tota AG recta linea data est, et per hypothesin ratio lineae AE ad lineam EG, quae eadem est rationi subtensae dupli circunferentiae AB ad subtensam dupli BG, erit etiam data linea AE, et portio reliqua ZE, ideoque, cum et recta DZ sit data, dabitur et in rectangulo triangulo EDZ, angulus qui sub EDZ, et totus angulus qui sub ADB. Ergo et circumferentia AB dabitur, et reliqua BG. Quod demonstrandum erat.
Hinc sequitur Secundum lemmation κυκλικὸν i. m. W quod, si dentur tota circumferentia AG et ratio subtensae duplo circumferentiae AB ad subtensam duplo circumferentiae BG, dabitur etiam utraque circumferentia AB et BG. Manente enim eadem figura connectatur recta AD, et a signo D deducatur perpendicularis DZ in lineam AEG. Quod igitur, circumferentia AG data, detur et angulus qui sub ADZ semissem eiusdem circumferentiae subtendens, et totum triangulum ADZ manifestum est. Deinde, quia tota AG recta linea data est, et per hypothesin ratio lineae AE ad lineam EG, quae eadem est rationi subtensae dupli circunferentiae AB ad subtensam dupli BG, erit etiam data linea AE, et portio reliqua ZE, ideoque, cum et recta DZ sit data, dabitur et in rectangulo triangulo EDZ, angulus qui sub EDZ, et totus angulus qui sub ADB. Ergo et circumferentia AB dabitur, et reliqua BG. Quod demonstrandum erat.
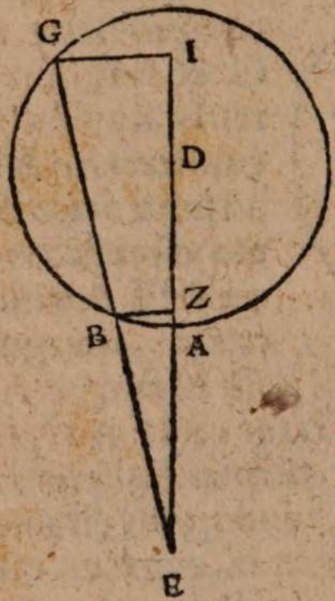 Rursus Tertium lemmation κυκλικὸν i. m. W sit circulus ABG circa centrum D et in eius circumferentia sumantur tria signa A, B, G, sic ut utraque circumferentia AB et BG sit minor semicirculo, —quod simililiter erit intelligendum, si deinceps sumantur circumferentiae—, et coniunctae rectae DA et GB producantur, et concurrant in signo E. Dico quod est subtensa dupli circumferentiae AG ad subtensam dupli circumferentiae AB, sicut recta GE ad rectam BE. Nam, quemadmodum in priori lemmate, si a signis B et G demittamus in rectam DA perpediculares BZ et GI, cum sint aequidistantes, erit sicut GI recta ad rectam BZ, sic recta GE ad rectam BE. Quare et subtensa dupli circumferentiae GA ad subtensam dupli AB est sicut recta GE ad rectam EB. Quod demonstrandum erat.
Rursus Tertium lemmation κυκλικὸν i. m. W sit circulus ABG circa centrum D et in eius circumferentia sumantur tria signa A, B, G, sic ut utraque circumferentia AB et BG sit minor semicirculo, —quod simililiter erit intelligendum, si deinceps sumantur circumferentiae—, et coniunctae rectae DA et GB producantur, et concurrant in signo E. Dico quod est subtensa dupli circumferentiae AG ad subtensam dupli circumferentiae AB, sicut recta GE ad rectam BE. Nam, quemadmodum in priori lemmate, si a signis B et G demittamus in rectam DA perpediculares BZ et GI, cum sint aequidistantes, erit sicut GI recta ad rectam BZ, sic recta GE ad rectam BE. Quare et subtensa dupli circumferentiae GA ad subtensam dupli AB est sicut recta GE ad rectam EB. Quod demonstrandum erat.
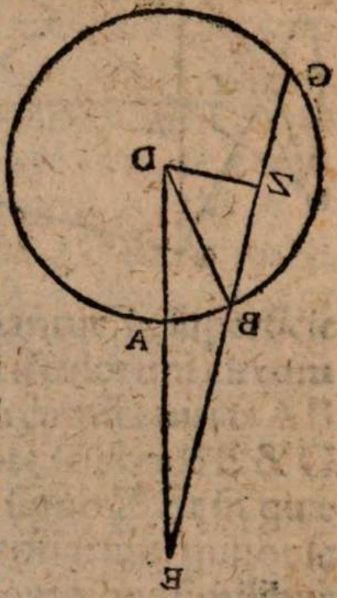 Ex his etiam sequitur Quartum Lemma κυκλικὸν i. m. W quod, si sola BG circumferentia detur una cum ratione subtensae dupli circumferentiae GA ad subtensam dupli AB, dabitur et circumferentia AB. Rursus enim in simili descriptione coniuncta recta DB, et in rectam BG deducta perpendiculari DZ erit angulus qui sub BDZ, subtendens semissem circumferentiae B G datus. Quare datum est et totum BDZ triangulum rectangulum. Deinde quia ratio rectae GE ad EB datur una cum recta GB, dabitur et recta EB, et tota porro EBZ. Quare cum DZ recta linea data est, dabitur et angulus qui sub EDZ eiusdem trianguli rectanguli, et angulus EBD reliquus. ltaque et AB circumferentia erit data.
Ex his etiam sequitur Quartum Lemma κυκλικὸν i. m. W quod, si sola BG circumferentia detur una cum ratione subtensae dupli circumferentiae GA ad subtensam dupli AB, dabitur et circumferentia AB. Rursus enim in simili descriptione coniuncta recta DB, et in rectam BG deducta perpendiculari DZ erit angulus qui sub BDZ, subtendens semissem circumferentiae B G datus. Quare datum est et totum BDZ triangulum rectangulum. Deinde quia ratio rectae GE ad EB datur una cum recta GB, dabitur et recta EB, et tota porro EBZ. Quare cum DZ recta linea data est, dabitur et angulus qui sub EDZ eiusdem trianguli rectanguli, et angulus EBD reliquus. ltaque et AB circumferentia erit data.
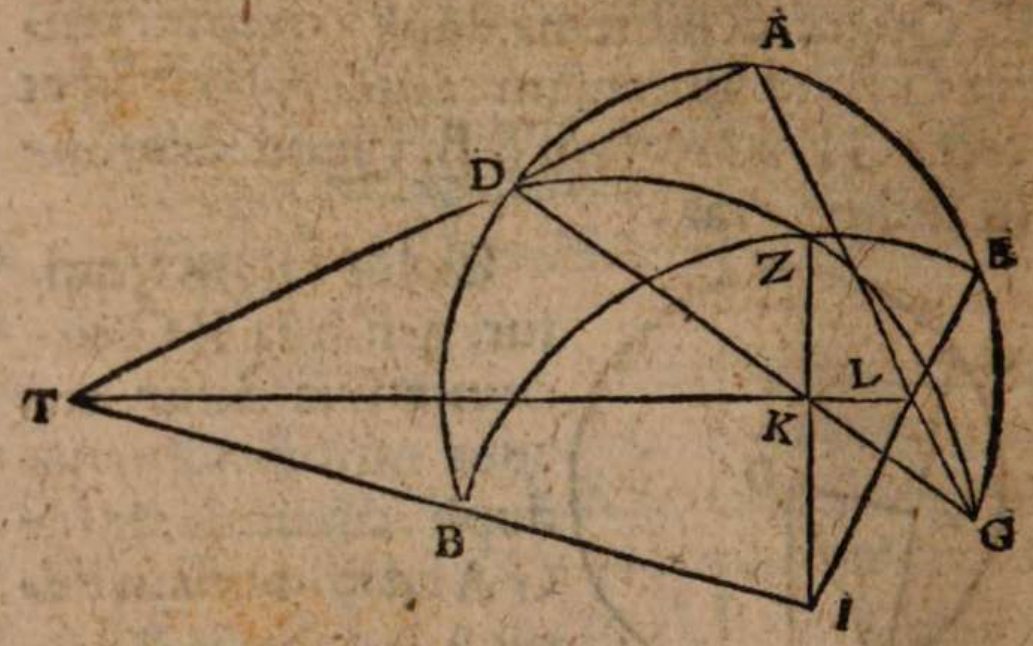 His praemissis, Primum theorema sphaere κατὰ διαίρεσιν i. m. W describantur in superficie sphaerae maximorum circulorum circumferentiae, ita, ut in duas circumferentias AB et AG aliae duae inscriptae, scilicet, BE et GD secent se invicem in signo Z. Et sit quaelibet earum circumferentiarum minor semicirculo, id quod in omnibus similibus descriptionibus intelligendum est. Dico, quod ratio subtensae dupli circumferentiae GE ad subtensam dupli EA componitur ex ratione subtensae dupli GZ ad subtensam dupli ZD, et ex ratione subtensae dupli DB ad subtensam dupli BA. Adsumatur enim centrum sphaerae, et sit I, et a centro I ad sectiones circulorum B, Z, E, ducantur IB et IZ, et IE, et coniuncta AD protrahantur, et concurrat cum recta IB protracta in puncto T. Similiter autem coniunctae rectae DG et AG intersecent lineas IZ, et IE in signis K et L. Sunt igitur in una recta linea T, K, L signa. Sunt enim in duobus simul planis, scilicet, in triangulo AGD, et in circulo BZE, Quae quidem recta TKL coniuncta efficit, ut rectae lineae TL, et GD deductae in duas rectas TA, et GA secent se in puncto K. Ratio igitur rectae GL ad rectam LA composita est ex ratione rectae GK ad rectam KD, et ex ratione rectae DT ad rectam TA. Sed sicut est recta GL ad rectam LA, sic subtensa dupli circumferentiae GE ad subtensam dupli circumferentiae EA. Et sicut recta GK ad rectam KD, sic subtensa dupli circumferentiae GZ ad subtensam dupli ZD. Sicut etiam recta DT ad rectam TA, sic subtensa dupli circumferentiae BD ad subtensam dupli BA. Ratio igitur igitur tur W subtensae dupli circumferentiae GE ad subtensam dupli EA componitur ex ratione subtensae GZ ad subtensam dupli ZD, ex ratione subtensae dupli DB ad subtensam dupli BA.
His praemissis, Primum theorema sphaere κατὰ διαίρεσιν i. m. W describantur in superficie sphaerae maximorum circulorum circumferentiae, ita, ut in duas circumferentias AB et AG aliae duae inscriptae, scilicet, BE et GD secent se invicem in signo Z. Et sit quaelibet earum circumferentiarum minor semicirculo, id quod in omnibus similibus descriptionibus intelligendum est. Dico, quod ratio subtensae dupli circumferentiae GE ad subtensam dupli EA componitur ex ratione subtensae dupli GZ ad subtensam dupli ZD, et ex ratione subtensae dupli DB ad subtensam dupli BA. Adsumatur enim centrum sphaerae, et sit I, et a centro I ad sectiones circulorum B, Z, E, ducantur IB et IZ, et IE, et coniuncta AD protrahantur, et concurrat cum recta IB protracta in puncto T. Similiter autem coniunctae rectae DG et AG intersecent lineas IZ, et IE in signis K et L. Sunt igitur in una recta linea T, K, L signa. Sunt enim in duobus simul planis, scilicet, in triangulo AGD, et in circulo BZE, Quae quidem recta TKL coniuncta efficit, ut rectae lineae TL, et GD deductae in duas rectas TA, et GA secent se in puncto K. Ratio igitur rectae GL ad rectam LA composita est ex ratione rectae GK ad rectam KD, et ex ratione rectae DT ad rectam TA. Sed sicut est recta GL ad rectam LA, sic subtensa dupli circumferentiae GE ad subtensam dupli circumferentiae EA. Et sicut recta GK ad rectam KD, sic subtensa dupli circumferentiae GZ ad subtensam dupli ZD. Sicut etiam recta DT ad rectam TA, sic subtensa dupli circumferentiae BD ad subtensam dupli BA. Ratio igitur igitur tur W subtensae dupli circumferentiae GE ad subtensam dupli EA componitur ex ratione subtensae GZ ad subtensam dupli ZD, ex ratione subtensae dupli DB ad subtensam dupli BA.
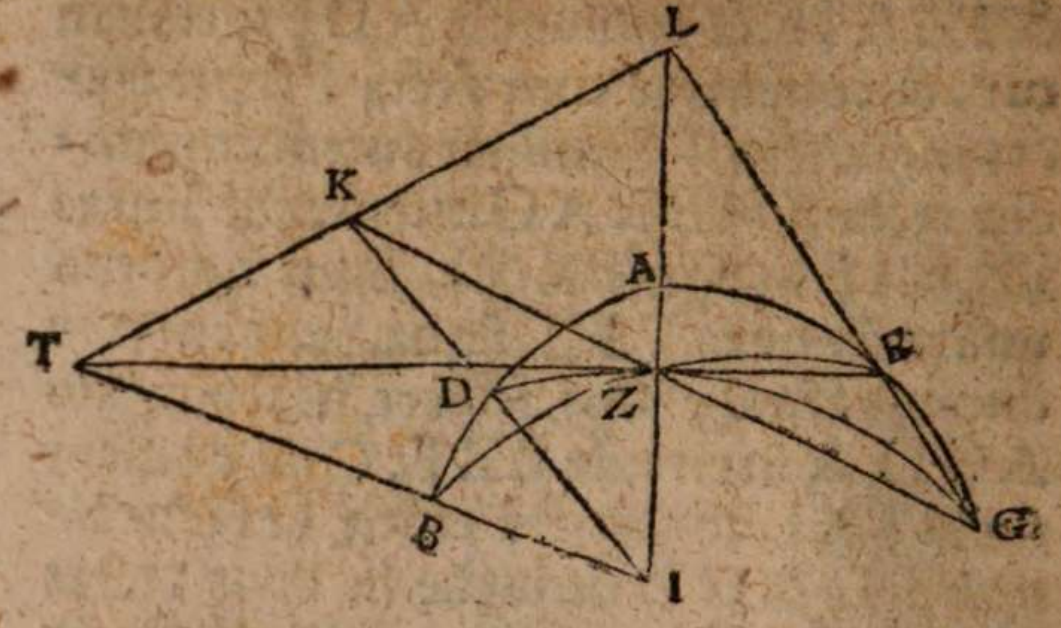 Et eodem modo, Alterum theorema sphaera κατὰ σύνθεσιν i. m. W sicut in plana descriptione rectarum linearum, demonstratur quod et ratio subtensae dupli GA ad subtensam dupli AE componitur ex ratione dupli GD ad subtensam dupli DZ, et ex ratione subtensae dupli ZB ad subtensam dupli ZB ad subtensam dupli BE. Quae prius erant demonstranda.
Et eodem modo, Alterum theorema sphaera κατὰ σύνθεσιν i. m. W sicut in plana descriptione rectarum linearum, demonstratur quod et ratio subtensae dupli GA ad subtensam dupli AE componitur ex ratione dupli GD ad subtensam dupli DZ, et ex ratione subtensae dupli ZB ad subtensam dupli ZB ad subtensam dupli BE. Quae prius erant demonstranda.
σχόλιον ex Theone. Dico quod ratio subtensae dupli circumferentiae GA ad subtensam dupli circunferentiae AE conponitur ex ratione subtensae dupli circunferentiae GD ad subtensam dupli circunferentiae DZ et ex ratione subtensae dupli ZB ad subtensam dupli BE. Coniunctae enim rectae GE et IA producantur et concurrant in signo L, similiter EZ, IB rectae coniunctae concurrant in signo T. Rursus denique GZ et ID coniunctae in signo K concurrant. Quoniam igitur signa T, K, L, sunt et in eo plano, in quo est triangulum GZE, propterea quod sunt in productis ipsius lateribus, et in plano illo etiam, in quo circulus ADB, quia sunt in lineis, quae ex centro eius producuntur, ideo signa T, K, L, sunt in communi sectione dictorum planorum, trianguli scilicet GZE et circuli ABD, ac propterea super eadem recta linea. Quare, si coniungatur haec recta T, K, L, existunt in duas GL, LT rectas deductae duae GK, TE secantes se in signo Z. Et sicut im primo rectilineo lemmatio κατὰ σύνθεσιν ratio GL ad LE componitur ex ratione GK ad KZ, ex ratione ZT ad TE. Ratio autem GL ad LE per tertium cyclicum lemmation eadem est rationi subtensae dupli circumferentiae GA ad subtensam dupli AE, ratio vero GK ad KZ eadem est rationi subtensae dupli circumferentiae GD ad subtensam dupli DZ. Ratio denique ZT ad TE eadem rationi subtensae dupli circumferentiae ZB ad subtensam dupli BE. Proinde ratio subtensae dupli circumferentiae GA ad subtensam dupli AE componitur ex ratione subtensae dupli GD ad subtensam dupli DZ et ex ratione subtensae dupli ZB ad subtensam dupli BE. Quod erat demonstrandum.
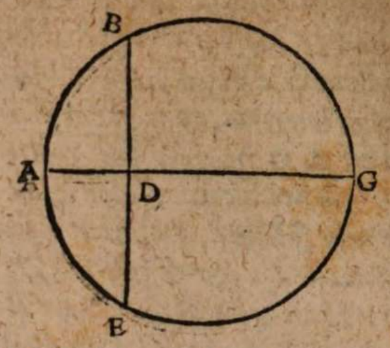 Recenset autem Theon plures casus seu πτώσεις huius posterioris theorematis κατὰ σύνθεσιν, quos casus nunc omitto. Sed addit postea Theon. Licet autem vel sine descriptione plani per rectas ex demonstratione κατὰ διαίρεσιν multo compendiosius ratiocinari demonstrationem circumferetiarum κατὰ σύνθεσιν, si breve hoc lemmation praemittatur. Esto semicirculus ABG super diametro AG, et accipiatur in circumferentia eius signum quodcunque B. Dico quod recta subtendens duplum circumferentiae AB subtendit et duplum circumferentiae BG, estque ex ipso diagrammate manifestum. Si enim absoluto circulo perpendicularem a B signo ad rectam BG actam produxerimus in E, recta BE subtendens circumferentiam BAE duplam circumferentiae BA subtendit etiam circumferentiam BGE duplam circumferentiae BG.
Recenset autem Theon plures casus seu πτώσεις huius posterioris theorematis κατὰ σύνθεσιν, quos casus nunc omitto. Sed addit postea Theon. Licet autem vel sine descriptione plani per rectas ex demonstratione κατὰ διαίρεσιν multo compendiosius ratiocinari demonstrationem circumferetiarum κατὰ σύνθεσιν, si breve hoc lemmation praemittatur. Esto semicirculus ABG super diametro AG, et accipiatur in circumferentia eius signum quodcunque B. Dico quod recta subtendens duplum circumferentiae AB subtendit et duplum circumferentiae BG, estque ex ipso diagrammate manifestum. Si enim absoluto circulo perpendicularem a B signo ad rectam BG actam produxerimus in E, recta BE subtendens circumferentiam BAE duplam circumferentiae BA subtendit etiam circumferentiam BGE duplam circumferentiae BG.
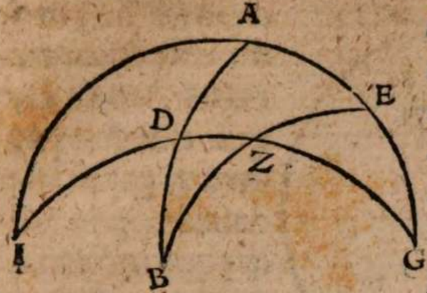 Hoc praemisso, exponatur circumferentiarum descriptio, et compleantur semicirculi GAI et GDI. Quoniam igitur in duas EI et EB circumferentias duae sunt deductae IDZ et BDA secantes se in signo D, ratio subtensae dupli circumferentiae IA ad subtensam dupli AE componitur ex ratione subtensae dupli ID ad subtensam dupli DZ et ex ratione subtensae dupli ZB ad subtensam dupli BE. Hoc enim demonstratum est. Sed subtendens duplum circumferentiae IA subtendit etiam duplum circunferentiae AG, quae reliqua est de toto circulo, atque subtensa dupli circumferentiae ID subtendit etiam duplum circumferentiae GD. Quare ratio subtensae dupli GA ad subtensam dupli AE componitur ex ratione subtensae GD ad subtensam dupli DZ et ex ratione subtensae dupli ZB ad subtensam dupli BE. Caetera Theonis nunc etiam omittimus.
Hoc praemisso, exponatur circumferentiarum descriptio, et compleantur semicirculi GAI et GDI. Quoniam igitur in duas EI et EB circumferentias duae sunt deductae IDZ et BDA secantes se in signo D, ratio subtensae dupli circumferentiae IA ad subtensam dupli AE componitur ex ratione subtensae dupli ID ad subtensam dupli DZ et ex ratione subtensae dupli ZB ad subtensam dupli BE. Hoc enim demonstratum est. Sed subtendens duplum circumferentiae IA subtendit etiam duplum circunferentiae AG, quae reliqua est de toto circulo, atque subtensa dupli circumferentiae ID subtendit etiam duplum circumferentiae GD. Quare ratio subtensae dupli GA ad subtensam dupli AE componitur ex ratione subtensae GD ad subtensam dupli DZ et ex ratione subtensae dupli ZB ad subtensam dupli BE. Caetera Theonis nunc etiam omittimus.
〈I.12〉 CAPUT XII: de circumferentiis inter aequinoctialem et obliquum circulum
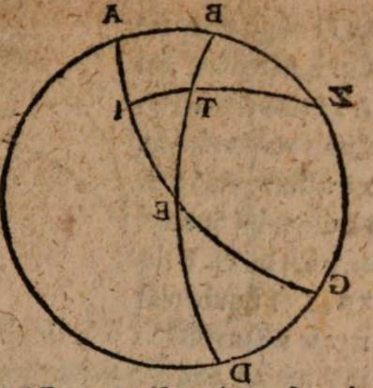 Exposito supra hoc theoremate, primam demonstrationem circumferentiarum, circumferen rentiarum W quas titulus proponit, faciemus hoc modo. Sit enim circulus ABGD qui transit per utrumque polum, videlicet per polum aequinoctialis et per polum eius qui est per medium signorum, et semicirculus circuli aequinoctialis sit AEG, semicirculus vero eius qui est per medium signorum BED, et punctum E sit communis intersectio in aequinoctio verno, ut B sit punctum tropicum brumale, D vero solstitiale. Sumatur autem in circumferentia ABG polus circuli aequinoctialis AEG, et sit punctum Z, et decidatur EI circumferentia eius qui est per medium signorum, supponaturque talium esse 30 partium, qualium maximus circulus est 360. Ac describatur per puncta Z, I circumferentia maximi circuli ZIT, sitque propositum circumferentiam IT invenire. Porro hic dictum sit de omnibus similibus demonstrationibus, ne saepius idem in singulis repeti oporteat, quoties incidit mentio de quantitate circumferentiarum aut rectarum linearum, quot sint partium vel portionum, universaliter in circumferentis tales partes intelligimus, Partes circumferentiae et diametri i. m. W qualium est circumferentia maximi circuli partium 360, in rectis vero tales, qualium est diameter 120. Ratiocinatur ex altero theoremate sphaerico, scilicet, κατὰ σύνθεσιν i. m. W Quoniam ergo in descriptione maximorum circulorum in duas circumferentias AZ et AE inscriptae sunt duae circumferentiae ZT et EB, quae sese intersecant in puncto I, sequitur rationem subtensae dupli ZA ad subtensam dupli AB componi ex ratione subtensae dupli ZT ad subtensam dupli TI et ex ratione subtensae dupli IE ad subtensam dupli EB. Porro duplum circumferentiae ZA est partium 180, et recta ei subtensa portionum 120, duplum vero circumferentiae AB secundum rationem 83 ad 11, sicut convenit nobis cum Eratosthene, partium est 47, scrupulorum 42, secundorum 40, recta vero ei subtensa portionum 48, scrupulorum 31, secundorum 55. Rursus duplum circumferentiae IE partium est 60, et recta ei subtensa portionum 60, duplum vero circumferentiae EB partium 180, et recta ei subtensa portionum 120. Si igitur a ratione quae est 120 ad portiones 48, scrupulorum 31, secundorum 55, auferamus rationem quae est 60 ad 120, relinquetur ratio subtensae dupli ZT ad subtensam dupli TI, quae est ratio 120 ad portiones 24, scrupula 15, secunda 57. Duplum autem circumferenttae ZT est partium 180, et recta ei subtensa portionum 120. Ergo et subtensa dupli TI est earundem portionum 24, et scrupulorum 15, secundorum 57. ltaque et duplum circumferentiae TI est partium 23, scrupulorum 19, secundorum 59. Circumferentia autem TI est earundem partium 11, scrupulorum 40 proxime.
Exposito supra hoc theoremate, primam demonstrationem circumferentiarum, circumferen rentiarum W quas titulus proponit, faciemus hoc modo. Sit enim circulus ABGD qui transit per utrumque polum, videlicet per polum aequinoctialis et per polum eius qui est per medium signorum, et semicirculus circuli aequinoctialis sit AEG, semicirculus vero eius qui est per medium signorum BED, et punctum E sit communis intersectio in aequinoctio verno, ut B sit punctum tropicum brumale, D vero solstitiale. Sumatur autem in circumferentia ABG polus circuli aequinoctialis AEG, et sit punctum Z, et decidatur EI circumferentia eius qui est per medium signorum, supponaturque talium esse 30 partium, qualium maximus circulus est 360. Ac describatur per puncta Z, I circumferentia maximi circuli ZIT, sitque propositum circumferentiam IT invenire. Porro hic dictum sit de omnibus similibus demonstrationibus, ne saepius idem in singulis repeti oporteat, quoties incidit mentio de quantitate circumferentiarum aut rectarum linearum, quot sint partium vel portionum, universaliter in circumferentis tales partes intelligimus, Partes circumferentiae et diametri i. m. W qualium est circumferentia maximi circuli partium 360, in rectis vero tales, qualium est diameter 120. Ratiocinatur ex altero theoremate sphaerico, scilicet, κατὰ σύνθεσιν i. m. W Quoniam ergo in descriptione maximorum circulorum in duas circumferentias AZ et AE inscriptae sunt duae circumferentiae ZT et EB, quae sese intersecant in puncto I, sequitur rationem subtensae dupli ZA ad subtensam dupli AB componi ex ratione subtensae dupli ZT ad subtensam dupli TI et ex ratione subtensae dupli IE ad subtensam dupli EB. Porro duplum circumferentiae ZA est partium 180, et recta ei subtensa portionum 120, duplum vero circumferentiae AB secundum rationem 83 ad 11, sicut convenit nobis cum Eratosthene, partium est 47, scrupulorum 42, secundorum 40, recta vero ei subtensa portionum 48, scrupulorum 31, secundorum 55. Rursus duplum circumferentiae IE partium est 60, et recta ei subtensa portionum 60, duplum vero circumferentiae EB partium 180, et recta ei subtensa portionum 120. Si igitur a ratione quae est 120 ad portiones 48, scrupulorum 31, secundorum 55, auferamus rationem quae est 60 ad 120, relinquetur ratio subtensae dupli ZT ad subtensam dupli TI, quae est ratio 120 ad portiones 24, scrupula 15, secunda 57. Duplum autem circumferenttae ZT est partium 180, et recta ei subtensa portionum 120. Ergo et subtensa dupli TI est earundem portionum 24, et scrupulorum 15, secundorum 57. ltaque et duplum circumferentiae TI est partium 23, scrupulorum 19, secundorum 59. Circumferentia autem TI est earundem partium 11, scrupulorum 40 proxime.
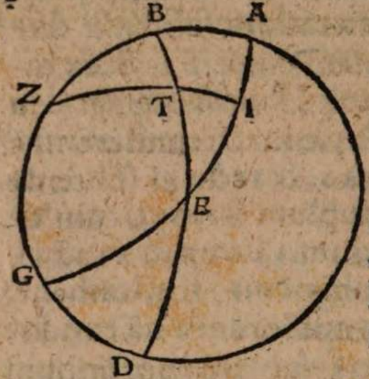 Rursus supponatur circumferentia EI partium esse 60, erit igitur, aliis non mutatis, duplum circumferentiae EI partium 120, recta vero ei subtensa portionum 103, scrupulorum 55, secundorum 23. Si ergo rursus a ratione quae est 120 ad portiones 48, scrupulorum 31, secundorum 55, subtrahamus rationem quae est iter. W portionum 103, scrupulorum 55, secundorum 23 ad portiones 120, relinquetur ratio quae est subtensae dupli ZT ad subtensam dupli TI, videlicet ratio 120 ad portiones 42, scupulorum 1, secundorum 48, estque subtensa dupli ZT portionum 120, quare et subtensa dupli TI earundem est portionum 42, scrupulorum 1, secundorum 48. Ergo et dupla circumferentia TI partium est 41, scrupulorum 0, secundorum 18, ipsa vero circumferentia TI earundem partium 20, scrupulorum 30, secundorum 9. Quod erat demonstrandum.
Rursus supponatur circumferentia EI partium esse 60, erit igitur, aliis non mutatis, duplum circumferentiae EI partium 120, recta vero ei subtensa portionum 103, scrupulorum 55, secundorum 23. Si ergo rursus a ratione quae est 120 ad portiones 48, scrupulorum 31, secundorum 55, subtrahamus rationem quae est iter. W portionum 103, scrupulorum 55, secundorum 23 ad portiones 120, relinquetur ratio quae est subtensae dupli ZT ad subtensam dupli TI, videlicet ratio 120 ad portiones 42, scupulorum 1, secundorum 48, estque subtensa dupli ZT portionum 120, quare et subtensa dupli TI earundem est portionum 42, scrupulorum 1, secundorum 48. Ergo et dupla circumferentia TI partium est 41, scrupulorum 0, secundorum 18, ipsa vero circumferentia TI earundem partium 20, scrupulorum 30, secundorum 9. Quod erat demonstrandum.
Eodem modo et in particularibus circumferentiis quantitates computando faciemus canonem quadrantis, videlicet 90 partium, qui continebit adpositas quantitates circumferentiarum similium demonstratis.
Sequitur canon.
CIRCUMFERENTIAE |
|||||||
zodiaci |
meridanorum |
zodiaci |
meridianorum |
||||
Part. |
Part. |
scru. |
sec. |
part. |
part. |
scr. |
sec. |
46 |
16 |
54 |
48 |
68 |
22 |
1 |
24 |
47 |
17 |
12 |
16 |
69 |
22 |
11 |
0 |
48 |
17 |
29 |
26 |
70 |
22 |
20 |
11 |
49 |
17 |
46 |
19 |
71 |
22 |
28 |
56 |
50 |
18 |
2 |
53 |
72 |
22 |
37 |
16 |
51 |
18 |
19 |
7 |
73 |
22 |
45 |
11 |
52 |
18 |
35 |
3 |
74 |
22 |
52 |
40 |
53 |
18 |
50 |
39 |
75 |
22 |
59 |
42 |
54 |
19 |
5 |
54 |
76 |
23 |
6 |
18 |
55 |
19 |
20 |
50 |
77 |
23 |
12 |
28 |
56 |
19 |
35 |
25 |
78 |
23 |
18 |
11 |
57 |
19 |
49 |
38 |
79 |
23 |
23 |
27 |
58 |
20 |
3 |
31 |
80 |
23 |
28 |
16 |
59 |
20 |
17 |
1 |
81 |
23 |
32 |
38 |
60 |
20 |
30 |
9 |
82 |
23 |
36 |
33 |
61 |
20 |
42 |
55 |
83 |
23 |
40 |
1 |
62 |
20 |
55 |
18 |
84 |
23 |
43 |
1 |
63 |
21 |
7 |
19 |
85 |
23 |
45 |
33 |
64 |
21 |
18 |
56 |
86 |
23 |
47 |
38 |
65 |
21 |
30 |
9 |
87 |
23 |
49 |
15 |
66 |
21 |
40 |
58 |
88 |
23 |
50 |
25 |
67 |
21 |
51 |
23 |
89 |
23 |
51 |
6 |
90 |
23 |
51 |
20 |
||||
CIRCUMFERENTIAE |
|||||||
zodiaci |
meridianorum |
zodiaci |
meridianorum |
||||
Partes |
part. |
scru. |
sec. |
par. |
par. |
scr. |
sec. |
1 |
0 |
24 |
16 |
23 |
9 |
5 |
32 |
2 |
0 |
48 |
31 |
24 |
9 |
28 |
5 |
3 |
1 |
12 |
46 |
25 |
9 |
50 |
29 |
4 |
1 |
37 |
0 |
26 |
10 |
12 |
46 |
5 |
2 |
1 |
12 |
27 |
10 |
34 |
47 |
6 |
2 |
25 |
22 |
28 |
10 |
56 |
41 |
7 |
2 |
49 |
30 |
29 |
11 |
18 |
25 |
8 |
3 |
13 |
35 |
30 |
11 |
39 |
59 |
9 |
3 |
37 |
37 |
31 |
12 |
1 |
21 |
10 |
4 |
1 |
36 |
32 |
12 |
22 |
31 |
11 |
4 |
25 |
32 |
33 |
12 |
43 |
29 |
12 |
4 |
49 |
24 |
34 |
13 |
4 |
15 |
13 |
5 |
13 |
11 |
35 |
13 |
24 |
48 |
14 |
5 |
36 |
53 |
36 |
13 |
45 |
7 |
15 |
6 |
0 |
31 |
37 |
14 |
5 |
13 |
16 |
6 |
24 |
1 |
38 |
14 |
25 |
4 |
17 |
6 |
47 |
26 |
39 |
14 |
44 |
42 |
18 |
7 |
10 |
45 |
40 |
15 |
4 |
5 |
19 |
7 |
33 |
67 |
41 |
15 |
23 |
12 |
20 |
7 |
57 |
2 |
42 |
15 |
42 |
4 |
21 |
8 |
20 |
0 |
43 |
16 |
0 |
40 |
22 |
8 |
42 |
50 |
44 |
16 |
18 |
59 |
45 |
16 |
37 |
2 |
||||
〈I.13〉 CAPUT XIII: De ascensionibus in recta sphaera
Sequitur deinceps, ut una demonstremus quantitates circumferentiarum circuli aequinoctialis factas a circulis qui transeunt per polos aequinoctialis et per quaecunque segmenta obliqui circuli proposita. Sic enim habebimus, in quot temporibus aequinoctialibus segmenta circuli qui est per medium signorum pertranseant meridianum ubique, propterea quod is horizon solus tunc describitur per polos aequinoctialis.
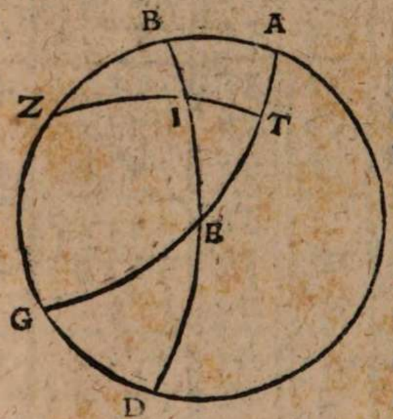 Proponatur Partes 30 Zodiaci. Ratiocinatur ex primo theoremate sphaerico, scilicet, κατὰ διάιρεσιν i. m. W ergo figura prius descripta, et data rursus circumferentia EI obliqui circuli, primum 30 partium, invenienda sit circumferentia aequinoctialis ET. Itaque eodem modo, ut supra, ratio subtensae dupli ZB ad subtensam dupli BA componitur ex ratione subtensae dupli ZI ad subtensam dupli IT et ex ratione subtensae dupli TE ad subtensam dupli EA. Sed duplum circumferentiae ZB est partium 132, scrupulorum 17, secundorum 20, et eius subtensa portionum expositarum 109, scrupulorum 44, secundorum 53. Duplum autem circumferentiae AB est partium 47, scrupulorum 42, secundorum 40, et eius subtensa portionum 48, scrupulorum 31, secundorum 55. Duplum vero circumferentiae ZI est partium 156, scrupulorum 40, secundorum 1, et eius subtensa portionum 117, scrupulorum 31, secundorum 15. Duplum vero circumferentiae IT est partium 23, scrupulorum 19, secundorum 59, et eius subtensa portionum 24, scrupulorum 15, secundorum 57. Si igitur a ratione quae est portionum 109, scrupulorum 44, secundorum 53 ad portiones 48, scrupula 31, secunda 55, auferamus rationem quae est portionum 117, scrupulorum 31, secundorum 15 ad portiones 24, scrupulorum 15, secundorum 57, relinquetur nobis ratio quae est subtensae dupli TE ad subtensam dupli EA, videlicet portionum 54, scrupulorum 52, secundorum 26 ad portiones 117, scrupulorum 31, secundorum 15, estque eadem ratio, quae est portionum 56, scrupulorum 1, secundorum 53, ad portiones 120. Cum autem duplum circumferentiae EA sit partium 180, et eius subtensa 120, sequitur et subtensam dupli TE esse iter. W subtensam portionum 56, scrupulorum 1, secundorum 53. Quare duplum circumferentiae ET erit partium 55 scrupulorum 40 proxime, et circumferentia TE earundum 27 partium scrupulorum primorum 50.
Proponatur Partes 30 Zodiaci. Ratiocinatur ex primo theoremate sphaerico, scilicet, κατὰ διάιρεσιν i. m. W ergo figura prius descripta, et data rursus circumferentia EI obliqui circuli, primum 30 partium, invenienda sit circumferentia aequinoctialis ET. Itaque eodem modo, ut supra, ratio subtensae dupli ZB ad subtensam dupli BA componitur ex ratione subtensae dupli ZI ad subtensam dupli IT et ex ratione subtensae dupli TE ad subtensam dupli EA. Sed duplum circumferentiae ZB est partium 132, scrupulorum 17, secundorum 20, et eius subtensa portionum expositarum 109, scrupulorum 44, secundorum 53. Duplum autem circumferentiae AB est partium 47, scrupulorum 42, secundorum 40, et eius subtensa portionum 48, scrupulorum 31, secundorum 55. Duplum vero circumferentiae ZI est partium 156, scrupulorum 40, secundorum 1, et eius subtensa portionum 117, scrupulorum 31, secundorum 15. Duplum vero circumferentiae IT est partium 23, scrupulorum 19, secundorum 59, et eius subtensa portionum 24, scrupulorum 15, secundorum 57. Si igitur a ratione quae est portionum 109, scrupulorum 44, secundorum 53 ad portiones 48, scrupula 31, secunda 55, auferamus rationem quae est portionum 117, scrupulorum 31, secundorum 15 ad portiones 24, scrupulorum 15, secundorum 57, relinquetur nobis ratio quae est subtensae dupli TE ad subtensam dupli EA, videlicet portionum 54, scrupulorum 52, secundorum 26 ad portiones 117, scrupulorum 31, secundorum 15, estque eadem ratio, quae est portionum 56, scrupulorum 1, secundorum 53, ad portiones 120. Cum autem duplum circumferentiae EA sit partium 180, et eius subtensa 120, sequitur et subtensam dupli TE esse iter. W subtensam portionum 56, scrupulorum 1, secundorum 53. Quare duplum circumferentiae ET erit partium 55 scrupulorum 40 proxime, et circumferentia TE earundum 27 partium scrupulorum primorum 50.
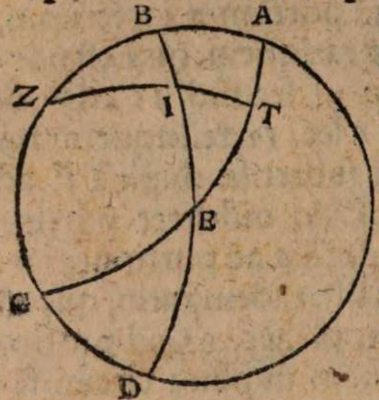 Rursus Partes 60 zodiaci i. m. W supponatur EI circumferentia partium 60, erit igitur, reliquis non mutatis, duplum circumferentiae ZI partium 138, scrupulorum 59, secundorum 42, et eius subtensa portionum 112, scrupulorum 23, secundorum 56. Duplum vero circumferentiae IT partium 41, scrupulorum 0, secundorum 18, et eius subtensa portionum 42, scrupulorum 1, secundorum 48. Si igitur a ratione quae est portionum 109, scrupulorum 44, secundorum 53 ad portiones 48, scrupulorum 31, secundorum 55, auferamus rationem quae est portionum 112, scrupulorum 23, secundorum 56 ad portiones 42, scrupulorum 1, secundorum 48, relinquetur ratio subtensae dupli TE ad subtensam dupli EA, videlicet, ratio quae est portionum 95, scrupulorum 2, secundorum 40 ad portiones 112, scrupula 23, secunda 56, eademque est ratio quae est portionum 101, scrupulorum 28, secundorum 20 ad portiones 120. Porro subtensa dupli circumferentiae EA est portionum 120, quare et subtensa dupli TE est earundem portionum 101, scrupulorum 28, secundorum 20. Duplum vero circumferentiae TE erit partium 115, scrupulorum 28 proxime. Ipsa vero circumferentia TE earundem partium 57, scrupulorum 44.
Rursus Partes 60 zodiaci i. m. W supponatur EI circumferentia partium 60, erit igitur, reliquis non mutatis, duplum circumferentiae ZI partium 138, scrupulorum 59, secundorum 42, et eius subtensa portionum 112, scrupulorum 23, secundorum 56. Duplum vero circumferentiae IT partium 41, scrupulorum 0, secundorum 18, et eius subtensa portionum 42, scrupulorum 1, secundorum 48. Si igitur a ratione quae est portionum 109, scrupulorum 44, secundorum 53 ad portiones 48, scrupulorum 31, secundorum 55, auferamus rationem quae est portionum 112, scrupulorum 23, secundorum 56 ad portiones 42, scrupulorum 1, secundorum 48, relinquetur ratio subtensae dupli TE ad subtensam dupli EA, videlicet, ratio quae est portionum 95, scrupulorum 2, secundorum 40 ad portiones 112, scrupula 23, secunda 56, eademque est ratio quae est portionum 101, scrupulorum 28, secundorum 20 ad portiones 120. Porro subtensa dupli circumferentiae EA est portionum 120, quare et subtensa dupli TE est earundem portionum 101, scrupulorum 28, secundorum 20. Duplum vero circumferentiae TE erit partium 115, scrupulorum 28 proxime. Ipsa vero circumferentia TE earundem partium 57, scrupulorum 44.
Demonstratum est igitur Ascensiones trium duodecimarum unius quadrantis i. m. W quod prima duodecima pars circuli qui est per medium signorum coascendit cum partibus aequinoctialis 27, scrupulis 50 iuxta expositum modum. Secunda vero pars duodecima ascendit cum partibus aequinoctialis 29, scrupulis 54. Nam demonstratum est, utranque cum partibus aequinoctialis 57, scrupulis 44. Tertia vero duodecima ascendit cum residuis partibus quadrantis aequinoctialis 32, scrupulis 16, quia aequali tempore ascendit totus quadrans obliqui circuli cum toto quadrante aequinoctialis, eo quod hi quadrantes a circulis qui describuntur per polos aequinoctialis aequaliter intercipiantur.
Eodem modo sequentes traditam demonstrationem computavimus, quantum de aequinoctiali coascendat cum singulis decem partibus obliqui circuli, quia in minoribus portionibus non percipitur differentia digna animadversione, sed pene aequalia sunt incrementa excessuum. Has igitur decades exponemus, Recenset decades unius quadrantis i. m. W ut sint in promptu, videlicet quot temporibus, quaelibet earum meridianum ubique et horizontem in sphaera recta transeat. Ac initium sumemus a prima decade, quae in puncto aequinoctiali incipit. Prima igitur decas continet tempora 9, scrupula 10, secunda 9 tempora, 15 scrupula, tertia 9 tempora, 25 scrupula prima. Unde colliguntur cum primo duodenario coascendere tempora 27, scrupula 50. Quarta vero decas continet tempora 9, scrupula 40, quinta continet tempora 9, scrupula 58, sexta continet tempora 10, scrupula 16. Colliguntur ergo cum secundo duodenario coascendere tempora 29, scrupula 54. Septima vero decas continet tempora 10, scrupula 34, octava continet tempora 10, scrupula 47, nona continet continet tempora 10, scrupula 55. Colliguntur ergo rursus cum tertio duodenario, qui exit ad solstitialia puncta coascendere tempora 32, scrupula 16. Atque ita cum toto quadrante continenter tempora 90. Manifestum est autem inde eundem esse ordinem reliquorum quadrantum, De reliquis quadrantibus zodiaci i. m. W quia eadem omnia iuxta unumquenque ipsorum contingunt. Sphaeram enim rectam esse subiicimus, hoc est in qua aequinoctialis nusquam ad horizontem inclinat.
Ad Lectorem studiosum. Deo iuvante, in proxima aeditione hanc institutam explicationem nostram rudiorem perpoliemus, et adiungemus reliqua ex Theone, quae ad Ptolemaei sententiam penitus intelligendam aliquid momenti adferunt. Interea bene vale, et hisce feliciter fruere.
Laus Deo.


