GEBRI FILII AFFLA HISPALENSIS, DE ASTRONOMIA LIBRI IX. IN QUIbus Ptolemaeum, alioqui doctissimum, emendauit: alicubi etiam industria superauit. omnibus Astronomiae studiosis haud dubie utilissimi futuri. foeliciter incipiunt.

⟨I⟩ LIBER PRIMVS continens quaedam elementa Geometrica, ad Astronomiam necessaria, nusquam alias obuia, sed ab ipso autore summa industria in lucem prodita.

⟨I.0a⟩ PROOEMIVM.

SCIENTIA species habet, quarum melior, post scientiam fidei, est, cuius scita fixa sunt, remanentia inalterata. et sunt uiae perducentes ad scientiam eorum, uiae necessariae, in quibus non est dubitatio, ducentes incedentem per eas ad ueritatem necessariam. Scientia itaque formae motuum Solis et Lunae et stellarum, et cognitionis orbium earum, et quod sequitur inde, est scientia melior pluribus alijs, propter aggregationem modorum meliorationis in ea. Eius namque scita fixa sunt, remanentia non alterata, usque ad horam in qua Deus illud praecipiet eis. Et uiae perducentes ad sciendum ea, sunt manifeste necessariae. Peruenit ergo ad eam melioratio ex modis. Ptolemaeus quidem Pheludensis aggregauit ea, quae comprehenderunt antiqui huius scientiae professores ante ipsum, et adiunxit ad ea, illa, quae ipse comprehendit post eos. et scripsit omnia illa in libro suo, qui nominatur Almagesti. et ipse quidem fuit nobis magni doni dominus, et maximae munificentiae largitor. Et factus est liber ille eius, comprehendens omnes intentiones huius scientiae. At uero est difficilis studenti in ipso, propter intentiones diuersas de quibus est, quod ipse aggregat Scientiam et Operationem. Quia fit necessarium ex uia operationis, multiplicare numeros quosdam in alios, et diuidere alios per alios, et inuenire radices eorum, et decenter praeparare tabulas, quae in operatione exercentur: quapropter prolongatur liber, et diuiditur scientia in ipso, et permiscetur cum operatione, quare fit difficilis legenti ipsum. Et de eis est, quod ipse utitur in plurimo suarum probationum figura sectore, quae est difficilis, et partitur in ramos plurimos, et diuersificatur in ea compositio proportionis uarietate extranea, quapropter fit difficilis aspicienti in ipso rememoratio eius, et ipsius comprehensio, et concludere eam quae concluduntur ex ea. Et de eis est etiam, quod ipse procedit in demonstrationibus suis secundum librum Theodosij et Milei, qui ambo sunt difficiles et graues, ita quod non praeparatur quaerenti et studenti cognitio eorum, et exercitatio in eis et in figura sectore, in minore spacio unius anni integri, quare quandoque pigritatur post illud, aut abscidit ipsum tempus ab introitu in librum. Et de eis est, quod ipse abbreuiauit sermonem suum in locis pluribus, qua difficile fit intelligere ea, et haesitat aspiciens in eo ambiguitate maxima, ita quod quandoque perducit eum illud ad pigritiam. Et de eis est, quod propter permutationem interpretum ipsius de lingua ad linguam accidit in eo antecessio et postpositio uerborum, et separatio inter intentiones eius, quod facit ambiguum lectorem, et haesitare, cum non possit componere intentiones quaesitas propter separationem earum, quare illud remouet cum quandoque ab assiduatione in aspiciendo. Nobis uero accidit ex amore huius scientiae, et dilectione eius propter res quas diximus, et propter ea, quae etiam ipse dixit in principio sui libri de rebus perducentibus ad amorem et studium eius, quod duxit nos ad assiduandam considerationem in eo, et tolerandum laborem et difficultatem accidentem legenti ipsum, usquequo peruenerunt ad nos per gratiam Dei, omnia quae comprehendit liber iste de scientia Astrologiae. Et non cessaui post illud assiduare considerationem, et continuare inquisitionem et cognitionem in eis, quibus possibile est, ut facilis fiat incessus huius scientiae magnae, et quibus proximus fiat intellectus libri huius magni. Acciderunt ergo nobis per gratiam Dei et bonitatem auxilij eius, propositiones faciles et breues, quibus excusamur a libro Milei, et a figura sectore, et a plurimo libri Theodosij. Et quibus extrahitur ignotum ex noto per quatuor numeros proportionales, non per sex numeros compositos, sicut praeparantur in figura sectore. Quamobrem fit facilis extractio ignoti ex noto, cum indigeamus in ea notis paucioribus, et fit per illis comprehensio eius facilis, incessus paucae inuolutionis et consolidationis. Et accidit in istis propositionibus quae diximus, de facilitate notorum in eis, et paucitate diuersitatis in compositione proportiones earum, quod ipsae perducunt ad uerificationem in omni quaesito, in quo administratur. Et non est necessarium cum eis uti lineis rectis, et angulis eorum, loco arcuum et angulorum suorum, sicut fecit Ptolemaeus in suo libro. Cum non fuerit possibile ei nisi illud, ut ingrediatur in hoc de propinquitate, quod non occultatur. Et ipse utitur in eis considerationibus quibus indiguit instrumentis quatuor, in quibus necessariae sunt armillae octo. Nobis autem accidit instrumentum unum, in quo non est necessaria nisi armilla una, et quarta alia, et regula. Et excusamur ab omnibus instrumentis, quae ipse dixit, et indiguit in cognitione quantitatis declinationis orbis Lunae decliuis ab orbe signorum consideratione, in regione cuius latitudo esset quasi triginta partes, ipsa existente in medietate diei, in parte Septentrionali, et loco eius uero ab orbe signorum in puncto tropici aestiui, et possibilis est eius consideratio cum hoc intrumento in omni terra. Et dixit etiam, quod centrum orbis deferentis trium stellarum superiorum, diuidit lineam quae est inter centrum motus aequalis, et inter centrum orbis signorum, in duo media. Et posuit illud ex rebus quae assumuntur absolute, cum non fuerit ei possibilis uia, qua perueniret ad cognitionem illius per demonstrationem. Nobis autem accidit per gratiam Dei uia, qua peruenimus ad cognitionem illius per demonstrationem manifestam. Et postquam considerationem ad ultimum perduximus, apparuit nobis, quod accidit ei, quod et uulgo accidit de diminutione propria naturae hominis. Quare laudatus sit singularis cum integritate, cuius nomen est sublime. Et illud est, quod diximus nuper de defectu eius, inuenimus cum errasse in locis pluribus libri sui, errore a quo excusari non potest. Et hoc est, quoniam eius demonstratio et operatio sunt fabricatae super errorem. Et postquam uidimus illud, perduxerunt nos omnia quae diximus ad componendum hunc librum. Quare praemisimus de libro Theodosij ea, quorum intellectus proximus est, et assumptio facilis, et adduximus demonstrationes super ea, ut liber sit stans per se, non indigens alio, nisi libro Euclidis, cum ab eo non excusetur. Et addimus ad ea propositiones, quae apparuerunt nobis, et quae uidimus esse praemittenda libro suo. Et ad omnia illa fecimus singularem tractatum, quem posuimus primum, et est adeo propinquus et facilis, quod possibile est consideranti in eo, ut sciat ipsum in hebdomada una. Et denudauimus in ipso Scientiam ab Operatione, et abbreuiauimus ipsum. Et conneximus alia alijs, cum lucrum libri Ptolemaei non sit nisi Scientia tantum, quoniam Operatio in ipso non est possibilis nunc propter causas multas. propterea expoliauerunt posteriores operationes eius in canonibus, quare sit facilioris comprehensionis. Explanauimus autem et exposuimus loca, in  quibus ipse abbreuiauit sermonem, secundum quantitatem qua potuimus, et attulimus demonstrationes super ea, quae ipse absolute sine demonstratione posuit, cum non fuerit possibilis demonstratio super ea. Et quia necessaria fuit inquisitio ueritatis, et facere ipsam uincere et apparere, et ut non timeatur ille, qui deuiat ab ea, quamuis sit magnus. Et imitauimus in hoc Aristotelem, cum intendit redire super magistrum suum Platonem, dixit excusando, Veritas et Plato ambo sunt amici, sed ueritas est magis amica. Visum est nobis, ut numeremus intentiones in quibus errauit, et dicamus loca earum in libro nostro hoc, ut perueniat ad ea facile qui uoluerit scire. Quod si fuerit uerum quod diximus, tunc lucrabitur ipse scientiam, et lucrabimur nos misericordiam. Sed si fuerit falsum, erit ei necessarium ut tueatur ueritatem, et reducat nos ex unda ignorantiae, et faciat nos lucrari scientiam, et lucretur ipse misericordiam et gratiam. et Deus sublimis perducet ad illud quod rectius est sua pietate. Ex illis itaque est, quoniam ipse errauit in capitulo secundo tractatus quarti libri sui, in temporibus Lunae reuolutionibus. Et errauit etiam in capitulo decimo tractatus quinti. et ego dixi illa ambo in tractatu quarto huius nostri libri. Et errauit in terminis eclipsium Solarium. et errauit in aequatione eclipsis Lunaris, et errauit in aequatione eclipsis Solaris, et in temporum eius quantitate, et omnia illa dicta sunt in tract. 5. huius nostri. Et errauit etiam in aequatione eclipsis Solaris, in definiendo diuersitatem aspectus Lunae in latitudine, quoniam adiunxit illud ad orbem signorum. Et non oportet nisi ut adiungat illud ad Lunam. et hoc est ex eis quae ego non dixi. quoniam non est necessarium nisi in compositione tabularum, quibus aequatur eclipsis Solaris, et est ex rebus operationis. Et errauit in principio tractatus noni sui libri, in hoc quod posuit ordinem duorum orbium Veneris et Mercurij sub orbe Solis. Nam illud quod dant radices suae, est, quod ambo sunt supra orbem Solis necessario. Et similiter errauit in sermone suo, quod ambo non uadunt per lineas, quae transeunt per uisus nostros et per Solem. Et errauit in inuentione longitudinis longioris Veneris et Mercurij, quoniam conuertit figuram tertiam et quartam capituli 8. tract. 9. libri sui. Et sunt ambae ex eis quae non conuertuntur. quia non intellexit, quid uoluerunt antiqui per longitudines oppositas duabus stellis, scilicet Veneris et Mercurij. Et errauit in hoc, quod posuit unamquanque linearum duarum k e et t e figurae quartae illius capituli, medietatem diametri orbis deferentis Mercurium, et non est ita, et illa sunt in tract. 7. huius. Et errauit in extractione duorum punctorum stationis stellae de stellis currentibus. Et errauit in hoc, quod posuit super fluitatem arcuum retrogradationis stellae secundum super fluitatem longitudinum centri orbis reuolutionis ex centro orbis signorum, et non est res ita. Et errauit, ponens considerationes stellae aequales absolute. et non est ita. Et errauit in terminando stationem stellae, et in quantitate temporis retrogradationis eius, ita quod possibile est, ut ingrediatur per illum errorem in tempore retrogradationis stellae Martis solum quasi 18. dies, et in tempore retrogradationis stellae Veneris quasi duo dies et dimidius, et non accidit illud nisi in superfluitate temporis. Sed secundum plurimum errorem in tempore retrogradationis harum duarum stellarum apparens manifestus sensui: in alijs uero ab eis duobus occultatur quantitas erroris, propter intentiones, quas dicendi hic non est locus. et omnia illa dicta sunt in tract. 8. huius. Et errauit in figura undecima tractatus tertij, decimi libri sui, et est in figura quarta tract. 9. huius nostri libri. Et rectificauimus omnia quae diximus in quibus errauit, et a summo Deo quaero tutamen ab errore et deuiatione, et ducatum ad ueritatem, in omni sermone et operatione, cum eius auxilio, cuius socius non est. Et hic incipio praemittere illa, quorum praemissio necessaria est.

⟨I.0b⟩ DIFFINITIONES.

ET incipiamus exponere intentiones nominum usitatorum in eo. Dico ergo Polus circuli signati super superficiem sphaerae, est punctum superficiei sphaerae, a quo omnes lineae egredientes ad circumferentiam circuli sunt aequales. Et circulus magnus ex circulis signatis super sphaeram, est circulus cuius centrum est centrum sphaerae, et est ille qui diuidit sphaeram in duomedia. Angulus est quem continent duo arcus se secantes duorum circulorum magnorum. Et angulus rectus est, quem continent duo arcus duorum circulorum magnorum. et sunt perpendiculares quae egrediuntur ex differentia communi ambobus, in superficie uniuscuiusque eorum continentes angulos rectos. Et est ille, cuius caput cum ponitur polus, et circumducitur cum quacunque longitudine quantumcunque magna possibile est, circulus est arcus cadens inter crura anguli quarta illius circuli. Et si fuerit ille arcus maior quarta circuli, nominabitur angulus expansus. et si fuerit minor, nominabitur acutus. Et sinus arcus est medietas cordis dupli eius. Et est etiam perpendicularis cadens ex extremitate eius arcus super diametrum exeuntem ex extremitate eius secunda. Et complementum arcus, est superfluitas quae est inter ipsum et quartam circuli, siue sit arcus minor quarta circuli siue maior. Et similiter complementum anguli, est superfluitas quae est inter ipsum et angulum rectum, siue angulus sit minor recto siue maior. Et duorum angulorum, quorum aggregatio duobus rectis angulis est aequalis, dicitur unusquisque continuatus. Et sunt quorum arcuum aggregatio est medietas circuli, et similiter duorum arcuum, quorum amborum aggregatio est medietas circuli, nominatur unusquisque continuatus.

⟨I.1⟩ PROPOSITIO I.

CVm superficies secat sphaeram, tunc differentia communis, illi superficiei et superficiei sphaerae est circumferentia circuli. Sit itaque sphaera a b, et superficies secans eam g d e z. Dico ergo, quod circumferentia g d e z est circumferentia circuli, cuius demonstratio haec est, Protraham ex centro sphaerae punctum h perpendicularem super superficiem g d, quae sit perpendicularis h t, et signabo super circumferentiam g d puncta g d e, qualitercunque cadant, et continuabo ea casui perpendiculari per lineas g c et d c et e c, et continuabo ea iterum centro sphaerae, 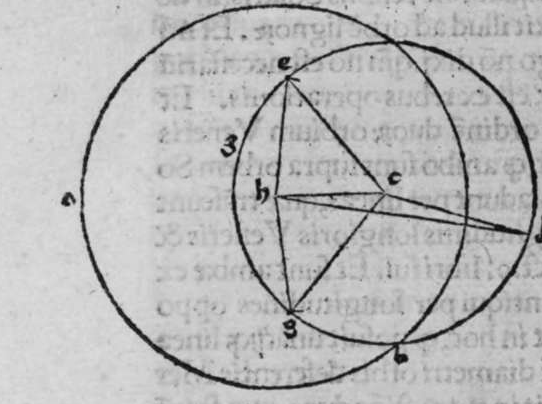lineis g h et d h et e h, propterea quia linea h t est perpendicularis super superficiem g d e, est erecta super omnes lineas quae sunt in illa superficie, per diffinitionem secundam undecimi Euclidis. Et propterea quod lineae g h et d h et e h sunt aequales, sunt lineae g t et d t et e t aequales. et similiter omnis linea egrediens a puncto t ad circumferentiam g d e est aequalis eis, ergo circumferentia g d z est circumferentia circuli, et centrum eius est punctum t. Et illud est, cuius declarationem uoluimus.

⟨I.2⟩ ⟨PROPOSITIO⟩ II.

CVm super sphaeram est circulus non magnus, et continuatur centrum eius centro sphaerae linea, tunc ipsa est perpendicularis super superficiem illius circuli: et si penetret in ambas partes, tunc ipsa transit per polos eius, et econuerso. Sit itaque super sphaeram circulus a b g d non magnus, sitque centrum eius punctum e, et centrum sphaerae punctum z, et continuabo ipsum centro circuli linea z e. Dico ergo quod linea z e est perpendicularis super superficiem circuli a b g, et faciam ipsam penetrare in ambas partes donec obuiet superficiei sphaerae super duo puncta h t. Dico ergo quod ipsa sunt duo poli circuli a b g, cuius haec est demonstratio. Signabo super circumferentiam a b g duo puncta a et b, qualitercunque cadant, et continuabo ea ambo centro circuli duabus lineis, a e et b e, et faciam eas penetrare, donec occurrant circumferentiae circuli super duo puncta g et d, et continuabo a b d g centro sphaerae lineis a z, b z, g z, d z, propterea igittur quod istae lineae sunt aequales, et lineae a e et b e et g e et d e, iterum sunt aequales, tunc linea z e communi, erunt duo anguli a e z, g e z aequales. per 8. primi Eucl. Vnusquisque igitur eorum est rectus, et similiter est unusquisque duorum angulorum b e z, d e z iterum rectus. ergo linea e z est perpendicularis super superficiem circuli a b g d. Et continuabo etiam duo puncta b c punctis a b g d, lineis h a et h b et h g et h d, et c a et c g et c d. Propterea, quia unusquisque angulorum, qui sunt apud punctum e, est aequalis, quoniam unusquisque 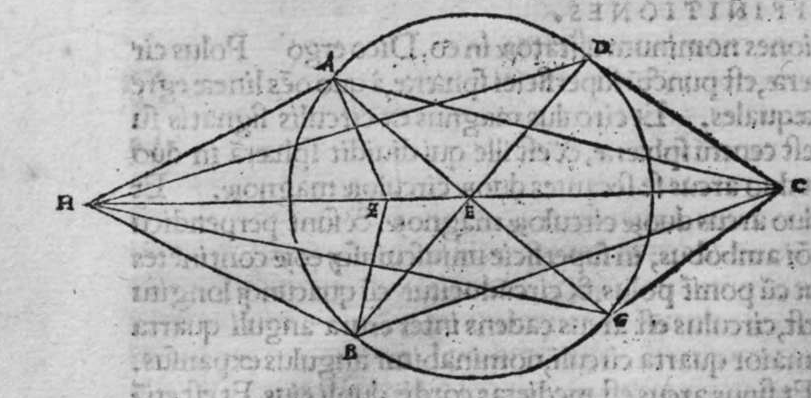eorum est rectus, et omnes lineae egredientes ex centro circuli, scilicet puncto e, ad circumferentiam sunt aequales, tunc linea e h communi sunt omnes lineae a h, h b, h g, h d, aequales, et similiter sunt omnes lineae exeuntes ex puncto c ad circumferentiam circuli a b g d aequales, ergo punctum h est polus circuli a b g. et similiter ostenditur etiam quod c est polus eius. Completa est eius declaratio. Et similiter, si protraximus ex centro sphaerae perpendicularem super superficiem circuli a b, quae sit linea e z, dico quod punctum e est centrum circuli a b g, et si fiat ut penetret in ambas partes, tunc ipsa transiet per polos eius, et illud, quoniam est angulorum a e z, b e z, g e z, d e z, unusquisque rectus, et lineae a z, b z, g z, d z, aequales, et sunt suppositae angulis rectis. tunc linea z e communi, sunt propter illud lineae a e, b e, g e, d e, aequales. Ergo punctum e est centrum circuli a b g. ergo cum fit ut linea e z, penetret in ambas partes transit per duos polos. Corollarium ex hoc etiam declaratum est, quod quando super sphaeram est cirulus non magnus, tunc puncta quatuor, scilicet duo poli, et centrum eius, et centrum sphaerae, sunt semper super lineam unam rectam, et quod illa linea est perpendicularis super superficiem eius. et quod si continuetur inter duo puncta eorum linea recta, et penetrando perducatur, tunc ipsa transit per duo puncta reliqua. et quod si protrahatur ab uno istorum perpendicularis super superficiem circuli, tunc ipsa transit per puncta tria remanentia.

⟨I.3⟩ ⟨PROPOSITIO⟩ III.

OMnis circulus signatur super sphaeram, a cuius polo lineae egredientis ad circumferentiam eius quadratus, est aequalis medietati quadrati diametri illius sphaerae, est circulus magnus. Sit ergo super sphaeram a b circulus b g d, et sit polus eius punctum a, et sit quadratus lineae egredientis ex puncto a, ad circumferentiam eius, quae sit linea a b, aequalis medietati quadrati diametri sphaerae, dico ergo quod circulus b g d est magnus, cuius demonstratio est haec. Continuabo punctum a, quod est polus circuli, centro eius, quod sit punctum e, lineam a e faciam penetrare donec concurrat superficiei sphaerae super punctum z, et continuabo lineam b z, propterea igitur quod circulus b g d signatus est super sphaeram, et continuatus est polus eius centro ipsius linea recta, cum ipsa transit per centrum sphaerae, et per polum eius secundum, et est perpendicularis super superificiem eius, ergp punctum z est polus circuli b g d, et linea a z est diameter sphaerae, quoniam transit per centrum sphaerae, quare quadratum eius est duplum quadrati lineae a b, secundum quod positum est. Et imaginabor superficium trianguli a b z  secantem sphaeram. erit ergo differentiae communis ei, et superficiei sphaerae circulus ab z g, propterea 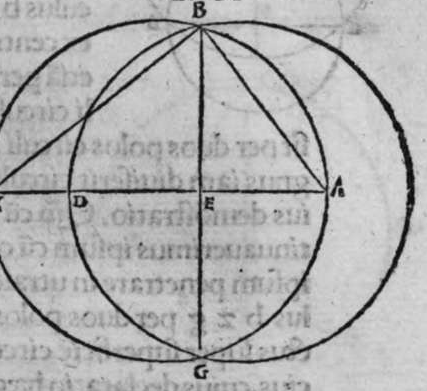igitur quod angulus a b z est rectus, quoniam ipse est in semicirculo a b z est quadratum lineae a z aequale duobus quadratis duarum linearum a b, b z. at quadratum lincae a b positum est aequale medietati quadrati lineae a z. Ergo quadratum lineae a b est aequale quadrato lineae b z, et propterea quod linea a e est perpendicularis super superficiem circuli b g d, est unusquisque duorum angulorum a e b et b e z rectus. Ergo quadratum lineae a b, est aequale duobus quadratis duarum linearum a e et e b, et similiter quadratum lineae b z est aequale duobus quadratis b e et e z. Ergo duo quadrata duarum linearum b e et e z, sunt aequalia duobus quadratis duarum linearum b e et e a, ablato ergo quadrato lineae b e communi, remanet quadratum lineae e z aequale quadrato lineae e a. Ergo linea e z est aequalis linea a e, et linea a e z est diameter sphaerae a b. ergo punctum e est centrum sphaerae, et centrum circuli b g d. Ergo circulus b g d est magnus. et illud est cuius uoluimus declarationem. Et hinc demonstratum est, quod omnis circuli magni super sphaeram linea egrediens a polo ad circumferentiam eius est aequalis lateri cadentis quadrati in eo.

⟨I.4⟩ ⟨PROPOSITIO⟩ IIII.

OStendere uolo qualiter transire faciam super duo puncta super superficiem spherae notae circulum magnum. Sit itaque sphaera nota a b, et duo puncta signata super eam a et b. Cum ergo uoluero ut super ipsam transeat circulus magnus, ponam puncta a polum, et mensurabo 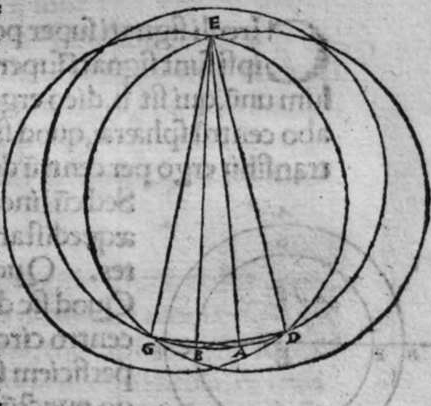cum longitudine lineae, cuius quadratum est aequale medietati quadrati quadratri ed. diametri sphaerae, quae sit linea a g, et circumducam circulum g e, et ponam iterum punctum b polum, et mensurabo illam longitudinem eandem, et circumducam circulum e d, et abscindant se isti duo circuli signati supra punctum e. propterea ergo quod a e est polus circuli g e, est linea a g aequalis a e. Et propterea quod punctum b est polus circuli e d, est linea b d aequalis lineae b e. At linea a g est aequalis lineae b d, ergo duae lineae a e et b e, sunt aequales. Cum ergo lineauerimus super polum e, et cum longitudine unius earum circulum transibit super extremitatem lineae alterius, ergo transibit per duo puncta a b. Sit itaque circulus a b g, dico ergo quod ipse est magnus. Cuius est demonstratio, quoniam quadratum uniuscuiusque duarum linearum a e et b e est aequale medietati quadrati diametri sphaerae a b, et unaqueque duarum linearum a e et e b, egreditur ex polo ciruli a b g ad circumferemtiam eius, ergo circulus a b g, est magnus, et transit per duo puncta a b, et hoc uoluimus declarare.

⟨I.5⟩ ⟨PROPOSITIO⟩ V.

CVm transit circulus magnus super duos polos circuli signati super sphaeram, tunc ipse secat eum in duo media, et est erectus super eum orthogonaliter, et econtra. Sit itaque circulus a b signatus super sphaeram, et sit polus eius punctum z, et transeat super eum circulus b g z magnus. Dico quod ipse diuidit circulum a b g in duo media, et est erectus super eum orthogonaliter, cuius declaratio haec. Continuabo centrum sphaerae, quod sit punctum e, cum polo circuli quod est punctum z, linea z e, et faciam ipsam penetrare donec concurrat lineae b g, quae est differentia communis duorum circulorum super punctum h. cum ergo h sit centrum circuli a b g, et circulus magnus iam transiuit per polum circuli a b g, ergo diuidit eum in duo media. Et est linea e z perpendicularis super eum, quoniam continuat inter centrum eius et centrum sphaerae, et omnis superficies uadens per lineam z h, est erecta super superficiem circuli a b g. ergo superficies circuli b z g magni est erecta super superficiem circuli a b g. Expleta est eius declaratio, Et sit ut circulus b z g iam diuiserit 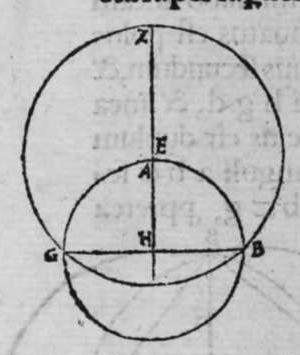circulum a b g in duo media, et sit superficies eius erecta super superficiem ipsius orthogonaliter, dico ergo quod circulus b z g magnus est, et quod ipse transit per duos polos circuli a b g, cuius demonstratio haec est. Quoniam circulus b z g diuidit circulum a b g in duo media, tunc ipse transit super centrum eius. Si ergo protraximus ex centro eius perpendicularem super superficiem ipsius, transibit per centrum sphaerae et per polum eius. Et quia circulus b z g erectus est super circulum a b g, erit perpendicularis egrediens ex centro circuli a b g, transiens per superficiem circuli b z g, et ipsa transit etiam per centrum sphaerae et per polos circuli a b g, ergo centrum sphaerae et poli circuli b a g, sunt in superficie circuli b z g, ergo ipse est magnus, et transit per duos polos circali a b g. completa est ius demonostratio. Et sit ut circulus b z g magnus iam diuiserit circulum a b g in duo media, dico ergo quod ipse transit per polos eius. cuius demonstratio. Quoniam cum diuidit eum in duo media, tunc transibit super centrum eius. Si ergo continuauerimus ipsum cum centro sphaerae, quod est centrum circuli b z g magni, et fecerimus ipsum penetrare in utrasque partes, transibit per duos polos circuli a b g, ergo transibit circulus b z g per duos polos circuli a b g. Et similiter si fuerit circulus b z g magnus erectus super superficiem circuli a b g, tunc ipse diuidet eum in duo media, et transibit per polos eius. cuius declaratio haec est, Quoniam si nos protraxerimus ex centro circuli b z g, quod est centrum sphaerae perpendicularem in superficie eius super lineam b g, quae est differentia communis duorum circulorum, erit perpendicularis super supficiem circuli a b g, et transibit per centrum et polos ipsius. Erit ergo propter illud superficies circuli b z g magni diuidens circulum a b g in duo media, cum iam transierit per polos eius. Et similiter si transibit circulus b g z per duos polos circuli a b g, tunc circulus b z g est magnus. Quoniam si continuauerimus inter duos polos circuli a b g linea recta, tunc illa linea erit in superficie circuli b z g, et transibit per centrum sphaerae, et per centrum circuli a b g. Erit ergo centrum sphaerae in superficie circuli b z g, ergo ipse erit circulus magnus. et illud est quod ostendere uoluimus.

⟨I.6⟩ ⟨PROPOSITIO⟩ VI.

CIrculi signati super polum unum sunt aequedistantes, et si sunt circuli aequedistantes, tunc ipsi sunt signati super polum unum. Sint itaque duo circuli a b g, d e z, signati super polum unum, qui sit h, dico ergo quod ipsi sunt aequedistantes, cuius haec est demonstatio. Continuabo centrum sphaerae, quod sit punctum c, cum polo duorum circulorum, scilicet cum puncto h, linea h c transibit ergo per centrum duorum circulorum, et erit perpendicularis super duas superficies earum. 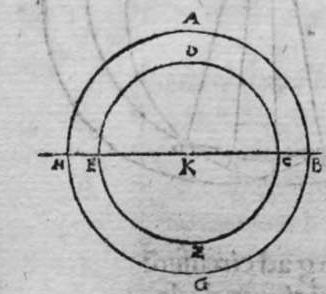Sed cum linea una est perpendicularis super duas superficies, tunc ipsae sunt aequedistantes. Ergo superficies duorum circulorum a b g, d e z, sunt aequedistantes. Quod si fuerint duo circuli aequedistantes, tunc polus eorum erit unus. Quod sic demonstratur. Continuabo centrum sphaerae, quod est punctum c, cum centro circuli a b g, quod est punctum k, et faciam ipsum penetrare usque ad superficiem secundam, et usque ad superficiem sphaerae, et usque ad punctum h. erit ergo punctum h polus circuli a b g, et erit c h perpendicularis super superficiem eius, et ipsa etiam erit perpendicularis super superficiem circuli d e z. Ergo transibit per centrum eius. et quando transit linea per centrum sphaerae et centrum circuli signati super sphaeram, tunc transibit per polos illius circuli. ergo linea c h transit per polum circuli d e z, et iam trasiuit per polum circuli a b g. ergo polus eorum est punctum unum, et est punctum h. Et illud est, cuius declarationem uoluimus.

⟨I.7⟩ ⟨PROPOSITIO⟩ VII.

CCirculi magni transeuntes per polos circulorum aequedistantium, separant in eo quod est inter eos de illis circulis aequedistantibus arcus similes. Sint itaque duo circuli a b, g d, aequedistantes, super quorum polum qui sit punctum e, transeant duo circuli magni, qui sint circuli 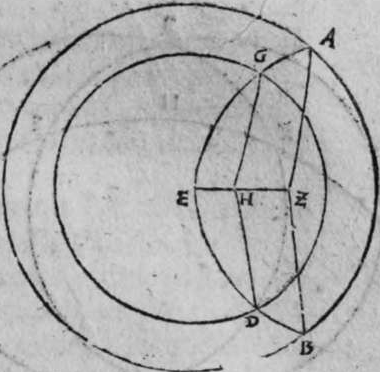a g e, et b d e, dico ergo quod duo arcus a b, g d, duorum circulorum aequedistantium sunt similes, cuius demonstratio haec est. Ponam centrum circuli a b punctum z, et centrum circuli g d punctum h, propterea igitur quod duo circuli a g e, et b d e, magni iam transierunt per polum circulorum aequedistantium, tunc transibunt per centrum eorum, transibunt igitur per duo puncta h et z. Sintque differentiae communes eis et circulis aequedistantibus lineae a z et g h, et b z et d h, quia ergo duo circuli a b, g d, sunt aequedistantes, et iam secuit utrosque circulos a g, sunt duae differentiae communes utrisque aequedistantes, ergo linea a z aequedistat lineae h g. Et similiter declaratur, quod linea b z aequedistat lineae d h. Angulus ergo b z b est aequalis angulo g h d, ergo arcus a b est similis arcui b g d, et illud uoluimus declarare.

⟨I.8⟩ ⟨PROPOSITIO⟩ VIII.

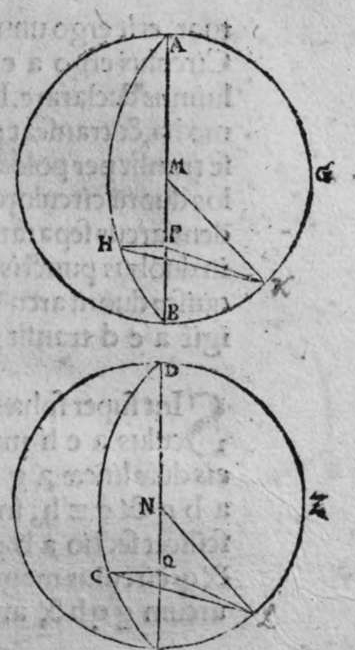CVm eriguntur supra duas diametros duorum circulorum a b g, et d e z aequalium orthogonaliter super superficiem utrorunque duae portiones a h b et d c e aequales, quae sint unius circuli crculi ed. aut duorum circulorum aequalium, et separantur ex arcubus ambarum portionum ab eo quod sequitur duo puncta e et b, duo arcus aequales, qui sint h b et c e. Et separantur ex duobus circulis a b et d e, duo arcus sequentes duo puncta e b etiam aequales, qui sint duo arcus b k et e l, et continuantur duae lineae h l et c l, tunc utraeque sunt aequales. Et econuerso illius etiam, scilicet quod si duae lineae h k et c l sunt aequales, et est unusquisque duorum arcuum h b et c e minor medietate portionis suae, tunc uterque arcus b k et e l sunt aequales. Ponam itaque in primis, quod duo arcus b k et e l et h b et c e sunt aequales. Dico ergo quod duae lineae h k et c l sunt aequales, cuius haec est demonstratio. Producam enim ex duobus punctis h et c, duas perpendiculares super duas lineas a b et d e, quae sint perpendiculares h p et c q, erunt ergo perpendiculares super duas superficies duorum circulorum a b k et d e z. Continuabo autem lineas p k et q l. Sitque centrum circuli a b k punctum m, quod continuabo cum puncto k, et centrum circuli d e z punctum n, quod continuabo puncto l. propterea igitur quod duo arcus b k et e l sunt aequales erunt duo anguli n m aequales. et propterea quod duo arcus h b et c e sunt aequales, et duae portiones a h b, et d c e sunt aequales. Et similes sunt duae lineae b p et q c. Et similiter duae lineae b p et q e etiam aequales sunt. Ergo sunt duae lineae m p et n q iterum aequales. At uero duo duae sic. lineae m k et n l sunt aequales. Sunt ergo propter hoc duae lineae p k et l q iterum aequales. Sed unusquisque duorum angulorum h p k, et c q l est rectus, pro pter hoc ergo sunt duae lineae h k et c l aequales. Completa est eius declaratio, et cum conuersione huius demonstrationis declarabitur conuerfio illius.

⟨I.9⟩ ⟨PROPOSITIO⟩ IX.

CVm super sphaera sese duo circuli secant, et transit circulus magnus super polos eorum, tunc ipse diuidit arcus separatos illorum duorum circulorum in duo media. Et econuerso si ipse diuidit arcus separatos cuiusque ilorum duorum circulorum in duo media, tunc ipse transit super polos eorum. Et similiter si diuidit arcus separatos unius duorum circuloum in duo media, et transit super medium polorum unius illorum, tunc ipse diuidet arcus separatos in duo media, et transit super polos amborum. Sint itaque duo circuli a b g, et g d b, sese super sphaeram secantes, super quorum polos transit circulus a e z magnus, dico ergo quod ipse diuidit arcus b a g, et b e g et b z g, et b d g, in duo media, quod sic demonstrat. Quoniam circulus a e z d, est magnus, et transit super duos polos duorum circulorum a b g, et d b g, tunc ipse est erectus super unum quenque eorum orthogonaliter. Sit itaque polus circuli b d g, punctum h, propterea ergo quod erecta est super diametrum circuli a b g, portio circuli orthogonaliter, et super circumferentiam signatum est punctum h, et arcus h z est minor mediate arcus a h z, et linea egrediens ex puncto h ad punctum b, est aequalis lineae egredienti ex eo ad punctum g. ergo propter illud arcus b z erit aequalis arcui g z. Et propterea quod unusquisque arcuum duorum a b z, et a g z est semicirculus, 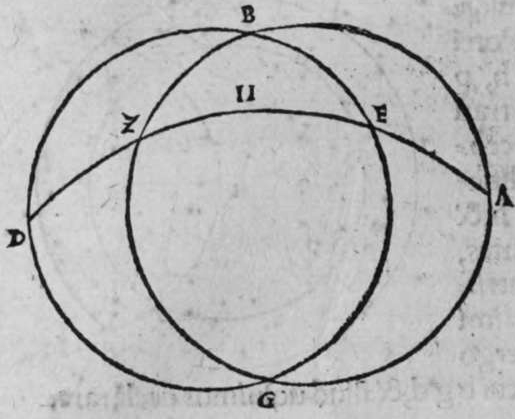remanet arcus a b aequalis arcui a g. Et quia portio z d est erecta super diametrum circuli a b g orthogonaliter, et separat ex eo arcus z b et z g aequales, et signatum est super circumferentiam portionis punctum d, qualitercunque cecidederit, tunc linea egrediens ex puncto d ad punctum b, est aequalis lineae egredienti ex puncto d ad punctum g. Ergo arcus b d est aequalis arcui g d. remanet itaque arcus b e aequalis arcui g e. Et sit quod circulus a e z d magnus diuiserit arcus separatos uniuscuiusque duorum circulorum a b et e b, in duo media. Dico ergo quod ipse transit per polos eorum, quod sic probatur. Quoniam si non transit per polos eorum, erit tunc circulus illius magnus transiens per polos eorum communicans cum circulo a e z d magno in punctis a e z d quatuor. erit ergo unusquisque arcuum a e, et e z, et z d semicirculus. hoc autem est impossibile. Circulus ergo a e z magnus, transit per polos duorum circulorum a b g et b e d, et hoc uoluimus declarare. Et si circulus a e z d iam diuiserit arcus separatos circuli a b g, in duo media, et transeat per polos eius, aut per polum circuli e b g, qui sit punctum h, dico ergo quod ipse transit per polos eorum, cuius demonstratio haec est. Quoniam si non transit arcus a e d per polos duorum circulorum, tunc erit circulus magnus per polos eorum amborum transiens, diuidens arcus separatos uniuscuiusque amborum in duo media, quare communicabit cum circulo a e d in duobus punctis a z, cum polo unius duorum circulorum, quod est punctum h. Quare erit unusquisque duorum arcuum a h et z h semicirculus. hoc uero contrarium est, et impossibile. Circulus igitur a e d transit per duos polos duorum circulorum a b g, et e b g, et illud uoluimus declarare.

⟨I.10⟩ ⟨PROPOSITIO⟩ X.

SInt super sphaeram duo circuli a b g et h z e aequedistantes et aequales, quorum utrunque circulus a e h magnus secet, et non transeat super polos amborum, et sint differentiae communes eis duae lineae a g et e h. Dico ergo, quod circulus a h e secat unumquenque duorum circulorum a b g et e z h, in duas sectiones diuersas. et quod sectiones coalternae utrorumque sunt aequales, scilicet sectio a b g aequalis sectioni h p e, et similiter sectio a d g aequalis sectioni e z h, et quod circulus magnus aequedistans duobus circulis a b g, et e z h, qui sit circulus q l, lecat arcum g q h et arcum a l e, in duo media super duo puncta l q. quod sic demonstratur. Ponam 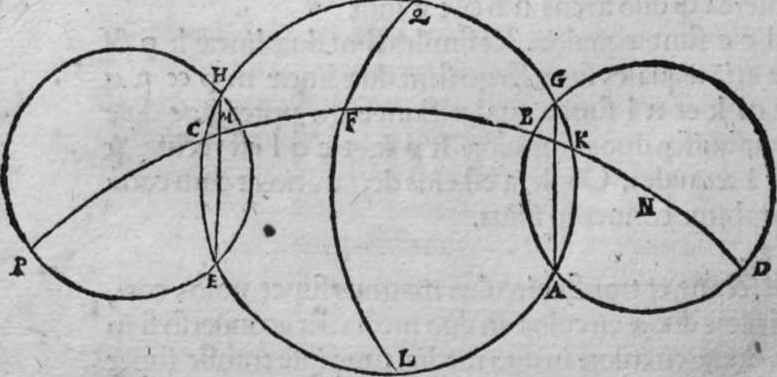enim duos polos duorum circulorum aequedistantium duo puncta, m, n, et polum circuli a g e punctum f, et transeat super duo puncta m f circulus magnus, qui sit d f m. Propterea ergo quod arcus m n est semicirculus, et arcus k c iterum semicirculus, erit arcus k n aequalis arcui m c. et propterea quod duo circuli a b g, et e z h sunt aequales, erunt duo arcus n b et m p aequales. remanent ergo duo arcus b k et p c aequales. et propterea quod circulus b f m transit per duos polos duorum circulorum a b et e z, et per polum circuli a g e, secantis eos ambos. erit circulus b f m erectus super unumquenque horum circulorum trium orthogonaliter. Et diuidit arcus separatos uniuscuiusque eorum in duo media. Et propterea quod arcus k n est aequalis arcui m c, et unusquisoque eorum amborum est minor medietate portionis suae. Et linea egrediens a puncto n ad punctum a, est aequalis lineae egredienti ex puncto m ad punctum e. Erit ergo arcus a k aequalis arcui e c. Sed arcus a k est aequalis arcui k g. Et similiter arcus e c est aequalis arcui h c, quare erit totus arcus a k g aequalis toti arcui e c h. Linea ergo a g c, est aequalis lineae e h. Et propterea quod duo circuli a b g, et e z h sunt aequales, erit portio a b g aequalis portioni e p h. Et similiter portio a d g aequalis portioni e z h Et propterea quod portio b f c transit per duos polos duorum circulorum a g h, et q l magnorum, et diuidit arcus separatos amborum eorum in duo media. Erit propter hoc unusquisque arcuum k l et k q et l c et c q quarta circuli. Et propterea quod iam demonstratum est, quod arcus a k est aequalis arcui e c, et similiter arcus b g aequalis arcui h c, remanet arcus a l aequalis arcui e l, et similiter arcus g q equalis arcui h k, et illud est quod uoluimus declarare.

⟨I.11⟩ ⟨PROPOSITIO⟩ XI.

ET quod plurimum in tractatu primo et secundo huius libri quaeritur, hoc non est nisi extractio ignotorum arcuum et angulorum ex notis eorum. Et figura trianguli est, in quam resoluuntur reliquae figurae. Et triangulus resoluitur in duos triangulos orthogonios. Et nos non scimus quantitatem alicuius arcuum circuli nisi per cognitionem quantitatis sinus eius de diametro. Et sinus est communis duobus arcubus, quorum unus est minor quarta circuli, et secundus maior quarta circuli. Oportet propter hoc ut praemittamus sermonem, quo sciamus, an latus quaesitum de lateribus trianguli orthogonij sit minus quarta circuli aut maius, et similiter arcus anguli eius quaesitus. et illud scitur per hoc quod narro. Dico itaque, quod omnes trianguli ex arcubus circulorum magnorum, in quo est angulus rectus, unumquodque duorum laterum continentium ipsum imitatur angulum cui subtenditur. Scilicet si angulus est rectus, illud latus ei suppositum est quarta circuli. Et si est maior recto, est maius quarta circuli. et si est minor recto, minus quarta circuli. Et similiter angulus imitatur latus sibi suppositum, scilicet si latus est quarta circuli, angulus cui ipsum subtenditur est rectus. et si est maius quarta circuli, est maior 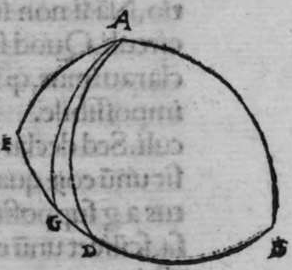recto. et si est minus, minor. Sit itaque triangulus a b g, sitque angulus eius b rectus, et sit angulus eius a rectus, dico ergo quod latus b g est aequale quartae ciculi, cuius haec est demonstratio. Quoniam angulus b est rectus, tunc polus circuli a b est super circulum b g. Et quia angulus a est rectus, erit etiam polus circuli a b super circulum a g, polus igitur circuli a b est punctum g, ergo latus b g est maius quarta circuli. Et ponam quod angulus a sit maior recto, dico quod latus b g est maius quarta circuli, quod sic probatur. Sit itaque angulus b a d rectus, erit punctum d polus circuli a b, secundum quod declarauimus, ergo arcus b d est quarta circuli. Latus ergo b g est maius quarta circuli. Sitque angulus b a g minor recto, dico quod latus b g est minus quarta circuli, cuius demonstratio ita. Sit angulus b a e rectus, erit punctum e polus circuli a b, est ergo propter hoc latus b e quarta circuli. latus igitur b g est minus quarta circuli. Et secundum hanc similitudinem declaratur, quod unusquisque duorum angulorum a g imitatur latus sibi suppositum, et illud est quod uoluimus declarare. Et dico iterum, quod si unum duorum laterum a b et b g, est quarta circuli tunc latus a g subtensum recto est quarta circuli, quod sic probatur. Quoniam si a b est quarta circuli, cum iam posuerimus angulum b rectum, erit propter hoc punctum a polus, arcus b g, ergo latus a g est quarta circuli. Et dico iterum, quod si unumquodque duorum laterum a b, et b g, continentium rectum, est minus quarta circuli, aut maius, tunc latus a g subtensum recto, est minus quarta circuli. Et si est unum eorum maius quarta circuli, et secundum minus, tunc a g subtensum recto est minus quarta circuli. Cuius haec est demonstratio. Nam si unumquodque duorum laterum a b et b g est minus quarta circuli, tunc ponemus unumquenque duorum arcuum b d et g e quartam circuli, et faciamus transire super duo puncta d e arcum circuli magni, qui sit d z e, et secet circulum a g super punctum z. Propterea ergo quod angulus b est rectus et latus b d est quarta circuli, erit punctum d polus circuli b g, ergo angulus e est rectus. et propterea quod angulus e est rectus, et latus e g quarta circuli, erit punctum g polus circuli d z e, ergo arcus g a z est quarta circuli, et latus a g est minus quarta circuli. Et ponam iterum unumquodque duorum laterum a b et b g, maius quarta circuli. Dico ergo quod latus a g subtensum recto est minus quarta circuli, quod sic probatur. Ponam enim unumquodque duorum arcuum b h et g c quartam circuli, et faciam transire super duo puncta h t circulum magnum, qui sit t h n, et secet circulum a g super punctum n, propterea igitur quod angulus b est rectus, et arcus b h est quarta qnarta ed. circuli, erit punctum h polus circuli b g. ergo angulus t est rectus et quia arcus t g est quarta circuli, erit punctum g polus circuli t h n, ergo g n est quarta circuli, latus igitur a g est minus quarta circuli. Et ponam latus a b maius quarta circuli, et latus b g minus quarta circuli. Dico ergo quod latus a g est maius quarta circuli, quod sic demonstratur. Ponam enim unumquenque duorum arcuum g e, b h quartam circuli, et faciam transire per duo puncta e h circulum magnum, qui sit circulus e h k. Propterea ergo quod angulus b est rectus, et arcus b h quarta circuli, erit punctum h polus circuli b g, ergo angulus e est rectus, et propterea quod arcus e g est quarta circuli, erit punctum g polus circuli e h k, ergo arcus g k est quarta circuli, latus igitur a g 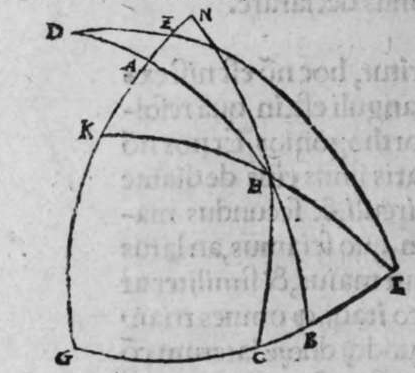est maius quarta circuli. Et quia duo anguli a et g, imitantur duo latera a b et b g, quae subtenduntur eis, oportet etiam ut latus a g suppositum recto imitetur duos angulos a et g, scilicet quod si unus eorum fuerit rectus, sit latus a g quarta circuli. Et si fuerit unusquisque eorum minor recto, aut maior recto, sit latus a g minus quarta circuli. Et si fuerit unus eorum minor recto, et secundus maior recto, sit latus a g maius quarta circuli. Ponam autem latus a g subtensum recto quartam circuli. Dico ergo quod unum duorum laterum a b, b g, est quarta circuli, quod sic probatur. Nam si non est unum duorum laterum a b, b g, quarta circuli, erit unumquodque eorum aut maius quarta circuli aut minus, aut unum eorum maius quarta circuli et secundum minus, sequitur ergo ex his quae nuper declarauimus, quod latus a g aut est maius quarta circuli aut minus. Nos autem iam posuimus ipsum quartam circuli, hoc contrarium est et impossibile. Vnum igitur duorum laterum a b, b g, est quarta circuli. Et si fuerit latus a g suppositum recto minus quarta circuli, tunc unum quodque duorum laterum a b, b g, aut erit maius quarta circuli aut minus, cuius haec est demonstratio. Nam si non sunt ita, tunc erit unum eorum maius, et secundum minus, aut erit unum eorum quarta circuli. Quod si unum eorum est maius quarta circuli, et secundum minus, sequitur ex eis quae declarauimus, quod latus a g est maius quarta circuli, ipsum enim iam positum fuit minus, et hoc est impossibile. Et similiter etiam si unum eorum est quarta circuli, sequitur quod sit latus a g quarta circuli. Sed declaratum est contrarium, quod sit unum eorum maius quarta circuli, et secundum minus, aut quod sit unum eorum quarta circuli. Erunt ergo unius speciei in magnitudine aut paruitate. et si laqus a g suppositum recto est maius quarta circuli, tunc duo latera continentia rectum sunt diuersa, scilicet unum eorum est maius quarta circuli, secundum minus, quod sic probatur. Quoniam si non est ita, tunc erunt unius speciei in magnitudine aut paruitate. Aut erit unum eorum quarta circuli, et si fuerit unumquodque eorum maius quarta circuli, aut minus, erit latus a g minus quarta circuli. Nos uer iam posuimus ipsum maius, et hoc est impossibile. erunt ergo ambo diuersa. Et similiter si fuerit unum eorum quarta circuli, sequitur quod sit latus a g quarta circuli. ipsum autem est maius, et hoc est contrarium. Contrarium igitur est quod sint speciei unius in paruitate aut magnitudine, aut quod sit unum eorum quarta circuli, unum igitur eorum est maius, et secundum minus. Et quoniam unusquisque duorum angulorum qui sunt super illud latus subtensum recto, imitatur latus sibi subtensum. Oportet ut sit indicium duorum angulorum qui sunt super illud latus subtensum recto, cum illo latere indicium duorum laterum subtensorum ipsorum eis ambobus, scilicet quia si fuerint subtensum recto quarta circuli, erit unus duorum reliquorum angulorum rectus. Et si fuerit minus quarta circuli, erit unusquisque eorum aut maior recto aut minor, et si fuerit maius quarta circuli, erit unus eorum maior recto, et secundus minor, et illud est quod uoluimus declarare. Istud est ergo quo scitur unumquodque laterum trianguli orthogonij an sit quarta circuli, aut maius aut minus, et similiter unusquisque duorum reliquorum angulorum eius, an sit rectus, aut maior aut minor. Qualiter uero sciatur quantitas cuiusque laterum eius et angulorum ad inuicem, praemittam ad illud figuram magnae excusationis et iuuamenti in hac intentione, et alijs ab ea et est haec.

⟨I.12⟩ ⟨PROPOSITIO⟩ XII.

CVm sint duo circuli magni super sphaeram, et non transit unus eorum per polum alterius, et signantur super circumferentiam unius eorum duo puncta, aut super circumferentiam uniuscuiusque ipsorum punctum, qualitercunque cadant, et producuntur ex unoquoque illorum duorum punctorum duo arcus ad circulum secundum, quorum unusquisque continuat cum arcu circuli ad quem ipse producitur angulum rectum, tunc proportio sinus arcus, quae est inter unum duorum punctorum, et inter unum duorum punctorum sectionis duorum circulorum ad sinum arcus producti ex illo puncto ad circulum secundum, est sicut proportio sinus arcus, quae est inter punctum secundum et inter unum duorum punctorum sectionis ad sinum arcus producti ex illo puncto ad circulum secundum. Sint ergo duo circuli x g d b, a e z b, magni super sphaeram, et signemus super circumferentiam circuli a g d b, qui est unus eorum, in primis duo puncta g d, et faciamus transire super utraque ea, et super polum circuli a e, duos arcus duorum circulorum maiorum, qui sunt arcus e g et z d, continentes cum arcu circuli a e z, duos angulos rectos. Dico ergo, quod proportio sinus arcus a g, ad sinum arcus g e est sicut proportio sinus a d ad sinum d z. Quod sic probatur. Producam enim ex duobus punctis g d, duas perpendiculares super superficiem circuli a e b, quae sint perpendiculares g k et d c, et protraham ex eis etiam duas perpendiculares super diametrum a b in superficie circuli a g d, quae 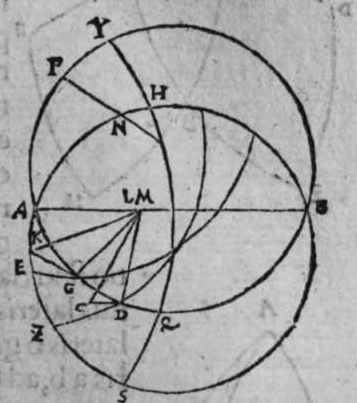sint perpendiculares g l et d m, et producam duas lineas k l et c m, propterea igitur quod duae perpendiculares g k et d c sunt aequedistantes, et similiter duae perpendiculares g l et d m aequedistantes, erunt et duo anguli l g k, et m d c aequales, et unusquisque duorum angulorum k et c est rectus, sunt ergo trianguli l g k et d m c similes. Ergo proportio lateris g l ad latus g k est sicut proportio lateris d m ad latus d c, ac latus g l est sinus arcus a g, et latus g k est sinus arcus g e, et similiter latus d m est sinus arcus a d, et latus d c est sinus arcus d z. Ergo proportio sinus arcus a g ad sinum arcus g e est sicut proportio sinus arcus a d ad sinum arcus d z. Completa est eius declaratio. Et quia sinus arcus a g est sinus arcus g b, et similiter sinus arcus a d est sinus arcus d b, oportet ut sit proportio sinus arcus b g ad sinum arcus g e, sicut proportio sinus arcus b d ad sinum arcus d z. Et ut sit etiam proportio sinus arcus a g ad sinum arcus g e sicut proportio sinus arcus b d ad sinum arcus d z. Et sit punctum g signatum alicubi in circumferentia circuli a g d, et signetur etiam alicubi in circumferentia circuli a e z punctum n, et protrahatur ad circulum a g d ex eo arcus circuli magni continens cum eo angulum rectum, qui sit arcus n p. Dico ergo quod proportio sinus arcus a g est ad sinum arcus g e, est sicut proportio sinus arcus a n ad sinum arcus n p, quod sic probatur. Faciam transire super polos duorum circulorum a g d et a e z, circulum magnum, qui sit y h q, ergo comprehendit cum duobus circulis a g d et a e z angulos rectos, et diuidit arcus separatos duorum circulorum in duo media. Erunt ergo propter hoc arcus a q, a s, et b q, et b s, et a h, et a y, et b h, et b y octo, omnes aequales, quoniam unusquisque eorum est quarta circuli. Et propter hoc etiam quod circuli magni secant se super medietates suas, cuius declaratio haec est, propinquae acceptionis, erunt arcus y h, et s q aequales, ergo proportio sinus cuiusque arcuum octo, ad sinum cuiusque duorum arcuum y h et s q, est sicut proportio una. Et propterea quod duo puncta n h sunt signata super circulum a n h, et ex eis productae sunt duae perpendiculares n p et y h, erit ex eis, quod declarauimus, proportio sinus arcus a n ad sinum arcus n p, sicut proportio linus arcus a h ad sinum arcus h y. Et similiter erit iterum proportio sinus arcus a g ad sinum arcus g e, sicut proportio sinus arcus a q, ad sinum arcus q s. At uero proportio sinus arcus a h, ad sinum h y, est sicut proportio sinus a q ad sinum q s. ergo proportio finus arcu a g ad sinum g e, est sicut proportio sinus a n, ad sinum n p, et illud uoluimus declarare.

⟨I.13⟩ ⟨PROPOSITIO⟩ XIII.

ET postquam ista iam exposita sunt, dico quod omnis trianguli ex arcubus circulorum magnorum proportio sinus cuiusque laterum ad sinum arcus anguli, cui subtensum est, est proportio una, cuius haec est demonstratio. Non enim est possibile, quin unusquisque angulorum trianguli sit rectus, aut sint duo angulorum eius recti, aut sit unus angulus ex eis rectus, aut non sit in eo angulus unus rectus. Quod si fuerint anguli eius tres recti, erit arcus cuiusque eorum quarta circuli, et erit etiam unumquodque laterum eius quarta circuli, quapropter erit proportio sinus cuiusque laterum eius, ad sinum arcus anguli cui subtensum est, proportio una, et est proportio aequalis. Et si sunt duo angulorum eius recti, caput reliqui anguli est polus circuli lateris sibi subtensi. quare illud latus est arcus anguli cui subtensum est. Ergo erit proportio sinus eius ad sinum arcus anguli cui ipsum subtensum est, proportio aequalis. Et similiter erit proportio sinus cuiusque duorum laterum reliquorum, ad sinum arcus anguli, cui subtensum est, proportio aequalis, quoniam unumquodque eorum est quarta circuli, et angulus cui subtensum est, est rectus. Et cum in triangulo est unus angulus rectus, declaratur illud in eo, secundum quod narro. Sint trianguli a b g, angulus b rectus. Dico ergo quod proportio sinus lateris a b ad sinum arcus anguli g, cui ipse subtendit, est sicut proportio sinus lateris b g ad sinum arcus anguli a, cui ipsum subtenditur. et sicut proportio sinus lateris a g ad sinum arcus anguli b, cui subtensum est. Quod sic demonstratur. Ponam unumquenque duorum arcuum a d et g e, quartam circuli, et similiter ponam unumquenque duorum arcuum a z, g h, quartam circuli, et faciam transire super duo puncta e h, arcum circuli magni, qui sit arcus h e, et faciam transire etiam super duo puncta z d, arcum circuli magni qui sit arcus z d, erit ergo punctum g polus arcus e h, et erit punctum a polus arcus d z, et erunt 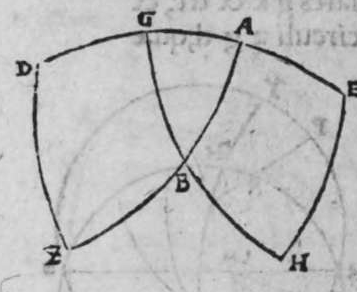duo circuli e g, g h, magni, et signata sunt super circumferentiam circuli e g. duo puncta a e, et egrediuntur ex eis duo arcus a b, et h e, perpendiculares super circulum g h, ergo proportio sinus arcus a g ad sinum arcus g e, est sicut proportio sinus arcus a b ad sinum arcus h e. Et similiter erit etiam proportio sinus a g ad sinum arcus a d, sicut proportio duorum arcuum sinus arcus g b ad sinum arcus d z. Sed unusquisque duorum arcuum g e, et a d, est quarta circuli, ergo unusquisque eorum est arcus anguli b recti. Et similiter arcus e h, est arcus anguli g, et arcus d z est arcus anguli a. Ergo proportio sinus lateris a g, ad sinum arcus anguli b, cui ipsum subtenditur, est sicut proportio g b, ad sinum arcus anguli a, cui ipsum subtenditur. Et similiter iterum proportio 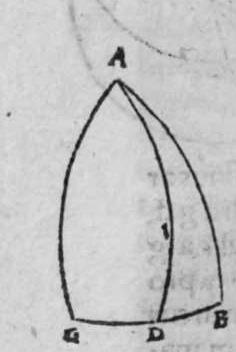sinus lateris a g, ad sinum arcus anguli b, cui subtensum est, est sicut proportio sinus lateris a b, ad sinum arcus anguli g, cui ipsum subtenditur. Proportio ergo sinus lateris b g, ad sinum arcus anguli a, cui subtensum est, est sicut proportio sinus lateris a b, ad sinum arcus anguli g, cui subtenditur. et illud est cuius uoluimus declarationem. Et non sit in triangulo a b g, angulus rectus, faciam itaque transire super punctum eius a, et super polum circuli b g, arcum circuli magni, qui sit arcus a d, et secet illam arcus in eo quod est inter duo puncta b et g, secundum quod est in figura secunda trianguli, ergo a d g angulus d est rectus. Ergo proportio sinus lateris a g, ad sinum lateris a d, est sicut proportio sinus arcus anguli d recti ad sinum arcus anguli g. Et similiter trianguli a d b angulus d est rectus. Ergo erit proportio sinus lateris a d 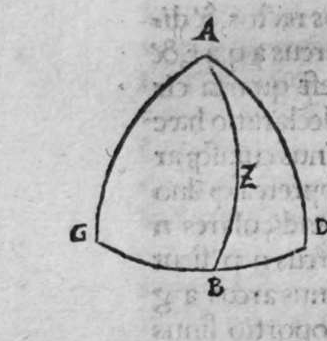eius, ad sinum lateris eius a b, sicut proportio sinus arcus anguli b, ad sinum arcus anguli d recti, ergo in proportione aequalitatis secundum proportionem * sic. muthrariba, erit proportio sinus lateris a g, ad sinum lateris a b, sicut proportio sinus arcus anguli b, ad sinum arcus anguli g. Cum ergo permutauerimus, erit proportio sinus lateris a g, ad sinum arcus anguli b, cui ipsum subtenditur, sicut proportio sinus lateris a b, ad sinum arcus anguli g, cui subtenditur. Et similiter si traxerimus ex puncto d perpendicularem super latus a g, declarabitur per hanc eandem demonstrationem, quod proportio sinus lateris a b, ad sinum arcus anguli g, cui est subtensum, est sicut proportio sinus lateris b g, ad sinum arcus anguli a, cui ipsum subtenditur. Et si arcus a d, qui est perpendicularis, ceciderit extra triangulum, sicut est in figura tertia, declarabitur etiam illa eadem demonstratione, quod proportio sinus lateris a g, ad sinum lateris a b, est sicut proportio sinus arcus anguli a b d ad sinum arcus anguli g. at sinus arcus anguli a b d, est ipse idem sinus arcus anguli a b g. quoniam aggregatio arcuationis amborum eorum est semicirculus, ergo proportio sinus lateris a g, ad sinum lateris a b, est sicut proportio sinus arcus anguli a b g, ad sinum arcus anguli g. Completa est eius declaratio.

⟨I.14⟩ ⟨PROPOSITIO⟩ XIIII.

HAec dico iterum, quod in omni triangulo ex arcubus circulorum magnorum, in quo est angulus unus rectus, est proportio sinus arcus unius duorum reliquorum ad sinum arcus anguli recti, sicut proportio sinus arcus complementi anguli reliqui, ad sinum arcus complementi lateris 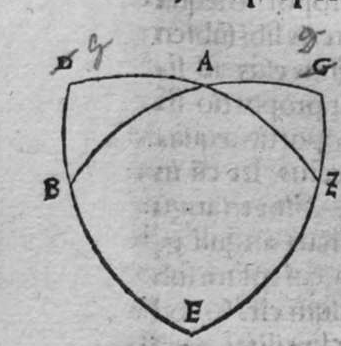subtensi ei. Sit itaque triangulus a b g, et sit eius angulus b rectus, dico ergo quod proportio sinus arcus anguli eius a, ad sinum arcus anguli b recti, est sicut proportio sinus arcus complementi anguli g reliqui ad sinum arcus coplementi lateris a b subtensi angulo g. Quod lic demontratur, ponam arcum d b quartam circuli, et protraham a puncto d perpendicularem super arcum a g, quae sit arcus d z, et occurrat arcui b g supra punctum e. Duo igitur arcus a g, a b iam secuerunt se supra punctum a, et signata sunt supra eos duo puncta g et d, a quibus productae sunt duae perpendiculares g b et d z. Est ergo ex eis quae praemisimus proportio sinus perpendicularis b g, ad sinum arcus a g, sicut proportio sinus perpendicularis d z, ad sinum arcus a d, at proportio sinus perpendicularis b g, ad sinum arcus a g est sicut proportio sinus arcus anguli a, ad sinum arcus anguli b recti, et perpendicularis d z, est arcus complementi anguli g, et arcus a d, est complementum lateris a b. proportio igitur sinus arcus anguli a ad sinum arcus anguli b recti, est sicut proportio sinus complementi arcus anguli g reliqui, ad sinum complementi lateris a b subtensi ei. et illud est cuius uoluimus declarationem.

⟨I.15⟩ ⟨PROPOSITIO⟩ XV.

ET dico iterum, quod proportio sinus complementi arcus subtensi recto ad sinum unius complementi duorum continentium ipsum, est sicut proportio sinus complementi lateris reliqui ad sinum quartae circuli, cuius haec est demonstratio. Eandem reiterabo figuram, ergo duo arcus etiam b d et d e secant se super punctum d, et super punctum d b. Vnde ergo signata sunt duo puncta b a, et progrediuntur ex eis duae perpendiculares super arcum d e, quare est ex eis quod declarauimus, 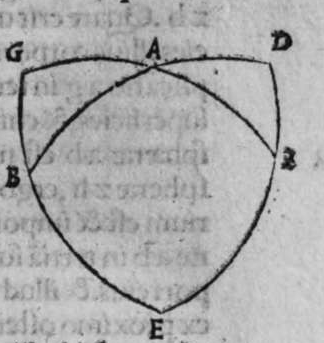Proportio sinus arcus a z ad sinum arcus e b, sicut proportio sinus arcus a d ad sinum arcus d b, sed arcus a z est complementum lateris a g, et arcus e b est complementum lateris b g, et arcus a d est complementum lateris a b, et arcus d b est quarta circuli. Proportio ergo sinus complementi lateris a g subtensi recto ad sinum complementi lateris b g unius duorum continentium ipsum, est sicut proportio complementi sinus lateris a b reliqui ad sinum quartae circuli, et illud est quod uoluimus declarare. Ex istis ergo tribus theorematibus extrahitur ignotum ex noto trianguli arcuum circulorum magnorum orthogonij, scilicet, quia cum ponuntur eius tria laterum et angulorum eius nota, tunc cum istis tribus theorematibus scientur tria reliqua laterum et angulorum ipsius per quatuor lineas proportionales, et excusabit illud a figura sectore, et propterea, quia non euacuatur in istis proportionibus, quando illud quod positum est in eis, sit sinus anguli recti, aut sinus quartae circuli, et unusquisque amborum est medietas diametri circuli. et illud est 60. Oportet ut declaremus qualiter multiplicetur numerus in ipsum et qualiter diuidamus numerum per ipsum. Cum ergo necesse est multiplicare in ipsum, excusat a multiplicatione eius in 60. si eleuetur unaquaeque pars ipsius numeri uno ordine, scilicet si ponantur pro unoquoque graduum duo signa, et pro unoquoque minutorum eius gradus, et pro unoquoque secundorum eius minutum, et similiter in reliquis partibus eius. Et si necessarium est iterum diuidere numerum per ipsum, scilicet per 60. excusat ab hoc, ut deponatur unaquaeque partium illius numeri uno ordine, scilicet, ut redeat gradus ad minuta, et minutum ad secunda, et similiter reliquae partes eius.

⟨I.16⟩ ⟨PROPOSITIO⟩ XVI.

QVod autem superest nobis super quod demonstrationem afferamus, super quod ipse in libro suo non attulit demonstrationem, est quod corporis omnis spherae embadum maius est embado omnis corporis plurium superficierum aequalium perpendicularium egredientium a centro 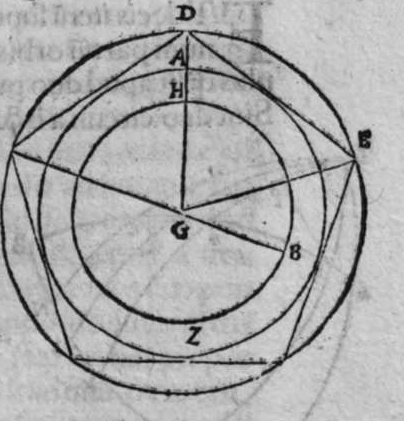ad superficiem ipsius, cuius superficies est aequalis superficiei illius spherae sperae ed., et hoc ex primo declarabitur, cum ostensum fuerit, quod embadum spherae sperae ed. surgit ex multiplicatione medietatis diametri eius in tertiam superficiei eius. Incipiamus ergo declarare illud. Sit itaque sphera a b, et medietas diametri eius sit linea a g, et centrum eius sit punctum g. Dico ergo, quod multiplicatio a g in tertiam superficiei spherae a b est aequalis embado corporis spherae a b, cuius haec est demonstratio. Si enim non est multiplicatio a g in tertiam superficiei spherae a b aequalis corpori spherae, tunc erit aequalis corpori spherae maioris sphera a b, aut minoris. Sit itaque in primis aequalis spherae maiori sphera a b, et sit sphera d e, quae sit cum sphera a b super centrum unum, possibile ergo est, ut sit in sphera d e figura corporis plurium basium, cuius bases sint non contingentes superficiem spherae a b. Quare erit unaquaeque perpendicularium productarum ex centro g super superficies eius maior linea a g. Si ergo continuentur anguli illius corporis euenientis in sphera d e cum centro spherae, prouenient piramides, quarum omnium capita erit centrum spherae, et earum bases erunt bases corporis, et embadum cuiuscunque piramidis earum proueniet ex multiplicatione suae perpendicularis in tertiam balis suae, et propterea quod linea a g, quae est medietas diametri spherae a b, erit minor unaquaeque illarum perpendicularium. Est propter illud multiplicatio lineae a g in tertiam cuiusque basis minor embado pyramidis, cuius est illa balis, ergo multiplicatio lineae a g in tertiam superficiei illius corporis, est minor embado corporis. at superficies illius corporis est maior superficie sphaerae a b, multiplicatio ergo lineae a g in tertiam superficiei sphaerae a b, est multo minor embado corporis, etiam fuit posita multiplicatio lineae a g in tertiam superficiei sphaerae a b, aequalis sphaerae d e, ergo oportet ut sit sphaera d e minor multum corpore, quod est intra ipsum, quod est contrarium et impossibile. Non ergo multiplicatio lineae a g in tertiam superficiei a b, est maior sphaera a b, et dico iterum, quod non est minor sphaera a b, quod si possibile est, tunc sit. erit ergo aequalis sphaerae, quae est minor sphaera a b, sicut est sphaera z h, quae sit super centrum g, et possibile iterum est ut sit in sphaera g a b corpus plurium basium, cuius bases non contingant superficiem sphaerae z b. Quare erit unaquaeque perpendicularium cadentium ex centro sphaerae a b super superficies illius corporis minor medietate diametri sphaerae a b, quae est linea a g, erit ergo multiplicatio a g in tertiam cuiusque superficiei earum maior embado piramidis, cuius basis est illa superficies, et cuius caput est centrum g. Multiplicatio ergo lineae a g in tertiam superficiei sphaerae a b est maior plurimum embado corporis. Iam autem posita fuit aequalis embado spherae z h, ergo sphaera z h est multo maior corpore, et ipsa est intra ipsum, hoc uero contrarium est et impossbile. Non ergo multiplicatio lineae a g, quae est medietas diametri sphaerae a b in tertiam superficiei suae est maior neque minor corpore eius, ipsa ergo est aequalis corpori eius. et illud est cuius uoluimus declarationem. Et quia iam declaratum est istud, tunc ex proximo ostendetur, quod omnis sphaerae embadum maius est embado omnis corporis plurium superficierum habentis perpendiculares, ex centro suo egredientes ad suas superficies aequales, cuius superficies superficiei illius sphaerae est aequalis. Ponam itaque sphaeram a b, et ponam superficiem eius aequalem superficiei corporis g plurium superficierum aequalium perpendicularium. Dico ergo, quod sphaera a b est maior corpore g, quod sic demonstratur. Imaginabor super sphaeram a b figuram corpoream similem figurae g, cuius superficies sint contingentes superficiem sphaerae a b, erit ergo superficies eius maior superficie sphaerae, ergo superficies eius erit maior superficie corporis g, et propterea, quia est simile corpori g, et superficies eius maior est superficie illius, erit perpendicularis eius maior perpendiculari corporis g, et propterea quod superficies eius sunt contingentes superficiem sphaerae a b, erit perpendicularis eius medietas diametri sphaerae a b, ergo medietas diametri sphaerae a b est maior perpendiculari figurae g. Sed embadum sphaerae surgit ex multiplicatione medietatis diametri eius in tertiam superficiei ipsius secundum quod ostendimus. Et embadum omnis corporis plurium superficierum aequalium perpendicularium consurgit ex multiplicatione perpendicularis eius in tertiam superficiei ipsius, ergo sphaera a b maior est corpore g, et illud est cuius uoluimus declarationem.

⟨I.17⟩ ⟨PROPOSITIO⟩ XVII.

ET de eis iterum super quae ipse non attulit demonstrationem est, quod superfluitas declinationum partium orbis signorum ab aequatore diei est apud duo puncta duarum aequalitatum plus quam sit apud duo puncta duorum tropicorum, et illud est quidem declaratum per id quod narro. Sint duo circuli a b et b g magni, sese secantes super punctum b, ex quibus separemus duos 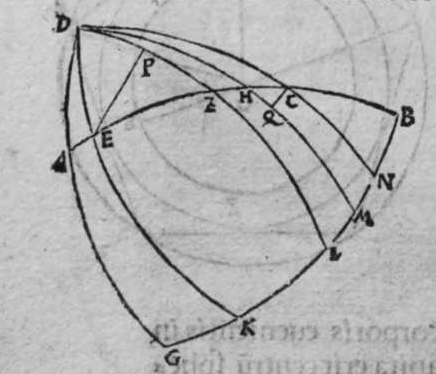arcus a b et b g, quorum unusquisque sit quarta circuli, et sit angulus a b g acutus, et sit polus circuli b g punctum d, et separemus ex arcu a b duos arcus e z et h t aequales, et faciemus transire super polum d, et super unumquodque punctorum e z h t circulum magnum. Sintque circuli d e k et d z l, et d h m et d t n, dico ergo, quod superfluitas arcus h m super arcum t n maior est superfluitate arcus e k super arcum z l, quod sic probatur. Producam a puncto t perpendicularem super arcum d m, qui sit arcus t q, et producam iterum a puncto e perpendicularem super arcum d l, qui sit arcus e p, propterea ergo, quia arcus h d est maior arcu z d, erit proportio sinus arcus h d ad sinum arcus d m maior proportione sinus arcus d z ad sinum arcus a d, et propterea quod duo circuli a b et d m secant se supra punctum h, et signantur super eos ambos duo puncta t et d, et producuntur ab eis duobus duae perpendiculares t q et d a, erit proportio sinus arcus h t ad sinum perpendicularem a d, et similiter sunt iterum super duos circulos a b et d l sese secantes supra punctum z, signata duo puncta e et d, et productae sunt ab eis utrisque duae perpendiculares e p et d a. Quare erit proportio sinus arcus z e ad sinum perpendicularem e p, sicut proportio sinus arcus z e ad sinum perpendicularem a d, proportio ergo sinus arcus h t ad sinum arcus t q est maior proportione sinus arcus e z ad sinum arcus p e. Sed arcus t h est aequalis arcui e z, ergo arcus e p est maior arcu t q. Ergo complementum arcus e p est minus complemento arcus p t q, ergo proportio sinus complementi arcus e z ad sinum complementi arcus e p, est maior proportione sinus complementi arcus h t ad sinum finum ed. complementi arcus t q, ergo proportio sinus complementi arcus z p ad sinum quartae circuli est maior proportione sinus complementi arcus h q ad sinum quartae circuli, ergo complementum arcus z p est maius complemento arcus h q, ergo arcus h q est maior arcu z p, et propterea quod est arcus d t maior arcu d q, oportet ut sit arcus q m maior arcu t n, ergo additio arcus h m super arcum t n est maior arcu z p, et propterea iterum quod arcus d e est maior arcu d p, est arcus p l maior arcu e k, ergo additio arcus p l super arcum z l, qui est arcus z p, est maior additione arcus e k super arcum z l, et iam fuit additio arcus h m super arcum t n maior arcu z p, ergo additio arcus h m super arcum t n est multo maior additione arcus e k super arcum z l, completa est eius declaratio.

⟨I.18⟩ ⟨PROPOSITIO⟩ XVIII.

ET de eis iterum super quae demonstrationem non attulit est, quod indiguit in tractatu tertio sui libri in diuersitate dierum cum noctibus suis, ut sciret punctum orbis signorum apud quod est plurimum diuersitas eius, quae est inter gradum orbis signorum, et inter eleuationem eius in orbe recto, et dixit illud absolute, et non attulit illud super demonstrationem, sed inuentio illius puncti est secundum quod narro. Sint duo circuli a b et b g magni super sphaeram, 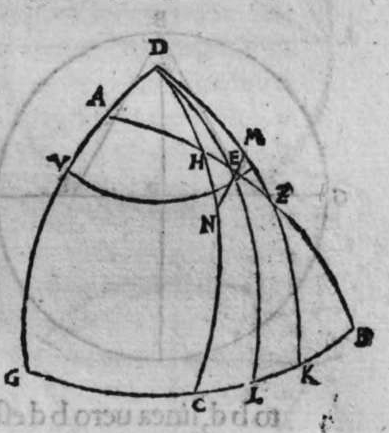qui se secant super punctum b, et separemus ex ambobus duos arcus a b g b, et sit unusquisque eorum quarta circuli, et faciamus transire super duo puncta g a arcum circuli magni, qui sit arcus d a g, et sit quarta circuli. Erit ergo propter illud punctum d polus circuli b g, et producamus lineam mediam in proportione inter sinum arcus d g, qui est medietas diametri circuli d g, et inter sinum arcus d a, qui est complementum partis declinationis circuli a b a circulo b g, et sit sinus arcus d n, et ponamus punctum t polum, et mensuremus longitudinem d n, et faciamus circulum n e, qui secet circulum b g super punctum l, et signemus super arcum b a duo puncta, a duobus lateribus puncti e, qui sint puncta duo h z, qualitercunque cadant, et faciamus transire super ea duos arcus d h t, d z k. Dico ergo, superfluitas arcus e b super arcum b l maior est superfluitate arcus z b super arcum k b, et quod superfluitas arcus l g super arcum a e est maior superfluitate arcus g t super arcum a h, cuius demonstratio est haec. Protraham ex puncto e perpendicularem super arcum d z, qui sit arcus e m, propterea ergo quod duo circuli d k et d l iam secuerunt se supra punctum d, et signata sunt ab illis duobus duae perpendiculares super unum eorum, scilicet duo puncta e l, et protractae sunt ab illis duobus duae perpendiculares e m et l k, erit proportio sinus arcus l k ad sinum arcus e m, sicut proportio sinus arcus l d ad sinum arcus d e. Verum proportio sinus arcus l d ad sinum arcus d e est sicut proportio sinus arcus d e ad sinum arcus d a. Et proportio sinus arcus d z ad sinum arcus d a est maior proportione sinus arcus d e ad sinum arcus d a, ergo proportio sinus arcus z d ad sinum arcus d a est maior proportione sinus arcus l k ad sinum arcus e m, et propterea iterum quod duo circuli a b et d k iam secuerunt se supra punctum z, et signata sunt super eos duo puncta e et d, et productae sunt ab eis duae perpendiculares e m et d a, erit proportio sinus arcus z d ad sinum arcus d a sicut proportio sinus arcus e z ad sinum arcus e m, sed iam fuit proportio sinus arcus z d ad sinum arcus d a maior proportione sinus arcus l k ad sinum arcus e m, ergo proportio sinus arcus z d e ad sinum arcus e m maior est proportione sinus arcus l k ad sinum arcus e m, ergo sinus arcus z e est maior sinu arcus l k, et unusquisque amborum est minor quarta circuli, ergo arcus z e est maior arcu k l, ergo superfluitas arcus e b super arcum b l est maior superfluitate arcus b z super arcum b k. Et similiter si protraxerimus a puncto e iterum perpendicularem super arcum d e, quae sit perpendicularis e n, erunt duo circuli l d et d t se secantes supra punctum d, et iam signata sunt super unum eorum duo puncta l e, et producuntur ab eis duae partes perpendiculares l t et e n, ergo proportio sinus arcus l t ad sinum arcus e n est sicut proportio sinus arcus l d ad sinum arcus d e. Verum proportio sinus arcus l d ad sinum arcus d e iam posita fuit sicut proportio sinus arcus d e ad sinum arcus d a, et proportio sinus arcus d e ad sinum arcus d a est maior proportione sinus arcus h d ad sinum arcus d a. Proportio ergo sinus arcus l t ad sinum arcus e n est maior proportione sinus arcus h d ad sinum arcus a d, et propterea iterum quod duo circuli a b et d t se secant supra punctum h, et iam signata sunt super ambos duo puncta e et d, et protrahuntur ex eis duae perpendiculares e n et a d, ergo proportio sinus arcus e h ad sinum arcus e n est sicut proportio sinus arcus h d ad sinum arcus a d, proportio ergo sinus arcus l t ad sinum arcus e n est maior proportione sinus arcus e h ad sinum arcus e n, ergo sinus arcus l t est maior sinu arcus e h, et unusquisque amborum est minor quarta circuli, ergo arcus l t est maior arcu e h, ergo superfluitas arcus l g supra arcum e a est maior superfluitate arcus t g super arcum a h. Et similiter est dispositio omnium duorum circulorum signatorum super arcum e b et e a, et illud est quod demonstrare uoluimus. Haec est ergo summa, quam necesse est praemittere eorum quibus consstit excusatio a figura sectore, et a libro Theodosij, et a libro Milei, et quibus declarantur, quae ipse dixit in libro suo sine demonstratione. Quare est liber iste noster stans per se, non egens alio sicut praemisimus.

⟨I.19⟩ ⟨PROPOSITIO⟩ XIX.

ET incipiamus nunc dicere ea quae necessaria sunt in extractione quantitate cordarum cadentium in circulo propter arcus suos et quantitatem arcuum propter cordas suas, et est, cum fuerit semicirculus a b g, et diameter eius a g, cuius centrum sit punctum d, et protrahatur ex eo super diametrum perpendicularis, quae sit linea b d, et diuiserimus lineam a d in duo media super 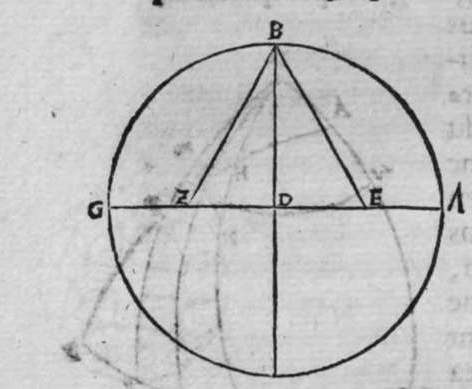punctum e, et continuauerimus lineam b e, et separauerimus ex linea e g, quod sit aequale lineae b e, et sit linea e z, et produxerimus lineam b z, tunc dico, quod linea d z est aequalis lateri decagoni cadentis in circulo a b g, et quod b z est aequalis lateri pentagoni cadentis in eo. Quod sic probat, propterea quod linea a d iam est diuisa in duo media super punctum e, et addita est in longitudine eius linea d z, fuerit multiplicatio lineae a z in z d, et quadratum e d aequalia quadrato e z. Sed quadratum e z est aequale quadrato e b, et quadratum e b est aequale quadrato d b, et quadrato d e, ergo multiplicatio lineae a z in z d, et quadratum e d sunt aequalia quadrato b d et quadrato e d. Proiecto ergo quadrato e d communi, remanet multiplicatio lineae a z in z d aequalis quadrato b d, linea uero b d est aequalis lineae a d, ergo multiplicatio lineae a z in z d, est aequalis quadrato a d, ergo linea a z iam diuisa est secundum proportionem habentem medium et duo extrema, et latus eius longius est linea a d, et est latus h exagoni cadentis in circulo a b g, ergo linea d z est latus decagoni cadentis in eo, et quadratum lineae z b est aequale duobus quadratis duarum linearum b d d z. Sed linea b d est latus exagoni, et linea z d est latus decagoni cadentium in circulo a b g, ergo linea b z est aequalis lateri pentagoni cadentis in eo, et illud est cuius uoluimus declarationem.

⟨I.20⟩ ⟨PROPOSITIO⟩ XX.

ET propterea quod latus exagoni cadentis in circulo est medietas diametri circuli, est latus exagoni notum etiam, et propterea quod quadratum diametri est aequale duplo lateris quadrati cadentis in eo, est iterum latus quadrati notum, et quoniam quadratum lateris trianguli cadentis in eo est triangulum quadrati medietais diametri eius, est iterum latus trianguli notum. Qualiter autem extrahatur quantitas cordae cadentis in circulo, scilicet proportio eius ad diametrum ipsius, propter arcum suum cum est notus, aut arcus ex corda sua cum est corda nota ex quantitate, cum qua diameter est nota figura, magnae excusationis consurgit ad illud in hac intentione, et est, cum in circulo est figura quadrilatera qualitercunque cadat. Sitque figura a b g d, et protrahantur duae diametri eius duabus lineis a g b d, tunc aggregatum ex multiplicatione laterum oppositorum eius ad inuicem, scilicet aggregatum ex multiplicatione a d in b g, et multiplicatione a b in g d et aequale multiplicationi unius duarum diametrorum in secundam scilicet lineae a g in lineam b d, quod sic probatur. 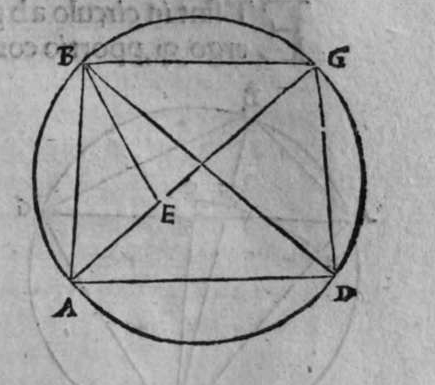Faciam super punctum b lineae a b angulum aequalem angulo g b d, qui sit angulus a b e, et angulo b a e aequali angulo b d g, remanet angulus b e a aequalis angulo b d g, ergo triangulus a b e est similis triangulo b g d. Multiplicatio ergo lineae a b in lineam g d est sicut multiplicatio a e in lineam b d, et proptetea iterum, quia angulus a b d est aequalis angulo e b g et angulus a d b est aequalis angulo b g e, remanet angulus b a d aequalis angulo g e b, ergo triangulus b e g est similis triangulo b d a quare est multiplicatio a d in b g aequalis multiplicationi b d in g e. Iam uero fuit multiplicatio a e in b d, sicut multiplicatio lineae a b in lineam g d, ergo multiplicatio totius lineae a g in lineam b d est aequalis multiplicationi lineae a b in g d, et sicut multiplicato lineae a d in b g. completa est eius declaratio.

⟨I.21⟩ ⟨PROPOSITIO⟩ XXI.

ET postquam declaratum est hoc, tunc ponamus in circulo a b g duas cordas a b et a g notas scilicet ut sit proportio cuiusque amborum ad diametrum circuli nota, et continuemus extremitates 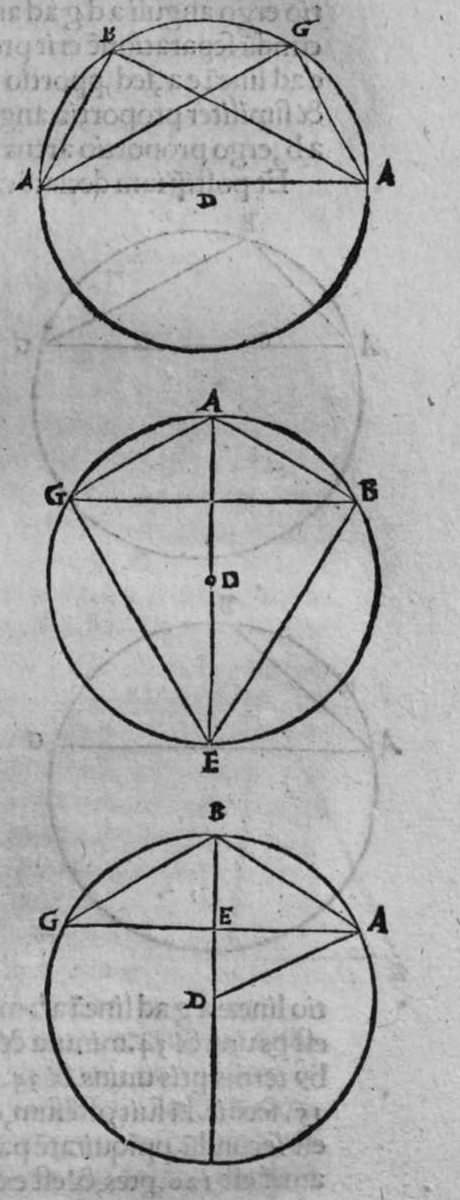earum cum corda b g. Dico ergo, quod corda b g iterum est nota, cuius haec est demonstratio. Continuabo punctum a, qui obuiat duabus lineis a b et a g cum centro circuli, quod est punctum d linea a d, et faciam ipsam penetrare ad circumferentiam circuli usque ad punctum e, et continuabo punctum e, quod est extremitas diametri duobus punctis b et g duabus lineis e b et e g, et propterea quod unaquaeque duarum linearum a b et a g posita est nota per quantitatem qua diameter est nota, et unusquisque duorum angulorum a b e et a g e est rectus, erit propter hoc unaquaeque duarum linearum b e et g e nota. Quare erunt quinque lineae quadrati a b g e notae, quae sunt lineae a b, a g, b e, g e, et diameter circuli scilicet linea a e, et sexta eius reliqua, quae est b g ignota, et egreditur nota, et illud est, quod declarare uoluimus. Et similiter si posuerimus duos arcus a b, a g sese ordinate sequentes secundum quod est in figura secunda, Dico iterum, quod b g continuans inter extremitates duorum arcuum est nota, quod sic probatur. Reiterabo figuram continuando punctum a iterum centro circuli linea a d e, et continuabo punctum e duobus punctis b g, ergo est unaquaeque ambarum nota per quantitatem, qua diameter a e est nota, quare sunt figurae a b e g quadrilatere lineae quinque notae, scilicet lineae a b a g et b e et e g et a e similiter notae, ergo linea b g residua est nota.

⟨I.22⟩ ⟨PROPOSITIO⟩ XXII.

ET iterum sit in circulo a b g corda a g nota, et diuidamus arcum eius in duo media supra punctum b, et continuemus duas lineas a b, g b, dico, quod unaquaeque ambarum est nota, cuius haec est demonstratio. Inueniam centrum circuli, quod est punctum d, et continuabo ipsum cum puncto b linea d b, et secet cordam a g supra punctum e, propterea ergo quod duo arcus a b, b g sunt aequales, secat linea d b cordam a g in duo media, et est super eam perpendicularis, ergo quadratum medietatis diametri, quae est linea a d, est aequale quadratis duobus duarum linearum a e et d e, et propterea quod linea a e posita est nota per quantitatem, qua medietas diametri a d est nota, et est medietas eius, quae est a e nota, remanet quadratum d e notum, ergo linea e d est nota, sed medietas diametri b d est nota, sit ergo propter illud linea b a nota, completa est declaratio eius.

⟨I.23⟩ ⟨PROPOSITIO⟩ XXIII.

ET sint in circulo a b g duae cordae a b, b g diuersae, et sit corda b g maior corda a b, dico ergo, quod proportio cordae b g ad cordam a b est maior proportione arcus b g ad arcum 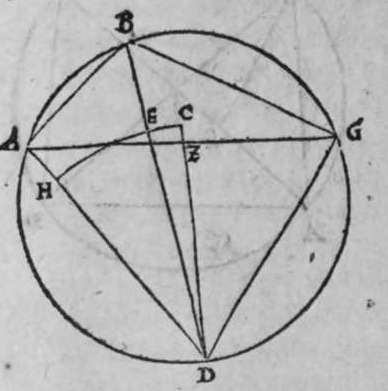a b, quod sic probatur. Producam lineam a g, et diuidam angulum a b g in duo media lineae b d, et producam duas lineas d a, d g, et protraham ex puncto d perpendicularem super lineam a g, quae sit perpendicularis d z, quare erit linea a d maior linea d e, et linea d e maior linea d z. Quod si posuerimus punctum d centrum, et cum longitudine d e fecerimus circulum c e h, cadet punctum c extra punctum z, et cadet punctum h in eo, quod est inter duo puncta a d secundum quod est in figura. Quare sector e d c est maior triangulo e d z, et sector e d h est minor triangulo e d a, quare proportio sectoris e d c ad sectorem e d h est maior triangulo e d z ad triangulum e a d, ergo proportio anguli z d e ad angulum e d a, est maior proportione lineae e z ad lineam e a, ergo secundum compositionem erit proportio anguli z d a ad angulum e d a maior proportione z a ad lineam a e. At linea a g est dupla lineae a z, et similiter angulus a d g est duplus anguli a d z, proportio ergo anguli a d g ad angulum a d e, est maior proportione lineae a g ad lineam a e, ergo secundum separationem erit proportio anguli g d e ad angulum a d e maior proportione lineae g e ad lineam e a, sed proportio lineae g e ad lineam e a est sicut proportio lineae g b ad lineam b a, et similiter proportio anguli g d e ad angulum a d e est sicut proportio arcus h g ad arcum a b, ergo proportio arcus b g ad arcum a b est maior proportione cordae b g ad cordam a b. Et postquam iam declarata sunt omnia quae diximus, tunc ponamus circulum a b g, et diuidamus 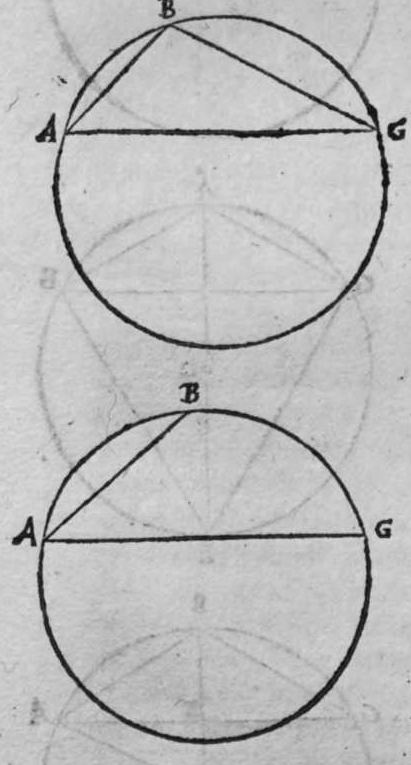circumferentiam eius in 300. et 60. partes aequales. quare est latus decagoni cadentis in eo, et est corda a b nota, scilicet, est proportio eius ad diametrum proportio nota, et latus exagoni, et est linea a g nota. Quare est per illud quod declarauimus linea b g continuans inter extremitates ambarum nota, quae est corda arcus 24. ergo corda medietatis eius, quae est 12. est per illud quod declarauimus iterum nota, et est corda 6. partium etiam nota, et similiter corda trium partium, et corda partis et semis, et corda trium quartarum partis omnes notae sunt, quare egreditur corda trium quartarum partis scilicet 47. minuta, et 8. secunda per partes, quibus diameter est 140. partes. Et ponamus in circulo a b g cordam a g cordam partis unius, et cordam a b cordam trium quartarum partis scilicet 47. minutorum et 8. secundorum, et iam declaratum est nobis nuper, quod proportio cordae a g ad cordam a b est minor proportione arcus a g ad arcum a b. Proportio ergo lineae a g ad lineam a b minor est proportione unius et tertiae ad unum, ergo est minor proportione partis unius ex duorum minutorum et 50. secundorum et 40. tertiorum ad 47. et 7. minuta et 8. secunda, quae sunt quantitas lineae a b, et haec proportio est proportio unius et tertiae ad unum. Quod si posuerimus iterum lineam a g cordam partis et mediae, et lineam a b cordam partis unius, declarabitur iterum, quod partis et mediae quantitas est pars una et 34. minuta et 15. secunda per partes, quibus diameter est 120. partes, et propterea, quod est proportio lineae a g ad lineam a b minor proportione partis unius et semis ad unum, et quantitas lineae a g est pars una et 34. minuta et 15. secunda. oportet ut sit corda a b, que est corda partis unius, plus duabus tertijs partis unius, et 34. minutorum et 15. secundum, ergo est plus parte una et duobus minutis et 15. secundis. Iam fuit ostensum, quod est minus parte una et 2. minutis, et 15. secundis, et 40. tertijs, ergo est secundum propinquitatem pars una, et duo minuta, et 15. secunda, et 20. tertia per partes, quibus diaameter est 120. partes, et est ex eo, cuius praecessit declaratio, corda medietatis partis nota, et prouenit etiam 31. minutum et 25. secunda fere. Et postquam illud ita est, tunc declaratae sunt omnes cordae cadentes in circulo. Corda quidem duarum partium declaratur propter compositionem cordae partis et semis, et cordae medietatis partis, et corda duarum partium et semis declarabitur propter cordam trium partium et cordam medietatis partis, et similiter reliquae cordae, et sunt eius declaratio.

⟨I.24⟩ ⟨PROPOSITIO⟩ XXIIII.

ET cum hoc iam sit decdaratum, tunc incipiamus ostendere semitam, qua, quod de lateribus trianguli rectilinei et angulis ipsius ignotum est, producatur propter illud quod de eis notum est, ne fiat sermo in intentione multotiens. Dico ergo, quando in triangulo a b g rectilineo duo latera a b, b g sunt nota, et angulus b, qui contineatur ab ilis duobus notus tunc latus a g est notum, et unusquisque duorum reliquorum angulorum est notus, cuius haec est demonstratio. Protraham a puncto a perpendicularem a d super lineam b g, propterea ergo, quod angulus a b g est notus, et linea b g nota, scitur qualiter cadat perpendicularis a d, scilicet an 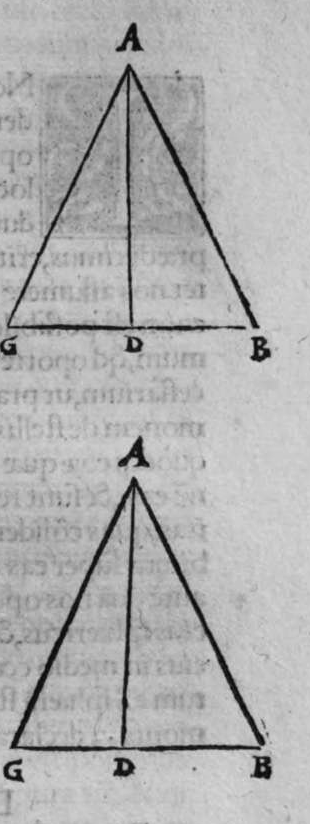cadat in eo, quod est inter duo puncta b et g, aut extra ab eis utrisque, et quoniam angulus d est rectus, est linea a b diameter circuli, qui continet triangulum a b d, et quoniam angulus b est notus, erit arcus illius circuli, qui est super lineam a d notus, corda ergo eius, quae est linea a d, est nota per quantitatem qua diameter circuli est nota. quare remanet linea b d nota, iam fuit linea b g nota per quantitatem, qua unaquaeque duarum linearum a b, b d est nota, Quare fit propter illud linea d g nota per illam quantitatem, et iam fuit ostensum, quod linea a d est nota, ergo oportet ut sit linea a g nota, ergo per quantitatem qua latus a g est 120. est perpendicularis a d nota, ergo arcus qui est super eam circuli continentis triangulum est notus, ergo angulus a g d est notus, et iam fuit angulus a b g notus, quare remanet angulus b a g notus, ergo triangulus a b g est notorum laterum et angulorum, completa est declaratio eius.

⟨I.25⟩ ⟨PROPOSITIO⟩ XXV.

ET si fuerint duo latera eius nota, duo latera a b et a g, et angulus eius notus angulus b, et est ille cui subtenditur unum duorum laterum notorum, tunc indigebit hoc problema conditione una, et tunc deligabitur, et est ut sciamus, angulus eius g, et est ille, cui subtenditur latus secundum duorum notorum, an sit expansus aut acutus. Nam si protrahatur perpendicularis a d, scietur per illud an cadat intra triangulum aut extra ipsum, et declarabitur sicut praemissum est, quod unumquodque duorum laterum a d et b d est notum per quantitatem qua linea a b est nota, et linea a g est nota per illam quantitatem, qua remanet linea d g nota per eam. Et est arcus, qui est super latus a d circuli, qui continet triangulum a g d notus, ergo angulus a g d est notus, et propterea, quod unaquaeque duarum linearum b d et g d iam prouenerunt notae, et propter illud linea b g nota, triangulus ergo a b g est laterum notorum et angulorum, et illud est cuius uoluimus declarationem.

⟨I.26⟩ ⟨PROPOSITIO⟩ XXVI.

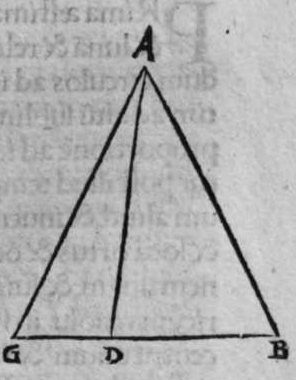ET si illud quod de triangulo notum est, est latera eius tertia, et illud cuius scientia queritur, est sinus angulorum eius, tunc protraham perpendicularem a d, tunc si fuerint duo latera a b a g aequalia, erunt duae lineae b d et g d aequales, quare unaquaeque earum erit nota. Et si fuerint duo latera a b a g diuersa, tunc sit eorum breuius linea a b, erit ergo superfluitas, quae est inter duo quadrata a b, a g nota, et est superfluitas, quae est inter duo quadrata b d, g d, quapropter diuidam superfluitatem illam per lineam b g, et accipiam superfluitatem quae est inter ilud quod exiuit, et inter lineam b g, et accipiemus medietatem illius superfluitatis, quaecunque sit erit linea b d. Multiplicabo ergo eam in seipsam, et proijciam quadratum eius ex quadrato a b, quare remanebit quadratum perpendicularis a d, erit ergo perpendicularis a d nota per quantitatem qua lineae a g et a b sunt notae, quapropter erit linea g d nota, ergo arcus qui est super perpendicularem a d circuli continentis triangulum a d g est notus, ergo triangulus g est notus. quare erit angulus b notus, quod si illud quod egreditur de diuisione superfluitatis, quae est inter quadrata duorum laterum a g et a b per latus b g, fuerit maius latere b g, erit quantitas quae egredit ab angulo b ipsa quantitas anguli, qui sequitur angulum trianguli quaesitum. Proijciam ergo ipsam ex duobus rectis, et remanebit angulus trianguli quaesiti, et propter quod angulus g est notus, remanet angulus a notus. Et si fuerint ea quae de triangulo a b g nota sunt tres anguli eius et inquisiuimus unumquodque trium laterum eius, erit proportio unius ad aliud nota, et illud ideo, quoniam unusquisque arcuum, qui sunt super latera eius circuli, qui continet ipsum, erit notus, ergo erit unaquaeque cordarum eorum, et sunt latera eius nota per quantitatem qua diameter illius circuli est nota, ergo proportio uniuscuiusque laterum eius ad unumquodque duorum reliquorum erit nota, ergo si fuerit unum laterum eius notum per aliquam quantitatem, erit unumquodque duorum reliquorum notum per illam quantitatem, et illud est cuius uoluimus declarationem.

⟨II⟩ LIBER SECVNDVS DE ORDINIBVS SPEcierum huius Scientiae.

INquit Ptolomeus, primum a quo nos oportet incipere in hoc libro, est consideratio in summa dispositionis totius terrae apud totum coelum, et primum, quod oportet sumere in ipso post illud, est inquisitio scientiae loci orbis decliuis, et locorum habitabilium de terra, deinde scientiae diuersitatis horizontum eorum secundum ordinem, qui est propter intentionem. Nam cum antecessit scientia eorum quae praediximus, erit inquisitio de illis, quae sunt absque eis facilioris uiae. Et secundum quod oportet nos assumere in eo, est inquisitio scientiae motus solis et lunae, et quae comitantur eos. non enim est possibile ante comprehensionem horum exquisite perscrutari scientiam stellarum. Et extremum, quod oportet nos sumere in eo, secundum quod ordini simile est, est sermo de stellis, et est necessarium, ut praemittamus sermonem de sphaera stellarum fixarum, deinde adiungamus illi sermonem de stellis quinque, quae nominantur haesitantes, et laborabimus, ut declaremus unum quodque eorum quae diximus, comprehendendo radices et principia, quae perducunt ad cognitionem earum, et sunt res apparentes manifeste sensui, et considerationes, in quibus non est ambiguitas, quas considerauerunt primi, et quae consideratae fuerunt in tempore nostro, et fabricabimus super eas totum quod sequitur eas cum uijs demonstrationum Geometricarum. Summa autem quam nos oportet praemittere in eo, est, ut declaremus quod coelum est sphaericum, et motus eius sphaericus, et quod figura terrae cum omibus partibus suis est sphaerica in sensu, et locus eius in medio coeli est sicut centrum, et quod ipsa est in spacio et magnitudine sicut punctum quantum ad sphaeram stellarum fixarum, et quod ipsa non habet motum localem, et nos praemittemus parum sermonis in declaratione uniuscuiusque istorum ad rememorandum.

⟨II.1⟩ De hoc quod coelum est sphaericum et motus eius sphaericus.

PRima aestimatio antiquorum ad illud quod diximus non fuit, nisi quoniam ipsi uidebant solem et lunam et reliquas stellas moueri semper ab oriente ad occidentem, et motus eorum secundum circulos ad inuicem aequedistantes, qui incipiunt ab infimo inferiore, et eleuantur paulatim ad altum sublimius, ac si ipsae eleuentur a terra, deinde descendunt post illud secundum illam proportionem ad inferius infimum, ac si ipsae cadant in terram, et cadant omnino, deinde morantur post illud tempore aliquo occulte, deinde oriuntur iterum et occidunt, ac si ipsis sit principium aliud, et inueniebant haec tempora quae sunt ab ortu ad occasum, et ab occasu ad ortum, et loca ortus et occasus alternata in maxima parte rei secundum ordinem unum et similitudinem unam, et fuit plurimum quod produxit eorum cogitationes ad firmandum motum esse sphaericum reuolutio stellarum sempiternae apparitionis, quoniam uidentur orbiculariter reuolui circa centrum unum et idem, quod est polus, et illud ideo, quoniam illud punctum circuli celesis oportet ut sit polus necessario, et quaecunque stellarum sunt plus proxime puncto, reuoluuntur in circulis paruis, et quaecunque earum sunt plus elongatae a puncto, reuoluuntur in circulis magnis, secundum quantitatem propinquitatis et elongationis, donec perueniat elongatio ad eas quae occidunt, et earum quae occidunt quaecunque sunt proximiores illis, quae sunt sempiternae apparitionis, sunt minoris morae in occasu, et quaecunque sunt longinquiores, sunt maioris morae secundum quantitatem propinquitatis et elongationis. Ex hoc ergo et sibi similibus tantum fuit primum, quod affirmauit eorum sententias, et fixit in eorum cogitationibus, quod motus coeli eorum est sphaericus. Et post illud consideratio cogitatiua perduxit ad inteligendum reliqua quae sequumtur illud, propterea quod totum quod uidetur in eo de rebus apparentibus est contrarium ei, super quod existit diuersificantium sententia, et illud est, ut nos ponamus, quod homo dicat, quod motus stellarum est secundum rectitudinem usque ad illud, cui non est finis, quemadmodum iam aestimauerunt quidam homines. Quibus ergo modis possibile est, ut uideatur unaquaeque earum in omni die oriri super nos ab ortu uno, et qualiter possibile est, ut redeat ad ortum suum motu eius secundum rectitudinem ad id, cui finis non est existente, et quomodo si redeunt secundum rectitudinem non uidentur redire, et qualiter non alterat eam longitudo, et minuit de lumine eius, et ipsius magnitudine, paulatim deinde occidit, imo uidetur secundum contrarium illius, quoniam ipsa magnificatur apud occasum suum, deinde tegitur paulatim, ac si ipsa a superficie terrae abscindatur. Et quod iterum dicitur, quod ipsae accenduntur a terra, deinde post illud extinguuntur in ea, est res longinquior ab eo, quod est conueniens. Et si nos affirmauerimus, quod sit hic ordo sublimis, qui est in magnitudine et quantitatum stellarum numeratione earum, et elongationibus ipsarum et locis earum, et temporibus ipsarum inanis et uanus, et quod sit natura quarundam partium terrae accendens, et quarundam earum extinguens, imo locus unus quibusdam hominibus sit accendens, et quibusdam hominibus extinguens, et quod sint eaedem stellae quibusdam hominibus accensae, aut quibusdam extinctae, et quibusdam non accendantur adhuc, aut non extinguantur, tunc si concesserimus hoc, licet sit derisio et illusio, ergo quod dicent hanc tenentes sententiam de stellis sempiternae apparitionis, quae non oriuntur neque occidunt, et propter quas causas stellae accensae extinctae extnctae ed. non oriuntur, et occidunt in omni loco, et apparentes quae non oriuntur neque occidunt non sunt apparentes in omni loco semper supra terram. Nam non potest aliquis dicere, quod eaedem stellae accendantur et extinguantur apud quosdam homines semper, et non accidit eis, nisi unum horum duorum apud quosdam. Cum uisibiliter stellae eaedem in quibusdam locis oriri et occidere, et in quibusdam non oriri neque occidere inueniantur, et omnino dico, quod quascunque figuras dederit dator in motu coelesti, praeter sphaericam, tunc necessarium est, ut sint elongationes a terra ad loca alta diuersae, ubicunque sit terra posita, et qualitercunque sit. Et propter illud oportebit, ut uideatur magnitudo quantitatum stellarum, et elongationes earum ab inuicem diuersae in loco uno et omni reuolutione, quoniam ipsae erunt quandoque in elongatione maiore, et quandoque in elongatione minore, de hoc nonnihil uidetur et illud, quod uidetur de additione in magnitudine earum, cum sunt apud horizonta, non uidetur propter propinquitatem earum et paruitatem elongationis apud horizonta. At uero, quoniam uapor humiditatis, qui continet terram, ponitur inter uisum, et eas, quare uidentur ita, sicut illud quod proijcitur in aquam uidetur maius, et quanto plus iungitur inferius, tanto plus est maius additum in magnitudine sua, et significat iterum affirmationem figurae sphaericae, quoniam non est possibilis conuenientia considerationum cum instrumentis, nisi secundum hanc figuram, et cum hac figura tantum, et quod motus coeli non est difficilis, imo est lenior motuum figurarum diuersarum, aut facilior eorum, et res quae est facilioris motus, de superficialibus est circulus, et de corporeis est sphaera, et quod figurarum diuersarum, quarum comprehensio est aequalis, quaecunque plures habet angulos, est maioris quantitatis, et propter illud oportet ut sit circulus maior superficierum, et sphaera maior corporum et coelum maius eo quo est praeter ipsum. Sermo quidem eius, quod figurarum diuersarum, quarum comprehensio est aequalis, quaecunque plures habet angulos, est maioris quantitatis, et propter illud oportet ut sit maior circulus superficierum, et sphaera maior corporum, et coelum maius eo, quod est praeter ipsum ex corporibus, est sermo in ultimo aggregationis, et est cum hoc uanitas sermonis, et hoc est primum, quod apparet de uanitate eius in arte geometriae. Et nunc quidem attendamus ad exponendum sermonem eius, et declarandum illud quod uoluit, et post illud declarandam uanitatem eius in ipso. Dico ergo illud, quod intelligo ex sermone eius, licet non dicitur illud ipsius dicto, sed det illud intentio, quam conatus est declarare, in quantum propterea quod fuit intentio finalis de coelo habita comprehensione plurium, et ut caperet de corporibus quam plurimum possibile est, oportuit ut esset figura eius figura dans illud ei, et est figura sphaerica, quoniam sphaera est maior unaquaque figurarum plurium angulorum, quarum comprehensio est aequalis comprehensioni sphaerae, et propter illud dixit, et sphaera est maior corporum, et coelum est maius eo quod est praeter ipsum ex corporibus, et declaratio huius intentionis, scilicet, quod sphaera est maior figuris plurium angulorum, quarum comprehensio est aequalis comprehensioni sphaerae, est facilis exceptionis secundum quod diximus in tractatu primo huius libri, et procedere ad ostendendum illud quod dat dictio eius, est declarare in primis figuris plurium angulorum aequalium comprehensionis, quod qaecunque earum est plurium angulorum est maioris quantitatis, et cum declaratum fuerit illud permutare iudicum ad circulum et sphaeram, et si non, quomodo ergo egredietur sermo eius, et propter illud oportet, quod circulus sit maior superficierum, et sphaera maior corporum. Et si sciuisset, quod declaratio huius intentionis in figuris ad inuicem esset difficilior plurium quam declaratio eius in figura et sphaera spaera ed., non processisset ad dicendum dispositionem figurarum ad inuicem, cum intentio qua intenditur non sit nisi declaratio dispositionis sphaerae cum figura plurium angulorum, non dispositionis figurae cum figura. Amplius egreditur ex uirtute sermonis eius in permutando iudicium de figuris ad circulum et sphaeram, et quod circulus est plenus angulis superficialibus et sphaera plena angulis corporeis. Et nunc quidem redeamus ad complendum sermonem eius in hoc capitulo, et est, et iam inuenimus uiam ad sciendum illud iterum ex rebus naturalibus de quibus est, quod aether est corpus coeli, est subtilior omnibus corporibus, et magis simile eis ad inuicem, et illa quae sunt similis superficiei ad inuicem, duo tantum sunt de superficialibus circulis et de corporibus sphaerae. Cum igitur ether non sit superficies, et neque sit nisi corpus tunc oportet, ut sit sphaericus, et de eis est, quod omnia corpora terrena, quibus accidit corruptio, creata sunt in figuris suis ex frustis rotundis diuersarum partium, et omnia corpora coelestia creata sunt in figuris suis sphaerica similium partium rotunda, et propter illud oportet, ut sit ether continens ea cum sit similis naturae eorum sphaericus, et quoniam partes eius sunt similes, erit motus eius rotundus cum aequalitate.

⟨II.2⟩ De hoc quod terra cum omnibus partibus suis sit sphaerica in sensu per comparationem ad totum.

ET declaratur nobis iterum, quod terra cum omnibus suis partibus sit sphaericae figurae in sensu. Nos namque uidemus solem et lunam et reliquas stellas non oriri et occidere in omni loco in hora una, sed ortus earum apud illos, qui sunt in oriente, antecedit ortum ipsorum qui sunt in occidente, et occasus eorum apud eos est iterum similiter et post illud, propterea quod nos inuenimus cosiderationes temporum eclipsium, et praecipue lunarum, quae sunt in tempore uno in libris illorum, qui firmauerunt eorum rememorationem antiquorum in locis diuersis, non aequalis spacij a meridie. Et inuenimus semper horas quas scripserunt illi, qui considerauerunt de orientalibus pluris antecessionis ad circulum meridiei, quam illae, quarum rememorationem scripserunt occidentales. Et quoniam iterum inuenimus diuersitatem horarum secundum quantitatem diuersitatis spacij inter loca, oportet ut dicamus, quod superficies terrae est sphaerica, quoniam assimilatio maximi partium terrae in aequalitate sit semper in locis, quae se sequuntur ad inuicem secundum comparationem unam, et si figura terrae foret non sphaerica, non esset ita, et possumus quidem scire illud iterum ex eo quod dicam: Si terra foret concaua, uidentur stellae oriri prius super occidentales, et si esset plana, orirentur super omnes omes ed. qui sunt in terra in hora una, et si esset triangula aut quadrata, aut alicuius alterius figurarum plurium angulorum, orirentur iterum stellae in hora una super omnes inhabitantes in superficie una super rectam lineam. Nos autem nihil horum uidemus, et non est terra figurae columnalis rotunditatis, cuius superficies sit ad orientem et occidentem, et duae superficies duarum basium eius sint ad duos polos mundi, sicut aestimauerunt quidam, quod est propinquius ad sufficientiam, quoniam si ipsa foret ita, non uiderentur aliquis eorum qui habitarent super rotunditatem eius aliquam stellarum apparentium semper, imo stellae aut omnes orirentur aut occiderent semper super omnes eorum, aut stellae eaedem, quarum elongatio ab unoquoque duorum polorum esset elongatio aequalis, sempiternae essent occultationis apud omnes eos, et nos quidem uidemus, quod quanto plus imus ad partem septentrionis, tunc secundum quantitatem nostri incessus in ea, multiplicatur illud quod occultatur a nobis de stellis meridianis, et quod apparet nobis de septentrionalibus. quare declaratur nobis per aequalitatem eius, quod regit rotumditas terrae a nobis, in hijs duabus partibus iterum cum comparantur ad inuicem in omnibus partibus suis quod ipsa est sphaerica, et similiter cum imus in mari ad montes, aut ad loca alta sublimia a quibuscunque horizontibus, aut ad quoscunque fuerimus, uidemus additionem eorum paulatim, ac si ipsi eleuentur ex mari, et quasi ipsi essent submersi in eo.

⟨II.3⟩ De hoc quod terra sit in medio coeli.

ET postquam scimus hoc sicut inquisiuimus, ut sciamus locum terrae, inueniemus, quod non est illud quod apparet nobis in ea, sicut uidemus, ut cum affirmauerimus locum eius in medio coeli, sicut centrum in sphaera tantum. Nam si non fuerit ita, tunc proculdubio terra erit aut egrediens ab axe aequalis longitudinis ab unoquoque duorum polorum, aut fixa super diametrum inclinata ad unum duorum polorum, aut ut non sit super diametrum, neque sit longitudo eius a duobus polis aequalis, quo contradicitur ei, qui dicit, quod locus eius sit primus trium, est illud quod narrabo. Si nos imaginaremur eam remotam cum hominibus a meridie ad superiora aut inferiora, tunc accideret eis cum essent in locis, in quibus est sphaera praeparata, ut non esset apud eos aequalitas noctis et diei semper, quoniam horizon secaret quod est supra terram, et quod est sub ea de coelo absque aequalitate tunc proculdubio. Et cum essent in locis, in quibus est sphaera decliuis, accideret eis, aut ut non aequarentur apud eos nox et dies penitus, aut non esset illud intra situm, qui est medium inter tropicum aestiualem et tropicum hyemalem, quoniam ista duo spacia essent necessario non aequalia, quoniam circulus quem secaret tunc horizon in duo media, non esset circulus aequalitatis, qui est maior circulorum qui reuoluuntur super duos polos motus totius, et neque esset nisi unus circulorum qui aequedistant ei, aut de illis qui sunt ad meridiem, etiam quidem affirmatum est apud omnes homines, quod haec duo spacia aequalia sunt in omni loco per illud quod inuenerunt de aequalitate additionis, quam addit dies aequalis in longitudine sua usque quo perueniat ad longiorem longitudinem suam in tropico aestiuali, eo quod minuit de longitudine sua, usquequo perueniat ad breuiorem breuitatem sui in tropico hyemali. Si imaginaremur terram remotam ad partem orientis aut occidentis, tunc accideret eis, ut non uiderent magnitudinem quantitatum stellarum et elongationes earum aequales secundum dispositionem unam in horizonte matutinali, et in horizonte uespertino, et ut non esset apud eos tempus, quod est ab oriente ad medium coeli aequale tempori quod est a medio coeli ad occidentem, et totum illud est contrarium ei quod apparet, et illud quod refellitur id quod dicit ille, qui ponit locum terrae esse secundum trium, cum est super axem, et inclinata ab uno duorum polorum, quoniam si eset secundum hunc modum superficies horizontis in omni climate non secaret quod est super terram, et quod sub ea est de coelo aequaliter, imo secaret eam cum diuersitate in modis pluribus semper, et unusquisque esset diuersus in seipso, et unusquisque apud alium, et non esset possibile, ut horizon secaret coelum in duo media, nisi ubi esset sphaera recta parata tantum. In decliui autem in qua fieret propinquior alter duorum polorum sempiternae apparitionis, minueretur, quod esset supra terram, et magnificaretur sub ea quod esset semper, et propter illud secaret superficies huius horizontis circulum magnum, qui transit super medium signorum absque aequalitate, et hoc est illud quod non apparet sic, quoniam omnes homines uident sex signa super terram, et sex reliqua occulta, deinde post illud apparent sex occulta supra terram, et occidunt alia residua. Declaratur ergo ex hoc, quod secat horizon circulum signorum semper in duo media, propterea, quod unaquaeque duarum medietatum huius circuli cum integritate sua est ipsamet quandoque supra terram, et quandoque sub ea, et ad ultimum accidet, si locus terrae non esset sub aequatione diei, et esset inclinata ad unum duorum polorum, ad septentrionem aut meridiem, ut non esset umbra gnomonum orientalis in aequalitate diei cum umbra gnomonum occidentali super unam lineam rectam super superficies aequedistantes horizonti, et nos uidemus aequalitatem eius super lineam unam in omni loco, et ex hoc declaratur, quod non affirmatur dictumm eius qui dicit, quod locus terrae est tertius trium quos diximus, quoniam totum quod accideret in duobus locis primis de diuersitate eius quod apparet, aggregaretur in tertio, et penitus dico, quod si alteraretur et permutaretur omnino totum quod affirmatur de antecessione additionis et diminutionis, quae est in die et nocte, non esset terra posita in medio, et non esset possibile, ut essent eclipses lunares in omnibus partibus coeli in oppositione lunae soli super diametrum, quoniam esset plurium eius quod non tegeret terram in oppositione, sed in spacijs, quae esent minora semicirculo.

⟨II.4⟩ Quod terra sit sicut punctum apud coelum.

MAius quo scitur, quod terra in sensu quantum ad spacium quod peruenit ad or bem stellarum fixarum sit sicut punctum, est quod magnitudo quantitatum stellarum et spacia quae sunt inter eas, uidentur in omni loco in una hora aequalia et similia, sicut inuenimus per considerationes, quae sunt earundem rerum in climatibus diuersis in una hora, non diuersas neque altera tas, et neque in re parua, et inuenimus iudicium gnomonum umbrae in quibuscunque partibus ponantur terrae, et caeterorum habentium armillas, sicut iudicium centri terrae ueri, et uidentur res quae uidentur per considerationem cum eis, et reuolutio umbrae conueniens rebus positis ad res quae apparent, sicut si esent supra punctum medij terrae, et significatio manifesta, quod hoc sit sicut diximus, est quod superficies quae egrediuntur ex uisibus nostris in omni loco quae nominantur horizontes, secant semper sphaeram coeli totam in duo media, et non esset possibile, ut illud es set magnitudo terrae sensata quantum ad spacium coeli, et neque esset nisi superficies, quae transit super centrum terrae, sola secans sphaeram in duo media. Superficies uero quae transiret super quemlibet locum superficiei terrae, quicunque esse, faceret semper partes quae essent sub terra maiores eis, quae supra eam essent, et nos non uidemus ita.

⟨II.5⟩ Quod terra non habeat motum localem.

ET per simile eius quod iam declaratum est in eis quae praemissa sunt, quod terra non est egrediens a centro declaratur, quod non est possibile, ut sit terrae motus ad aliquam partium, neque motus localis omnino a centro, quoniam si foret, acciderent illa accidentia quae acciderent, si esset locus eius extra medium, et propter hoc uidi, quod perscrutari de causis motus ad medium iterum est superfluum, cum iam demonstratum sit semel, quod terra sit in medio mundi, et quod grauia omnia redeunt ad ipsam, et leuis quod apparet ex eis, quorum appropinquat acceptio in inuentione eius quod diximus, est, quod cum eo quod ostendimus, quod figura terrae est sphaerica, et locus eius est medium totius, est quod motus corporum grauium proprij eius, et partes motus in omni hora et in omni loco terrae sunt secundum rectos angulos super superficiem ponderatam egredientem ad locum casus super contactum. Manifestum est ergo, cum hoc sit secundum quod diximus, quod ipsa peruenienient per motus suos ad centrum, si non superficies terrae resisteret eis, et perhiberet ea, quoniam linea recta quae transit super centrum a loco, in quo superficies tangit sphaeram, est iterum secundum rectos angulos super superficiem. Et illi quidem, qui aestimauerunt, quod de mirabilibus est, ut corpus terrae non sit sustentatum super aliquod, et non subiungatur et inferius descendat propter multitudinem suae grauitatis, errauerunt, quia posuerunt comparationem per id quod accidit eis, non per id quod comitatur totum. Et si ipsi scirent, quod comparatio terrae apud corpus continentis, est comparatio puncti et centri, non uiderent hoc esse mirum, quoniam ipsi uident quod possibile est hoc modo, ut sit illud quod est in fine paruitatis per comparationem ad illud, quod est in fine magnitudinis retentum propter illud quod est in fine magnitudinis similium partium, ita, ut sit illud quod est in fine paruitatis remanens in suo loco, et impellatur per illud quod est in circuitu eius ex omnibus partibus eius, quod est in fine magnitudinis in pulsione simili et aequali, quoniam mundus in seipso non habet superius neque inferius, quemadmodum neque imaginatur illud in sphaera. Corpora autem quae sunt in eo per quantitatem motuum eorum propriorum naturalium parua uadunt quae ex eis sunt leuia subtilia ad manifestam mundi superficiem, scilicet continentem ipsum, Quare aestimant, quod motus eorum ad superiora est, et hoc est apud omnes homines, quoniam illud quod est super capita nominatum supra, est in partes superficiei continentis. Verum grossa grauia intendunt ad centrum, et aestimant, quod cadant ad inferiora, quoniam id quod sequitur pedes omnium hominum, nominatum inferius est in parte centri terrae, et propter illud aggregantur in circuitu medij ex impulsione ad inuicem ex omnibus partibus impulsione aequali simili, et propter hoc res graues si sint paruae, consequuntur totalitatem terrae, licet magna sit quantitas eius apud quntitatem eius quod uenit ad eam, quoniam ipsa est fixa, recipiens totum quod cadit ad eam ab omnibus partibus. Et si terrae et corporibus grauibus, quae sunt praeter ipsam, inesset motus unus communis, terra superfluitatem suae magnitudinis et grauitatis uinceret omne quod est praeter eam, quare inferius descenderet et dimiteret animalia, et quae sunt praeter eam de rebus grauibus, et penetraret uelociter omnia quae continent ipsam et corpus coeli omnino. Verum aestimare hoc et similia est risus, uerum tamen quidam postquam non fuit apud eos quo contradicerent huic sententiae, concedunt illuo, et aestimant, quod si ipsi dixerint, quod coelum non mouetur, et quod terra mouetur super axem unum ab oriente ad occidentem, et quod reuolutio eius est in omni die reuolutio una fere secundum propinquitatem, aut quod coelum et terra simul mouentur super axem unum, sicut diximus, et per quantitatem qua unum eorum consequitur alterum, non erit aliquid contradiens illi, et erit sermo eorum secundum eorum aestimationem sufficiens. Et ignotum est eis, quoniam propter illud quod apparet de stellis non prohibet illud, quin sit licut dicunt secundum aestimationem absolutam, uerum propter illud quod accidit in nobis et in aere declaratur, quod sermo eorum est maxima ignorantia. Et si nos concesserimus eis illud quod est contrarium naturae, ut leue subtile similium partium aut non moueatur omnino aut ut sit modus eius non diuersus a motu eius, quod contrarium est ipsi in natura, quamuis nos uideamus uerisimiliter aerem et res alias minus subtiles eo uelocioris motus, eo quod est terrenum, et concessimus eis iterum, ut sit graui grosso diuersarum partium motus proprius uelox aequalis, quamuis uideamus res terrenas difficilis receptionis, ut alia moueant eas. Nam ipsi concedunt, quod motus terrae est uelocior omnibus motibus qui sunt in circuitu eius, propter reditionem ipsius ad locum suum in huiusmodi hora breui. Et si esset res ita, omnia quae non essent firmata super eam, sentirentur semper mota contra motum terrae, et non uideremus motum nubium ad orientem, neque alicuius auium, neque alicuius eorum quae proijciuntur, propterea quod terra uinceret omnem rem semper propter uelocitatem sui motus ad orientem, et existimaretur, quod illud quod esset praeter eam moueretur semper ad partes occidentis. Quod si ipsi dixerint, quod aer mouetur iterum cum terra motu aequali motui eius in uelocitate, tunc oportebit, ut uideatur semper motus corporum quae sunt in ipso diminutus ex motibus amborum simul. Quod si dixerint illa fixa annexa in aere, quasi consolidata mouentur cum eo, tunc consequeretur, ut non uideantur antecedere neque postponi, imo sunt fixa semper, et non sit eis motus localis, et neque redeant, neque in transitu eorum quae de ipsis transeunt, neque in uolatu eorum quae uolant, neque in cursu eorum quae de ipsis proijciuntur, sed nos uidemus totum illud uisibiliter, et quod non consequitur omnino aliquid eorum uelocitas neque tarditas propter motum terrae. Iam ergo sufficit nobis id quod diximus de radicibus quae praecesserunt per necessitatem rerum particularium quae ponuntur in hac scientia, et rerum quae sequuntur eas secundum intentionem abbreuiationis et breuitatis, et affirmabuntur et uerificabuntur secundum complementum per testimonium conuenientiae eius, quod ostendimus in sequenti de eis quae sunt fabricata super cas propter illud quod apparet sensui.

⟨II.6⟩ Quod species motuum, qui sunt in coelo, sunt duae.

ET cum eo quod diximus, oportet ut sit ex summa eius quod praecessit iterum ut sint motus primi, qui sunt in coelo, duo, quorum unus est ille, qui mouet totum semper ab oriente ad occidentem cum dispositione una, et cum reuolutionibus aequalis uelocitatis, et super circulos aequedistantes adinuicem, quorum reuolutio est super duos polos sphaerae, quae reuoluit totum cum aequalitate, et nominatur maior horum circulorum aequator diei, quoniam circulus horizontis cum sit de circulis maioribus, diuidit semper hunc circulum inter eos in duo media. Cum ergo transit sol super eum, aequantur nox et dies, et aequantur quantum ad sensum in omni terra, et motus alter qui mouet sphaeram stellarum currentium ad contrarium motus primi, est super duos polos alios, et non affirmamus illud quod narramus, nisi quoniam consideramus omnia quae sunt in coelo in omni die uidemus ea cum sensu in die uno oriri, et mediare coelum, et occidere super loca similia in forma aequedistantia aequatori diei, et haec est proprietas motus primi. Cum ergo considerauerimus in diebus continuis, uidebimus omnes stellas, praeter solem et lunam et stellas erraticas habentes spacia ab inuicem fixa, adhaerentes locis proprijs cum motu primo secundum comparationem rei, et uidebimus solem et lunam stellas haesitantes moueri motibus diuersis, non aequalibus adinuicem, ueruntamen omnes per comparationem ad motum primum mouentur ad orientem, scilicet ad partes, in quibus dimittunt eas post se, stellas habentes fixa spacia ab inuicem, quasi illae quas reuoluit motus unus. Et si esset motus stellarum erraticarum et solis et lunae iterum super circulos aequedistantes aequatori diei super duos polos motus primi, esset in affirmatione nostra, quod motus totius esset motus unus, et quod motus iste sequeretur motum primum sufficienter, et esset de probabilibus, ut diceremus, quod motus earum ad contrarium non eset, nisi per aestimationem, non quod esset eis motus secundum contrarium. Nos uero uidemus eis cum motibus earum ad orientem, motus ad septentrionem et meridiem, et uidemus quantitatem elongationum earum in eis diuersam, et forsitan accidit, ut aestimetur, quod declinatio earum illa in eis ambobus sit propter res impellentes eas, uerum si declinatio earum esset secundum hunc modum, esset diuersa non ordinata. Quia ergo ei est ordo, tunc oportet ut sit propter circulum decliuem ab aequatore diei et ex hoc inuenimus hunc circulum esse circulum unum, et eundem proprium stellis erraticis, et inuenimus motum solis signantem ipsum secundum ueritatem, et super duo latera huius circuli, et super ipsum est transitus lunae et quinque erraticarum, et transitus earum a septentrione ad meridiem, et a meridie ad septentrionem, praeter quod aliqua earum pertranseat quantitatem spacij determinati sibi ab utroque latere eius, neque in paruo. Et nos uidemus hunc circulum ex circulis magnis, propterea quod declinatio solis ad septentrionem et meridiem ab aequatore diei est quantitatis unius, et super hunc eundem circulum et a duobus lateribus eius sunt motus stellarum erraticarum omnium ad orientem, ergo oportet necessario ut affirmemus esse motum alium secundum, praeter motum primum, qui fiat super duos polos huius circuli, et ad contrarium partis motus primi. Nam si nos imaginati fuerimus circulum magnum signatum super polos duorum circulorum, scilicet circuli aequatoris diei, et circuli decliuis ab eo, sciemus necessario quod ipse secat unumquenque duorum circulorum in duo media et orthogonaliter, et inueniemus in circulo decliui quatuor puncta, quorum duo sunt super quae secat ipsum circulus aequatoris diei, quorum unumquodque est alteri oppositum nominata aequantia diem, quorum unum est illud, super quod est transitus a meridie ad septentrionem, nominatum uernale, et alterum illud super quod est transitus a septentrione ad meridiem nominatum autumnale, et duo puncta reliqua, super quae secat ipsum circulus magnus signatus super polos duorum circulorum, quorum unumquodque iterum alteri est oppositum nominata tropica, quorum unum est illud quod est in eo, quod sequitur meridiem, ab aequatore diei nominatum tropicum hyemale, et alterum quod est in eo quod sequitur septentrionem, ab aequatione diei nominatum tropicum aestiuum. Scitum ergo est, quod motum primum continentem omnes motus alios designat, et quasi comprehendit et determinat iste circulus magnus signatus super polos duorum circulorum cum reuolutionibus suis, et cum reuolutionibus omnium quas secum facit ab oriente ad occidentem, et est fixus super duos polos aequatoris diei, sicut figitur circulus, qui nominatur circulus meridiei super eos ambos, qui per id quod dicemus tantum differet a circulo quem diximus, signato super polos duorum circulorum, et est, quod ipse non est signatus super duos polos orbis decliuis, et quoniam ipse iterum est orthogonalis super horizonta in omni hora, nominatur circulus meridiei, propter quod illud, cuius narratio est haec, cum secet unamquanque duarum medietatum sphaerae celestis, scilicet quae est supra terram, et quae est sub ea, in duo media, determinat medium duorum temporum scilicet diei et noctis, et motum quidem secundum multarum diuersitatum continet motus primus, et continet ipse sphaeras omnium stellarum erraticarum, et mouet eas motus primus, quem diximus, ab oriente ad occidentem, et mouetur ipse ad contrarium motus illius super duos polos circuli decliuis, qui sunt fixi semper in circulo, qui terminat motum primum, scilicet circulo signato super polos duorum circulorum, et sunt moti cum eo, et sunt adhaerentia in motu secundo, qui est ad contrarium primi loca amborum in circulo magno reuoluto cum eis decliui ab aequatore diei.

⟨II.7⟩ De scientijs particularibus.

INquit auctor, quoniam primum harum scientiarum particularium est cognitio quantitatis eius quod est inter arcum, qui est inter duos tropicos, et non fuit uia ad cognoscendum illud sine instrumento, quo consideretur elongatio solis a summitate capitum in hora meridiei, et huius instrumenti praeparatio non praeparatur nisi super lineam meridiei, oportet ut praemittamus sermonem inueniendo lineam meridiei in horizonte quolibet, et est secundum quod narrabo. Describam in superficie marmoris, super quod praeparatur instrumentum, circulum, super quem sint a b, cuius centrum sit b, et ponam super punctum g perpendicularem super superficiem maioris marmoris, qui sit perpendicularis g d. Sitque longitudo eius tantae quantitatis, ut abbreuietur umbra eius in hora meridiei a circumferentia circuli, et pertranseat eam in extremitatibus diei, et ponam illud marmor in superficie horizontis, ita, ut si inpendamus super illam perpendicularem, et est illud quod nominant artifices cementarij plumbum, et non cessabimus fulcire ipsum rebus minutis subtilibus tandem, donec fiat illa perpendicularis fixa in centro circuli aequedistans lineae plumbi. Erit ergo tunc perpendicularis, ita, quod si fieret, ut penetraret, transiret per zenith capitum, et considerabimus umbram illius perpendicularis ante meridiem, donec fiat extremitas umbrae eius, et est linea a g figurae super circumferentiam circuli punctum a, et considerabimus ipsam iterum post meridiem, donec fiat extremitas umbrae eius, quae est linea a g super circumferentiam circuli, et signabimus super ipsam punctum b, et diuidam arcum, qui transit per duo puncta a b, in duo media super punctum e, et producam lineam g e et faciam ipsam penetrare in ambas partes. Dico ergo, quod ipsa est linea meridiei, quod sic probatur. Ponam circulum horizontis z h, et circulum super quem reuoluitur sol l t k m, et sit punctum super quem est sol 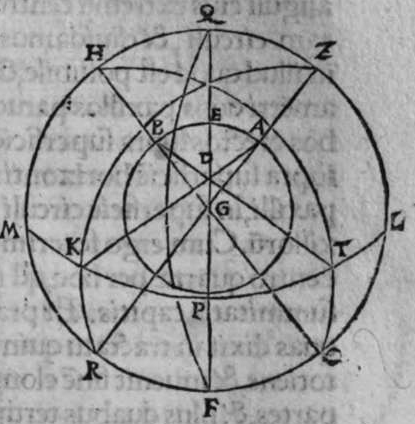ante meridiem, scilicet, quando est umbra perpendicularis linea g a punctum k, et linea radij k d a, et post meridiem quando est umbra perpendicularis linea g b punctum t, et linea radij linea t d b, et sit zenith capitum punctum s, et faciamus transire super ipsum et suum unumquodque duorum punctorum k et t duos circulos magnos, qui sunt duo circuli z k r, h t o, et sit circulus meridiei circulus q s p, et differentia communis ei et circulo horizontis linea q g f, propterea ergo, quod linea a g est aequalis lineae b g linea g d communi, et duobus angulis a g d et b g d aequalibus, quoniam unusquisque eorum est rectus, erunt duo anguli g d a et b d g aequales, ergo duo anguli s d k, s d t sunt aequales. Et propterea quod non est differentia inter punctum d et inter centrum, erit arcus s k aequalis arcui s t, et propterea quod circulus meridiei, scilicet circulus f s q est transiens per duos polos circuli l t k m, est erectus super ipsum orthogonaliter, est portio p s q erecta super circulum l t k m super diametrum eius, et iam signatus est super ipsam punctus s, et arcus p s minor est semicirculo, et linea egrediens ex puncto s ad punctum k est aequalis lineae egredienti ex puncto s ad punctum t, ergo est arcus k p aequalis arcui p t, et propterea quod circulus meridiei diuidit arcus diei in duo media est arcus l p aequalis arcui p m, quare remanet arcus l t aequalis arcui m k, et propterea quod duo arcus s t, s k sunt aequales, remanent duo arcus t o, k r aequales. Quare sunt duae portiones o s h et r s z erectae super diametrum circuli z h orthogonaliter, et iam signata sunt super eas duo puncta k t, et arcus k r et t o sunt aequales, et unusquisque eorum est minor semicirculo, et linea egrediens ex puncto k ad punctum m est aequalis lineae egredienti ex puncto t ad punctum l, ergo est arcus m r aequalis arcui l, propterea quod circulus f s q est transiens super duos polos duorum circulorum z h, et l t k m est diuidens arcus separatos eorum amborum in duo media, quapropter erit arcus f l aequalis arcui f m, ergo remanet arcus f o aequalis arcui f r, ergo duo anguli e g f et r g f sunt aequales, ergo duo anguli a g e et b g e sunt aequales, ergo linea f g q, quae est differentia communis circulo meridiei et circulo horizontis, diuidit arcum a e b in duo media supra punctum e, et illud est quod uoluimus declarare. Postquam ergo extraxerimus illud secundum hunc modum, accipiemus armillam de aere aequalis quantitatis in latitudine sua et sua grossitie, sapienti arte factam, uerificatae rotunditatis, et diuidam unam facierum eius in 300. et 60. partes, et diuidam partes illas usque ad illud quod est possibile, et ponam hunc circulum loco circuli meridiei, ita, ut ponam ipsum supra marmor, et ponam marginem eius super illam lineam productam in marmore, et erigam eam super superficiem marmoris super rectos angulos, donec uerificetur quod ipsa est in superficie circuli meridiei, et sit intra ipsam armilla altera subtilis, quae reuoluatur in extremitate huius armillae, et sit in eius superficie. Postquam nos posuerimus in extremitatibus duabus diametri eius duo ligna aequalia in longitudine et latitudine erecta super superficiem eius secundum rectos angulos, et posuerimus in medio latitudinis amborum duo instrumenta obuiantia superficiei armillae maioris, et sit marmor illud in loco detecto soli, et non cessemus considerare solem in hora in qua sit sol super marginem armillae maioris secundum ueritatem, ita, ut reuoluamus superficiem armillae minoris, donec obumbretur lignum inferius a superiore secundum aequalitatem totum, faciet ergo nos uidere tunc extremitas instrumenti, quod est in medio latitudinis ligni superioris, per illud super quod cadit de partibus signatis in superficie armillae maioris, elongationem solis a puncto summitatis capitis, et non cessemus considerare ipsum in hora, in qua scimus quod sol approximat puncto tropici aestiui, donec sciamus finem latitudinis eius aut propinquitatis ipsius a puncto summitatis capitis in illa regione, in qua est consideratio, deinde consideremus eum iterum in hora, in qua est proximus tropico hyemali, deinde inueniamus punctum in quo est longinquior, et illud in quo est propinquior, quam esse potest a summitate capitis, quare sciemus tunc ex longitudine, quae est inter illa duo puncta in superficie armillae maioris, quantitatem arcuis circuli meridiei, quae est inter duos tropicos, et est arcus, qui est inter reuolutionem capitis signi Cancri, et reuolutionem capitis Capricorni. Et praeparatur consideratio illius iterum, si sumamus laterem aut frustum ligni quadratum uehementis leuitatis, quod in sua quadratura bene sit praeparatum, et ponamus punctum anguli eius extremum centrum, et mensuremus latitudinem unius laterum eius, et faciamus quartam circuli, et diuidamus eam in 90. partes aequales, et diuidamus unamquanque partem earum in illud quod est possibile, et figamus in angulo quem posuimus centrum, et in extremitate diametri duos paxillos paruos aequales, et similes ab omnibus partibus, et ponamus eos ambos erectos supra superficiem portionis secundum rectos angulos, et praeparemus eam erectam supra superficiem horizontis super lineam meridiei, ita, ut sit superficies eius, in qua sunt duo paxilli, in superficie circuli meridiei, suspendendo perpendiculum in extremitatem duorum paxillorum. Cum ergo fecerimus illud, significabit nobis umbra paxilli superioris, qui est in centro quartae per hoc, quod ipsa secat arcum quartae elongationem solis in meridie a puncto summitatis capitis. Et praeparatur consideratio illius iterum cum duabus regulis longis, quas dixit in tractatu quinto libri sui, dixit enim, quod continuauerit considerationem illius multotiens, et inuenit finem elongationis solis in meridie et septentrione a summitate capitis 47. partes, et plus duabus tertijs partis, et minus medietate et quarta partis, et dixit, quod illud fuit conueniens ei quod inuenerunt Arcusianus et Abrachis, et est possibile per hanc considerationem consequi declinationem habitationis, in qua sit illa consideratio ab aequatore diei, ita, ut diuidamus arcum, qui est inter duo puncta, in duo media. Illud ergo erit punctum, super quod circulus meridiei secat circulum aequatoris diei, quare sciemus quantum est inter illud punctum et summitatem capitis, et illud est latitudo illius regionis in qua fit consideratio, quae est aequalis eleuationi poli super illum horizonta, propterea quod postquam declarata fuit ei quantitas arcus, qui est inter duos tropicos, et illud est 47. partes et plus duabus tertijs partis, et minus medietate et quarta partis, mediauit eam, et fuit illud finis declinationis orbis signorum a circulo aequatoris diei, et est arcus, qui est circuli magni transeuntis per duos polos aequatoris diei, et per illam partem, cuius declaratio quaeritur ab aequatore diei. Ipse uero inuenit eam per figuram sectorem cum sex lineis diuersis, et possibile est inuenire illam cum quatuor quantitatibus proportionalibus, propter illud quod praemisimus secundum hunc modum. Sit itaque aequator diei 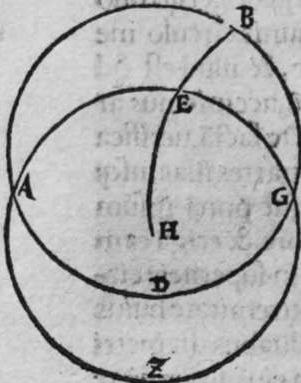circulus a b g d, et orbis signorum circulus a e g z, et sit polus punctum h, et sit punctum e orbis signorum datum, scilicet sit arcus a e eius scitus, qui sit elongatio puncti e a capite arietis aut librae, et imaginemur circulum magnum transeuntem super duo puncta h e, et secet circulum aequatoris diei super punctum b, propterea ergo quod triangulus a b e est ex arcubus circulorum maiorum, erit proportio sinus lateris a e ad sinum arcus anguli b, cui est subtensus, sicut proportio sinus lateris e b quaesiti ad sinum arcus anguli a, sed angulus a est notus, quoniam eius arcus est summa declinationis, et illud est 23. partes et 51. minutum, et 20. secunda, ergo eius sinus est notus, et sinus arcus anguli b est notus iterum, quoniam est diametri medietas, et sinus arcus a e est notus cum sit datus, quare oportet, ut sit sinus arcus e b notus, et est minor quarta circuli, quoniam arcus b e h est quarta circuli, quare oportet ut sit arcus e b notus, et illud est quod uoluimus declarare. Et de manifesto est, quoniam cum sciuerimus quantitates declinationum partium unius quartae orbis signorum, erunt declinationes partium cuiusque trium quartarum reliquarum scitae propter similitudinem dispositionis in eis. At uero cognitio quantitatum partium, quae eleuantur de circulo aequatoris diei cum partibus datis orbis signorum in orbe recto, et est circulus meridiei omnis horizontis, erit iterum nota per illam eandem uiam. Ponamus ergo in illa eadem figura arcum a e orbis signorum notum, et uoluimus scire quantitatem arcus a b aequatoris diei, et quoniam triangulus a e b est ex arcubus circulorum maiorum, et angulus eius b est rectus, tunc proportio sinus complementi lateris a e subtensi recto ad sinum complementi lateris a b unius duorum continentium rectum, est sicut proportio sinus complementi lateris e b reliqui ad sinum quartae circuli. Verum sinus complementi lateris a e est notus, et similiter sinus complementi lateris e b est notus, et est etiam declinatio et sinus quartae circuli notus, quapropter erit sinus complementi lateris b a notus, sed latus b a est minor quarta ciculi, ergo ipsum est notum, et illud est cuius uoluimus declarationem. Et de manifesto est, quod sciuerimus illud quod eleuatur cum partibus quartae unius orbis signorum, erit illud quod eleuatur cum partibus cuiuscunque trium quartarum reliquiarum notum, propter similitudinem dispositionis in eis. Et similiter si ponatur nobis longitudo diei alicuius graduum orbis signorum in horizonte dato, erit arcus horizontis, qui est inter ortum illius gradus, et inter ortum capitis arietis aut librae notus, et illud est, quoniam cum nos posuerimus, ut sit circulus aequatoris diei b e d, et sit punctum z horizontis, ipsum punctum supra quod oritur, punctum datum orbis signorum, et sit longitudo diei illius puncti nota. Sit itaque polus punctum h, 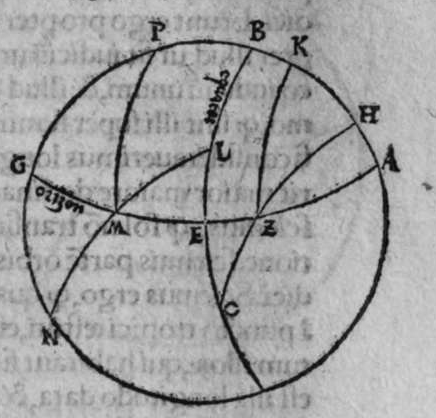et faciam transire super ipsum et super punctum z arcum circuli magni, qui sit arcus h z t, et sit circulus z k circulus, super quem reuoluitur punctum z orbis signorum, propterea ergo quod duo puncta z t perueniunt super circumferentiam orbis meridiei, scilicet circuli a b g in tempore uno, est arcus t b aequatoris diei similis arcui k z. At arcus k z est notus, quoniam est arcus medij diei dati, ergo arcus k t est notus, uerum arcus b e est quarta circuli, ergo arcus e t est notus Est ergo triangulus e t z ex arcubus circulorum magnorum et angulus eius t est rectus, ergo proportio sinus complementi lateris e z subtensi recto, ad sinum complementi lateris e t unius duorum continentium eius, est sicut proportio sinus complementi lateris t z reliqui ad sinum quartae circuli. At arcus t z est notus, quoniam ipse est declinatio gradus positi, et arcus quartae circuli est notus, et arcus e t est notus, ergo sinus complementi arcus e z est notus, sed ipse est minor quarta circuli, ergo ipse est notus, et illud est quod uoluimus declarare. Et per huiusmodi iterum scitur altitudo poli, cum fuerint arcus isti dati, aut cum fuerit longior dies datus. Ponamus ergo punctum z horizontis punctum, super quod oritur principium signi cancri, et sit arcus e z notus. Dico ergo, quod eleuatio poli in illo horizonte est nota, cuius demonstratio haec est. Quoniam triangulus e t z ex arcubus circulorum magnorum, et angulus eius t est rectus, tunc proportio sinus lateris e z noti ad sinum lateris t z noti, est sicut proportio sinus arcus anguli t noti, quoniam ipse est rectus ad sinum arcus anguli t e z, ergo sinus arcus anguli t e z est notus, et ipse est minor recto, ergo arcus eius est notus, et est arcus a d, ergo est propter illud arcus h a, et est altitudo poli notus. completa est demonstratio eius. Et similiter iterum, si fuerit longior dies datus, et est duplum arcus b t, cum sit similis arcui z k, erit ergo propter illud arcus e t notus, et est additio medietatis diei dati supra medietatem diei aequalis, quare est proportio sinus complementi lateris e z ad sinum complementi lateris e t, sicut proportio linus complementi lateris t z ad sinum quartae circuli. Est ergo propter illud sinus complementi lateris e z notus, sed ipse est minor quarta circuli, ergo est notus propter illud, propter illud ergo est altitudo poli nota, sicut ostensum est nuper, et illud est cuius uoluimus declarationem. Et si posuerimus punctum m horizontis punctum super quod oritur principium signi capricorni, et punctum n polum meridiei super quod transeat, et super punctum m arcus circuli magni, qui sit arcus l m n, et posuerimus circulum m p circulum aequedistantem aequatori die, super quem transit punctum m, declarabitur ex proximo, quod arcus m e est aequalis arcui z e, et quod arcus diei capitis cancri est aequalis arcui noctis capitis capricorni, et nox capitis cancri aequalis diei capitis capricorni, et illud ideo, quoniam propterea quod arcus t z est aequalis arcui l m, et angulus t e z aequalis angulo l e m, erit proportio sinus arcus z t ad sinum arcus anguli z e t, sicut proportio sinus arcus l m ad sinum arcus anguli l e m. Proportio ergo sinus arcus e z ad sinum finum ed. arcus anguli t recti, est sicut proportio sinus arcus e m ad sinum arcus anguli e l m, quare oportet, ut sit sinus arcus z e aequalis sinui arcus e m, sed unusquisque nunsquisque ed. eorum est minor quarta circuli, ergo arcus z e est aequalis arcui m e, et illud recte sequitur in omnibus punctis duobus orbis signorum, quorum longitudo a puncto aequalitatis una est longitudo aequalis, scilicet est elongatio ortus amborum in horizonte ex puncto e longitudo aequalis, et propter illud sunt duae differentiae communes inter circulum horizontis, et inter unumquenque duorum circulorum z, p m aequales, et proprerea quod arcus z h est aequalis arcui m n, erunt duo circuli z k, p m aequales, et cordae aequales secant in circulis aequalibus arcus aequales, oportet ergo propter illud, ut sit portio circuli z k, quae est supta terram, aequalis portioni circuli p m, quae est sub terra, et sit portio, quae est sub terra circuli z k aequalis portioni, quae est supra terram, circuli p m secundum coalternationem. Sit ergo propter illud dies puncti z orbis signorum aequalis nocti puncti m eius, et nox puncti est aequalis diei puncti m secundum coalternationem, et propterea quod omnium duorum punctorum orbis signorum, quorum longitudo ab uno et eodem tropico longitudo est aqualis, est longitudo a circulo aequatoris diei longitudo aequalis, et est propter illud longitudo amborum ab unoquoque duorum punctorum longitudo aequalis, oportet propter illud, ut sit transitus amborum super circulum unum de circulis aequedistantibus aequatori diei. Erunt ergo propter illud dies amborum aequales, et noctes eorum aequales, et oportet propter illud, ut sit iudicium uniuscuiusque eorum cum suo relatiuo, scilicet, quod est unius diameter cum eo iudicum unum, et illud est quod nos uoluimus declarare. Et declaratur nobis ex proximo, quod sint illi super summitatem capitum, quorum uadat sol, et quando et quotiens accidat illud si considerauerimus longitudinem summitatis capitum a circulo aequatoris diei. Nam si fuerit maior maiore declinatione, cuius summa est 23. partes et 51. minutum, et 20. secunda, sciemus, quod sol non transit super summitatem capitum eorum, et si fuerit minor maiore declinatione, sciemus partem orbis signorum, cuius illa latitudo est quantitas declinationis ab aequatore diei. Sciemus ergo, quod quando sol erit in illa parte orbis signorum, et in parte, cuius latitudo a puncto tropici aestiui, est sicut longitudo illius partis ab eo transibit per summitatem capitum illorum, qui habitant sub illo circulo aequedistante aequatori diei, cuius elongatio ab eoest illa longitudo data, et sunt horizontes, super quos est eleuatio poli similis illi longitudini. Et si uoluerimus scire proportionem gnomonum ad umbras suas in duabus aequalitatibus, et duobus tropicis in horizonte dato, ponemus circulum meridiei illius horizontis circulum a b g et summitatem capitis in eo punctum a, et centrum eius punctum e, et producam diametrum 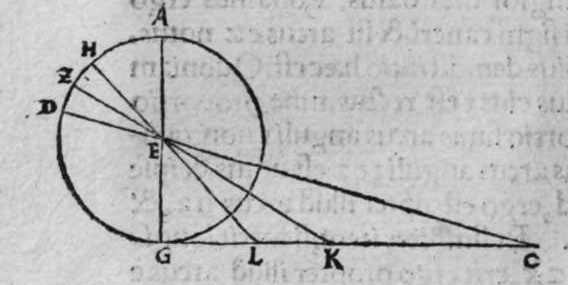a e g, et protraham a puncto g lineam tangentem circulum a b g, quae sit linea g t, et proculdubio ipsa est aequedistans differentiae communi inter circulum horizontis et circulum meridiei, et quoniam quantitas corporis sphaerae terrae apud orbem solis, est sicut quantitas puncti et centri, ita, ut non sit inter centrum e et caput gnomonis differentia neque diuersitas, ponam caput instrumenti centrum e, et imaginabor gnomonem lineam e g, et lineam g t lineam supra quam cadunt in meridie extremitates umbrarum, et sit sol, quando est super punctum tropici hyemalis super punctum d, et quoniam est in aequalitate uernali et autumnali supra punctum z, et quando est in tropico aestiuo super punctum h, et protraham lineas d e t, z e k, h e l, est ergo l inea d e t radius solis in meridie. quando sol est in tropico hyemali, et linea z e k radius eius, cum est in duobus punctis duarum aequalitatum, et linea h e l radius eius quando est in tropico aestiuo, ergo erit linea g t umbra gnomonis in tropico hyemali, et linea g umbra eius in duabus aequalitatibus, et linea g l umbra eius in tropico aestiuo. Propterea ergo quod arcus a z est notus, et est arcus latitudinis regionis datae, et unusquisque duorum arcuum z h, z d est notus, erit unusquisque angulorum g e t et g e c et g e l notus, et angulus g est rectus, ergo remanet unusquisque angulorum g t e et g k e et g l e notus. Erunt ergo arcus qui sunt super hos angulos continentes triangulos g e t et k g e et l e g noti, ergo proportio uniuscuiusque cordarum t g, k g, l g ad gnomonem e g erit nota. Et declaratur conuersio illius etiam, et est, quando positae fuerint duae de his tribus proportionibus, erit altitudo poli nota et erit arcus, qui est inter duos tropicos notus, et illud ideo, quoniam cum positi fuerint duo de angulis qui sunt apud punctum e, erit angulus reliquus notus, quoniam duo anguli e d z et z e h sunt aequales. Verum inuentio illius per considerationes secundum quod praecessit, est uerius et firmius, quoniam ex tremitates umbrarum in tropicis hyemalibus comprehendere est difficile, et alteratio quantitatum umbrarum in duabus aequalitatibus est uelox, et fortasse non comprehenditur, et illud est ideo, quoniam alteratio declinationum partium orbis signorum ab aequatore diei prope duas sectiones est magis secundum diuersitatem eius, quae est super eam in duobus tropicis, et illud est manifestum per illud quod praemisimus in tractatu primo huius libri, propter illud ergo uelox fit elogatio solis a summitate capitis, fit ergo propter illud necessario alteratio umbrarum, completa est eius declaratio. Qualiter autem sciantur quantitates arcuum aequatoris diei, quae eleuantur cum arcubus datis orbis signorum in horizonte dato, hoc scitur secundum quod narro, et praemittamus ante illud, et demonstremus, quod arcus aequales orbis signorum, quorum elongatio ab uno puncto duarum aequalitatum est elongatio una, eleuantur in omni horizonte semper cum arcubus aequalibus circuli aequatoris diei. Sit ergo circulus horizontis dati circulus a e g, et circulus meridiei circulus 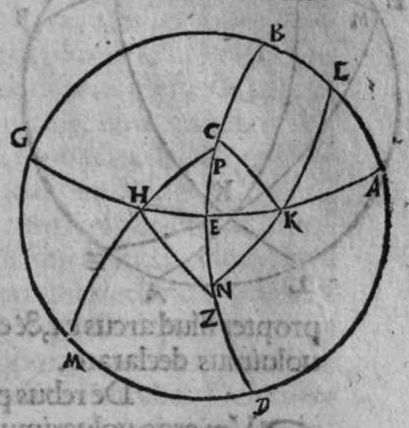a b g d, et circulus aequatoris diei circulus b e d, et sit unusquisque duorum punctorum z d punctum uernale, et arcus d k orbis signorum aequalis arcui z h, et sunt duo compares a duobus lateribus puncti aequalitatis uernalis. Dico ergo, quod arcus e t aequatoris diei, et est ille qui eleuatur cum arcu t k super horizonta a g, est aequalis arcui e z, et est ille qui eleuatur cum arcu z h, cuius haec est demonstratio. Ponam enim polum septentrionalem punctum l, et polum meridianum punctum m, et faciam transire super ea ambo, et super duo puncta k h duos arcus duorum circulorum magnorum, qui sint duo arcus l k n, m h p, propterea ergo quod duorum punctorum k h orbis signorum a puncto aequalitatis unius longitudo est longitudo aequalis, sunt amborum declinationes ab aequatore diei, et sunt duo arcus k n, h p aequales, et sunt duo arcus e k et e h circumferentiae horizontis aequales. Et propterea quod triangulus e k n est ex arcubus circulorum magnorum, et angulus eius n est rectus, erit proportio sinus complementi lateris n e residui ad sinum quartae circuli. Et similiter iterum in triangulo h e p proportio sinus complementi lateris e h ad sinum complementi lateris h p, est sicut proportio sinus complementi lateris e p ad sinum quartae circuli. At proportio sinus complementi lateris e k ad sinum complementi lateris k  n, est sicut proportio complementi lateris e h ad sinum complementi lateris h p, propter aequalitatem uniuscuiusque eorum ad sinum comparem alterius trianguli. Oportet ergo propter illud, ut sit proportio sinus complementi lateris n e ad sinum quartae circuli, sicut proportio sinus complementi lateris e p ad sinum quartae circuli, ergo sinus complementi lateris e p est aequalis sinui complementi lateris e n, et unusquisque eorum est minor quarta circuli, ergo arcus e p est aequalis arcui e n, et propterea quod duo arcus t k et z h orbis signorum sunt aequales, et sunt a duobus lateribus puncti unius duorum punctorum duarum aequalitatum, erunt eleuationes eorum in orbe recto, et sunt duo arcus t n et z p aequales, quare remanent duo arcus t p et z n aequales, ergo duo arcus e t, e z sunt aequales, et illud est quod uoluimus declarare. Et dico iterum, quod omnium duorum arcuum orbis signorum aequalium et aequalis elongationis a puncto tropici unius, et eiusdem aggregatio eleuationum in omni horizonte, est aequalis aggregationi eleuationum eorum in sphaera praeparata. Sit itaque horizon datus circulus 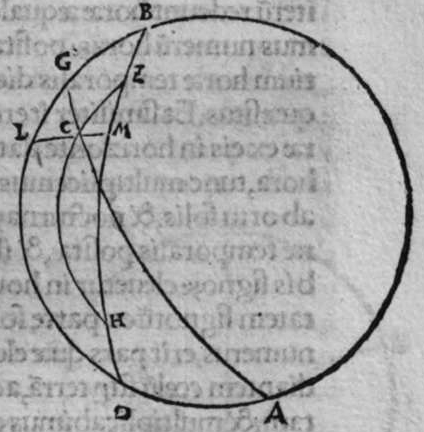a e g, et circulus meridiei circulus a b g d, et sint duo puncta h z duo puncta duarum aequalitatum, scilicet uernalis et autumnalis, et duo arcus h t, t z orbis signorum sint aequales, et aequalis elongationis ab uno et eodem tropico. Sequitur ergo propter illud, ut sint eleuationes eorum similes super punctum unum horizontis, et est punctum t, et sit polus meridianus punctus l, et faciamus transire super ipsum et super punctum t arcum circuli magni qui sit arcus l t m. Eleuabitur ergo arcus z t in sphaera praeparata cum arcu z m, et arcus h t eleuabitur cum arcu m h, ergo aggregatio eleuationum eorum in sphaera recta est arcus z h. Et similiter arcus z t eleuatur in horizonte a e g cum arcu e b z, et arcus h t eleuatur in eo cum arcu e h, et aggregatio amborum est arcus z h, ergo aggregatio eleuationum amborum in horizonte a e g est aequalis aggregationi eleuationum eorum in sphaera recta, et illud est quod uoluimus declarare. Sequuntur ergo ex hoc, quod cum sciuerimus in horizonte posito quantitates eleuationis partium cuiusque trium reliquarum quartarum. Incipiamus ergo nunc declarare quantitates declinationis partium eleuationis unius 4. quartarum orbis signorum in horizonte posito. Sitque horizon datus circulus a e g, et circulus meridiei circulus a b g d, et circulus aequatoris diei circulus b e d, et circulus signorum circulus h l t, et sit punctum t punctum uernale, 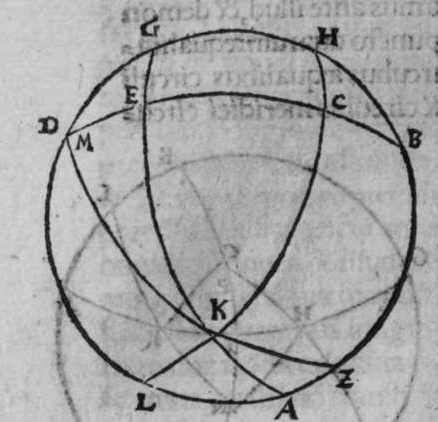et sit arcus t k orbis signorum notus, et uolumus scire arcum et aequatoris diei, et est ille, qui eleuatur cum arcu t k. Sit ergo polus septentrionalis punctum z, et faciamus transire super ipsum et punctum k arcum circuli magni, qui sit arcus 3/Z k m, propterea ergo quod punctum k orbis signorum est notum, declinatio eius, quae est arcus k m, est nota, et similiter est iterum arcus k e horizontis notus, et est triangulus k e m ex arcubus circulorum magnorum, et angulus m eius est rectus, ergo proportio sinus complementi lateris e k noti ad sinum complementi lateris e m, est sicut proportio sinus complementi lateris k m noti ad sinum quartae circuli. Est ergo propter illud sinus complementi lateris arcus e m notus, et est minor quarta circuli, ergo est notus, et arcus t m est notus, cum sit eleuationis arcus t k in orbe recto. Est ergo propter illud arcus e t, et est eleuationis eius in horizonte posito notus, et illud est quod uoluimus declarare.

⟨II.8⟩ De rebus particularibus quae sciuntur per scientias eleuationum.

CVm ergo uoluerimus scire longitudinem diei gradus alicuius orbis signorum, aut noctis eius in horizonte dato, sciemus, quod debetur de eleuationibus in illo horizonte medietati orbis signorum, cuius principium est ex illo gradu, si quaesitum fuerit dies, aut ex eius opposito, si fuerit nox, et quod fuerit de partibus aequatoris diei diuidemus per 15. qui est numerus graduum horae aequalis, et quod proueniet, erit numerus horarum aequalium illius diei aut noctis et accipiemus partem ex 12 et quod fuerit, erit quantitas horae temporalis, et inueniemus iterum quantitatem horae temporalis absque hoc, et est, ut consideremus quantum sit inter caput arietis et partem illam in qua est sol et accipiamus quod debetur ei de gradibus eleuationum in horizonte recto, et in horizonte de quo intenditur, et accipiamus sextam superfluitatis inter eas ambas, et quod fuerit, seruemus illud. Quod si fuerit pars, in qua est sol, de signis septentrionalibus, addemus illud super 15. gradus ad horas diurnas, et inueniemus illud ad horas nocturnas. Et si fuerit de signis meridianis, faciemus contrarium illius, scilicet, minuemus illud ex 15. gradibus ad horas diurnas, et addemus illud ad horas nocturnas, et quod fuerit, erit numerus partium horae temporalis quaesitae. Et similiter cum ponitur numerus horarum temporalium, et uolumus scire quantus numerus sit aequalium, tunc multiplicabimus numerum horarum positarum, horarum quidem diurnarum in partes horae temporalis illius diei, et horarum noctis in partes horae temporalis illius noctis, et eius quod aggregatur, accipimus partem quintamdecimam, et quod prouenit, est numerus horarum aequalium illius temporis positi in illa regione, et cum conuersione illius iterum redeunt horae aequales, cum ponuntur nobis ad horas temporales, scilicet, ut multiplicemus numerum horarum positarum 15. uicibus, et illud quod aggregatur diuidamus per numerum partium horae temporalis diei aut noctis dati, et quod prouenit, est numerus horarum temporalium quaesitus. Et similiter iterum, si ponatur nobis numerus horarum temporalium, et quantitas horae ex eis in horizonte dato noctis sit ille aut diei, et uoluerimus scire partem orientem in illa hora, tunc multplicemus numerum horarum positarum, diurnarum quidem scilicet illarum quae sunt ab ortu solis, et nocturnarum illarum, scilicet quae sunt ab occasu solis, in numerum partium horae temporalis positae, et illud quod aggregatur, sciemus cum quarta parte de partibus orbis signorum eleuetur in horizonte posito, et illud quod fuerit, proijciemus secundum continuitatem signorum ex parte solis, si fuerit dies, aut ex eius opposito, si fuerit nox, et ubi proueniet numerus, erit pars quae eleuatur in illa hora posita. Et cum uoluerimus inuenire partem mediantem coelum super terram, accipiemus horas quae sunt a medio die praeterito usque ad horam datam, et multiplicabimus eas in tempora horarum relatarum eis, scilicet diurnas in diurnarum, aut nocturnas in nocturnarum, et quod aggregabitur, sciemus cum quarto eleuetur de partibus orbis signorum in sphaera praeparata, et quod fuerit, proijiciemus ex parte solis, et ubi prouenerit numerus, erit pars medians coelum in illa hora data. Et similiter iterum sciemus partem mediantem coelum propter partem orientem, ut consideremus, quantum sit spacium partis orientis a capite arietis, et accipiemus quod debetur ei, quod fuerit de eleuationibus in regione data, et quod fuerit, proijciemus de illo 90. si fuerit plus 90. et si fuerit minus, addemus super ipsum reuolutionem unam, et minuemus ex eo 90. et illud quod remanserit de partibus eleuationum, sciemus cum quanto eleuatur de partibus orbis signorum in sphaera recta, et quod fuerit, proijciemus a principio arietis secundum continuitatem signorum, et ubi peruenerit numerus, erit pars medians coelum in illa hora posita. Et econuerso illius, quando nos uoluerimus scire partem orientem ex parte mediante coelum, tunc sciemus quanta sit elongatio illius partis a capite arietis, et sciemus quod debeatur ei, quod fuerit de eleuationibus in sphaera recta, et super illud quod fuerit, addemus 90. et proijciemus ex eo reuolutionem, si fuerit plus reuolutione, et sciemus illud cum quanto eleuetur de partibus orbis signorum in regione data, et quod fuerit, proijciemus secundum continuitatem signorum a principio arietis, et ubi perueniet numerus, tunc illa pars erit oriens. Et manifestum est, quod elongatio solis a medio die et media nocte eorum, qui habitant sub uno circulorum meridiei, est longitudo una ex horis aequalibus, et super illos qui non habitant sub uno circulorum meridiei, diuersitas meridiei est cum temporibus de temporibus aequalitatis, quorum numerus est aequalis numero partium, qui sunt inter circulos meridiei eorum. Et postquam declaratae sunt res istae, ergo incipiamus nunc declarare quantitates angulorum, qui proueniunt ex circulo signorum et circuli meridiei, et quoniam illud quod prouenit ex sectione omnium duorum circulorum sese secantium, est 4. anguli, tunc oportet, ut determinemus angulum quem uelimus de eis, et ipse quidem est angulus septentrionalis orientalis. Demonstremus ergo in primis, quod omnes duo anguli, qui sunt super omnia duo puncta orbis signorum, quorum longitudo ab uno duorum punctorum duarum aequalitatum est longitudo aequalis, ex circulo 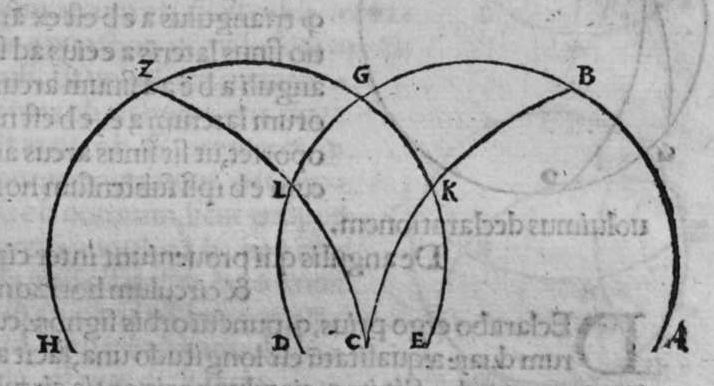meridiei sunt aequales. Sit itaque orbis signorum circulus a b g d, et orbis aequatoris diei circulus e g z h, et punctum g unum duorum punctorum duarum aequalitatum, et sint duo arcus b g, g l aequales, et sit polus septentrionalis punctum t, et faciamus transire super ipsum et super duo puncta b l duos arcus duorum circulorum magnorum, qui sint duo arcus t k b et t l z Dico ergo, quod duo anguli g b k et t l d sunt aequales. Quod sic probatur, quoniam triangulus b g k est ex arcubus circulorum magnorum, ergo proportio sinus lateris k g ad sinum lateris b g, est sicut proportio sinus arcus anguli b ad sinum arcus anguli k. Et similiter in triangulo g l z iterum proportio sinus lateris g z ad sinum lateris g l, est sicut proportio sinus arcus anguli l ad sinum arcus anguli z, uerum arcus b g est aequalis arcui g l, et arcus g k est aequalis arcui g z, quoniam ambo sunt eleuationes illorum utrorumque in sphaera praeparata. Et similiter angulus k est aequalis angulo z, quoniam unusquisque amborum est rectus, oportet ergo, ut sint propter illud duo sinus duorum angulorum b l aequales, et ipsi sunt sequentes duo latera k g, g z aequalia, ergo oportet ut sint aequales, ergo angulus b trianguli g b k est aequalis angulo l trianguli g l z. Sed iste angulus est aequalis angulo t l d, ergo angulus k g b quaesitus est aequalis angulo t l d quaesito iterum, et illud est, cuius uoluimus declarationem. Et dico 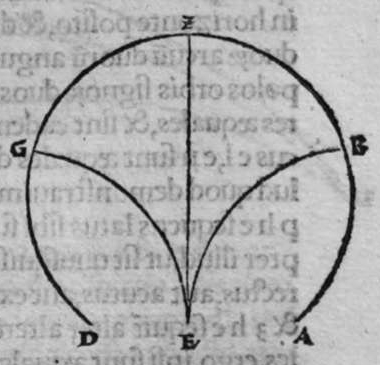iterum, quod duorum angulorum anguloum ed. qui proueniunt apud duo puncta, quorum longitudo ab uno et eodem tropico est longitudo una, aggregatio est aequalis duobus angulis rectis. Sit itaque orbis signorum circulus a b g d, et punctum tropici punctum z, et sint duo arcus b z, g z aequales, et sit polus septentrionalis punctum e, et faciamus transire super ipsum et super duo puncta b g duos arcus duorum circulorum magnorum, qui sint duo arcus e b, e g. Dico ergo, quod duo anguli e b g, e g d sunt aequales duobus angulis rectis, cuius haec est demonstratio. Quoniam triangulus e b g est ex arcubus circulorum magnorum, ergo proportio sinus lateris e g ad sinum lateris e b, est sicut proportio sinus arus anguli e b g ad sinum arcus anguli e g b, uerum arcus e b est aequalis arcui e g, ergo sinus arcus anguli e b g est aequalis sinui arcus anguli e g b. Et si nos imaginati fuerimus arcum circuli magni transeuntem per duo puncta e z, erit unusquisque duorum angulorum z rectus, erit ergo propter illud unusquisque duorum angulorum e b z, e g z sequens arcum e z, ergo hi duo anguli sunt sequentes se, scilicet, si fuerit unus eorum rectus aut maior aut minor, erit alter aequalis ei, quamobrem oportet ut sint arcus amborum aequales, ergo duo anguli sunt aequales, erunt ergo propter illud duo anguli e b g et e g d quaesiti aequales duobus angulis rectis, et illud est, cuius uoluimus declarationem. Et quia iam patefactum est nobis illud, tunc nos contenti erimus cognitione angulorum euenientium in partibus unius quatuor quartarum orbis signorum, et excusabit nos illud a cognitione angulorum in tribus quartis residuis. Inquiramus ergo nunc quantitates angulorum, qui proueniunt apud partes quartae unius. Dicamus ergo, quod angulus qui prouenit apud punctum tropici, est rectus, et illud manifestum est, et quoniam angulus, qui sit apud punctum aequalitatis, est superfluitas recti super angulum sectionis, qui est inter circulum signorum et circulum aequatoris diei, et est ille, cuius arcus est finis declinationis, tunc est angulus quaesitus 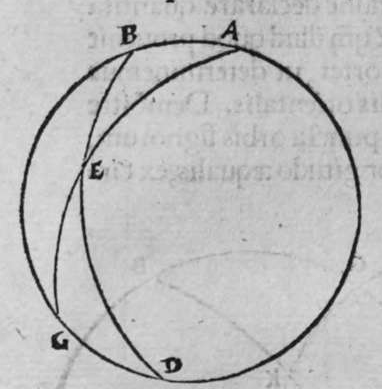notus. Ponamus ergo de partibus quartae quamcunque partem uoluerimus, et inquiramus quantitatem anguli qui prouenit apud eam, ponamus ergo orbem signorum circulum a e g, et circulum meridiei circulum a b g, et circulum aequatoris diei circulum b e d, et sit punctum e punctum autumnale, et sit punctum a de orbe signorum notum, et uolumus scire quantitatem anguli e a b, propterea ergo quod triangulus a e b est ex arcubus circulorum magnorum, erit proportio sinus lateris a e eius ad sinum lateris e b, sicut proportio sinus anguli a b e ad sinum arcus anguli e a b, uerum unumquodque duorum laterum a e, e b est notum, et angulus a b e est rectus, ergo oportet, ut sit sinus arcus anguli e a b notus, et ipse est sequens arcum e b ipsi subtensum notum, ergo est notus, et illud est, cuius uoluimus declarationem.

⟨II.9⟩ De angulis qui proueniunt inter circulum orbis signorum et circulum horizontis.

DEclarabo ergo prius, quod punctum orbis signorum, cuius longitudo ab uno duorum punctorum duarum aequalitatum est longitudo una, facit angulos, qui proueniunt ei apud horizontem, aequales. Sit itaque circulus horizontis circulus d e b, et circulus meridiei circulus 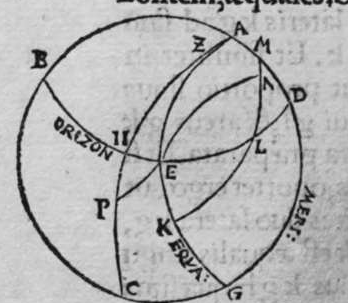a b g, et circulus aequatoris diei circulus a e g, et sit unumquodque duorum punctorum k z punctum autumnale, et duae portiones orbis signorum aequales sicut duo arcus k l et z h. Dico ergo, quod duo anguli e l k et e h z sunt aequales, cuius demonstratio haec est. Triangulus k l e est ex arcubus circulorum magnorum, ergo proportio sinus lateris k l ad sinum lateris k e, est sicut proportio sinus arcus anguli k e l ad sinum arcus anguli k l e. Et similiter etiam proportio sinus lateris z h trianguli e z h ad sinum lateris e z, est sicut proportio sinus arcus anguli z e h ad sinum arcus anguli z h e, et duo latera k l, k e sunt aequalia duobus lateribus e z, z h, unumquodque latus suo relatiuo, propterea quod duo arcus e k, e z sunt eleuationes duorum arcuum k l, z h in horizonte posito, et duo anguli h e z et l e k sunt aequales, ergo oportet, ut sint duo sinus duorum arcuum duorum angulorum k l e, z b e aequales, et faciam transire per punctum e, et per duos polos orbis signorum duos arcus duorum circulorum magnorum, qui sint duo arcus e n, e p, existentes aequales, et sint cadentes ad partem unam ex duobus angulis n l e et p h e, et quoniam duo arcus e l, e n sunt aequales duobus arcubus e h, e p, unusquisque suo relatiuo, oportet propter illud quod demonstrauimus in his quae praemissa sunt, ut sit unusquisque duorum angulorum n l e p h e sequens latus sibi suppositum, scilicet arcus e n, e p, et ipsi sunt aequales. Oportet ergo propter illud, ut sit unusquisque duorum angulorum n l e, p h e sequens alterum, scilicet, si sit unus eorum rectus, aut acutus, aut expansus, sit alteri similis, unusquisque eorum ergo duorum angulorum k l e et z h e sequitur alter alterum, et duo sinus duorum arcuum ipsorum, ut iam ostensum est, quod sunt aequales, ergo ipsi sunt aequales, et illud est cuius uoluimus declarationem. Et dico iterum, quod duo anguli, qui sunt in duobus punctis diametralibus orbis signorum, scilicet orientalis et occidentalis, sunt aequales duobus angulis rectis. Sit ergo circulus horizon circulus a b 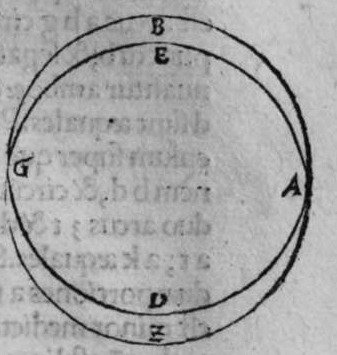g d, et circulus orbis signorum a e g z. Dico ergo, quod duo anguli e a d et z g d sunt aequales duobus angulis rectis, cuius haec est demonstratio. Angulus e a d est aequalis angulo e g d, et duo anguli e g d, z g d sunt aequales duobus angulis rectis, ergo duo anguli e a d, z g d sunt aequales duobus angulis rectis, et illud est, cuius uoluimus declarationem. De manifestis ergo est, quod quando nos sciuerimus quantitates angulorum, qui eueniunt orbi horizontis cum una quartarum orbis signorum, contenti erimus per illud ab inuentione angulorum prouenientium in tribus quartis reliquis. Speculemur ergo nunc inuentione quantitatum angulorum prouenientium in quarta una. Ponamus ergo orbem horizontis positi circulum a b g, et 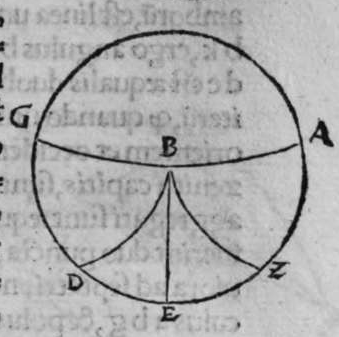circulum meridiei circulum a e g, et ponam arcum e b aequatoris diei, et duos arcus z b et d b orbis signorum, et punctum b punctum uernale aut autumnale, sit ergo punctum z tropicum aestiuum, et punctum d tropicum hyemale, propterea ergo, quod altitudo poli in regione posita est nota, erit arcus a e notus, sed arcus e z est notus, propter illud est ergo arcus a z, notus, et similiter arcus a d notus, ergo unusquisque duorum angulorum a b z, a b d est notus, et illud est, cuius uoluimus declarationem. Et reiteremus figuram, et ponamus orbem horizontis dati circulum g b h, et ponam ex orbe signorum arcum e h, et sit orbis aequationis diei circulus z e b, et sit punctum e punctum uernale, et arcus e h 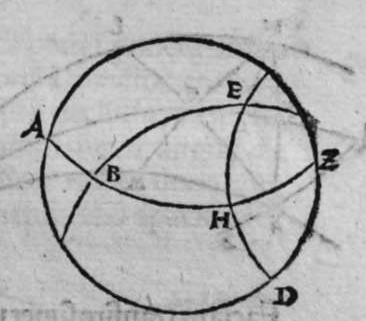sit notus, et non sit maior quarta circuli. Et uolo scire quantitatem anguli e h b, propterea ergo, quod arcus e h est notus, erit eleuatio eius in horizonte posito nota, et est arcus e b, et propterea quod triangulus e b h est ex arcubus circulorum magnorum, erit proportio sinus lateris h e ad sinum lateris e b notorum, sicut proportio sinus arcus anguli e b h ad sinum arcus anguli e h b. Sed angulus e b h est notus, quoniam altitudo poli est posita, ergo sinus arcus anguli e h b est notus, et ipse est in eo, quod est infra aequatorem diei ad septentrionem, et est illud quod inhabitatur de terra proueniens, ergo est notus. completa est eius declaratio.

⟨II.10⟩ De scientia arcuum et angulorum prouenientium ab orbe signorum, et circulo altitudinis.

PRaemittamus ergo ante illud, quod puncta orbis signorum, quae sunt aequalis elongationis a puncto tropico et eodem, et est eorum longitudo a circulo meridiei ad orientem et occidentem cum temporibus aequalibus, tunc arcus euntes per ea et per summitatem capitis, erunt aequales, et anguli quos continent isti arcus et orbis signorum secundum partem narratam sunt aequales duobus angulis rectis. Sit itaque orbis meridiei arcus a b g, et punctum g 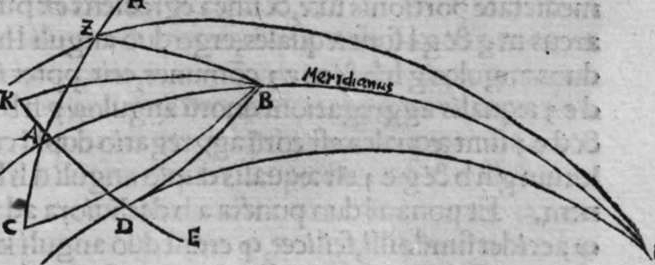sit polus septentrionalis, et zenith capitis sit punctum b, et duo arcus a d e, a z h sunt duae portiones orbis signorum, et sit longitudo duorum punctorum d z illorum amborum a puncto tropici aestiui longitudo aequalis, et faciam transire super ea ambo et super zenih capitis arcum b d et arcum b z, et sit longitudo duorum punctorum d z a circulo a b g ad orientem et occidentem longitudo aequalis. Dico ergo, quod arcus b d est aequalis arcui b z, et quod duo anguli b d e et b z a sunt aequales duobus angulis rectis, cuius ista est demonstratio. Faciam transire super polum g, et super duo puncta d z duos arcus duorum circulorum magnorum, qui sunt duo arcus g d, g z, propterea ergo, quod duorum punctorum d z longitudo est a puncto tropico est longitudo aequalis, est incessus eorum cum motu totali super unum circulorum aequedistantium aequatori diei. Erecta est ergo iam super diametrum huius circuli portio circuli, et est arcus a b g circuli meridiei orthogonaliter, et signatum est super circumferentiam portionis punctum b, et separati sunt ex circulo ab utraque parte arcus portionis duo arcus aequales, et continuantur amborum extremitates, scilicet duo puncta d z cum puncto b, ergo duo arcus b z, b d sunt aequales. Ponam autem punctum z polum, et mensurabo longitudinem b z, et reuoluam circulum super quem sint b t, et similiter ponam iterum punctum d polum, et mensurabo longitudinem b d, et circumuoluam circulum b k, propterea ergo, quod duo arcus b z, b d sunt aequales, erunt duo arcus z t et d k aequales, sed duo arcus a d, a z sunt aequales, remanent ergo duo arcus a t, a k aequales. Super duas ergo diametros duorum circulorum b t, b k aequalium erectae sunt duae portiones a t, a k orthogonaliter, et arcus a t est aequalis arcui a k, et unusquisque eorum est minor medietate portionis suae, et linea egrediens ex puncto a ad punctum b uniuscuiusque amborum, est linea una, et est corda arcus a b. Propter illud ergo est arcus b t aequalis arcui b k, ergo angulus b z t est aequalis angulo b d k, ergo aggregatio duorum angulorum b z a et b d e est aequalis duobus angulis rectis, et illud est, cuius uoluimus declarationem. Et dico iterum, quod quando unius puncti orbis signorum elongatio ab utroque latere circuli meridiei ad orientem et occidentem cum temporibus aequalibus, tunc arcus transeuntes per ipsum et per zenith capitis, sunt aequales, et duo anguli, quos isti arcus continent, et circulus signorum aggregati sunt aequales duplo anguli, qui accidit isti portioni apud circulum meridiei. Cum fuerint duo puncta, super quae circulus signorum secat circulum meridiei in utrisque sitibus decliuiora ad septentrionem a zenith capitis, aut ad meridiem ab eo. Sit ergo circulus meridiei circulus a b g, e polus septentrionis sit super quem est punctum d, et zenith capitis sit punctum g, 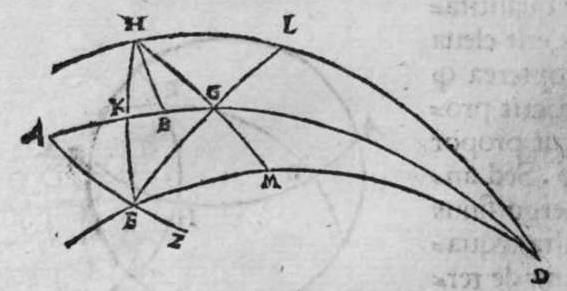et sint duo arcus a e z, et b h t duae portiones orbis signorum, et punctum e eius quod est a parte orientis circuli meridiei ad orientem et ad occidentem, sit cum temporibus aequalibus, et duo arcus g e, g h sint transeuntes per ea ambo, et per zenith capitis, dico ergo, quod ambo sunt aequales, et ponam in primis unumquodque duorum punctorum a b ad partem meridiei a zenith capitis. Dico ergo, quod aggregatio duorum angulorum g e z et g h b est aequalis duplo anguli d h b, quod sic demonstratur. Faciam transire super unumquodque duorum punctorum h e, et super polum duos arcus duorum circulorum magnorum, qui sint duo arcus d h, d e, et sit transitus duorum punctorum e h super circulum e k h, erit ergo arcus e k huius circuli aequalis arcui k h, erit ergo propter illud arcus g h aequalis arcui g e. Ponam autem punctum h polum, et mensurabo longitudinem g h, et circumuoluam circulum g l, et similiter ponam punctum e polum, et mensurabo longitudinem e g, et circumuoluam circulum g m, propterea ergo, quod duo arcus d e, d h sunt aequales, et duo arcus e m et h l aequales, sunt duo arcus d m et d l aequales super diametros, ergo duorum circulorum g m et g l aequalium erectae sunt duae portiones aequales d m et d l duorum circulorum magnorum aequalium, et separantur de duabus portionibus duo arcus d m et d l aequales, et unusquisque eorum est minor medietate portionis suae, et linea egrediens ex puncto d ad punctum g, est communis utrisque, et duo arcus m g et g l sunt aequales, ergo duo anguli l h g et m e g sunt aequales. Et si posuerimus duos angulos g h b et m e z communes, erit propter illud aggregatio duorum angulorum d h b et d e 3 aequalis aggregationi duorum angulorum g h b et g e z, et propterea, quod duo anguli d h b et d e z sunt aequales, est eorum aggregatio duplum cuiusque eorum, ergo aggregatio duorum angulorum g h b et g e z est aequalis duplo anguli d h b, et illud est, cuius uoluimus declarationem. Et ponantur duo puncta a b decliuiora ad septentrionem a zenith capitis. Dico ergo, quod accidet simile illi, scilicet, quod erunt duo anguli k e z et l h b aequales duplo anguli d e z, cuius haec est demonstratio. Ponam punctum e polum, et mensurabo spacium e g, et circumducam circulum n p g, et ponam iterum punctum h polum, et mensurabo longitudinem h g, et circumducam circulum s q g, propterea ergo, quod duo arcus g e et g h sunt aequales, erunt duo arcus n e et s h aequales, quare manent duo arcus d n et d s iterum aequales, erectae sunt ergo iam super diametros duas duorum circulorum n p g et s q g aequalium duae portiones d n et d s duorum circulorum aequalium, et separantur ex eis duo arcus d n e d s aequales, et unusquisque 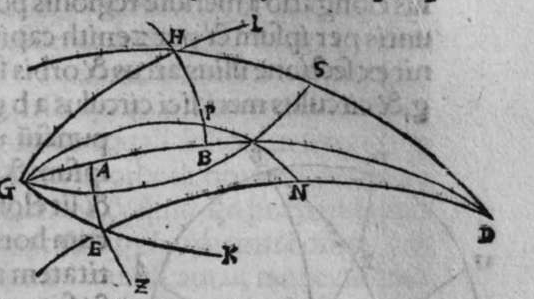eorum est minor medietate portionis suae, et linea d g est communis utrisque, et est propter illud arcus n p g aequalis arcui s q g, ergo duo anguli d h g et d e g sunt aequales, quare remanent duo anguli d e k et d h l aequales. Si ergo posuerimus aggregationem duorum angulorum d h b et k e z communem, erit aggregatio duorum angulorum l h b et k e z aequalis aggregationi duorum angulorum d h b et d e z, uerum isti duo anguli sunt aequales, ergo aggregatio duorum angulorum l h b et k e z est aequalis duplo anguli d e z, et illud est, quod uoluimus declarare. Et ponatur punctum a portionis orientalis orbis signorum, et est illud super quod secat haec portio circulum meridiei decliuius ad meridiem a puncto g, quod est supra zenith capitis. Dico ergo, quod aggregatio duorum 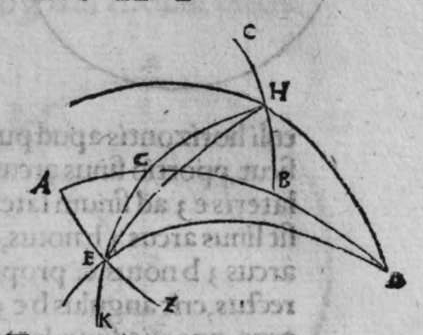angulorum g e z et l h b est maior duplo anguli d e z per duos angulos rectos, quod sic probatur. Ostendam quemadmodum nuper praemissum est, quod duo anguli d h g et d e g sunt aequales, et remanent duo anguli d h l et d e k iterum aequales, sed duo anguli d h b et d e z sunt aequales, ergo angulus l h b est aequalis aggregationi duorum angulorum d e k et d e z. Si ergo posuerimus angulum g e z communem, erunt duo anguli l h b et g e z aequales aggregationi angulorum d e k et d e z et g e z. Aggregatio autem horum angulorum est aequalis duplo anguli d e z, et duobus angulis erectis, ergo aggregatio duorum angulorum l h b et g e z est maior duplo anguli d e z per duos angulos rectos, et ilud est, cuius uoluimus declarationem. Et ponatur punctum medians coelum portionis orientalis, et est punctum a decliuius ad septentrionem a puncto zenith capitis et punctum medians coelum portionis occidentalis, et est punctum b decliuius ad meridiem. Dico ergo, quod aggregatio duorum angulorum k e z et g h b est minor duplo anguli d e z per duos angulos rectos, cuius haec est demonstratio. Ostendam sicut nuper declaraui, quod duo arcus g h et g e sunt aequales, et ponam punctum e polum, et mensurabo spacium g e, 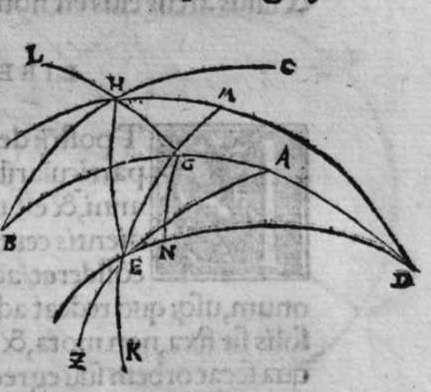et circumducam circulum n g, et similiter ponam punctum h polum, et mensurabo spacium g h, et describam circulum g m, declarabitur ergo sicut praemissum est, quod duo anguli m h g et n e g sunt aequales, ergo aggregatio duorum angulorum d e k, d h g est aequalis duobus angulis rectis, ergo aggregatio duorum angulorum d e z et d h b addit super aggregationem duorum angulorum k e z et g h b duos angulos rectos, sed angulus d e z est aequalis d h b, ergo aggregatio duorum b e 3/Z, g h b est minor duplo anguli d e z per duos angulos rectos, et illud est quod declarare uoluimus. Quod si fuerit punctum positum orbis signorum in circulo meridiei, erit angulus quaesitus ipse angulus, cuius praecessit declaratio, scilicet ex angulis, qui eueniunt orbi signorum et circulo meridiei, et erit arcus transiens per zenith capitis notus, quoniam eius elongatio aequatoris diei erit nota, et elongatio zenith capitis ab aequatore diei posita. Erit ergo propter illud elongatio eius ab illo puncto nota. Et si fuerit punctum positum super horizonta, erit arcus transiens per ipsum et per zenith capitis quarta circuli, ergo erit notus, et erit angulus quem continet iste arcus cum circulo horizontis angulus rectus, quoniam ipse est transiens per polum horizontis, et iam quidem praemissum est nobis, qualiter anguli quos horizon continet et orbis signorum egrediantur noti. Erunt ergo propter illud anguli, quos arcus transiens per zenith capitis et orbis signorum continent apud horizonta noti. completa est eius declaratio. Et manifestum quidem est, quod cum nos sciuerimus quantitates arcuum et angulorum, qui eueniunt ab arcu transeunte per zenith capitis et medietate orbis signorum, quae est ab initio cancri usque ad initium capricorni in declinatione posita quae sunt ante meridiem, sciemus ex eis per illud, cuius declaratio praecessit quantitates arcuum et angulorum, qui eueniunt medietati secundae orbis signorum ante meridiem, et post ipsum. Ponamus ergo nunc punctum aliquod orbis signorum, cuius elongatio a meridie regionis positae sit nota, et uolumus scire quantitatem arcus transeuntis per ipsum et per zenith capitis illius regionis positae, et quantitatem anguli, qui euenit ex sectione illius arcus et orbis signorum. Sit ergo circulus horizontis positi circulus a e g, et circulus meridiei circulus a b g, et orbis signorum circulus d z e, et punctum positum eius 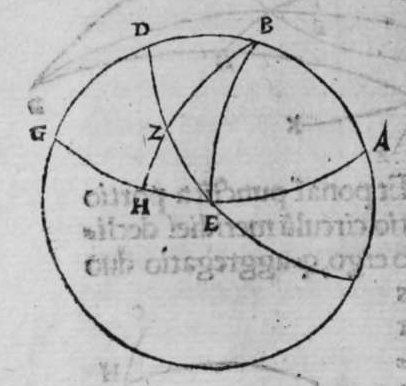punctum z, et zenith capitis sit punctum b, et faciamus transire super ipsum et super punctum z circulum circuli magni, qui sit arcus b z h et sit elongatio puncti z a circulo meridiei, scilicet circulo a b g cum horis positis, et uolumus scire quantitatem arcus b z, et quantitatem anguli e z b, faciamus ergo transire super zenith capitis et super punctum, supra quod orbis signorum secat circulum horizontis, et est pars oriens in illa hora, scilicet punctum e arcum circuli magni, qui sit arcus b e, et propterea quod elongatio puncti z a meridie est horae positae, est pars oriens in illa hora nota. Est ergo propter illud arcus e z notus, ergo est triangulus z e h ex arcubus circulorum magnorum, et angulus eius h est rectus, et angulus eius e est notus, et est angulus, qui prouenit ex sectione orbis signorum, et circuli horizontis apud punctum e notum, ergo proportio sinus lateris e z ad sinum lateris z h est sicut proportio sinus arcus anguli h recti ad sinum arcus anquli e noti, ergo proportio sinus lateris e z ad sinum lateris z h est proportio nota, et latus e z est notum. Oportet ergo, ut sit sinus arcus z h notus, et ipse est minor quarta circuli, tunc ipse est notus, ergo remanet arcus z b notus, et propterea quod angulus z e h, sicut diximus, est notus, et angulus k e h est rectus, erit angulus b e z notus, ergo triangulus b e z est ex arcubus circulorum magnorum, ergo proportio sinus lateris e b ad sinum lateris b z, est sicut proportio sinus arcus anguli b z e ad sinum arcus anguli b e z. Sed proportio sinus arcus b e ad sinum arcus z b est nota, quoniam unusquisque eorum est notus, ergo proportio sinus arcus anguli b e z noti ad sinum arcus anguli b z e est nota, ergo sinus arcus anguli b z e notus est, et propterea quod angulus h trianguli z e h est rectus, et latus z e subtensum ei est notum, et latus z h est notum, oportet ut sit latus e h reliquum comprehensum, ergo angulus e z h suppositus ei est comprehensus, et sinus arcus eius est notus, ergo ipse est notus, et illud est quod uoluimus declarare.

⟨III⟩ LIBER TERTIVS DE MOTV SOLIS.

ET postquam declaratum est illud, cuius demonstratio praecessit de istis scientijs particularibus, oportet post illud ut incipiat declarare quantitatem temporis anni, et est tempus, in quo incipit sol per motum a puncto aliquo sui orbis egredientis centri, usquequo redeat ad ipsum. Inquirit ergo illud tempus ita, ut consideret aduentum solis ad unam duarum aequalitatum, aut unam duarum conuersionum, usque quo redeat ad illam aequalitatem aut conuersionem, et fabricauit secundum quod aux solis sit fixa, non mota, et propter illud inquirit motum solis medium scilicet sectionem eius, qua secat orbem suum egredientis centri, ita, ut incipiat sol a puncto orbis signorum, usque quo redeat ad ipsum, scilicet ab aequalitate aut a conuersione usque ad reditum suum ad illam aequalitatem aut conuersionem. Et si declaretur ei, quod aux solis esset mobilis, non inquireret sectionem solis, qua secat orbem suum egredientis centri per sectionem eius, qua secat orbem signorum, et poneret duas reditiones aequales, considerauit ergo solem cum armilla, qua consideratur aequalitas apud aduentum suum ad aequalitatem autumnalem, et uerificauit illam horam et accepit de considerationibus Abrachis considerationem aequalitatis autumnalis, in cuius certitudine non fuit ambiguitas. Fuit ergo spacium, quod fuit inter duas considerationes, continens reditiones integras solis in orbe signorum, et reditiones integras, quarum numerus fuit aequalis in orbe egredientis centri, diuisit ergo illud tempus, quod fuit inter duas considerationes et exiuit inde tempus, in quo sol secat orbem suum egredientis centri proprium sibi. Et illud est 365. dies, et minus quarta diei parte tricentesima diei secundum propinquitatem, et auctorizauit certitudinem temporis huius reditionis, quam inuenit per conuenientiam eius cum eo, quod inuenit Abrachis, et per comparationem considerationis suae in conuersione aestiua ad considerationem minutam et auctam in illa eadem conuersione, et consideratio quidem haec praeparata est cum duabus armillis, quibus consideratur declinatio, aut cum duabus regulis longis, aut cum laterculo. Et postquam declarata est ei quantitas temporis anni, incepit post illud declarare modum, secundum quem erit res in diuersitate solis. Demonstrauit ergo quod possibile est, ut stella moueat in orbe suo sibi proprio motu aequali, scilicet, ut secet de eo in temporibus aequalibus arcus aequales, et uideatur moueri in orbe signorum motu diuerso, scilicet, ut secet de eo in temporibus aequalibus arcus diuersos, et illud quod praeparatur uno duorum minutorum, et illud est, aut ut stella moueatur motu aequali super circumferentiam orbis, cuius centrum est egrediens a centro orbis signorum, quod est centrum mundi, aut ut moueatur motu aequali super circumferentiam orbis, cuius centrum est centrum mundi, et nominatur iste orbis orbis deferens orbem reuolutionis. Secundum unamquanque igitur istarum duarum radicum mouetur stella motu aequali, et uideatur moueri in orbe signorum motibus diuersis, et demonstratur illud secundum quod narro. Sit orbis egredientis centri circulus a b g d in circuitu centri 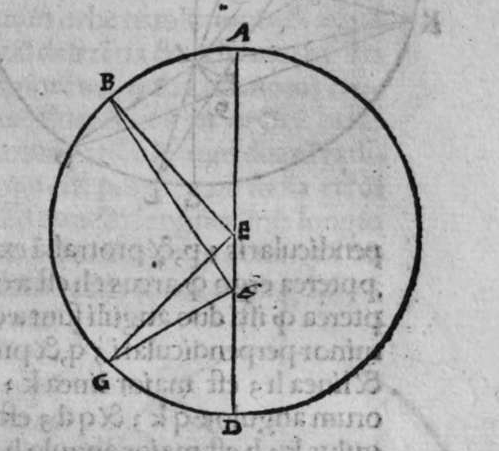e, et sit centrum orbis signorum punctum z, et continuabo lineam z e, et faciam ipsam penetrare in utramque partem usque ad circumferentiam circuli, et occurrat ei super duo puncta a d, erit ergo ipsum punctum a ipsa longitudo longior, et punctum e propinquior propinquitas, et separabo ab una parte duorum punctorum a d duos arcus aequales, qui sint duo arcus a b, g d, et continuabo lineas b e, b z, g e, g z, erunt ergo duo anguli a e b et g e d aequales, et duo anguli a z b et g z d diuersi, et angulus a z b est ille, quem secat stella per uisum in tempore in quo secat arcum a b, et similiter iterum angulus g, z d est ille quem secat per uisionem in tempore, in quo secat arcum g d stella, ergo secat de orbe signorum in temporibus aequalibus arcus diuersos. Et simile illi eidem accidit in radice orbis reuolutionis, et illud est, quoniam si nos posuerimus 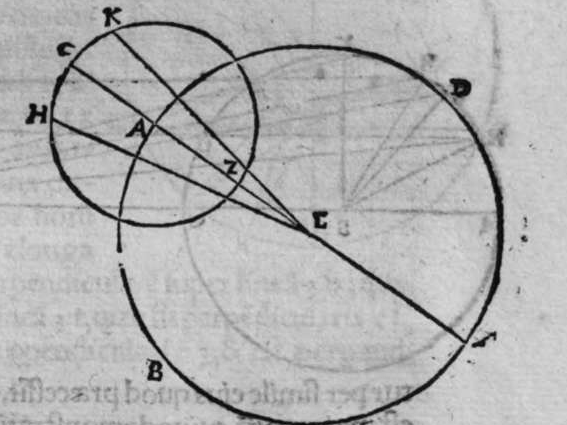orbem signorum circulum a b g d in circuitu centri e, et posuerimus or bem reuolutionis, cuius centrum mouetur super circumferentiam circulum k t h in circuitu centri a, et continuauerimus duo puncta e a linea a e, et fecerimus ea penetrare in utrasque partes, donec occurrat circumferentiae orbis signorum supra punctum g, et circumferentiae orbis reuolutionis supra duo puncta t z, erit tunc punctum t longior longitudo, et punctum z propinquior propinquitas. Cum ergo mouetur centrum orbis reuolutionis super circumferentiam orbis signorum motu aequali ad partem succesionis signorum, et mouetur stella motu aequali super circumferentia orbis reuolutionis circa centrum eius a puncto t, quod est longitudo longior, tunc si fuerit motus eius ab eo ad partem succesionis signorum, et ad partem motus centri orbis reuolutionis, sicut si ipsa mota sit in arcu t h, erit angulus qui prouenit apud centrum orbis signorum, scilicet angulus t e h additus super angulum, quem mouit centrum orbis reuolutionis circa centrum orbis signorum, erit ergo motus stellae ipsius propter illud maior motu centri orbis reuolutionis per angulum t e h. Cum ergo prouenit stella super punctum z quod est propinquior propinquitas, deinde permutatur ad partem longitudinis longioris, sicut si ipsa permutetur ad punctum k, erit motus eius contrarius motui centri orbis reuolutionis, scilicet ipse erit ad contrarium successionis signorum, erit ergo angulus, qui accidet apud centrum orbis signorum, scilicet angulus t e k diminutus a motu centri orbis reuolutionis. Erit ergo motus propter illud minor motu centri orbis reuolutionis per illum angulum, ergo uidebitur stella secare in temporibus aequalibus orbis signorum arcus diuersos. Et si moueatur stella a puncto t quod est longior longitudo ad contrarium successionis signorum, scilicet ad contrarium motus centri orbis reuolutionis, erit res econtrario illius, scilicet, erit motus uisibilis a longitudine longiore minor motu aequali. Cum ergo peruenit in punctum z, quod est propinquior propinquitas, erit motus uisibilis a longitudine propinquiore proginquiore ed. maior motu aequali. Et haec quidem intentio declaratur in duabus radicibus simul per id quod est communis, eo quod ipse dixit, scilice, ut sint arcus diuisi medietatis circuli orbis egredientis centri in quocunque loco uoluerimus. 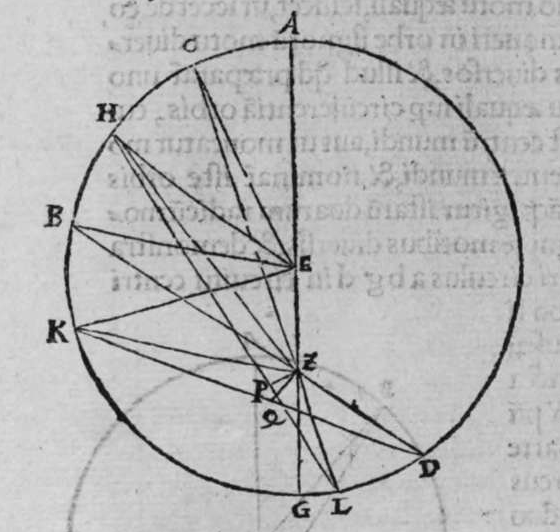Sit itaque orbis egredientis centri circulus a b g in circuitu centri e, et centrum orbis signorum sit punctum z, et diameter transiens per longitudinem longiorem et propiorem sit linea a e g, et separabo in medietate circuli a b g duos arcus aequales, in quocunque loco eius uoluerimus, continuos aut separatos, et sint duo arcus h t, k b, et continuabo extremitates cum duobus centris e z per lineas h e, t e, k e, b e, h z, t z, k z, b z, erunt ergo duo anguli h e t et k e b aequales. Dico ergo, quod duo anguli h z t et k b z sunt diuersi, et quod angulus k z b est maior eorum, cuius demonstratio haec est. Faciam penetratre duas lineas b z, t z usque ad circumferentiam circuli a b g, donec occurrant ei super duo puncta d l, et continuabo punctum l cum puncto h linea l h, et punctum d cum puncto k linea d k, et protraham a puncto z perpendicularem super lineam l h, quae sit perpendicularis z p, et protraham ex eo perpendicularem super lineam d k, quae sit perpendicularis z q, propterea ergo quod arcus t h est aequalis arcui k b, est angulus h l t aequalis angulo k d b. Et propterea quod isti duo anguli sunt aequales, et linea l z est minor linea z d, est perpendicularis z p minor perpendiculari z q, et propterea quod perpendicularis z p est minor perpendiculari z q, et linea h z est maior linea k z, est angulus q k z maior angulo p h z, ergo aggregatio duorum angulorum q k z et q d z est maior aggregatione duorum angulorum p h z et p l z, ergo angulus k z b est maior angulo h z t, et illud est, cuius uoluimus declarationem. Et similiter 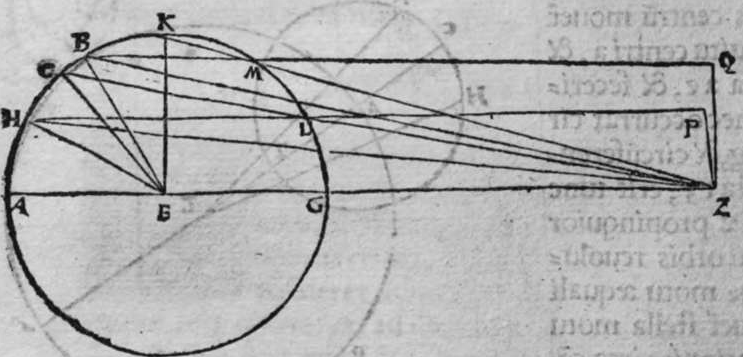si posuerimus orbem reuolutionis circulum a b g in circuitu centri e, et centrum orbis signorum punctum z, et continuauerimus lineam llneam ed. e z et fecerimus eam penetrare usque ad punctum quod est longior longitudo, et separauerimus de medietate a b g duos arcus aequales, qui sint duo arcus h t et b k, et continuauerimus extremitates amborum cum puncto z per lineas h z, t z, b z, k z, declarabitur per simile eius quod praecessit, quod duo anguli h z t, b z k sunt diuersi, et quod angulus h z t est maior eorum, cuius demonstratio haec est. Continuabo duas lineas h l, b m, et faciam eas penetrare ad partem puncti z, et protraham super utrasque duas perpendiculares z p, z q, propterea ergo, quod duo arcus h t, b k sunt aequales, sunt duo anguli h l t, b k m aequales. Erunt ergo duo anguli z l p, z m q iterum aequales, et propterea, quod linea z m est longior linea z l est, perpendicularis z q maior perpendiculari z p, et propterea quod perpendicularis z q est maior perpendiculari z p, et linea z b est minor linea h z, est angulus z b q maior angulo z h p, et angulus b m k est aequalis angulo h l t, ergo remanet angulus h z t maior angulo b z k, et angulus h z t est superfluitas inter motum aequalem et uisibilem in tempore, in quo stella secat arcum h t, et similiter angulus b z k est superfluitas inter motum aequalem et uisibilem in tempore, in quo stella secat arcum b k, et propterea quod duo arcus h t et b k sunt aequales, sunt duo tempora, in quo secat eos ambos, aequalia, sequuntur ergo propter illud, quod stella per uisionem secat de orbe signorum in temporibus aequalibus arcus diuerios, et illud est quod uoluimus declarare. Et demonstrabitur per illud, quod superfluitas in angulis diuersitatis secundum unamquanque duarum radicum est maior quae esse potest in duabus longitudinibus longiore et propinquiore stellae, et non cessat superfluitas minorari, donec peruenit stella ad transitum suum medium, et est punctum, cuius elongatio a puncto longitudinis longioris per uisionem est quarta circuli, tunc enim priuatur haec superfluitas in diuersitatibus inter motum aequalem et uisibilem, et fiunt tunc aequales, et propter illud nominatur punctum hoc punctum transitus medij stellae, et illud est, quoniam motus uisibilis in eo est medius motuum eius. In quaecunque ergo stellarum sunt duo modi diuersitatis, possibile est duas intentiones simul componi, scilicet radicis, in qua agitur secundum orbem egredientis centri, et radicis, in qua agitur secundum orbem reuolutionis, quemadmodum declarabitur illud in eo quod sequitur post in stellis concurrentibus. In ea uero, cui inest diuersitas una duarum radicum, et est totum quod sequitur ab unaquaque earum, conueniens ei quod apparet uisibiliter, cum fuerint proportiones seruatae, et fuerint motus in utrisque aequales, scilicet, ut sit proportio lineae, quae est inter duo centra in radice egredientis centri ad medietatem diametri eius, sicut proportio medietatis diametri orbis reuolutionis ad medietatem diametri orbis deferentis eum, cum centrum est orbis signorum, et ut sit motus stellae in orbe egredientis centri aequalis motui eius in orbe reuolutionis, et aequalis iterum motui centri orbis reuolutionis super circumferentiam deferentis, et ut sit motus stellae in orbe reuolutionis suae, cum est in longitudine eius longiore ad contrarium motus centri orbis reuolutionis, ut sit motus eius ille minor motuum eius, sicut sequitur in radice orbis egredientis centri. Primum ergo, quod oportet me ostendere de assimilatione harum duarum radicum es, quod angulus diuersitatis in unaquaque earum est maior, qui esse potest, cum stella est in transitu suo medio, et illud est, cum eius elongatio per uisionem a puncto longitudinis longioris est quarta circuli, et quod ille, qui appropinquat huic angulo, est maior eo, qui elongatur ab eo. Demonstrabo ergo illud secundum hunc modum. Sit orbis egredientis centri circulus a b g d, et centrum 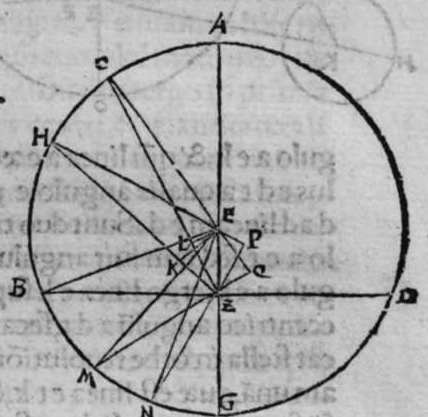eius sit punctum e, et centrum orbis signorum sit punctum z, et linea transiens per ea utraque linea a e z g, erit ergo punctum a longitudo longior, et punctum g longitudo propinquior, et protrahamus ex puncto z perpendicularem super lineam a g, quae sit linea z b, et faciamus ipsam penetrare usque ad d, et continuabo duo puncta b e linea b e, ergo erit angulus e b z ipse angulus diuersitatis inter angulum a e b, qui est motus eius aequalis, et inter angulum a z b, qui est motus eius uisibilis. Signabo autem super circumferentiam circuli a b g duo puncta h t, et continuabo ea cum duobus punctis z e per lineas h z, h e, t z, t e erit ergo angulus h ipse angulus diuersitatis inter duos angulos a e h et a z h, et angulus t iterum angulus diuersitatis inter duos angulos a e t et a z t. Dico ergo, quod angulus b est maior horum angulorum, et quod angulus h proximus est maior angulo t elongato ab eo, quod sic demonstratur. Potraham a puncto e perpendicularem super lineam z h, quae sit linea e k, et protraham ab eo iterum perpendicularem super lineam z t, quae sit perpendicularis e l, erit ergo unaqaeque harum duarum perpendicularium minor perpendiculari e z, et est perpendiculare 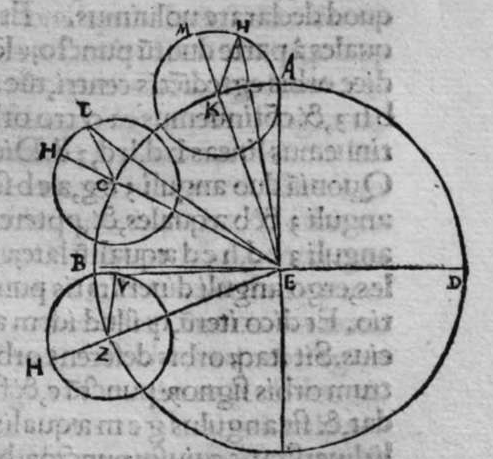e k, quae est una ambarum maior perpendiculari e l, et propterea quod lineae e b, e h, e t sunt aequales, sequitur, ut sit angulus b, cui subtenditur perpendicularis longior, maior angulo h, et angulus h maior angulo t, et accidet illi eidem simile si fuerint duo puncta h t in eo, quod est inter duo puncta b g. Et sit iterum in radice orbis reuolutionis orbis signorum circulus a b g in circuitu centri e, et sit linea a e g diameter, super quam est centrum orbis reuolutionis, cum stella est in sua longitudine longiore a puncto e, quod est centrum orbis signorum, et sit orbis reuolutionis circulus h n in circuitu centri z, et continuabo centrum eius a centro orbis signorum per lineam e z h. Est ergo punctum h orbis reuolutionis ipsa longitudo eius longior, et est illud, in quo est stella, quando est centrum orbis reuolutionis eius supra punctum a, et sit angulus n z h aequalis angulo a e z, et continuabo lineam n e, propterea ergo, quod duo motus centri orbis reuolutionis super circumferentiam orbis signorum est aequalis motui stellae super circumferentiam orbis reuolutionis eius, est stella super punctum n orbis reuolutionis eius, et est linea n z aequedistans lineae a e, ergo angulus a e n est aequalis angulo z n e. Si ergo fuerit angulus a e n rectus, tunc angulus z n e erit rectus, et erit linea e b contingens circulum orbis reuolutionis, et erit angulus b e z maior angulorum diuersitatis. Et si nos signauerimus super arcum a b duo puncta, quae sint t k, et posuerimus unumquodque eorum centrum orbis reuolutionis, et posuerimus angulum l t h aequalem angulo a e t, erit punctum l orbis reuolutionis, ipse locus planetae in ipso, cum fuerit centrum orbis reuolutionis supra punctum t. Et similiter, si posuerimus angulum h k m aequalem angulo a e k, erit punctum m ipse locus stellae in orbe reuolutionis eius, cum fuerit centrum eius supra punctum k. Et manifestum est, quod angulus t e l est maior angulo k e m, et similiter erit, si fuerit centrum orbis reuolutionis in eo, quod est inter duo puncta z g, et illud est, quod uoluimus declarare. Et ponam iterum orbem egredientis centri circulum a b g 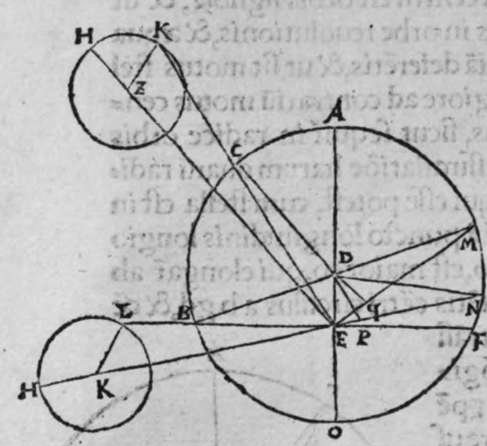in circuitu centri d, et centrum orbis signorum punctum e, et lineam transeuntem per longitudinem longiorem et propinquiorem lineam a e g, et ponam stellam supra punctum t, et continuabo duas lineas e d, e t, et protraham ex puncto e lineam aequedistantem lineae t d, quae sit linea e h, et signabo super ipsam punctum z qualitercunque accidat, et sit proportio lineae d e ad lineam a d, sicut proportio lineae h z ad lineam z e, et protraham ex puncto z lineam aequedistantem linea a d, quae sit linea z k, et ponam punctum z centrum, et mensurabo spacium z h, et circumducam circulum h t. Est ergo orbis reuolutionis stellae, et secat lineam k z supra punctum k, et continuabo lineam k e. Dico ergo, quod ipsa transit super punctum t, et quod ipsa cooperit lineam e t, cuius haec est demonstratio. Quoniam linea k z est aequedistans lineae a g, tunc angulus z k e est aequalis angulo a e k, et quoniam linea a e aequedistat lineae k z, et linea e z aequedistat lineae d t, et est angulus e d t aequalis angulo e z k, et proportio lineae e z ad lineam z k, est sicut proportio lineae t d ad lineam e d. Sunt duo trianguli k z e, t d e similes, ergo angulus e z k est aequalis angulo a e t, sed iam fuit angulus e k z aequalis angulo a e k, ergo angulus a e t est aequalis angulo a e k, ergo linea e k supraponitur lineae e t, ergo sunt linea una. Cum ergo secat stella in ecentrico angulum a d t, secat in illo tempore centrum orbis reuolutionis angulum a e z, et secat stella in orbe reuolutionis angulum h z k, et uidetur in unaquaque duarum radicum super lineam unam, quae est linea e t k, et est eius elongatio a linea a e in utrisque radicibus angulus a e t et sunt duo anguli diuersitatis, qui sunt duo anguli d t e et k e z aequales, et est angulus z k e in orbe reuolutionis aequalis semper angulo, qui est elongatio stellae a linea transeunte per longitudinem longiorem et propinquiorem, scilicet angulo a e k, ergo uidetur stella propter illud semper secundum unamquanque duarum radicum super lineam unam, quae est linea e k, et illud est, quod declarare uoluimus. Et si stella iterum iam separauit de orbe signorum duos arcus aequales a parte duorum punctorum longitudinis longioris, et propinquioris propinquitatis in radice orbis egredientis centri, tunc anguli diuersitatis erunt aequales. Sit itaque stella super puncta b h z, et continuemus ea centro orbis signorum, et sint anguli a e b et h e g et z e g aequales, et continuemus lineas b d, h d, z d. Dico ergo, quod anguli b et h et z sunt aequales, quod sic probatur. Quoniam duo anguli z e g, a e b sunt aequales, est propter illud linea e b z recta, et sunt duo anguli z et b aequales, et propterea iterum, quod duo anguli z e g, h e g sunt aequales, sunt duo trianguli z e d, h e d aequalium laterum et angulorum, ergo duo anguli z et h eorum amborum sunt aequales, ergo anguli diuersitatis punctorum b et h et z sunt aequales. completa est eius demonstratio. Et dico iterum, quod illud idem accidit in radice, in qua agitur secundum orbem reuolutionis eius. Sit itaque orbis deferens orbem reuolutionis circulus a z g, et centrum eius quod est centrum orbis signorum punctum e, et faciamus transire super ipsum lineam b e d qualitercunque accidat, et sit angulus g e m aequalis unicuique duorum angulorum a e b et d e g.Dico ergo, quod anguli diuersitatis cuiusque punctorum b m d sunt aequales. Sit itaque centrum orbis reuolutionis, quando stella est supra punctum b in puncto z, et continuabo lineam z e, et faciam ipsam penetrare usque ad h, et sit centrum orbis reuolutionis, quando stella etiam est supra punctum m in puncto k et continuabo k m, k e, et sit centrum orbis reuolutionis, quando stella est supra punctum d super punctum n, et continuabo duas lineas n d, n e. Dico ergo, quod anguli b e z et k e m et n e d sunt aequales, cuius haec est demonstratio. Producam lineas b z, z t, k f, n q, propterea igitur, quod anguli a e b, m e g, d e g sunt aequales, et lineae b z, m k, q n, sunt aequedistantes lineae a g, erunt anguli t b z, k m f, d q n iterum aequales, ergo trianguli b z t, f k m, n d q sunt aequalium laterum et angulorum, scilicet unumquodque latus suo relatiuo, et omnis angulus suo relatiuo, ergo latera b t, f m, d q sunt aequalia, et multiplicatio lineae b e in e t, est sicut multiplicatio f e in e m, et sicut multiplicatio lineae d e in e q, oportet ergo propter illud, ut sint lineae b e, f e, d e aequales, ergo trianguli e b z, et e f k et e d n sunt aequalium laterum, scilicet omne latus suo relatiuo et aequalium angulorum omnis angulus suo relatiuo, ergo anguli b e z et f e k et d e n, qui sunt anguli diuersitatis, sunt aequales, et illud est, quod declarare uoluimus. Et sequitur ob hoc, ut sit angulus z e k, qui est motus aequalis angulo b e f, qui est motus uisibilis, et est ille, quem diuidit linea transiens per duos transitus medios in duo media, et illud est, quod declarare uoluimus.

⟨III.1⟩ De diuersitate Solis.

ET postquam declaratum fuit ei totum, cuius praecessit declaratio, incepit post illud declarare quantitatem diuersitatis quae uidetur in sole. Dixit ergo propterea quod haec diuersitas una, et tempus, quod est a minore motu solis ad medium motum eius, est semper maius tempus, quod est a medio motu eius usque ad maiorem, oportet ut amministretur in hac diuersitate radix orbis egredientis centri, quamuis casus illius etiam praeparetur per radicem, in qua agitur secundum orbem reuolutionis, ita, ut sit motus stellae ipsius in orbe reuolutionis in longitudine longiore eius ad contrarium successionis signorum, quemadmodum est praemissum. Verumtamen haec radix, scilicet radix orbis egredientis centri, est planior et lenior, quoniam completur motu uno, uerum radix orbis reuolutionis non completur nisi motibus duobus. Inquirit ergo in primis locum orbis signorum, in quo est longitudo longior orbis egredientis centri, et quantitatem lineae quae est inter duo centra. Accepit ergo ad illud tres considerationes solis, quarum unam constituit per aequalitatem uernalem, et secundam statuit per conuersionem aestiuam, et tertiam statuit per aequalitatem autumnalem. Inuenit ergo tempus quod est ab aequalitate uernali ad aequalitatem autumnalem longius medietate temporis anni, ergo sciuit, quod aux solis cadit in medietatem quae est ab aequalitate uernali ad aequalitatem autumnalem, et reperit tempus, quod est ab aequalitate uernali ad conuersionem aestiuam longius tempore, quod est a conuersione aestiua ad aequalitatem autumnalem. Sciuit ergo propter illud, quod aux cadit in hac quarta, et illud est, quia ipse inuenit tempus, quod est ab aequalitate uernali ad conuersionem aestiuam 94. dies, et 30. minuta, et tempus quod est a conuersione aestiua ad aequalitatem autumnalem 92. dies, et 30 minuta. Extraxit ergo ex superfluitate, quae est inter hos arcus, illud quod est inter duo centra et locum longitudinis longioris secundum hunc modum, scilicet, ut sit orbis signorum circulus a b g in circuitu centri e, et ponam punctum a punctum aequalitatis uernalis, et punctum b conuersionem aestiuam, et punctum g aequalitatem autumnalem, et punctum d conuersionem hyemalem, et iam demonstratum est, quod longitudo longior orbis ecentrici non cadit nisi in arcu a b. Describam ergo orbem egredientis centri circulum h t k, et centrum eius n, et continuabo lineam e n m, ergo linea e n est illud quod est inter duo centra, et punctum m orbis signorum est locus longitudinis longioris, ergo sol abscidit arcum 3 h orbis egredientis centri in 94. diebus et 30. minutis, et arcum h t in 92. diebus et 30. minutis, et protraham super punctum n duas lineas aequedistantes duabus lineis a g, b d, propterea ergo, quod unumquodque temporum, in quibus sol secat arcus z h, h t, t p orbis egredientis centri, est notum, et unusquisque horum arcuum notus, cum iam praecessit scientia quantitatis temporis reditionis solis, et propter illud sunt sectiones z f, q h notae, et sunt earum sinus, et sunt lineae n c, c e noti. Est ergo propter illud linea n e, quae est inter duo centra nota et illud est duae partes et 29. minuta per quantitatem, qua est medietas diametri orbis egredientis centri 60. partes, et erit iterum angulus n e c notus, ergo erit arcus a m, et est longitudo augis ab aequalitate uernali, notus, et est 65. partes et 30. minuta. Comprehensio uero augis et eius, quod est inter duo centra, praeparatur per tres considerationes absque istis conditionibus, scilicet, ut sint loca considerata orbis signorum, praeter puncta aequalitatis et conuersionis, ueruntamen est difficilis, et ingredietur eam propinquitas propter multitudinem multiplicationis multipilcationis ed. et diuisionis, et inueniendi radicem. Et postquam patuit ei locus augis solis orbis signorum, et quod est inter duo centra, possibile ei fuit inuenire quantitates diuersitatum particularium in omnibus partibus orbis signorum secundum hunc modum. Ponam ergo orbis egredientis centri circulum a b g in circuitu centri d, et sit diameter eius a d g, et ponam centrum orbis signorum super eam punctum e, et separabo ex orbe egredientis centri arcum a b per quamcunque quantitatem fuerit, et continuabo punctum b cum centro orbis egredientis centri, et cum centro orbis signorum per duas lineas b d et b e, propterea ergo, quod linea e d, quae est inter duo centra, est nota per quantitatem, qua medietas diametri orbis egredientis centri est nota, tunc est unumquodque duorum laterum b d, d e trianguli b d e notum, et angulus eius b d e est notus, ergo angulus eius d b e est notus, et iste angulus est angulus diuersitatis, quae est inter motum aequalem et uisibilem, scilicet inter duos angulos a d b et a e b. Minuatur itaque ex partibus anguli a d b positi, si fuerit sol in medietate, quae est a longitudine longiore ad longitudinem propiorem, scilicet, si fuerit arcus a b positus minor semicirculo, et addatur super eas, si fuerit in medietate secunda, scilicet, si fuerit arcus a b maior semicirculo, quod ergo est post additionem aut diminutionem, est quantitas anguli a e b, qui est elongatio solis in orbe signorum a puncto a, et iam ostensum fuit, quod locus huius puncti orbis signorum est notus, ergo propter illud est locus solis orbis signorum notus, et illud est, quod uoluimus declarare. Et similiter si fuerit angulus positus angulus a e b, sciemus iterum quantitatem anguli b per illam eandem demonstrationem, sciemus ergo ex eo quantitatem anguli a d b. Et similiter si sol mouetur super orbem reuolutionis, ponam ergo or bem signorum circulum a b in circuitu centri e, et sit super circumferentiam eius orbis reuolutionis d h, et sit centrum eius super circumferentiam huius orbis punctum b, et continuabo lineam e b d, et ponam punctum a circumferentiae orbis signorum punctum super quod est sol cum centro orbis reuolutionis, cum est in longiore longitudine orbis reuolutionis, scilicet, cum est supra punctum d, et continuabo punctum a cum centro orbis signorum per lineam a e g, et sit arcus a b qui est motus solis medij positus per quamcunque quantitatem uolumus, et sit arcus d h orbis reuolutionis, qui est motus diuersitatis aequalis ei, et continuabo punctum h cum centro orbis reuolutionis per lineam h b, et quoniam trianguli e b h angulus b est notus, et duo latera eius e b, b h sunt nota, est angulus h e b notus, et est angulus diuersitatis. Minuatur ergo aut addatur secundum locum solis in orbe signorum, et illud est, quod uoluimus declarare. Et similiter si fuerit notus angulus a e h, scilicet motus solis uerus, et uoluerimus scire motum eius medium, scilicet angulum a e b. Nos namque extrahemus angulum b e h, propterea quod angulus b h e est aequalis angulo a e h, ergo est notus, et unumquodque duorum laterum e b, h b est notum, est ergo propter illud angulus b e h notus, minue ergo ipsum aut adde secundum locum solis in orbe reuolutionis eius, et quod fuerit post additionem aut diminutionem, erit quantitas anguli a e b. completa est declaratio.

⟨III.2⟩ De diuersitate dierum cum noctibus suis.

ET postquam, speculatus est in diebus cum noctibus suis, inuenit eos in ueritate diuersos, et illud est, quoniam dies cum nocte sua est tempus, in quo incipit sol ab horizonte, aut circulo meridiei, usquequo redeat ad illum eundem circulum, et hoc tempus est, in quo reuoluuntur partes circuli aequatoris diei, et additio ad illud eius quod eleuatur de eo cum partibus orbis signorum, quas abscidit sol in illo tempore, et hoc tempus additum consequitur diuersitas duobus modis, quorum unus est, quod sol abscidit de orbe signorum in temporibus aequalibus arcus diuersos, et secundus est, quod partes aequales orbis signorum eleuantur ab horizonte, aut orbe meridiei cum partibus diuersis aequatoris diei. Et est tempus quidem anni solis, ipsum tempus in quo reuoluitur circulus aequatoris diei reuolutionibus, quarum numerus est numerus dierum anni, et additio ad illud reuolutionis unius, et est illa, quae reuoluitur cum partibus orbis signorum, quas abscidit sol in tempore anni. Cum ergo diuiduntur illae reuolutiones per numerum dierum anni, egreditur inde uni diei et nocti suae reuolutio una aequatoris diei, et additio ad illud 59. minutorum de eo secundum propinquitatem, et est illud quod egreditur de diuisione circuli aequatoris diei additum super reuolutiones supra numerum dierum anni. Est ergo propter illud tempus diei medij cum nocte sua ipsum tempus, in quo reuoluuntur partes circuli unius aequedistantis aequatori diei, et 59. minuta eius secundum propinquitatem. Tempus ergo diei cum nocte sua uera ingreditur diuersitas duobus modis, quorum unus est, quod consequitur ista 59. minuta de diuersitate, et secundus est, quod consequitur ea de diuersitate eleuationum apud horizonta, et apud circulum meridiei, ueruntamen haec diuersitas in die una est insensata. In diebus non pluribus aggregatur ex ea quantitas de qua curatur, et propterea quod plurimum superfluitatis inter diuisiones orbis egredientis centri, et diuisiones orbis signorum non est, nisi in duabus medietatibus orbis egredientis centri, quas diuidunt longitudo longior et propinquior in duas medietates, oportet ut plurimum diuersitatis, quae consequitur dies cum noctibus suis propter diuersitatem solis, non sit, nisi in istis duabus diuisionibus orbis signorum, et est summa eius in duabus medietatibus temporis anni circiter nouem partes et medietatem partis, propterea quod una earum addit super medietatem circuli 4. partes et 3. quartas partis, et secunda minuit a medietate circuli, quantum sunt illae eaedem partes. Et propterea, quod superfluitas inter partes orbis signorum, et inter illud quod eleuatur aut occidit, cum eis de aequatore diei diuersificatur secundum diuersitates horizontum, et haec diuersitas in curculo meridiei omnis horizontis est una et eadem quae non alteratur, oportet propter illud, ut ponantur principia dierum a medietate diei aut noctis. Erit ergo tempus diei unius cum nocte sua a medietate diei aut noctis ad medietatem diei aut noctis, post ipsum plurimum uero superfluitatis, quae est inter partes orbis signorum et inter eleuationes earum a circulo meridiei, est in duobus signis, quae sequuntur unum duorum punctorum duarum aequalitatum, et in duobus signis quae sequuntur unum duorum punctorum duarum conuersionum, et peruenit illud circiter 4. partes et medietatem partis, et praeparatur comprehensio illius per illud, quod praemisimus in tractatu huius libri. Est ergo superfluitas inter ea cum quibus eleuatur, et eleuationes nouem partes, ergo diuisio orbis signorum pertinens additioni est illa, in qua aggregantur istae duae superfluitates, scilicet superfluitas, quae est propter diuersitatem solis, et superfluitas, quae est propter diuersitatem eleuationum in circulo meridiei additae simul, et est diuisio, quae est a principio signi scorpionis usque ad medium signi aquarij, et diuisio proportionata diminutioni, est diuisio, in qua aggregantur istae duae superfluitates diminutae simul, et est residuum circuli, scilicet, quod est a medio aquario usque ad finem librae, et est summa illius propter diuersitatem quidem solis tria tempora, et duae tertiae temporis, et propter diuersitatem quidem eleuationum quatuor tempora, et duae tertiae temporis, donec sit aggregatum ex duabus superfluitatibus simul octo tempora, et tertia temporis, et illud est quasi medietas horae et pars octauadecima horae, et haec quidem quantitas, si negligatur in sole et in alijs stellarum, non ingreditur ex ea de errore quantitas sensata. In luna autem propter uelocitatem motus eius est illud, quod prouenit inde circiter tres quintae partis, et est illud, quod ipsa abscidit in hora una et nona horae praedictum. Cum ergo uoluerimus reducere dies diuersos ad dies aequales, sciemus cursum solis medium et uerum in illo tempore posito, et sciemus eleuationes cursus ueri in sphaera recta, et accipiemus superfluitatem inter illas eleuationes et cursum medium, et illius superfluitatis quaecunque fuerit, accipiamus partem quintamdecimam, et quantacunque fuerit unius horae. Si eleuationes fuerint plus cursu medio, addemus illud super dies positos, et si fuerit minus, minuemus illud de diebus positis, et quod fuerit post additionem aut diminutionem, erit dies aequalis, et per conuersionem illius reducantur dies aequales ad dies diuersos, et illud est, quod uoluimus declarare.

⟨IV⟩ LIBER QVARTVS. DE LVNA ET eius diuersitatibus.

ET postquam declaratum est ei totum quod praemissum est de esse solis, possibile est ei inquirere de re lunae. Inquirit ergo primo de considerationibus, quibus oportet uti in illo, uidet ergo, quod loca solis in eclipsibus significant loca lunae. In solaribus quidem earum loca eius sunt loca lunae. In lunaribus autem loca solis sunt opposita locis lunae secundum ueritatem. Loca uero solis in eclipsibus solaribus non sunt nisi loca lunae uisibilia de orbe signorum, non loca eius uera, et illud est, quoniam ipsi non fiunt, nisi apud incessum lunae per lineam quae transit per uisus nostros, et per centrum solis, non transitum eius per lineam, quae transit per centrum terrae et per centrum solis, scilicet lineam quae determinat loca stellae uera in orbe signorum. Nam si imaginemur penetrationem eius usque ad superficiem sphaerae orbis signorum, et imaginemur circulum magnum signatum super polum orbis signorum, et super extremitatem huius lineae, tunc punctum super quod iste circulus secat signorum circulum, est locus stellae uerus in eo, sicut locus eius uisibilis est punctum, super quod circulum signorum secat circulus, qui signatur super duos polos orbis signorum, et super extremitatem lineae productae ex superficie terrae, non illius quae egreditur de centro eius. Propter illUD ergo sunt loca eius ipsa loca uisibilia non uera, propterea uero, quod causa faciens eclipses lunares non est nisi introitus lunae in pyramidem umbrae terrae, et est pyramis quae accidit ex casu radij solis super illud, quod est in directo eius de corpore terrae, et separat corpus terrae, tunc inter lunam et radium solis quo illuminatur, et sequitur ob hoc, ut sit locus lunae de orbe signorum in medio tempore eclipsis super axem huius pyramidis, scilicet super lineam transeuntem per caput eius et per centrum terrae, et centrum basis eius, quae est corpus solis, ergo est locus lunae uerus secundum oppositionem loci solis ueri super extremitatem diametri, oportet ergo propter illud, ut utamur in inuestigatione de locis lunae ueris eclipsibus lunaribus, non solaribus. Et propterea quod luna mouetur secundum diuersitatem in longitudine et in latitudine scilicet, quia non est motus eius in parte una orbis signorum motus unus et idem, neque eius latitudo in eo est latitudo una et eadem semper, imo mouere in parte una medio motuum eius et maiore eorum et minore ipsorum, et similiter eius latitudo in ea est maior quae esse potest ad septentrionem et ad meridiem, et quandoque non est in ea latitudo, tunc significatur inde quod reditio eius in diuersitate sua diuersa est a reditione ipsius in orbe signorum, et quod nodus orbis eius decliuis iterum est imitatus super partes orbis signorum. Aspexerunt ergo in modo quo peruenirent ad cognitionem reditionis eius in diuersitate sua et reditionis eius in orbe signorum, et intenderunt, ut esset illud per eclipses lunae fugientes ab eo quod ingreditur diuersitas aspectus lunae, sicut diximus, et propterea quod lunae sunt motus diuersi, scilicet motus uelox et motus tardus et motus medius, oportet ut sint ei in orbe suo sibi proprio 4. puncta in uno, quorum sit uelocior, qui esse potest, et in secundo opposito illi sit tardior qui est, et sint ista duo puncta ipsa longitudo longior et longitudo propinquior orbis sui proprij, et duo puncta fibi opposita, in quibus sit motus medius inter istos duos motus, et sint duo transitus medij huius orbis proprij. Haec ergo 4. puncta diuidunt hunc or bem in quatuor sectiones, quarum una est illa, in qua est motus eius a uelociore motu ipsius ad motum medium eius primum, et est motus uelox diminutus, et motus eius in sectione secunda est motus medius diminutus etiam, et motus eius in sectione tertia est motus tardus additus, et motus eius in sectione quarta est motus medius additus iterum. Oportet ergo propter illud, ut sciatur secundum grossitudinem aspectus in omni hora terminata, in qua harum 4. sectionum sit. Posuerunt autem antiqui inquirentes duas eclipses lunares in unaquaque quarum esset motus lunae unus horum 4. motuum. Aestimauerunt ergo propter illud secundum grossitudinem aspectus, quod iam redijt in secunda eclipsi in orbe suo proprio ad locum suum in ipso in eclipsi prima, et quod illud spacium, quod est inter duas eclipses, continet reditiones integras lunae in orbe suo sibi proprio, et quia uoluerunt experiri et uerificare inquisiuerunt duas eclipses alias in unaquaque, quarum esset motus lunae motus unus, et diuersus motui in duabus eclipsibus primis, et essent duo spacia, quae fuerunt inter has eclipses quatuor aequalia, et secaret luna in unoquoque horum duorum spaciorum de orbe signorum arcus aequales, aut reuolutiones integras tantum, aut reuolutiones integras et arcus additos super reuolutiones aequales. Cum ergo inuenerunt illud secundum has conditiones narratas, sciuerunt quod luna iam redijt in duabus eclipsibus primis ad punctum unum sui orbis proprij sibi, et quod iam redijt iterum in duabus eclipsibus postremis ad punctum secundum eius etiam, unumquodque ergo duorum spaciorum aequalium erit continens reuolutiones integras lunae in orbe suo sibi proprio. Retulit ergo Ptolomeus ab antiquis hanc uiam, et non propalauit has conditiones quas diximus in istis motibus lunae in eclipsibus quaesitis, et quamuis ipse non propalauerit illud, tamen ipsa intentio dat, quod istae conditiones sunt quaesitae in istis eclipsibus, et si non esset secundum hunc modum, non fabricaret ab integro reditiones. At uero unde declaretur, quod quando istae quatuor eclipses fuerint secundum has conditiones, tunc unumquodque duorum spaciorum inter eas continebit reditiones lunae in orbe suo sibi proprio integras aequalis numeri, iliud declaratur secundum quod narro. Moueatur luna super orbem reuolutionis qui sit circulus a b g d in circuitu centri e, et centrum orbis signorum sit punctum z, et linea transiens per longitudinem longiorem et propinquiorem, et centrum orbis signorum sit 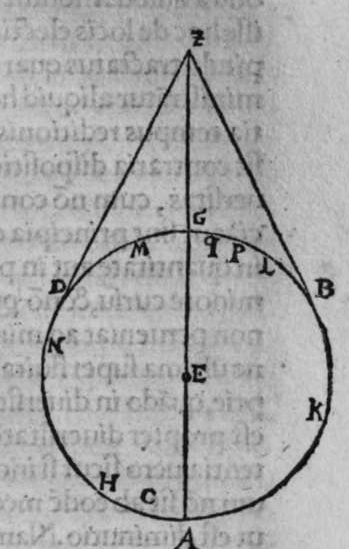linea a e g z, et longitudo longior sit punctum a et propior punctum g, et protrahamus ex puncto z duas lineas contingentes circulum a b super duo puncta b et d, quae sint duae lineae b z et d, erunt ergo duo puncta b et d duo transitus medij, et sit luna in eclipsi prima supra punctum h, et in eclipsi tertia supra punctum p, et sint duo incessus eius super ista duo puncta secundum quod diximus, scilicet quod ipsi ambo sint diuersi, et sit incessus eius in puncto h, ipse incessus eius secundum grossitudinem aspectus in secunda, et incessus eius in tertia, ipse incessus eius iterum in quarta, et duo spacia sint aequalia, et sectiones orbis signorum in utrisque sint aequales. Dico ergo iam, quod redit in eclipsi secunda ad ipsummet punctum h, et in quarta ad ipsummet punctum p, cuius demonstratio est haec. Quoniam si non redit in secunda in punctum h, tunc sit in ea supra punctum t, et si non redit in quarta ad punetum p, tunc sit in ea super punctum q, propterea ergo, quod duo spacia sunt aequalia, oportet propter illud, ut sint duo arcus h t et p q aequales, et propterea quod incessus lunae in duobus punctis h et l est diuersus ab incessu eius in duobus punctis p et q secundum quod conditionatum est, erit unus duorum arcuum h t et p q faciens in motu lunae medio additionem, et secundus faciens in eo diminutionem, et propterea, quod duo spacia sunt aequalia, oportet ut sit motus in utrisque aequalis, ergo necesse est propter illud, ut sit motus lunae uerus in spacio primo diuersus motui eius in secundo, per aggregationem duorum diuersorum simul, scilicet duorum angulorum, qui sunt apud centrum orbis signorum, quibus subtenduntur duo arcus h t et p q. Luna ergo iam secuit in illis duobus spacijs aequalibus orbis signorum duos arcus diuersos, et est fuperfluitas inter eos ambos ipsa aggregatio duarum diuersitatum, quas faciunt duo arcus h t et p q, et nos posuimus quod luna iam secuit in istis duobus spacijs aequalibus orbis signorum post reuolutiones integras duos arcus aequales, hoc ergo est contrarium, quod esse non potest. Contrarium ergo est, quod luna sit in eclipsi secunda super punctum aliud a puncto h, et similiter in eclipsi quarta super punctum aliud a puncto p, ipsa ergo iam redijt in eclipsi secunda ad locum suum in prima, et in quarta ad locum suum in tertia, et illud est cuius uoluimus declarationem. Et propterea quod diuersitas inter duos arcus quos abscidit luna in duobus spacijs aequalibus, si non redit luna ad locum suum primum, est aggregatio duarum diuersitatum quas faciunt duo arcus h t et p q, oportet ut sint eclipses electae in inquisitione huius temporis reuolubilis, ipsae eclipses in quibus loca lunae faciunt diuersitatem plurimam inter motum medium et uerum, et ista loca sunt duo puncta longitudinis longioris et propinquioris, et eius quod appropinquat utrisque, et quanto plus elongantur loca lunae in eclipsibus a duobus punctis longitudinis longioris et propinquioris, tanto plus longinquiora sunt ad electionem. Oportet ergo ut necessario deuitetur, quod locus lunae sit in eclipsi prima et in tertia in duobus transitibus medijs, aut prope eos utrosque secundum contrarium eius quod dixit Ptolomeus. Nam si luna fuerit in eclipsi prima supra punctum m, quod est propinquum puncto d quod est transitus medius, tunc propterea quod motus lunae in eo quod appropinquat puncto d est motus unus, qui plurimum non alteratur, possibile est, ut sit in eclipsi secunda super punctum n, et nos aestimamus quod est in duabus eclipsibus super punctum unum, et possibile est iterum ut sit in eclipsi tertia super punctum k, cuius longitudo a puncto b est sicut longitudo puncti n a puncto d, et est possibile iterum ut sit in eclipsi quarta in puncto l, cuius longitudo a puncto b est sicut longitudo puncti m a puncto d, et nos aestimamus quod in duabus eclipsibus sit in puncto uno, oportet ergo propter illud, ut sit diuersitas quam facit arcus m n aequalis diuersitati quam facit arcus k  l, et sint ambae generis unius, scilicet, quod ambo faciant simul in motu uero additionem aut diminutionem. Sequitur ergo ex hoc, quod luna iam secuit in orbe signorum post reuolutiones integras in duobus spacijs aequalibus duos arcus aequales, et non redit in orbe reuolutionis suae, et illud idem sequitur, si fuerit locus lunae in eclipsi prima punctum transitus medij primi, et in quarta transitus medij alterius, et in unaquaque duarum scilicet secundae et tertiae unum duorum punctorum n et k, aut l et m, ita, ut secet in orbe reuolutionis suae duos arcus aequales, et elongationis aequalis a longitudine longiore aut propinquiore, et haec est una trium positionum a quibus monuit cauendum, et a quibus iussit abstinendum, et nos inuenimus ipsum posuisse hoc de locis electis lunae in istis considerationibus, et illud est, quia dixit in secundo capitulo tractatus quarti, cuius narratio est haec. Non oportet ergo ut sit in spacijs quae amministrantur aliquid horum accidentium, ut aestimemus in eis, quod sint in ueritate comprehendentia tempus reditionis diuersitatis, imo non oportet, nisi ut eligamus ex eis, quorum dispositio sit contraria dispositionibus horum, scilicet spacia quibus proprie sit possibile ut appareat diuersitas, cum non continent reditiones reditones ed. integras de reditionibus diuersitatis, scilicet, ut non sufficiat ut sint principia eius a cursibus diuersis tantum, imo a cursibus magnae diuersitatis, aut in quantitate aut in potentia. In quantitate quidem, sicut si incipiat in uno duorum spaciorum a minore cursu, et non perueniat ad maiorem cursum, et incipiat in spacio alio a maiore cursu, et non perueniat ad minorem cursum, istis enim modis erit superfluitas additionis in longitudine ultima superfluitatis, et illud est, quoniam non possunt esse diuersitatis reditiones integrae, et proprie, quando in diuersitate una consequitur quarta una, aut tres quartae, est superfluitas quae est propter diuersitatem, tunc duae superfluitates per quas sunt duo spacia non aequalia. Impotentia uero sicut si incipiat in unoquoque duorum spaciorum a cursu medio, ueruntamen principium non sit ab eodem medio, imo sit in uno amborum a cursu, ut est additio, et sit in altero a cursu ut est diminutio. Nam secundum hunc modum etiam proprie diuersitates longitudinis diuersificantur ad inuicem ultima diuersitate, praeter quod diuersitas iam reuersa sit, et cum in diuersitate una consequitur quarta iterum, et tres quartae, est superfluitas, quae est propter diuersitatem duae superfluitates, et quando est illud quod consequitur ipsam medietas circuli est super fluitas 4. et propter illud inuenimus Abrachis etiam aestimasse, quod ipse sollicitus fuit cum ultimatione sollicitudinis quae est possibilis in eligendo spacia, quibus utuntur in hac inquisitione. Vsus est ergo superfluitate in luna secundum quod initium unius duorum spaciorum sit a maiori cursu, et non perueniat ad minorem cursum, et principium spacij alterius sit a minori cursu, et eius peruentio non sit apud maiorem cursum. Haec est ergo narratio sermonis Ptolomei, ipse autem posuit de eclipsibus electis in inquisitione huius temporis reuolubilis eclipses in quibus fuit luna in uno duorum spaciorum, in uno duorum transituum mediorum, et fuit in spacio secundo in transitu medio altero, et ipse nuper ostenderat, quod illud ualde longinquum est ab electione, et quod est una trium positionum a quibus cauere monet in inquisitione horum spaciorum, et praecipit abstinendum ab eis, iam ergo elegit et non percepit quod cauere ab eo monuerat, et praeceperat ab eo abstinendum. Sermo uero eius. Haec est uia qua incessit ille, qui fuit in inuentione harum rerum, et possibile est tibi ut scias, quod haec uia non est facilis incessus, neque proximae acceptionis, imo est necessaria in ea consideratio uehemens et comprehensio exquisita eius quod narro et quod continuatur cum hoc est sermo non comprehensus, et illud est, quoniam non oportet ut huiusmodi dicat sermonem, ut si ipse iam ueniat cum uia alia faciliori hac, et non sit necessarium in ea illud quod in hac uia necessarium est de pertransitione, et cum hoc non indigeat uia qua uenerunt antiqui. Sed non fuit ei possibile de illo, imo non uenit nisi cum uia, qua uerificauit et minorauit superfluitatem intrantem propter considerationes, quibus usi sunt antiqui inueniendo tempus reuolubile, et non fuit ei possibile illud nisi ita, ut uteretur in eo quantitatibus motuum, quas inuenerunt antiqui per hoc tempus reuolubile. Totum ergo cum quo uenit, non est fabricatum nisi secundum hoc tempus reuolubile, quod inuenerunt antiqui cum hac uia. Sermo autem eius, ponamus itaque in primis quod tempora spaciorum inueniantur aequalia secundum certitudinem, dico in primo, quod non confert illud nisi superfluitas, quae est propter diuersitatem solis, aut penitus non sit unoquoque duorum spaciorum, aut sit una et eadem, et quod continuatur cum eo est sermo uanus, et illud est quod conditionat in spacijs quaesitis, ut sint aequalia, et luna in eis abscidat de orbe signorum arcus aequales, et cum illud fuerit ita, ut sol sit in medio tempore omnis eclipsis oppositus secundum ueritatem lunae, oportet ut sol iterum iam secuerit in illis duobus spacijs aequalibus de orbe signorum duos arcus aequales, et illud non fit nisi ita, ut non sit ei diuersitas penitus, aut ut sit diuersitas una, et illud fit ita, ut sit secundum unam quatuor positionum quas dixit. Ponit ergo quod sequitur a posito absolute, et est res manifesta per se, et similiter quod dixit post hoc ex eo quod sequitur, ut caueatur a locis lunae in orbe reuolutionis suae in eclipsibus usis in inquisitione horum spaciorum, et sunt loca in quibus possibile est, ut abscidat de orbe signorum in temporibus aequalibus arcus aequales, et non redeat in diuersitate sua, et illud est ita, ut luna in eclipsi prima incipiat a longitudine longiore orbis reuolutionis suae, et perueniat in eclipsi secunda ad longitudinem propiorem, et in tertia incipiat a longitudine propiori, et perueniat in quarta ad longitudinem longiorem, aut ut abscidat in uno quoque duorum spaciorum de orbe reuolutionis suae arcum unum et eundem, aut ut abscidat de eo duos arcus aequales, et aequalis elongationis a longitudine longiore aut propiore, scilicet, ut sit duorum locorum eius in eclipsi prima et quarta elongatio ab utroque latere lineae transeuntis per longitudinem longiorem et propiorem aequalis. Et similiter iterum duo loca eius in eclipsi secunda et tertia, quare sequitur in unaquaque harum trium positionum, ut luna de orbe signorum in duobus spacijs aequalibus abscidat duos arcus aequales, et non redeat in orbe reuolutionis suae, non indiget hac cautela et exquisitione, quoniam non est possibile, ut luna sit, cum ipsi inquirunt ista spacia secundumm aliquam harum conditionum. Quoniam primum quod inispicitur de esse lunae est, ut sint duo incessus eius in eclipsi prima et secunda, scilicet illi qui continent spacium unum incessus unus secundum grossitudinem aspectus, donec aestimetur, quod iam redijt in orbe reuolutionis suae, in eclipsi secunda ad locum suum in eo in prima, ut spacium contineat reditiones integras lunae in orbe reuolutionis suae. Et similiter iterum si cursus eius in eclipsi tertia et quarta, cursus unus et idem etiam secundum grossitudinem aspectus, ita ut iterum aestimetur de ea, quod iam redijt in orbe reuolutionis suae. Haec enim conditio destruit, quod luna sit in eclipsi prima et quarta in longitudine longiore, et sit in secunda et tertia, et in propinquitate propiore. Duas autem positiones reliquas, scilicet in una, quarum secat luna de orbe reuolutionis suae in duobus spacijs unum et eundem arcum et positionem, in qua secat in duobus spacijs duos arcus aequales et aequalis elongationis a longitudine longiore aut propiori, destruit illud quod conditionauit iterum et est, ut sit cursus lunae in duabus eclipsibus, primus diuersus a cursu eius in duabus eclipsibus postremis, quoniam in unaquaque harum duarum positionum sequitur, ut sit cursus lunae in duabus eclipsibus primis, ipse cursus eius in duabus eclipsibus postremis, et hoc est diuersum ab eo quod conditionat. Cum ergo conditionantur in spacijs quaesitis istae conditiones in cursu lunae, non est necessarium aliquid eorum quae ipse dixit de cautela et perscrutatione subtili, neque in luna neque in sole. Haec est ergo uia qua incesserunt antiqui in inueniendo hoc tempus reuolubile, et Ptolomeus quidem refert de Abrachis, quod ipse inuenit quantitatem huius 126007. dies, et horam unam de horis aequalibus, et continentur in ipso de mensibus 4267. menses, et de reditionibus diuersitatis completis 4573. reditiones, et de reuolutionibus orbis signorum 4612. reuersiones, exceptis septem partibus et medietate partis fere, et sunt partes quas minuit sol in 345, reuolutionibus, et hoc quidem secundum quod in reditionibus harum rerum non agatur, nisi secundum comparationem ad stellas fixas. Cum ergo diuiserunt istos dies quos inuenerunt huic tempori reuolubili per numerum mensium qui sunt in eo, exiuit tempus mensis medij 29. dies, et 31. minutum, et 50. secunda, et 8. tertia, et 9. quarta, et 20. quinta cum propinquitate, et cum multiplicantur dies mensis per minuta, quae abscidit sol per motum suum medium in die uno, et sunt 59. minuta et 8. secunda et 17. tertia, et 13. quarta, et 12. quinta, et 31. sexta, est inde quod abscidit sol in tempore mensis medij. Cum ergo adiunguntur ad illud partes circuli unius, et sunt 360. partes, erit illud in quo mouetur luna in longitudine per medium in tempore mensis medij, et cum diuiditur illud per numerum dierum mensis, egreditur motus lunae medius in longitudine in die uno, et illud est 13 partes et 10. minut. et 34. secunda et 58. tertia, et 33. quarta, et 30. quinta, et 30. sexta fere. Cum ergo minuitur ex illo motus solis medius in die uno, remanet motus longitudinis inter eos per medium in die, et illud est 12. partes et 11. minuta, et 26. secunda, et 41. tertia, et 20. quarta, et 17. quinta. Et iterum, cum multiplicantur reditiones diuersitatis, quas comprehendit illud tempus reuolubile per partes circuli unius, et diuiditur aggregatum per numerum dierum illius temporis reuolubilis, egreditur quod abscidit luna in die uno de orbe reuolutionis suae, et illud est 13. partes, et 3. minuta, et 53. secunda, et 56. tertia, et 29. quarta, et 30. quinta, et 30. sexta fere. Motum autem lunae in latitudine comprehenderunt ita quod quaesierunt spacium inter duas eclipses lunares, in quibus fuit quantitas eclipsati de diametro lunae una, et fuit luna in utraque in uno et eodem puncto orbis reuolutionis suae, et fuit eclipsatum ex superficie lunae in parte una a septentrione aut a meridie apud unum et eundem nodum. Nam per aggregationem harum conditionum sequitur necessario, ut sit longitudo lunae in prima duarum eclipsium eius a nodo aequalis longitudini eius in secunda ab illo eodem nodo in eadem parte. Illud ergo spacium continet reuolutiones completas lunae in latitudine, et centri orbis reuolutionis eius in orbe decliui. Dixit ergo, quod Abrachis reperit has duas secundum has conditiones, et inuenit tempus quod est inter eas continere 5458. menses, et de reuolutionibus latitudinis 5923. reuolutiones. Cum ergo diuiditur illud spacium per numerum reditionum latitudinis, egreditur tempus reditionis unius, et cum diuiditur per illum numerum numerus partium circuli unus, et est 360. partes, egreditur, quod luna abscidit per motum suum medium in latitudine in die uno, et illud est 13. partes, et 13. minuta, et 45. 45, ed. secunda, et 39. tertia, et 40. quarta, et 17. quinta, et 19. sexta. Per hanc ergo uiam comprehenderunt antiqui motus lunae in latitudine et diuersitate et longitudine. Ptolomeus uero propterea quod antecessit eum Abrachis, et iam comprehenderat motus lunae secundum hos modos, et scripserat eos, et intendit rectificare eos, et experiri per hanc uiam quam narro, et illud est, quoniam ipse uidit, quod si in istis motibus scriptis est appropinquatio propter comsiderationes, tunc cum assumetur ex ea quantitati alicui temporis parui, erit appropinquatio in illa quantitate temporis magna. Cum ergo extrahitur propter assumptum ex ea motus quantitati alicui temporis magni, et diuiditur illa appropinquatio parua, quae est propter considerationes per numerum reuolutionum illius temporis magni, tunc est portio reuolutionis unius de illa appropinquatione insensibilis omnino, et erunt motus comprehensi hac uia certiores qui esse possunt, et fecit illUD currere secundum semitam indagationis subtilis. Intendit ergo ad rectificandos hos motus comprehensos, ita, quod inquirit tres eclipses lunares, quarum considerationes uerificatae fuerunt ex antiquioribus earum quas inuenit, et extraxit propter has tres eclipses locum lunae in orbe reuolutionis suae, scilicet elongationem eius a longitudine longiori eius in tempore unius illarum eclipsium, et locum centri orbis reuolutionis eius in orbe signorum, et quantitatem proportionis medietatis diametri orbis reuolutionis eius ad medietatem diametri orbis deferentis ipsum secundum quod narro. Ponam tres eclipses, quarum considerationes uerificatae sunt et loca earum, et ponam orbem reuolutionis lunae, super quem sunt a b g, et sit luna in eclipsi prima super punctum a, et in secunda super punctum b, et in tertia super 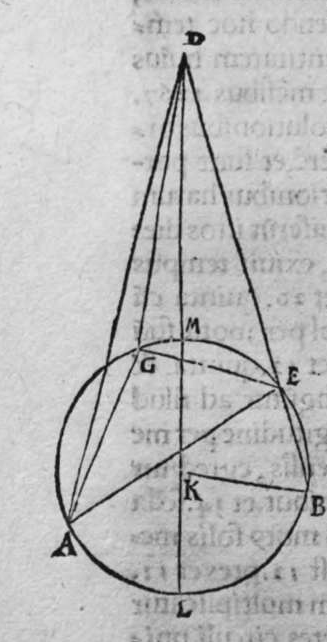punctum g, et sit centrum orbis signorum punctum d, et continuabo lineas d a, d b d g, a g, a e, g e, arcus ergo quem abscidit luna ab eclipsi prima ad eclipsim secundam est arcus a g b, et a secunda ad tertiam arcus b a g, et arcus quidem isti sciti sunt ex motibus scriptis, et quod abscindit in orbe signorum per motum suum medium in longitudine, est notum iterum ex illis motibus extractis per tempus reuolubile, et loca lunae in ueritate in orbe signorum nota propter loca solis, ergo sectio eius in ueritate de orbe signorum est nota, ergo angulus a d b est notus, quoniam ipse est superfluitas inter motum eius medium et uerum in longitudine, quem secat luna in spacio, quod est inter eclipsim primam et secundam, et similiter angulus a d g est notus per illum modum, et quoniam arcus a b orbis reuolutionis est notus, erit angulus a e b notus, ergo angulus d e a est notus, ergo triangulus a d e est notorum angulorum, ergo per quantitatem qua est latus d e 60. partes, est per eam unumquodque duorum laterum a d, a e notum, et propterea quod angulus a d e est notus, et angulus a d g est notus, est angulus g d e notus, et angulus g e d est notus, quoniam ipse est superfluitas duorum rectorum super angulum g e b notum, ergo triangulus g e d est notorum angulorum, igitur unumquodque duorum laterum g e, g d est notum per quantitatem qua est latus e d 60. partes. Et similiter iterum angulus a e g est notus, quoniam arcus a g est notus, et duo latera trianguli a e g, a e, e g sunt nota, et angulus e eius est notus, ergo latus a g est notum per quantitatem qua est linea d e 60. partes. Sed linea a g est nota per quantitatem qua est medietas diametri orbis reuolutionis 60. partes, quoniam arcus a g orbis reuolutionis est notus, linea ergo g e est nota per quantitatem qua est medietas diametri orbis reuolutionis 60. partes, et similiter linea d e iterum est nota per illam quantitatem, ergo arcus g e est notus, remanet ergo e b notus, ergo corda eius quae est linea e b est nota per quantitatem qua est medietas diametri orbis reuolutionis 60. partes, propter lineam ergo e b et arcum e b a scitur locus centri orbis reuolutionis in sectione. Ponam ergo ipsum in sectione e a b, sitque punctum k, et continuabo lineam d k l et lineam k b, et propterea ergo, quod duae lineae b e, e d sunt notae per quantitatem qua est b k 60. partes, tunc b d et d e sunt notae per illam quantitatem, ergo superficies b d in d e est aequalis superficiei l d in d m, ergo superficies l d in d m est nota, et quadratum m k est notum, ergo quadratum d k est notum, ergo d k est nota per quantitatem qua est b k 60. partes. Iam ergo ostensum est, quod proportio medietatis diametri orbis reuolutionis ad medietatem diametri orbis deferentis est nota, et iterum, quia triangulus d k b est notorum laterum, sunt anguli eius noti, ergo angulus l k b est notus, ergo arcus l b est notus, et ipse est longitudo lunae in eclipsi secunda, quae est apud punctum b a longitudine longiori orbis reuolutionis. Per hanc ergo uiam inuenerunt ex tribus eclipsibus antiqui proportionem medietatis diametri orbis reuolutionis ad medietatem diametri orbis deferentis, et longitudinem lunae in una eclipsium a longitudine longiori orbis reuolutionis, et sciuerunt iterum, propterea quod angulus l d b est notus, longitudinem loci centri orbis reuolutionis, qui est locus lunae, per medium in longitudine a puncto b, quod sequitur locum eius uerum in una eclipsium. Deinde accepit tres considerationes in eclipsibus modernis uerificatorum locorum et temporum, et exemplificauit in eis hanc eandem uiam, et exiuit ei proportio diametri orbis reuolutionis ad diametrum orbis decliuis, existens illa eadem proportio quae exiuit ei per eclipses antiquas, et sciuit iterum locum centri orbis reuolutionis, scilicet locum lunae per medium ex orbe signorum in una eclipsium modernarum, et elongationem lunae in orbe reuolutionis suae a longitudine longiori eius. Diuisit ergo reditiones et arcus superfluentes, si fuerint motui medio et diuersitati per tempus, quod fuit inter illas duas eclipses, scilicet antiquam et modernam, et exiuit ei inde motus longitudinis diei uni 13. partes et 10. minuta, et 34. secunda, et 18. tertia teria ed., et 33. quarta, et 30. quinta, et 30. sexta, et illud quod fuit conueniens ei quod inuenit Abrachis, et inuenit motum diuersitatis diei uni qui est secundum quod firmauit ipsum 13. partes et 3. minuta, et 53. secunda, et 56. tertia, et 17. quarta, et 51. quinta, et 59. sexta, et exiuit ei per eclipses antiquas et modernas proportio medietatis diametri orbis decliuis ad medietatem diametri orbis reuolutionis proportio 60. partium ad quinque partes et quartam. De motu uero latitudinis dixit, quod in primis usus fuit in eo, eo quo usus fuit Abrachis, et illud est, quia ipse retulit de Abrachis, quod ei uisum fuit, quod luna mensurat orbem suum decliuem 650. uicibus fere, et mensurat circulum umbrae duabus uicibus et semis in longitudine mcdia in considerationibus, et cum posuit illud et posuit quantitatem declinationis orbis lunae decliuis ab orbe signorum, et posuit quantitatem eclipsati de luna, sciuit inde elongationem lunae ipsius in orbe suo decliui a nodo, et sciuit propter 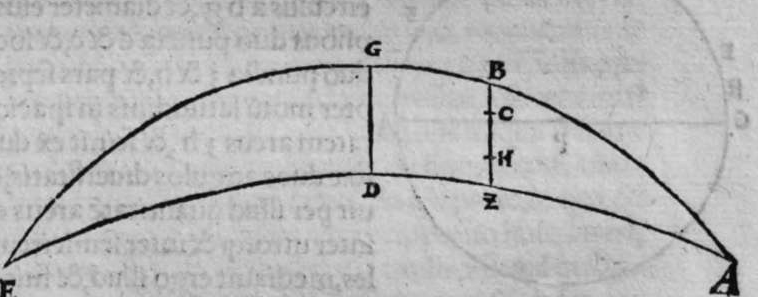superfluitatem diuersitatis quae est lunae longitudinem centri orbis reuolutionis ab illo nodo, et cognitio quidem huius est secundum quod narro, ut ponamus orbem signorum circulum a b g e, et orbem lunae decliuem circulum a d e, et sit unusquisque duorum arcuum g a et d a quarta circuli, et sit arcus g d circuli magni, et ponamus cenrum lunae in medio tempore eclipsis supra punctum z, et sit punctum b centrum circuli umbrae in longitudine lunae media, et faciamus transire per duo puncta z b arcum circuli magni, qui sit arcus b z, et medietas diametri circuli umbrae subtendatur arcui b h, et medietas diametri lunae sit corda arcus c z, erit ergo eclipsatum de luna arcus h c, propterea ergo quod diameter lunae mensurat circulum a d magnum, qui est aequalis circulo b z iterum magno, et mensurat iterum circulum umbrae, erit portio arcus b h de circulo suo nota, et propterea quod eclipsatum de diametro lunae est notum, erit propter illud arcus b z totus notus, et proportio sinus eius ad sinum arcus a z est sicut proportio sinus arcus g d noti ad sinum arcus a d noti. Est ergo propter illud sinus arcus a z notus, et est minor quarta circuli, ergo arcus a z est notus, ergo longitudo lunae ipsius in tempore medio eclipsis positae a puncto a, quod est unus duorum nodorum est nota, et propterea quod locus lunae in orbe reuolutionis suae est notus, est angulus diuersitatis lunae in medio tempore eclipsis notus, ergo longitudo centri orbis reuolutionis in medio tempore eclipsium a nodo a est nota, Cum ergo posuit eclipsim aliam particularem iterum sciuit per illam uiam longitudinem centri orbis reuolutionis in medio tempore a nodo appropriato ei, sciuit ergo per illud quantitatem reditionis latitudinis, postea uero, quoniam Ptolomeus uidit, quod hanc uiam ingreditur appropinquatio non parua, propterea quod in mensuratione qua luna mensurat orbem suum decliuem sibi proprium, et circulum umbrae non confiditur ei, et quia fuit ei possibile, assumpsit duas eclipses, inter quas fuit tempus magnum, et fuit eclipsatum in utrisque unum, et fuit elongatio lunae a longitudine sua longiore orbis reuolutionis suae una, et per harum aggregationem conditionum sequitur necessario, ut sit quantitas longitudinis lunae ipsius in unaquaque duarum eclipsium a nodo una, ergo propter illud spacium quod est inter duas eclipses, continebit reditiones lunae ipsius in latitudine. Et si fuerit luna in unaquaque duarum eclipsium in una et eadem parte orbis reuolutionis suae, tunc illud spacium continebit iterum reditiones integras centri orbis reuolutionis in orbe decliui, sicut reditiones lunae ipsius. Et si non fuerit in utrisque in una et eadem parte, imo in duabus partibus, quarum elongatio a longitudine longiori est aequalis, tunc reditiones centri orbis reuolutionis minuent in illo spacio a reditionibus lunae ipsius, aut addent super eas per quantitatem duarum diuersitatum lunae in duabus eclipsibus. Postquam ergo Ptolomeus inuenit duas eclipses secundum conditiones praedictas, praeter quod luna fuit in eis utrisque in parte una orbis reuolutionis suae, si fuit in duabus partibus, quarum elongatio a longitudine longiori est aequalis, assumpsit reditiones lunae ipsius in orbe suo decliui in illo spacio, quod fuit inter duas eclipses, et minuit illud quod fuit necessarium duabus diuersitatibus, quoniam in spacio quod inuenit diuersitas in utrisque fecit necessariam additionem. Deinde diuisit residuum per tempus, quod fuit inter duas eclipses, et exiuit ei inde motus lunae medius in latitudine in die uno, et est motus centri orbis reuolutionis supra circumferentiam orbis sui decliuis 13. 45. 39. 48. 56. 37. Deinde quoniam post illud uoluit inuenire in hora aliqua posita elongationem centri orbis reuolutionis ab uno duorum nodorum, incepit determinare illas duas eclipses lunares, quae fuerunt in una parte scilicet septentrionis aut meridiei, et fuit quantitas eclipsati in utrisque una, et fuit elongatio lunae in orbe reuolutionis suae circiter aequalitatem, excepto quod nodus non fuit in utrisque unus, sed fuit in prima contrarius ei qui in secunda, et sequitur ab illo, ut sit longitudo lunae in unaquaque duarum eclipsium a nodo appropriato sibi longitudo aequalis. Postquam 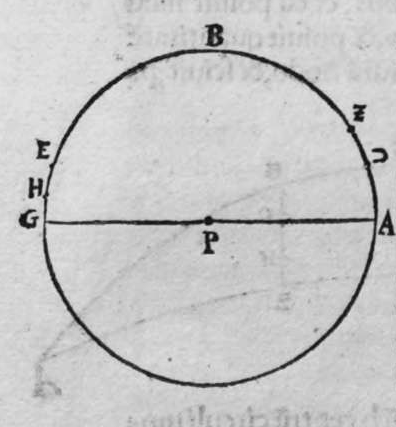ergo inuenit duas eclipses secundum has conditiones, declarauit ex eis quantitatem longitudinis centri orbis reuolutionis a parte septentrionali in una duarum eclipsium secundum hunc modum. Sit orbis decliuis circulus a b g, et diameter eius a g, et sit locus lunae in duabus eclipsibus duo puncta d et e, et locus centri orbis reuolutionis in utrisque duo puncta z et h, et pars septentrionalis punctum b. Sciuit ergo propter motum latitudinis in spacio quod fuit inter duas eclipses quantitatem arcus z h, et sciuit ex duobus locis lunae in orbe reuolutionis suae duos angulos diuersitatis, et sunt duo arcus z d et e h, ergo sciuit per illud quantitatem arcus d e. Sciuit ergo superfluitatem, quae est inter utrosque et inter semicirculum, et illud est duo arcus a d et e g aequales, mediauit ergo illud, et fuit quantitas a d, addit ergo super ipsum arcum d z, et fuit aggregatum quantitas arcus a z, et est longitudo centri orbis reuolutionis in eclipsi eclpsi ed. prima a nodo a. Addidit ergo super ipsum 270 partes, et fuit aggregatum quantitas arcus b g a z, et est longitudo centri orbis reuolutionis in eclipsi prima a parte septentrionali, et illud est, cuius uoluimus declarationem, et figura eius est supra quam est nota p.

⟨IV.1⟩ De arte instrumenti quo considerantur stellae.

ET quoniam indiguit considerationibus lunae in temporibus alijs ab eclipsibus et considerationibus aliarum stellarum in eo quod futurum est de scientia dispositionum earum, fecit instrumentum quo considerauit lunam et stellas, et sciuit per ipsum loca earum in orbe signorum in longitudine et latitudine, et est instrumentum quod nominatur habens armillas. Narrauit ergo artem huius instrumenti, et qualiter consideretur per ipsum, dixit ergo: Accipiemus duas armillas moderatae magnitudinis decentis rasurae quadratarum superficierum aequales, similes in omni modo, et componemus unam earum in alia super diametrum in duobus locis oppositis orthogonaliter super superficies suas, et imaginabimur unam earum orbem signorum, et alteram or bem meridiei transeuntem per duos polos orbis signorum, et duos polos aequatoris diei, et inueniemus super hanc propter latus quadrati duo puncta, quae distinguunt duos polos orbis signorum, et figemus in eis simul duos paxillos rotundos aequales, in grossitudine aequales, penetrantes a duabus superficiebus, scilicet extrinseca et intrinseca, fixos in eis utrisque, et componemus in eis ambabus armillam aliam deforis, cuius superficies concaua contingat superficiem duarum armillarum intrinsecarum gibbosam ab omnibus partibus tactu uero, et ponemus eam facilis reuolutionis et transitus in longitudine super duos polos orbis signorum quos diximus. Et similiter componemus armillam aliam iterum in eis ambabus deintus secundum illud exemplum, cuius superficies iterum gibbosa contingat ab omnibus lateribus suis superficiem illarum duarum armillarum concauam tactu uero, et sit facilis reuolutionis et transitus sicut altera, et tolleret ut reuoluatur in longitudine super istos duos polos secundum multitudinem armillae quae est deforis. Et diuidemus hanc armillam quae est deintus, et armillam quam nos ereximus loco circuli orbis signorum in partes, per quas de consuetudine nostra est, ut diuidamus circumferentiam circuli, et sunt 360. partes, et in illud in quod possibile est diuidere has partes ex partibus, et componemus iterum in hac armilla, quae deintus est, compositione decenti armillam aliam subtilem paruam, in qua sint duo foramina secundum diametrum eminentia super superficiem armillae, in qua praeparentur ut reuoluantur in superficie illius armillae uersus unumquenque duorum polorum narratorum propter illud, quod est necessarium de consideratione latitudinis. Et postquam factae erunt armillae istae secundum quod narrauimus, perueniemus ad arcum, qui est inter duos polos polum orbis signorum, et polum aequatoris diei, cuius quantitatem iam ostendimus in ilis quae praemissa sunt. Accipiemus ergo quantitatem eius ab unoquoque duorum polorum orbis signorum in orbe meridiei, de quo aestimatur, quod ipse sit descriptus super polos, et ponemus illic duas notas oppositas, et componemus eas iterum in duobus polis fixis in armilla alia simili armillae meridiei, quam narrauimus in tractatu primo in considerationibus arcus orbis meridiei inter duos tropicos, ut cum haec armilla fixa fuerit in illo loco, in quo fuit illa, scilicet cum fuerit erecta supra superficiem horizontis, et secundum altitudinem poli loci, in qua sit consideratio, et fuerit in superficie orbis, qui est uere orbis meridiei, sit reuolutio armillarum, quae sunt intra ipsam in circuitu duorum polorum aequatoris diei ab oriente ad occidentem, sequens motionem localem motus totius primi. Cum ergo praeparauerimus instrumentum, secundum hunc modum considerabimus. Cum ergo praeparabit, ut sint sol et luna apparentes simul supra terram, ponemus armillam, quae est extrinseca armillarum considerationis, currens super duos polos orbis signorum super partem, in qua inuenitur sol in illa hora cum ultimatae propinquitatis, et reuoluemus armillam quae transit super duos polos ad hoc, ut fiat sectio duarum, quae est super partem solis opposita soli secundum ueritatem, tunc enim obumbrabunt seipsas totas duae armillae, scilicet armilla orbis signorum, et armilla quae transit per polos ipsius, quod si fuerit loco solis aliqua stellarum quae consideratur, et cuius locus scitur, reuoluemus armillam quae transit ad hoc, ut cum unus duorum circulorum fuerit super unum duorum laterum armillae quae est deforis in illa parte, in qua est stella ab orbe signorum, uideat etiam stellam in hac armilla a latere altero opposito huic lateri, quod est coram ea quasi ipsa sit annexa duabus superficiebus duarum armillarum simul in superficie quae transit per ipsas ambas, deinde perueniemus ad armillam aliam quae est inter armillas considerationis diuisa, et reuoluemus eam uersus lunam, aut uersus aliam stellarum de illis, cuius uolumus considerationem usquequo cum affirmatione nostra cum instrumento loci solis aut alterius de eis, super quae praeparatur consideratio, uideamus iterum lunam et quod uoluerimus de stellis per duo foramina simul, quae sunt in armilla subtili composita in armilla intrinseca diuisa. Nos enim taliter sciemus locum lunae et alterius stellarum quae quaeritur in longitudine partium orbis signorum ex partibus armillae, quam aestimauimus orbem signorum, et diuisimus in potentia secundum diuisionem eius, et sciemus quanta sit elongatio lunae aut stellae a superficie orbis signorum ad septentrionem, aut ad meridiem in orbe descripto super duos polos orbis signorum ex partibus quae reperiuntur in armilla diuisa intrinseca per numerum qui est inter medium foraminis, quod sequitur stellam ex duobus foraminibus, quae sunt in armilla parua et inter lineam, quae est diameter orbis signorum transiens per locum stellae in ipso.

⟨IV.2⟩ De diuersitate secunda quae accidit lunae.

ET postquam praeparatum fuit ei hoc instrumentum secundum hunc modum, assiduauit considerationem lunae cum eo in reliquis elongationibus eius a sole, cum est in medio coeli ascendens, ita, ut non sit ei diuersitas aspectus in longitudine, erit ergo propter illud locus uisibilis in orbe signorum ipsemet locus eius uerus. Inuenit ergo locum eius extractum per considerationem quandoque conuenientem loco eius egredienti per computationem, et quandoque diuersum ei, et diuersitas quandoque fuit parua, et quandoque fuit multa, et illud est, quoniam inuenit locum eius per considerationes apud oppositiones et coniunctiones per medium et conuenientem ei, quod ipse comprehendit propter eclipses, et ei, quod exiuit iterum per computationem, et cum fuit in longitudine longiori aut propinquiori orbis reuolutionis suae, et fuit in reliquis longitudinibus suis a sole, non inuenit iterum diuersitatem inter locum eius comprehensum per considerationem, et inter locum eius egredientem per computationem, et inuenit, quando fuit luna in transitu medio orbis reuolutionis suae, diuersitatem inter comprehensum per considerationem, et inuentum per computationem, et inuenit hanc diuersitatem maiorem quae erit, cum luna est in quadratura quadraturam ed. solis, et est in transitu suo medio orbis reuolutionis suae, scilicet, cum est centrum orbis reuolutionis secundum longitudinem quartae circuli a medio solis, et est luna super lineas contingentes or bem reuolutionis, et illud est, quoniam ipse inuenit, si diuersitas fuerit diminuta, locum lunae magis diminutum, eo quem exigit computatio, et si est addita, inuenit locum magis additum, eo quem exigit computatio. Significauit ei ergo illud, quod diuersitas eius est maior ea quam computatio exigit, et illud non erit, nisi ita, ut sit centrum orbis reuolutionis propinquius centro orbis signorum, quoniam magnificatur propter illud angulus diuersitatis, et quoniam magnificatio eius finitur apud unamquanque duarum quadraturarum, oportet ut sit centrum orbis reuolutionis tunc propinquius quod est centro orbis signorum, et illud praeparatur ita, ut centrum orbis reuolutionis moueatur super orbem egredientis centri, erit ergo in longitudine eius longiore apud oppositionem et coniunctionem, et in propinquitate ipsius propinquiori in unaquaque duarum quadraturarum, et quia fuit in propinquiore propinquitate eius ad terram in unaquaque duarum quadraturarum, significauit ei illud, quod ipsum secat or bem egredientis centri in mense medio lunari duabus uicibus, et istud non praeparatur nisi ita, ut centrum orbis egredientis centri moueatur in circuitu centri orbis signorum ad diuersitatem continuitatis signorum per quantitatem quam addit duplum longitudinis mediae, scilicet longitudinis centri orbis reuolutionis a medio solis supra motum suum medium in latitudine, et demonstrabo illud per exemplum secundum hunc modum. Ponam itaque circulum 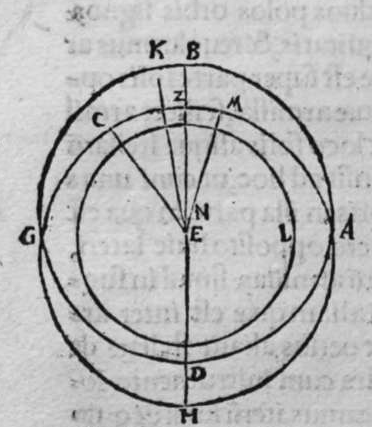signorum circulum a b g d, et circulum orbis decliuis circulum a z h, et duos nodos duo puncta a et g, et centrum horum duorum orbium, scilicet centrum terrae punctum e, et duo puncta a et g orbis decliuis, quae sunt duo nodi, moueantur in circuitu orbis centri signorum, et ad diuersitatem successionis signorum per quantitatem qua superat motum in longitudine motus in latitudine, et illud circiter tria minuta in die uno, et sit sectio communis circulo orbis decliuis, et circulo transeunti per duos polos eius, et per duos polos orbis signorum linea z e h, et secet circulus iste transiens per polos orbis signorum supra punctum b, et sit orbis egredientis centri deferens centrum orbis reuolutionis circulus z l in circuitu centri n, et longitudo eius longior sit punctum z, et est punctum longitudinis longioris deferentis, et medius solis in coniunctione, aut nadir medij eius in oppositione de orbe signorum sit supra punctum b. Cum ergo mouetur centrum orbis reuolutionis in circuitu centri orbis signorum ex puncto z secundum succesionem signorum, et est motus latitudinis et est in superficie orbis decliuis, moueatur punctum a eius secundum contrarium successionis signorum. Accidit ergo ex superfluitate motus centri orbis reuolutionis per comparationem ad superficiem orbis signorum, et moueatur sol per motum suum medium ex puncto b ad punctum k, scilicet angulo b e k, et moueatur centrum deferentis scilicet punctum n ad diuersitatem successionis signorum per motum lineae z n e ad punctum o, et permutatur longitudo longior deferentis scilicet punctum z ad punctum m circumferentiae orbis decliuis, et erit angulus z e m quem mouet cum angulo b e k, quem mouet sol per medium in illo tempore aequalis semper longitudini centri orbis reuolutionis a medio solis, scilicet, quod erit angulus k e m semper aequalis angulo k e t, erit ergo angulus m e t semper duplus angulo t e k, qui est angulus longitudinis inter duos medios duarum lunarium. Sequitur ergo ob hoc, ut sit motus longitudinis longioris deferentis ad diuersitatem successionis signorum per quantitatem eius, quod addit duplum longitudinis inter duos medios duorum lunarium, scilicet angulus t e m super motum latitudinis scilicet anguli b e t, et sequitur ab illo, ut sit centrum orbis reuolutionis in longitudine propinquiori deferentis in reuolutione una duabus uicibus, et illud est, cum existit in duabus quadraturis a medio solis. Et postquam declaratum est ei per assiduationem considerationis, quod haec diuersitas est secundum hunc ordinem et modum, accepit post illud ad declarandam quantitatem eius considerationem, in qua fuit luna per medium in quadratura a medio solis, scilicet fuit centrum orbis reuolutionis in longitudine propinquiori orbis deferentis, et in transitu medio orbis reuolutionis, et ipsa in medio coeli ascendens, ut per illud priuaretur diuersitate aspectus in longitudine. Sciuit ergo locum eius uisibilem, et est uerus in orbe signorum, et sciuit propter comprehensionem horae considerationis locum eius medium scilicet centri orbis reuolutionis eius in orbe signorum. Inuenit ergo inter locum eius per medium et uerum septem partes et duas tertias partis loco quinque partium, quae sunt maior diuersitas apud oppositiones et coniunctiones medias, et similiter iterum inuenit eam per considerationem quam narrauit ab Abrachis aequalem huic quantitati. Et postquam declarata fuit ei quantitas anguli, cui subtenditur medietas diametri orbis reuolutionis, cum est in longitudine propinquiori, ostendit quantitatem lineae, quae est inter duo centra secundum quod narro. Sit orbis deferens centrum orbis reuolutionis circulus 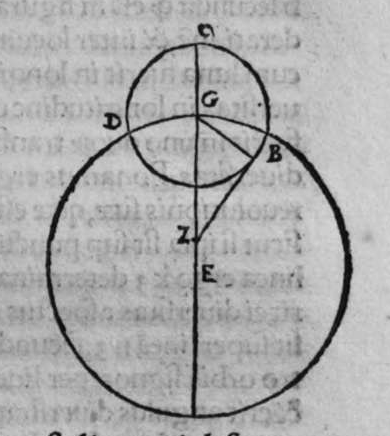a b g d in circuitu centri e, et sit centrum orbis signorum punctum z, et longitudo longior punctum a, et longitudo propinquior punctum g, et sit supra ipsum centrum orbis reuolutionis in hora considerationis scilicet in quadratura punctum g, et orbis reuolutionis sit circulus h b t d, et protraham a puncto z quod est centrum orbis signorum lineam contingentem orbem reuolutionis supra punctum h, erit ergo angulus g z h notus, et est 7. partes et duae tertiae partis, et angulus g h z est rectus, ergo triangulus g z h est notorum angulorum, ergo proportio laterum eius adinuicem est nota, ergo proportio lateris eius g z ad latus g h est proportio nota. Sed proportio lineae a z quae est medietas diametri orbis decliuis ad lineam g h, quae est medietas diametri orbis reuolutionis, est nota, ergo proportio lineae z g ad lineam a z est nota, ergo per quantitatem qua est linea a z 60. partes, est linea z g nota, ergo propter illud est tota linea a z g, quae est diametri deferentis per illam quantitatem nota, ergo medietas eius quae est linea e g per eam est nota, et iam fuit linea z g per illam quantitatem nota, ergo linea 3 e per eam est nota. Exiuit ergo ei linea z e quae est inter duo centra 10. partes et 19. minuta, per quantitatem qua est medietas diametri orbis decliuis 60. partes, et illud est cuius uoluimus declarationem declationem ed..

⟨IV.3⟩ De declinatione orbis reuolutionis et euis reflexione.

DEinde post illud continuauit considerationem in reliquis elongationibus eius a sole, et est, cum fuerit centrum orbis reuolutionis in eo quod est inter longitudinem longiorem et propinquiorem orbis egredientis centri. Inuenit enim locum eius per considerationem, cum fuit centrum orbis reuolutionis in medietate ecentrici, quae est a longitudine longiori ad longitudinem propinquiorem, scilicet, cum fuerit inter duos medios duorum lunarium minus quarta circuli, et fuit luna in parte longitudinis longioris orbis reuolutionis suae, diminutum a loco suo comprehenso per computationem, et cum fuit in parte longitudinis propioris orbis reuolutionis, inuenit locum eius per considerationem additum super locum eius comprehensum per computationem. Et cum fuit centrum orbis reuolutionis in medietate secunda orbis egredientis centri, scilicet, cum fuit inter duos medios duorum lunarium plus medietate circuli, fuit res econtrario illius et inuenit hanc diuersitatem maiorem quae est, cum fuit centrum orbis reuolutionis in transitu medio orbis egredienis centri, scilicet in sextilitate solis et in eius triplicitate, et fuit luna prope longitudinem longiorem aut propiorem orbis reuolutionis. Et si fuerit centrum orbis reuolutionis in longitudine longiori aut propinquiori ecentrici, aut fuit luna in transitu medio orbis reuolutionis, non fuit ei diuersitas. Significauit ergo illud, quod diameter orbis reuolutionis transiens per longitudinem longiorem et propiorem, non semper recte respicit per motum centri orbis reuolutionis centrum orbis signorum, imo semper recte respicit punctum, cuius elongatio a centro orbis signorum est aequalis elongationi centri deferentis ab eo ad contrarium partis eius, et demonstrabo illud per exemplum secundum hunc modum. Sit orbis deferens orbem 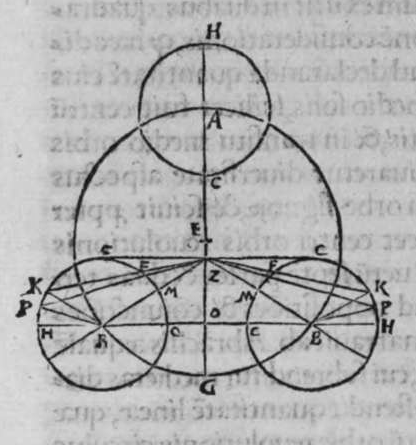reuolutionis circulum a b g d in circuitu centri e, et centrum orbis signorum sit punctum z, et sit linea transiens per longitudinem longiorem et propinquiorem linea a g, et sit orbis reuolutionis circulus h t, et centrum eius sit supra punctum a quod est longior longitudo, et longitudo longior eius sit punctum h, et longitudo eius propior sit punctum t. Cum ergo fuerit centrum orbis reuolutionis super hoc punctum, ubicunque fuerit luna in orbe reuolutionis suae, non erit inter duo loca eius comprehensa per considerationem et per computationem diuersitas penitus. Cum ergo permutatur centrum orbis reuolutionis per motum ad partem puncti b, quod est in sextilitate medij solis, inuenitur diuersitas inter duo loca eius comprehensa per considerationem et computationem, et non cessat haec diuersitas addi, usquequo perueniat centrum orbis reuolutionis super punctum b secundum quod est in figura, erit enim diuersitas tunc inter locum eius comprehensum per considerationem, et inter locum eius comprehensum per computationem maior, quae erit praecipue, cum luna fuerit in longitudine longiori aut propinquiori orbis reuolutionis suae, et erit diuersitas in longitudine eius propinquiori maior ea in longitudine eius longiori. Et si luna fuerit in uno duorum transituum mediorum orbis reuolutionis, non inuenietur inter duo loca eius diuersitas. Ponamus ergo centrum orbis reuolutionis super punctum b, et lunam in loco orbis reuolutionis suae, quae est inter longitudinem eius longiorem, et unum transituum eius mediorum sicut si ipsa sit super punctum k, et continuabo ipsum cum centro orbis signorum per lineam k z, linea ergo k z determinat locum eius uerum comprehensum per considerationem, cum non fuerit ei diuersitas aspectus in longitudine, et inueniemus eam ad succesionem signorum quasi ipsa sit super lineam n z, secundum quod est in figura, et continuabo centrum orbis reuolutionis cum centro orbis signorum per lineam z b l, erit ergo punctum l longitudo longior orbis reuolutionis et erit angulus diuersitatis l z n. Si ergo diameter orbis reuolutionis, quae est linea h t, non permutaretur a rectitudine sua cum puncto z, quod est centrum orbis signorum, ad rectitudinem suam ad aliud, esset longitudo longior orbis reuolutionis semper punctum unum circumferentiae suae, et non alteraretur, et esset locus lunae comprehensus per considerationem ipsemet locus eius comprehensus per computationem. At uero propterea quod diameter h t, cum separatur centrum orbis reuolutionis a duobus punctis a et g, recte dirigitur ad punctum aliud a puncto z, sicut ad punctum o secundum quod est in figura, ita, ut moueatur circulus orbis reuolutionis in circuitu centri e, et moueatur iterum punctum h, quod est longitudo longior, et reflectatur a rectitudine puncti z ad rectitudinem puncti o, secundum quod est in figura, ergo habebit tunc orbis reuolutionis duas diametros, quarum una quae est linea h t, recte respicit punctum o, et secunda linea l m, et est illa, quae recte respicit centrum orbis lignorum, et duo puncta eius l m semper permutantur super circumferentiam orbis reuolutionis, et duo puncta diametri primae h t semper manent fixa super circumferentiam orbis reuolutionis et punctum eius h, est quo terninantur motus lunae in orbe reuolutionis suae. Cooperiunt ergo se istae duae diametri, cum fuerit centrum orbis reuolutionis super unum duorum punctorum a et g, et elongantur eorum extremitates per abscisionem, cum mouetur centrum orbis reuolutionis ab his duobus punctis, et maior elongatio, quae est inter ambarum extremitates, erit, cum fuerit centrum orbis reuolutionis super unum duorum punctorum b et d, quae sunt prope sextilitatem medij solis et eius triplicitatem, erit ergo propter illud elongatio lunae in orbe reuolutionis suae ab his duobus punctis, scilicet duobus punctis h l, diuersa per quantitatem arcus h l. Verum portio lunae accepta in aquatione eius non est nisi arcus h k, non arcus l k, cum per punctum h terminentur motus lunae in orbe reuolutionis suae, sicut diximus. Cum ergo ceperimus a parte puncti l quantitatem arcus h k, quasi sit ipse arcus h k l n, et continuauerimus punctum n cum centro orbis signorum per lineam z n, terminabit haec linea locum eius comprehensum per computationem, et linea h k terminabit locum eius per considerationem secundum quod posuimus illud prius, iam ergo fit locus eius per computationem ad successionem signorum a loco eius per considerationem. Et cum luna fuerit in eo, quod est inter longitudinem eius propiorem orbis reuolutionis suae, et unum transituum eius mediorum, quasi ipsa sit super punctum f, et continuauerimus ipsum cum centro orbis signorum per lineam z f, terminabit haec linea locum eius per considerationem, et portio eius assumpta ad aequationem eius non erit, nisi arcus h f, non arcus l f. Cum ergo separauerimus a parte puncti l arcum aequalem arcui h f, sicut est arcus l c, et continuauerimus punctum c cum centro orbis signorum per lineam z c, terminabit haec linea locum comprehensum per computationem. Iam ergo factus est locus eius per computationem ad contrarium successionis signorum a loco suo per considerationem. Et cum fuerit luna in uno duorum transituum eius mediorum, non erit ei diuersitas sensibilis propter paucitatem superfluitatis, quae est tunc inter duas lineas z f et 3 c, et cum permutatur centrum orbis reuolutionis ad punctum g, quod est longitudo propinquior, incipit diuersitas in descensione propter approximationem puncti l ad punctum h, et puncti m ad punctum t, donec peruenit centrum circuli orbis reuolutionis super centrum g, tunc enim cooperit diameter l m lineam h t, fiunt ergo propter illud duo puncta l et h punctum unum, et similiter punctum m et t, erit ergo propter illud locus eius comprehensus per computationem ipsemet locus eius comprehensus per considerationem. Cum ergo mouetur centrum orbis reuolutionis a puncto g ad partem puncti d, quod est super triplicitatem medij motus solis, incipit haec diuersitas addi, donec sit centrum orbis reuolutionis super punctum d, tunc enim haec diuersitas est maior quae est, sed est supra contrarium eius super quod fuit, cum centrum orbis reuolutionis fuit super punctum b, scilicet quia est locus eius comprehensus per computationem, cum luna est inter longitudinem eius longiorem et unum duorum transituum mediorum ad contrarium successionis signorum a loco suo comprehenso per considerationem, et cum est luna in eo quod est inter longitudinem eius propinquiorem, et unum duorum transituum mediorum est locus comprehensus per computationem ad partem successionis signorum a loco suo comprehenso per considerationem, et ad summam, diuersitas eius in duabus medietatibus ecentrici, quas determinat diameter a e g, est secundum proportionalitatem et assimilationem eius quod est in parte, diuersitas enim, quae est ei in medietate a b g, si exegerit diminutionem diuersitas, quae est in medietate a d g, exiget additionem. Et si illa exegerit additionem, exiget illa quae est in medietate a d g diminutionem, et postquam illud est ita, oportet ut abscidatur, quod punctum ad quod reflectitur diameter h t, semper sit super lineam a z g. Accipit ergo post illud ad ostendendam elongationem huius puncti a puncto z, scilicet centro orbis signorum unam ex considerationibus Abrachis, in qua fuit centrum orbis reuolutionis prope triplicitatem medij solis, et fuit luna in ea prope longitudinem propiorem orbis reuolutionis suae, quoniam haec diuersitas est magis apparens, quae fit in huiusmodi cursibus. Sciuit ergo locum lunae per considerationem in orbe signorum et ille super 21. partem et duas tertias partes piscis, et inuenit ei diuersitatem aspectus in longitudine circiter 13. minuta ad successionem signorum, et factus est locus eius secundum ueritatem propter illud super 21. partem et tertiam et octauam piscis, et inuenit locum eius per medium super 22. partes et 13. minuta, fuerunt ergo inter locum eius per medium, et locum eius per ueritatem 46. minuta. Oportet ergo secundum illud, ut sit luna abbreuiata a longitudine propiore orbis reuolutionis suae per sex partes et tertiam partis, et est arcus orbis reuolutionis, qui exigit 46. minut. quae reperit inter locum eius per medium et per ueritatem, et inuenit eam in diuersitate super 185. partes, et medietatem a longitudine longiori orbis reuolutionis. Pertransierat ergo ipsa longitudinem propiorem eius per 5. partes et medietatem partis. Iam ergo reflectitur longitudo propinquior media, scilicet, quae recte respicit punctum o figurae praecedentis rememorationis a longitudine propiori uera, scilicet quae transit per centrum orbis signorum et per aggregationem duorum arcuum simul orbis reuolutionis, scilicet sex partium et tertiae partis, et 5. partium et medietatis partis, et illud est 11. partes et medietas et tertia partis, et exemplicemus exemplum quo declaretur illud quod narrauimus de illo, et ostendamus cum eo locum puncti quaesiti, scilicet elongationem eius a centro orbis signorum. Ponamus ergo orbem egredientis centri deferentem circulum a b g in circuitu 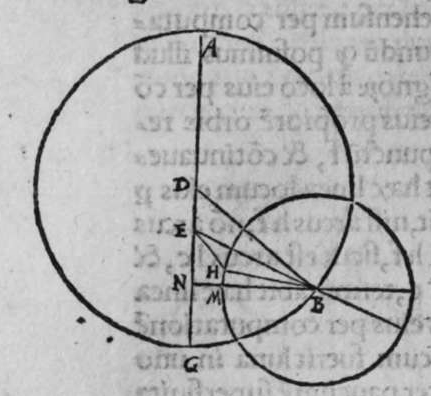centri d, et centrum orbis signorum punctum e, et lineam transeuntem per duo centra lineam a d e g, et sit orbis reuolutionis circulus z m in circuitu centri b, et copulabo ipsum cum centro orbis signorum per lineam b t e, erit ergo punctum t longitudo propior, propterea ergo quod luna fuit in hora considerationis per ueritatem super 21. partem, et tertiam et octauam partis piscis, et locus eius per medium scilicet punctum b, secundum quod extraxit eum computatio, fuit super 32. partes et 13. minuta eius, erit locus eius per ueritatem abbreuiatus a loco eius per medium scilicet a puncto b per 46. minuta de orbe signorum. Ponamus ergo lunam super punctum h orbis reuolutionis, et continuemus duas lineas e h, b h, ergo angulus b e h est 46. minuta, et sequitur ob hoc, ut sit angulus e b h scilicet arcus t h orbis reuolutionis sex partes et tertia partis, et iam fuit, et computatio dat quod elongatio eius in hora considerationis a longitudine longiore media orbis reuolutionis eius fuit 185. partes et medietas partis, ergo longitudo propior media orbis reuolutionis est abbreuiata a luna per 5. partes et medietatem. Sit ergo super punctum m ita, ut sit illud quod est inter longitudinem propiorem mediam, quae est punctum m, et inter longitudinem propiorem ueram, quae est punctum t arcus t m, et illud est 11. partes, medietas et tertia partis. Si ergo nos fecerimus transire per duo puncta b m lineam, et fecerimus eam transire donec occurrat lineae a g super punctum n, erit hoc punctum ipsum, quod recte respicit diameter orbis reuolutionis transiens per longitudinem longiorem et propiorem medias, et scitur elongatio huius puncti a centro orbis signorum secundum hunc modum, et illud est, quod continuabimus centrum orbis reuolutionis cum centro deferentis per lineam b d, propterea ergo quod angulus b e d est notus, et duo latera eius b d, d e sunt nota, erit latus b e notum. Et similiter latus b h est notum, et angulus e b h est notus, et ille est 6. partes et tertia partis, et angulus h b m est notus, et ille est 5. partes et medietas, erit ergo angulus e b n totus notus, et illud est 11. partes et medietas et tertia, et angulus b e n notus, et latus b e notum, ergo oportet ut sit linea e n nota. Inuenit ergo eam 10. partes et 18. minuta, et est propinqua quantitati lineae e d, cum iam inuenerit quantitatem lineae e d 10. partes et 19. minuta, et illud est cuius uoluimus declarationem. Deinde post illud accepit unam de considerationibus Abrachis iterum, in qua fuit centrum orbis reuolutionis in transitu medio altero deferentis, et fuit luna in ea prope longitudinem suam longiorem orbis reuolutionis, et operatus est secundum operationem suam in consideratione praecedente, et inuenit lineam e n propinquam ei quod inuenit eam nuper, et dixit, quia inuenit eam iterum aequalem illi quantitati per considerationes alias plurimas praeter istas. Quare certificatum est apud eum per illud, quod diameter orbis reuolutionis in motu suo semper directe tendit ad punctum diametri a g, cuius elongatio a centro orbis signorum est proxima elongationi centri orbis deferentis ab eo, et illud est cuius uoluimus declarationem. Deinde post illud rememoratus est, qualiter inuenit propter motus lunae reuolubiles in hora posita cursum lunae rectum, scilicet 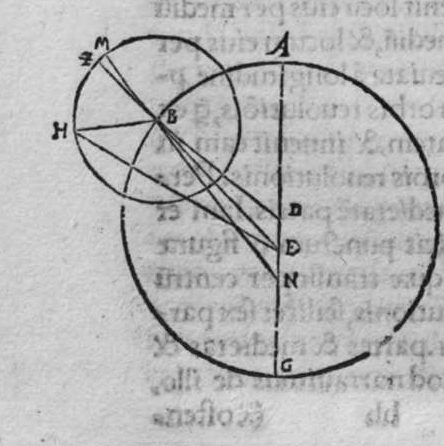locum eius uerum in orbe signorum, declarauit ergo illud secundum hunc modum. Sit orbis deferens or bem reuolutionis circulus a b g in circuitu centri d, et sit centrum orbis signorum punctum e, et linea transiens per longiorem longitudinem et propiorem linea a d e g, et longitudo longior sit punctum a et propior punctum g, et sit punctum ad quod recte dirigitur diameter orbis reuolutionis punctum n, et sit orbis reuolutionis circulus m z h t in circuitu centri b, et ponamus angulum, cuius elongatio a medio solis sit nota. Erit ergo propter illud angulus a e b notus, cum sit duplus anguli longitudinis, et sit luna in orbe reuolutionis suae supra punctum h, et continuabo centrum orbis reuolutionis cum centro orbis signorum per lineam b e, et faciam ipsam penetrare usque ad punctum z, ergo erit longitudo longior uera orbis reuolutionis, et continuabo centrum eius cum puncto n per lineam b n, et faciam ipsam penetrare usque ad m, ergo erit longitudo longior media ergo erit longitudo lunae a puncto m nota, et est arcus h m, et continuabo h b, b e, d b, propterea ergo quod angulus d e b est notus, et linea d e est nota, et linea d b quae est medietas diametri deferentis nota, erit linea e b nota. Et propterea quod linea e n est nota, et angulus b e n est notus, erit angulus e b n notus, ergo angulus m b z est notus, et iam fuit arcus m h notus, erit propter illud angulus z b h, qui est longitudo lunae a longitudine sua longiori uera notus, ergo erit angulus e b h notus, et unumquodque duorum laterum b h, b e est notum, ergo erit angulus b e h notus, et est angulus diuersitatis inter motum medium et uerum, addatur ergo aut minuatur ex angulo a e b, qui est duplus anguli longitudinis, et erit angulus a e h notus, et illud est cuius uoluimus declarationenm. De hoc quod non fit propter egressionem centri deferentis a centro orbis signorum in continuationibus diuersitas, de qua sit curandum, propterea quod possibile est, ut sit unumquodque duorum lunarium in continuationibus ueris secundum maiorem diuersitatem sui, et diuersitas unius eorum exigat additionem, et secundi diuersitas exigat diminutionem, oportet ut sit tunc, quod est inter duo loca amborum per medium in hora coniunctionis uerae, et illud quod aggregatur ex maiore diuersitate amborum, et summa illius est 7. partes et 24. minuta, quoniam maior diuersitas lunae in continuationibus est 5. partes et minutum unum, et maior diuersitas solis est duae partes et 23. minuta. Et propterea quod longitudo medij lunae semper a longitudine longiori deferentis, est duplum longitudinis medij eius a medio solis, tunc possibile est, ut sit longitudo lunae medij, scilicet centri orbis reuolutionis eius in hora continuationis uerae a longitudine longiori deferentis duplum partium aggregatarum ex maioribus duabus diuersitatibus, et illud est quasi 14. partes et 48. minuta. Et cum illud ita est, sequitur, ut sit centrum orbis reuolutionis lunae tunc propinquius centro orbis signorum, quam sit, cum est in longitudine longiori deferentis, sicut est in continuationibus medijs, erit ergo propter illud angulus diuersitatis, et est ille, cui subtenditur medietas diametri orbis reuolutionis in hora continuationis uerae maior, quam sit ille, qui erit in hora continuationis mediae. Sequitur ergo inde in ueritate in extractione loci continuationis uerae superfluitas, et illa quidem maior erit, cum luna fuerit secundum maiorem diuersitatem suam, scilicet, ut sit super lineam contingentem orbem reuolutionis. Sed cum luna fuerit in longitudine longiore aut propiore orbis reuolutionis suae, tunc illud quod erit tunc de loco medij lunae, et loco medij solis in hora continuationis uerae, est maior diuersitas solis tantum, et illud est duae partes et 23 .minuta, et erit longitudo centri orbis reuolutionis a longitudine longiori deferentis duplum ilius, et est 4. partes et 4 6. minuta. Et propter reflexionem orbis reuolutionis a centro orbis signorum, erit longitudo longior media orbis reuolutionis, praeter longitudinem longiorem ueram, non erit luna tunc super ipsam longitudinem longiorem aut propiorem ueram, sequitur ergo quod erit ei angulus diuersitatis, cui est quantitas. Sequitur ergo inde in extractione loci continuationis uerae diuersitas, ueruntamen quando contingit, ut sit diuersitas prima maior, quae est, scilicet, cum luna est super lineam contingentem orbem reuolutionis, est haec diuersitas secunda insensata omnino, quoniam superfluitates angulorum diuersitatis erunt tunc insensatae. Et cum diuersitas secunda, et est illa, quae est propter reflexionem maior, quae est scilicet, cum luna est in longitudine longiori aut propiori orbis reuolutionis suae, tunc diuersitas prima non est nisi secundum diuersitatem solis tantum, aut non erit omnino, aut erit insensibilis. Et cecidit narratio in hoc libro ab hac intentione errata in ultimo erroris, et illud est, quoniam ipse dixit, quod diuersitas quae accidit in duabus intentionibus simul, non est nisi secundum longitudinem, quae est inter duo loca continuationis uerae et mediae, et res non est ita, imo haec diuersitas non est nisi secundum longitudinem, quae est inter duos medios duorum lunarium in hora continuationis uerae. Et demonstratio quam ipse attulit in extractione quantitatis uniuscuiusque harum duarum diuersitatum est conueniens ei quod diximus, et diuersa ab eo, quod ipse prius dixit ante demonstrationem, et illud est, quoniam ipse dixit illud, cuius narratio est haec. Et potest esse, ut diuersificet continuatio uera continuationem quae inuenitur media per duas superfuitates simul, quae sunt propter diuersitatem, possibile ergo est, quod translator libri non intellexit illud quod uoluit Ptolomeus, ergo alterauit narrationem propter illud, ergo alterata est intentio quam ipse uoluit, quamuis ego iam perquisiui ab hoc in libris pluribus translationis Hunani et translationis Alhahazeg, et non inueni in eis diuersitatem nisi paruam in dictionibus. In intentione uero non inueni in duabus translationibus diuersitatem omnino, et propterea quod est impossibile, ut utraeque diuersitates simul aggregentur, scilicet diuersitates quae sunt propter diuersitatem duorum lunarium, et propter reflexionem orbis reuolutionis, tunc necesse est, ut unamquanque earum singulariter ponamus per se, et ponemus eam secundum maius quod erit, et demonstrabimus quantitatem quae ingreditur ex ea de appropinquatione in continuatione uera. Ponam ergo deferentem circulum a b g circa centrum d, et centrum orbis signorum punctum e 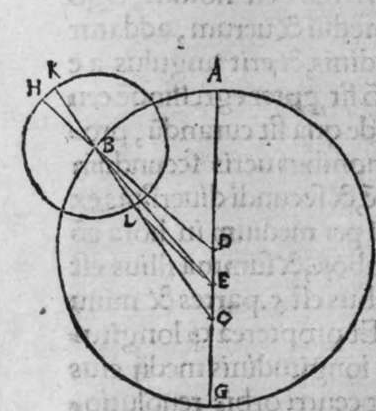et orbem reuolutionis circulum z h circa centrum b, et protraham a centro orbis signorum lineam contingentem orbem reuolutionis super punctum z quae sit linea e z, et sit luna super punctum z Et continuabo centrum orbis reuolutionis cum centro orbis signorum per lineam b e, et centrum orbis reuolutionis cum puncto z per lineam b z, et continuabo iterum centrum orbis reuolutionis cum centro deferentis per lineam b d, propterea ergo quod possibile est, sicut diximus, ut inter duos medios duorum lunarium in hora continuationis uerae sit illud quod aggregatur ex maioribus diuersitatibus amborum, quod est 7. partes et 24. minuta, sequitur, ut sit angulus a e b duplum harum partium quod est 14. partes et 48. minuta. Trianguli ergo b d e duo latera b d, d e erunt nota, et angulus eius d e b erit notus, oportet ergo ut sit latus eius e b notum, et erit unumquodque duorum laterum trianguli b z e, b e, b z notum, et angulus eius b z e notus, ergo oportet ut sit angulus eius z e b notus. Exiuit ergo quantitas huius anguli 5. partes et 3. minuta, et iam ostensum est, quod eius summa, cum centrum orbis reuolutionis est super punctum a, est 5. partes et minutum unum. Iam ergo erpo ed. augmentatus est secundum angulum a e b duobus minutis, et illud est de quo non curatur, cum non ingrediatur propter illud de approximatione in comprehensione spacij eclipsium, nisi ualde parum. Et consideremus iterum quantitatem eius quae ingreditur de approximatione propter diuersitatem secundam, scilicet ex reflexione orbis reuolutionis. Ponamus ergo in illa eadem forma angulum a e b duplum maioris diuersitatis solis, quae erit, et illud est 4. partes et 46. minuta, et ponamus lunam super propinquiorem propinquitatem orbis reuolutionis, cum maius, quod est de diuersitate propter reflexionem orbis reuolutionis, non sit nisi cum luna est in propinquiori propinquitate eius, et sit punctum, ad quod reflectitur orbis reuolutionis, punctum t, et continuabo ipsum cum centro orbis reuolutionis per lineam t l b k, et sit luna supra punctum l, et continuabo ipsum cum puncto e, quod est centrum orbis signorum per lineam l e, propterea ergo quod angulus d e b trianguli d e b est notus, et unumquodque duorum laterum b d, d e est notum, erit linea b e nota. Et propterea quod unumquodque duorum laterum b e, e t trianguli b e t est notum, et angulus eius b e t est notus, erit angulus e b t eius notus, et propterea quod unumquodque duorum laterum b e, b l trianguli b e l est notum, et angulus eius e b l est notus, erit angulus eius b e l notus. Egreditur ergo quantitas huius anguli 3. minuta, et est maius quod est de approximatione in continuationibus ueris propter reflexionem diametri orbis reuolutionis, et illud est cuius uoluimus declarationem.

⟨V⟩ LIBER QVINTVS. DE ACCEPTIONE instrumenti quo scitur diuersitas aspectus lunae.

ET propterea quod non est quantitas sphaerae terrae apud sphaeram orbis lunae, sicut quantitas puncti et centri, fit proportio diametri terrae ad diametrum orbis eius proportio sensata, et propter illud inter locum eius in orbe signorum per ueritatem et uisionem diuersitas sensata, et est diuersitas aspectus eius sensata, et est possibile scire eam secundum quantitatem longitudinis eius a terra, cum non sit possibile cognoscere longitudinem alicuius stellarum a terra, nisi per diuersitatem aspectus eius, si fuerit ei illud, et cui non est diuersitas aspectus, non est uia ad comprehendendam longitudinem eius a terra, sicut non est uia ad sciendam diuersitatem aspectus eius per computationem, nisi post scientiam longitudinis eius a terra, ueruntamen est possibile extrahere diuersitatem aspectus eius per considerationem, ita, ut sciatur quantitas longitudinis eius a zenith capitis per instrumenta, sicut scitur illud in sole apud extractionem quantitatis arcus, qui est inter duos tropicos. Deinde scitur post illud per computationem quantitatis longitudinis eius a zenith capitis in omni hora, ita, ut sciatur locus eius uerus in orbe signorum, et quantitas latitudinis eius in illa hora. Scitur ergo ex longitudine loci eius ueri in orbe signorum a zenith capitis, et ex eius latitudine quantitas ipsius longitudinis eius a zenith capitis. Quod ergo est inter longitudinem eius extractam per computationem a zenith capitis et longitudinem eius ab eo per considerationem de diuersitate, est diuersitas aspectus eius, et propterea quod per duo instrumenta praedicta in principio libri non extrahitur nisi quantitas longitudinis solis a zenith capitis per umbram eius, lunae uero neque alicui stellarum est umbra, per quam sciatur illud, oportet ut ponamus instrumentum tertium, per quod sit possibile inuenire longitudinem lunae aut stellae a zenith capitis, ponit ergo illud secundum hunc modum. Inquit ergo: Accipiemus duas regulas habentes quatuor angulos, quarum quaedam longitudo non sit minor 4. cubitorum, ut sit possibile diuidere longitudinem in partes plurimas, quantitas uero quam continet unaquaeque earum sit quantitas bona, media quantitatum, et cum quantitate qua non torqueantur propter longitudinem earum, imo sit uehementis rectitudinis et planiciei secundum subtilius et melius, quod possibile est de rectitudine unumquodque laterum earum. Deinde lineabimus in unaquaque earum per medium latitudinis laterum earum in longitudine lineas, et componemus in ambabus extremitatibus unius earum duas tabellas quadratas aequales, erectas supra superficiem, quarum medium sit erectum super lineam, quae est in medio superficiei, et perforabimus in medio cuiusque earum secundum ueritatem foramen, et ponemus medium cuiusque duorum foraminum super ueritatem lineae quae est in medio regulae, et ponemus foramen super quod ponit considerator oculum minus, et illud quod sequitur lunam maius cum quantitate qua aspiciens cum considerat cum uno oculorum suorum per foramen minus, possit uidere lunam totam per foramen aliud quod opponitur ei, postea perforabimus unamquanque duarum regularum aequaliter super duas lineas quae sunt in medio in una duarum extremitatum apud tabellam in qua est foramen maius, et intromittemus in eis meguar quo ligentur latera duarum regularum, in quibus sunt duae lineae, ita, ut sint sicut centrum utrisque, et fiat praeparatio, ut in ea reuoluatur regula habens duas tabellas ad omnia latera, praeter quod flectatur, aut eam cum torqueatur, et figemus regulam, in qua non sunt tabellae, in basi, deinde signabimus super lineam quae est in medio cuiusque earum punctum ab eo quod sequitur extremitatem, quae est apud basim, cuius longitudo a centro meguar in eis utrisque sit aequalis, et quanto plus possibile est, ut sit aequalis, et diuidemus lineam distinguentem in regula habente basim in 60. partes per id quod poterimus de diuisionibus. Et praeparabimus iterum in hac regula in posterioribus eius apud extremitates eius duas tabellas, sicut duos paxillos erectos supra superficiem eius secundum angulos rectos, et figemus medium earum super lineam signatam in medio regulae, ut possimus suspendere filum transiens per eas ambas, ut praeparetur illa regula supra superficiem horizontis secundum rectos angulos, et assumemus iterum regulam aliam paruam subtilem rectam, et componemus eam cum clauo subtili, qui etiam sit facilis reuolutionis in extremitate, quae sequitur basim lineae diuisae, et ponemus longitudinem eius infra longitudinem lineae diuisae. Reuoluemus ergo regulam habentem duas tabellas ad duo latera uersus lunam, usquequo aspiciens uideat centrum lunae ex utrisque foraminibus, et ex medio foraminis maioris, signabimus super regulam subtilem longitudinem comprehensam tunc inter duas extremitates duarum linearum, quae sunt in duabus regulis, deinde ponemus eam super lineam quae est in regula praeparata diuisam per 60. Inueniemus ergo per illud numerum partium lineae longitudinis quam diximus per quantitatem, qua est medietas diametri circuli, quem continet reuolutio in superficie orbis reuolutionis meridiei 60. partes, deinde accipiemus arcum, cui subtenditur linea huius longitudinis, et dicemus, quod ipse est arcus longitudinis quae fuit inter centrum lunae quod uideatur, et inter punctum zenith capitis in orbe magno descripto super zenith capitis et centrum lunae. Et contingit excusatio ab omnibus instrumentis praedictis in hoc libro per armillam unam et duas regulas secundum quod narrabo, et illud est, quia ego accipiam armillam aeris, cuius diameter sit quasi sex palmarum, aequalis grossitudinis, ita, ne torqueatur, decentis rotunditatis, bonae rasurae, quae sit armilla a b, et diuidam circumferentiam circuli a b, qui est maior circulorum continentium armillam, in 360. partes, et diuidam unamquanque harum partium usque ad illud quod possibile est, et sit medium grossiciei extremitatis armilae punctum a, quod sit initium signi cancri, et medium grossiciei extremitatis eius secundae punctum b, quod sit initium signi capriconi, et sit in medio huius diametri quod est centrum armilae foramen, in quo reuoluitur paxillus g d rotundus, aequalis grossiciei, reuolutione 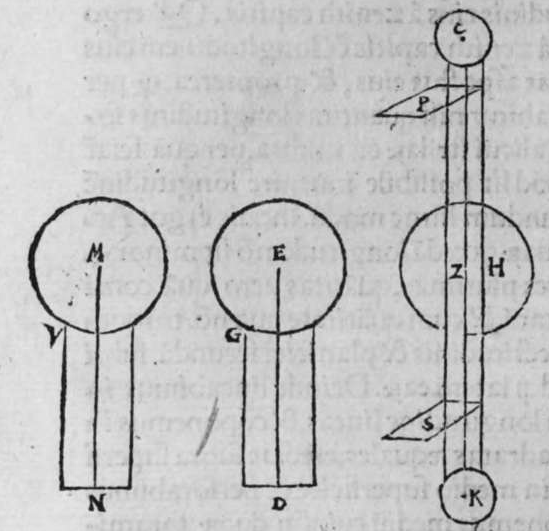facili, non currente, sicut est reuolutio fusorij aquae, et sit in capite huius paxilli tabula rotunda amplitudo superficiei, cuius sit quasi grossitudo 4. digitorum, et sit centrum eius punctum e, et grossitudo eius sit medietas grossitudinis paxilli g d, et communicet haec tabula cum circulo z h regulae k z t in meguar, transeunte per duo centra duorum circulorum, scilicet duo puncta e et z, et sit motus regulae k z t in circuitu huius meguar motus facilis, non currens, et in superficie una semper sicut motus duorum crurium circini, et communicet iterum circulus t regulae k z t cum circulo m regulae m n in meguar, transeunte per duo centra duorum circulorum, scilicet per duo puncta t m, et sit reuolutio circuli m in circuitu huius meguar reuolutio facilis, non currens, et sit in medio regulae k z t semper sicut reuolutio crurium circini iterum, et sit longitudo, quae est inter duo puncta, scilicet linea z t, sicut longitudo puncti z, quando componitur perpendicularis g d in foramine medij diametri a circumferentia circuli a b diuisi, et linea z k sit minor medietate diametri circuli minoris armillae parum, et sit longitudo regulae m n scilicet linea 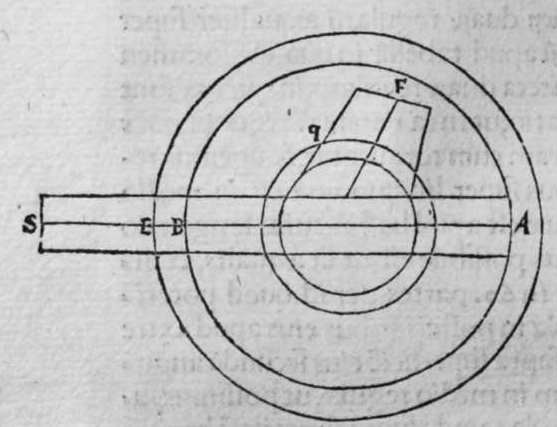m n aequalis lateri quadrati cadentis in circulo medietas diametri, cuius est linea z t, et diuidam longitudinem lineae m n per diuisiones, per quas linea z t est 60. partes aequales, et diuidam omnem diuisionem usque ad illud quod possibile est, et sint in duabus extremitatibus regulae k z t duae tabellae orthogonaliter super eius superficiem, et sit medium cuiusque earum super lineam k z t, et sit in medio latitudinis cuiusque earum foramen super rectitudinem lineae k z t, et sint duae tabellae p et s, et sit in dorso diameter a b, et in medio longitudinis eius paxillus q f rotundus, et sit grossitudo eius sicut grossitudo paxilli g d, et contineat iste paxillus cum longitudine diametri b a angulum addentem super angulum rectum, cuius summa sit 23. partes et 51. minutum, et est angulus maioris declinationis, et sit in puncto e gibbositatis armillae a b, et est punctum quod est cum duobus punctis q b perpendicularis q f super lineam unam rectam perpendicularis e s, et est super rectitudinem lineae q b, et sit longitudo eius 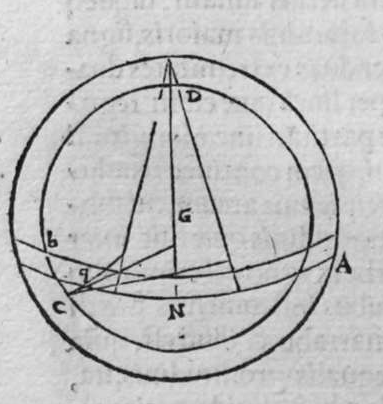paxilli q f, et grossitudo eius sicut grossitudo illius. Cum ergo uoluerimus scire per hoc instrumentum quantitatem arcus, qui est inter duos tropicos, accipiemus marmor, cuius facies sit uehementis aequalitatis et leuitatis, et sit in medio eius foramen, et sint in hoc foramine duae armillae aeris, in quibus reuoluatur perpendicularis c s reuolutione facili, non currente, et sit linea s c b q n, et est illa quae transit per duos paxillos f q et c s erecta super superficiem marmoris orthogonaliter. Erit ergo propter illud armilla a b erecta iterum super illam superficiem orthogonaliter, et praeparabitur illud marmor in loco detecto sol in podio, cuius altitudo a terra sit quasi 4. palmorum, et ponam superficiem illius marmoris in superficie horizontis, erit ergo propter illud punctum n armillae ipsum punctum summitatis capitis, et extraham in superficie illius marmoris lineam meridiei, et reuoluam armillam a b donec ponam superficiem eius in superficie circuli meridiei, et componam paxillum g d in foramine, quod est in medio armillae, et non cessabo considerare solem in medietate diei in omni die, cum fuerit in propinquitate puncti tropici, ita, ut reuoluam regulam t k in circuitu meguar z, donec obumbretur tabella inferior tota per superiorem. Sciemus ergo per illud elongationem solis in medio 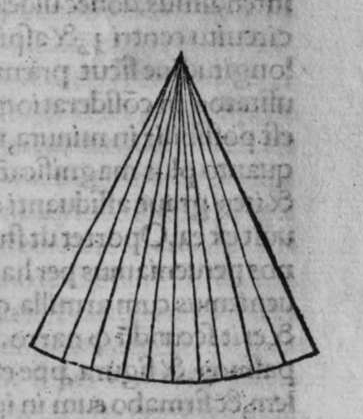diei cuiusque a puncto summitatis capitis, et faciam illius simile in hora in qua erit sol prope tropicum secundum. Sciemus ergo superfluitatem quae est inter elongationem solis a puncto summitate capitis in illis duabus horis, quantitatem arcus, qui est inter duas reuolutiones duorum punctorum duorum tropicorum. Et similiter sciemus altitudinem lunae aut alicuius stellarum in omni hora, ita, ut reuoluamus armillam ad lunam aut stellam, donec uideamus eam in superficie armillae, deinde reuoluemus tunc regulam z h t, et considerabimus ex duobus foraminibus duarum tabellarum donec uideamus lunam aut stellam. Sciemus ergo casum lineae m n in circumferentia circuli a b diuisae, super quam partem est a summitate capitis. Et cum uoluerimus considerare cum hoc instrumento unamquanque duarum aequalitatum, erigemus in loco directo soli duos pedes, altitudo cuiusque, quorum sit quasi status unus, et ponemus unum eorum directum ad medium orientis, et secundum directum ad medium occidentis, et extendemus super capita amborum trabem de ligno, et signemus in medio eius lignum, cuius extremitas sit eminens super latitudinem trabis parum, et componam in superficie huius ligni duas armillas paruas cuiusque, quarum superficies sit erecta super superficiem eius orthogonaliter, et amplitudo cuiusque earum sit, ut reuoluatur in eis paxillus f q reuolutione facili, non currente, et intromittam in eis paxillum aeris cuius grossitudo sit sicut grossitudo paxilli f q, et sit in eo eminens ab extremitate ligni quantitas quae ingrediatur in foramine, quod est in medio diametri armillae a b, et extendam filum super dorsum duarum armillarum fixarum in dorso ligni, contingens eas ambas, et ponam illud filum transiens per duos polos mundi, et tunc constringam duas extremitates trabis in capite duorum pedum constrictione cum qua non sit possibile ut torqueatur, neque ut moueatur, et extraham tunc paxillum g d cum regulis continuatis cum eo ex foramine, quod est in medio armillae, et componam illud medium in illo paxillo, qui est in duabus armillis paruis fixis in ligno. Erunt ergo tunc superficies armillae a b in superficie circuli aequatoris diei, considerabimus ergo tunc solem donec uideamus concauitatem armillae a b obumbrari totam, sciemus ergo quod sol tunc est super circumferentiam circuli aequatoris diei. Et cum uoluerimus scire cum hoc instrumento locum lunae uisibilem in orbe signorum in longitudine et latitudine, cum luna fuerit apparens in die supra terram, extrahemus paxillum ex duabus armillis, et intromittemus 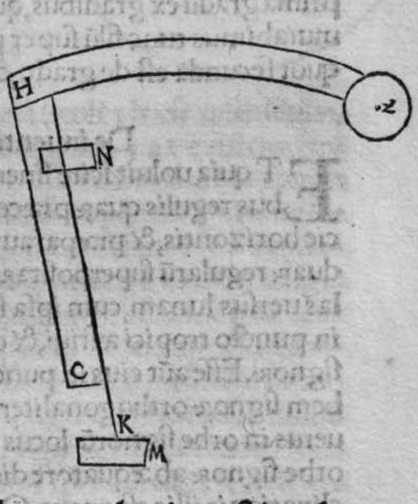in eis paxillum f q, et componemus paxillum g d in foramine armillae, sicut fuit prius, et reuoluemus armillam a b donec transeat superficies eius per solem, sciemus ergo quod armilla a b tunc est in superficie circuli transeuntis per medium signorum. Reuoluemus ergo tunc regulam z t circa paxillum g d, et in circuitu meguar z, et aspiciemus ad lunam donec uideamus eam in superficie in qua sunt duae regulae z t et m n, reuoluemus ergo tunc regulam z t, et aspiciemus ex duobus foraminibus duarum tabellarum quae sunt in ea, donec uideamus lunam ex utrisque foraminibus, et ponam marginem regulae m n super circumferentiam circuli a. Sciemus ergo ex casu lineae m n in hac circumferentia locum lunae in longitudine in circulo signorum, et sciemus ex partibus lineae m n quae sunt inter punctum m et inter partem, quae est super circumferentiam circuli a b quantitatem partium cordis arcus latitudinis lunae uisibilis in orbe signorum. Arcuabimus ergo illam cordam, et arcus qui fuerit, erit latitudo eius uisibilis in illa hora. Et cum uoluerimus scire locum olcum ed. alicuius stellarum in orbe signorum in longitudine et latitudine, cum iam nobis praecessit scientia loci lunae uisibilis in orbe signorum in longitudine et latitudine, aut alicuius stellarum, ponemus lineam m n regulae m n super locum lunae uisibilem, aut stellae in orbe signorum scilicet ponemus lineam m n super illam partem circumferentiae circuli a b, et reuoluemus armillam a b uersus lunam aut stellam, donec uideamus eam in superficie sua, et tunc reuoluemus regulam z h in circuitu paxilli g d uersus stellam longitudinis, cuius et latitudinis scientiam intendimus, donec uideamus eam in superficie regularum, reuoluemus ergo tunc regulam z t in circuitu centri z, et aspiciemus ex duobus foraminibus, sciemus ergo tunc locum stellae in longitudine sicut praemissum est in luna. Et propterea quod omnium instrumentorum usitatorum in considerationibus diuisio non est possibilis in plura, nisi in minuta, et diuisio non est possibilis in minuta, nisi in armilla, cuius diameter est maior 12. palmis, et cotingit, quod quanto plus magnificatur armilla, sit difficile facienti eius rectificationem et ipsius diuisionem, et iterum graue assiduanti considerationem cum ea, praeparare eam secundum ueritatem eius quod uult ex ea. Oportet ut studiose utamur speculatione in instrumento, cum quo sit possibile, ut nos perueniamus per hanc armillam, cuius diameter est quasi sex palmorum ad illud ad quod perueniemus cum armilla, cuius diameter est 100. palmorum, aut plus, ut diuidatur in secunda, et erit secundum quod narro. Et est, quod ego assumam tabulam planam, cuius longitudo sit quasi 4. palmorum, et figura prope extremitatem eius, et in medio latitudinis ipsius paxillum ferreum subtilem, et firmabo eum in ipsa, ita, ut non moueatur, et accipiam regulam subtilem, et perforabo in extremitatibus eius duo foramina, et sit inter ea sicut medietas diametri armillae a b diuisae, et intromitam foramen unum super perpendicularem ferri subtilem, et intromittam in foramen secundum clauum acutae extremitatis, et firmabo eum in ipso, ut non moueatur, et lineabo in illa tabula portionem circuli, postquam posuero illam tabulam in podio eleuato a terra quasi palmo uno, et stringam eam in illo podio bene, ita, ut non moueatur. Et accipiam tabulam aliam planam iterum et ponam eam in podio secundo, cuius altitudo a terra sit altitudo prima, et continuabo regulas longas, donec perueniant omnes ex paxillo ferri ad hanc tabulam, quae est in secundo podio, et sit longitudo quae est inter duas tabulas, quae nobis possibile est, et ponam in extremitate harum regularum continuatarum clauum acutum, et intromittam extremitatem eius secundam super paxillum ferri fixum in tabula prima, et lineabo cum extremitate claui in tabula secunda portionem circuli, et diuidam portionem primam quae est in tabula prima per diuisiones armillae a b, et accipiam filum sericum tortum in ultimo subtilitatis, et faciam in extremitate eius circulum qui reuoluatur in paxillo ferri, qui est in tabula prima, et extendam ipsum super partes portionis circuli primi, et ubi cadit filum in portione secunda maiore, quae est in tabula secunda, signabimus illud in tabula secta in circumferentia portionis, deinde diuidemus illud quod est inter omnes duas lineas per illud quod poterimus de diuisionibus. Cum ergo ceciderit nobis in hora considerationis linea m n super partem supra quam cadit de circumferentia circuli a b, accipiemus cum circino subtilium extremitatum eius quod fuerit inter illam partem et inter lineam primam gradum ex gradibus, quae sint in circumferentia circuli, postea ponemus circinum et permutabimus tunc filum super partem portionis circuli maioris, qui est in tabula secunda, super quot secunda est de gradu, et haec est forma illius.

⟨V.1⟩ De inuentione quantitatis finis latidunis lunae.

ET quia uoluit scire finem latitudinis lunae ab orbe signorum, considerauit lunam cum duabus regulis quarum praecessit rememoratio, ita, quod ante inuenit lineam meridiei in superficie horizontis, et praeparauit instrumentum tali praeparatione, quod in ea fuit superficies earum duarum regularum superpositarum in superficie circuli meridiei, et reuoluit habentem duas tabellas uersus lunam, cum ipsa fuit in circulo meridiei, et locus eius uerus in orbe signorum in puncto tropici aestiui, et cum hoc fuit in longitudine sua longiori in septentrione ab orbe signorum. Esse autem eius in puncto tropici aestiui, fuit, ut circulus meridiei esset erectus super orbem signorum orthogonaliter, propter illud ergo fuit arcus latitudinis ex eo, et fuit locus eius uerus in orbe signorum locus eius uisibilis, et est in eadem electione, quod declinatio loci illius in orbe signorum ab aequatore diei est in fine propinquitatis ueritatis, quoniam superfluitas arcuum declinationis illic est parua. Quod ergo ingreditur de approximatione in loco lunae, non facit accidere in declinatione diuersitatem cui sit quantitas, de qua sit curandum, et propter illud iterum latitudo eius ab orbe signorum, cum est in fine latitudinis suae super ultimum uerificationis, fuit ergo longitudo corporis eius ab aequatore diei secundum uerius quod possibile est, ut aggregetur ex hoc quod luna est in fine septentrionali orbis sui decliuis, et locus eius uerus in puncto tropico aestiui, quod corpus lunae est propinquius quod possibile est, ut sit a zenith capitis ne diuersitas aspectus eius sit sensata. Sciuit ergo per considerationem suam in luna cum duabus regulis, ipsa existente in istis dispositionibus quantitatem longitudinis corporis eius a puncto summitatis capitis in Alexandria, inuenit enim eam duas partes et octauam partis fere. Adiunxit ergo illud fini declinationis puncti tropici aestiui ab aequatore diei, et est illud 23. partes et 51. minutum, et accepit superfluitatem inter aggregatum ex illo, et inter latitudinem Alexandriae, quae est 30. partes et 58. minuta, fuit ergo illa superfluitas latitudo lunae ab orbe signorum, et illud est 5. partes fere. Et inuentio quidem finis latitudinis lunae est possibilis cum hoc instrumento, quod ostendimus in omni terra, et in quocunque loco fuerit orbis signorum, et inuentio proportionum elongationum eius a centro terrae ad medietatem diametri eius secundum quod narro, et illud est, quia nos considerabimus cum fuerit in uno duorum nodorum in hora, in qua sit in medio coeli ascendens in regione in qua est consideratio. Sciemus ergo secundum quod rememorati fuimus in eis quae praemissa sunt, quantitatem longitudinis eius loci uisibilis a puncto orbis signorum, deinde suspendemus filum perpendiculi super centrum armillae a b, ergo sciemus per ipsum locum zenith capitis in circumferentia quartae z h, ergo sciemus longitudinem uniuscuiusque locorum eius per ueritatem et uisionem in illa hora a zenith capitis. Quod ergo fuerit inter duas longitudines, erit diuersitas aspectus eius in circulo altitudinis, et propterea quod ipsa est in superficie orbis signorum, erit illUD quantitas latitudinis eius uisibilis, et sciemus locum lunae in orbe reuolutionis eius in illa hora, et locum centri orbis reuolutionis eius in orbe egredientis centri, ergo sciemus inde longitudinem lunae ipsius a centro terrae in illa hora. Sciemus itaque propter diuersitatem aspectus eius in circulo altitudinis proportionem longitudinis eius a centro terrae ad medietatem diametri eius secundum hunc modum. Sit circulus continens corpus terrae circulus a b in circuitu centri g, et circulus per centrum lunae 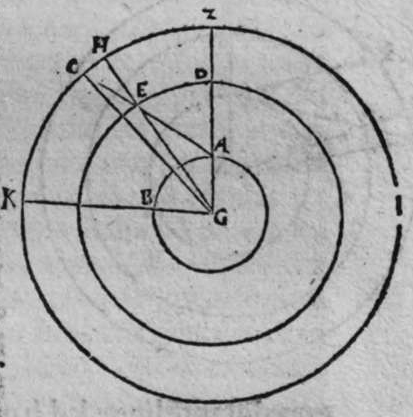et per zenith capitis in hora considerationis sit circulus d e, et sit zenith capitis punctum d, et luna punctum e, et sit circulus transiens per medium signorum, et est ille apud quem quantitas sphaerae tertae est sicut punctum, et centrum circulus z h t, et sit summitas capitis in eo punctum z, et continuabo punctum a quod est locus uisus, et punctum g quod est centrum terrae cum puncto e, quod est centrum lunae per duas lineas a e t et g e h, erit ergo punctum h locus lunae uerus in orbe signorum, et punctum t locus eius uisibilis in eo, et arcus z t longitudo centri lunae uisibilis a zenith capitis inuenta per considerationem, et arcus z h longitudo loci eius ueri a zenith capitis, et arcus h t est diuersitas aspectus eius in circulo altitudinis, et est latitudo eius uisibilis, et propterea quod fuit unusquisque duorum arcuum z h et z t notus, oportet ut sit arcus h t notus, et propterea quod medietas diametri terrae apud medietatem diametri circuli z h est insensibilis, oportet ut sit angulus a t g insensibilis, erit ergo propter illud angulus z a t existens fere angulus z g t, et angulus z g t est notus, et est ille, qui est inuentus per considerationem, ergo angulus z a t est notus, ergo erit propter illud angulus e a g notus, et angulus a g e est notorum angulorum, ergo proportio laterum z g h est notus, ergo trianguli a g e est notorum angulorum, ergo proportio laterum eius adinuicem est nota, ergo proportio lineae g e quae est longitudo centri lunae a centro terrae in hora considerationis ad lineam a g, quae est medietas centri diametri terrae est nota. completa est eius declaratio. Et postquam sciuerimus illud, considerauimus lineam cum hoc instrumento, ipsa erit in una duarum finium eius, cum fuit in medio coeli ascendens, et sciuerimus secundum quod nuper praemissum est longitudinem loci eius uisibilis a zenith capitis in illa hora, et fuit quasi arcus esset z t huius figurae. Et sciuerimus longitudinem loci eius ueri in orbe signorum a zenith capitis iterum, et fuit quasi sit arcus z k, erit ergo propter illud arcus k t notus, et est latitudo eius uisibilis in illa hora, et sciuerimus longitudinem centri eius in illa hora a centro terrae quae est linea g e, ergo erit proportio lineae g e ad lineam a g, quae est medietas diametri terrae nota, ergo erit unumquodque duorum laterum trianguli a g e, a g et g e notum, et angulus e a g eius est notus, ergo erit propter illud angulus eius a g e notus, et iam fuit angulus z g k, qui est longitudo loci lunae ueri in orbe signorum a zenith capitis notus, tunc erit propter illud angulus h g k, et est finis latitudinis lunae notus, et illud est, cuius uoluimus declarationem. ET postquam declaratum fuit ei illud quod praemissum est de motibus lunae et diuersitatibus eius, incepit post illud ostendere quantitates proportionum longitudinum eius a centro terrae ad medietatem diametri eius, cum hoc praemissum fuerit in inquisitione super reliquas habitudines lunarium, et illud quidem non est possibile, nisi post inuentionem quantitatis diuersitatis aspectus lunae in circulo altitudinis. Considerauit ergo propter illud lunam cum duabus regulis, cum erat super circulum meridiei, et locus eius uerus in orbe signorum prope punctum tropici hyemalis, et ipsa erit prope finem septentrionalem orbis sui decliuis, et fuit complementum electionis in hac consideratione, ut esset luna in parte meridiana orbis decliuis, ut esset quam magis possibile est ipsam esse longinquam a zenith capitis secundum contrarium, quod fuit electio in consideratione praecedente, cum intentio intenta in hac consideratione non fuit, nisi ut sciret quantitatem diuersitatis aspectus in circulo altitudinis, ut inueniret inde longitudinem eius a centro terrae, et quanto plus elongatur a zenith capitis, magnificatur quantitas huius diuersitatis. Inuenit ergo longitudinem eius a zenith capitis in Alexandria per uisionem 50. partes et 55. minuta, deinde inuenit per computationem ante inuentionem horae considerationis locum lunae in longitudine in orbe signorum, et in latitudine in orbe suo decliui. Sciuit ergo quantitatem latitudinis eius, et quantitatem longitudinis loci eius ueri in orbe signorum a zenith capitis, ergo sciuit per illud longitudinem eius ueram a zenith capitis, inuenit ergo inter eam et inter longitudinem uisibilem inuentam per considerationem partem unam et 7. minuta. Et postquam declaratum fuit ei illud, incepit declarare proportionem longitudinis eius a centro terrae ad medietatem diametri eius, ostendit ergo illud secundum quod narro. Sit circulus transiens per corpus lunae et per zenith capitis circulus g d in circuitu centri k quod est centrum mundi, et sit luna super punctum eius d, et zenith capitis super punctum g, et sit differentia communis inter illa duo et inter centrum sphaerae terrae circulus a b, et sit circulus apud quem locus terrae est locus puncti circulus e z, et continuabo punctum d super quod est centrum lunae in hora considerationis cum centro terrae per lineam k d, et faciam ipsam penetrare usque ad punctum h, ergo erit locus lunae uerus in circulo altitudinis, et continuabo centrum centum ed. terrae cum zenith capitis per lineam k g, et faciam ipsam penetrare usque ad e, et continuabo iterum punctum a quod est locus uisuum cum puncto d, super quod est corpus lunae, per lineam a d, et faciam ipsam penetrare ad punctum t, erit ergo punctum t locus lunae uisibilis, et protraham a puncto a lineam aequedistantem lineae k d h quae sit linea a z. Arcus igitur e h est notus, cum sit longitudo loci lunae ueri a zenith capitis, ergo angulus a k d est notus, et arcus h t est notus, cum sit diuersitas aspectus lunae inuenta per considerationem, et propterea quod medietas diametri terrae est insensibilis apud medietatem diametri k d h, erit arcus z h insensibilis apud circumferentiam circuli e z h. Erit ergo arcus z t sicut arcus h t apud sensum, et similiter angulus z a t, qui est apud punctum a, ac si esset apud punctum k, cum linea a k sit insensibilis apud longitudinem k e, erit ergo propter illud quantitas anguli z a t fere quantitatis anguli qui est super arcum h t, cum fuerit super centrum k, ergo est notus, ergo angulus a d k, cum sit aequalis ei, iterum est notus, ergo trianguli a k d anguli tres sunt noti. Proportio ergo laterum eius ad inuicem est nota, ergo per quantitatem qua latus a k est notum, erit latus k d iterum notum. Iam ergo comprehensa est per hoc proportio longitudinis centri lunae a centro terrae in hora considerationis ad medietatem diametri eius, et illud est cuius uoluimus declarationem. Deinde quia post illud possibile fuit ei scire proportionem longitudinis lunae mediae in applicationibus et in quadraturis, scilicet longitudinis duorum punctorum longitudinis longioris, et longitudinis propioris orbis egredientis centri a centro terrae ad medietatem diametri cius, tunc declarauit illud secundum hunc modum. Sit orbis deferens centrum orbis reuolutionis circulus a b g in circuitu centri d, et sit orbis reuolutionis circulus h t in circuitu centri b, et sit luna in hora illius 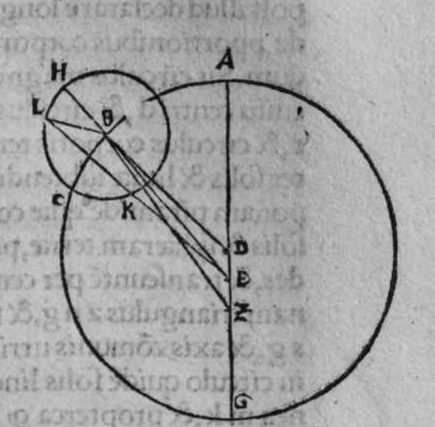considerationis super punctum eius l, et sit centrum orbis signorum punctumm e, et punctum quod sequitur declinatio orbis reuolutionis, et eius reflexio punctum z, et continuabo lineas b d, b z, b e, et faciam eam penetrare ad punctum h, et continuabo iterum l b, l e, propterea ergo quod angulus d e b est notus, quia est duplum longitudinis inter duos medios duorum lunarium in hora considerationis, et unumquodque duorum laterum d e, d b est notum per quantitatem qua linea a d est 60. partes, est latus e b iterum notum, et linea e z iterum est nota, ergo duo latera e b, e z sunt nota, et angulus b e z est notus, ergo angulus e b z est notus, et punctum k est longitudo media proprior orbis reuolutionis, et arcus k l est longitudo lunae in hora considerationis ab illa longitudine propiore, et ipse est notus, ergo angulus l b k est notus, ergo angulus l b e totus propter illud est notus, ergo angulus ungulus ed. l b e trianguli l b e est notus, et unumquodque duorum laterum eius l b et e b iterum est notum, ergo latus l e iterum eius est notum, et illud totum est per quantitatem qua linea a d est 60. partes. At linea l e quae est longitudo lunae a centro terrae in hora considerationis iam ostensum est quod est nota per quantitatem qua medietas diametri terae est pars una, ergo erit linea a d iterum nota per illam quantitatem. Et similiter linea a e, et linea e g quae sunt duae longitudines lunae mediae in applicationibus et in quadraturis iterum notae per illam quantitatem, ergo manifestum fuit, quod linea a e quae est logitudo media in applicationibus, est 59. partes per quantitatem, qua medietas diametri terrae est pars una, et linea quidem e g quae est longitudo eius in quadraturis est 38. partes et 43. minuta, et linea quidem b l quae est medietas diametri orbis reuolutionis est 5. partes et 10 minuta, et illud est quod declarare uoluimus. AMplius quia post illud uoluit scire longitudinem solis a centro terrae, tunc non fuit ei possibile illud inuenire ex diuersitate aspectus eius sicut fecit in luna, cum non sit diuersitati aspectus eius quantitas magna. At inuentio illius fuit, quia sciuit quantitatem angulorum quibus subtenduntur diametri solis et lunae et umbrae apud centrum terrae, quoniam iam sciuit longitudines lunae in applicationibus, et uidit quod in inuentione horum angulorum per illud quod dixerunt de instrumentis per aquam et tempora ascensionum aequalitatis non est confidentia. Dixit ergo, quod considerauit cum duabus regulis, et inuenit diametrum solis continere angulum qui fortasse erit in omni loco unus et idem, propterea quod egressio centri orbis eius a centro terrae est parua per comparationem ad longitudinem eius ab eo, et inuenit diametrum lunae subtendi huic eidem angulo, cum fuerit in maiore suarum longitudinum a terra, et illud est, cum centrum orbis reuolutionis est in longitudine longiore ecentrici, et luna est in longitudine longiore orbis reuolutionis. Sciuit ergo quantitatem huius anguli per duas eclipses lunares, in prima eclipsi, quarum fuit eclipsatum de diametro lunae quarta eius, et eclipsatum de ea in secunda fuit medietas eius, et fuit luna in unaquaque duarum eclipsium prope longitudinem longiorem orbis reuolutionis, deinde inuenit per computationem longitudinem centri lunae in duobus medijs temporibus duarum eclipsium a fine septentrionali in circulo deliui, ergo sciuit per illud longitudinem ab orbe signorum in circulo transeunte per centrum lunae erecto super or bem decliuem orthogonaliter in unaquaque duarum eclipsium. Inuenit ergo longitudinem in eclipsi prima 48. minuta et medietatem minuti, et in eclipsi secunda 40. minuta et duas tertias minuti, ergo accepit superfluitatem inter istas duas longitudines, et illud quidem est 7. minuta et medietas et tertia minuti. Sciuit Space is missing in the print. itaque quod haec quantitas quartae arcus, cui subtenditur diameter lunae cum fuerit eclipsatum ex ea in eclipsi prima quarta eius, et in secunda medietas ipsius, erit ergo propter illud summa arcus cui subtenditur diameter lunae 31. minutum et tertia minuti. Et propterea quod in eclipsi secunda inuenit longitudinem lunae ab orbe signorum in circulo traseunte per eam, erecto super orbem decliuem orthogonaliter 40. minuta et duas tertias minuti, et iam eclipsatum erat de luna medietas diametri eius, erit propter illud quantitas medietatis arcus cui subtenditur medietas diametri circuli umbrae 40. minuta et 40. secunda, cum centrum umbrae semper sit super superficiem orbis signorum, erit ergo propter ilud arcus cui subtenditur diameter circuli umbrae pars una et 2 1. minuta et tertia, et dixit, quod huiusmodi quantitates inuenit per considerationes eclipsium plurium aliarum ab istis. Et postquam declaratae sunt ei res istae, incepit post illud declarare longitudinem solis a centro terrae, et quod declaratur cum declaratione eius de proportionibus corporum solis et lunae adinuicem, ergo declarauit illud secundum hunc modum. Sit circulus magnus secundum propinquitatem qui est corporis solis circulus a b g in circuitu centri d, et circulus corporis lunae in longitudine magna circulus e h circa centrum t, et circulus corporis terrae circulus k l circa centrum n, et quia iam ostensum fuit, quod diameter solis et lunae subtenditur angulo uni, cum luna est in sua longitudine longiori a terra, tunc ponam piramidem quae continet utrosque, piramidem a n g, et piramidem quae continet sphaeram solis et sphaeram terrae, piramidem a s g, et imaginabor superficiem secantem has duas piramides, et transeuntem per centra ambarum, et sit sectio communis ei et piramidi, quae continet lunam triangulus a n g, et sectio communis ei et piramidi quae continet solem et terram triangulus a s g, et axis communis utrisque urrisque ed. linea d t n s, et sint lineae quae continuant inter puncta contactus in circulo quidem solis linea a g, et in circulo quidem lunae linea e h, in circulo quidem terrae linea m k, et propterea quod luna non eclipsatur nisi per introitum suum in piramidem umbrae terrae, sciuimus, quod extremitas huius piramidis pertransit orbem lunae. Sequitur ergo propter illud, ut sit linea n s maior linea n t, quae est longior longitudo lunae a terra, secabimus ergo lineam n f aequalem lineae n t, et producam a puncto f perpendicularem super lineam n s, quae sit linea c q diameter circuli umbrae, quae eclipsat lunam in longitudine sua longiori a terra. Et manifestum est, quod istae lineae a g et e h, et m k et c q sunt aequedistantes et aequales in sensu diametris illorum circulorum, et quod isti circuli iterum appropinquant apud sensum circulis magnis qui sunt super illas sphaeras. Vnaquaeque igitur duarum linearum t n, n f est nota per quantitatem 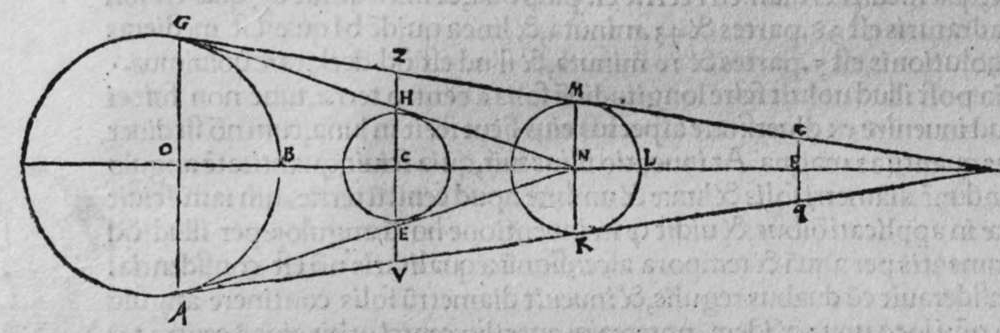qua linea k n quae est medietas diametri terrae, est pars una, et quoniam angulus e n t, cui subtenditur medietas diametri lunae in maiori suarum longitudinum a terra est notus, et angulus e t n iterum est notus, quoniam est rectus, et latus n t est notum per quantitatem qua linea l n est pars una, erit linea e t iterum nota per illam quantitatem, et erit iterum linea q f nota per eam cum sit nota per quantitatem qua linea e t est nota, sicut ostensum est in his quae praemissa sunt, ergo proportio n f ad f s est nota, et linea n f est nota, ergo linea n s est nota iterum per illam quantitatem, et linea n t iterum est nota per eam, ergo tota linea t s est nota per eam, ergo proportio t s ad s n est nota, et ipsa est proportio n t ad k n, ergo linea n t est nota per quantitatem qua linea l n est pars una, sed iam fuit linea e t nota per illam quantitatem, ergo remanet linea u e iterum nota per eam, ergo proportio n a ad a e est nota, et est proportio n d ad d t, sed linea n t est nota, ergo linea n d est nota. Et similiter proportio g d ad t h est nota, quia est sicut proportio n d ad n t nota, exiuit ergo ei per hanc lineam linea n d, et est longitudo solis a centro terrae 1210. per quantitatem qua medietas diametri terrae est unum, et longitudo quidem extremitatis piramidis umbrae a centro terrae iterum 268. per illam quantitatem, et iam fuit manifestum ei, quod longitudo lunae media scilicet centri orbis reuolutionis in continuationibus est 59. illius quantitatis, et istae sunt res quarum intendit declarationem, ergo ostensa est per haec proportio cuiusque duarum diametrorum lunarium ad diametrum terrae. Proportio ergo diametri lunae ad diametrum terrae est proportio unius ad tria et duas quintas, et proportio quidem diametri solis ad diametrum terrae, est proportio 5. et medij ad unum. et proportio quidem diametri solis ad diametrum lunae est proportio 18. et 4. quintarum ad unum. Erit ergo proportio corporis lunae ad corpus terrae sicut proportio unius ad 39. et quartam fere, et erit proportio corporis solis ad corpus terrae iterum proportio 166. ad unum fere, et erit proportio corporis solis ad corpus lunae proportio 6644. et medij ad unum. completa est declaratio declararatio ed. eius. ET postquam declarata fuit proportio longitudinum lunarium a centro terrae ad medietatem diametri eius, fuit possibile ei post illud inuenire diuersitates aspectus utrorumque in circulo altitudinis, cum sit unaquaeque longitudinum amborum a zenith capitis et a centro terrae nota, ut inuenirentur inde diuersitates aspectus in longitudine et latitudine, declarauit ergo illud secundum hunc modum. Ponam unamquanque duarum longitudinum lunae, scilicet longitudinem eius a zenith capitis in circulo atitudinis et longitudinem eius a centro terrae nota, et uolo scire quantitatem diuersitatum aspectus eius in circulo altitudinis, scilicet circulo 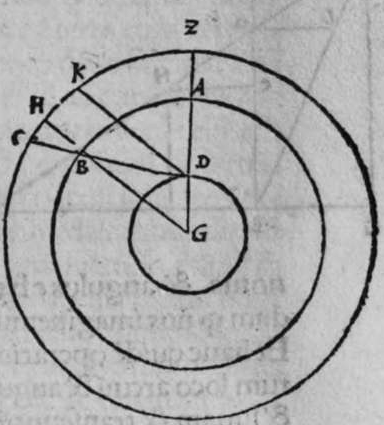a b, qui transit per zenith capitis et per lunam et centrum eius, quod est centrum mundi sit punctum g, et zenith capitis sit punctum a, et corpus lunae sit punctum b, et continuabo puncta ista cum centro terrae per lineam b h, et sit sectio communis huius circuli, et sphaerae terrae circulus d e, et sectio communis inter ipsum et inter orbem signorum qui est orbis, apud quem locus terrae est locus puncti circulus z h, et faciam penetrare lineam g b ad punctum h, et continuabo g a, et faciam penetrare ipsum iterum ad punctum z, erit ergo punctum d in superficie terrae locus uisuum. Continuabo ergo eum cum centro lunae per lineam d b, et faciam ipsam penetrare ad t, ergo locus lunae in circulo z h est per comparationem ad centrum terrae punctum h, et per comparationem ad uisum est punctum t. Arcus igitur quaesitus est arcus h t, ergo sciemus quantitatem huius arcus, cum fuerit longitudo g b, et angulus a b g noti, ita, ut extrahamus a puncto d lineam aequedistantem lineae g h, quae sit linea d k, propterea ergo quod medietas diametri terrae est insensibilis apud longitudinem g h, erit arcus k h insensibilis apud magnitudinem circuli k h t, et propterea quod longitudo g b est nota per quantitatem qua g d est unum, et angulus d g b est positus, erit angulus d b g notus, ergo angulus k d t aequalis ei est notus. Et propterea iterum, quod medietas diametri terrae est insensibilis apud longitudinem g h, erit punctum d sicut centrum circuli h t, ergo erit angulus k d t ipse angulus arcus k t secundum propinquitatem, ergo erit propter illud arcus k t notus, et est secundum propinquitatem aequalis arcui h t, cum non sit arcui k h quantitas sensibilis apud circulum z h, erit ergo propter illud arcus h t notus secundum propinquitatem. Cum ergo fuerint longitudines lunae a zenith capitis, et a centro terrae notae, scies arcum h t secundum hunc modum. Longitudo autem a centro terrae in hora posita scitur propter comprehensionem loci eius in orbe reuolutionis ipsius, et propter comprehensionem loci centri orbis reuolutionis ipsius in orbe ecentrico in illa hora. Loco autem longitudinis eius a zenith capitis utitur ipse in inuentione diuersitatum aspectus eius in eclipsibus longitudine loci eius ueri in orbe signorum, cum non sit inter has duas longitudines in continuationibus eclipticis quantitas de qua curetur. completur eius declaratio. Diuersitates autem aspectus in longitudine et latitudine inuenit propter diuersitates aspectus in circulo altitudinis, scilicet arcum h t praemissae rememorationis, et propter angulum quem continent arcus transiens per corpus lunae et zenith capitis et arcus orbis signorum, ita, quod usus est in eo eius angulo quem continent arcus orbis signorum et arcus transiens per zenith capitis et locum eius uerum in orbe signorum secundum hunc modum. Sit portio orbis signorum supra quem sunt a b g, et sit zenith capitis punctum e, et luna sit punctum d, et faciamus transire per haec duo puncta arcum circuli magni, qui sit arcus e d z, et sit arcus d h ipsa diuersitas aspectus in circulo altitudinis, erit ergo locus lunae uisibilis in eo punctum h, et protrahamus a duobus punctis d h duos arcus duorum circulorum magnorum erectos super arcum orbis signorum, qui sint duo arcus d b, h k, erit ergo arcus d b latitudo lunae uera, et punctum b locus eius uerus in orbe signorum, et arcus h k latitudo eius uisibilis, et punctum k locus eius uisibilis in orbe signorum, ergo erit arcus k b diuersitas aspectus in longitudine, et superfluitas quae est inter duos arcus h l et d b est diuersitas aspectus in latitudine, et protrahamus a puncto h arcum orthogonaliter super arcum b d qui sit arcus h t, ergo arcus h t est diuersitas aspectus in longitudine, quia est secundum propinquitatem aequalis arcus k b, et arcus d t est diuersitas aspectus in latitudine, quia est iterum secundum propinquitatem aequalis superfluitati quae est inter duos arcus d b, h k. Inuenit ergo quantitatem cuiusque horum duorum arcuum, scilicet arcuum h t, t d propter arcum h t notum, et propter angulum d h t secundum quod latera duorum triangulorum d h t et d b z sint lineae rectae, et secundum quod angulus t trianguli d h t sit rectus, et angulus eius h aequalis angulo z, qui est secundum propinquitatem aequalis angulo e b g noto. Post hoc declarauit quomodo 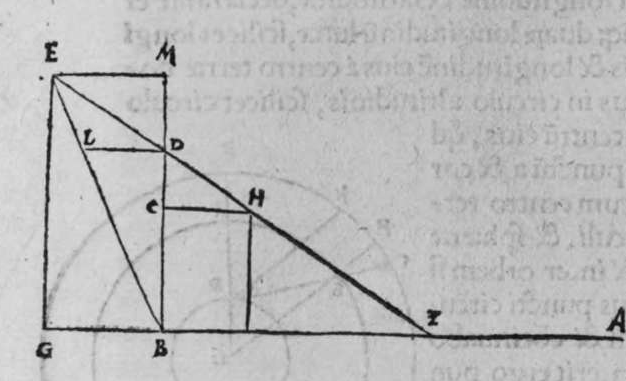extrahatur quantitas arcus d e per arcum e b et angulus z per angulum e b g notum, ita, quod duxit a puncto d arcum orthogonaliter super arcum e b, qui est arcus d l, et fabricauit rem secundum quod latera duorum triangulorum d l b et d e l sint lineae rectae, propterea ergo quod angulus d b g est rectus, et angulus e b g est notus, erit angulus d b l notus, et latus d b est notum, et angulus l est rectus, ergo erit unumquodque duorum laterum d l, l b notum, erit ergo latus l e notum, et propterea quod angulus l est rectus, et unumquodque duorum laterum d l, l e trianguli l d e est notum, erit latus e d notum, et angulus eius e est notus, et angulus e b g iam positus fuit notus, ergo erit angulus trianguli e z b notus secundum quod nos imaginemur iterum, quod latera eius sint lineae rectae. completa est eius ostensio. Et hanc quidem operationem ingreditur approximatio in utendo lineis rectis et angulis eorum loco arcuum et angulorum eorum, praecipue in arcubus transeuntibus per zenith capitis et lunam, et transeuntibus per zenith capitis et locum lunae, et per locum lunae uerum in orbe signorum unumquodque, quorum possibile est peruenire prope quartam circuli, et est possibile scire illud secundum ueritatem per illud quod narro. Ponamus ergo formam praecedentem secundum dispositionem suam, et sit arcus e m erectus super arcum b d m, ex quo est arcus latitudinis, triangulus ergo e m b est ex arcubus circulorum magnorum, et angulus eius m est rectus, erit ergo ex eis quae ostensa sunt in triangulis arcuum proportio sinus lateris e b ad sinum lateris e m, sicut proportio sinus arcus anguli m ad sinum arcus anguli b eius, sed angulus b eius est notus, quia angulus e b g est rectus, et arcus anguli m est quarta circuli, et arcus e b est notus, ergo oportet, ut sit sinus arcus m e notus, et ipse est minor quarta circuli, ergo est notus. Et propter illud quod ostensum est in triangulis iterum, erit proportio sinus complementi arcus e b noti ad sinum complementi arcus m e noti, etiam sicut proportio sinus complementi arcus b m ignoti ad sinum arcus quartae circuli, ergo oportet ut sit sinus arcus b m notus, et ipse est minor quarta circuli, ergo arcus est notus, et arcus b d est notus, quoniam ipse est arcus latitudinis, ergo erit arcus m d notus, et erit trianguli d m e unumquodque duorum laterum d m, m e notum, et angulus m est rectus, ergo erit ex eis quae praemissa sunt latus eius reliquum e d notum, et similiter simiter ed. erit angulus eius e d m iterum notus, similiter per ea quae praemissa sunt. Iam ergo ostensa est quantitas anguli h d t, e z k, et quantitas arcus d e, qui est longitudo corporis lunae a zenith capitis absque approximatione, quae ingrediatur in operatione, nisi quae ingreditur propter computationem a qua non est excusatio, et non est plus quam ea quae ingreditur in opere ius. Inuenimus ergo in longitudine corporis lunae a zenith capitis, et propter longitudinem eius a centro terrae quantitatem arcus h d secundum quod praemissum est, erit ergo triangulus d h t ex arcubus circulorum magnorum, et angulus eius t est rectus, et angulus eius d est notus, et latus eius d h est notum, ergo erit propter illud unumquodque duorum laterum d t, h t eius notum, uerum superfluitas inter duos arcus h t, k b est insensibilis, et similiter superfluitas quae est inter duos arcus h k, d b, quae est diuersitas aspectus in latitudine, est aequalis in sensu arcui d t et illud est cuius uoluimus declarationem. ET postquam manifestum fuit ei totum quod praemisum est de dispositionibus duorum lunarium, incepit post illud declarare causam eclipsium amborum. Speculatus est ergo prius in declaratione terminorum eclipsium, scilicet terminationis locorum orbis decliuis, inter quos et inter nodum a quo euasit, cum fuerit locus applicationis mediae, erit eclipsis posibilis, et cum erit in eo quod est inter eos, et inter partem, quae est ultra eos, erit impossibilis, declarauit ergo illud secundum hunc modum, et ilud est, quia declarata fuit ei in eis, quae sunt praemissa, quantitas arcus cui subtenditur diameter lunae circuli transeuntis per eam, cum ipsa est in longiori longitudine sua a terra in applicationibus. Hos autem terminos non oportet inquirere. nisi luna existente in sua propinquiore propinquitate orbis reuolutionis, ergo necessarium fuit ei declarare quantitatem arcus, cui subtenditur diameter lunae, cum ipsa fuerit in longitudine propiori in applicationibus. Declarauit ergo sicut illud praemissum est per duas eclipses lunares, quas considerauit luna existente in unaquaque ambarum prope longitudinem suam propiorem orbis reuolutionis. Inuenit ergo eam 35. minuta et tertia minuti, et per illud iterum sciuit quantitate arcus, cui subtenditur diameter umbrae in illa eadem longitudine, ergo inuenit eam partem unam et 32. minuta, et operatus est secundum quod quantitas huius circuli, scilicet circuli umbrae non diuersificetur in una longitudine lunae a terra, cum uere diuersificetur propter exitum centri circuli solis a centro mundi, ueruntamen diuersitas in ea est parua, propterea quod egressus huius centri non est plurimus, et propter illud non curauit de hac diuersitate, et iam quidem fuit ei declarata in eis quae sunt praemissa quantitas arcus, cui subtenditur diameter solis circuli magni transeuntis per ipsum, et illud est 31. minutum et tertia. Et similiter diuersificatur iterum iste arcus uere propter egressum centri circuli solis, ueruntamen eius diuersitas iterum est insensibilis. Aggregatum ergo ex duabus medietatibus duarum diametrorum lunarium est 33. minuta et 20. secunda, propter illud ergo cum fuerit in eclipsi solis inter duo centra solis et lunae quae uidentur 33. minuta et 20. secunda, tunc primum possibile est, ut sit situs lunae, qui uidetur super contactum solis, et lineauit ad illud exemplum secundum hunc modum. Sit portio circuli signorum supra quem sunt a b, et portio orbis decliuis supra quam sint g d, et ponantur cursus elipsium amborum aequedistantes, et sit centrum lunae in circulo decliui in tempore coniunctionis uisibilis punctum d, et locus eius uisibilis punctum e, et 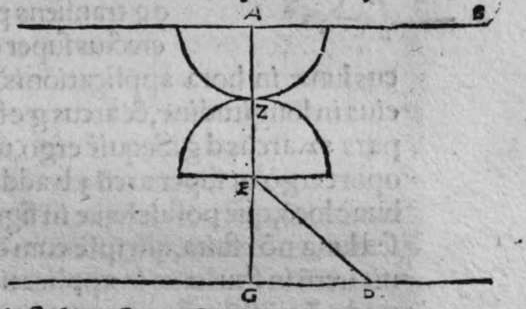sit arcus d e diuersitas aspectus eius uniuersalis, et sit punctum a centrum solis, et sit arcus a e g circuli magni erecti super orbem decliuem orthogonaliter, qui est quantum ad sensum erectus iterum super orbem signorum, erit ergo arcus e g diuersitas aspectus in latitudine, et arcus g d diuersitas aspectus in longitudine, et sit punctum super quem contingunt se corpora duorum lunarium in illa coniunctione uisibili punctum z, ergo arcus a e est ille, qui est aggregatio duarum medietatum diametrorum duorum lunarium, cuius summam possibile est esse 33. minuta et 20 secunda, et arcus e g, qui est diuersitas aspectus in latitudine maior summa ad quam peruenire potest in toto quod de terra habitatur, scilicet ab ultima regione, cuius longior dies est 13. horae, usque ad ultimam regionem, cuius longior dies est 16. horae in propiori longitudinum lunae in applicationibus, postquam computatur cum diuersitate aspectus solis ab ea quidem parte eius, quae sequitur meridiem, est 58. minuta, et ab ea parte quidem eius quae sequitur septentrionem, est 8. minuta, et arcus g d, qui est diuersitas aspectus in longitudine, ut multum erit, cum fuerit arcus g e 58. minuta, 15. minuta, et cum fuerit quidem 8. minuta 30. minuta. Arcus ergo a e g maior summa ad quam possibile est peruenire, cum luna quidem fuerit septentrionalis a zenith capitis, et fuerit secundum maiorem diuersitatem aspectus eius, qui possibilis est ab eo quod sequitur meridiem est pars una et 31. minutum, et quidem quando est meridiana ab eo, et est secundum plus diuersitatis aspectus eius, quod est ab ea parte eius quae sequitur septentrionem est 41. minutum. Deinde ipse duplicauit hunc arcum, scilicet arcum a e g 11. et semis, propterea quod proportio eius ad arcum, quae est a nodo ad ipsum, est secundum propinquitatem proportio unius ad 11. et medium. Fuit ergo illud summa arcus qui est a nodo ad ipsum, cum arcus quidem a g est pars una et 31. minutum, 17. partes et 26. minuta, et erit cum arcu g d, qui erit tunc 15. minuta, 17. partes et 41.minutum, et cum quidem arcus a g est 41. minutum, est 7. partes et 52. minuta, et erit cum arcu g d, qui erit tunc 30. minuta 8. partes et 22. minuta. Propter illud ergo, quia longitudo loci lunae ueri in circulo decliui ab uno duorum nodorum est quidemm, cum fuerit septentrionalis a sole 17. pars et 41. minutum, et cum quidem est meridiana a sole, est 8. partes et 42. minuta tunc in regione posita in primis, cum est possibile, ut sit situs eius uisibilis, uidetur super contactum solis. Deinde post illud acceptum plurimum diuersitatis, quod est unicuique duorum lunarium, et aggregauit utrunque, et accepit inde partem tertiamdecimam, et est illud quod sol perlabitur in tempore in quo luna perambulat partes duarum diuersitatum simul secundum approximationem, et addidit super illam partem, partem 13. iterum, et est illud quod percurrit sol iterum in tempore, in quo luna pertransit pertansit ed. illam partem. Quod ergo fuit, est secundum propinquitatem illud quod perambulat sol donec consecuta fuerit ipsum luna, et illud fuit 37. minuta. Adiunxit ergo illud super plurimum quod de diuersitate solis, et quod fuit, est plurimum, quod est inter duas applicationes mediam et ueram in longitudine, et aequale illi fere est in latitudine, et illud est tres partes. Adiunxit ergo istas tres partes super finem lunae a nodo in orbe decliui in hora applicationis uisibilis, in qua sit situs lunae uisbilis super contactum solis, scilicet spacium puncti g a nodo. Partes ergo orbis decliuis quae fuerunt, sunt finis longitudinis loci applicationis mediae ab uno duorum nodorum, in quo sit situs lunae, qui uidetur super contactum solis, et illud quidem est, cum luna est septentrionalis a sole 20. partes et 41. minutum, et cum est meridiana ab eo est 11. partes et 22. minuta. Et errauit in hoc, quod posuit tres partes quae sunt plurimum, quod est inter duo loca duarum applicationum super longitudinem corporis lunae a nodo in hora applicationis uerae, quoniam istae tres partes non sunt nisi plurimum, quod est inter locum applicationis mediae et locum applicationis uerae, non quod est inter locum applicationis mediae et applicationis uisibilis. Ostendam ergo illud, et ponam figuram secundum quod est in ueritate, scilicet, ut sit 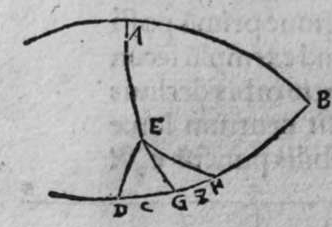portio orbis signorum arcus circuli magni, qui sit arcus a b, et centrum solis super quod est punctum a, et portio orbis decliuis arcus d b, et centrum lunae super quod est punctum d, et sit arcus d e portio circuli transeuntis per ipsum et zenith capitis, et sit centrum lunae uisibile punctum e, erit ergo arcus d e diuersitas aspectus eius totalis circuli altitudinis, et sit arcus a e g transiens per centrum solis et per centrum lunae uisibile orhogonaliter erectus super or bem signorum. Erit ergo punctum g orbis decliuis ipse locus lunae in hora applicationis uisibilis, et erit arcus d g existens fere diuersitas aspectus eius in longitudine, et arcus g e fere diuersitas aspectus eius in latitudine, et sit arcus g z pars 12. arcus d g. Sequitur ergo, ut sit punctum z ipse locus lunae in hora applicationis uerae, oportet oport ed. ergo ut super arcum z b addantur tres partes super g b, sicut fecit, ergo oportet, ut super hunc locum, quem posuit lunae in figura hac, sit in terminis additio per quantitatem arcus g z, sed luna non est ita, quoniam ipse cum errore suo in additione trium partium super arcum g b, errauit iterum in situ lunae in applicatione uisibili, et illud est, quia ponit situm eius longinquius a nodo quam punctum g, et non oportuit, nisi ut esset situs lunae, propinquior nodo quam punctum g, ac si sit super punctum h huius figurae, et sit arcus e h diuersitas aspectus totalis, et arcus g h diuersitas aspectus in longitudine, ergo est propter illud locus lunae in hora coniunctionis uerus longinquior a nodo quam punctum g per quantitatem arcus partis 12. arcus g h, ac si sit punctum t, et est arcus g t ipsa pars 12. arcus g h. Addemus ergo tres partes super arcum t b, non super arcum z b sicut sequitur ex situ, super quem posuit lunam, oportet ergo secundum ueritatem, ut sit in terminis, quos inuenit additio quantitatis arcus g t, et est in termino maiori, in quo diuersitas aspectus in longitudine est 15. minuta 13. minuta et tres quartae minuti, et in termino minori, et est ille, in quo diuersitas aspectus in longitudine est 30. minuta. Terminos uero eclipticos lunares inuenit secundum hunc modum, et illud est, quia ipse adiunxit arcum cui subtenditur medietas diametri lunae in propiori propinquitate sua orbis reuolutionis, qua est 17. minuta et 40. secunda, arcui cui subtenditur medietas diametri circuli umbrae ad illam longitudinem propiorem quae est 45. minuta et 50. secunda, et accepit quod exigit illud de circulo decliui, fuit ergo illud finis longitudinis corporis lunae a nodo in hora medij temporis eclipsis, et illud est 12. partes et 12. minuta. Addidit ergo illud super tres partes praedictas quae sunt maius, quod est inter duo loca duarum applicationum in longitudine, et est fere illud, quod est in latitudine. Est ergo illud ultimum longitudinis loci applicationis mediae ab uno duorum nodorum, in quo est luna super contactum circuli umbrae, et illud est 15. partes et 13. minuta. Iste ergo est terminus inter applicationes medias, in quibus possibile est lunam eclipsari, et applicationes, in quibus non est possibile, et illud est cuius uoluimus declarationem. Et postquam ostensum fuit ei illud, fuit ei necessarium addere qualiter comprehenditur tempus mensium, in quibus possibile est redire eclipsim, ne consideranti post eclipsim aliquam esset necessarium aspicere in omnibus applicationibus quae sequuntur illam eclipsim, sed attendat ad applicationes quae sunt in hoc tempore quaesito. Ostendit ergo quod possibile est post spacium 6. mensium, ut eclipsentur sol et luna, et illud est, quoniam ex cursu lunae medio in latitudine in 6. mensibus aggregantur 148. partes et minutum unum et 15. secunda, et quod comprehenditur ex partibus arcuum, qui sunt inter terminos eclipticos lunares, qui sunt quidem infra semicirculum est minus illo, et qui quidem sunt plus semicirculo, est maius illo, propter illud ergo possibile est, ubi eclipsentur sol et luna bis in sex mensibus. Et similiter declarauit iterum quod possibile est, ut eclipsetur luna post longius spacium quinque mensium quod est, et illud est, quia quandoque sequitur ut sit in hoc spacio cursus solis maior qui esse potest, et cursus lunae in eo minor qui esse potest, ut sit spacium mensium uerorum addens super tempus mensium mediorum per duas diuersitates simul, et illud quidem, quod comprehenditur de cursu duorum lunarium cuiusque in longitudine in quinque mensibus medijs, est 145. partes et 32. minuta, et motus lunae in orbe reuolutionis suae in hoc tempore est 129. partes et 5. minuta, et partes quidem 145. et minuta 32. que sunt solis addunt in maiori cursu, qui est a duabus partibus propioris longitudinis super cursum medium 4. partes et 38. minuta, et partes orbis reuolutionis lunae, scilicet 129. partes et 5 minuta, minuunt in minori cursu, qui est a duabus partibus longitudinis longioris a cursu medio 8. partes et 40. minuta. In tempore ergo medio quinque mensium, quando cursus solis est maior qui est, et cursus lunae qui est minor qui est, sol etiam praecedit lunam per partes quae aggregantur ex duabus diuersitatibus simul, et sunt 13. partes 18. minuta. Cum ergo acceperimus partem 12. illius propter illud, cuius praecessit declaratio, proueniet nobis pars pars sic. una et 6. minuta, et est illud quod addit per motum usquequo consequatur eum linea, et quoniam solem consequatur ex additione propter diuersitatem suam sibi propriam 4. partes 38. minuta, et consequuntur eum usquequo reuoluatur et compleatur applicatio uera pars una et 6. minuta, tunc maius tempus quod est quinque mensium, addit super tempus medium quinque mensium in longitudine 5. partes et 44. minuta. Haec ergo fere est summa additionis cursus lunae iterum in latitudine in circulo decliui super partes, quae aggregantur latitudini in tempore medio quinque mensium, quod est 253. partes et 21.minutum fere. Propter illud ergo cursus uerus, qui inuenitur in latitudine in maiori tempore, quod est quinque mensium, aggregant 159. partes et 5. minuta, uerum termini, qui sunt a duobus lateribus orbis lignorum habentes eclipsim in longitudine lunae media comprehendunt in circulo quidem magno, qui significantur in eis per duos polos circuli decliuis partem unam fere, propterea quod ipsi comprehendunt in longitudine propiori partem unam et tria minuta et 36. secunda, et in longitudine eius longiori 56. minuta et 24. secunda, et in circulo quidem decliui est eorum summa secundum longitudinem a duobus nodis 11. partes et 30. minuta, et arcus qui est inter eos, in quo non cadit eclipsis propter illud 157. partes, et istae partes sunt minus partibus quae superfluunt de circulo decliui in maiori tempore, quod est 5. mensium, quae sunt 159. partes et 5. minuta, per duas partes et 5. minuta. Apparet ergo inde quod possibile est in maiori tempore quinque mensium quod est, ut cum luna eclipsatur ex prima oppositione in eis, quoniam recedit ab uno duorum nodorum, quicunque nodus suerit, redeat et eclipsetur in postrema oppositione in eis, cum uadit ad nodum sequentem illum nodum, et erunt tenebrae in duabus eclipsibus simul ab una et eadem parte de duabus partibus orbis signorum, et nunquam erunt a duabus partibus contrarijs. Et similiter etiam ostendit, quod non est possbile, ut eclipsentur sol et luna post maius tempus quod est 7. mensium, et illud est, quoniam propterea iterum quod in tempore medio 7. mensium cursum medium cuiusque duorum lunarium consequuntur de additione 203. partes et 45. minuta, et cursum lunae in orbe reuolutionis suae consequuntur de additione 180. partes et 43. minuta, et 200. quidem et tres partes et 45.minuta, quae sunt solis, cum cursus eius qui est minor, qui est a duobus lateribus longitudinis longioris, minuunt ex motu medio eodem 4. partes et 42. minuta, et 180. partes et 43. minuta, quae sunt lunae in orbe reuolutionis suae, cum cursus eius qui est maior, qui est a duobus lateribus longitudinis propioris, addunt super cursum medium 9. partes 58. minuta, tunc in tempore paruo 7. mensium, cum sol currit cursu suo qui est minor qui est, et luna currit cursu suo qui est maior qui est luna iam transit per partes quae aggregantur de duabus diuersitatibus simul, quae sunt 14. partes et 40. minuta. Cum ergo acceperimus de illo propter illud, cuius praecessit declaratio partem 12, et addiderimus eam super partes quae minuuntur propter diuersitatem solis, quae sunt 4. partes et 42. minuta, erunt partes quae colliguntur, quae sunt quinque partes et 55. minuta ipsae partes, quibus postponitur cursus in longitudine in minori tempore septem mensium, quod erit a cursu in tempore mediorum eorum, et minuuntur cursus in latitudine secundum hanc similitudinem a partibus latitudinis, qua aggregantur in tempore medio septem mensium, quae sunt 214. partes et 42. minuta, ergo in minori tempore quod est 7. mensium, consequuntur lunam de additione in latitudine in circulo decliui 208. partes et 47. minuta. Sed arcus magnus totus qui est inter duos terminos habentes eclipsim in luna in longitudine media circuli decliuis, scilicet terminum qui est, cum uadit ad unum duorum nodorum, et terminum qui est, cum separatur a nodo sequente ipsum, non est nisi 203. partes tantum. Non est ergo possibile, ut luna eclipsetur post minus tempus quod est quinque mensium, declarauit secundum hunc modum, et illud est, quia ipse comprehendit in primis quantitatem duarum medietatum duarum diametrorum lunarium in longitudine lunae media, sicut fecit in comprehensione duarum diametrorum lunae et umbrae, inuenit ergo illud 32. minuta et 20. secunda. Deinde comprehendit etiam arcum orbis decliuis, quem perambulat luna per motum suum uerum in maiori tempore quinque mensium, quod est secundum quod praecesit, et sciuit quantitatem cuiusque duorum arcuum aequalium transeuntium per duas extremitates huius arcus circuli transeuntis per duos polos orbis signorum et illud est 55. minuta fere, et illud est maius aggregatione duarum medietatum duarum diametrorum duorum lunarium in longitudine longiori lunae per 22. minuta et medietatem. Sciuit ergo quod quando non accidit lunae diuersitas aspectus in latitudine, non est possibile, ut redeat eclipsis solis post maius tempus quod est quinque mensium et quando accidit ei diuersitas aspectus in una duarum eclipsium, aut in ambabus simul a parte una lunae, quae superfluat super 45. minuta, quae sunt duplum 22. minutorum et medij, tunc possibile est, ut redeat eclipsis. Comprehendit ergo tempus quod est in maiori spacio, quod est quinque mensium per hoc quod accepit maius, quod est de duabus diuersitatibus duorum lunarium in illo tempore, et addit super aggregatum ex eis partem duodecimam quae est illud, quod perambulat sol donec consequatur cum luna, quod ergo fuit, diuisit super motum medium lunae in die. Addidit ergo quod exiuit super tempus quinque mensium mediorum, et quod fuit, est tempus maius, quod est quinque mensium, et illud est 148. dies et 18. horae aequales, ergo est tempus coniunctionis secundae post tempus coniunctionis primae per 18. horas aequales, et propterea quod sol in hoc tempore in maiori cursu suo secat duos arcus aequales a duobus lateribus longitudinis propioris orbis sui ecentrici, quae est super quinque partes et mediam signi sagittarij, et luna perambulat in illo spacio quod est maiori tempore, quod est quinque mensium per cursum suum minorem de orbe signorum quasi 151. partem secundum propinquitatem, erit propter illud coniunctio prima in duabus tertijs aquarij. Oportet ergo ut inquiramus ubi et quando sit possibile, ut accidat lunae de diuersitate aspectus in latitudine in his duobus locis orbis signorum in una duarum coniunctionum, aut utrisque ab una parte lunae plus 45. minutis secundum hoc, ut sint inter duo tempora duarum coniunctionum 18. horae aequales additae super 148. dies, quae sunt dies quinque magnorum, scilicet, ut sit inter duas longitudines lunae a circulo meridiei in duobus temporibus duarum coniunctionum arcus 18. horarum aequalium, uerum non est possibile in loco eius quod habitatur, ut proueniat summa diuersitatis aspectus lunae in latitudine in parte septentrionis eius, quae sit in illa quantitas, propter illud ergo sit impossibile, ut eclipsetur sol in maiori tempore quod est 5. mensium bis in cursu lunae in meridie ab orbe signorum, scilicet, quando est in coniunctione prima, recedens a nodo caudae, et est in coniunctione secunda uadens ad nodum capitis, sed a parte meridiei eius est possibile, ut perueniat summa diuersitatis aspectus eius in latitudine in his duobus signis, quando fuerit occidens in coniunctione prima duae tertiae uirginis, et fuerit illud quod mediat coelum in coniunctione secunda duae tertiae aquarij. Postquam computata fuerit cum diuersitate aspectus solis apud illos quidem qui habitant sub aequatore diei, cum locus eius fuerit in duabus tertijs uirginis ad hoc, ut sit 22. minuta, et cum fuerit super duas tertias aquarij 14. minuta. Sed ubi est longior dies 12. horae et media, est possibile, ut sit summa diuersitatis aspectus eius, est quidem in duabus tertijs uirginis occidentalis 27. minuta, cum est quidem medians coelum in duabus tertijs aquarij 22. minuta. Erit ergo aggregatio ambarum plus 4 5. minutis, propter illud ergo est possibile in hoc loco habitabili, ut bis eclipsetur sol in longiori tempore, quod est quinque mensium, in eo uero quod sequitur hunc locum ad partem septentrionis, quanto plus est diuersitas aspectus a parte meridiei, maior est possibilitas illius apud eos maior, et illud non est nisi cum cursus lunae est a parte septentrionis ab orbe signorum tantum, scilicet, quando est in eclipsi prima recedens a nodo capitis, et est in secunda eclipsi uadens ad nodum caudae. Et per simile huiusmet ostenditur, quod est possibile iterum, ut eclipsetur sol apud illos, qui sunt unius et eiusdem regionis, bis in breuiori tempore, quod est 7. mensium, cum cursus lunae iterum est in septentrione ab orbe signorum, et non est possibile illud cursu eius in meridie ab eo in loco de eo quod habitatur, et illud est, quia ipse sciuit per illud quod praemissum fuit quantitatem arcus orbis decliuis, quem perambulat luna per motum suum uerum in breuiori tempore, quod est 7. mensium, et illud est 208. partes et 47. minuta, et est arcus in eo quod est inter accessionem, ad unum duorum nodorum et recessionem a nodo secundo 192. partes et 24. minuta. Clarum est ergo, quod cum lunae non est diuersitas aspectus, non est possibile inuentio illius, propterea quod arcus circuli decliuis, qui est minori tempore quod est 7. mensium, est maior maiori arcu sparso inter duos terminos habentes eclipsim in sole per partes, quarum summa est in circulo decliui 16. partes et 31. minuta, et in circulo quidem, qui transit per duos polos orbis signorum pars una et 25. minuta. At uero ubi est possibile, ut accidat ei de diuersitate aspectus in una duarum coniunctionum, aut in utrisque a parte una, quod sit plus parte una et 25. minutis, tunc illis est possibile, ut apud eos bis eclipsetur in minori tempore quod est 7. mensium. Inuenit ergo per simile eius quod praecessit quantitatem dierum, qui sunt in hoc tempore, et illud est 205. dies et 12. horae aequales. Sequitur ergo quod sit tempus coniunctionis secundae post 12. horas a tempore coniunctionis primae, et propterea quod sol in hoc tempore perlabitur de orbe signorum duos arcus aequales a duobus lateribus longitudinis longioris, quorum summa est 197. partes et 50. minuta, erit coniunctio prima in fine aquarij, et coniunctio secunda in medio uirginis. Oportet ergo, ut quaeramus ubi et quando sit possibile, ut sit lunae in uno istorum locorum, aut utrisque de diuersitate aspectus in latitudine a parte una eius, quod addat super partem unam et 25. minuta secundum hoc, ut sit luna in unae duarum coniunctionum super horizonte orientali, et in secunda super horizonte occidentali, quoniam per hunc modum tantum praeparatur, ut sint duae eclipses simul supra terram, cum sint inter duo tempora earum 12. horae, erit ergo una earum in mane et altera in sero. Diuersitas uero aspectus eius quae est septentrionalis, non est possibile, ut sit summa in aliquo loco de eo quod habitatur, neque apud eos quorum habitationes sunt sub aequatore, nedum apud alios maior 23. et propter illud fit impossibile, ut sol bis eclipsetur in breuiori tempore quod est 7. mensium, cum cursus lunae est in meridie ab orbe signorum, scilicet cum est in coniunctione prima, uadens ad nodum capitis, et in coniunctione secunda recedens a nodo caudae. Diuersitatis autem aspectus eius, qui est meridianus in regione, cuius longior dies est 14. horae, et media, est summa in longitudine lunae media in applicationibus, cum est postremum aquarij orientale, et est medium uirginis occidentale. Postquam computatur cum diuersitate aspectus solis quasi 46. minuta in unoquoque duorum locorum horum, donec sit quod aggregatur ex duabus diuersitatibus aspectus in utrisque plus parte una et 25. minutis. Propter illud ergo est possibile, ut apud eos sol bis eclipsetur in breuiori tempore, quod est 7. mensium, et propterea quod diuersitas aspectus magnificatur apud illos, quorum habitationes sunt in parte septentrionis ab hoc loco, tunc possibilitas illius apud eos est maior, et non erit illud nisi cum cursus lunae fuerit in septentrione ab orbe signorum tantum, scilicet, cum in eclipsi prima est uadens ad nodum caudae, et in eclipsi secunda est recedens a nodo capitis. Deinde Deind ed. ipse declarauit post illud, quod non est possibile, ut sol bis eclipsetur in mense uno in loco eius quod habitatur, neque in climate uno et eodem, neque in duobus climatibus diuersis, et si ponatur conuenientia eius, cuius est impossibilis conuenientia, scilicet, ut sit luna in sua propiori propinquitate in applicationibus, ut illud quod accidit ei de diuersitate aspectus sit maius quod est, ut sit tempus mensis breuius quod est possibile, ut sit additio cursus in latitudine in mense super cursum, quem continet terminus eclipsis solis minor, qui esse potest, et ut non consequatur separatio, neque ex horis, neque ex signis, in quibus illud quod accidit ei de diuersitate aspectus, est maius quod est. Declarauit ergo per simile eius quod praecessit quantitatem arcus orbis decliuis, quem perambulat luna per motum suum uerum in breuiori tempore quod est mensis, et illud est 29. partes et 14. minuta, et pertinet unicuique duarum medietatum huius arcus, scilicet, cum nodus est in medio eius de circulo transeunte per duas extremitates eius, et duos polos orbis decliuis pars una et 16. minuta et medietas fere. Sed summa arcus huius circuli in duobus terminis teminis ed. eclipsis in longitudine sua lunae propiori in applicationibus et 33. minuta, et illud est aggregatio duarum medietatum duarum diametrorum lunarium, et illud est minus parte una et 16. minutis et medietate per 43. minuta. Non est ergo possibile, ut sol bis eclipsetur in mense uno, nisi ut luna non habet diuersitatem aspectus in latitudine in una duarum eclipsium, et sit ei in secunda de diuersitate aspectus plus parte una et 27. minutis, quae sunt duplu 43. minutorum et medietatis, aut sit ei in unaquaque duarum eclipsium diuersitas aspectus in parte una, et sit superfluitas inter utrasque maior parte una et 27. minutis, aut sit in unaquaque duarum eclipsium diuersitas aspectus in duabus partibus contrarijs, et sit utrarumque aggregatio maior parte una et 27. minutis. Verum non est in terra locus in quo lunae accidat de diuersitate aspectus in latitudine, postquam computatur cum diuersitate aspectus solis plus parte una, propter illud ergo non est possibile solem bis eclipsari in minori tempore quod est mensis, neque quando non est lunae diuersitas aspectus in una duarum coniunctionum, neque quando est diuersitas aspectus eius in parte una ipsius, cum superfluitas inter eas ambas non sit maior parte una, et sit necesse, ut sit maior parte una et 27. minutis. Iam ergo superest, ut illud non sit nisi ita, ut sit ei diuersitas aspectus in duabus partibus contrarijs eius, et aggregatio ambarum maior parte una et 27. minutis. In parte autem una et eadem de partibus duabus aequatoris diei, non est illud possibile in aliqua dispositionum, quoniam finis ad quem peruenit diuersitas aspectus lunae in latitudine apud illos quidem, quorum habitationis locus est sub aequatorae diei, est circiter 25. minuta ad septentrionem et ad meridiem, et apud illos quidem, quorum habitatio in ultimo septentrionis a meridie ab aequatore diei, non est maior parte una, donec sit aggregatum de duabus diuersitatibus aspectus contrarijs per partem minus parte una et 27. minutis. In eo autem quod est in haec duo loca, scilicet aequatorem diei et unam duarum finium, scilicet septentrionalem aut meridianam, propterea quod unaquaeque duarum diuersitatum aspectus contrarium per partem addit apud eos paruitatem, tunc possibilitas illius apud eos addit elongationem, in duobus uero locis duarum partium contrariarum ab aequatore diei, scilicet septentrionalis aut meridianae, est possibile, ut eclipsetur sol in loco partis septentrionalis ab aequatore diei, deinde redeat post mensem unum, et eclipsetur in loco alio partis meridianae ab eo, quoniam possibile, ut summa diuersitatis aspectus sit in una quaque harum duarum partium pars una, sicut praemissum est. Non est ergo possibile, ut sol bis eclipsetur in mense uno, neque apud illos qui sunt unius eiusdem regionis in loco uno terrae, neque in duabus regionibus diuersis in parte una ab aequatore diei, et neque est illud possibile nisi in duobus locis duarum partium aequatoris diei, scilicet, ut sit una septentrionalis ab aequatore diei et altera meridiana ab eo et illud est, cuius uoluimus declarationem. ET de illis quorum praemissio est necessaria ad inueniendum quantitates eclipsium et temporum earum, de quibus non rememoratus est Ptolomeus, est illud quod narro. Sit arcus g b portio signorum, et arcus a b portio decliuis lunae, et sit punctum g centrum solis in eclipsi solari 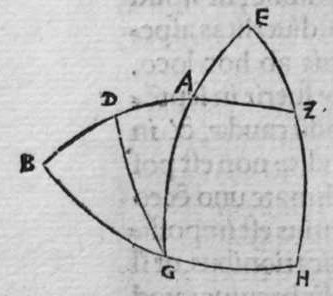et centrum circuli umbrae in eclipsi lunari, et sit arcus a g orthogonaliter erectus super arcum b g, ergo punctum a est centrum lunae in applicatione uera, et arcus a g est latitudo eius uera, et sit arcus g d erectus orthogonaliter super arcum a b, ergo erit punctum d ipsum punctum super quod est centrum lunae in medio temporis eclipsis, et erit arcus d g ipse arcus super quem erit centrum duorum lunarium in medio temporis eclipsis solaris, et centrum lunae et circuli umbrae in medio temporis eclipsis lunaris, et ex quantitate arcus d g sciemus quantitatem eclipsati de diametro tecti duorum lunarium. Quantitas autem arcus a g, qui est latitudo lunae in applicatione uera, erit nota, propterea quod arcus a b, qui est longitudo lunae a nodo in orbe decliui est notus, et proportio sinus eius ad sinum arcus a g est sicut proportio medietatis diametri ad sinum totius declinationis orbis declinationis, et propterea quod tres sinus sunt noti, erit quartus, et est sinus arcus a g notus, et ipse est minor quarta circuli, ergo est notus. In arcu uero g d usus est licentia Ptolomeus, et posuit eum aequalem arcui a g. Et similiter posuit arcum a b aequalem arcui d b, et dixit, quod ultimum quod est inter eos est duo minuta sed illud quod est inter eos, est circiter 4. minuta, et possibilis est scientia quantitatis arcus g d secundum uerificationem per faciliorem inquisitionem, et illud est, quia si fecerimus nos penetrare arcum a g donec transeat per polum arcus b g qui sit punctum e, et arcus e z h transeat per duos polos duorum circulorum a b, b g, tunc erit unusquisque duorum angulorum z et d rectus, et angulus e a z est aequalis angulo g a d, erit ergo ex eo quod declarauimus proportio sinus lateris a g ad sinum lateris g d, sicut proportio sinus arcus a e ad sinum arcus z e, et unus quisque sinuum arcuum a g, a e, z e est notus, ergo oportet ut sit arcus g d notus, et arcus g d est minor quarta circuli, ergo est notus. completa est eius declaratio. ET ut sciamus quomodo extrahatur propter longitudines lunae a centro terrae in applicationibus quantitates diametri lunae, et diametri circuli umbrae, et scientia illius est secundum quod narro. Sit orbis reuolutionis luna circulus a b g circa centrum d, et sit centrum terrae 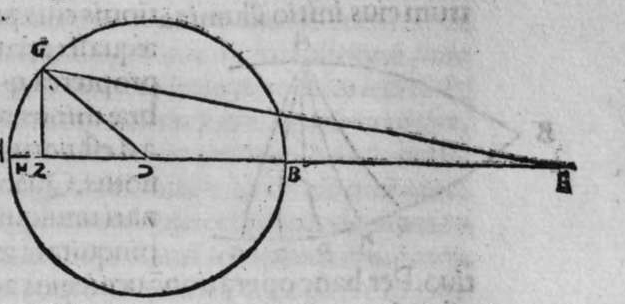punctum e, et continuabo e b, b d et a d, ergo erit punctum a ipsa longior longitudo lunae a terra in applicationibus, et punctum b propinquior longitudo in eis, et superfluitas inter eas quae est linea a b iam ostensum est quod est 10. partes per quantitatem qua est linea e d 60. partes, et iam praecessit nobis scientia quantitatis diametri lunae, et quantitatis diametri circuli umbrae, ad unamquanque duarum longitudinum a b, et singulariter ponamus lunam super punctum g orbis reuolutionis, et uoluimus scire quantitatem diametri eius, et quantitatem diametri circuli umbrae ad longitudinem e g, ergo extrahamus perpendicularem g z, propterea ergo quod arcus a g est positus, et est arcus diuersitatis in hora applicationis uerae, erit sinus eius qui est perpendicularis g z notus, et similiter erit sinus eius uerus qui est linea a z notus, ergo remanet linea e z nota, ergo linea e g quae est longitudo lunae a centro terrae est nota, et sit linea e h aequalis ei, et sit diameter lunae ad longitudinem a e linea t l, et diameter eius ad longitudinem b e linea t k, et superfluitas quae est inter eas est linea l k, et quantitas diametri lunae ad longitudinem e g quae est aequalis lineae e h. Sit linea t m, et uolo scire quantitatem eius, propterea 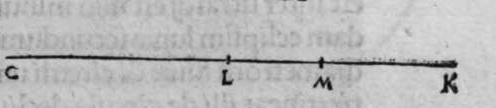ergo quod linea t l est diameter lunae ad longitudinem a e et linea t k est quantitas eius ad longitudinem e b, et superfluitas inter eas est linea l k, erit secundum propinquitatem proportio lineae a h quae est superfluitas, quae est inter duas longitudines a e, e h ad lineam a b, quae est superfluitas inter duas longitudines a e, b e, sicut proportio lineae m l quae est superfluitas diametri lunae ad longitudinem e h super diametrum eius ad longitudinem a e ad lineam l k, quae est superfluitas inter duas quantitates duarum diametrorum, quae sunt ad duas longitudines a e, b e. Sed superfluitas quae est inter duas longitudines e a, b e est nota, quae est diameter orbis reuolutionis tota. Et similiter superfluitas quae est inter duas longitudines a e et e h est nota, quae est linea a h nota, et similiter linea l k quae est superfluitas inter duas diametros t k et t l est nota, ergo oportet propter illud, ut sit linea l m quae est superfluitas inter duas diametros t m, t l nota. Adiungam ergo eam ad lineam t l, et erit linea t m nota, et est diameter lunae ad longitudinem notam. completa est eius declaratio. Et per illud idem simile incedam in quantitate diametri circuli umbrae ad longitudinem g e positam, et propterea quod diameter solis in omnibus longitudinibus suis a terra non alteratur alteratione magna propter paruitatem lineae quae est inter centrum ecentrici eius et centrum orbis signorum, et iam ostensa fuit ei quantitas ipsius per hoc, quod reperit eam aequalem quantitati diametri lunae in longitudine sua longiori in applicationibus, et fuit propter illud diameter solis nota, tunc cum nos posuerimus portionem orbis signorum arcum a b, et portionem orbis decliuis lunae arcum g b, et punctum a centrum solis in eclipsibus solaribus, aut centrum circuli umbrae in eclipsi lunari, et posuerimus punctum g centrum lunae, et arcum a g aequalem aggregationi duarum medietatum duarum diametrorum, scilicet diametri lunae et diametri solis in eclipsi solari, aut diametri lunae et diametri circuli umbrae in eclipsi lunari, et fuerit arcus a d erectus super arcum b g orthogonaliter, erit punctum d ipsum medium tempus eclipsis. Separabo autem arcum d e aequalem arcui g d, erit ergo arcus e d continens medietatem temporis eius secundam, et propterea quod latitudo lunae in hora applicationis uerae est nota secundum quod praemisimus, erit etiam arcus a d qui est uadens per duo centra eclipsantis et eclipsati in medio tempore eclipsis notus secundum quod nuper ostendimus. Proijciam ergo ipsum de aggregatione duarum diametrorum, et remanebit quantitas eclipsantis de quantitate eclipsati nota, et propterea quod linea a g quae est quantitas duarum medietatum duarum diametrorum est nota, et arcus a d est notus, et angulus d est rectus, erit ex eo quod ostendimus in triangulis arcuum latus g d notum, et propterea quod circulus umbrae est magnus, erunt eclipsi lunari 4. dispositiones, quarum duae sunt communes duabus eclipsibus, scilicet solari et lunari, et sunt initium eclipsis et finis eius, et per alias duas dispositiones fit singularis eclipsis lunaris, quarum una est impletio, et est, cum eclipsatur luna tota, et secunda est initium illuminationis, et est, cum incipit exire a circulo umbrae. Sit ergo centrum lunae in fine impletionis eius punctum z, et centrum eius initio illuminationis eius punctum h, ergo erit arcus g z secundum propinquitatem 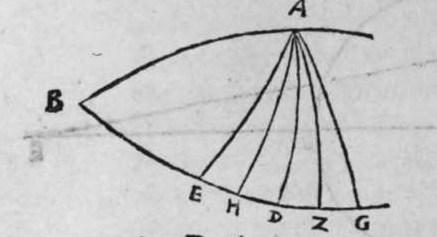aequalis arcui h e, et similiter arcus z d aequalis fere arcui d h, et propterea quod arcus a z subtenditur medietati diametri circuli umbrae minus medietate diametri circuli lunae, erit notus, sed arcus a d est notus, ergo arcus z d est notus, et iam fuit arcus g d totus notus. Quamobrem remanet arcus g z notus ergo erit in eclipsi lunari unusquisque duorum arcuum g z, z d notus, et sunt secundum propinquitatem aequales duobus arcubus d h, h e, quisque arcus suo relatiuo. Per hanc operationem ueniemus ad scientiam quantitatis eclipsantis de diametro eclipsati, et quantitatis temporum eclipsis, scilicet temporis quod ab initio eclipsis lunae ad medium eius, et temporis quod est ab initio eclipsis lunae ad finem impletionis eius, et temporis quod est in fine impletionis ad medium temporis eclipsis, et quod est a medio temporis eclipsis ad initium illuminationis eius, et quod est ab initio illuminationis eius usque ad finem ipsius sine propinquitate quae consequitur eam. Operatio aut cuius rememoratur Ptolomeus, est operatio suscipiens propinquitatem duobus modis, quorum unus est, quia ipse utitur lineis rectis loco arcuum, et secundus, quia ipse ponit arcum qui est inter duo centra eclipsantis et eclipsati in medio tempore eclipsis aequalem latitudinem lunae uere, et dixit, quod illud quod est inter utrasque est duo minuta, et est plus illo. Deinde post hoc composuit tabulas ad aequdam eclipsim lunae secundum quod narro, et illud est, quia aggregauit duas medietates duarum diametrorum lunae et circuli umbrae in longitudine longiori orbis reuolutionis, et sciuit quid pertineat illi de circulo decliui, et inuenit illud 10. partes et 48. minuta. Eiecit ergo illud de 90. et remanserunt 79. partes et 12. minuta, et sunt longitudo a parte septentrionis. Posuit ergo eas in prima arearum tabulae, quae est ad longitudinem maiorem, et accepit iterum aggregationem duarum medietatum diametrorum ad longitudinem minorem, et sciuit quod competeret illi de circulo decliui, et illud est 12. partes et 12. minuta, proiecit ergo illud de 90. et remanserunt 77. partes et 8. minuta, et scripsit illud in prima arearum tabulae secundae, quae est ad longitudinem minorem, et fecit tabulam minutis, quorum proportio de 60. minutis est sicut proportio superfluitatis longitudinis maioris super longitudinem lunae a terra in hora eclipsis ad diametrum orbis reuolutionis, quae est superfluitas inter maiorem et minorem ipsius. Et dixit in aequatione eclipsis, ut fiat introitus cum numero latitudinis in unaquaque duarum tabularum, et sumatur quod est coram eo in unaquaque earum, et scribatur unumquodque unumqnodque ed. per se, deinde intromittantur partes diuersitatis in areas numeri, qui est in tabula minutorum, et sumatur quod est coram eis de minutis, et quod fuerit de 60. minutis, sumatur talis proportio, qualis est illa, de superfluitate quae est inter illud quod sumptum est de utrisque tabulis, et quod fuerit, addatur super illud quod sumptum est de tabula prima, et quod fuerit de digitis, est eclipsatum de diametro lunae. Et si numerus latitudinis non inuenitur in tabula prima, sed inuenitur in secunda, solum accipiatur quod est coram eo de digitis, et erit illud quantitas eclipsati de diametro lunae, haec est operatio quam ipse dixit:Quod si fuerit numerus latitudinis 79. partes, non inueniemus ipsum in tabula prima, et inueniemus coram ipso in tabula secunda de digitis plus duobus digitis. Dicemus ergo quod luna eclipsabitur plus duobus digitis, et hoc quidem non erit, nisi cum luna fuerit in propiori propinquitate sua orbis reuolutionis suae, quod si luna fuerit tunc in longitudine sua longiori, aut circa eam taliter, ut sit aggregatio duarum diametrorum illic aequalis latitudini lunae, aut minor ea, tunc de luna non eclipsabitur aliquid omnino, et nos iam diximus, quod de ea eclipsabitur plus duorum digitis, et hoc quidem est ultimum inconueniens, ut iudicetur quod de luna eclipsabitur plus sexta ipsius, et nihil de ea penitus eclipsetur, et huiusmodi quidem non est possibile, ut dimittat aliquis auctorum Aziget, super quos non sunt demonstrationes. Quomodo ergo est possibile quod Ptolomeus dimiserit illud qui per se usus est demonstrationibus ueris super omnem questionem de questionibus huius scientiae, donec ipse ad hoc peruenit, ut excitaret super hoc, quod tempus quod est ab initio eclipsis ad medium eius, est maius tempore, quod est a medio eius usque ad finem ipsius, et aequauit illud, et non dimisit expergefacere super illud, quamuis sit ualde parum, quod sensus non comprehendit. Quomodo ergo potest esse, ut qui hac subtilitatis quantitate subtiliatus est, et expergefecit experfecit ed. super hanc rem uilem, quae non intromittit nocumentum in aliqua rerum, neque sentitur, dimitteret rem in qua exiret ad falsitatem, et ut indicaret casum rei qui penitus non eueniet, et quam uisus detegit, et fuit ei possibile peruenire ad uerificandum per leuiorem inquisitionem, hoc est ergo de eo in quo non dubitat, qui facit uincere concessionem, et dimittit contrarietatem et diuersitatem, quoniam haec res ignota fuerit ei et non sciuit eam, et praecipue, quia nos inuenimus in libro eius intentiones fuisse ei ignotas, quae sunt propinquiores hac multum. Laudatus sit ergo singularis perfectus, cuius gloria est gloriosa et fama sublimis. Et de eis quae remanserunt nobis ad declarandum, est, quomodo sciatur ex quantitate quae eclipsatur de diametro, quantitas quae eclipsatur de facie eclipsati, et illud quidem declaratur secundum hunc modum. Ponam circulum magnum qui est super sphaeram corporis lunae circulum d t b e in circuitu 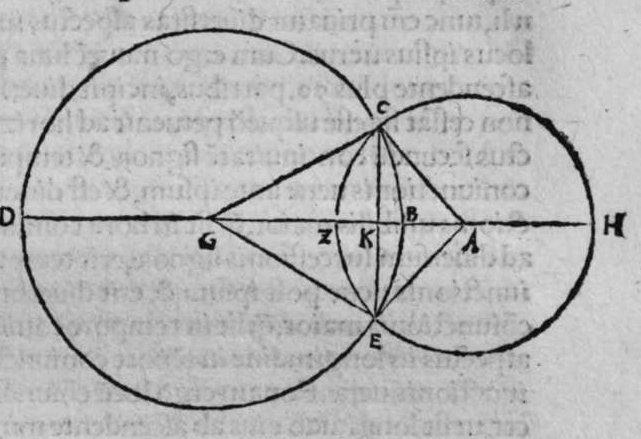centri g, et circulum solis in eclipsi solari, et circulum umbrae in eclipsi lunari circulum t h e in circuitu centri a, et sit linea a g transiens per duo centra horum duorum circulorum in medio tempore eclipsis solaris aut lunaris, et sit portio eclipsata de corpore solis aut corpore lunae existens illa, quam continent duo arcus t z e et t b e. Dico ergo, quod cum linea z b quae est illud quod eclipsatum est de diametro, fuerit nota, tunc area huius portionis, quem continent duo arcus e z t, e b t erit nota per quantitatem qua erit circulus eclipsati notus. Producam ergo lineam t e, ergo erit perpendicularis super lineam a g, et continuabo unumquodque duorum punctorum cum duobus centris duorum circulorum per lineas t g, e g, t a, a e, propterea ergo quod unaquaeque duarum linearum g t, a t est nota per quantitatem unam, erit mensuratio cuiusque duorum circulorum earum nota per quadratum illius quantitatis. Et si nos diuiserimus superfluitatem quadratorum eorum super lineam a g notam, exibit inde superfluitas quae est inter duas lineas g k, a k, erit ergo haec superfluitas nota. Sed tota linea a g est nota, ergo erit unaquaeque duarum linearum g k, a k nota per illam quantitatem, per quam unaquaeque duarum linearum g t, a t est nota, et angulus g k t est rectus, ergo erit propter illud linea k e nota per illam quantitatem, ergo duplum eius quod est linea e t est notum per eam, ergo unusquisque duorum triangulorum t g e, t a e est notus per quadratum illius quantitatis, quod est quadratum per quod unaquaeque superficies duorum circulorum est nota, et quoniam linea e t est nota per illam quantitatem, per quam unaquaeque duarum medietatum diametrorum duorum circulorum est nota, erit unusquisque duorum arcuum t b e et t z e notus, ergo unusquisque duorum sectorum t g e b et t a e z erit notus per illam quantitatem, per quam unusquisque duorum circulorum est notus, et iam fuit unusuquisque duorum triangulorum t g e et t a e notus per eam, ergo remanet unaquaeque duarum portionum t z e k et t b e k nota, ergo portio tota est nota, ergo proportio superficiei huius portionis ad superficiem circuli eclipsati de duobus circulis t d e, t h e est nota. completa est eius declaratio. IN eclipsibus uero solaribus comprehensio quantitatum eclipsati, et quantitatum temporum eclipsis earum est propter comprehensionem arcus transeuntis per duo centra duorum lunarium quae uidentur, scilicet per coniunctionem uisibilem, et illud quod erit per hoc, ut aequemus ex tempore coniunctionis uerae et loco eius tempus coniunctionis uisibilis et locum in regione in qua queritur illud, et loca lunae uera in longitudine et latitudine, et diuersitate ad illam coniunctionem uisibilem, et illa quidem aequatio eget explanatione explanitione ed. per illud quod narro. Sit itaque circulus b z e g circulus horizontis, et zenith capitis ad illum horizonta 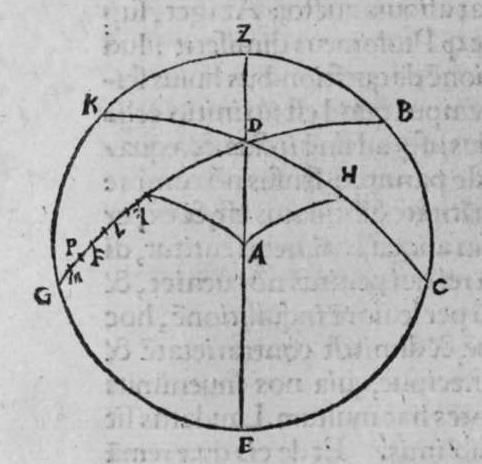sit punctum a, et linea meridiei sit linea z a e, et sit unusquisque duorum arcuum b d g et t d kmedietas circuli orbis signorum, et sit ascendens in hora coniunctionis uerae unum duorum punctorum g et k, et faciamus transire super duos polos cuiusque duorum arcuum b d g et t d k, et super zenith capitis duos arcus duorum circulorum magnorum qui sint duo arcus a n, a h, unumquodque ergo duorum punctorum h n diuidit medietatem circuli sui in duo media. Si ergo fuit locus coniunctionis uerae super unum duorum arcuum g n, h k, scilicet, si fuerit longitudo eius ab ascendente minus 90. partibus, tunc diuersitas aspectus in longitudine cadet ad successionem signorum. Et si fuerit super unum duorum arcuum b n, h t, scilicet, si fuerit longitudo eius ab ascendente plus 90. partibus, tunc diuersitas aspectus in longitudine cadet ad diuersum successionis signorum, et diuersitas quidem aspectus in longitudine cum fuerit super horizonte orientali, erit maior quae est, et non cessat minorari cum eleuatione lunae per motum totalem usquequo peruenit luna ad medietatem coeli ascendens, scilicet ad unum duorum punctorum n h, tunc enim priuatur diuersitas aspectus in longitudine, et fit locus lunae uisibilis, ipse idem locus ipsius uerus. Cum ergo mouetur luna per motum totalem, et sit longitudo eius a parte ascendente plus 90. partibus, incipit diuersitas aspectus magnificari per motum totalem, et non cessat sic esse usquequo peruenit ad horizonta occidentalem. Et si ceciderit diuersitas aspectus secundum continuitatem signorum, et tempus quidem coniunctionis uisibilis antecedit tempus coniunctionis uerae ante ipsum, et est diuersitas aspectus in longitudine in hora coniunctionis uisibilis maior, quam sit in hora coniunctionis uerae. Et si ceciderit diuersitas aspectus ad diuersum successionis signorum, erit tempus coniunctionis uisibilis posterius tempore coniunctionis uerae post ipsum, et erit diuersitas aspectus in longitudine in tempore uisibilis coniunctionis maior, quam sit in tempore coniunctionis uerae. Erit ergo propter illud diuersitas aspectus in longitudine in tempore coniunctionis uisibilis maior semper quam sit in tempore coniunctionis uerae. Ponam ergo locum coniunctionis uerae secundum unam duarum positionum, scilicet, ut sit longitudo eius ab ascendente minus 90, aut sit longitudo eius ab ascendente plus 90. et sit sicut super arcum n g, et sicut ipsa sit punctum l, et sit diuersitas aspectus eius in longitudine arcus l m, et locus eius uisibilis punctum m, et locus uisibilis solis punctum r, et diuersitas aspectus in longitudine arcus l r, et uolo scire punctum orbis signorum in quo cum luna fuerit, uere sit per uisionem super punctum r. Cum ergo acceperimus diuersitatem aspectus lunae totalem ad punctum l, et eiecerimus ex ea diuersitatem aspectus solis totalem, et aequauerimus ex residuo diuersitatem aspectus lunae in longitudine, erit illud arcus m r. Si ergo separauerimus ex latere puncti l arcum aequalem arcui r m ad contrarium parti eius, quasi ipse sit arcus l c, erit arcus c r aequalis arcui l m, qui est diuersitas aspectus eius in longitudine, tunc si imaginauerimus lunam super punctum c, et si esset diuersitas aspectus eius in puncto c aequalis diuersitati aspectus in puncto l, qui est arcus l m, esset locus eius uisibilis super punctum r, et esset illud quod uoluimus, sed diuersitas aspectus eius in puncto c est maior quam ipsa sit in puncto l, sit ergo quasi ipsa sit arcus c p, iam ergo addidit super intentionem nostram arcum r p. Si ergo separauerimus ex latere puncti c arcum aequalem arcui r p, qui sit arcus c q, erit arcus r q aequalis arcui p c. Si ergo imaginauerimus lunam super punctum q, tunc si esset diuersitas eius in puncto q aequalis diuersitati aspectus eius in puncto c qui est c p, esset locus eius uisibilis punctum r, et esset illud nostra inquisitio, sed diuersitas aspectus eius in puncto q est maior quam ipsa sit in puncto c. Sit ergo diuersitas aspectus eius in puncto q ipse arcus q f, si ergo addiderimus ad arcum q r arcum aequalem arcui r f, si fuerit sensatus g, et posuerimus illud super punctum q, sicut ipse sit arcus s q, erit fere punctus s existens punctum quaesitum, et est illud super quod cum fuerit luna per ueritatem, erit per uisionem super punctum r, quod est locus solis uisibilis, erit ergo punctum r ipse locus coniunctionis uisibilis. Et rememoremur hic operationis in hac eclipli solari, ut explanetur per eam illud quod diximus, et fiat facilis eius intellectus, et declaretur per eam iterum illud, in quo errauit Ptolomeus in operatione sua quam dixit ei, et in terminatione temporum eius. Dico ergo, in primis inuenimus diuersitatem aspectus lunae totalem in hora coniunctionis uerae, et proijciamus ex ea diuersitatem aspectus solis, et ex eo quod remanet, scimus diuersitatem aspectus lunae in longitudine quae est arcus r m huius figurae, diuidemus ergo eam per motum lunae uerum in hora coniunctionis uerae, et quod prouenerit de temporibus horarum considerabimus, tunc si diuersitas aspectus in longitudine ceciderit ad successionem signorum, et iam praecessit discretio eius, minuemus illa tempora de tempore illius coniunctionis uerae. Et si ceciderit ad diuersum successionis signorum, addemus super tempus illius coniunctionis uerae, et quod fuerit post additionem et diminutionem de horis, inueniemus per illud diuersitatem aspectus lunae in longitudine secundo, quae est arcus c p. Accipiemus ergo superfluitatem quae est inter duas diuersitates aspectus qui est arcus r p, et sciemus in quanto tempore secat luna per motum suum uerum arcum p r, et addemus illa tempora super tempus in quo luna est super punctum c, aut minuemus illa ex eo secundum quod dat illud longitudo coniunctionis uerae a parte ascendente in illa hora, et quod fuerit ex temporibus, inueniemus per illud diuersitatem aspectus in longitudine tertio, et erit illud arcus q f, et accipiemus superfluitatem inter ipsum et inter arcum diuersitatis aspectus puncti c, qui est aequalis arcui q r, et erit illud arcus r f. Adiungemus ergo illud ad ipsum partem eius, si fuerit sensata sicut pars eius ex arcu r p, et addemus illud super arcum q r, et erit illud arcus s r, erit ergo punctum s existens secundum propinquitatem punctum super quod cum fuerit luna per ueritatem, erit per uisionem super punctum r. Cum ergo sciuerimus hoc punctum scilicet arcum s r, diuidemus ipsum per motum lunae uerum in hora illius coniunctionis uerae, et quod exierit de temporibus considerabimus, tunc si diuersitas aspectus in longitudine fuerit ad successionem signorum, minuemus illa tempora de tempore coniunctionis uerae, et si fuerit ad diuersum successionis signorum, addemus ea super ipsum, et quod fuerit post additionem aut diminutionem, erit tempus coniunctionis uisibilis. Sciemus ergo loca lunae in longitudine et latitudine et diuersitate ad illud tempus, ergo sciemus inde latitudinem eius ueram et diuersitatem aspectus eius in latitudine, et sciemus ex latitudine eius uisibili quantitatem eius quod est inter duo centra in medio temporis eclipsis, deinde sciemus ex loco lunae in orbe reuolutionis suae quantitatem medietatis diametri lunae, et adiungemus eam ad medietatem diametri solis, et accipiemus superfluitatem inter illud quod fuerit, et inter illud quod inuenimus inter duo centra in medio temporis eclipsis, et quod fuerit, erit quod eclipsatum est de diametro solis. Sciemus ergo ex illo, quod eclipsatum est de facie ipsius secundum quod praemissum est, et similiter sciemus iterum ex eo quod est inter duo centra in medio temporis eclipsis, et ex aggregatione duarum medietatum duarum diametrorum arcum, qui est ab initio eclipsis ad medium eius, et a medio eius ad finem ipsum secundum quod praemissum est. Addemus ergo super ipsum partem eius 12. quae est illud quod perambulat sol donec consequatur ipsum luna, et quod fuerit, erit arcus quem perambulat luna per motum suum uisibilem ab initio eclipsis ad medium eius, et a medio eius usque ad finem ipsius. Et propterea quod diuersitas aspectus lunae in longitudine diuersificatur in temporibus eclipsis tribus, scilicet principio eius et ipsius medio et fine eius, oportet propter illud, ut sit motus lunae uisibilis ab initio eclipsis ad eius medium inaequalis motui eius uisibili a medio eius ad ipsius finem, et propterea quod isti duo arcus sunt aequales, et motus lunae in eis est diuersus, oportet ut sit tempus quod est ab eius initio ad ipsius medium diuersum tempori quod est ab eius medio ad ipsius finem. Ostendam ergo qualiter inueniatur unumquodque horum duorum temporum secundum ultimam ueritatem quam super illud possumus, et exemplificemus exemplum ad illud, ut sit demonstratio super illud manifestior. Sit itaque portio orbis otbis ed. decliuis arcus a b, et punctum a sit locus lunae uisibilis in initio eclipsis, et punctum e sit locus eius in medio ipsius, et punctum b sit eius locus in ipsius fine, et sit sol in medio eclipsis super punctum d, et in eius initio super punctum t, et in ipsius fine super punctum k, et unusquisque duorum arcuum a t et b k est aggregatio duarum medietatum duarum diametrorum duorum lunarium, et propterea quod ipsi ambo fere sunt aequales, sunt duo arcus a e et e b aequales, et diuersitas aspectus lunae in longitudine in initio eclipsis arcus a z, et in medio eius arcus e h, et sunt ambo diuersi, ergo erit luna per ueritatem super duo puncta a et e, et per uisionem super duo puncta 3 et h, ergo in tempore in quo luna perambulat arcum z h per uisionem, secat per ueritatem arcum a e, et superfluitas quae est inter duos arcus a e et z h, est superfluitas inter duos arcus a z et h e, qui ambo sunt duae diuersitates aspectus in longitudine. Si ergo ceciderit diuersitas aspectus in longitudine ad successionem signorum, consequitur ut sit diuersitas aspectus in initio eclipsis maior quam sit in eius medio, erit ergo propter illud arcus z h maior arcu a e, quamobrem erit motus uisibilis tardior uero. Et si ceciderit diuersitas aspectus ad diuersum successionis signorum, erit diuersitas aspectus in initio eclipsis minor quam in eius medio, erit ergo iterum arcus z h maior arcu a e, ergo erit motus uisibilis semper tardior motu uero, et hoc idem consequitur in arcu e b, quod si nos acceperimus superfluitatem inter duos arcus a z et e h, et addiderimus eam super arcum a e, erit illud arcus z h. Diuidemus ergo illud super motum lunae uerum, et quod exibit, erit tempus in quo luna secat per motum uisibilem arcum a e, et simile illius eiusdem accidit in arcu e b, ita, ut addamus superfluitatem inter duas diuersitates aspectus in duobus punctis e et b super arcum e b, et propterea quod superfluitas diuersitatis aspectus in longitudine est maior, quae est apud medium coeli ascendens, et minor, quae est apud partem ascendentem aut occidentem, et hoc declaratur ex eo quod diximus in superfluitate angulorum diuersitatis quae est propter ecentricum, tunc oportet si fuerit in tempore eclipsis totius longitudo lunae a parte ascendente minor 90. partibus, ut sit tempus casus in eclipsi minus tempore reditionis. Et si fuerit longitudo eius in ea ab ascendente plus 90. erit res econtrario, scilicet quod erit tempus casus in eclipsi maius tempore reditionis repletionis. Et cum fuerit luna in medio eclipsis in medio coeli ascendens, tunc erunt duo tempora aequalia, et non est res secundum quod dixit Ptolomeus, et illud est, quia ipse dixit: Si fuerit medium temporis eclipsis in hora meridiei, erunt duo tempora aequalia, et haec est error, quoniam quandoque est inter partem mediantem coelum et inter partem que est in medio coeli ascendens in regione septentrionali arcus cui est quantitas, et peruenit summa eius in climate septimo circa 37. partes. Si ergo fuerit luna in eclipsi in hoc arcu, et fuerit post meridiem longitudo eius ab ascendente minor 90. aut ante meridiem, et longitudo eius ab ascendente maior 90. erunt tempora in magnitudine et paruitate, tunc secundum diuersum quod dixit, et similiter illud quod dixit de additione temporum quae pertinet arcubus diuersitatum aspectus in longitudie semper super longitudinem temporis coniunctionis uerae a circulo meridiei ante ipsum uel post ipsum, est error, quia non pertinet ei illud semper, nisi in eclipsi in qua est ascendens a capite arietis aut librae, tunc enim pars medians coelum est medium coeli ascendens. Cum autem fuerit ascendens praeter haec duo puncta, erunt istae duae partes alteratae. Quod si fuerit coniunctionis locus uerae inter istas duas partes, et est quod sit ante meridiem et eius longitudo maior 90. post meridiem, et longitudo eius ab ascendente minor 90. tunc consequitur, ut minuantur tempora quae pertinent diuersitati aspectus in longitudine de temporibus longitudinis quae est coniunctionis uerae a circulo meridiei, et ipse addit ea, ergo accidit ex illo errore in tempore coniunctionis uisibilis diuersitas, cui est quantitas, quoniam diuersitati aspectus in longitudine in regione septentrionali, est tunc quantitas bona. Accidit ergo diuersitas in tempore coniunctionis uisibilis per illud quod pertinet de tempore duplo diuersitatis in longitudine, et similiter est eius intentio iterum in determinatione partis diuersitatis aspectus lunae in latitudine, ut inueniat ex ea latitudinem lunae uisibilem, et illud est, quia dicit, si fuerit diuersitas aspectus in latitudine ab eo quod sequitur septentrionem ab orbe signorum considerabimus. Si ergo fuerit luna uersus nodum capitis, addemus, et si fuerit uersus nodum caudae, minuemus, et si fuerit aspectus diuersitatis in latitudine ab eo quod sequitur meridiem ab orbe signorum, faciemus contrarium illius, ergo addit diuersitatem aspectus in latitudine in hoc loco ad orbem signorum, et non oportet ut addat eam nisi ad lunam ipsam, non ad orbem signorum, et ingreditur inde in partes quae sunt longitudo a nodo, diuersitas ergo ego ed. sit ingressus in tabulas cum minori et maiori eo, cum quo oportet ut ingrediatur secundum ueritatem. Sequitur ergo inde, ut sit in latitudine latitudind ed. eius uisibili, et est illa quae inuenitur coram eo, cum quo fit ingressus in tabulas diuersitas plurima, et similiter erit iterum in partibus casus in eclipsi et reditione impletionis et propter hoc excitauimus super illud in hoc loco. Et ex eo quod remansit de esse eclipsium est ut sciamus punctum horizontis oppositum puncto obtenebrato in unaquaque hora temporum, scilicet temporum trium eclipsis solis, et temporum quinque eclipsis lunae, et hoc quidem punctum est quod prouenit a sectione circuli horizontis cum circulo transeunte per duo centra duorum lunarium in unaquaque hora horum temporum. Ptolomeus enim inuenit hoc punctum per uiam in ultimo a ueritate longinqua, et pertransit in illo pertransitione qua esset ei melius ne eius rememoraretur, et ut liber eius penitus ex ipso uacuaretur, et esset simile de eo, et casus eius ex libro ipsius leuius ei quam illud per quod apparet illud quod est de debilitate eius in Geometria, et ipsius ignorantia in ea, et illud est, quoniam non sufficit ei quod usus est in illo erectione linearum rectarum et angulorum earum loco arcuum et angulorum eorum, donec ipse posuit angulum quem continet orbis signorum, et arcus transiens per duo centra, unum semper siue sit apud zenith capitis, siue apud horizonta, et eguit in illo tabulis et circulis, et prolongauit in illo prolongatione horribili, et est possibile peruenire ad illud faciliori labore et propinquiori acceptione secundum hunc modum. Sit horizon circulus a b g d, et medietas orbis signorum a h e g, et punctum 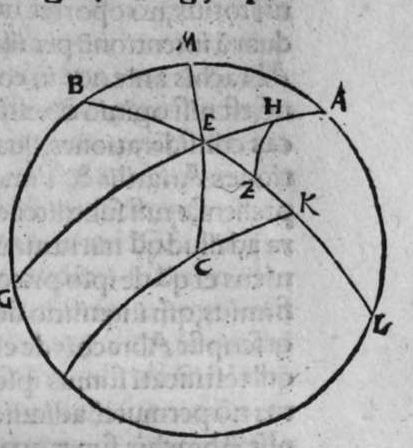e eius centrum solis, aut centrum circuli umbrae in aliqua horarum temporum eclipsis praedictorum, et centrum lunae in illo punctum z, et latitudo eius uera arcus z h, et arcus circuli transeuntis per duo centra, scilicet centrum lunae et centrum solis in eclipsi solari, aut centrum lunae et centrum circuli umbrae in eclipsi lunari arcus l z e b. Volo autem scire in hac hora posita ex horis eclipsis longitudinem puncti b oppositi eclipsato ex luna, aut puncti l, et est oppositum eclipsato ex sole ab uno punctorum 4. quae sunt super horizonta, et sunt illa quae signat circulus aequatoris diei, et circulus meridiei, scilicet duo puncta medij orientis et occidentis, et duo puncta meridiei et septentrionis. Sit itaque zenith capitis punctum t, et sit arcus t k erectus super semicirculum l k b orthogonaliter, et faciam penetrare arcum t e m per zenith capitis et per centrum solis, scilicet punctum e, et secet horizonta super punctum m, propterea ergo quod triangulus z h e est ex arcubus circulorum magnorum, et angulus eius h est rectus, erit proportio sinus lateris eius e z ad sinum lateris z h, sicut proportio sinus arcus anguli h eius ad sinum anguli eius e, uerum unumquodque duorum laterum eius e h et z e est notum, quoniam latus z h est latitudo lunae, et latus z e est illud quod est inter duo centra in hora posita ex horis eclipsis, et angulus eius h est rectus. Oportet ergo ut sit sinus arcus anguli eius e notus, et ipse est minor recto, quoniam arcus z h subtensus ei est minor quarta circuli, ergo angulus est notus, et angulus t h e est notus, quoniam punctum e orbis signorum, et est locus solis, est notus, erit ergo angulus k e t notus, et angulus k est rectus, et latus e t trianguli t k e est notum. Est ergo propter illud arcus t k notus, et arcus t d est quarta circuli, ergo arcus k t d est notus, et punctum b est polus eius, ergo angulus b est notus, angulus ergo e b m est notus, et proportio sinus eius ad sinum arcus anguli b e m noti, est sicut proportio sinus lateris e m ad sinum lateris b m. At latus e m est notum, quoniam arcus e t est notus, ergo latus b m est notum, et propterea quod latus e g trianguli e m g est notum, et angulus m est rectus, et angulus g e m est notus, tunc latus m g est notum, et longitudo puncti g ex propinquioribus punctis ad ipsum ex 4. punctis est nota, cum punctum g horizontis positi sit eleuatio puncti g orbis signorum quod est notum, ergo latitudo puncti b ab uno duorum punctorum 4. est nota, et similiter scitur iterum trianguli a e l latus a l, ergo longitudo puncti l, et est oppositum eclipsato ex sole a puncto a, et est occasus partis occidentis orbis signorum nota, et longitudo puncti a in horizonte posito ab uno 4. punctorum est nota, ergo longitudo puncti l ab illo puncto est nota, et illud est cuius uoluimus declarationem.

⟨VI⟩ LIBER SEXTVS. DE STELLIS FIXIS.

QVod stellae fixae sunt communicantes proprietates suorum locorum cum quantitate spacij unius semper inter se ad inuicem, inquit Ptolomeus, et postquam narrauimus in eis quae praecedunt hunc sermonem illud quod accidit in sphaera recta, et in sphaera sqhaera ed. decliui, et iterum quod accidit in partibus motuum solis et lunae, et quod uidetur in eis de figuris secundum quod oportet, tunc incipiamus nunc secundum quod simile est ei de ordinatione ordinum qui se adinuicem sequuntur in hac scientia loqui in stellis, et propter illud quod conuenit ex ordine, incipiamus prius loqui in stellis quae nominantur fixae, non haesitantes, et ante omnem rem praemittamus earum nominationem. Propterea quidem, quod stellae omnes uidentur comitari semper figuras suas fixis spacijs quantitatum, quae sunt inter eas simili motu aequali, tunc bonum est, ut nominentur fixae, non motae, et propterea quidem, quod tota sphaera earum in qua sunt ceu solidata et orta, uidetur habere motum localem sibi appropriatum cum mensuratione una ad successionem signorum ad orientem econtrario motui totius, non oportet, ut nominetur sphaera fixa immobilis, ita inuenimus unamquanque harum duarum intentionum per illud quod uidimus in hoc tempore longo, et per illud quod aestimauit Abrachis ante nos in eo quod uidit in istis duabus intentionibus intentionihus ed. in longitudine temporis, quod non est nisi opinio et aestimatio, et non est comprehensum, quoniam ipse non inuenit nisi ualde paucas considerationes, quae fuerunt ante ipsum stellarum fixarum non haesitantium, scilicet considerationes Arsatilis et Timonialis scriptas tantum, et istae quidem considerationes non fuerunt comprehensae nisi subtiliter exquisitae, et nos iterum comparauimus, quod testificati fuimus in hac hora ad illud quod narratur in illa hora, et fuit illud super quod stetimus de scientia illius conueniens ei quod de ipso praecessit. Veruntamen illud super quod stetimus de illo nunc fit certius et firmius, quoniam inquisitio de eo cecidit ex tempore longo, et quoniam illud quod cecidit nobis ex eo quod scripsit Abrachis de esse stellarum fixarum, et est illud ad quod proprie comparauimus illud quod testificati sumus ipse perscrutatus est ultima perscrutatione. Verum quod stellarum fixarum situs non permutetur adinuicem, etiam usque ad hanc horam manifestum est, imo figurae earum quas scripsit Abrachis, super quas stetit per considerationem, inueniuntur in hac hora etiam illae eaedem figurae, in quibus non est diuersitas, et non est conuenientia in illo, quod non est nisi in hoc tantum scilicet in figuris stellarum quae sunt in orbe signorum adinuicem, aut in figuris stellarum egressarum ab eo per comparationem ad illas quae sunt secundum huiusmodi dispositionem, et illud est quod sequeretur si res curreret secundum radicem primam quam narrauit Abrachis, quod stellae, quae sunt in ipso orbe signorum line alijs permutantur occurrendo motui totius, imo conuenientia ex eo inuenitur iterum in figuris stellarum quae sunt in orbe signorum, quando comparantur cum stellis quae sunt extra ipsum longinquae ab eo. Iam ergo facile scire illud omni quod elegit, ut enunciet in hac inquisitione, et utatur in ea ratiocinatione cum cautela ueritatis, et sciat an illud quod uidetur in hac hora sit conueniens quod scripsit Abrachis. Verumtamen nos ponemus in hac intentione quaerentes facilitatem in experientia et probatione parum ex eo, quod ipse scipsit de illo, cuius intellectus proprie est facilis, et est possibile ipsum scire secundum comparationem omnem, ita, ut uideantur species figurarum, quas continent stellae quae sunt extra orbem signorum, conuenientes ad conseruationem formarum suarum adinuicem, et apud illas quae sunt in orbe signorum. Dico ergo, quod ipse scripsit scipsit ed. de stellis quae sunt in cancro, quod stella quae est in meridiano labio cancri, et stella lucida quae antecedit istas, et antecedit caput serpentis audacis, et stella lucida ex stellis quae sunt in cane, pertinente ad antecessionem, sunt proxime ad hoc, ut sint secundum rectitudinem, inquit: Nam media earum non recedit a linea recta quantum sit per duas extremitates uersus septentrionem et meridiem, nisi digito uno et medietati digiti, et duae longitudines inter utrasque sunt aequales. Et scripsit de stellis quae sunt in leone, quod duae 4. stellarum, quae sunt in capite leonis, quae sunt ab eo quod sequitur orientem, et stella quae est in origine duorum brachiorum audacis sunt secundum rectitudinem, et iterum, quod linea quae transit super caudam leonis, et super stellam, quae est in extremitate caudae ursae, pertransit a parte occidentis stellam lucidam quae est sub cauda ursae, et inter illam et eam est digitus unus. Et similiter iterum, quod linea recta quae transit super stellam, quae est sub cauda ursae, et super caudam leonis continuat inter duas stellas antecedentes ex stellis quae sunt in terra. Et scripsit de stellis quae sunt in uirgine in eo quod est inter duos pedes uirginis septem, et inter duos pedes alangue dextros duas stellas, quarum una et est meridiana lucida similis pedi, recedit a linea recta quae transit per duos pedes uersus orientem, et septentrionalis quidem earum quae est super extremitatem digitorum, est super rectitudinem duorum pedum. Nam antecedunt stellam ex his duabus stellis quae est super extremitatem digitorum duae stellae lucidae, facientes cum stella quae est super extremitatem digitorum trianglum duorum dnorum ed. aequalium crurium, cuius caput stella quae est super extremitatem digitorum, et istae duae stellae sunt secundum rectitudinem Asimek arami et pedem meridianum uirginis. Et scripsit iterum in eo quod est inter Azimek Alahazel et inter stellam secundam etremitatis caudae audacis sunt tres stellae positae secundum rectitudinem adinuicem, et media earum est secundum rectitudinem Azimek arami et stellae secundae extremitatis caudae audacis. Et scripsit in stellis quae sunt in libra, quod stella ex eis quae in septentrione est secundum propinquitatem rectitudinis duarum stellarum luminosarum quae sunt in duabus lancibus, et est stella luminosa tripla, et illud est, quoniam super unumquodque duorum laterum eius est stella parua. Et scripsit in stellis quae sunt in scorpione, quod linea recta quae transit super stellam duarum stellarum quae sunt in fronte scorpionis, et super genu dextrum latoris serpentis Alangue, diuidit in duo media spacium in eo quod est inter duas stellas antecedentes in pede dextro latoris serpentis, et quod nodus quintus est secundum rectitudinem stellae lucidae quae est in medio latoris, et quod decliuior duarum stellarum quae sunt in basi latoris ad septentrionem, est in medio secundum propinquitatem rectitudinis spondilis quintae, et stellae quae est in medio latoris, et longitudo quae est ab unaquaque eius earum est prope aequalitatem. Et scripsit in stellis quae sunt in sagittario, quod in eo quod sequitur orientem et meridiem circuli, qui est sub sagittario, sunt duae stellae lucidae, inter quas est spacium quasi trium cubitorum, et quod decliuior harum duarum stellarum ad meridiem et earum luminosior, et est super pedem sagittarij, est secundum propinquitatem rectitudinis stellae mediae trium stellarum manifestarum in circulo in quo sunt positae ab eo quod sequitur orientem proprie et stellae secundae duarum stellarum lucidarum, quae sunt super duos angulos oppositos in quadri latero, et quod spacia inter utrasque sunt aequalia, sed septentrionalis earum recedit ab hac linea uersus orientem, uerum secundum rectitudinem duarum stellarum lucidarum quae sunt super duos angulos oppositos in quadrilatero. Et scripsit in stellis quae sunt in aquario, quod duae compares quae sunt in capite equi et humero secundo effundentis, sunt super lineam propinquam rectitudini, et aequedistat huic lineae linea quae egreditur ex humero antecedente effundentis ad stellam quae est in mandibula equi, et iterum, quod humerus antecedens effundentis, et luminosior duarum stellarum quae sunt in oculo equi, et stella quae est in summitate equi, sunt secundum rectitudinem, et duo spacia inter utrasque sunt aequalia, et quod linea recta quae transit super musidam equi, et super stellam quae est ab eo quod sequitur orientem ex illis quatuor alangue, secat lineam quae transit per duas stellas compares, quae sunt in capite equi in duo media et orthogonaliter secundum propinquitatem. Et scripsit in stellis quae sunt in duobus piscibus, quod stella quae est in musida piscis meridiani, et stella lucida quae est in duobus humeris equi, et stella luminosa quae est in pectore eius, sunt secundum propinquitatem rectitudinis. Et scripsit in stellis que sunt in ariete, quod antecedens stellarum basis trianguli uersus orientem separatur digito uno a linea recta quae transit super stellam, quae est in musida arietis et super pedem sinistrum mulieris, et iterum quod duae stellae antecedentes ex stellis quae sunt in capite arietis, sunt secundum rectitudinem praeparationis basis trianguli. Et scripsit iterum in stellis quae sunt in capite tauri, quod duae stellae quae sequuntur orientem ex lateribus formae, quam Graeci nomine literae Alpha in lingua sua, et haec est eius forma et stella sexta ex stellis iaculi, et illa quae est in manu audacis sinistra, quando eius stellae numerantur ex parte meridiei sunt snnt ed. secundum rectitudinem, et quod linea liuea ed. recta quae transit super stellam antecedentem oculi tauri, et super stellam septimam ab eo quod sequitur meridiem ex stellis quae sunt in iaculo, pertransit stellam luminosam ex stellis formae similis literae laude nominatae Aldebaran, ad partem inferiorem inter eam et inter ipsam digito uno. Et scripsit in stellis quae sunt in geminis, quod secundum rectitudinem capitis geminorum sunt duae stellae diuersae super caput secundum ex capitibus eorum per triplum spacij quod est inter duas mulieres, et quod haec eadem stella est iterum secundum rectitudinem duarum stellarum meridionalium ex stellis 4. quae sunt in uolutabro. Nihil ergo horum et quae eis simulantur ex figuris quae comprehendunt comparationem inter loca stellarum in plurimo duarum partium sphaerae totius, inuenimus nos usque ad hoc ultimum alterari, et accideret quidem ita, quod sensus consequeretur illud comprehensione manifesta in hoc toto spacio temporis quod fuit inter nos et Abrachis, et eius summa est 200. et circiter 60. anni, si non mouerentur ex stellis uersus orientem, nisi stellae quae sunt in orbe signorum sine alijs. Et ut dimittamus eis qui prouenient post nos quo experiatur illud in tempore longo propter figuras compares illis quas diximus ex eo quod est plus et laboriosius quam illud quod diximus ex eis, addemus ad illud quod narrauimus aliquid, cuius non rememorati sunt illi qui praecesserunt nos. Veruntamen nos continuabimus eius cosiderationem propinquius et facilius, quod possibilis est eius intellectus et scire ipsum, et incipiemus a stellis quae sunt in ariete. Dico ergo, quod duae stellae septentrionales quae sunt ex stellis tribus, quae sunt in capite arietis, et stella lucida quae est in genu meridiano delatoris caput noctuae, et stella nominata alaiot sunt super lineam rectam, et iterum linea recta quae transit super nominata alaiot, et super aldebaran pertransit stellam quae est in pede ante retinentis habenas, et inter ipsam et illam est res modica. Et stella nominata alaiot et algofe, et stella communis pedi retinentis habenas tertia et extremitati cornu septentrionalis tauri, et stella quae est in humero antecedente superbi sunt super lineam rectam, et iterum duae stellae lucidae quae sunt in capite geminorum, et stella luminosa quae est in collo serpentis audacis, sunt secundum propinquitatem rectitudinis. Et iterum duae stellae compares quae sunt in pede antecedente ursae, et stella quae est super extremitatem labij cancri, septentrionalis, et septentrionalis asini, sunt super lineam rectam. Et similiter iterum superbus meridianus, et stella lucida quae est iussahare assenna, et stella lucida quae est inter utrasque, et est antecedens caput audacis, sunt secundum propinquitatem rectitudinis. Et iterum linea recta quae egreditur ex stella luminosa media stellarum, quae sunt in collo leonis ad stellam luminosam in audace pertransit illam quae est super cor leonis ab eo quod sequitur orientem, et inter eam et ipsam est res parua. Et linea recta quae egreditur ex stella luminosa, quae est in dente leonis ad stellam luminosam quae est in coxa secunda ursae, et stella meridiana latoris secundi quadrilateri pertransit duas stellas stelles ed. compares, quae sunt in pede tertio ursae ab eo quod sequitur occidentem, et inter ipsam et inter eas est res parua. Et iterum linea recta quae egreditur ex stella quae est in postremo coxae uirginis ad stellam secundam extremitatis caudae audacis, pertransit stellam nominatam azimek alahazel ab eo quod sequitur occidentem, et inter ipsam et eam est res modica. Et linea recta quae egreditur ex azimek alahazel ad stellam quae est in capite noctuae, pertransit pertansit ed. azimek alahazel. Et duae stellae quae sunt super duas alas corui sunt secundum rectitudinem, et stella quae est super coxam tertiam uirginis, est stella septentrionalis luminosa ex tribus stellis quae sunt in crure antecedente alangue, sunt secundum rectitudinem. Et iterum duae stellae luminosae quae sunt in duabus lancibus librae, et stella quae est in extremitate caudae audacis, sunt secundum propinquitatem rectitudinis, et stella luminosa quae est lanx meridiana et azimek arami, et stella media trium quae sunt in cauda ursae maioris, sunt secundum rectitudinem, et iterum stella luminosa quae est in lance septentrionali et azimek arami, et stella quae est in coxa tertia ursae, sunt secundum rectitudinem. Et iterum stella quae est super acutum cruris tertiae latoris serpentis, et stella quae est in spondili quinta scorpionis, et stella antecedens duarum stellarum comparium quae sunt in aculeo, sunt secundum rectitudinem. Et stella antecedens ex stellis tribus quae sunt in pectore scorpionis cum duabus stellis quae sunt in duobus genibus latoris serpentis, facit triangulum duorum aequalium crurium, cuius caput est stella antecedens ex stellis quae sunt in pectore scorpionis, et iterum stella quae est super calcaneum antecedentem meridianum sagittarij, et est magnitudinis secundae, et stella quae est super hastulam sagittae, et stella quae qnae ed. est in genu tertio latoris serpentis, sunt secundum rectitudinem. Et stella quae est in genu huius pedis eiusdem sagittarij est prope alfetati, et stella quae est super hastulam sagittae, et stella quae est in genu antecedente latoris serpentis, sunt secundum rectitudinem. Et iterum linea recta quae continuat inter stellam luminosam ex stellis coclearis, et est uultur cadens, et inter duas stellas quae sunt in cornu capricorni, pertransit stellam luminosam quae est in uulture uolante ab eo quod sequitur septentrionem, et inter ipsam et eam est res parua. Et iterum linea recta quae continuat inter stellam luminosam, quae est in uulture uolante, et inter stellam quae est in ore piscis meridiani magnitudinis primae diuidit spacium quod est inter duas stellas luminosas, quae sunt super caudam capricorni in duas sectiones propinquas aequalitati. Et iterum linea recta quae continuatur ex stella quae est in ore piscis meridiani magnitudinis primae ad stellam paruam, quae est in musida equi pertransit stellam luminosam, quae est in humero sequente effundentis. Et iterum duae stellae quae sunt in orificijs duorum piscium, et duae stellae antecedentes quadrilateri quod est in equo, sunt secundum rectitudinem. Veruntamen si quis uelit comparare has easdem figuras cum eo quod scripsit Abrachis de formis stellarum, quae sunt in sphaera connexa, inueniet loca earum nunc conuenientia secundum ultimum propinquitatis locis quae narrauit per illud quod considerauit in illa hora, et quod sunt eis ex sphaera quando figurantur.

⟨VI.1⟩ Quod sphaera stellarum fixarum ad successionem signorum moueatur.

QVod autem comparatio stellarum quae dicuntur fixae omnium absolute adinuicem sit una et eadem, et motus earum unus et idem ex istis rebus, et his similibus possibile est scire. Sed quod sphaera earum iterum habet motum proprium occurrentem motui totius, scilicet occurrentem motui qui fit per circulum magnum qui signatur transiens per duos polos simul, scilicet duos polos aequatoris diei, et duos polos orbis signorum, apparet nobis per illud quod ego narro proprie, et est, quod stellae unae et eaedem non seruant unam et eandem longitudinem in antiquo et in nostro tempore a duobus punctis duorum tropicorum, et duobus punctis duarum aequalitatum, sed semper in postremo tempore inuenitur earum longitudo secundum signorum continuitatem ab his eisdem punctis maior earum longitudine in illo quod praecessit in eo, et illud est quod Abrachis, propterea quod narrauit in sermone suo in duobus punctis duorum tropicorum, et duobus punctis duarum aequalitatum, eclipses lunae ex eis quas considerauit in diebus suis consideratione exquisita, et ex eis quas considerauit ante ipsum Timocaris, et inuenit per illud, quod longitudo Azimek alahazel a puncto aequalitatis autumnalis anterius secundum suum quidem tempus sex partes, et secundum tempus quidem Timocaris 8. partes fere. Ipse namque nanque ed. post omnia quae loquutus est in hoc capitulo, dixit sermonem hunc: Quia ergo fuit azimeck alahazel antecedens punctum autumnale in longitudine signorum prius 8. partibus, et in hac hora non antecedit ipsum nisi 7. partibus, et caetera quae sequuntur, tunc forsitan in reliquis stellis eadem comparatio amministratur, contingit iam separatae sunt occurrendo toti per quantitatem illius, et nos iterum postquam comparauimus illud quod sciuimus in nostro tempore de longitudinibus stellarum fixarum a duobus punctis duorum tropicorum, et duobus punctis duarum aequalitatum ad illud quod considerauit, et scripsit Abrachis: Inuenimus longitudines harum stellarum secundum continuitatem signorum accidere secundum ratiocinationem permutationis, cuius narratio praecessit, et non alterat eas omnino, et illud quo experti fuimus illud, ita, quod sciuimus ipsum, est instrumentum quod sumpsimus ad considerationes longitudinum lunae particularium a sole. Nam nos praeparauimus unam duarum armillarum, quas fecimus ad experientiam stellarum secundum quod exigebat, quod sciuimus in hora considerationis de cursu lunae qui uidetur, et reuoluimus armillam aliam ad stellam quam experiri uoluimus, donec uidimus per instrumentum lunam et stellam simul, scilicet unamquanque in loco suo in quo est. Scimus ergo per illud propter longitudinem lunae locum cuiusque stellarum luminosarum, et nos rememoramur ad illud exemplum unum. Dico ergo, quod in anno secundo annorum Antonij in mense eius ex mensibus Aegyptiorum nominato barmodhi, in nono die eus in hora occasus solis in Alexandria postrema parte geminorum, existente in medio coeli post medietatem iomin noni quinque horis et media aequalibus, considerauimus lunam secundum uisionem, et inuenimus longitudinem eius a sole, cum iam inuenissemus eam per instrumentum in tribus partibus piscis 92. partes et octauam partis, deinde comparauimus stellam quae est super cor leonis post medietatem horae, cum iam sol occubuisset, et mediasset coelum pars 4. geminorum, secundum quod luna per instrumentum fuit in illo eodem loco per uisionem, et inuenimus per unam duarum armillarum longitudinem eius a luna per uisionem in illa hora, propterea quod longitudo eius fuit secundum continuitatem signorum 92. partes et 8. partis, 5. partes et sextam partis fere geminorum, et illud est quod oportuit esse secundum principia nostra radicem eius ex partibus. Deinde post medietatem horae oportuit ut moueretur luna secundum continuitatem signorum circiter quartam partis, et ut separetur per diuersitatem aspectus sui anterius a locis suis uis ed. in quibus fuit prius fere parte 12. partis unius, fuit ergo radix lunae per uisionem post medietatem horae 5. partes et tertia geminorum, oportuit ergo iterum ut esset radix stellae, quae est super cor leonis, quia inuenimus longitudinem eius a luna secundum continuitatem signorum per uisionem 57. partes et 10. partis, duae partes leonis et medietas partis, et fuit longitudo eius a tropico aestiuo 32. partes et medietas partis. Verum in anno 56. reuolutionis tertiae ex reuolutionibus Philippi, dixit Abrachis in libro suo, quod ipse considerauit hanc stellam, et inuenit longitudinem eius secundum continuitatem signorum a puncto eiusdem tropici aestiui 29. partes et medietatem, et tertiam partis. Iam ergo elongatur stella quae est super cor leonis secundum secundnm ed. continuitatem signorum duabus partibus, et duabus tertijs partis, et anni aggregati ex hora considerationis Abrachis usque ad initium annorum Antonij, et est hora in qua fuit plurimum nostrae considerationis qua considerauimus cursus stellarum fixarum, sunt 265. anni. Colligitur ergo inde, ut sit remotio in omnibus 100. annis secundum propinquitatem, pars una secundum continuitatem signorum, secundum quod inuenimus Abrachis iterum aestimasse in eo quod ipse scripsit de quantitate anni, ubi dixit, quoniam propter istas causas duo puncta duorum tropicorum, et duo puncta duarum aequalitatum permutantur ad anterius signorum in anno non minus parte centesima partis unius, tunc per hoc oportet, ut in 300. annis non permutentur minus tribus partibus. Et secundum hunc modum, postquam probauimus azimek alahazel et luminosiores stellas quae sunt in orbe signorum propter lunam. Deinde probauimus post propter istas stellas reliquas, facilius illo inuenimus longitudines inter quasdam earum, et inter quasdam iterum conuenientes secundum propinquitatem ei quod inuenit Abrachis, longitudines autem inter eas et inter duos tropicos, et duas aequalitates inuenimus in unaquaque earum iam remotas ab eo quod descripsit Abrachis secundum continuitatem signorum per duas partes, et duas tertias partis secundum propinquitatem. Quod huiusmodi motus fiat super polis eclipticae, et non aequatoris diei. IAm ergo ostensum est nobis declaratione manifesta per res istas, quod sphaera stellaru fixarum iterum permutatur secundum continuitatem signorum hac permutatione, cuius summam diximus secundum propinquitatem, et quia continuatur cum illo, ut inquiramus de modo, super quem currit res in hoc motu, scilicet an sit super duos polos aequatoris diei, aut super duos polos circuli decliuis, qui transit per media signorum, tunc illud esset manifestum ex ipsa elongatione in longituditudine circuli magni, qui describuntur transeuntes per duos polos unius duorum circulorum quos diximus, secent ex altero arcus inaequales, si elongatio in longitudine non esset in hac quantitate temporis parua ualde, adeo, ut superfluitas quae accidit in hac causa, cuius praecessit rememoratio non comprehendat sensus. Veruntamen huius intentionis scientia sit facilis per cursum stellae proprie in latitudine in eo quod praecessit ex tempore, et in hoc nostro tempore. Nam inter quemcunque duorum circulorum ex duobus circulis aequatoris diei et circuli signorum, inueniuntur stellae seruare longitudinem semper, et inter se manifestum est, quod motus sphaerae earum iterum non est, nisi super duos polos illius circuli ex illis duobus. Sed et Abrachis iterum sciuit, quod iste motus non est, nisi super duos polos orbis signorum, et illud est, quoniam ipse continuauit in sermone suo in locali motu duorum punctorum duorum tropicorum, et duorum punctorum duarum aequalitatum azimek alahasel. Iterum per illud quod considerauit Timocaris, et per illud quod ipsemet considerauit, quod ipsa non seruat quantitatem elongationis in longitudine, nisi per comparationem ad orbem signorum, non aequatorem diei, et quod ipsa est magis declinata ad meridiem ab orbe signorum primo, et postremo per duas partes, et propter illud affirmauit in sermone suo in quantitate anni motum solum, qui est super duos polos orbis signorum. Veruntamen ipse adhuc erat in dubitatione secundum quod ipse dixit, propterea quod considerationes quae fuerunt secundum tempus Timocaris, non sunt ex eis quae merentur, ut in eis fiducia habeatur, cum non sint assumptae, nisi secundum grossitudinem speculationis, et secundum apparitionem, propterea quod superfluitas quae accidit inter duo tempora, non est adhuc sufficiens in scientia per quam fiducia habeatur in illo. Nos autem propterea quod inuenimus hanc intentionem consideratam in tempore longiori in illo, et in pluribus stellis fixis, tunc uisum est nobis necessario, ut iudicemus superfluitatem confidentiae, quod iste motus non est istis stellis, nisi super duos polos orbis decliuis, et illud est, quoniam postquam considerauimus elongationem cuiusque earum in latitudine ab orbe signorum in circulo magno, qui describitur transiens per polos eius, inuenimus eam fortasse conuenientem ei quod scripsit Abrachis, et comprehendit de longitudinibus earum, aut diuersificatur ab eo paruissime, et per quantitatem quod possibile est refugere inde, et non comprehendatur ex ipsis considerationibus, de elongationibus uero earum ab orbe aequatoris diei in circulo magno, qui describitur descrihitur ed. transiens per polos eius, inuenimus illud quod scripsimus, non conuenit ei quod scripsit Abrachis, ex eo quod currit hac semita, et quod considerauit Abrachis iterum non fuit conueniens ei quod considerauerat ante Timocaris, et ego quidem iam firmaui de illo iterum, quod conuenit ei quod diximus, et cum affirmat illud magis quod casus ex latitudine non est nisi unus et idem per comparationem ad orbem signorum, et illud est, quod stellarum quae sunt in medietate sphaerae, quae est a tropico aestiuo, capiendo uersus punctum uernale ad tropicum hyemale, inuenitur longitudo ab aequatore diei decliuior ad septentrionem, quam illa quae fuit eis in eo quod praecessit de tempore, et stellarum quae sunt in medietate sphaerae contraria huic medietati decliuior ad meridiem, et quaecunque stellarum appropinquat duobus punctis duarum aequalitatum, superfluitas illius est in eis magna, et quae earum approximat duobus punctis duorum tropicorum, superfluitas illius est in eis parua, et fortasse contingit, ut sint quantitates huius superfluitatis secundum superfluitatem partium reliquarum orbis signorum septentrionalium ab aequatore diei apud permutationem earum oppositam illi, et ut addamus in expositione eius quod diximus, narrabo rem paucarum stellarum quas facile est scire. Nos enim rememorabimur in unaquaque duarum medietatum sphaerae quarum praecessit rememoratio, longitudines earum in latitudine ab aequatore diei in circulo magno, qui describitur transiens per duos polos eius secundum quod affirmauit Timocaris, et scripsit, et secundum quod affirmauit Abrachis, et secundum quod nos sciuimus illud etiam per illum modum. Dico ergo, quod de stella luminosa in uulture uolante Timocaris quidem scripsit, quod ipsa est inclinata ad septentrionem ab aequatore diei 5. partibus et 4. quintis partis, et similiter scripsit iterum Abrachis. Nos uero inuenimus eam decliuiorem ad septentrionem 5. partibus et medietate et tertia. Et de stella media pliadum scripsit Timocaris, quod ipsa est inclinata ad septentrionem ab aequatore diei 14. partibus et medietate, Abrachis uero 15. partibus et medietate, nos autem 16. partibus et quarta, et de aldebaran scripsit Timocaris, quod est inclinata ad septentrionem ab aequatore diei 8. partibus et medietate et quarta, Abrachis uero 9. partibus et medietate et quarta, et nos quidem 11. partibus. Et de stella quidem quae est luminosior stellarum tenentis habenas quae dicitur alaiot, scripsit Arsatilis, quod est inclinata ad septentrionem ab aequatore diei 40. partibus, Abrachis uero 40. partibus et quinta partis, nos autem inuenimus eam 41. parte et sexta partis. Et de stella quae est in humero antecedente superbi, scripsitTimocaris, quod ipsa est inclinata ad septentrionem ab aequatore diei parte una et duabus quintis partis, et Abrachis quidem parte una et 4. quintis partis, nos uero inuenimus eam duabus partibus et medietate. Et de stella quae est in humero secundo superbi scripsit Timocaris, quod est inclinata ad septentrionem ab aequatore diei tribus partibus et medietate et tertia, et Abrachis quidem quatuor partibus et tertia partis, nos uero 5. partibus et quarta. Et stella luminosa quae est in ore canis, et est aschere alhaabor, scripsit Timocaris, quod est inclinata ad meridiem ab aequatore diei 16. partibus, nos autem inuenimus eam 15. partibus et medietate et quarta. Et de stella antecedente ex duabus stellis luminosis quae sunt in capite geminorum scripsit Arsatilis, quod ipsa est inclinata ad septentrionem ab aequatore diei 33. partibus, et Abrachis quidem 33. partibus et medietate partis, nos uero inuenimus eam 33. partibus et medietate. Et de stella sequente earum scripsit Arsatilis, quod est inclinata ad septentrionem ab aequatore diei 30. partibus, et Abrachis iterum similiter scripsit, nos uero inuenimus eam 30. partibus et sexta partis. Iam ergo inuenimus situm stellarum omnium, quarum situs in longitudine est in medietate in qua est aequalitas uernalis ex duabus medietatibus sphaerae quas diximus, cum comparantur cum aequatore diei decliuiorem ad septentrionem ab eo, super quod fuit in duobus temporibus praecedentibus, in illis quidem, quae ex eis sunt apud duo puncta duorum tropicorum ipsorum re parua ualde, et in illis quidem quae sunt apud duo puncta duarum aequalitatum cum eo, cui est quantitas de qua curatur. Illud ergo est conueniens, ut motus localis secundum continuitatem signorum non sit nisi super duos polos orbis decliuis, propterea quod sectiones etiam quae secundum continuitatem signorum ex hac medietate circuli sunt semper decliuiores ad septentrionem, quam sectiones eius antecedentes, et in illis, quae ex eis sunt apud duo puncta duarum aequalitatum superfluitas est maior, et in illis quae ex eis sunt apud duo puncta duorum tropicorum superfluitas est minor. Et in medietate sphaerae iterum contraria isti medietati scripsit Timocaris de stella quae est super cor leonis, quod est inclinata ad septentrionem ab aequatore diei 21. parte et tertia, Abrachis uero 20. partibus et duabus tertijs, nos autem inuenimus declinationem eius 19. partes et medietatem et tertiam partis. Et de stella quae, dicitur azimek alahazel, scripsit Timocaris, quod declinat ad septentrionem ab aequatore diei parte una et duabus quintis partis, Abrachis uero tribus quintis partis tantum, nos autem inuenimus eam declinatam ad meridiem ab aequatore diei medietatem partis. Et de stella ex tribus stellis quae sunt in cauda ursae maioris, quae est in extremitate caudae, scripsit Arsatilis, quod est inclinata ad septentrionem ab aequatore diei 61. parte et medietate partis, Abrachis uero 60. partibus et medietate et quarta, nos uero inuenimus declinationem eius 59. partes et duas tertias partis. Et de stella extremitatis sequente, et est illa, quae est in medio caudae, scripsit Arsatilis, quae est declinata ab aequatore diei ad septentrionem 67. partibus et quarta partis, Abrachis uero 66. partibus et medietate, nos uero inuenimus eius declinationem 65. partes. Et de stella tertiae extremitatis, quae est quasi ipsa sit origo caudae, scripsit Arsatilis, quod ipsa declinat ad septentrionem ab aequatore diei 68. partibus et medietate partis, Abrachis uero 67. partibus et duabus tertijs partis, nos autem inuenimus eius declinationem 66. partes et quarta partis. Et de azimek arami scripsit Timocaris, quod declinat ad septentrionem ab aequatore diei 31. parte et medietate partis, Abrachis uero 31. parte, nos autem inuenimus eius declinationem 29. partes et medietatem partis. Et de stella ex duabus stellis luminosis, quae sunt in rubetiae scorpionis, quae est in extremitate azubenae meridiani, scripsit Timocaris, quod declinat ad meridiem ab aequatore diei 5. partibus, Abrachis uero 5. partibus et tribus quintis partis, nos autem inuenimus eius declinationem 7. partes et medietatem partis. Et de stella quae est in extremitate azubenae septentrionalis ex eis, scripsit Timocaris, quod declinat ad septentrionem ab aequatore diei parte una et quinta partis, Abrachis uero duabus quintis partis, nos autem inuenimus eam declinatam ad meridiem ab aequatore diei parte una. Et de stella luminosa quae est in pectore scorpionis, quae dicitur cor scorpionis, scripsit Timocaris, quod declinat ad meridiem ab aequatore diei 18. partibus et tertia partis, Abrachis uero 19. partibus, nos autem inuenimus eius declinationem 20. partes et quartam partis. Et de istis stellis etiam omnibus secundum quod sequitur quaecunque sunt oppositae illis stellis, inueniuntur cursus earum in latitudine omnes, quando comparantur cum aequatore, decliuiores ad meridiem secundum illam comparationem quam fuerunt in duabus partibus antecedentibus, et peruenit per ista omnia, quod motus localis sphaerae stellarum fixarum in longitudine secundum continuitatem signorum est iterum pars una secundum quod praecessit ex sermone nostro in omnibus 100. annis secundum propinquitatem, et duae partes et duae tertiae partis in 265. annis, qui sunt inter considerationem Abrachis et nostram considerationem, et comprehensio illius est per superfluitatem quae inuenitur in latitudine stellis, quae sunt apud duo puncta duarum aequalitatum est manifestior, et illud est, quoniam stellam mediam pliadum Abrachis quidem inuenit declinatam ad septentrionem ab aequatore diei 15. partibus et sexta partis, nos uero inuenimus declinationem eius 16. partes et quarta partis. Iam ergo declinat ad septentrionem quidem in tempore, quod fuit inter nos et inter Abrachis parte una et duabus 12. partis unius. Et manifestum est, quod illud est propinquum quantitati qua superfluit latitudo ab aequatore diei duarum partium et duarum tertiarum partis orbis signorum, quae sunt in postremo arietis ex motu locali in hoc eodem tempore in longitudine secundum succesionem signorum. Et stellam quidem quae dicitur alhaioch, inuenit Abrachis declinatam ad septentrionem ab aequatore diei 40. partibus et quinta partis, nos uero inuenimus eius declinationem declinatinationem ed. 21. partem et 5. partis, facta est ergo decliuior ad septentrionem 4. quintis partis, et illud iterum est quantitas, qua superfluit latitudo ab aequatore diei duarum partium et duarum tertiarum partis orbis signorum, quae sunt in medio tauri. Et stellam stella ed. quae est super humerum antecedentem superbi, inuenit Abrachis quidem declinatam ad septentrionem ab aequatore diei parte una et 4. quintis partis, nos uero inuenimus eius declinationem duas partes et medietatem. Facta est ergo decliuior ad septentrionem, quasi duabus tertijs partis, et illud fortasse est quantitas, qua superfluit latitudo ab aequatore diei duarum partium, et duarum tertiarum partis orbis signorum quae sequuntur finem tauri. Et similiter iterum de stellis quae sunt in medietate sphaerae, opposita huic medietati, inuenit Abrachis quidem stellam quae dicitur azimek alahazel declinatam ad septentrionem ab aequatore diei 3. quiuintis partis, nos autem inuenimus eam declinatam ad meridiem ab aequatore diei medietatem partis. Facta est ergo decliuior, quoniam fuit ad meridiem parte una et 10. partis, et illud iterum est summa eius, quo superfluit latitudo ab aequatore diei duarum partium, et duarum tertiarum partis orbis signorum, quae sunt in fine uirginis. Et stellam quae est in extremitate caudae ursae, et est benetnassi maioris, Abrachis quidem inuenit declinatam ad septentrionem ab aequatore diei 60. partibus et medietate et quarta, nos autem inuenimus eius declinationem 59. partes et duas tertias partis. Iam ergo declinat uersus meridiem parte una et 12. partis, et est summa eius, quo superfluit latitudo ab aequatore diei duarum partium, et duarum tertiarum partis orbis signorum, quae sunt in principijs signi librae. Et azimek alrameha Abrachis quidem inuenit declinatam ab aequatore diei 31. parte, nos autem inuenimus declinationem eius 29. partes et medietatem et tertiam. Iam ergo declinat uersus meridiem parte una et 6. partis, et illud est propinquum summae eius, quo superfluit latitudo ab aequatore diei secundum illam similitudinem duarum partium, et duarum tertiarum partis orbis signorum, quae sunt in principijs librae. Et illud ad quod intendimus, fit manifestius et planius per illud quod dicemus iterum de considerationibus. Timocaris enim scripsit, quod ipse considerauit in Alexandria hac in anno 47. reuolutionis primae ex reuolutionibus Philippi in die octaua mensis nominati astranon, et die 29. mensis ex mensibus Aegyptiorum nominati atur, apud consumationem horae eius tertiae, et inuenit per uisionem medietatem meridianam lunae iam cooperuisse tertiam, aut medietatem sequentem pliadum secundum ueritatem, et fuit illud tempus in anno 465. termini Nabuchodonozor in die 29. mensis eorum ex mensibus Aegyptiorum nominati atur in nocte, quam sequitur dies 30. eius ante mediationem noctis, quasi tribus horis temporalibus, scilicet aequalibus tribus horis et tertia, propterea quod sol fuit super 7. partes aquarij. Computauit ergo dies cum noctibus suis aequalibus, et fortasse fuit hora ante mediationem noctis per hanc quantitatem etiam horarum, et in hac hora fuit radix lunae uerae secundum radices, quarum declaratio praecessit super 30. partes et 20. minuta et fuit inclinata ad septentrionem ab orbe signorum tribus partibus et 45. minutis, et fuit uisa in Alexandria radix eius in longitudine super 29. partes et 29. minuta arietis. Et eius declinatio in septentrione ab orbe signorum tres partes et 35. minuta, quoniam medians coelum fuit pars secunda geminorum. Fuit ergo longitudo partis sequentis pliadum in illa hora ab aequalitate uernali secundum continuitatem signorum 29. partes et medietas fere, et illud est, quoniam centrum lunae praecedebat eam aliquantulum, et erat decliuis ad septentrionem ab orbe signorum tribus partibus et duabus tertijs partis fere, et illud est quoniam fuit iterum declinata parumper ad septentrionem a centro lunae. Agrinus autem considerauit in ciuitate nominata Athene, et scripsit, quod in anno 12. annorum Dustaguasiae in mense nominato matrath, in nocte septima eius, in principio horae tertiae eius, cooperuit cornu lunae meridianum extremitatem pliadum sequentem meridianam, et fuit hoc tempus in anno 840. a termino Nabuchodonosor in die secundo mensis ex mensibus Aegyptiorum nominati cobi, in nocte eius quam sequitur dies tertius ante mediationem noctis 4. horis temporalibus, sed ex aequalibus quinque horis, propterea quod sol fuit super sex partes sagittarij. Fuit ergo haec consideratio secundum circulum meridiei, qui transit per Alexandriam ante mediationem noctis 5. horis et tertia ex horis aequalibus. Secundum dies uero cum noctibus suis aequales ante mediationem noctis 5. horis et medietate et quarta, et in hac hora fuit radix centri lunae secundum ueritatem super tres partes et 7. minuta tauri, et fuit declinata ad septentrionem ab orbe signorum 4. partibus et medietate et tertia, et fuit uisus in ciuitate Athene locus eius in longitudine super tres partes et 15. minuta tauri. Et eius declinatio in septentrionem ab orbe signorum fuit 4. partes, quoniam medians coelum fuit pars secunda piscis, fuit ergo longitudo partis sequentis pliadum in longitudine in illa hora ab aequalitate uernali secundum continuitatem signorum 33. partes et quarta, et fuit declinata ad septentrionem ab orbe signorum tribus partibus et duabus tertijs partis. Propter illud ergo est manifestum, quod pars sequens pliadum, in latitudine quidem fuit decliuis ad septentrionem ab orbe signorum in illa hora, et in hac hora per unas et easdem partes, et sunt tres partes et duae tertiae partis in circulo magno, qui describitur transiens per polos eius. In longitudine autem mouetur secundum continuitatem signorum, elongatur ergo ab aequalitate uernali tribus partibus et 45. minutis, propterea quod ipsius elongatio ab ea fuit in consideratione quidem prima 29. partes et medietas, et in consideratione quidem secunda 33. partes et quarta. Et temporis quidem quod fuit inter duas considerationes, summa fuit 375. anni, pars ergo sequens pliadum mouetur in 100. annis secundum continuitatem signorum parte una. Et iterum Timocaris scripsit, quod ipse considerauit in Alexandria in anno 30. reuolutionis primae ex reuolutionibus Philippi in die 15. mensis nominati alhosul, et die quinto mensis nominati cobi in initio horae tertiae, et tunc comprehenderat luna in medio sui per illud quod opponitur orienti aequalitatis ex duobus lateribus eius azimek alahazel, et comprehenderat eam azimek alahazel, et iam de portione lunae ab eo quod sequitur septentrionem tertiam eius secundum ueritatem, et fuit tempus illud in anno 454. ex tempore Nabuchodonosor in die quinto mensis ex mensibus Aegyptiorum nominati cobi, in nocte eius quam sequitur dies sextus ante mediationem noctis 4. horis temporalibus et aequalibus secundum propinquitatem, propterea quod sol fuit super 15. partem piscis, et haec est summa quae aggregatur ex horis secundum propinquitatem ex aequatione, quae est secundum dies cum noctibus suis aequales. Et in illa hora fuit iterum centrum lunae secundum ueritatem in longitudine super 21. partem et 21. minutum uirginis, scilicet longitudo eius fuit a tropico aestiuo secundum continuitatem signorum 81. pars et 21. minutum, et fuit declinata ad meridiem ab orbe signorum parte una et medietate et tertia, et uidit longitudinem eius a tropico aestiuo in longitudine 82. partes et 12. minuta, et declinatio eius in meridie ab orbe signorum est duae partes fere, et illud est, quoniam medians coelum fuit postremum medij cancri. Fuit ergo longitudo azimek alahazel propter illud, cuius rememoratio praecessit in longitudine in illa hora a tropico aestiuo 82. partes et tertia. Et fuit declinata ad meridiem ab orbe signorum duabus partibus ut multum, et dixit iterum secundum hanc similitudinem, quod in anno 48. eiusdem reuolutionis remanentibus sex diebus mensis nominati barusion, et transactis diebus 9. mensis nominati numinati ed. tut, postquam transierat de hora 10. quantitas medietatis eius, postquam eleuata fuerit luna ab horizonte, uidit azimek alahazel contingentem in ueritate latus septentrionale eius, et fuit illud tempus in anno 466. ex tempore Nabuchodonosor in die septimo mensis ex mensibus Aegyptiorum nominati tut, in nocte eius quam sequitur dies octauus, secundum quod ipse quidem dicit. Postquam praeterierunt de ea post ipsius mediationem tres horae temporales et medietas, sed ex horis aequalibus tres horae et octaua fere, propterea quod sol fuit in medio scorpionis. Secundum uero, quod oportet post duas horas et medietatem a mediatione noctis, et illud est, quoniam post mediationem noctis per illud, cuius haec summa est ex horis aequalibus, fuit medians coelum 22. partes et medietas geminorum, et ascendit propinquum istarum partium de uirgine, et illud est summa harum partium quas dixit de luna iterum, quibus fuit locus eius in ea post ipsius ortum, et secundum dies cum noctibus suis aequales. Inuenimus nos horam fuisse post mediationem noctis duabus horis tantum ex horis aequalibus, et in illa hora fuit iterum longitudo centri lunae secundum ueritatem a tropico aestiuo 81. pars et 30. minuta, et fuit declinata ad meridiem ab orbe signorum 2. partibus et medietate, et fuit eius longitudo per uisionem 82. partes et medietas, et eius declinatio in meridiem duae partes et quarta. Fuit ergo azimek alahazel per hanc considerationem etiam declinata ad meridiem ab orbe signorum, quasi per illam eandem quantitatem, et est duae partes, et fuit eius longitudo a tropico aestiuo 82. partes et medietas partis. In 12. ergo annis, qui sunt inter duas considerationes, mota est azimek alahazel secundum continuitatem signorum, et elongata a tropico aestiuo per sextam partis fere. Et dixit Mileus Geometer, quod ipse considerauit Romae in anno primo annorum tubianos in mense nominato machur, in 15. die eius in nocte, quam sequitur dies 16. apud consumationem horae decimae eius, et inuenit lunam iam cooperuisse azimek alahazel, et illud, quoniam non uidebatur. Inquit, sed postquam consumata est hora 11. uisa est praecedere centrum lunae per minus diametri lunae, et fuit longitudo eius a duobus cornibus lunae aequalis, et tempus illud est in anno 845. ex tempore Nabuchodonosor in 15. die mensis nominati mesir ex mensibus Aegyptiorum in nocte, quam sequitur dies 16. post mediationem eius quatuor horis temporalibus, et est hora, in qua fuit centrum lunae secundum propinquitatem ita, quod iam conuenerat azimek alahazel, et fuit ex horis aequalibus post quinque horas a mediatione noctis, propterea quod sol fuit super 20. partes capricorni, et fuit secundum circulum meridiei, quae transit per Alexandriam post sex horas et tertiam a mediatione noctis. Secundum dies uero cum noctibus suis aequales post sex horas et 4. horae, aut plus parum, et in illa hora fuit longitudo centri lunae secundum ueritatem a tropico aestiuo 85. partes et medietas et 4. et fuit declinata ad meridiem ab orbe signorum parte una et 3. fere, et fuit longitudo eius per uisionem in longitudine 86. partes et 4. et declinatio eius in meridiem 2. partes, quoniam medians coelum fuit quartus librae ut multum, iste ergo fuit in illa hora locus azimek alahazel. Iterum manifestum est, quod simile illius est illUD quod scripsit Timocaris, et quod diximus nos post ipsum de longitudine eius in meridiem ab orbe signorum, et est 2. partes, in longitudine uero iam recessit secundum continuitatem signorum a loco in quo inuenta fuit per considerationem quae fuit in anno 36. tribus partibus et 55. minutis, et summa annorum quae fuit inter duas considerationes, est 391. annus, et recessit a loco in quo inuenta est per considerationem in anno 48. tribus partibus et 45. minutis. Et summa annorum que fuit inter duas considerationes 379. anni, donec fit comprehensio eius quo mota est azimek alahazel secundum continuitatem signorum, propter istas considerationes consierationes ed. etiam quasi pars una in omnibus 100. annis. Et iterum Timocaris dixit, quod ipse considerauit in Alexandria in anno 36. reuolutionis primae ex reuolutionibus Philippi in die 25. mensis nominati berse dierum, in die 16. mensis nominati censi in principio cum incepit hora 10. et uidit lunam iam dilatatam esse multum per latus septentrionale a duabus partibus stellae septentrionalis ex stellis quae sunt in fronte scorpionis, et illud tempus est in anno 454. ex tempore Nabuchodonosor in mense ex mensibus Aegyptiorum nominati cusi, in die 16. eius in nocte quam sequitur dies 17. post mediationem noctis tribus horis temporalibus, ex horis uero aequalibus tribus horis et 2. quintis horae, propterea quod sol fuit in 26. partibus sagittarij. Secundum uero cum noctibus suis aequales 3. horis et sexta, et in hac hora fuit elongatio centri lunae secundum ueritatem ab aequalitate autumnali 31. pars et 4. et fuit declinata ad septentrionem ab orbe signorum parte una et tertia. Et fuit longitudo eius per uisionem in longitudine 32. partes, et declinatio eius ab orbe signorum pars una et pars 12. partis unius, quoniam medians coelum fuit tunc medium leonis, ergo stellae septentrionalis ex stellis quae sunt in fronte scorpionis, fuit elongatio in longitudine in illa hora ab aequalitate autumnali, sicut illae partes, et sunt 32. partes, et fuit declinata ad septentrionem ab orbe signorum parte una et tertia fere. Et dixit Mileus secundum illam similitudinem, quod ipse considerauit Romae in anno primo annorum trabianos in die 18. mensis nominati messur, in nocte quam sequitur 19. apud consumationem horae 11. et uidit cornu lunae meridianum secundum rectitudinem stellae mediae, et stellae meridionalis ex stellis quae sunt in fronte scorpionis, et uidit centrum lunae postrematum diuersificatum a rectitudine longitudo eius stellis medijs, est summa longitudinis stellae mediae abbreuiatae a stella meridiana, et aestimauit, quod in stella septentrionali ex stellis quae sunt in fronte iam fixa est luna, dixit et illud, quoniam non fuit uisa penitus, et illud tempus iterum fuit in anno 845. a tempore Nabuchodonosor in die 18. mensis ex mensibus Aegyptorum nominati mesir, in hac nocte quam sequitur dies 19. post 5. horas temporales a mediatione noctis. Sed ex horis aequalibus post sex horas et sextam, quoniam sol fuit in 23. parte capricorni, et secundum circulum meridiei qui transit per Alexandriam post 7. horas et medietatem. Et haec etiam summa horarum fuit secundum dies cum noctibus suis aequales, et in illa hora fuit longitudo centri lunae secundum ueritatem sub aequalitate autumnali 35. partes et tertia, et fuit declinata ad septentrionem ab orbe signorum quasi 2. partibus et sexta partis, et fuit uisa elongatio eius in longitudine 35. partes et 55. minuta, et eius declinatio in septentrionem pars una et tertia, et illud, quoniam medians coelum fuit postremum librae. Magis ergo elongatae stellae frontis scorpionis in septentrione fuit locus in illa hora secundum propinquitatem illius eiusdem loci, propter illud ergo iam manifestum est in consideratione considtratione ed. in hac stella iterum, quod eius longitudo in latitudine ab orbe signorum est longitudo una et eadem in antiqua et moderna. In longitudine uero additur, et elongatur ab aequalitate autumnali secundum continuitatem signorum 3. partibus et 55.minutis, in tempore quod fuit inter duas considerationes, et summa eius est 391. annus, et sequitur ex illo iterum, quod permutatio harum stellarum est in omnibus 100. annis pars una.

⟨VI.2⟩ In descriptione differentiarum tabularum fixarum stellarum

INquit et postquam affirmatum est apud nos per considerationem et comparationem, quae euenerunt secundum secundam ed. similitudinem unam inesse harum stellarum luminosarum, et per casum longitudinum reliquarum stellarum ad illud quod expertum est de eis, et scitur secundum esse eius, quod sphaera stellarum fixarum iterum separatur uersus continuitatem signorum a punctis duorum tropicorum et duarum aequalitatum recessione, cuius summa est quam erigit haec quantitas temporis, et cum illo, quod permutatio eius non est nisi super duos polos orbis signorum, non super duos polos aequatoris diei, scilicet duos polos super quos est reuolutio motus primi, uidimus quod oportet, ut intendamus ad unamquanque harum stellarum, et aliarum stellarum fixarum, et scribamus quod consideratum est, et quod dictum est de locis earum in hoc nostro tempore in latitudine et in longitudine, non quod uidetur ex eis per comparationem ad aequatorem diei, sed quod uidetur separari ex eis per comparationem ad orbem signorum in circulis magnis, qui signantur transeuntes per polos eius, et per unamquanque stellarum, et sunt circuli, in quibus oportet secundum radicem quam praemisimus, et posuimus radicem huic motui, ut sit cursus earum in latitudine per comparationem ad orbem signorum unus et idem semper, in quo non sit diuersitas, et sit separatio earum in longitudine secundum successionem signorum in temporibus aequalibus, scilicet, separent ex eis arcus aequales, propter illud ergo usi sumus etiam illo instrumento, quoniam duarum armillarum quae sunt in illo, reuolutio non est nisi super duos polos circuli decliuis. Considerauimus ergo, quod nobis fuit possibile comparare ex eis ad illud quod est in magnitudine sexta, praeparauimus ergo semper unam duarum armillarum instrumenti, quas diximus, secundum aliquam stellarum luminosarum quam praemisimus, et inuenimus locum in quo ipsa est ex orbe signorum per lunam. Armillam uero aliam diuisam totam, quam iterum possibile est reuolui in latitudine super duos polos circuli decliuis, nos praeparauimus secundum stellam de qua inquisiuimus, donec uideremus stellam iterum per foramina huius armillae secundum conuenientiam stellae positae, Nam cum illud accidit, apparet nobis apparitione manifesta cursus stellae quaesitae, scilicet locus stellae in longitudine, et locus eius in latitudine simul per armillam quae cadit super eam, et illud est, quoniam elongatio eius in longitudine separatur a differentia communi, quae est inter hanc armillam et inter orbem signorum, et elongatio eius in latitudine separatur ab arcu eius, qui continuat inter hanc sectionem, cuius rememoratio praecessit, et inter foramen, quod est supra terram. Vt ergo sit nobis iste modus ex modis stellarum in sphaera corporea positus situs, descripsimus eum secundum semitam tabularum in 4. diuisionibus, et firmauimus in esse cuiusque stellarum quae sunt in unoquoque signo. In diuisione quidem prima formas earum, et in diuisione quidem secunda loca earum in longitudine signorum, in quibus sunt per considerationes in principio regni Antonij, secundum quod principia 4. sint ex punctis duorum tropicorum et duarum aequalitatum. Et in diuisione quidem tertia longitudines earum in latitudine ab orbe signorum in duas partes, secundum quod est in ea locus cuiusque earum in septentrione aut in meridie. Et in diuisione quidem quarta ordines quantitatum earum in magnitudine, et longitudines quidem earum in latitudine semper sunt fixae secundum habitudinem unam. Per loca uero earum in longitudine in hac hora possibile est facile scire cursus earum etiam in alio tempore, ut intendamus ad partes quae pertinent tempori, quod est inter locum stellae nunc et inter radicem eius in hora quaesita, secundum quod portio omnium 100. annorum sit pars una. Proijciemus ergo eas ex partibus loci in hac hora, cum tempus quaesitum fuerit antiquius ea, et addemus eas super partes radicis in hac hora, cum tempus quaesitum fuerit in hac hora, fuerit recentius ea, et oportet, ut intelligamus ad ilud, quod currit in formis earum secundum radicem quae ponitur in hoc modo locorum stellarum, et secundum sectiones quae cadunt duobus polis orbis signorum, et illud est, quoniam nos dicimus stellam antecedere stellam, aut stellam sequi stellam, et nos significamus stellas, quarum loca ista narrata sunt super partes orbis signorum antecedentes aut sequentes, et dicimus stellam decliuiorem ad meridiem, aut decliuiorem ad septentrionem, et significamus stellas quae sunt propinquiores duobus polis orbis signorum, quam stellae eius relatae in nominatione et in formis iterum ipsis quae sunt cuiusque summae stellarum, non sumus sequuti illud quo usi sunt illi, qui fuerunt ante nos, ita, ut non alteramus illud. Et similiter iterum non sunt sequuti illi illud quo usi sunt, qui ante eos fuerunt, imo nos usi sumus in locis plurimis earum alijs formis secundum rem magis licitam, et similiorem et magis necessariam figurationi in parte. Verbi gratia: Duas stellas quas Abrachis posuit esse super duos humeros uirginis, nominamus nos super duo latera eius, propterea quod spacium inter utrasque et inter stellam, quae est in capite uirginis, est maius spacio inter utrasque, et inter duas spatulas eius, et cuius spacium est, hoc spacium melius est in ea, ut sit super duo latera. Si autem fuerit super duas spatulas, erit illud extra illud quod consuetum est, ueruntamen sit facilis, et appropinquat per ipsam comparationem quae est in locis, quae firmantur eis scientia esse stellarum ad quas innuimus ex eis, in quarum nominatione diuersificati sumus ab antecessoribus nostris, et ita currit res in ordine earum.

⟨VI.3⟩ De affirmatione stellarum quae sunt in medietate septentrionali sphaerae, et positione earum in tabulis.

INquit, ubi inuenimus apud magnitudinem quae est in tabulis stellarum fixarum notam m, et supra notam e, sciuimus quod intentio illius est, quod est plus illa magnitudine parum. Et ubi inuenimus apud magnitudinem notam e, et supra eam notam l, scimus quod significat illud esse minus illa magnitudine parum. Omnes ergo stellae meridianae sunt 316, de quibus in magnitudine prima sunt 7. et in secunda 18. et in tertia 63. et in quarta 164. et in quinta 54. et in sexta 9. et nebulosa una. Omnes ergo stellae fixae in septentrione et meridie et orbe signorum ex eis, quae magnitudinem habent, sunt 1022. stellae, de quibus in magnitudine prima sunt 15. et in magnitudine secunda 45. et in magnitudine tertia 208. et in magnitudine quarta 474. et in magnitudine quinta 203. et in magnitudine sexta 49. et ex nebulosis 5. et ex tenebrosis 9. Et stella nominata cometa non ingreditur in numerum, et ista est descriptio tabularum quas qui uult, sumat ex libro Ptolomei.

⟨VI.4⟩ In descriptione almaiarati siue uiae lacteae.

HOc ergo est quod narrauimus de ordinibus stellarum fixarum, et nos sumus adiungentes ad illud, secundum quod oportet, dispositiones circuli lactei iterum. Conabimur ergo quanto plus poterimus, et secundum quod comprehendimus per considerationem unamquanque partium eius, ut describamus quod uidemus de dispositionibus eius particularibus. Dico ergo, quod haec uia lactea non est circulus secundum ueritatem, imo est cingulum in quo toto sit, quasi color lactis communis, et propter illud nominatur hoc nomine deriuato a nomine lactis, et hoc idem cingulum non est iterum aequale in omnibus partibus suis, neque ordinatum, imo est diuersum in latitudine et in colore, et in spissitudine, et in loco, et ipsum in quibusdam partibus suis est spissum duplum, fit ergo facile scire illud ei, qui intuetur illud uisu suo intuitu tantum nedum alij. Res autem eius particulares, de quibus necessarium est superfluum studium et credulitas, et inuenimus secundum quod narro, et est, quod portionis duplicis huius anguli una duarum extremitatum quae sunt ei, est in eo quod est ei simile continuationi apud larem, et altera extremitas est apud gallinam, et cingulum praecedens non continuatur cingulo alij in aliquo locorum, et illud est, quoniam inter ea sunt foramina in loco illius continuationis quae est apud larem, et in loco illius continuationis quae est apud auem. Cingulum uero tertium est continuatum cum residuo almaiarati, faciens cum eo angulum unum, et est illud super quod iterum transit circulus qui est ex maioribus circulis signatis super medium eius proprie, et nos quidem incipimus nunc loqui de hoc cingulo, et incipimus ex finibus eius meridianis. Dico ergo illud, quod ex eo est ab hac parte transit per pedes centauri, qui nominatur Arabice adholmen, et est uehementius rarum et rarificatum, et occultioris coloris. Stella ergo quae est in interioris pedis eius posterioris dextri, est inclinata parumper ad meridiem a linea septentrionali almaiarati, et similiter etiam stella, quae est super genu pedis sinistri, et stellam quae est sub genu eius posteriore dextro. Stella uero in quae est brachio posteriori sinistro, est posita in medio almaiarati. Stellae autem secundae quae est in hoc calcaneo, et stella quae est super calcaneum dextrum longitudo in septentrione a duabus extremitatibus eius meridianis, est duae partes fere per partes, quibus maiores circuli sunt 360. partes, et illud quod est in maiarati super duos pedes eius posteriores, est uehementioris spissitudinis parum. Deinde post illud extremitas almaiarati septentrionalis elongatur a stella, quae est in inferiori dorso lupae fere parte una et media, et in duabus extremitatibus eius meridianis continetur stella, quae est super accessionem primae, et tangit stellam septentrionalem ex duabus stellis comparibus, quae sunt in loco ignis laris, et stellam meridianam ex duabus stellis, quae sunt in base laris. Stella autem quae est in parte septentrionali loci ignis, et stella quae est in medio loco ignis, sunt positae in almaiarati ipsa, et haec portio est uehementioris raritatis. Deinde in portione almaiarati septentrionali tres scorpionis spondiles continentur, quae sunt sub serpente, et continet rete sequens serpentem. Duae uero extremitates eius ab eo quod sequitur meridiem tangunt stellam in calcaneo pedis dextri sagittarij, et continetur in eis stella quae est super manum eius sinistram. Stella uero quae est super latus meridianum equi, est extra almaiarati, sed stella quae est super hastulam sagittae, est in medio eius, et duae quidem stellae quae sunt in parte septentrionali arcus, sunt iterum positae in almaiarati, ueruntamen longitudo cuiusque earum a duabus extremitatibus extrexmitatibus ed. eius est parum plus parte una. Septentrionalis quidem earum longitudo est haec longitudo ab extremitate eius meridiana, et meridianae quidem ab extremitate eius contraria huic, et extremitates eius quae sunt super spondiles tres, sunt spissiores parum, et quod de ea est post illud, est rarius parumper, et extenditur, donec peruenit ad uulturem uolantem, et fortasse conseruat latitudinem unam. Et stellae quae est super extremitatem caudae serpentis, et retinet eam lator serpentis, est, quando est in aere puro longitudo eius ab extremitate almaiarati antecedente plus parum parte una. Duae uero stellae antecedentes ex stellis luminosis positis sub eo, sunt positae in ipsa almaiarati, et stellae meridianae ex eis utrisque longitudo ab extremitate almaiarati sequente, est longitudo una, et stellae septentrionalis earum longitudo ab utrisque est duae partes. Stella uero sequens ex duabus stellis, quae sunt super humerum dextrum uulturis uolantis, tangit hanc extremitatem, sed antecedens utrarumque continetur inter almaiarati, et similiter stella luminosa antecedens ex duabus stellis quae sunt in ala septentrionali uulturis. Stella autem luminosa quae est inter duos humeros eius, et duae stellae quae sunt secundum rectitudinem cum ea, deficiunt parumper ab hoc, ut consequantur suo tactu hanc marginem. Deinde post illud comprehendit almaiarati sagittam totam, et continetur in ea stella quae est super extremitatem hastulae, distans a margine eius qui sequitur occidentem duabus partibus, et quod est de almaiarati ab eo quod sequitur uulturem uolantem, est spissius parum, et quod remanet post illud, est rarius. Deinde almaiarati capit uersus uolantem et terminant marginem eius super foramina, ab eo quod sequitur septentrionem et occidentem stella, quae est super humerum meridianum uolantis, et stella quae est sub ea in illa ala, et duae stellae quae sunt super pedem eius meridianum, et determinat marginem eius ab eo quod sequitur orientem stella, quae est super extremitatem decimae meridianae, et comprehendit super duas stellas quae sunt sub hac ala, egredientes ex formis, quarum longitudo ab ea est circiter duae partes, et quod est ex almaiarati ab eo quod sequitur hanc alam, est parum spissius, et quod est post illud, continuatur cum hoc cingulo. Veruntamen est uehementioris spissitudinis multum, et uidetur quasi incipiat inceptione alia, et illud est, quoniam declinat uersus posteriora cinguli alterius, ueruntamen accidit inter ipsum et illud foramen, deinde continuatur ex latere suo meridiano cum hoc cingulo, quod narrauimus in hoc loco, et est rarum ualde in loco continuationis, et incipit inspissari post illud, quod accidit ei de foramine inter ipsum et inter cingulum aliud ex stellis de luminosioribus stellis, quae sunt in cauda uolantium, et ex nebulosis quae sunt in genu eius septentrionali. Deinde permutatur parumper usquequo peruenit ad pileum ekifros, et terminant teminant ed. latus eius septentrionale stella meridiana ex stellis tribus quae sunt in pileo, et stella sequens tres, et apud illam stellam diuiduntur ex ea duo rami, quorum unus declinat uersus septentrionem et orientem, et alter uersus meridiem et orientem. Deinde almaiarati tendit super habentem sedem, et est habens palmam delibutam totam, et excepta stella eius quae est in pede, et terminat marginem eius ab eo quod sequitur meridiem, stella quae est in capite habentis sedem, et terminat marginem eius ab eo quod sequitur septentrionem, stella quae est in pede sedis eius, et stella quae est in crure habentis sedem. Reliquae uero stellae contentae cum eo omnes sunt positae in almaiarati, et ei quod est ex ipsa ab eo quod sequitur marginem eius, accidit uehementior raritas, et eius quod de ea est in medio, habentis sedem marginem ab eo quod sequitur septentrionem, et est in ultimo raritatis, determinat stella sola, quae est extra genu deferentis caput algol dextrum, et determinat marginem eius ab eo quod sequitur meridiem, et est in ultimo spissitudinis stella luminosa, quae est super latus dextrum, et duae stellae sequentes ex stellis tribus meridianis ab eo, et comprehendit iterum almaiara super recitationem nebulosam, quae est super manubrium et super stellam, quae est in capite eius, et super stellam quae est super humerumm eius dextrum, et super stellam quae est super cubitum eius dextrum. Quadrilaterum uero quod est in genu eius dextro, et stella iterum quae est in lacerto cruris eius, sunt posita in medio almaiarati, stella uero qua est in colo eius dextro, est iterum sub latere eius meridiano ad interiora parumper. Deinde cingulum transit per tenentem habenas, et uidetur nitor eius rarior parum. Stella autem quae est super humerum eius sinistrum, et dicitur alaioch, et duae stellae quae sunt super brachium eius dextrum deficiunt ab hoc, ut consequantur suo tactu marginem almaiarati, qui sequitur orientem et septentrionem. Stella audem parua quae est supra pedem eius sinistrum in margine, quae est super pedem eius dextrum, est sub eodem latere ad interiora medietate partis, duae uero stellae compares quae sunt super brachium sinistrum, et dicuntur duo hoedi, sunt positae in medio cinguli. Deinde post illud transit almaiara per duos pedes geminorum, et apparent post eam stellae quae sunt in duobus pedibus a spissitudine eius parua ad longitudinem aliquantulam. Stella autem sequens ex stellis tribus quae sunt secundum rectitudinem, quae sunt in pede tenentis habenas dextro, et stella sequens ex duabus stellis quae sunt in uirga superbi habentis canes, et duae stellae septentrionales ex stellis 4. quae sunt in palma eius, terminant marginem antecedentem almaiarati. Stella autem lucida quae est sub manu dextra tenentis habenas, et stella quae est in pede sequente sequentis geminorum, sunt intra latus eius sequens parte una, stella uero quae est in extremitate reliqua pedum, est in medio almaiarati. Deinde cingulum ab hoc loco separat in eo quod est inter stellas canis, et pertransit stellas canis ab eo quod sequitur orientem, et fiunt omne extra almaiarati exitu non paruo, et pertransit stellas canis ab eo quod sequitur occidentem, donec forsitan istae iterum omnes fiunt extra eam, et illud est, quoniam super stellam quae est super aures coprehendit arcus almaiarati simul obscurationem, et stellae tres quae sunt post eam, sequentes ipsam quae sunt in collo canis deficiunt parum ab hoc, ut occurrant almaiarati, et stella quae est supra caput canis, egrediens cum longitudine sola, est intra uentrem eius, quae sequitur orientem duabus partibus et media fere, et haec nebulositas est rarior parum. Deinde post illud transit almaiarati per nauem, et stella quae est septentrionalis antecedens ex stellis quae sunt in loco cotheli eius simili scuto, quem Graeci acstus nominant uersus marginem cinguli, ab eo quod sequitur occidentem, et stella quae est in medio huius loci simili scuto, et duae stellae quae sunt sub eo compares, et stella luminosa quae est in initio alfarassi, quae est apud sekem eius et stella quae est apud medium trium stellarum, quae sunt in ligno super quod augumentatur nauis deficiunt parum ab occursu lateris eius. Stella autem septentrionalis ex stellis tribus quae sunt in antenna, terminat marginem eius ab eo quod sequitur orientem. Stella autem luminosa quae est in extremitate nauis, ab eo quod sequitur pectus, est intra latus almaiarati haec parte una. Stella uero luminosa quae est sub scuto sequente, QUOD est in alfaras, est extra hanc marginem eius parte una. Stella autem meridiana ex duabus stellis luminosis quae sunt in medio alssara anten nae tangit marginem eius hanc. Duae uero stellae luminosae quae sunt in sectione ligni, super quod fabricata est nauis, sunt intra marginem eius antecedentem duabus partibus fere. Deinde almaiarati continuatur ex hoc loco cum incisione quae transit per duos pedes centauri et haec quidem nebulositas iterum quae transit per nauim, est subtilis parum, et inspissatur de ea proprie quod continetur cum scuto, et quod continetur cum antenna, et quod continetur cum portione ligni super quod est fabricata nauis. Et cingulum quidem antecedens, sicut diximus, separatur a cingulo quod narrauimus apud almaiarati, fit ergo principium eius ex illo loco, et transit in eam tribus uicibus ab eo quod sequitur corpus scorpionis. Stella autem sequens ex stellis tribus quae sunt in corpore scorpionis, est extra marginem eius quae sequitur occidentem parte una, sed stella quae est in spondili 4. scorpionis, est posita in aere claro inter duo cingula, et longitudo eius ab unoquoque eorum est fere aequalis, et est plus parte una parum. Deinde cingulum, cuius praecessit rememoratio, permutatur uersus orientem secundum similitudinem portionis circuli, et terminat latus antecedens almaiarati stella quae est super genu dextrum latoris serpentis, et determinat marginem eius sequentem, stella quae est super acutum cruris eius dextri, et stella antecedens ex stellis quae sunt in pede dextro, fortasse tangunt hoc latus eius, et iterum terminat post illud marginem eius quae sequitur scorpionem, stella quae est sub cubito dextro latoris serpentis, et determinat marginem eius qui sequitur orientem, stella antecedens ex duabus stellis quae sunt in palma huius manus. Deinde post hunc locum est foramen magnum in quo est aer purus, et in eo sunt duae stellae quae sunt super caudam serpentis post stellam quae est in eius extremitate, et iste terminus quem narraui huius cinguli est totus ex nebulatione subtili ualde propinqua aeri, praeter portionem eius quae comprehendit super tres spondiles, ipsa namque est parum spissior. Deinde post hoc incipit iterum almaiarati inceptione alia a stellis 4. sequentibus humerum dextrum latoris serpentis, et determinat marginem huius cingulum quod sequitur orientem, stella luminosa quam fortasse tangit illam quae est sub cauda uulturis uolantis sola, et determinat marginem eius contrarium illi longinquior stellarum quatuor, quarum praecessit rememoratio ab eo quod sequitur septentrionem, deinde hoc cingulum ab hoc loco aggregatur et constringitur ex raritate coram stella quae est in rostro auis, ita, ut opinetur abscisio eius ex ipsa. Residuum uero huius cinguli quod est inter stellam, quae est in rostro auis, et inter stellam quae est in pectore eius, est latius et spissius multum, et in medio huius loci spissi est stella quae est in collo auis, et declinat pars eius rara uersus septentrionem in loco in quo est stella quae est in pectore auis, et usque ad locum in quo est stella quae est in humero alae dextrae, et duae stellae compares quae sunt in extremitate pedis eius dextri, et ab hoc loco fit inter hoc cingulum, sicut diximus nuper, et inter cingulum alterum foramen purum existens a stellis quas diximus ex stellis auis usque ad stellam luminosam quae est in cauda eius.

⟨VI.5⟩ De fabricatione sphaerae solidae.

ISte ergo est modus situs eius quod uidetur in almaiarati, et ut praeparemus iterum exemplum per sphaeram solidam conuenientem radicibus quae firmatae sunt in sphaera stellarum fixarum, apparet quod hanc sphaeram etiam reuoluit secundum similitudinem sphaerarum stellarum haesitantium motus primus ab oriente ad occidentem in circuitu duorum polorum aequatoris diei, et permutatur iterum ad contrarium huius partis circa duos polos orbis solis, qui transit per media signorum, tunc nos ponemus artem eius et uiam ad descriptionem stellarum in ea secundum hunc modum. Ponam colorem huius sphaerae spaerae ed. aliquem ex coloribus inbibitis, ita, ut sit magis similis aeri in nocte, et est ille, in quo apparent stellae iterum non aeri in die, et signabo super eam duo puncta uere per diametrum opposita, et describam ea secundum quod ipsa sint duo poli circuli ex maioribus circulis quae semper ponam in eo quod est post in superficie orbis signorum, et describam circulum alium magnum orthogonaliter super hunc circulum transeuntem per polos eius, et incipiam ab una duarum sectionum quae cadunt inter eas et inter circulum primum. Diuidam ergo circulum signorum per 360. diuisiones, et diuidam diuisiones horum numerorum per illud quod uidebimus esse facile, deinde accipiam ex materia forti grossa armillas duarum quartarum superficierum abrasarum ab omnibus partibus rasione decenti, quarum una maior altera parumper erit, et ponam, ut minor earum contingat totam superficiem concauam maioris, et lineabo medium superficiei gibbosae cuiusque earum cum linea diuidente latitudinem eius secundum ueritatem, et diuidam unamquanque reuolutionem harum duarum linearum in duas medietates, deinde secabo loca diuisionis unius duorum laterum quae transeunt a duobus lateribus lineae cuiusque duarum armillarum, et diuidam duas medietates duorum circulorum quae sunt inter duas sectiones per 180. partes, et cum fecerimus illud, figemus armillam minorem circuli qui semper transit per polos duorum circulorum simul, scilicet circuli aequatoris diei, et circuli signorum, et transit iterum per duo puncta duorum tropicorum cum superficie sua in qua cadit diuisio, quam diximus, et perforabimus eam duobus foraminibus per diametrum oppositis medium, quorum erit apud extremitates superficiei diuisae, et figemus in eis duos clauos, et firmabimus eos in loco duorum polorum orbis signorum, quos posuimus in sphaera fixione qua praeparetur, ut reuoluatur super superficiem sphaerae totius, et ut nos ponamus firmationem stellarum fixarum in sphaera initium quod non alteretur, neque discedat, cum fixio duorum punctorum duorum tropicorum, et duorum punctorum duarum aequalitatum secundum ipsum circulum signorum in sphaera non sit possibilis, propterea quod stellarum quae firmantur in ea longitudines ab ipsa, non sunt longitudines eaedem, signabimus luminosiorem harum stellarum, scilicet stellam quae est in ore canis super circulum signorum apud partem quae est principium diuisionis, et ponam longitudinem eius a circulo signorum uersus polum meridianum, eius partes quas firmauimus ei in latitudine, deinde sciemus unamquanque reliquarum stellarum fixarum secundum ordinem per foramen, reuoluendo faciem armillae diuisae circa duos polos circuli signorum, et illud est, quia nos semper ponemus superficiem lateris diuisi super punctum circuli signorum longitudo partium, cuius ab initio numeri est pars quae transit per aschere alahabor, deinde considerabimus in latere diuiso amillae quae reuoluitur, et superpunctum eius longitudo partium, cuius iterum a circulorum est per numerum partium longitudinis stellae illius ab eo quod sequitur polum circuli signorum septentrionalem aut meridianum, signabimus locum illius stellae, postea nos firmabimus eam cum colore flauo, aut cum colore cum quo uidentur quaedam stellae cum mensuratione conuenienti ei quod firmauimus unicuique earum de quantitate magnitudinis mangitudinis ed. eius per figurationem formarum pertinentium unicuique signorum. Nos enim ponemus eam puram in ultimo quod est possibile, ita quod lineabimus super stellas intrantes in unaquaque forma cum lineis tantum, et non ponemus colorem eius iterum diuersum a sphaera in qua cadit, et non erit nostra multiplicatio cum coloribus diuersis, auferens nobis exemplum ab hoc, ut sit simul rei uerae, et de eo quo sit nobis facile comprehendere stellas et earum rememorationem, donec sciamus eas, cum eas contemplamur est, ut nosipsi studeamus imaginari stellas in exemplo sphaerico, etiam et earum erectionem in nostris mentibus, unde deinde nos firmabimus iterum in hac sphaera galaxiam secundum quod praemisimus, et significauimus super eam de locis suis, et suis figuris et dispositionibus suis. Iterum in spissitudine et raritate et foraminibus, et componam armillam maiorem, et est armilla quam semper erigimus loco circuli meridiei super armillam minorem continentem sphaeram, et figam eam in ipsa super duos polos qui sunt duo poli circuli aequatoris diei, et haec duo puncta in armila quidem maiore quae est circulus meridiei, ponemus apud duas extremitates lateris diuisi in duas medietates, quod ex eis est diuisum, et est illud quod posuimus supra terram unum eorum contra aliud secundum diametrum. In arnilla uero minori, et est illa quae transit per polos duorum circulorum simul, ponemus ea apud extremitates duorum arcuum, quorum longitudo ab unoquoque duorum polorum a duobus polis orbis signorum secundum diametrationes est partes declinationis, et sunt 23. partes et 50. minuta. Postquam posuerimus super loca sectionum duarum armillarum additiones paruas secantes tolerantes, ut in eis cadunt foramina in quibus figuntur duo claui. Cum latere autem diuiso armillae minoris, quia semper est circulus meridiei qui transit per duo puncta duorum tropicorum, cooperiemus in unaquaque hora punctum partium circuli signorum, longitudo partium cuius ab initio Sahare alhahabor est per numerum partium longitudinis Sahare alhahabor in hora in qua intenditur a tropico aestiuo secundum quod longitudo initij Sahare alhahabor a tropico aestiuo in principio regni Antonij in parte antecedente fuit 12. partes et tertia partis. Armillam uero meridiei praeparabimus orthogonaliter super basim quam erigemus loco horizontis, cuius superficies apparens diuidat ipsam in duas medietates, et ponam hanc armillam ita, ut possit moueri in ipsa sua superficie, ut quando uoluerimus eleuare per diuisiones circuli meridiei polum septentrionalem ab horizonte secundum arcum alicuius climatum positorum, non cadat super illud diminutio, propterea quod non inuenimus uiam ad hoc, ut firmemus circulum aequalitatis et duo puncta duorum tropicorum in hac ipsa sphaera, et illud est, quoniam puncti lateris diuisi circuli meridiei quod est inter duos polos aequatoris diei, et longitudo eius ab unoquoque eorum est 90. partes, quae sunt partes quartae uirtus est, uirtus puncti tropici aestiui, et eius quidem quod est ab eo quod sequitur meridiem uirtus, est uirtus puncti tropici hyemalis, ita, ut stellarum in quibus consideratur in aliqua horarum, cum permutatur motus primus, qui est ab oriente ad occidentem secundum latus diuisum armillae meridiei sit possibile, ut sciatur hoc idem experimentum per hanc eandem diuisionem etiam longitudines a circulo aequatoris diei, aut a duobus punctis duorum tropicorum in circulo qui transit per duos polos aequatoris diei.

⟨VI.6⟩ De uarietatibus figurarum quas habent stellae fixae.

ET quia iam significauimus hunc modum etiam super quem proprie oportet, ut currat res in firmatione stellarum fixarum, tunc oportet nunc, ut conuertamus sermonem ad species figurae earum. Dico ergo, quod species figurae inuentas in stellis fixis post species figurae, quae est quibusdam earum apud quasdam remanens secundum dispositionem unam, sicut quod quaedam earum quando comparantur cum quibusdam, sunt secundum rectitudinem, et quaedam earum quando comparantur cum quibusdam quibunsdam ed., sunt in figura trianguli, aut quae sunt ei similes, inueniuntur quaedam earum per comparationem ad stellas haesitantes et solem et lunam tantum, aut partes signorum, et quaedam earum inueniuntur ad terram simul, et stellas haesitantes, et solem et lunam, aut partes signorum tantum. Ipsae namque inueniuntur secundum rem quidem communem, quando aliqua stellarum fixarum et stella ex haesitantibus sunt, aut super unum et eundem circulorum, qui describuntur transeuntes per duos polos orbis signorum, aut super duos circulos diuersos, ueruntamen una earum est in triplicitate alterius, aut in eius quadratura, aut in sextilitate ipsius, scilicet, ipse continet angulum rectum, aut angulum addentem super rectum tertiam recti, aut minuentem ab eo tertiam recti. Et secundum rem quidem propriam inueniuntur in stellis, sub quibus possibile est currere quasdam stellas haesitantes, et istae stellae sunt stellatum quod est in sparsione orbis signorum, quae continet cursus haesitantium in latitudine, et ex illo figurae quidem earum per comparationem ad stellas haesitantes quinque inueniuntur apud comparilitatem earum ad eas, et cooperiunt eas. Figurae uero earum per comparationem ad solem, inueniuntur apud alistisar aut alistinia, aut apud altissere. Nos namque significamus per alistisar, ut stella incipiat occultari cum tendit ad intrandum in radios luminarium, et intelligimus per alistinia, ut cooperiat ipsam centrum unius duorum luminarium, et significamus per tassirie, ut incipiat uideri cum tendit ad exitum ex radijs luminarium. Species autem figurae quae est stellis fixis per comparationem ad terram solum sunt 4. summatim autem nominant eas quidam hominum cardines et centra, secundum distinctionem uero nominant eas ascendens et medians coelum supra terram et occasum, et medians coelum sub terra. Vbi enim est aequator diei super zenith capitis, illic stellae fixae omnes oriuntur et occidunt, et mediant coelum in omni reuolutione super terram semel, et semel sub ea, quod quidem est, propterea quod duo poli aequatoris diei occurrunt horizonti, quia fit, ut nulus circulorum aequedistantium sit apparens semper, neque occultus semper. Vbi uero poli sunt eius supra zenith capitis, nulla stellarum oritur neque occidit, cum locus aequatoris diei sit tunc locus horizontis. Vna itaque duarum medietatum sphaerae quas ipse separat, reuoluitur semper super terram, et medietas altera sub terra, unaquaeque ergo harum stellarum mediat coelum in reuolutione una bis. Illae quidem quae sunt in medietate prima supra terram, et illae quidem quae sunt in medietate secunda sub terra, in reliquis uero declinationibus quae sunt inter haec duo loca, cum quidam circuli sunt apparentes semper, et quidam semper occulti, stellae quas comprehendunt isti circuli, ab eo quod sequitur duos polos, non oriuntur neque occidunt semper, et mediant coelum in omni reuolutione bis, stellae quaedam quae sunt in circulo semper apparente supra terram, et stellae quaedam quae sunt in circulo semper occulto sub terra. Reliquae uero stellae, et sunt illae, quae sunt in istis circulis aequedistantibus maioribus, oriuntur et occidunt et mediant coelum in omni reuolutione semel supra terram, et semel sub ea, et post sunt tempora. Tempus quidem in quo incipit stella ab aliquo cardinum usquequo redit ad illum eundem cardinem est unum et idem in omni loco, et illud est, quoniam comprehendit reuolutionem unam in sensu. Et tempus quidem in quo incipit stela ab aliquo cardinum usquequo peruenit ad cardinem condiametralem ei, si consideratur in eo per comparationem ad circulum meridiei, et est unum et idem iterum semper in omni loco, et illud est, quoniam comprehendit ipsum medietas reuolutionis. Et si consideratur in eo per comparationem ad horizonta, si est aequator diei supra zenith capitis, tunc tempus iterum est unum et idem, et illud est, quoniam unumquodque horum duorum temporum comprehendit medietatem reuolutionis, quod quidem, quoniam circulos aequedistantes omnes tunc non solum diuidit in duas medietates circulus meridiei, imo circulus horizon etiam. In reliquibus uero declinationibus non est tempus quod est supra terram, neque tempus quod est sub terra secundum suam singularitatem aequale in eis omnibus, neque in aliqua earum secundum se est tempus quod est supra terram aequale tempori quod est sub ea, nisi in stellis quibus accidit, ut sint super ipsum aequatorem diei, quia aequatorem diei, cum sit inter reliquos circulos, diuidit horizon in sphaera, quamuis sit decliuis in duas sectiones aequales, et reliqui circuli aequedistantes ei omnes non diuiduntur in sphaera decliui, nisi in arcus non similes et non aequales. Deinde post illud tempus, in quo incipit stella ab ortu aut occasu, usquequo peruenit ad unum duorum mediantium coelum in unoquoque circulorum aequedistantium, est aequale tempori quod est inter illud medians coelum quod est ei, et inter ortum eius, aut inter ipsius occasum, propterea quod circulus meridiei diuidit semper sectionem circulorum aequedistantium quae est supra terram, et illam quae est sub ea in duas medietates. Tempus autem quod est inter ortum stellae aut occasum eius, et inter unumquodque duorum mediantium coelum est in sphaera, quando est decliuis non tempus unum. Sed in sphaera, quando est recta, est aequale, quoniam in hoc loco solo diuisiones circulorum aequedistantium quae sunt supra terram, omnes sunt aequales sectionibus circulorum quae sunt sub terra omnibus, et propter illud oportet in sphaera ubi est recta, ut stellae quae mediant coelum in ea simul oriantur semper simul, dum non fit permutatio earum circa duos polos orbis signorum sensata, et oportet in sphaera, quando est decliuis, ne stellae quae mediant coelum simul, oriantur simul, neque occidant simul, sed stellarum quae sunt decliuiores ad meridiem, tardatur semper ortus, ab ortu stellarum quae sunt ad septentrionem cum antecessione occasus earum. Species uero figurae quae inueniuntur per comparationem ad terram, et stellas haesitantes simul, et partes signorum sciuntur secundum summam quidem iterum propter ortum earum cum una stellarum haesitantium, aut cum aliqua partium signorum, aut per hoc, quod ipsae mediant coelum cum ea, aut occasu earum cum ea, et secundum distinctionem quidem, quoniam species figurae quae sunt per comparationem ad solem, inueniuntur secundum nouem modos. Primus itaque modus figurae nominatur ortus matutinus et illud est, quando stella est cum sole in horizonte a parte orientis, et huiusmodi sunt tres species, una earum scitur per ortum in matutinis sequentem, quae non uidetur, et illud est, quando stella incipit iestasar, non moratur post ortum solis quin oriatur, et species alia scitur per ortum in matutinis separatum, uerum et illud est, quando sit stella cum sole in hora una in horizonte ab eo quod sequitur orientem, et species tertia scitur per ortum in matutinis antecedentem quae uidetur, et illud est, quando stella iam incipit esse orientalis, oritur ante ortum solis. Modus uero secundus figurae dicitur medians coelum matutinalis, et illud est, quando stella, cum sol est in horizonte a parte orientis, est super circulum meridiei, aut supra terram, aut sub ea, et huic modo sunt tres species, una earum nominatur medians coelum in matutinis sequens, quae non uidetur, et illud est, quando stella moratur quin mediat coelum postquam oritur sol, et species alia nominatur medians coelum cum matutinis separata uera, et illud est, quando stella cum ortu solis mediat coelum, et species tertia nominatur medians coelum antecedens, et illud est, quod quando stella mediat coelum oritur sol statim, et quod est ex hoc modo supra terram uidetur. Et modus quidem tertius ex modis figurae dicitur occasus matutinus, et illud est, quando stella, cum sol est in oriente, est in horizonte a parte occidentis, et huic modo etiam sunt tres species, una earum nominatur occasus in matutinis sequens, quae non uidetur, et illud est, quod quando stella, cum oritur sol, occidit statim, et species secunda nominatur occasus in matutinis separatus uerus, et illud est, quando stella occidit cum ortu solis aequaliter, et species tertia nominatur occasus in matutinis antecedens, quae non uidetur, et illud est, cum contingit, ut quando stella occidit, oritur sol statim. Et modus quartus figurae est, qui dicitur ortus ad hohorin, et illud est, quando stella, cum sol est in circulo ad hohorin, et est circulus meridiei, est in horizonte ortus, et huic modo etiam sunt duae species, una earum est diurna quae non uidetur, et illud est, quando stella cum sol mediat coelum supra terram oritur, et species secunda est nocturna quae uidetur, et illud est, quando stella, cum sol mediat coelum, sub terra oritur. Et modus quintus dicitur medians coelum ad hohorin, et illud est, quando sol et stella simul fiunt in circulo meridiei, et huic modo sunt etiam duae species diurnae, quae non uidentur, et sunt sole mediante coelum supra terram, quando stella tunc mediat coelum cum eo iterum super terram, aut sub terra secundum diametrationem, et duae species nocturnae quae sunt, cum sol mediat coelum, sub terra, et una duarum specierum harum non uidetur, et illud est, quando stella simul est cum sole in circulo meridiei sub terra, et altera earum uidetur, et illud est, quando stella supra terram est opposita soli secundum diametrum. Et modus sextus figurae est, qui dicitur occasus ad hohorin, et illud est, quando stella cum sole in circulo meridiei est in horizonte, ab eo quod sequitur occidentem, et huic modo iterum sunt duae species, quarum una est diurna quae non uidetur, et illud est, quando stella, cum sol mediat coelum supra terram, occidit, et altera est nocturna quae uidetur, et illud est, quando sol cum stella mediat coelum sub terra occidit etiam. Et modus septimus figurae dicitur ortus uespertinus, et illud est, quando stella, cum sol est in horizonte ab eo quod sequitur occidentem, est in horizonte ab eo quod sequitur orientem, et huic modo iterum sunt tres species, quarum una dicitur ortus uespertinus sequens, qui uidetur, et illud est, quando stella, cum occidit sol, oritur statim. Et secunda species dicitur ortus uespertinus diuisus uerus, et illud est, quando stella oritur cum occasu solis aequaliter. Et species tertia nominatur ortus uespertinus antecedens qui non uidetur, et illud est, quando stella antecedit et oritur, occidit sol statim. Et modus octauus figurae dicitur medians coelum uespertinus, et illud est, quando stella, cum sol est in horizonte a parte occidentis, est in circulo meridiei, aut supra terram, aut sub ea, et huic modo iterum sunt tres species, quarum una dicitur medians coelum uespertinus sequens, et illud est, quando stella cum sol occidit statim mediat coelum, et quod ex illo est supra terram uidetur, et alia dicitur medians coelum dispertitus uerus, et illud est, quando mediat coelum stella cum occasu solis aequaliter. Et species tertia nominatur medians coelum uespertinus antecedens qui non uidetur, et illud est, quando cum stella mediat coelum, occidit sol statim. Et modus nonus figurae dicitur occasus uespertinus, et illud est, quando stella cum sole fit in horizonte ab eo quod sequitur occidentem, et huic modo sunt etiam tres species, quarum una dicitur occasus uespertinus sequens qui uidetur, et illud est, quando stella postquam incipit tegi occidit post occasum solis statim, et alia dicitur occasus uespertinus dispertitus uerus, et illud est, quando stella occidit cum occasu solis in loco uno. Et species tertia dicitur occasus uespertinus antecedens qui non uidetur, et illud est, quando stella incipit iam oriri, et occidit ante occasum solis.

⟨VI.7⟩ De declinatione et mediatione coeli.

ET postquam ostensae fuerunt ei res istae, et sciuit per considerationem loca harum stellarum in orbe signorum, et longitudines earum ab ipso in altitudine, possibile fuit ei, ut sciret partes orbis signorum et aequatoris diei quae mediant coelum, et quae oriuntur, et quae occidunt cum stella in climate posito, declarauit ergo illud per figuram sectorem, scilicet per 6. lineas compositas, et illud quidem ostenditur per quatuor quantitates proportionales secundum radices quas praemisimus in principio huius libri secundum hunc modum. Sit circulus transiens per duos polos 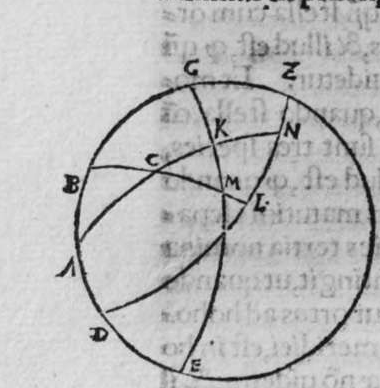orbis signorum circuls a b g, et aequator diei circulus d h z, et orbis signorum circulus g h e, et punctum h sit punctum uernale aut autumnale, et polus aequatoris diei sit punctum b, et polus orbis signorum punctum a, et sit stella super punctum t, et faciam transire super ipsum et super duo puncta a b, quae sunt duo poli duos arcus duorum circulorum magnorum, et sunt duo arcus b t m et a t k, et sit nostra intentio in primis, ut sciamus punctum l aequatoris diei, qui mediat coelum cum stella t, propterea ergo quod triangulus n h k est ex arcubus circulorum magnorum, et angulus eius k est rectus, et angulus eius h est notus, et latus eius h k est notum, et proportio sinus complementi lateris eius h k noti ad sinum complementi arcus anguli h n k subtensi et ignoti, est sicut proportio sinus arcus anguli k recti ad sinum arcus anguli h noti, et est sinus arcus anguli h n k notus, et est comprehensus, quoniam latus h k subtensum ei est notum. Oportet ergo propter illud, ut sit angulus h n k notus, triangulus ergo n h k est trium notorum angulorum, et propterea quod proportio sinus lateris h k eius noti ad sinum arcus anguli h m k subtensi ei noti, est sicut proportio sinus omnis lateris eius ad sinum arcus anguli cui subtenditur, erit propter illud sinus cuiusque laterum h n, n k notus, et unumquodque eorum est comprehensum, et unumquodque eorum est notum. Et quoniam arcus t k qui est latitudo stellae, est notus, erit arcus t n notus, ergo trianguli t l n angulus l est rectus, ergo proportio sinus lateris eius t n noti ad sinum anguli l recti, cui subtenditur, est sicut proportio sinus lateris t l ad sinum arcus anguli t n l subtensi ei noti, propter illud ergo sinus lateris t l est notus, et est comprehensus, quoniam angulus t n l, cui ipse subtenditur, est notus, ergo propter illud latus t l est notum, et proportio sinus complementi eius noti ad sinum complementi lateris t n subtensi recto noto, est sicut proportio sinus quartae circuli ad sinum complementi lateris n l, ergo sinus complementi lateris n l est notus, sed latus n l est minus quarta circuli, ergo est notum, et iam fuit latus n h trianguli h n k notum, ergo arcus l h est notus, ergo punctum aequatoris diei quod mediat coelum cum stella t est notum, et propterea quod arcus h m orbis signorum oritur in orbe recto cum arcu h l aequatoris diei, erit iterum punctum m orbis signorum, et est ille, qui mediat coelum cum stella t notum. completa est eius declaratio. Qualiter autem sciatur punctum aequatoris diei et orbis signorum, qui oritur aut occidit cum stella, quando punctum quod mediat coelum est notum, est secundum hunc modum. Sit circulus transiens per duos polos mundi circulus a b g d, et circulus aequatoris diei circulus b e d, et polus eius sit punctum n, et circulus horizontis circulus a e g, et sit stella oriens super punctum h, et faciam transire super hunc punctum, et super polum aequatoris diei arcum circuli magni, qui sit arcus n h t, erit ergo punctum t aequatoris diei ipsum punctum quod mediat coelum cum stella h, ergo est notae longitudinis ab uno duorum punctorum sectionum per illud quod nuper praemissum est, et arcus h t, qui est longitudo 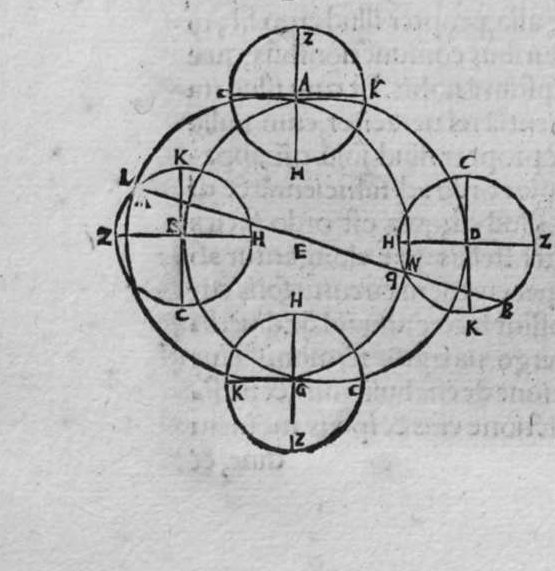stellae ab aequatore diei, iterum est notus per illud quod praemissum est, ergo triangulus e t h est ex arcubus circulorum magnorum, et angulus eius t est rectus, ergo proportio sinus complementi lateris eius t h noti ad sinum complementi arcus anguli t h e subtensi ei noti, est sicut proportio sinus arcus anguli t recti ad sinum arcus anguli t h e, oportet ergo ut sit sinus arcus anguli h notus, et similiter angulus e eius est notus, et propterea quod altitudo poli in regione posita nota est, tunc proportio sinus e ad sinum arcus anguli h est nota, ergo oportet ut sit sinus arcus anguli h notus, et similiter angulus e eius est notus, et haec proportio est proportio sinus lateris t h noti ad sinum e t quaesitum, oportet ergo ut sit latus e t notum, et ipsum est minus quarta circuli, ergo est notum, ergo longitudo puncti aequatoris diei, et est illud quod oritur cum stella ab uno duorum punctorum sectionis est nota. Et si nos secauerimus arcum t k aequalem arcui e t, erit punctum k aequatoris diei ipsum quod accidit cum stella h, ergo longitudo eius a puncto sectionis est nota etiam. Et similiter punctum orbis signorum quod oritur cum puncto e aequatoris diei, et punctum quod occidit cum eo, erit notum, sicut ostensum est in initio libri. Iam ergo declaratum est qualiter inueniatur punctum aequatoris diei et orbis signorum quod mediat coelum, et quod oritur et occidit cum stella, et illud est, cuius uoluimus declarationem. Scientia autem arcuum orbis signorum, qui sunt inter solem et stellam in principio apparitionis eius et ipsius occultationis, erit manifesta, cum declarabitur qualiter inueniatur quantitas eorum in fine libri in stellis currentibus secundum rectitudinem.

⟨VII⟩ LIBER SEPTIMVS. DE STELLIS quinque errantibus.

ET quia ostensum fuit ei totum, cuius praecessit declaratio de ese solis et lunae et stellarum fixarum, oportuit ut consideraret in dispositionibus stellarum currentium, et uidit quod primum in quo oportet considerare, est indagatio de ordine sphaerarum earum abinuicem, dixit ergo in hoc illud, cuius haec est narratio. Dico, quod inuenimus antiquos ex opificibus disciplinarum omnes simul conue nisse in quantum aestimo super hoc, quod istae sphaerae omnes sunt sub sphaera stellarum fixarum, et supra sphaeram lunae, et super hoc, quod sphaerae tres, scilicet quod sphaera Saturni, quae est maior earum, et sphaera Iouis, quae est secunda in magnitudine ex sphaeris quae sunt sub sphaera stellarum fixarum, et sphaera Martis, quae est sub istis, sunt supra sphaeras reliquarum stellarum et supra sphaeram Solis. Sphaeram autem Veneris et Mercurij quidam eorum quorum tempus praecesit, posuerunt sub sphaera solis, et quidam eorum ex illis qui uenerunt post eos, posuerunt eam iterum supra sphaeram solis, propterea quod non inueniunt eos tegere solem in aliqua dispositionum. Nobis uero uidetur, quod haec ratiocinatio non est ex eis in quibus fiducia habetur, et illud est, quoniam possbile est, ut aliqua stellarum sit sub sole, et non sit proculdubio in aliqua superficierum quae transeunt per solem et per uisus nostros, imo sit in superficie alia, propter illud ergo fit, quod non inuenitur cooperire solem, quemadmodum inuenimus in pluribus coniunctionibus, quae sunt lunae cum sole, luna enim tunc currit sub sole, et non tegit ipsum a nobis. Et cum illud ita sit, et nos secundum alium modum peruenire pernenire ed. non possumus ad scientiam rei ueraciter, cum nulla harum stellarum faciat aliquid sensibile de diuersitate aspectus, et propter illud solum quando apparet, inueniuntur longitudines stellarum, tunc uidemus quod propinquior ordo ad sufficientiam et dignior ad incipiendum est ordo eorum quorum tempus praecessit, et illud est, quia est ordo faciens rem magis similem rei naturali ex hoc, quod solem facit medium inter stellas quae elongantur ab eo longitudine tota, et inter stellas quae non sunt ita, imo semper currunt in circuitu solis cursu cum quo non elongantur ab eo usque inferius longitudine, ut possint facere aliquid de diuersitate aspectus, an sit quantitas de qua sit curandum. Haec est ergo narratio sermonis eius in ordine sphaerarum stellarum, et ego quidem miror omni admiratione de esse huius uiri, et haesito haesitatione magna propter illud, quod apparet de contradictione eius et ipsius inquietudine, et ipse non percepit illud, et res huiusmodi quidem elongatur ultima longitudine ab eo qui studet, sicut ipse studuit ex sermone in istis rebus notabilis quantitatis, et ipse non percepit contradictionem suam, et illud est, quoniam ipse dixit, quod sol habet diuersitatem aspectus sensibilem, et quod maior quantitas eius est 2. minuta et 51. secundum, et lineauit ad illud tabulas, et minuit eam in eclipsi solis ex diuersitate aspectus lunae. Et dixit, quod non inuenit ueneri et mercurio, quamuis sint in propinquiori propinquitate eorum a terra, diuersitatem aspectus cui sit quantitas de qua sit curandum, et ipse demonstratione probat in eo QUOD uenit post, quod medietas diametri orbis reuolutionis ueneris est 43. partes et 6. partis, per partes quibus medietas diametri ecentrici utriusque eorum est 60. partes, et quod linea quae est inter duo centra, scilicet centrum orbis ecentrici et centrum orbis signorum, est pars una et quarta partis per illam quantitatem. Cum ergo fuerit stella ueneris in longiori longitudine sua, oportet ut sit longitudo eius a centro terrae maior 104. partibus, et cum fuerit in propinquiori propinquitate sua, erit longitudo eius a centro terrae minor 16. partibus. Cum ergo sit sol super eam, et erit longitudo eius semper a centro terrae plus 104. partibus, et est ei diuersitas aspectus, cuius summa est fere tria minuta, tunc quia non inuenitur, ut stellae ueneris, cum inter ipsam et inter centrum terrae est minus 16. partibus diuersitas aspectus, cui sit quantitas manifesta, et oportet, ut sit secundum quod partium eius longitudini circiter tertiam partis, et oportet iterum, si stella mercuij est sub sole, ut sit diuersitas aspectus eius, quando est in longitudine propiori orbis reuolutionis suae fere 7. minuta, licet diuersitas aspectus utriusque in istis locis non sit possibilis, propterea quod uterque est in constructione solis, sed est possibilis in eo quod appropinquat eis. Cum autem stella ex eis utrisque est super lineas contingentes or bem reuolutionis, tunc acceptio diuersitatis aspectus eius est possibilis ualde, quia sunt super finem longitudinis suae a sole, prolongatur ergo propter illud mora earum supra terram, et cum centrum orbis reuolutionis earum est tunc in uno duorum nodorum, est unaquaeque duarum stellarum in superficie orbis signorum quia est diuersitas aspectus utrisque nuda a latitudine earum, et est diuersitas aspectus ueneris tunc quasi 6. minuta, et diuersitas aspectus mercurij quasi 4. minuta. Cum ergo non inueniatur eis utriusque diuersitas aspectus, cui sit quantitas de qua sit curandum secundum quod ipse dixit, et soli sit diuersitas aspectus sensibilis, cui sit quantitas de qua est curandum, quomodo sunt sub sole. Illud quo contradixit ratiocinationi antiquorum, qui crediderunt quod ipse supra solem per hoc, quod ipsi non inueniunt eas utrasque tegere solem in aliqua dispositionum, quia diit, quod stella quandoque est sub sole, et non tegit ipsum a nobis, quoniam est superficies quae non sunt superficies, quae transeunt per uisus nostros et per solem, sicut accidit in pluribus coniunctionibus quae sunt lunae cum sole, non destruit ratiocinationem earum nisi postquam demonstratur, quod duae stellae uenus et mercurius non transeunt semper super lineas quae transeunt per uisus nostros et per solem, et illud quod dat sermo eius, est quod ipse credit illud. Res uero non est sicut ipse credidit, imo declaratur per demonstrationem ueram ex summa quam dabimus in tractatu 13. libri sui in radicibus super quas currit esse suarum latitudinum, quod ipsae transeunt per lineas transeuntes per uisus nostros et per solem necessario. Incipiamus ergo nunc in declaratione illius. Sit itaque orbis egredientis centri circulus a b g d, et orbis signorum circulus a m g n circa centrum e, et est locus uisuum, et sit punctum a unus duorum nodorum orbis egredientis 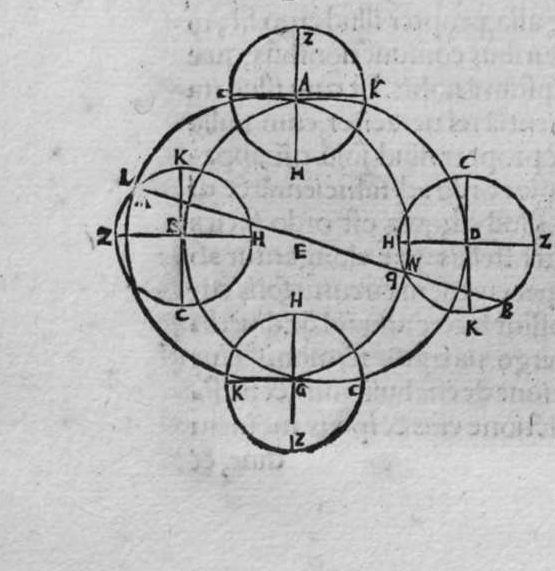centri stellae, et punctum g nodus secundus, et punctum b una duarum partium, et punctum d pars secunda, et sit orbis reuolutionis stellae circulus 3 h, et sit centrum eius in primis super punctum a, quod est unus duorum nodorum, et diametri eius transiens per longitudinem eius longiorem et propinquiorem linea 3 h, et diameter erecta super eam orthogonaliter linea t h. Et Ptolomeus quidem ostendit in tractatu 13. libri sui, quod pars septentrionalis et meridionalis duorum orbium suorum mouentur ad septentrionem et meridiem a superficie orbis signorum, et quod ultimum quo elongantur ab eo. In stella quidem ueneris est 6. partis, et in stella quidem mercurij est 3. quartae partis, et quod duae extremitates duarum diametrorum z h et t k quae sunt duo puncta z et t mouentur semper super duas circumferentias duorum circulorum paruorum aequalium, et inclinant duas extremitates harum duarum diametrorum ab orbe signorum ad septentrionem et meridiem, et quod reuersio cuiusque harum duarum extremitatum in circumferentia circuli, est aequalis reditioni orbis reuolutionis in orbe egredientis centri, et quod quando est centrum orbis reuolutionis super punctum a, quod est unus duorum nodorum, est diameter t k in superficie orbis signorum, quia est sectio communis, et sunt orbis reuolutionis et diameter z h secantes signorum, et sunt duo puncta z et h super finem longitudinis suae ab eo, unum eorum in septentrionem, et secundum in meridiem. Et cum sit centrum orbis reuolutionis super punctum b quod est una duarum partium, sit res econtrario illius, scilicet, quia est tunc diameter t k secans superficiem orbis signorum, quia sunt duo puncta t et k super finem longitudinis ipsorum ab eo unum eorum in septentrione, et secundum in meridie, et est diameter z h in superficie orbis ecentrici, quia sunt duo puncta z et h opposita centro orbis signorum. Cum ergo peruenit centrum orbis reuolutionis ad punctum g quod est nodus secundus, redit diameter t k ad superficiem orbis signorum, et fit sectio communis ei et superficiei orbis reuolutionis. Et fit diameter z k secans superficiem orbis signorum, et eius extremitates sunt super finem longitudinis suae ab eo in septentrione et meridie, extremitas quidem quae est septentrionalis ab eo cum sit centrum orbis reuolutionis teuolutionis ed. super punctum a, est meridiana, et extremitas quae est meridiana ab ipso a puncto a est septentrionalis ab eo. Et similiter est dispositio in his duabus diametris per motum centri orbis reuolutionis a puncto g ad punctum d et ex puncto d ad punctum a. Sequitur ergo ab hoc, ut extremitas sectionis communis inter superficiem orbis signorum et superficiem orbis reuolutionis moueatur ex puncto a ad partem puncti b. Nam extremitas eius quae est punctum t, mouetur ad partem puncti z, et extremitas eius quae est punctum k mouetur ad partem puncti h. Cum ergo sit centrum orbis reuolutionis super punctum b, fit extremitas huius sectionis communis, et est linea l q opposita centro orbis signorum, ergo cum currit centrum orbis reuolutionis in quarta a b, mouetur extremitas una ex puncto t ad punctum z, et mouetur extremitas secunda ex puncto k ad punctum h. Et cum mouetur centrum orbis reuolutionis in quarta b g, mouetur extremitas una ex puncto z ad punctum k, et extremitas secunda ex puncto h ad punctum t. Et apud motum centri orbis reuolutionis in quarta g d, mouetur extremitas una ex puncto k ad punctum h, et extremitas secunda ex puncto t ad punctum z secundum illud super quod fuit, cum centrum orbis reuolutionis fuit in quarta a b et opponuntur suae extremitates centro orbis signorum quando fit super d, et quando mouetur centrum orbis reuolutionis in quarta d a, mouetur extremitas una ex puncto h ad punctum t, et extremitas secunda ex puncto z ad punctum k, secundum illud super quod fuit, cum centrum orbis reuolutionis fuit in quarta b g, et propterea quod plurimum diuersitatis solis est duae partes et 24. minuta, et illud est plurimum, quo corpus solis elongatur a duobus lateribus centri orbis reuolutionis harum duarum stellarum, et illud est minus plurimum quam arcus orbis signorum, cui subtenditur medietas diametri orbis reuolutionis stellae, scilicet linea a t, quia iste arcus in stella ueneris est plus 43. partibus, et in mercurio est plus 22. partibus. Oportet necessario ut in motu centri orbis reuolutionis in unaquaque quartarum a b et b g, et g d et d a occurrat una duarum extremitatum huius differentiae communis motarum lineae continuanti inter corpus solis et centrum orbis signorum, quod est locus longitudinum. Est ergo ille locus orbis signorum loco unius duorum nodorum orbis decliuis lunae, et propterea quod motus stellae in orbe reuolutionis suae est diuersus in uelocitate motui centri orbis reuolutionis suae, oportet necessario ut stella in quibusdam horis sit super unum illorum 4. punctorum. Est ergo tunc super lineam transeuntem per uisus nostros et solem, et hoc sine dubio est, quod crediderunt illi antiquorum qui fuerunt posteriores, et propter illud abscise dixerunt, quod istae duae stellae sint supra solem, quia inuenerunt eas per hanc uiam uel tegere, et quandoque essent super lineas quae transeunt per uisus nostros et solem, et non inuenerunt eas ipsi, neque qui eos praecesserunt, eclipsare solem in aliqua dispositionum, dixerunt ergo prorsus propter illud, quod ipsae sunt supra solem, et propterea quod Ptolomeus non percepit hoc, imo credidit, quod ipsae non sunt semper super lineam transeuntem per uisus nostros et per solem, destruxit propter illud ratiocinationem eorum, et elongatus est ultima elongatione secundum quod aestimo in hac intentione nobilis quantitatis, quia pertransiuit super eum, quod eclipsis non est nisi per duas conditiones, una earum est, ut eclipsatum sit supra eclipsantem, et secunda est ut unum eorum transeat per lineam transeuntem per uisus nostros et per secundum. Illud autem quod dixit Ptolomeus, quod similis est rei naturali ut sol sit medius inter stellas quae elongantur ab eo longitudine tota. Et inter stellas quae non sunt ita, est sermo in ultimo temporis, imo similius rei naturali est, ut sint sol et luna, quia sunt ambo luminaria in parte, et sint stellae omnes simul continue in parte, quia sunt in pluribus dispositionibus similes ultima simulatione, scilicet in compositione orbium suorum, et in diuersitatibus suis, et in eo quod accidit eis de statione et retrogradatione, ergo similius rei naturali est, ut non separentur abinuicem per alia. Et si esset similius rei naturali, ut sit illud quod elongatur a sole longitudine tota in parte, et illud quod non elongatur ab eo longitudine tota in parte, esset luna cum stellis tribus superioribus, quia elongatur a sole longitudine tota sicut elongantur illae, et non licet expositori ut exponat in sermone eius, elongatur a sole longitudine tota, illud quod exposuit quidam considerantium de illis quae sunt huius nostri temporis, et est, quod ipse uoluit per longitudinem totam tempus reditionis solis. Nam hic per longitudinem non uoluit nisi longitudinem in tempore non in loco, propterea quod istarum stellarum trium non aggregatur aliqua cum sole, nisi post complementum reditionis aut reditionum solis, et quod unaquaeque harum duarum stellarum et luna aggregatur cum sole ante complementum reditionis eius. Qui ergo exponit sermonem eius hac expositione, uacat rem quam firmare non potest, quoniam testis sermonis Ptolomei destruit uocationem eius, et illud est, quoniam adunxit ad sermonem suum non est ita, imo ipsae semper currunt in circuitu suo, cursu cum quo non elongatur ab eo ad inferius longitudine quam possibile sit facere aliquid diuersitatis aspectus, cui sit quantitas de qua sit curandum. Ex isto ergo sermone non intelligitur aliquo modorum longitudo in tempore, et non intelligitur ex eo, nisi longitudo in loco, quoniam inferius et circuitus non dicuntur in tempore, et neque dicuntur nisi in loco, et diuersitatem quidem aspectus non facit esse necessaria longitudo in tempore, et neque facit eam necessariam nisi longitudo in loco. Et si uoluisset tempus, narrasset de illo absque hac narratione, imo dico similius rei est, ut sit sol medius inter stellas quae sunt tardiores eo, et inter illas quae sunt uelociores, et de eis iterum quae significant, quod ipse non uoluit per longitudinem totam, nisi circumferentiam circuli, non tempus reditionis, est sermo eius in capitulo 6. tractatus 10. libri eius. Demonstrationes quidem quibus rectificantur quantitates cuiusque duarum diuersitatum et longitudo longior cuiusque earum nos non inuenimus semitam, ut incedamus in inuentione earum in istis tribus uiam qua incessimus in illis duabus, propterea quod istae stellae elongantur a sole longitudine tota, et non apparet ex considerationibus sicut apparet in maiori longitudinum in stella mercurij et stella ueneris, quando sit stella super locum, super quem tangit linea extracta ex uisibus nostris orbem reuolutionis, et in hoc est ostensio sufficiens ei qui eligit concedere ueritatem, et dimittit falsitatem et diuersitatem.

⟨VII.1⟩ In eo quod oportet praemittere de motibus quinque stellarum errantium.

STellarum quidem currentium quinque inuenit ipse, et qui eum praecesserunt moueri in omnibus partibus orbis signorum motu aequali, neque moueri in parte una eadem motibus aequalibus, scilicet, quia mouetur in ea maiori motuum suorum et medio eorum, et minori ipsorum. Significatum est ergo eis super illud, quod reditus cuiusque earum in orbe suo proprio est diuersus a reditu suo in orbe signorum, et inuenimus hanc diuersitatem redire cum reditione stellarum ad partem unam orbis signorum, et ad longitudinem unam a medio solis, scilicet, quando stella est et medius solis unusquisque eorum in parte aliqua orbis signorum, deinde redit unusquisque eorum ad partem in qua fuit in primis, et est motus stellae tunc in illa parte aequalis motui eius in ea in primis. Et postquam consequuti sunt, inuenerunt motum stellae in parte una, et longitudines eius a medio solis diuersas, et inuenerunt tempus quod est a maiori motuum eius in illa parte ad medium eorum maius semper tempore, quod est a medio motuum eorum ad minorem ipsorum, et huius quidem casus non praeparatur nisi per radicem, in qua agitur secundum orbem reuolutionis tantum, ita, ut stella moueatur in longitudine longiori, cuius ad partem successionis signorum non ad diuersitatem successionis eorum sicut est in luna, deinde ipsi considerauerunt stellam ex eis in partibus diuersis orbis signorum, et longitudines eius a medio solis aequales. Quare inuenerunt motus eius in illis partibus diuersos, et inuenerunt tempus quod est a minori motuum eius ad medium eorum minus semper tempore, quod est a medio eorum ad maiorem ipsorum, et sequitur, ut sit hoc secundum unamquanque duarum radicum, ueruntamen magis licite et proprius per radicem, in qua agitur secundum orbem egredientis centri, quoniam completur motu uno, et propterea etiam quod diuersitatis primae non praeparatur casus nisi per radicem, in qua agitur secundum orbem reuolutionis eius tantum, tunc propter illud oportet, ut sit haec diuersitas secundum radicem, in qua agitur secundum or bem egredientis centri. Inuenerunt ergo uniuscuiusque harum quinque motuum ordinari secundum quod dat eis aggregatio harum duarum radicum secundum quod narro quod est, quia ex stellis est quae mouetur super circumferentiam orbis reuolutionis eius motu aequali, quandoquidem est in longitudine longiori eius ad partem successionis signorum, et quandoquidem est in longitudine propinquiori eius ad diuersitatem successionis eorum. Et completur reditus eius in eo cum reuersione stellae ad longitudinem a medio solis aequalem longitudini quae fuit ei ab eo ante, et centrum orbis reuolutionis mouetur etiam ad partem successionis signorum motu aequali circa centrum egressum a centro orbis signorum, et quia illud confitetur, coeperunt inquirere tempus reditus cuiusque harum duarum diuersitatum in unaquaque harum quinque stellarum. Inquisiuerunt ergo illud per hoc, quod considerauerunt stellas ex eis in parte aliqua orbis signorum, et in longitudine aliqua a medio solis usquequo redijt ad illam eandem partem, et ad illam longitudinem a medio solis eandem. Diuiserunt ergo illud tempus super numerum reditionum stellarum ad longitudines suas aequales a medio solis, et exiuit tempus reditionis reditonis ed. eius in orbe reuolotionis suae, et similiter diuiserunt ipsum etiam super numerum reditionum stellae ipsius in orbe signorum, et exiuit inde tempus reditus eius in ipso. Sciuerunt ergo per illud tempus cuiusque reditionum harum duarum diuersitatum, et inuenerunt in stellis tribus altis, scilicet Saturno et Ioue et Marte, quod numerus redituum stellae ex eis in tempore reuolubili in orbe reuolutionis suae cum numero redituum orbis reuolutionis suae in orbe signorum, est aequalis numerus redituum solis in illo tempore reuolubili, et illud quidem est conueniens ei quod apparet in eis quod est, quia stella ex eis quando est in parte aliqua orbis signorum tecta secundum propinquitatem solis, est in uelociori motuum suorum in illa parte. Et quando est in diametratione medij solis, est in tardiori motuum suorum in illa parte, imo est rediens in ea, et quando est in quadratura medij solis, est in mediali motuum suorum in illa parte. Significauerunt ergo ex illo, quia quando est in tectura, scilicet quando est aggregata cum sole, est in longitudine longiori orbis reuolutionis suae, et quando est diametrata medio solis, tunc ipsa est in propinquitate propinquiori orbis reuolutionis suae. Et quando est in quadratura eius, tunc ipsa est in transitu medio orbis reuolutionis, et sequitur ab hoc, ut sit linea quae egreditur ex centro orbis reuolutionis ad stellam aequedistans semper lineae quae continuat inter medium solis et centrum orbis signorum, aut continuata cum ea secundum rectitudinem, sicut ostendam in eis quae sunt post. Reditus autem centri orbis reuolutionis ueneris et mercurij est aequalis reditui medij solis, et ipsi duo per motum suum in orbe reuolutionis suae reuoluuntur semper circa medium solis, quia sunt in longitudine longiori et propinquiori orbis reuolutionis, quando sunt in medio solis et in duobus transitibus eius medijs, quando sunt in ultimo longitudinis suae a medio solis. Ptolomeus autem uerificauit tempora horum redituum per considerationes suas et considerationes antiquorum, et processit in uerificatione illius uia qua processit in uerificatione redituum lunae. Modus autem secundum quem currit res in ordine orbium harum stellarum quinque, est secundum hanc maneriem, quod est, quia quatuor stellae ex eis, scilicet Saturnus, Iupiter, Mars et Venus, conuenientes sunt in ordinibus orbium suorum, quod est, quia stella ex eis mouetur aequaliter super circumferentiam orbis reuolutionis suae, quando quidem est in longitudine longiori eius ad continuitatem signorum, et quando est in longitudine propinquiori ad contrarium continuitatis eorum, et centrum orbis reuolutionis mouetur ad partem successionis signorum super circumferentiam orbis, cuius centrum est egrediens a centro orbis signorum, et est orbis deferens eum, motus uero eius aequalis non est in circuitu centri huius orbis deferentis, sed est in circuitu centri alterius, cuius longitudo a centro deferentis est sicut longitudo centri deferentis a centro orbis signorum. Ista uero tria centra, scilicet centrum orbis signorum, et centrum deferentis orbem reuolutionis, et centrum motus aequalis super unam consistunt lineam, et est linea transiens per longitudinem longiorem et propiorem. Stella autem Mercurij mouetur etiam motu aequali in circuitu centri orbis reuolutionis suae, cum quidem est in longitudine longiori ad partem continuitatis signorum. Sed cum est in longitudine propiori ad contrarium illius, et centrum orbis reuolutionis eius mouetur ad partem succesionis signorum super circumferentiam orbis centri egredientis ab orbe signorum, et est orbis deferens ipsum. Verum centrum huius orbis deferentis mouetur in circuitu centri egredientis a centro orbis signorum iterum motu aequali ad contrarium successionis signorum, aequali in uelocitate motui centri orbis reuolutionis aequali, et nominatur hoc centrum reuoluens orbem deferentem. Fit ergo propter illud quod centrum orbis reuolutionis abscidit circumferentiam huius orbis deferentis in reuolutione una, scilicet in tempore anni bis, fit ergo in longitudine sua longiori, et in propinquitate sua propiori duabus uicibus in tempore anni unius. Motus autem centri orbis reuolutionis eius aequalis est in circuitu centri, qui diuidit spacium quod est inter centrum orbis signorum et centrum in circuitu, cuius mouetur centrum deferentis, et est illud quod nominatur reuoluens deferentem in duo media, et longitudo centri deferentis semper in motu suo ab hoc centro reuoluente ipsum, est sicut longitudo huius centri reuoluentis a centro motus aequalis, et sicut longitudo centri motus aequalis a centro orbis signorum. Ita uero tria centra, scilicet centrum orbis signorum et centrum motus aequalis, et centrum reuoluens deferentem, sunt super lineam unam, et est linea transiens per longitudinem longiorem et propiorem orbis ecentrici, et nos quidem explicabimus ad omnia quae diximus exemplum, ut per illud alleuietur formatio horum orbium quae sunt stellis, et ordo eorum. Ponam ergo in primis in radice secundum quam agitur in stellis quatuor orbem 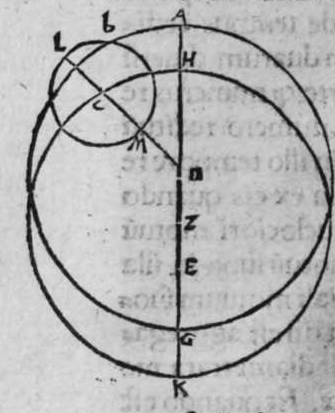egredientis centri, circa cuius centrum est motus aequalis, circulum a b g circa centrum d, et sit diameter eius transiens per punctum d, et diameter orbis signorum linea a g, et sit super ipsam centrum orbis signorum punctum e, et punctum longioris longitudinis punctum a, et propioris propinquitatis punctum g, et diuidam lineam d e in duo media super punctum z, et lineabo super centrum z, et cum longitudine a d circulum h t k, erit ergo iste circulus orbis deferens orbem reuolutionis, et signabo in circuitu puncti t orbem reuolutionis super quem sint l m, et continuabo centrum eius quod est punctum t cum centro d, quod est centrum motus aequalis per lineam d m t l, erit ergo punctum l longitudo longior, et punctum m longitudo propior. Mouetur ergo linea d e l ad successionem signorum motu aequali circa centrum d, quia mouetur motu eius centrum orbis reuolutionis super circumferentiam circuli h t k, et mouetur stella super circumferentiam orbis reuolutionis suae motu aequali super centrum suum, quandoquidem est in puncto l quod est longior longitudo eius ad continuitatem signorum, et quando est super punctum m ad contrarium illius. IN stella autem Mercurij ponemus orbem egredientis centri circa centrum, cuius est motus aequalis, circulum a b g in circuitu centri d, et sit diameter eius transiens per ipsum et 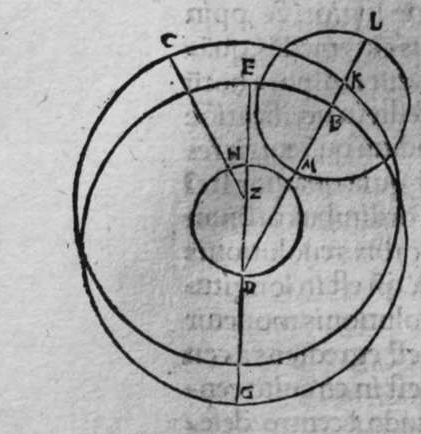per centrum orbis signorum linea a d g, et sit centrum orbis signorum super ipsam punctum e, et punctum longitudinis longioris punctum a, et longitudinis propioris punctum g, et secabo lineam d z aequalem lineae d e, erit ergo punctum existens centrum reuoluens centrum deferentis, et protraham ab ipso lineam z h t. Sitque linea z h aequalis lineae z d, et signabo in circuitu centri z, et cum longitudine z d circulum h d, et secabo lineam h t aequalem lineae a d, quae est medietas diametri circuli a b g, et ponam punctum h centrum, et reuoluam circulum t k, erit ergo iste circulus ipse orbis deferens centrum orbis reuolutionis, et sit centrum orbis reuolutionis super ipsum punctum k, et continuabo ipsum cum puncto d quod est centrum motus aequalis cum linea d m l, erit ergo linea m k l diameter eius, et erit punctum l longitudo eius longior, et punctum m longitudo eius propior, et erit motus huius diametri aequalis in circuitu centri d ad successionem signorum. Mouebitur ergo motu eius centrum orbis reuolutionis, scilicet punctum k super circumferentiam circuli t k, et linea z h t mouetur etiam motu aequali ad contrarium successionis signorum, aequali in uelocitate motui lineae d k, et stella mouetur motu aequali super circumferentiam orbis reuolutionis in circuitu centri eius, cum quidem est in longitudine sua longiori scilicet puncto l ad partem successionis signorum. Et quando est in propinquitate sua propiori ad contrarium illius, propter illud ergo centrum orbis reuolutionis abscidit circumferentiam orbis deferentis in tempore reditionis suae in orbe signorum, scilicet tempore anni bis, quia fit in unaquaque longitudinis eius longioris et propinquitatis eius propinquioris in reuolutione una duabus uicibus. Ex eis autem quae oportet me ostendere iterum de eo quod sequitur ab istis radicibus, est, quod quando est longitudo centri orbis reuolutionis a duabus partibus longitudinis longioris ecentrici longitudo aequalis, et est longitudo stellae in orbe reuolutionis suae a duabus partibus longitudinis longioris longitudo aequalis, tunc duo anguli diuersitatis pertinentes ad orbem signorum sunt aequales, et similiter duo anguli utrique, quorum subtenditur medietas diametri orbis reuolutionis apud centrum orbis signorum sunt aequales. Sit itaque in radice secundum quam agitur in stellis quatuor orbis deferens centrum orbis reuolutionis circulus a b g d in circuitu centri e, et diameter transiens per longitudinem 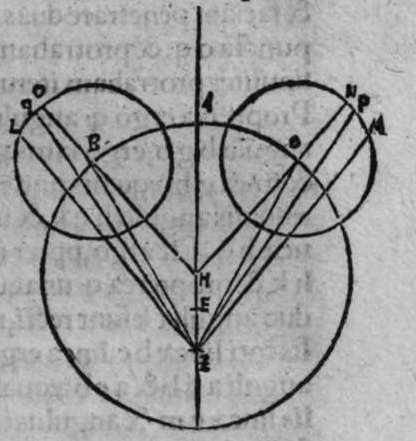longiorem et propiorem linea a e g, et punctum a longitudo longior, et punctum g longitudo propior, et centrum orbis signorum punctum z, et centrum motus aequalis punctum h, et secabo duos arcus aequales a duabus partibus longitudinis, qui sunt a d, a b, et sit punctum b centrum orbis reuolutionis, et similiter punctum d etiam, et signabo super unumquodque eorum orbem reuolutionis o l et n m, et continuabo centrum eorum cum centro motus aequalis per duas lineas o b h et n d h. Erunt ergo duo puncta o n existentia longitudo longior orbis reuolutionis, et continuabo centra eorum cum centro orbis signorum per duas lineas d z et b z. Sitque stella in duobus orbibus reuolutionis supra duo puncta l m, et sit arcus o l aequalis arcui n m, et continuabo duo puncta l m cum centro orbis signorum per duas lineas l z, m z. Dico ergo, quod duo anguli h b z, h d z sunt aequales, et quod duo anguli b z l et d z m etiam sunt aequales, cuius demonstratio est, quia linea b h est aequalis lineae d h, et linea h z est communis, et angulus b h z est aequalis angulo d h z, tunc angulus h b z est aequalis angulo h d z, et linea b z est aequalis lineae d z, et propterea iterum quod angulus o b l est aequalis angulo n d m, et angulus h b z aequalis angulo h d z, remanet angulus l b z aequalis angulo m d z, et latus b z aequale lateri d z, et similiter latus b l aequale lateri d m, ergo angulus b z l est aequalis angulo d z m. Si ergo nos protraxerimus a puncto z duas lineas aequedistantes duabus lineis b h, d h, quae sint lineae duae z q, z p, erit angulus b z q aequalis angulo d z p, et remanet q z l aequalis angulo p z m, uerum unaquaeque duarum linearum z q, z p transit per medium solis in stella ueneris tantum. Sequitur ergo propter illud, ut sint longitudines eius a medio solis in istis cursibus aequalibus a duabus partibus longitudinis longioris, et sunt duo anguli q z l, p z m aequales, et sequitur ab hoc, ut sint duae longitudines maiores stellae contrarie aequales. completa est eius declaratio. Et ostendam illud etiam in stella mercurij. Sit itaque centrum orbis 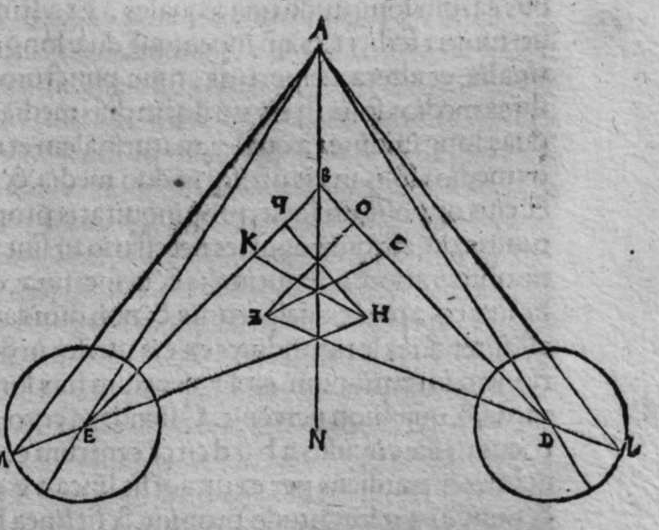signorum punctum a, et centrum motus aequalis punctum b, et centrum reuoluens centrum deferentis punctum g, et ponam duas lineas e b, d b, continentis cum linea b g duos angulos aequales, qui sint duo anguli g b e et g b d, et sit unumquodque duorum punctorum e d centrum orbis reuolutionis stellae mercurij in duobus cursibus aequalibus a duobus lateribus longitudinis longioris et propioris, et sit stella super duo puncta m l, et sit longitudo eius puncto longitudinis longioris orbis reuolutionis a duobus lateribus eius longitudo aequalis, et continuabo duo puncta m l cum centro orbis signorum per duas lineas a m, a l, et similiter duo puncta d e per duas lineas a d, a e. Dico ergo, quod duo anguli a d b et a e b, et sunt duo anguli diuersitatis in orbe signorum aequales, et quod duo anguli d a l et e a m iterum sunt aequales, quod sic demonstratur. Faciam super punctum g lineae g n, quae est transiens per longitudinem longiorem et propiorem angulum aequalem angulo d b g qui sit angulus z g n, et similiter faciam super ipsum a latere altero lineae g n angulum aequalem angulo g b e qui sit angulus h g n et sit unaquaeque duarum linearum z g, h g aequalis lineae b g. Propterea ergo quod motus centri orbis reuolutionis apud punctum b est aequalis motui centri deferentis circa punctum g, est linea g z existens linea transiens per centrum deferentis per longitudinem eius longiorem, erit ergo punctum z centrum deferentis, continuabo ergo ipsum centro orbis reuolutionis, scilicet puncto d, ergo linea d z est medietas diametri deferentis, et similiter erit punctum h centrum deferentis, quando est centrum orbis reuolutionis super punctum e, ergo continuabo ipsum cum puncto per lineam e h, erit ergo linea e h medietas diametri deferentis, et faciam penetrare duas lineas z g, h g donec occurrant duabus lineis b d, b e super duo puncta o q, et protraham a puncto z perpendicularem super lineam b d quae sit linea z t, et similiter protraham iterum a puncto h perpendicularem super lineam b e, quae sit linea h k. Propterea ergo quod angulus z g n est aequalis angulo g b o, ergo angulus g b o est aequalis angulo b g o, ergo latus g o est aequale lateri b o, et similiter est latus b q aequale lateri g q et linea g h aequalis lineae g z, ego tota linea q h est aequalis toti lineae z o, et angulus z o t aequalis angulo h q k, et unuiquisque duorum angulorum t k est rectus, et linea z o est aequalis lineae h q. Est ergo propter illud linea b t aequalis lineae b k, et similiter linea z t aequalis lineae h k, et propterea quod unaquaeque duarum linearum d z et e h est medietas diametri deferentis, et duo anguli t k sunt recti, remanet linea d t aequalis lineae e k, ergo tota linea b d est aequalis toti lineae b e, linea ergo b a communi et duobus angulis a b d et a b e aequalibus, erunt duo anguli a d b et a e b aequales, et linea a d aequalis lineae a e, et propterea quod linea d l est aequalis lineae e m, et angulus l d a aequalis angulo m e a, est angulus d a l aequalis angulo e a m, et illud est cuius uoluimus declarationem. Et similiter sequitur per illud quod ostendimus in stella ueneris, ut sint longitudines duae stellae a medio solis aequales, haec autem demonstratio est diuersa a demonstratione Ptolomei, quoniam demonstratio eius est erronea, quod est, quia ipse ponit puctum h centrum deferentis, quando centrum orbis reuolutionis est super punctum d, et similiter ponit punctum z centrum deferentis, quando est centrum orbis reuolutionis super punctum e, et continuat duas lineas d h, e z, et ponit unamquanque earum medietatem diametri deferentis. Non autem est ita, imo centrum deferentis punctum d non est nisi punctum z, non punctum h, et similiter centrum eius ad punctum e non est nisi punctum h, non punctum z, quod si ipse non crederet hoc, non poneret lineam d h aequalem lineae e z, et non declararetur ei illud, et non est possibilis declaratio aequalitatis ambarum nisi post declarationem aequalitatis duarum linearum d b et e d, et per eas ambas declaratur quaesitum. Cadit in demonstratione circulari, et quando declarabitur illud oportebit ut sint duae longitudines magnae stellae a medio solis matutinalis et uespertina, in quibus sit longitudo centri orbis reuolutionis a duobus lateribus earum longitudo una aequales. Et aestimauit Ptolomeus quod hoc est ex eis quae conuertuntur, scilicet, quod quando inueniuntur duae longitudines magnae aequales, quarum una sit matutinalis, et altera uespertina, tunc punctum longitudinis longioris diuidit quod est inter duos medios solis in eis utrisque in duo media. Inquirit ergo unicuique harum duarum stellarum duas longitudines aequales, matutinalem et uespertinam, et diuidit arcum qui est inter duos medios solis in eis utrisque in duo media, et est illud locus longioris longitudinis stellae, et eius oppositum locus propinquitatis propioris, hoc autem est ex eis quae non conuertuntur, quod est, quia oportet necessario ut sint stellae ex eis utrisque longitudines multae infinitae numerationis matutinalis et uespertinae, quarum unaquaeque ex matutinalibus sit aequalis suae compari ex uespertinis, et non diuidat punctum longitudinis longioris llud quod est inter duas longitudines ex eis utrisque in duo media, et illud declarabitur post declarationem intentionum consequentium has longitudines, et sunt illae, quas ignorauit Ptolomeus, et quas non percepit. Ostendam ergo illud secundum hunc modum. Sit orbis ecentricus stellae circulus a b g d circa centrum e, et centrum orbis signorum sit punctum z, et diameter transiens per ea utraque sit linea a e z g, erit ergo punctum a longitudo longior, et punctum g longitudo propior, et sit linea b z d stans super lineam a g super rectos angulos, erit ergo punctum b transitus medius primus, et punctum d transitus medius secundus. Et quando est longitudo magna stellae, cum est centrum orbis reuolutionis in locis a duobus punctis a et g, et est angulus medietatis diametri orbis reuolutionis adiuncto ad 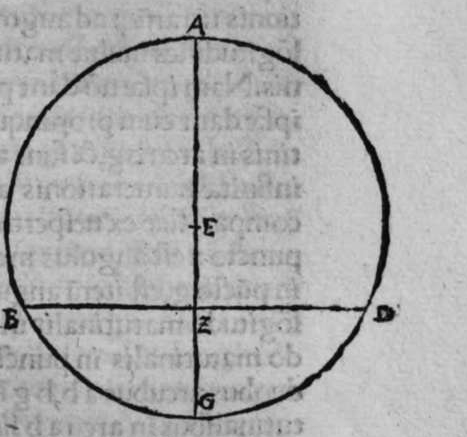ipsum, aut diminuto ex eo angulo diuersitatis, quae est propter ecentricum. Et quando mouetur centrum orbis reuolutionis a puncto a, uadens ad partem puncti b, augmentatur angulus medietatis diametri orbis reuolutionis, et augmentatur angulus diuersitatis, oportet ut sit longitudo matutinalis, cum sit aggregatio duorum angulorum in toto arcu a b augmentata, et longitudo uespertina continuata ei, non referatur cum additione neque cum diminutione, propterea quod est superfluitas anguli medietatis diametri orbis reuolutionis super angulum diuersitatis. Et quando mouetur cenrum orbis reuolutionis a puncto b ad partem puncti g, augmentatur iterum angulus medietatis diametri orbis reuolutionis, et minuitur angulus diuersitatis ecentrici. Et propterea quod longitudines matutinales in toto arcu b g sunt aequales aggregationi earum ambarum, et longitudines longituines ed. uespertinae in eo sunt superfluitas anguli medietatis diametri orbis reuolutionis super angulum diuersitatis, oportet ut sint longitudines uespertinae augmentatae manifesta additione, et longitudinum matutinalium continuitas eis non referatur aliqua ex eis additione, neque cum diminutione. Et quando mouetur centrum orbis reuolutionis a puncto g ad partem puncti d, minuitur angulus medietatis diametri orbis reuolutionis, et augmentatur angulus diuersitatis, et propterea quod longitudines matutinales in toto arcu g d sunt superfluitas anguli medietatis diametri orbis reuolutionis super angulum diuersitatis, et longitudines uespertinae in eo continuatae eis sunt aggregatio ambarum, oportet propter illud, ut sint longitudines matutinales diminutae manifesta diminutione, et longitudines uespertinae continuatae eis non proferantur cum additione, neque cum diminutione. Et quando mouetur centrum orbis reuolutionis a puncto d ad partem puncti a, minuitur angulus medietatis diametri orbis reuolutionis, et minuitur etiam angulus diuersitatis et propterea quod londitudines uespertinae in toto arcu d a sunt aggregatio duorum angulorum, et sunt longitudines matutinales in eo continuatae eis superfluitas anguli medietatis orbis reuolutionis super angulum diuersitatis, oportet propter illud, ut sint longitudines uespertinae diminutae manifesta diminutione, et longitudines matutinales in eo continuatae, non proferantur cum additione neque diminutione. Erunt ergo longitudines augmentatae manifesta additione ipsae matutinales in arcu a b, et uespertinae in arcu b g, et diminutae apparente diminutione, ipsae matutinales in arcu g d, et uespertinae in arcu a d. Erunt ergo propter illud longitudines uespertinae in arcu a d contrarie longitudinibus matutinalibus in arcu a b, quia istae uespertinae sunt diminutae manifesta diminutione, et istae matutinales augmentatae manifesta additione, et similiter longitudines uespertinae in arcu b g, et matutinales in arcu g d, quia sunt istae uespertinae augmentatae manifesta additione, et istae matutinales diminutae apparente diminutione. Reliquae autem longitudines continuatae eis, non merentur nomen contrarietatis, cum non proferatur aliqua earum cum additione neque cum diminutione. Longitudines autem matutinales in arcu a b, cum uerspertinis in arcu b g non sunt contrarie etiam, quoniam ipsae omnes sunt augmentatae manifesta additione, et similiter longitudines matutinales in arcu g d et longitudines uespertinae in arcu a d, quoniam ipsae omnes sunt diminutae manifesta diminutione. Longitudines uero matutinales in arcu a b cum longitudinibus uespertinis in arcu d g, non sunt etiam contrarie, quoniam istae matutinales sunt augmentatae, et uespertinae non proferuntur cum diminutione, et similiter longitudines matutinales, quae sunt in arcu b g, non sunt contrarie longitudinibus uespertinis in arcu a d, quoniam uespertinae in arcu a d sunt diminutae apparente diminutione, et matutinales in arcu b g non proferuntur cum additione. Longitudines ergo contrariae secundum ueritatem sunt matutinales in arcu a b cum uespertinis in arcu a d, et uespertinae in arcu b g cum matutinalibus in arcu g, d. Qando ergo inueniuntur ex eis duae contrariae aequales punctum longitudinis longioris, diuidit arcum qui est inter duos medios solis in eis utrisque in duo media, sed longitudines aequales quae sunt continue istis, quamuis ponamus nos quod punctum longitudinis longioris diuidat etiam arcum qui est inter duos medios solis in duo media, tamen inuentio dua rum aequalium ex eis secundum ueritatem est illud in quo non est fiducia, propter paruitatem mutationis utrarumque ad augmentum aut ad diminutionem. Posibile est enim ut sint in parte una longitudines multae matutinales aequales secundum propinquitatem, et similiter in uespertinis. Nam ipsae non dant propter illud locum longitudinis longioris secundum ueritatem, sed ipsae dant eum propinquum. In longitudinibus uero matutinalibus et in arcu a b cum uespertinis in arcu b g, et sunt augmentatae simul, oportet necessario ut sint longitudines multae infinitae numerationis aequales, scilicet unaquaeque ex matutinalibus in arcu a b aequalis compari suae ex uespertinis in arcu b g, quod est, quoniam propterea quod longitudo matutinalis in puncto a est angulus medietatis diametri orbis reuolutionis tantum, et longitudo uespertina in puncto g, est iterum angulus medietatis diametri orbis reuolutionis tantum, oportet ut sit longitudo matutinalis in puncto a minor uespertina in puncto g, et propterea quod longitudo matutinalis in puncto b est maior uespertina in ipso, oportet propter illud ut sint in duobus arcubus a b, b g longitudines multae infinitae numerationis, quarum unaquaeque ex matutinalibus in arcu a b sit aequalis suae compari ex uespertinis in arcu b g, et propterea quod augmentum longitudinum matutinalium non fit nisi per motum centri orbis reuolutionis ad partem puncti b, et augmentum longitudinum uespertinarum per motum centri eius ad punctum g, oportet propter illud ut sint puncta, quae diuidunt quod est inter longitudines aequales ex eis in duo media multae infinitae numerationis, et oportet ut sit unumquodque eorum secundum demonstrationem eius punctum longitudinis longioris stellae, et simile illius eiusdem sequitur in longitudinibus matutinalibus in arcu g d cum uespertinis in arcu d a, et sunt diminutae simul. Longitudinum autem matutinalium in arcu a b cum uespertinis in arcu g d, et sunt illae, quarum una augmentatur, et secunda non profertur cum diminutione, si fuerit in unaquaeque duarum longitudinum aequalium scilicet matutinalis puncto b, et uespertina in puncto d, maior uespertina in puncto g, tunc sequitur necessario, ut sint in duobus arcubus a b et g d longitudines multae infinitae numerationis aequales, quarum unaquaeque ex matutinalibus in arcu a b sit aequalis compari suae ex uespertinis in arcu g d, et sint iterum puncta quae diuidunt quod est inter duas longitudines aequales ex eis in duo media infinitae numerationis. Nam si nos usi fuerimus inuentione loci puncti longitudinis longioris duabus longitudinibus, uespertina et matutinali aequalibus, et non conditionauerimus in eis utrisque, ut sit una earum augmentata manifesta additione, et secunda diminuta apparente diminutione, et possibile est, ut fiat una istarum longitudinum, non contrariarum, quas diximus, et egrediatur nobis locus puncti longitudinis longioris, aut inconstans, et in quo non sit fiducia, et est illae, quem dant nobis longitudines continuatae longitudinibus contrarijs secundum quod ostendimus, aut ut sit non locus eius et sint stellae puncta multa infinitae numerationis, quorum unumquodque est longitudo eius longior. In hoc uero est de absurditate quod non occultatur. Significatur autem manifestus quod Ptolomeus non percipit aliquid harum intentionum annexarum his longitudinibus, et quod ipse non intellexit illud quod uoluerunt antiqui per longitudines contrarias, est quod non exposuit aliquid de illo in libro suo, neque innuit ad illud, quoniam ipse utitur in inuentione duorum punctorum longitudinis longioris harum duarum stellarum considerationibus contrarijs, et sunt illae, quas diximus, et considerationibus non contrarijs, quod est, quia ipse utitur inuentione puncti longitudinis longioris stellae mercurij duabus considerationibus contrarijs, et sunt duae considerationes primae, quoniam sunt uespertina in arcu b g, et matutinalis in arcu g d. Duae uero considerationes postremae, quas dixit secundum uiam apparitionis, sunt non contrariae, quoniam sunt matutinalis in arcu b g, et uespertina in arcu g d. Nos uero iam ostendimus, quod sunt non contrariae, quoniam nulla earum profertur cum additione, neque cum diminutione, et similiter longitudinum antiquarum, quibus utitur iterum in hac stella, duae sunt contrariae, quoniam sunt matutinalis in arcu b g, et uespertina in arcu a d, et duae non contrariae, quoniam sunt matutinalis in arcu b g, et uespertina in arcu g d. In stella autem ueneris utitur iterum duabus considerationibus contrarijs, quae sunt matutinalis in arcu a b et uespertina in arcu a d, et in duabus considerationibus non contrarijs quae sunt matutinalis in arcu b g, et uespertina in arcu g d, et propterea quod ipse iam usus est in unaquaque duarum stellarum duabus considerationibus contraijs, fecit nos scirc et credere, quod duo loca quae ipse inuenit longitudini longiori utrarumque sunt sana, uerum quod ipse inuenit illud, fuit per accidens, non essentialiter. Exiuit ergo ei longitudo longior stellae mercurij super 10. partes librae, et longitudo propior ei super 10. partes arietis, et exiuit ei longitudo longior stellae ueneris super 25. partes tauri, et longitudo propior super 25. partes scorpionis. Et postquam inuenit locum longitudinis longioris et propioris cuiusque duarum stellarum per considerationes suas, et considerationes quae fuerunt secundum tempus suum, inuenit iterum per considerationes antiquorum locum longitudinis longioris stellae mercurij, et inuenit ipse motum esse in spacio, quod fuit inter duo tempora quantum est motus stellarum fixarum, et illud est in omnibus 100. annis gradus unus. In stella autem ueneris non inuenit in considerationibus antiquorum quod possibile sit inuenire illud. Postea ipse inuenit per considerationes duas longitudines maiores contrarias uniuscuiusque harum duarum stellarum in longitudine longiori, et similiter in longitudine propior, quamuis non rememoratus sit illius in libro suo, ueruntamen extrahitur ex toto quod ipse dixit inesse harum duarum stellarum, quod ipse inuenit illud quod centrum orbis reuolutionis utrarumque aggregatur cum medio solis in reuolutione duabus uicibus, semel in longitudine longiore londiore ed., et semel in longitudine propiori, et fit, quod linea transiens per centrum orbis reuolutionis, et centrum motus aequalis cooperit diametrum transeuntem per longitudinem longiorem et propiorem, et in locis alijs ab istis duobus sunt aequedistantes. Et postquam exposuit illud, incepit ostendere proportionem medietatis diametri orbis reuolutionis stellae mercurij, et linea quae est inter duo centra, scilicet centrum orbis reuolutionis, et centrum motus aequalis ad medietatem diametri orbis deferentis centrum orbis reuolutionis, ipse enim sciuit per considerationem quantitatem longitudinis maioris quae est ei, quando est medius solis in puncto longitudinis longioris ecentrici, et quantitatem longitudinis maioris quae est ei, medio solis existente in longitudine propiori eius, et sciuit ex quantitate cuiusque harum duarum longitudinum ex superfluitate inter utrasque proportionem medietatis diametri orbis reuolutionis ad medietatem diametri deferentis secundum hunc modum. Sit linea transiens per duo centra, scilicet centrum orbis obis ed. signorum 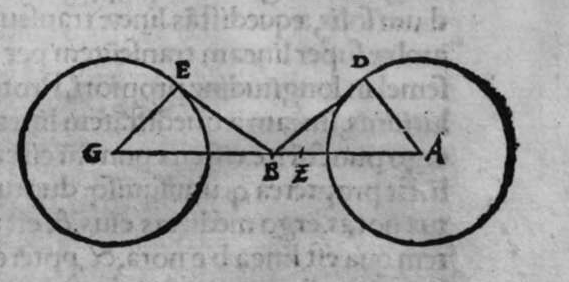super ipsum punctum b, et longitudo longior punctum a et longitudo propior punctum g, et sint duo circuli d et e duo orbes reuolutionis stellae, et sit centrum circuli d punctum a, et centrum circuli e punctum g, et protraham duas lineas b d et b e contingentes duos circulos super duo puncta d et e, et sit stella super ea in hora considerationis, et continuabo duas lineas a d et g e, propterea ergo quod angulus g b e est notus, et est longitudo stellae a medio solis, quando est et medius solis in puncto longitudinis propioris, est linea g e, quae est medietas diametri orbis reuolutionis nota per quantitatem qua est linea g b 120. partes. Et propter illud etiam est linea a d quae est iterum medietas diametri orbis reuolutionis nota per quantitatem qua est linea a b 120. partes, et est iterum linea b g per illam quantitatem nota, et est linea a g per illam quantitatem nota, ergo medietas eius, et est linea a z, per illam quantitatem nota. Declarabitur ergo inde, quod per quantitatem qua est linea a z nota, est per eam medietas diametri orbis reuolutionis mercurij nota, et linea b z et b e etiam nota, et punctum z, aut est centrum deferentis orbem reuolutionis, aut est centrum circa quod mouetur centrum deferentis or bem reuolutionis. Nam secundum horum unum duorum modorum tantum praeparatur, ut sit centrum orbis reuolutionis in his duobus locis longitudo a puncto z longitudo aequalis. Verum si ipse esset centrum deferentis, esset longitudo longior, quae est magna, stellae in puncto g quod est propinquior propinquitatis eius maior longitudinum eius, uerum inueniuntur stellae mercurij duae longitudines maiores hac longitudine, et est, quod quando est longitudo medij solis a puncto longitudinis longioris in unaquaque duarum longitudinum contrariarum 120. partes. Est enim tunc aggregatio duarum longitudinum magnarum huius stellae in his duobus locis maior aggregatione duarum longitudinum eius, quando est medius solis super punctum g, quod est longitudo propior ecentrici. Significat ergo illud, quod centrum orbis reuolutionis eius, quando est super unumquenque horum duorum locorum, quorum longitudo a puncto a, quod est longitudo longior est 120. partes, tunc est propinquius centro orbis signorum, quam est, quando est super punctum g, et hoc non praeparatur nisi ut obis deferens moueatur ad contrarium successionis signorum motu suo aequali in circuitu puncti z aequali in uelocitate motui centri orbis reuolutionis. Est ergo propter illud centrum orbis reuolutionis in longitudine propiori deferentis duabus uicibus in reuolutione una, sicut fuit illud in luna. Inuentio autem puncti in circuitu, cuius mouetur centrum orbis reuolutionis huius stellae motu aequali, est, quod ipse inuenit ipsum per hoc quod considerauit ei duas longitudines magnas contrarias, scilicet uespertinam et matutinalem, et medij solis in utrisque simul in puncto uno orbis signorum longitudo a loco longitudinis longioris eius quarta circuli. Inuenimus ergo per superfluitatem, quae est inter has longitudines magnas, quae est quantitas longitudinis puncti in circuitu, cuius est motus aequalis a centro orbis signorum hac uia. Sit diameter transiens per longitudinem longiorem et propiorem mercurij figurae praecedentis linea a g, et centrum orbis signorum punctum b, et centrum reuoluens centrum 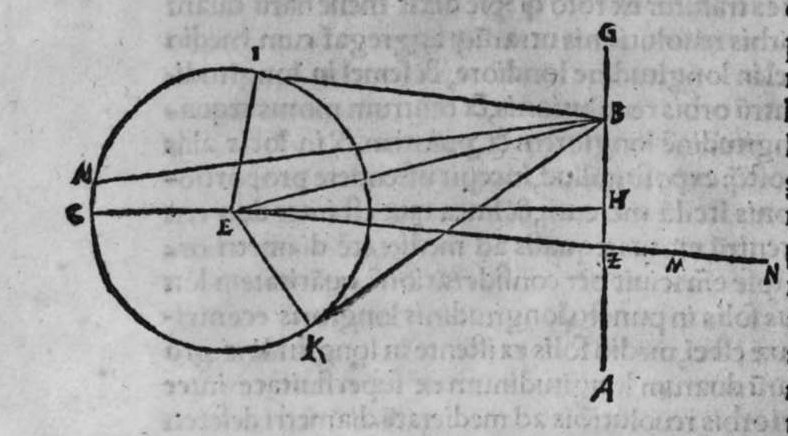deferentis punctum z, et sit linea transiens per medium solis in duabus considerationibus linea b m, et sit centrum orbis reuolutionis in utrisque punctum e, et orbis reuolutionis circulus k l, et sint duae lineae tangentes ipsum duae lineae b k, b l, et continuabo duas lineas e k, e l, et continuabo punctum e cum centro orbis signorum per lineam b e. Et quoniam iam ostensum est, quod motus centri orbis reuolutionis aequalis, est aequalis semper motui solis medio, et quod medius solis aggregatur semper cum centro orbis reuolutionis super duo puncta longioris longitudinis et propioris ecentrici, est propter illud semper linea transiens per medium solis, aequedistans lineae transeunti per centrum orbis reuolutionis, et supponuntur simul ambae super lineam transeuntem per longitudinem longiorem et propiorem duabus uicibus semel in longitudine propiori. Protrahamus ergo ex puncto e quod est centrum orbis reuolutionis, lineam aequedistantem lineae b m transeunti per medium solis, et sit linea e h, erit ergo punctum h existens punctum circa quod mouetur centrum orbis reuolutionis motu aequali. Et propterea quod unusquisque duorum angulorum k b m, l b m est notus, erit angulus k b l totus notus, ergo medietas eius, et est angulus t b l, est nota, ergo est linea e l nota per quantitatem qua est linea b e nota, et propterea quod unusquisque duorum angulorum e b l et m b l notus, erit angulus e b m notus, et ipse est aequalis angulo b e h, ergo angulus b e h est notus, et angulus h est rectus, ergo linea b h est nota per quantitatem qua est linea b e 60. partes, et medietas diametri orbis reuolutionis per eam iterum est nota. Iam autem fuit ostensum in figura quae praemissa est, quod per illud quo medietas diametri orbis reuolutionis est nota, est linea b z nota, ergo linea b h est nota per quantitatem qua linea b z est nota, et per quam medietas diametri orbis reuolutionis est nota, prouenit ergo quod punctum h, et est centrum motus aequalis, diuidit lineam quae est inter centrum orbis signorum et centrum reuoluens centrum deferentis in duo media. Cognitio autem quantitatis lineae, quae est inter centrum deferentis et inter reuoluens ipsum, scitur per hoc, ut protrahatur in hac figura a puncto z, quod est centrum reuoluens centrum deferentis, perpendicularis super lineam a z g, quae sit sinea n z aequalis lineae a z, quae est composita ex medietate diametri deferentis, et illa linea quaesita, et sit super ipsam centrum deferentis punctum m, et continuabo lineam e z, et quoniam duae lineae h e, z n sunt conuenientes in reditione utrarumque in tempore uno, et duo anguli a h e, a z n sunt aequales, est, quod quando mouetur longitudo longior deferentis per angulum a z n, mouetur centrum orbis reuolutionis in illo tempore per angulum a h e, et propterea quod est angulus n z h rectus, et angulus e z h approximat recto erit linea n z e fere recta, et est linea n z nota per quantitatem qua medietas diametri orbis reuolutionis est nota, et linea e z nota per illam quantitatem, quoniam est aequalis lineae e h, de qua nuper, ostensum fuit, quod est nota, ergo erit linea n z e tota nota, ergo medietas eius, et est linea m n, est nota, et iam fuit linea n z nota, ergo remanet linea m z nota. Inuenit ergo lineam aequalem unicuique duarum linearum b h, h z, inuenit ergo, quod per quantitatem qua est linea m n, quae est meditetas diametri deferentis 60. partes, est unaquaeque linearum m z et z h et h b tres partes, et per eam est medietas diametri orbis reuolutionis 22. partes et medietas. Ex eis autem quae oportet nos etiam ostendere, est, quod in istis radicibus positis stellae mercurij sequitur, ut sit longitudo centri orbis reuolutionis a centro orbis signorum, quando est super 120. partes a longitudine longiore in duabus partibus contrarijs minor longitudine eius ab eo, quando est in longitudine propinquiori deferentis, et illud declaratur secundum hunc modum. Sit linea transiens per longitudinem longiorem et propiorem linea a b g, et sit super ipsam centrum orbis signorum 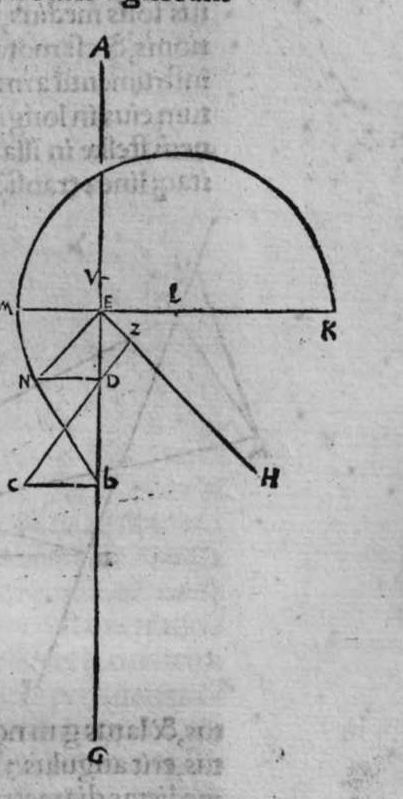punctum b, et centrum motus aequalis punctum d, et centrum reuoluen centrum orbis reuolutionis punctum e, et centrum deferentis punctum n, et sit centrum orbis reuolutionis super punctum t lineae d t. Sitque angulus a d t 120. partes, per partes, quibus quatuor anguli recti sunt 360. partes, et sit centrum deferentis tunc punctum z, et sit linea e z h ipsa linea transiens per centrum reuoluens deferentem, et punctum h longitudo longior deferentis, et protraham ex puncto e perpendicularem super lineam a e g quae sit e k. Sitque linea e l aequalis lineae e n, et linea l k aequalis lineae a n, quae est medietas diametri deferentis, et ponam punctum l centrum, et reuoluam cum longitudine l k circulum k m n, et faciam penetrare lineam k e, donec occurrat circumferentiae eius super puctum m, et protraham a puncto d lineam aequedistantem lineae e m, quae sit linea d n, erit ergo punctum n circumferentiae deferentis ipsum super quod est centrum orbis reuolutionis in longitudine propiori, et copulabo iterum duo puncta n t cum puncto b, quod est centrum orbis signorum per duas lineas b n, t b. Dico ergo, quod linea t b est minor linea n b, cuius demonstratio est. Quoniam propterea quod fuit angulus a e h aequalis angulo a d t, oportet ut sint duo anguli z e d et z d e trianguli z d e aequales, et unusquisque eorum est 60. partes, per partes quibus quatuor anguli recti sunt 360. partes. Remanet ergo angulus eius 360. partes etiam, ergo triangulus e z d est aequalium laterum, ergo latus eius z d est aequale lineae e l, et propterea quod linea z k est medietas diametri deferentis, oportet ut sit linea e m residua aequalis lineae d t residuae, et propterea quod linea n d est perpendicularis super lineam e b, et linea b d est aequalis lineae d e. Si continuauerimus duas lineas n e, n b, erunt aequales, uerum linea e n est maior linea e m, ergo linea b n est maior linea e m, ergo est etiam maior linea d t, de qua iam ostensum est, quod est aequalis lineae e m, et propterea quod de linea d b iam ostensum est, quod est tres partes per partes, quibus linea z t est 60. partes, est linea d t maior linea d b, ergo angulus d b t est maior multo angulo d t b, sed aggregatio duorum angulorum d b t, d t b est aequalis angulo a d t, qui iam positus fuit 120. partes, quibus 4. anguli recti sunt 360. partes, ergo angulus d b t est maior multo 60. partibus, ergo est multo maior angulo t d b. Ergo linea b t est multo minor linea d t, et iam fuit ostensum iterum, quod linea d t est minor b n, ergo linea b t est multo minor linea b n, et illud est cuius uoluimus declarationem. Sequitur ergo ex hoc, quod aggregatio duarum longitudinum magnarum contrariarum stellae mercurij, quando centrum orbis reuolutionis est super longitutinem 120. a longitudine longiori, est maior duabus longitudinibus quae sunt ei, quando est centrum orbis reuolutionis in longitudine propiori deferentis, et simile illius eiusdem sequitur, quando est centrum orbis reuolutionis in parte secunda in longitudine longiori super longitudinem aequalem longitudini puncti t ab ea, et illud est cuius uoluimus declarationem. Et nos quidem iam inuenimus per considerationes, quod aggregatio duarum longitudinum contrariarum, quando centrum orbis reuolutionis est in longitudine propiori deferentis, est 46. partes et medietas partis, et quod aggregatio duarum longitudinum contrariarum, quando est centrum orbis reuolutionis super longitudinem 120. partium a longitudine longiori in unaquaque duarum partium contrariarum est 47. partes et medietas et quarta. Postquod ergo uerificauit longitudines quae sunt inter centra, scilicet centrum orbis signorum, et centrum motus aequalis, et centrum reuoluens deferentem, et centrum deferentis, et quod istae longitudines sunt aequales, et sciuit proportionem cuiusque earum, et proportionem medietatis diametri orbis reuolutionis ad medietatem diametri deferentis, oportuit ut ostenderet quod sequitur ex unaquaque earum ex istis radicibus, quod aggregatio duarum longitudinum magnarum contrariarum, quando cum ea est centrum orbis reuolutionis a longitudine longiori 120. partes, est 47. partes et medietas et quarta partis, sicut inuenimus per considerationes, declarauit ergo illud per numeros, et inuenit quantitates eius conuenientes ei quod inuenit per considerationes. Et postquam declarata sunt ei omnia quae praecesserunt, oportuit ut consideraret in certificatione quantitatum motuum huius stellae. Motus uero eius medius in longitudine, est motus solis medius, non ergo fuit necessarium uerificare ipsum. Motum autem eius in orbe reuolutionis, et est motus qui nominatur motus diuersitatis, certificauit ipse per hoc, quod sciuit per instrumentum armillarum locum stellae de orbe signorum in hora aliqua, et inuenit propter motum eius in longitudine, et propter medietatem diametri orbis reuolutionis eius longitudinem stellae in illa hora a longitudine longiori media orbis reuolutionis per hanc uiam. Sit itaque linea transiens per centra linea a e, et sit centrum orbis signorum super ipsam punctum d, et 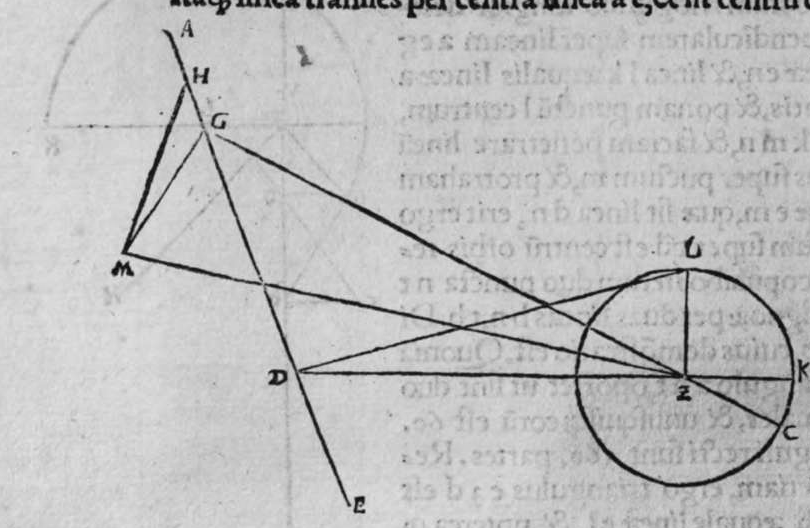centrum motus aequalis punctum g, et sit orbis reuolutionis circulus k l, et cen trum eius z, et sit stella super punctum l, et protraham lineas l d, l z, et sit centrum reuoluens deferentem punctum h, et sit angulus m h g aequalis angulo z g d, et sit centrum deferentis punctum m, et continuabo m z et z d et z g, propterea ergo quod motus stellae in longitudine est notus in hora considerationis propter locum solis medium in illa hora per illud, quod inuenit ipsum ex quantitate motus augium stellarum, erit propter illud angulus z g d notus, et ipse est aequalis angulo g h m est notus, erit angulus h g m eius notus, et latus g m notum erit. Et propterea quod angulus z g d est notus, et angulus h g m notus, erit angulus z g m notus, et latus m g notum, et similiter latus m z notum, quoniam est medietas diametri deferentis, ergo trianguli z g m, duo latera g m et m z sunt nota, et angulus eius z g m est notus, ergo latus eius g z est notum. Et E ed. propterea quod latus g d iterum est notum, et angulus z g d est notus, ergo erit angulus g z d notus, et latus z d notum, et angulus z g d notus. Et propterea quod stella in hora considerationis fuit uisa super lineam l d, et locus eius de orbe signorum est notus per considerationem, et locus longitudinis longioris in illa hora est notus, erit angulus a d l notus, iam autem fuit angulus g d z notus, remanet ergo angulus l d z notus, ergo trianguli l z d duo latera l z et z d sunt nota, et angulus l d z est notus, ergo erit angulus l z d notus, ergo angulus l z k est notus. Sed angulus k z t est notus, ergo totus angulus l z t est notus, ergo longitudo stellae a puncto t quod est longitudo longior media orbis reuolutionis nota. Inuenit ergo per hanc uiam longitudinem stellae a puncto t in hora considerationis antiquae ex antiquioribus considerationibus quas reperit, deinde considerauit ipse etiam stellam, et sciuit locum eius per uisum in orbe signorum, et sciuit per hanc uiam quantitatem longitudinis eius a puncto t etiam, deinde comprehendit quod est inter duo tempora duarum considerationum, et uerificauit illud, et diuisit super illud numerum reditionum quae fuerunt stellae in orbe reuolutionis suae secundum quod accepit illud ex antiquis, qui fuerunt ante ipsum, et additionem ad illam superfluitatem quae fuit inter duo loca stellae. Comprehensa est ergo ei per illud quantitas motus stellae in orbe reuolutionis suae in die una secundum ultimitatem uerificationis, et illud est gradus tres 24. 59. 35. 50. et illud est cuius uoluimus declarationem. Postea ipse inuenit, quod ligatur comprehensio motuum harum stellarum in hora in qua ligata est comprehensio motuum solis et lunae, et est hora regni Nabuchodonosor, et uerificauit illud, et sciuit quod fuit ei necessarium de motu stellae in orbe reuolutionis suae. Sciuit ergo per illud locum stellae in orbe reuolutionis sue, scilicet longitudinem eius a longitudine media, quae est punctum t in hora regni Nabuchodonosor, inuenit ergo eam in illa hora super 21. partem et 55. minuta, a longitudine longiori orbis reuolutionis. Comprehensio autem motus longitudinis eius, est comprehensio solis ipsamet quae est 45.minuta piscium, longitudo autem longior eius est super partem et sextam partis librae. Deinde exemplificauit omnia illa in stella ueneris secundum similitudinem eius quod fecit in stella mercurij ipsamet, scilicet, quia inuenit per hanc uiam locum longitudinis longioris eius ex orbe signorum, et proportionem medietatis diametri orbis reuolutionis eius ad medietatem diametri deferentis ipsum, et proportionem eius quod est inter centrum motus aequalis, et centrum orbis signorum ad medietatem diametri deferentis, et similiter etiam sciuit proportionem eius, quae est inter centrum orbis signorum et centrum deferentis ad medietatem diametri deferentis. Inuenit ergo quod centrum deferentis huius stellae diuidit quod est inter centrum orbis signorum et centrum motus aequalis eius in duo media. Inuenit ergo longitudinem longiorem huius stellae cadere super 25. partes tauri, et inuenit medietatem diametri orbis reuolutionis 43. partes et sextam partis per quantitatem qua est medietas diametri deferentis ipsum 60. partes, et linea quae est inter centrum deferentis et centrum orbis signorum per illas partes, partem unam et quartam partis cum propinquitate. Et lineam quae est inter centrum deferentis et centrum motus aequalis aequalem illi, et inuenit quantitatem motus huius stellae in diuersitate in die uno minuta 36. 59. 25. 53. 114. 22. et reperit locum stellae in diuersitate in hora ligationis comprehensionis super 71. partem et 7. minuta a longitudine longiori orbis reuolutionis, locum autem longitudinis super locum solis, et inuenit longitudinem longiorem huius stellae super 16. partes et 10. minuta tauri, et illud est cuius uoluimus declarationem. Reliquae autem tres stellae, scilicet Saturnus, Iupiter et Mars, propterea quod elongantur a sole elongatione tota, non fuit statio super horam in qua est stella super lineam contingentem orbem reuolutionis suae, ut sciatur per illud ex dispositionibus suis quod scitur in duabus stellis uenere et mercurio, uerum transitur ad illud earum per dispositiones extremitatis noctis, et sunt dispositiones, in quibus stella est condiametralis loco medij solis, tunc enim est super propinquitatem suam propinquiorem uisibilem orbis reuolutionis suae. Est ergo propter illud centrum orbis reuolutionis tunc super condiametrationem medij solis, est ergo locus eius medius ex orbe signorum notus, et est ipsemet locus stellae et eleuatur tunc diuersitas eius quae est propter solem, et fit singularis diuersitas pertinens orbi signorum, possibile est ergo propter illud, ut sciatur quantitas motus in ecentrico, cum non cadat cum ea aliquid de diuersitate comparata ad solem, et ostendam illud per exempla. Ponam ergo deferentem centrum orbis reuolutionis circulum a b g, et centrum motus aequalis 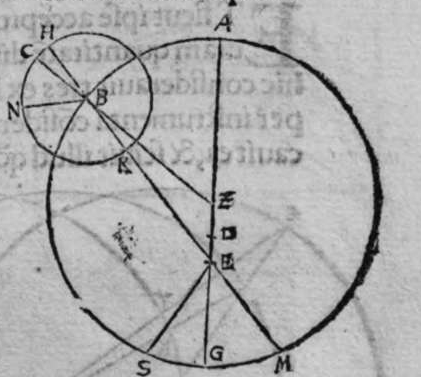punctum z, et centrum orbis signorum punctum e, et diametrum transeuntem per longitudinem longiorem et propiorem lineam a d g, et orbem reuolutionis circulum h t, et centrum eius punctum b, et continuabo ipsum cum centro orbis signorum per lineam e b h, et faciam ipsam transire ad circumferentiam deferentis a parte secunda usque ad punctum m. Dico ergo, quod quando stella est super lineam e h, est super medium solis super illam lineam. Nam si fuerit stella super punctum h, quod est longitudo longior uisibilis, erit currens cum sole. Erit ergo per cursum suum medium super lineam b e, et quando erit super punctum e, quod est longitudo propinquior, erit condiametralis medio solis, scilicet, quod medius solius erit tunc super ipsum punctum m, quod est, quoniam propterea quod est numerus reuolutionum stellae in orbe reuolutionis suae cum numero reuolutionum centri orbis reuolutionis suae in orbe signorum aequalis numero reuolutionum solis in illo tempore, sequitur inde, ut sit semper longitudo centri orbis reuolutionis stellae a puncto longitudinis longioris, et longitudo stellae ipsius a longitudine longiori orbis reuolutionis, quando aggregantur cursus solis medius ab illo principio eodem. Sit ergo medius stellae et medius solis apud punctum a, et stella sit tunc super punctum t orbis reuolutionis suae, deinde moueatur centrum orbis reuolutionis ad punctum b, et continuemus ipsum cum centro motus aequalis per lineam t b z, et moueatur stella in illo tempore per quantitatem arcus t k h, et fiat super punctum h quod est longitudo longior uisibilis. Sequitur ergo ex eo, quod pro radice positum est in motibus harum stellarum, ut sint motus stellae in orbe reuolutionis suae, scilicet arcus t k h, et motus centri orbis reuolutionis suae, scilicet arcus a b aequales motui solis medio, quo mouetur in illo tempore a puncto a quod est principium ei et stellis et orbi reuolutionis suae, propterea ergo quod angulus h b t est illud quod minuitur a reuolutione stellae in orbe reuolutionis suae, et angulus a z b est aequalis duobus angulis z b e et z e b, oportet ut sit angulus a z b, quem perambulauit centrum orbis reuolutionis cum motu stellae in orbe reuolutionis suae, addens super reuolutionem unam angulum z e b, et propterea quod illud est aequale motui solis medio in illo tempore, oportet ut sol etiam sit motus iam a puncto a reuolutione una ex reuolutionibus orbis signorum et additione anguli z e b. Sequitur ergo propter illud, ut sit sol per medium super lineam e b, est ergo medius eius cum stella et cum centro orbis reuolutionis suae in puncto uno orbis signorum. Et si nos posuerimus stellam super punctum k orbis reuolutionis suae, et est longitudo propior, iam abscidit de orbe reuolutionis suae arcum t k in tempore, quo abscidit orbis reuolutionis arcum a b, et abscidit sol per medium suum in illo tempore, quod est aequale aggregationi utrorumque, et angulus a z b est aequalis duobus angulis z b e, z e b, qui est angulus m e g, oportet ergo ut medius solis iterum iam perambulauit in illo tempore a puncto a medietatem circuli orbis signorum, et additionem anguli m e g. Sequitur ergo propter illud ut sit super punctum m quod est condiametrale puncto k, et sequitur ab hoc iterum, ut sit linea transiens per stellam et centrum orbis reuolutionis eius, aut cooperiens super lineam transeuntem per medium solis et centrum orbis signorum, et illud est, quando stella est super unum duorum punctorum h et k, aut aequedistans, et illud est, quando stella est super loca quae sunt alia ab his duobus punctis. Ponamus ergo singulariter stellam super punctum n, et continuemus lineam b n, et protraham a puncto e lineam aequedistantem lineae b n, quae sit linea e s. Erit ergo angulus a z b, et est ille, quem perambulat centrum orbis reuolutionis cum angulo t b n, et est ille, quem perambulat stella in illo tempore aequalis motui medio solis in illo tempore, propterea ergo quod angulus a z b est aequalis duobus angulis z b e et z e b, est aggregatio motus amborum aequalis aggregationi duorum angulorum h b n et z e b, et propterea quod linea b n est aequedistans lineae e s, erit angulus h b n aequalis angulo b e s, ergo aggregatio motus stellae in orbe reuolutonis suae, et motus orbis reuolutionis suae est aequalis angulo a e s. Oportet ergo propter illud, ut medius solis in illo tempore sit motus per quantitatem anguli a e s, ergo est super punctum s, et est super lineam aequedistantem lineae b n, et illud est cuius uoluimus declarationem.

⟨VII.2⟩ Ad ostendendum egressionis motus aequalis cuiusque harum stellarum a centro orbis signorum, et locum longitudinis longioris earum.

ET sicut ipse accepit in luna loca trium eclipsium lunarium et tempora earum, et ostendit per uiam quantitatem diuersitatis eius, et locum longitudinis longioris eius. Similiter etiam hic considerauit tres ex habitudinibus noctis, et uerificauit loca stellarum in unaquaque earum per instrumenta considerationis, et numerauit etiam tempora quae fuerunt inter eas, et uerificauit ea, et sciuit illud quod conuenit unicuique eorum per motum stellae medium in longitudine, secundum 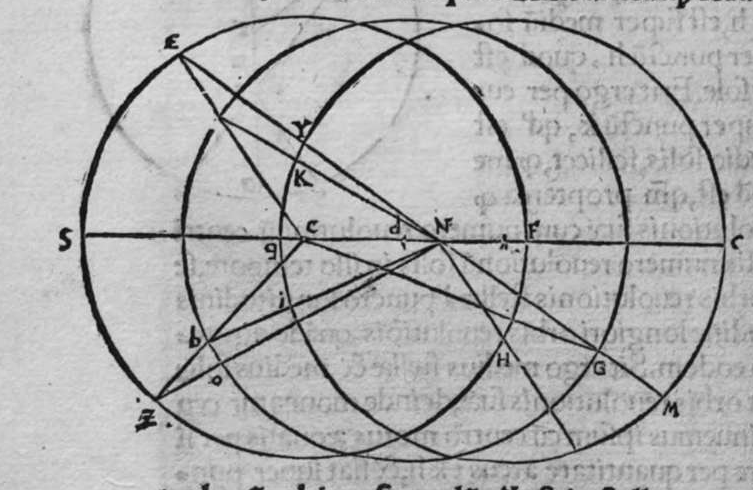quod fecit in duabus stellis uenere et mercurio, cum non ingrediatur in illo de propinquitate, aliquid faciens in istos motus errorem de quo curetur, et processit in illo uia quam narrabo. Sint ergo in superficie orbis signorum tres circuli aequales, et sit unus eorum orbis deferens centrum orbis reuolutionis, et sit circulus a b g in circuitu centri d, et alius sit orbis ex centro in circuitu centri, cuius est motus aequalis stellae, qui sit circulus e z h in circuitu centri t, et tertius orbis, cuius centrum est orbis signorum, qui sit circulus k l m, in circuitu centri n, et diameter quae transit per centra tria linea s q f c, et ponantur centra horum orbium secundum quod est in stella ueneris, ex hoc, quod centrum orbis deferentis diuidit quod est inter centrum motus aequalis et centrum orbis signorum in duo media, et accepit illud absolute, quia non fuit ei possibile peruenire ad cognitionem illius per demostrationem, sicut ostendit in uenere et mercurio, et propterea quod istae stellae elongantur a sole longitudine tota non ergo sciuit uere quando sunt super lineas contingentes orbes reuolutionum, et dixit, quod apparet ei quod est super hunc modum per probationem continuam, et ipsa est res, cuius narratio est impossibilis propter grauitatem eius. Acceperunt ergo hoc absolute, et apparuit postea totum quod apparet ex dispositionibus harum stellarum conueniens, et cooperiens illud quod sequitur ab istis radicibus positis eis. Sit ergo stella et centrum orbis reuolutionis eius in habitudine prima super punctum a, et in secunda super punctum b, et in habitudine tertia super punctum g, et continuabo lineas t a e, t b z, t h g, n k a, n l b, n g m. Erit ergo arcus e z orbis ecentrici ipsae partes quas abscidit centrum orbis reuolutionis per motum suum aequalem a tempore habitudinis primae, usque ad tempus habitudinis secundae, et arcus z h partes quas abscidit centrum orbis reuolutionis a tempore habitudinis secundae ad tempus habitudinis tertiae. Et arcus k l orbis signorum partes longitudinis primae quae uidentur, scilicet arcus orbis signorum quem secat stella per uisionem ab habitudine prima ad habitudinem secundam, et similiter arcus l n parte longitudinis secundae, scilicet quas abscidit per uisionem ab habitudine secunda ad habitudinem tertiam. Si ergo duobus arcubus e z, z h orbis ecentrici subtenderentur duo arcus k l, d m orbis signorum, non esset necessarium ad ostendendum egressionem a centro plus illo, uerum propterea quod isti duo arcus orbis signorum non subtenduntur nisi duobus arcubus a b, b g orbis deferentis, et sunt non dati, et quando producuntur lineae n y e, n o z, n h i, non erunt duo arcus, qui supponuntur duobus arcubus e z, z h orbis ecentrici, nisi duo arcus y o, i o orbis signorum, sed isti iterum non sunt dati. Manifestum ergo est, quod necesse est in primis, ut abscisiones superfluitatum quae sunt arcus k y, l o, m i sint datae, et tunc praeparatur cognitio ueritatis quantitatis egressionis a centro in eo, quod est inter duos arcus e z, z h compares, et inter duos arcus y o, i o compares etiam. Verum propterea quod iterum non est possibile, ut sciantur isti duo arcus secundum ueritatem, nisi sciatur ante illud quantitas egressionis a centro, et longitudo longior, et est possibile, ut sciantur secundum propinquitatem pronpinquitatem ed., quamuis non praecedat eos scientia illorum secundum ueritatem, propterea quod non cadit in utrisque de superfluitate quantitas de qua sit curandum, tunc fabricauit rem in primis in computatione sua qua computauit quantitatem egressionis a centro, et locum longitudinis longioris secundum quod non sit inter duos arcus k l, l m, et inter duos arcus y  o et o i superfluitas, cui sit quantitas de qua curetur. Ostendam ergo illud secundum hunc modum. Sit orbis ecentricus in circuitu centri, cuius est motus aequalis circulus a b g, et centrum orbis signorum sit punctum e, et sit locus stellae in habitudine prima super lineam 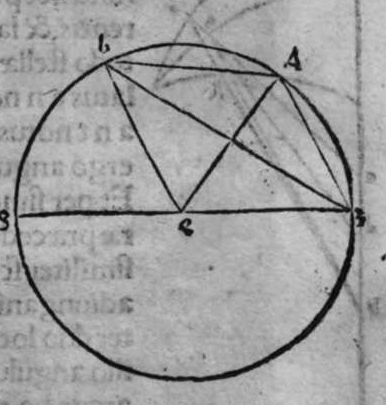e a, et in secunda super lineam b e, et in tertia super lineam g e, et faciam ipsam penetrare usque ad circumferentiam orbis ecentrici usque ad punctum z, et continuabo lineam a z, et lineam a b, et lineam b z. Est ergo unusquisque duorum angulorum a e b, b e g notus, et sunt duo arcus a b, b g orbis ecentrici noti per illud quod diximus de motibus quos scripserunt antiqui, propterea ergo quod duo anguli a e b et b e g sunt noti, erit angulus a e z notus et propterea quod arcus a b g est notus, erit angulus a z g notus, ergo triangulus a z e est notorum angulorum, ergo proportiones laterum eius adinuicem sunt notae, ergo per quantitatem qua linea z e est nota, erit unaquaeque duarum linearum a z a e nota. Et propterea quod arcus b g est notus, erit angulus b z g notus, et angulus b e z est notus, ergo triangulus z b e est notorum angulorum, ergo proportiones laterum eius adinuicem sunt notae, per quantitatem ergo qua latus z e est notum, est unumquodque duorum laterum b e, b z notum. Et propterea quod angulus a e b est notus, et unumquodque duorum laterum a e, b e est notum, erit latus a b notum per quantitatem qua est linea z e nota, et propterea quod arcus a b est notus, erit corda eius nota per comparationem ad diametrum circuli, ergo linea z e est nota per comparationem ad ipsam, et unusuquisque duorum angulorum b a e, e a z est notus, ergo angulus z a b est notus, ergo arcus z a b est notus, et arcus b g est notus, ergo totus arcus z a b g est notus, ergo corda z g est nota per quantitatem qua diameter circuli est nota, et iam fuit linea e z per illam quantitatem nota. Remanet ergo linea e g nota per illam quantitatem, ergo linea 3 e g, et unaquaeque duarum sectionum eius, scilicet z e, e g est nota per qutitatem qua est diameter circuli a b gnota. Et postquam illud est ita, tunc ponam in figura unius orbis ecentrici circulum a b g, et cordam z g in ipso 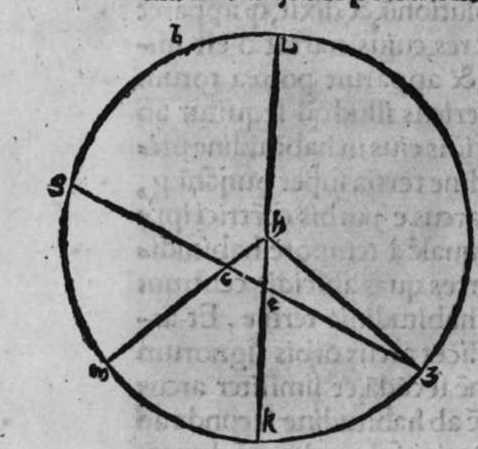notam per quantitatem diametri eius, et unamquanque duarum sectionum eius, scilicet duas lineas 3/e, e g notam. Sitque centrum circuli punctum h, et continuabo lineam e h, et faciam eam penetrare usque ad duo puncta l k, et protraham perpendicularem h t m Dico ergo, quod linea h e, et est illa quae est inter duo centra, est nota, et quod longitudo cuiusque duorum punctorum l k, quae sunt duo puncta longitudinis longioris et propioris ab uno punctorum a et b et g est nota. Quod sic probatur, quoniam linea z g est nota, tunc medietas eius, et est linea z t, et medietas diametri circuli quae est linea h z est nota, et angulus t est rectus. Erit ergo propter illud h t nota, et propterea quod unaquaeque duarum sectionum g e et e z est nota, est multiplicatio g e in e z nota, et quadratum z t, ergo linea e h quae est inter duo centra, est nota per quantitatem qua medietas diametri circuli est nota. Et propterea quod e t est nota, erit angulus t h k notus, ergo arcus m k est notus. Et propterea quod arcus g n z est notus, erit medietas eius, et est arcus g n nota, et arcus k m notus, ergo totus arcus k m g est notus, ergo duo arcus g l et l a sunt noti, et propterea quod angulus h e t est notus, est longitudo puncti l nota, ergo longitudo puncti l, et est longitudo longior a puncto g, quod est locus stellae per uisionem in orbe signorum in habitudine tertia est nota, et similiter est arcus a l, qui est illud quod est inter longitudinem longiorem et locum habitudinis primae notus, ergo locus longitudinis longioris et propioris de orbe signorum est notus, et illud est cuius uoluimus declarationem. Postquam autem sciuit illud quod est inter duo centra et locum longitudinis longioris secundum hanc semitam, incepit post illud in ostensione quantitatum superfluitatum, de quibus non curauit prius, declarauit ergo illud secundum hunc modum. Ponam orbes tres praedictos in primis secundum quod positi sunt in figura praecedente, et ponam in eis habitudinem primam, scilicet punctum a, et continuabo ipsum cum tribus centris per lineas a n, a d, a t, et faciam penetrare lineam a t, donec occurrat 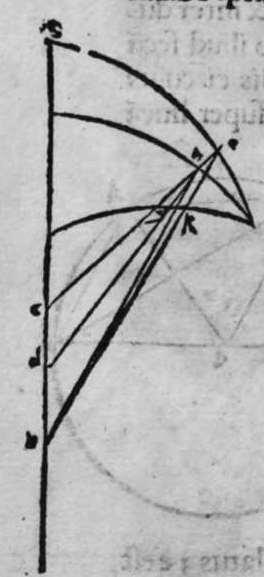circumferentiae ecentrici super punctum e, et uolo scire superfluitatem k y, pro pterea ergo quod arcus e s orbis ecentrici, et est ille, qui est ab habitudine prima ad longitudinem longiorem, est notus, est angulus e t s notus, ergo angulus e t n est notus, et propterea popterea ed. iterum quod latus a d trianguli a d n est medietas diametri deferentis, et latus n d eius est notum, et angulus a n d est notus, quoniam ipse est longitudo stellae in habitudine prima a loco longitudinis longioris, est propter illud latus a n notum, et propterea quod latus a n est notum, et latus t n notum, et angulus a n t notus, erit angulus n a t notus, et iam fuit angulus n e t notus. Remanet ergo angulus a n e notus, ergo arcus y k, et est arcus superfluitatis, est notus. Et per similitudinem huius uiae eiusdem sciemus quantitatem superfluitatis l o figurae praecedentis, et est superfluitas quae comprehenditur in habitudine secunda, et similiter sciemus iterum arcum m i, et est superfluitas apud habitudinem tertiam, adiungantur ergo duo arcus y k, l o ad quantitatem arcus k l, et est ille qui est inter duo loca stellae ex orbe signorum in habitudine prima, et in secunda, tunc erit ex illo angulus e n z, et est ille qui est secundum ecentricum notus, et minuantur duo arcus l o, m i ex partibus arcus l m, et est ille qui est inter duo loca stellae in habitudine secunda et habitudine tertia, et erit arcus o i, et est ille qui est secundum ecentricum notus. Inuenimus ergo propter duos arcus e z et z h ecentrici, et propter duos arcus y o et o i orbis signorum quantitatem egressionis a centro et locum puncti s, et est longitudo longior secundum quod praemissum est, et sciemus per illud, quantum est inter locum longitudinis longioris et punctum a ecentrici, quod est punctum habitudinis primae, exibunt ergo istae res diuersae ab eo quod exiuerunt in primis, deinde inuenimus propter illud, quod est inter duo centra et locum longitudinis longioris, et longitudinem eius ab habitudine prima in orbe ecentrico, quantitates superfluitatum y k et l o et m i, secundo secundum similitudinem qua inuentae sunt prius, inuenientur inueuientur ed. ergo quantiates earum diuersae ab eo quod inuentae sunt prius. Addantur ergo duae superfluitates y k, l o super arcum k l, et minuantur duae superfluitates l o, m i ex quantitate arcus l m, et erunt tunc duo arcus y o et l o. Inueniamus ergo ex eis utrisque et ex duobus arcubus e z, z h ecentrici, quod est inter duo centra tertio, et locum longitudinis longioris, et longitudinem eius a puncto a, quod est locus stellae per uisionem, et inuenitur illud propinquum ei quod inuentum est secundo, et non cesset iteratio huius operis, donec inueniatur quantitas eius quae est inter duo centra, et locus longitudinis longioris non diuersificari ab eo quod inuentum est ante. Scitur ergo tunc quod illae quantitates inuentae per duas operationes, sunt quantitates uere quaesitae, deinde experiar post illud, ut inueniam per istas quantitates quae inuentae sunt, esse partes lineae quae sunt inter duo centra et loci longitudinis longioris, quantitates duorum arcuum k l, l m orbis signorum, quare inuenientur conuenientes ei secundum quod sunt per considerationem, et inuenientur quantitates horum duorum arcuum secundum quod narrabo. Propterea ergo quod angulus a t s, qui est apud centrum ecentrici, est notus, et est ille qui inuentus est, partes quae sunt inter longitudinem longiorem et habitudinem primam, sunt trianguli a t d duo latera a d, d t nota, et angulus a t d notus, ergo angulus a d t est notus, ergo trianguli a d n duo latera a d, d n sunt nota, et angulus a d n eius est notus, ergo angulus a n d eius est notus, et ipse est illud quod est inter stellam in habitudine prima, et longitudinem longiorem de orbe signorum, et similiter scietur quantitas eius quod est inter longitudinem longiorem de orbe signorum, et locum stellae in habitudine secunda. Inuenietur ergo arcus orbis signorum extractus per quantitates praedictas, postremo per illud quod est inter duo centra et loci longitudinis longioris conueniens ei quod inuentum est per considerationem, et similiter faciemus in arcu orbis signorum, qui est inter locum stellae in habitudine tertia, et inter longitudinem propiorem. Adiungetur ergo ad arcum qui est inter longitudinem secundam illud quod est ita, accipitur superfluitas quae est inter ipsum et inter medietatem circuli, et est propter illud arcus orbis signorum, qui est inter duo loca stellae in habitudine secunda, et in habitudine tertia, et inuenitur illud conueniens ei quod est secundum considerationem. Certificatur ergo per illud, quod istae quantitates quae inueniuntur ei quod est inter centra tria et locum longitudinis longioris sunt, secundum quod sunt uere, quando inuenitur quod sequitur ab eis conueniens, et suppositum ei quod apparet uisibiliter. Et Ptolomeus quidem comparatur in eo quod intendit in hoc loco uiro debilis uisus, qui uacillat in siluis spissis, in quibus sunt uiae strictae et semitae occultae, et per debilitatem sui uisus non est ei possibile incedere super eas. Incipit ergo uacillare dextrorsum et sinistrorsum, et ante et retro, et conatur ingenium in euasione, et qualiter eueniet ei, uia uero perducens ad inuentionem huius quaesiti secundum ultimam certitudinem, est secundum quod narrabo. Dico in primis, quia propterea quod pars longitudinis longioris et propioris cuiusque harum stellarum apud nos est inuenta secundum multam considerationem per illud quod apparet de quantitatibus motuum earum in partibus orbis signorum, et sunt duo motus stellae in duabus medietatibus orbis signorum, quas determinant longitudo longior et propior aequales, oportet propter illud, ut sint anguli diuersitatis quae est propter egressionem a centro in illis duabus medietatibus aequales, omnis angulus suo compari medietatis alterius, et illud non est nisi ita, ut sit centrum deferentis centrum orbis reuolutionis super lineam transeuntem per centrum orbis signorum et per centrum motus aequalis, et est linea quam terminant duo puncta longitudinis longioris et propioris. Et propterea quod non est possibile nobis peruenire ad cognitionem alicuius altitudinum stellarum, nisi post cognitionem puncti orbis signorum super quod est aux eius, oportet necessario ut praemittatur sermo in ostensione uiae perducentis ad cognitionem loci augis stellae, et illud erit per hoc, ut assumantur stellae quatuor ex habitudinibus qua nominatur extremitas noctis, quarum duae sunt in medietate orbis signorum, quam determinant longitudo longior et propior secundum multam considerationem, et duae reliquae in medietate secunda, et sit tempus quod est inter illas duas primas aequale tempori quod est inter istas duas postremas. Cum ergo inuenerimus has habitudines secundum hanc conditionem, diuidemus arcum orbis signorum, qui est inter duo loca stellae in duabus habitudinibus, quae sequuntur longitudinem longiorem secundum multitudinem considerationis, et erit ille locus augis eius secundum ultimum finem certitudinis. Cuius exemplum est, ut ponamus orbem signorum circulum a b g circa centrum e, et sint habitudines consideratae secundum conditionem praedictam, ipse in quibus est stella super lineas a e et b e et g e et d e, et sit tempus quod est inter duas horas duarum habitudinum a et b, aequale tempori quod est in eo, quod est inter duas habitudines g et d, et diuidemus arcum b g in duo media 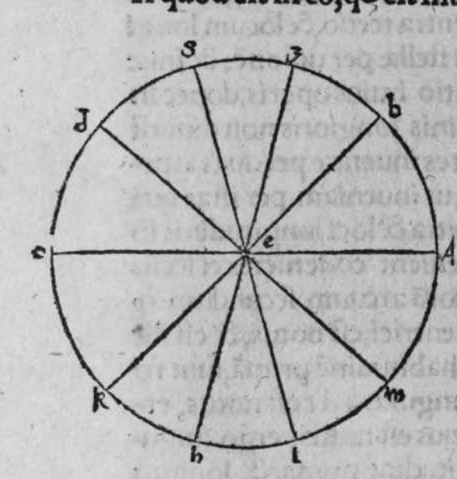super punctum z, et continuemus ipsum cum centro orbis signorum per lineam z e h. Dico ergo, quod linea z h transit per longitudinem longiorem et propiorem, cuius demonstratio est, quod nos faciemus penetrare lineas a e et b e et g e et d e, donec occurrant circumferentiae circuli super puncta t et k et l et m. Erunt ergo puncta ista loca medij solis in horis habitudinum consideratarum, et propterea quod tempus quod fuit inter horam duarum habitudinum a et b, est aequale tempori quod est in eo, quod est inter horam duarum habitudinum g et d, oportet ut sit tempus in quo abscidit sol per motum suum medium arcum t k, aequale tempori in quo abscidit arcum l m, ergo duo arcus sunt aequales, ergo duo arcus a b et g d iterum sunt aequales. Iam ergo abscidit stella de orbe signorum in duabus partibus aequalibus duos arcus, et non est aliquis eorum medietas circuli, et illud non est nisi ita, ut sit longitudo extremitatis utriusque a puncto augis eius longitudo aequalis, ergo linea h z est linea transiens per longitudinem longiorem et propiorem, et illud est cuius uoluimus declarationem. Et quando declaratum est nobis qualiter inueniantur duo loca longitudinis longioris et propioris orbis signorum, possibile lest nobis post illud cognoscere quantitates longitudinum quae sunt inter centra tria, scilicet centrum orbis signorum et centrum motus aequalis, et centrum deferentis secundum hunc modum. 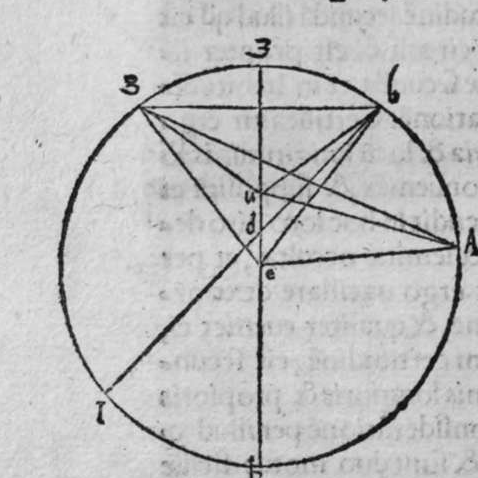Ponam circulum a b g circulum deferentem centrum orbis reuolutionis stellae, et sit centrum eius punctum d, et sit tertia habitudinum consideratarum, et sunt habitudines a et b et g, et linea transiens per longitudinem longiorem et propiorem sit linea z h, et sit centrum orbis signorum super eam punctum e, et centrum motus aequalis punctum u, et continuabo lineas a e et b e et g e, et lineas a u, b u, g u, et sit linea z h diuidens spacium quod est inter duas lineas b e et g e in duo media secundum quod est in figura prima, et continuabo iterum lineas a b et b g et a g, et continuabo lineam b d, et faciam eam penetrare usoque ad circumferentiam circuli ad punctum l. Erit ergo linea b d l diameter deferentis, propterea ergo quod tempus quod est inter duas horas duarum habitudinum b et g est notum, erit angulus b u g notus, ergo eius medietas quae est angulus b u z est nota, ergo angulus b u e est notus, et propterea quod locus longioris longitudinis est notus, et punctum b est locus stellae est notum, erit angulus b e z notus, ergo triangulus b e u est notorum angulorum, ergo proportiones laterum eius adinuicem sunt notae. Et per simile illius ostendit, quod triangulus a e u est notorum angulorum, ergo proportiones laterum eius adinuicem sunt iterum notae, ergo per quantitatem qua linea e u est nota, est unaquaeque linearum a e et b e et a u et b u nota. Et propterea quod angulus a u b est notus, et duo latera a u, b u sunt nota, erit latus a b notum, et angulus a b u notus, et similiter illius iterum erit latus b g notum, et angulus b g u notus, et duo latera a b et b g sunt nota, et angulus a b g est notus. Erit ergo propter illud angulus b a g notus, ergo arcus b g est notus, ergo corda eius, et est linea b g est nota per quantitatem qua est medietas diametri circuli a b g nota, et iam fuit linea b g nota per quantitatem qua est linea e u nota, ergo linea e u est nota per quantitatem qua est medietas diametri deferentis nota. Et propterea quod arcus b g est notus, remanet arcus g l notus, ergo angulus g b l notus, ergo angulus u b l est notus, et propterea quod linea b u est nota per quantitatem qua est linea e u nota, oportet ut sit linea b u nota per quantitatem qua est medietas diametri deferentis nota, et duo latera b d, b u sunt nota, et angulus d b u est notus, ergo latus d u est notum, et iam fuit linea e u nota, remanet ergo linea d e nota, et illud est cuius uoluimus declarationem. Dixit ergo, quia inuenit per illud, quod ei praemissum est de illo opere, punctum longitudinis propinquioris stellae martis super 25. partes et medietatem partis capricorni punctum longitudinis longioris super partem condiametralem huic parti, et est 25. pars et medietas cancri, et lineam quae est inter centrum orbis signorum et centrum motus aequalis 12. partes propinquae propinpuae ed., per partes quibus medietas diametri ecentrici est 60. partes. Et inuenit longitudinem longiorem stellae Iouis super 11. partes uirginis, et longitudinem propinquiorem super partem condiametralem ei, et illud est super 11. partes piscis, et inuenit lineam quae est inter centrum orbis signorum et centrum motus aequalis 5. partes et medietatem partis, quibus est medietas orbis ecentrici 60. partes, et inuenit punctum longitudinis longioris stellae Saturni super 23. partes scorpionis, et longitudinem propiorem super partem condiametralem ei, et est 23. pars tauri, et lineam quae est inter centrum orbis signorum et centrum motus aequalis 6. partes et 50. minuta, per partes quibus est medietas diametri orbis ecentrici 60. partes. Et propterea quod ostensum fuit ei hoc, incepit post illud ligare comprehensionem motus alicuius harum stellarum trium in longitudine et diuersitate in tempore unius habitudinum trium consideratarum secundum hunc modum. Ponam ergo 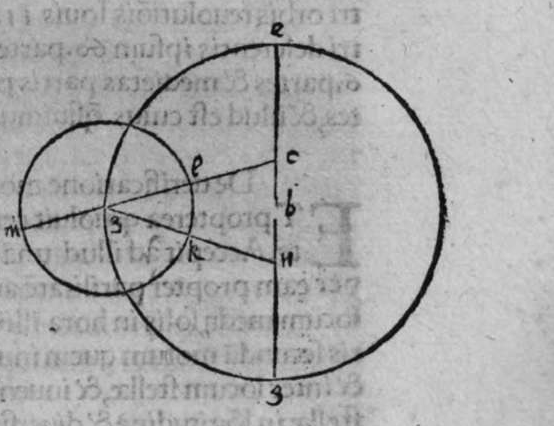orbem deferentem stellam circulum e g circa centrum d, et centrum motus aequalis punctum t, et centrum orbis signorum punctum n, et centrum orbis reuolutionis in habitudine tertia ex habitudinibus consideratis, et sunt habitudines quibus extrahitur locus longitudinis longioris punctum g, et continuabo g n, ergo uidebitur stella super hanc lineam in hac habitudine tertia, et continuabo t g m, propterea quod illud quod est inter punctum longitudinis longioris et locum stellae per medium in hora considerationis tertiae, et est quantitas anguli e t g, est notum, et angulus e n g est notus, et est longitudo stellae in orbe signorum per uisionem in hora habitudinis tertiae a puncto longitudinis longioris, remanet angulus t g n notus, et est apud centrum orbis reuolutionis, ergo erit arcus k l orbis reuolutionis notus, et est illud quod est inter stellam et longitudinem propiorem mediam orbis reuolutionis in hora habitudinis tertiae, erit ergo propter illud arcus m k, et est longitudo eius a longitudine longiori media in hora habitudinis tertiae notus, erit ergo propter illud longitudo centri orbis reuolutionis iterum, et est medius stellae a puncto longitudinis longioris nota, et illud est cuius uoluimus declarationem. Et propterea quod ostensum fuit illud, possibile fuit ei, ut sciret quantitatem orbis reuolutionis stellae, scilicet proportionem medietatis diametri eius ad medietatem diametri deferentis ipsum, ita, quod considerauit stellam cum instrumento considerationis post considerationem eius in consideratione tertia post tres dies, aut quasi ipsi, et uerificauit considerationem suam qua considerauit stellam ex stellis fixis, et cum luna. Inuenit ergo locum eius in orbe signorum, quia sciuit quantitatem arcus quem abscidit de orbe signorum in illis diebus et horis, qui fuerunt inter duas considerationes, et proportionem medietati s diametri orbis reuolutionis eius de medietate diametri deferentis ipsum secundum hunc modum. Sit itaque orbis deferens stellam circulus a b g circa centrum d, et centrum orbis 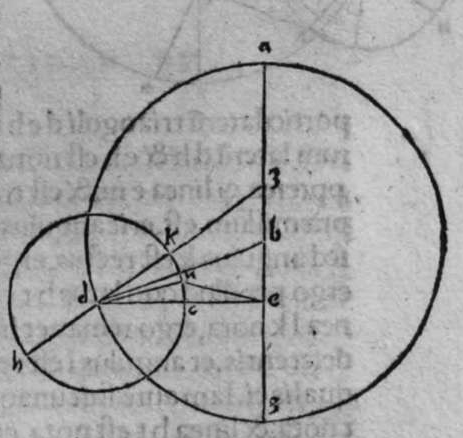signorum punctum e, et centrum motus aequalis punctum z et linea transiens per longitudinem longiorem et propiorem linea a e g, et orbis reuolutionis circulus h t k circa centrum b, et sit stella in orbe reuolutionis suae in hora considerationis secundae super punctum n, et continuabo lineas z b h et d b et e b, et continuabo duas lineas e n, b n, propterea ergo quod tempus quod fuit inter illam horam habitudinis tertiae et horam considerationis secundae, est notum, et quod conuenit ei de motu longitudinis medio et diuersitatis, secundum quod scripserunt illud antiqui, est notum, quamuis sit in illo propinquitas, et non est in huiusmodi tempore paruo. Et quantitas de qua curetur, erit illud, quo mouetur centrum orbis reuolutionis in illo tempore, et quod mouet stellam in eo notum est, et longitudo centri orbis reuolutionis in hora habitudinis tertiae a puncto a fuit nota, et similiter longitudo stellae a puncto longitudinis propioris mediae orbis reuolutionis iterum nota. Oportet ergo propter illud, ut sit unusquisque duorum angulorum a z b et b n notus, et propterea quod trianguli d z b, duo latera d z, d b sunt nota, et angulus d z b est notus, est linea z b nota. Et propterea quod trianguli e z b, duo latera e z et z b sunt nota, et angulus e z b eius est notus, erit unusquisque duorum angulorum eius z e b et z b e notus, et latus eius e b notum, et iam fuit angulus n b k notus. Remanet ergo angulus n b t notus, et propterea quod fuit angulus g e n notus, et est longitudo stellae in hora considerationis tertiae a longitudine propiore, remanet angulus n e b notus, ergo trianguli e n b anguli tres sunt noti, ergo proportiones laterum eius adinuicem sunt notae, ergo proportio lineae n b ad lineam b e est nota, et linea c b iam exiuit nota per quantitatem qua est linea d b quae est medietas diametri deferentis 60. Sed proportio lineae b n ad lineam d b quae est medietas diametri orbis deferentis, est proportio nota, exiuit ergo ei in stella martis, quod est medietas diametri orbis reuolutionis, 39. partes et medietas partis per quantitatem qua est medietas deferentis 60. partes. Et exiuit iterum quantitas medietatis diametri orbis reuolutionis Iouis 11. partes et 30. minuta per quantitatem qua est medietas diametri deferentis ipsum 60. partes, et exiuit ei medietas diametri orbis reuolutionis Saturni 6. partes et medietas partis per quantitatem qua est medietas diametri deferentis 60. partes, et illud est cuius quaesiuimus declarationem.

⟨VII.3⟩ De uerificatione motuum stellarum reuolubilium in longitudine et diuersitate.

ET propterea quod uoluit certificare motus stellae reuolubiles in longitudine et diuersitate. Accepit ad illud unam ex antiquioribus considerationibus quas inuenit, et fuit firmus per eam propter parilitatem aut propinquitatem uehementem alicui stellarum fixarum, et sciuit locum medij solis in hora illius considerationis, et locum longitudinis longioris et propioris secundum motum quem inuenit augibus stellarum. Sciuit ergo per illud quod fuit inter ipsum et inter locum stellae, et inuenit ex illo et ex medietate diametri orbis reuolutionis locum stellae in longitudine et diuersitate per medium, scilicet longitudinem puncti centri orbis reuolotionis a longitudine longiori media ecentrici, et longitudinem planetae a longitudine longiori orbis reuolutionis secundum quod ego narro. Sit orbis deferens circulus a b g circa centrum d, et linea transiens per longitudinem longiorem et propiorem linea a z, et centrum motus 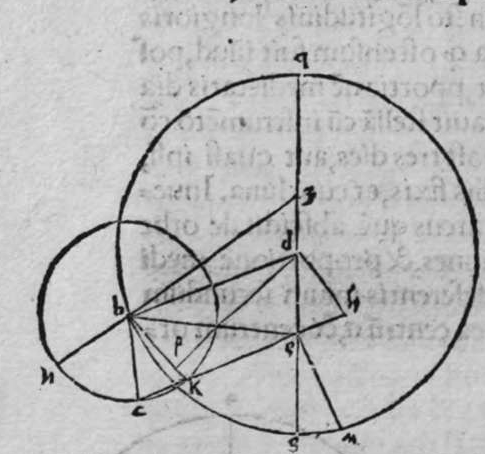aequalis super ipsam punctum z, et punctum centri orbis signorum punctum e, et orbis reuolutionis circulus n t circa centrum b, et sit stella in hora considerationis illius super ipsum punctum t, et continuabo lineas z b n et d b, et sit medius solis super lineam e m, et continuabo punctum t cum centro orbis signorum per lineam e t, et protraham super ipsam a puncto d perpendicularem quae sit linea d h, et a puncto b perpendicularem quae sit b k et protraham super ipsam a puncto d perpendicularem quae sit linea d l. Est ergo superficies d h k l aequedstantium laterum, ergo latera opposita sunt aequalia, et propterea quod fuit longitudo stellae a puncto longitudinis propioris in hora considerationis nota, est angulus g e t notus, ergo angulus d e h est notus, sed angulus h est rectus, remanet ergo angulus h d e notus, ergo proportio laterum trianguli d e h adinuicem est nota, et latus e d est notum, ergo unumquodque duorum laterum d h et e h est notum. Sed linea d h est aequalis lineae k l, ergo linea k l est nota, et propterea quod linea e m, et est transiens per medium solis, est aequedistans lineae b t, secundum quod praemissum est, erit angulus m e t notus aequalis angulo b t e, ergo angulus b t e est notus, sed angulus k est rectus, ergo triangulus b k t est notorum angulorum, ergo est notorum laterum, ergo per illud quo latus b t est notum, est latus b k notum, et iam fuit per illam quantitatem linea l k nota, ergo remanet linea b l nota. Sed linea d b est nota, quoniam est medietas diametri deferentis. et angulus l est rectus, ergo erit linea l d nota, ergo linea h k est nota, cum sit aequalis ei. Iam autem fuit unaquaeque duarum linearum h e et t k nota, est ergo propter illud linea e t nota, et linea b t est nota, et angulus b t e est notus, ergo unusquisque duorum angulorum b e t, e b t est notus, et latus e b est notum. Et propterea quod angulus t e g est notus, et est longitudo stellae a longitudine propiori in hora considerationis, erit angulus b e g totus notus. Remanet ergo angulus d e b notus, et duo latera d e et e b, ergo unusquisque duorum angulorum e b d, e d b est notus, ergo totus angulus d b t est notus. Et propterea quod angulus e d b est notus, remanet angulus z b d notus, et unumquodque duorum laterum z d, d b est notum, ergo unusquisque duorum angulorum d z b quod d b z est notus, ergo angulus a z b est notus, et est longitudo centri orbis reuolutionis in hora considerationis a puncto longitudinis longioris, et similiter angulus d b t iam fuit ostensum quod est notus, ergo totus angulus z b t est notus. Remanet ergo angulus n b t notus, ergo longitudo stellae a puncto longitudinis longioris mediae orbis reuolutionis in hora considerationis etiam est nota, et alliud est cuius uoluimus declarationem. Iam autem fuit locus stellae medius in longitudine et diuersitate in hora considerationis tertiae, quae fuit secundum tempus suum notus. Verificauit ergo quod est inter duo tempora, et diuisit super ipsum numerum reuolutionum centri orbis reuolutionis, et numerum reditionum stellae in orbe reuolutionis suae, et superfluitates additas, exiuit ergo quantitas motus stellae reuolubilis in longitudine et diuersitate, et illud est cuius uoluimus declararationem. Inuenit ergo motum diuersitatis in die uno Saturni quidam 57. minuta et 7. secunda et 43. tertia et 41. quartum et 43. quinta et 40. sexta per propinquitatem. Et Iouis quidem 54. minuta et 9. secunda et duo tertia et 46. quarta et 26. quinta. Et Martis quidem 27. minuta et 41. secundum et 40. 40 ed. tertia et 19. quarta et 20. quinta et 58. sexta. Et Veneris quidem 36. minuta et 59. secunda et 25. tertia et 53. quarta et 11. quinta et 20. sexta. Et Mercuij quidem tres partes et 6. minuta et 24. secunda et 6. tertia et 59. quarta et 35. quinta et 50. sexta. Postea ipse minuit ex motu solis medio diei motum cuiusque stellarum trium in die, et remanet motus longitudinis eius. Inuenit ergo illud Saturni quidem duo minuta 0. secunda et 33. tertia et 31. quartum et 28. quinta et 51. sextum. Et Iouis quidem 4. minuta et 59. secunda, et 14. tertia et 26. quarta et 46. quinta et 31. sextum. Et Martis quidem 31. minutum et 26. secunda et 36. tertia et 53. quarta et 51. quintum et 30. sexta.

⟨VII.4⟩ De ligatione comprehensionis motuum stellae in longitudine et diuersitate.

ET propterea quod uoluit scire in hora regni Nabuchodonosor loca stellarum trium in longitudine et diuersitate, accepit tempus quod fuit inter regnum Nabuchodonosor et inter horam considerationis antiquae, et uerificauit ipsum, et sciuit illud quod conuenit ei de reuolutionibus longitudinis et diuersitatis, et propter illud ex locis stellarum in hora illius considerationis, et sciuit per illud duo loca stellae per medium in longitudine et diuersitate in hora regni Nabuchodonosor. Inuenit ergo locum Saturni in longitudine super 26. partes et 43. minuta capricorni, et in diuersitate super 32. partes et duo minuta a longitudine longior, et locum Iouis in longitudine super 4. partes et 41. minutum librae, et in diuersitate super 144. in longitudine longiori, et locum Martis in longitudine super tres 32. arietis, et in diuersitate super 320. 13. a longitudine longiori. Et similiter comprehendit loca augium harum stellarum in illa hora, inuenit ergo augem Saturni in 20. 10. scorpionis, et Iouis super duas nouem uirginis, et Martis super 16. 40. cancri.

⟨VIII⟩ LIBER OCTAVVS. DE STATIONE ET retrogradatione stellarum.

PRopterea quod uir iste rememoratus est inuentionis stationis stellarum, secundum quod non sit ei nisi diuersitas una tantum, et est illa, quae est per comparationem ad solem, et propterea quod huius diuersitatis casus praeparatur secundum unamquanque duarum radicum, scilicet radicem orbis ecentrici et radicem orbis reuolutionis, fuit ei necessarium erigere demonstratrionem secundum assimilationem habitudinis stationis et temporis eius in unaquaque duarum radicum, uisum est nobis, ut abbreuiemus illud, com non sit nobis necessarium prolongare et frustra uociferare, propterea quod iam uerificauimus, quia est uanum, et quod res in stellis est secundum contrarium illius, quod est, quia ipse iam demonstratiue probauit quod stella habet duas diuersitates, quarum una est secundum orbem ecentricum, et secunda secundum orbem reuolutionis suae. Incipiamus ergo nunc praemittere quod praemittendum est in inuentione loci stellae, secundum quod sint ei duae diuersitates, sicut iam ostensum est in eo quod praemissum est. Dico ergo propterea quod iam contingit in unaquaque stellarum quinque, ut sit proportio medietatis diametri orbis reuolutionis suae ad lineam, quae est inter centrum orbis signorum et propinquitatem propinquiorem orbis reuolutionis maior semper proportione motus sui medij in longitudine ad motum suum in diuersitate, oportet ut contingat stellae in loco aliquo orbis reuolutionis suae, ut uideatur stans, deinde uideatur post illud rediens per aliquod tempus, deinde redeat ad stationem secundam. Deinde dirigatur, et est punctum stationis cuius ipsum punctum, super quod secat or bem reuolutionis apud propinquitatem propinquiorem, linea egrediens a centro orbis signorum proportio medietatis eius, quae cadit ex ea in orbe reuolutionis ad illud quod cadit de ea extra ipsum, est sicut proportio motus medij in longitudine ad motum diuersitatis, uerum alleuiatur formatio eius quod diximus, si exemplificemus ad illud exemplum. Ponamus ergo reuolutionis circulum ab g circa 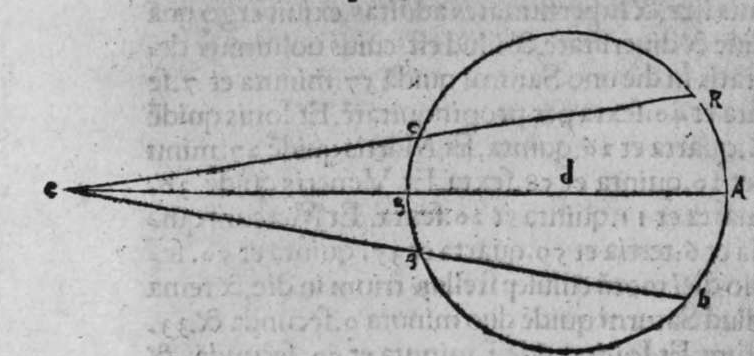centrum d, et centrum orbis signorum punctum e, et continuemus e g a, et contingit in unaquaque harum quinque stellarum, ut sit proportio linae d g ad lineam e maior proportione motus centri orbis reuolutionis suae ad motum suum in orbe reuolutionis suae, et quando illud est ita, tunc possibile est, ut protrahamus a puncto e lineam e z b, et sit proportio medietatis lineae b z ex ea ad lineam e z, sicut proportio motus orbis reuolutionis ad motum stellae in orbe reuolutionis. Dico ergo quod quando stella est super punctum z, imaginatur nobis quod ipsa est stans, et similiter si protraxerimus lineam aliam in medietate secunda orbis reuolutionis secundum hanc proportionem quae sit sicut linea e t k, imaginatur nobis iterum quando est super punctum t quod est stans, et quod in toto arcu z g t est retrograda, quod in toto arcu t a z est directa, et hoc est ita, ut ostendamus quod omnis arcus qui abscinditur a parte puncti z ad partem g, et a puncto t ad punctum g, iterum est arcus retrogradationis stellae, et quod omnis arcus qui separatur ad partem a iterum ab ambobus punctis, est arcus directionis, et propter illud sequitur, ut quando stella sit super duo puncta z et t, imaginetur nobis, quia est stans. Praemittamus ergo ad ostensionem illius illud, cuius praemissio necessaria est. Dico ergo, quod quando est triangulus a b g, et est latus b g longius latere a g, et secatur ex latere b g longiore linea, quae non sit minor linea a g, quae sit linea g d, tunc proportio lineae g d sectae ad lineam b d reliquam, est maior proportione anguli b eius ad angulum g, cuius demonstratio est, ut continuetur linea a d, et protrahatur a puncto g linea aequedistans lineae a d quae sit linea g z, et fiat ut penetret linea a b, donec occurrat ei super punctum z, et protrahatur linea a e aequedistans lineae b g, propterea ergo quod linea d g non est minor linea a g, erit linea a e non minor linea a g. Si ergo erpo ed. posuerimus punctum a centrum, et mensurabimus longitudinem 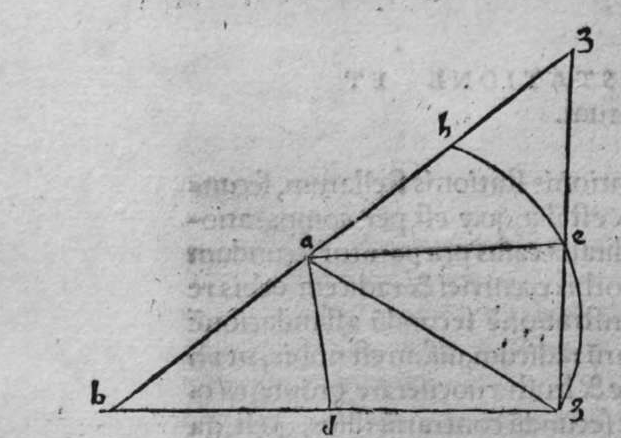a e, et circumduxerimus circulum e h, transibit per punctum g, aut extra ipsum, et propterea quod linea g d non est minor linea a g, est linea a b longior b d, ergo angulus a d b est maior angulo b a d, ergo angulus a e z est maior angulo a z e, ergo linea a z est longior linea a e. Cadet ergo punctum h circuli e h in eo quod est inter duo puncta a e, ergo proportio trianguli a z e ad triangulum a e g est maior proportione sectoris a h e ad sectorem a e g. Sed proportio trianguli z a e ad triangulum e a g, est sicut proportio lineae z e ad lineam g e, et proportio sectoris a h e ad sectorem a e g, est sicut proportio anguli h a e ad angulum e a g, et propterea quod linea a e est aequedistans lineae b g, erit angulus h a e aequalis angulo a b g, et angulus e a g aequalis angulo a g b, ergo proportio lineae z e ad lineam e g est maior proportione anguli g b a ad angulum a g b, ergo proportio lineae z a ad lineam a b est maior proporuione anguli a b g ad angulam a b g, ergo proportio lineae g d ad lineam d b est maior proportione anguli a b g ad angulum a g b, et illud est cuius uoluimus declarationem. Et quia iam expositum est illud, tunc sit circulus a b g orbis reuolutionis stellae circa centrum e, et sit punctum z centrum orbis signorum, et sit diameter a e g transiens per centrum orbis signorum, et sit proportio medietatis lineae a g ad lineam g z maior propottione uelocitatis centri reuolutionis suae 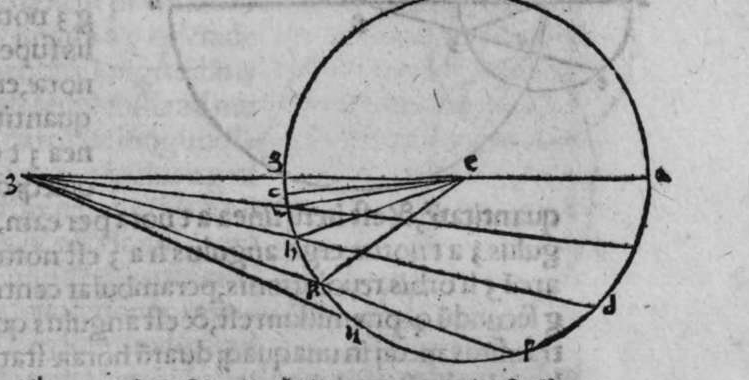ad uelocitatem stellae in orbe reuolutionis, sicut est in stellis quinque, et protraham a centro orbis signorum lineam quae secet orbem reuolutionis, donec sit proportio medietatis eius quod cadit intra circulum ad illud quod cadit de ea etra ipsum, sicut proportio uelocitatis orbis reuolutionis ad uelocitatem stellae. Sit ergo linea illa existens linea b h z. Dico ergo, quod quando stella sit super punctum h orbis reuolutionis uidetur stans, et quod si secetur a parte puncti h ad partem longitudinis longioris arcus cum quacunque quantitate fuerit, tunc ipse erit arcus directionis, scilicet quod quando stella est in eo, uidetur directa. Et si secetur in parte longitudinis propioris, est arcus retrogradationis, scilicet, quia uidetur in eo retrograda, secabo ergo in primis arcum k h a parte longitudinis longioris, et continuabo lineam z k l, et continuabo k e, h e, k b, erit ergo trianguli z k b latus z b maius latere b k, et separatur ex latere z b linea quae non est minor latere b k, quae est linea b h, ergo proportio lineae b h ad h z, est maior proportione anguli z ad angulum b, ergo proportio medietatis lineae b h ad lineam z h est maior proportione anguli z ad duplum anguli b, uerum angulus h e k est duplus anguli b, ergo proportio medietatis lineae b h ad lineam z h est maior proportione anguli z ad angulum h e k. Sit ergo sicut proportio anguli b z n ad angulum h e k, et propterea quod fuit proportio medietatis lineae b h ad lineam z h existens sicut proportio uelocitatis orbis reuolutionis ad uelocitatem stellae, erit proportio uelocitatis orbis reuolutionis ad uelocitatem stellae, sicut proportio anguli b z n ad angulum h e k, uerum angulus h e k est uelocitas stellae in orbe reuolutionis suae, et angulus b z n est uelocitas orbis reuolutionis. In tempore ergo in quo abscidit stellae arcum k h orbis reuolutionis, abscidit centrum orbis reuolutionis angulum b z n, ergo uidetur stella directa per quantitatem anguli k z n, qui est superfluitas anguli b z n super angulum b z k, et si separetur arcus h m ad partem longitudins propioris, et continuentur lineae z m et b m et m e, erit trianguli b z m latus b z maius latere z m, et iam separata fuit linea z h non minor linea z m, ergo proportio lineae z h ad lineam h b est maior proportione anguli z b m ad angulum b z m. Cum ergo conuerterimus, erit proportio lineae b h ad lineam h z minor proportione anguli b z m ad angulum z b m, ergo proportio medietatis lineae b h ad lineam h z, est minor proportione anguli b z m ad duplum anguli b z m. Ergo proportio uelocitatis orbis reuolutionis ad uelocitatem stellae est minor proportione anguli b z m ad angulum h e m. Sit ergo sicut anguli b z m ad angulum h e t, ergo i tempore, in quo percurrit centrum orbis reuolutionis angulum b z m, percurrit stella arcum h t orbis reuolutionis, uidetur ergo retrograda per quantitatem anguli cui subtenditur apud centrum orbis signorum, et illud est cuius uoluimus declarationem. Et quia iam declaratae sunt res istae, tunc incipiamus post illud declarare quantitates temporum in unaquaque stellarum quinque, et propterea quod motus stellae reuolubilis in longitudine diuersificatur secundum diuersitatem longitudinum centri orbis reuolutionis a centro orbis signorum, et secundum diuersitatem huius motus diuersificatur tempus retrogradationis, tunc ostendam quantitatem illius in primis, quando centrum orbis reuolutionis est in hora quae nominatur extremitas noctis in transitu medio ecentrici, ubi est motus stellae in longitudine reuolubilis secundum propinquitatem motus eius, qui uidetur secundum centrum orbis signorum secundum hunc modum. Sit orbis deferens centrum orbis reuolutionis circulus a b, et sit centrum orbis reuolutionis super ipsum in transitu medio quod sit punctum a, et orbis reuolutionis circulus d e, et linea b g a transiens per centrum orbis reuolutionis quod est punctum a, et per centrum orbis signo rum, et est punctum g, et sit proportio medietatis lineae e z ad lineam z g, sicut proportio motus stellae in longitudine ad motum eius in diuersitate, qui ambo sunt reuolubiles, et continuabo lineam a z, et protraham a puncto a puncto a puncto ed. a super lineam z e perpendicularem a t, propterea ergo quod proportio lineae t z ad lineam g z 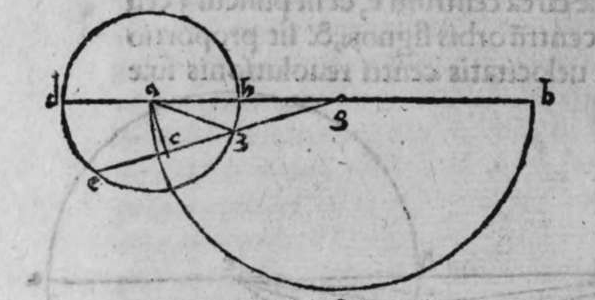est nota, cum sit sicut proportio motus stellae in longitudine ad motum eius in diuersitate, qui ambo sunt reuolubiles, erit iterum proportio lineae e g ad lineam g z nota, et superficies quam continent nota, cum sit aequalis superficiei quam continent duae lineae d g, g h quae sunt notae, ergo unaquaeque duarum linearum e g, z g est nota per quantitatem qua est medietas diametri a d nota, et linea z t est nota per illam quantitatem. Et similiter unaquaeque duarum linearum g a et g t iterum est nota per illam quantitatem, et est iterum linea a t nota per eam, ergo angulus g est notus, et similiter erit angulus z a t notus, ergo angulus h a z est notus, ergo in tempore in quo perambulat stella arcum z h orbis reuolutionis, perambulat centrum orbis reuolutionis angulum minorem angulo g secundum quod praemissum est, et est angulus qui est inter centrum orbis reuolutionis et punctum transitus medij in unaquaque duarum horarum stationis, et est tempus in quo percurrit stella per longitudinem reuolubilem illum eundem angulum notum, et est medietas temporis retrogradatioonis, et est superfluitas inter hunc angulum et angulum g nota, et est medietas arcus retrogradationis, et illud est cuius uoluimus declarationem. Quando ergo est centrum orbis reuolutionis in loco alio a trasitu medio ab orbe ecentrico, sciemus longitudinem centri eius a centro orbis signorum in illo loco, et sciemus superfluitatum quantitatem angulorum diuersitatis, quae lest propter ecentricum illic. Nam si fuerit centrum orbis reuolutionis in sectione ecentrici quam determinant duo transitus medij, in cuius medio est punctum longitudinis longioris, inuenimus illas superfluitates quae sunt angulorum diuersitatis illic ex motu medio in longitudine. Et si fuerit in sectione secunda eius, scilicet in cuius medio est punctum longitudinis propioris, addemus illas superfluitates super motum medium, quod ergo fuerit post additionem aut diminutionem, est quantitas motus longitudinis uisibilis in illo loco. Si ergo nos protraximus lineam a centro orbis signorum, quae secat orbem reuolutionis secundum proportionem huius motus uisibilis ad modum diuersitatis, et exemplificauerimus opus quod praecessit iterum nuper, proueniet nobis punctum stationis stellae, et quantitas temporis retrogradationis eius in illo loco. Et totum quod fecit Ptolomeus in inuentione loci stationis stellae et quantitatis temporis retrogradationis eius, quando est centrum orbis reuolutionis in loco qui est alius a transitu medio ecentrici, est error, quod est, quia quando extrabitur linea secans or bem reuolutionis secundum quod sit proportio medietatis eius quod cadit ex ea in orbe reuolutionis ad illud quod cadit ex ea extra ipsum, sicut proportio proporio ed. motus longitudinis uisibilis ad motum diuersitatis, reuolubilem non uisibilem, tunc ingreditur ingreeditur ed. in illud de errore illud quod ostendam in eo quod est post, et propter illud uisum est nobis, ut afferamus omnia quae ipse fecit in hac intentione, ut ostendatur error eius in illo. Dico ergo, quod propterea quod declarata ei est quantitas anguli quae est longitudo centri orbis reuolutionis a puncto transitus medij ecentrici in unaquaque duarum horarum stationis, fuit ei possibile aequare duos motus stellae in longitudine et diuersitate qui uidentur, quando stella est uersus longitudinem longiorem aut propiorem ecentrici, ut inueniret per illud quantitatem temporis retrogradationis stellae, quando est in habitudine quae nominatur extremitas noctis ab uno duorum punctorum longitudinis longioris aut propioris ecentrici, ostendit ergo illud in longitudine longiori in primis secundum hunc modum. Sit in forma simili huic formae praecedenti linea transiens per longitudinem longiorem et propiorem linea m g n, et sit super eam centrum motus aequalis punctum l, et longitudo longior punctum m, et longitudo propior punctum n, et sit longitudo centri orbis reuolutionis quod est punctum a a puncto m, quod est longitudo longior, sicut longitudo eius a puncto transitus medij in hora stationis, et est angulus m g a. Sciemus ergo ex hoc angulo quantitatem longitudinis centri orbis reuolutionis a centro orbis signorum, et est linea a g, et sciemus iterum quantitatem anguli g a l, qui est angulus diuersitatis, et angulum a l m, et est angulus longitudinis reuolubilis. Diuidemus ergo partes anguli g a l super numerum partium anguli a l m, et quod exibit, erit portio diuersitatis partis unius longitudinis reuolubilis, minuemus ergo illud ex parte una longitudinis reuolubilis, et addemus super illud quod conuenit illi parti de motu diuersitatis reuolubilis, et quod fuit post additionem et diminutionem, est motus stellae qui sunt uisibiles in longitudine et diuersitate secundum longitudinem 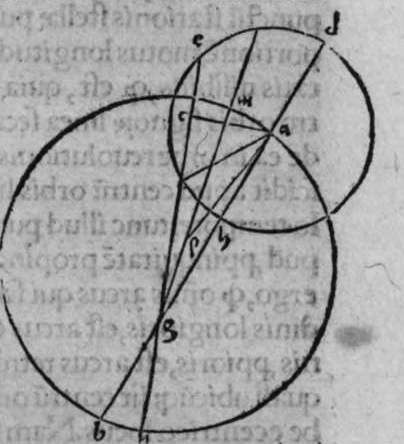a g, postea ponemus proportionem medietatis lineae e z ad lineam z g, sicut proportionem illius motus uisibilis in longitudine ad illum motum uisibilem in diuersitate, et ostendam sicut praemissum est per quantitatem anguli z a h, et quantitatem anguli a g e, deinde sciemus illud quod conuenit angulo z a h ex partibus longitudinis reuolubilis per proportionem motus longitudinis reuolubilis ad motum diuersitatis uisibilis. Quod ergo fuerit de partibus longitudinis reuolubilis, et seruabimus illud, et propterea quod angulus a g m non est secundum ueritatem longitudo centri orbis reuolutionis a puncto longitudinis longioris in hora stationis, et non est nisi angulus longitudinis a transitu medio, cum isti anguli diuersificantur secundum diuersitatem longitudinis centri orbis reuolutionis a centro orbis signorum, et proportio motus uisibilis in longitudine ad motum uisibilem in diuersitate mutatur secundum mutationem longitudinis centri orbis reuolutionis a longitudine longiori. Et istae partes longitudinis reuolubilis seruatae non inueniuntur nisi secundum proportionem acceptam in longitudine anguli a g m et g a l, si inuenerimus angulum diuersitatis illarum partium seruatarum, et minuerimus eas ex partibus anguli z a h, quae sunt partes diuersitatis mediae, et est longitudo stellae in hora stationis a puncto longitudinis propioris aequalis orbis reuolutionis. Sciemus ergo illud quod conuenit illi de motu longitudinis reuolubilis secundum proportionem motuum mediorum, quod ergo est, est partes longitudinis aequalis centri orbis reuolutionis a puncto longitudinis longioris secundum propinquitatem in hora stationis, et sunt partes quas perambulat centrum orbis reuolutionis per motum suum aequalem ab hora stationis ad horam habitudinis quae nominatur extremitas noctis, scilicet medium temporis retrogradationis, et tempus in quo perambulat centrum orbis reuolutionis illud, est medietas temporis retrogradationis, ergo medietas temporis retrogradationis est nota. Deinde minuemus ex partibus illius longitudinis aequalis angulum diuersitatis, quod ergo remanebit, erit longitudo centri orbis reuolutionis a longitudine longiori secundum centrum orbis signorum. Minuemus ergo illud ex partibus anguli a g e, et quod remanebit, erit medietas partium retrogradationis stellae ergo illud etiam notum, et uia huic et deuiae simili iuit in inuentione horum temporum in longitudine propiori ecentrici, et in reliquis partibus orbis ecentrici. Verumtamen propter inquisitionem alleuiationis in opere componuntur ad illud tabulae per quas inueniuntur tempora retrogradationis rerrogradationis ed. in omnibus partibus orbis ecentrici ex temporibus retrogradationis in istis tribus longitudinibus, scilicet transitu medio et longitudine longiori et longitudine propiori secundum propinquitatem. Exemplificauit ergo in illo illud quod fecit in angulis medietatis diametri orbis reuolutionis, qui sunt apud centrum orbis signorum, quod est, quia ipse inuenit eos per proportiones minutorum ex 60. minutis, quae sunt proportiones superfluitatum longitudinum centrorum orbis reuolutionis a centro orbis signorum adinuicem, et illud est cuius uoluimus declarationem. Comprehenduntur ergo ei per hoc opus quantitates dierum retrogradationis omnium. Stellae quidem quide ed. Saturni in maiori longitudine eius a terra 140. dies et duae tertiae diei, et in longitudine ipsius media 138. dies, et in minori longitudine sua 136. dies. Stellae autem Iouis in maiori longitudine sua 123. dies, et in longitudine ipsius media 120. dies, et in minori longitudine sua 118. dies. Stellae uero Martis in maiori longitudine sua 80. dies, et in sua longitudine media 73. dies, et in propinquiori longitudine sua 64. partes et medietas. Stellae uero Veneris in maiori sua longitudine 43. dies, et in longitudine sua media 41.dies, et duae tertiae diei, et in minori sua longitudine 40. dies et duae tertiae diei. Stellae autem Mercuij in sua maiori longitudine 21. dies, et in longitudine sua media 22. dies et medietas, et in minori sua longitudine 23. dies. Totum uero quod attulit in hoc tractatu de inuentione loci stationis stellae, quando centrum orbis reuolutionis est in longitudine longiori aut propiori ecentrici est error, quod est, quia ipse ponit proportionem lineae t z figurae praecedentis ad lineam g z, sicut proportionem motus uisibilis in longitudine ad motum uisibilem in diuersitate, scilicet ad motum stellae in orbe reuolutionis suae post additionem anguli diuersitatis, quae est propter ecentricum ad diminutionem eius ab eo, et fabricauit rem secundum hoc quod sit punctum z punctum stationis stellae, uerum res non est sicut dixit, erit autem punctum stationis stellae punctum quod secat de orbe reuolutionis linea egrediens secundum proportionem motus longitudinis uisibilis ad motum diuersitatis reuolubilis, non ad motum diuersitatis uisibilis, quod est, quia iam ostensum est per demonstrationem certam, quod quando producitur a centro orbis signorum linea secans or bem reuolutionis, et est proportio medietatis eius quod cadit de ea in orbe reuolutionis ad illud quod cadit de ea extra ipsum, sicut proportio anguli quem abscidit apud centrum orbis signorum ad angulum qui est apud centrum orbis reuolutionis suae in illo tempore, tunc illud punctum super quod secat haec linea circumferentiam orbis reuolutionis apud propinquitatem propinquiorem eius, est punctum in quo apparet stella stans. Manifestum est ergo, quod omnis arcus qui secatur de orbe reuolutionis a parte illius puncti ad partem longitudinis longioris, est arcus directionis stellae, et omnis arcus qui absciditur ad partem longitudinis propioris, est arcus retrogradationis, et haec quidem demonstratio est secundum communitates, quasi ubicunque sit centrum orbis reuolutionis in circumferentia ecentrici, non appropriatur ei in orbe ecentrico locus. Nam si producatur ad or bem reuolutionis linea alia secans ipsum, et sit proportio medietatis eius quod cadit de ea intra or bem reuolutionis ad illud quod cadit de ea extra ipsum, sicut proportio illius anguli apud centrum orbis signorum ad angulum qui est apud centrum orbis reuolutionis cum additione diuersitatis super ipsum, aut diminutione ab eo, sicut dixit, erit tunc illud punctum per aestimationem eius longitudo stationis stellae, erit ergo arcus orbis reuolutionis qui est in eo, quod est inter duo puncta per comparationem ad punctum unum arcus directionis, et per comparationem ad punctum alterum arcus retrogradationis. Cum ergo stella est in illo arcu, oportet ut sit directa et retrograda in habitudine una, hoc uero est de manifestioribus impossibilibus. Sequitur ergo ex opere eius illo inuentione puncti stationis stellae, quando est in loco, qui non est transitus medius ecentrici, ut sit stella per opus eius illud directa, et uideatur retrograda, aut sit per opus eius illud retrograda, et uideatur directa. Et similiter currit super eum autumnatio in inuentione longitudinum punctorum stationis stellae a longitudine propiori uisibili, quando est centrum orbis reuolutionis super puncta alia ab istis punctis quatuor, scilicet longitudine longiori et propiori, et duobus punctis transitus medij, quod est, quia ipse dicit, qualiter inueniantur istae longitudines ex longitudinibus quas ipse inuenit punctis stationum, quando est centrum orbis reuolutionis super ista puncta quatuor, ita, quod ponit proportionem superfluitatum in partibus harum longitudinum quae sunt punctis stationum secundum superfluitates longitudinum centri orbis reuolutionis a centro orbis signorum, quod est, quia ipse dixit in capitulo 7. huius tractatus, quia secundum has longitudines proprie inuenitur diuersitas in stationibus. Haec autem res non certificatur, imo inuenitur contrarium illius ex hoc, quia possibile est, ut mutentur longitudines centri orbis reuolutionis a centro orbis signorum, et non alterentur etiam puncta stationis a longitudine propiore uisibili, 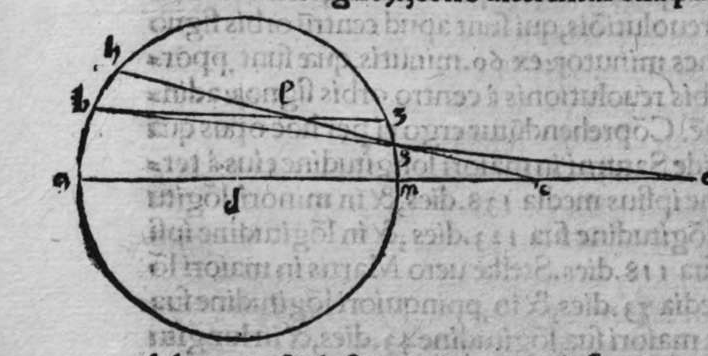et illud est, quia si nos posuerimus orbem reuolutionis a b g circa centrum d, et centrum orbis signorum punctum e, et continuemus lineam a d m e, et protraxerimus lineam b g e secundum quod sit proportio medietatis b g ad lineam g e, sicut proportio motus longitudinis uisibilis ad motum diuersitatis reuolubilis, erit tunc punctum g punctum stationis stellae longitudini e d, et protrahamus a puncto b lineam aequiedistantem lineae a e, quae sit linea b z, et signemus super arcum b h z punctum h, et continuemus ipsum cum puncto g per lineam g h, et faciamus ipsam penetrare donec occurrat lineae a e super punctum t, et propterea ergo quod linea b z est aequedistans lineae a e, erunt duo trianguli b g l, e g t similes, ergo erit proportio lineae g h ad lineam t g maior proportione lineae b g ad lineam e g. Si ergo fuerit longitudo centri orbis reuolutionis in parte orbis ecentrici a centro orbis signorum, sicut longitudo eius a puncto t scilicet, sicut linea d t, erit possibile ut sit punctum stationis stellae in illa longitudine d t, sicut est ei in longitudine d e, et sit longitudo eius a puncto longitudinis propioris uisibilis quod est punctum m longitudo aequalis, quod est, quia quanto plus minorantur longitudines centri orbis reuolutionis a centro orbis signorum, magnificatur motus uisibilis in longitudine. Est ergo proportio eius ad motum diuersitatis in longitudinibus minoribus maior proportione eius in longitudinibus maioribus. Sequitur ergo propter illud, ut sit proportio linearum quae producuntur a centro orbis signorum quae separant de circumferentia orbis reuolutionis puncta stationis stellae secundum illam semitam, scilicet, ut sit proportio eius quod cadit in orbe reuolutionis de lineis protractis longitudinibus minoribus ad illud quod cadit de eis extra orbem reuolutionis maior proportione eius quod cadit ex eis ex longitudinibus maioribus ad illud quod cadit extra, sicut declaratur illud in hoc, ut sit proportio lineae g h ad lineam g t maior proportione lineae b g ad lineam e g. Cum ergo illud est possibile, ut sit punctum g punctum stationis longitudinis aequalis lineae t d, erit ergo quod alterabuntur longitudines centri orbis reuolutionis a centro orbis signorum, et non alterabuntur longitudines punctorum stationis a puncto longitudinis propioris uisibilis. Necessitas ergo prouocat ad inueniendum puncta stationis stellae in omni parte ex partibus ecentrici, sicut inuenimus eas in eo quod praemissum est. Sciemus ergo quantitatem longitudinis puncti stationis a puncto longitudinis propioris uisibilis, et illud est cuius uoluimus declarationem. Et similiter etiam cucurrit super eum aestimatio in hoc, ut duplicaret partes orbis reuolutionis, quae sunt inter locum stationis primae, et inter propinquitatem propiorem uisibilem. Est ergo illud secundum eius aestimationem locus stationis secundae, hoc autem non certificatur nisi ita, ut sit centrum orbis reuolutionis in hora habitudinis, quae nominatur extremitas noctis super unum duorum transituum mediorum ecentrici. Verum quando est centrum orbis reuolutionis in sectione ecentrici, in qua est longitudo longior, aut in sectione in qua est longitudo propior, scilicet duabus sectionibus, quas determinant duo transitus medij. Non ergo certificatur illud propter motum propinquitatis propinquioris uisibilis, quod est, quia nos ponemus or bem reuolutionis circulum a b g circa 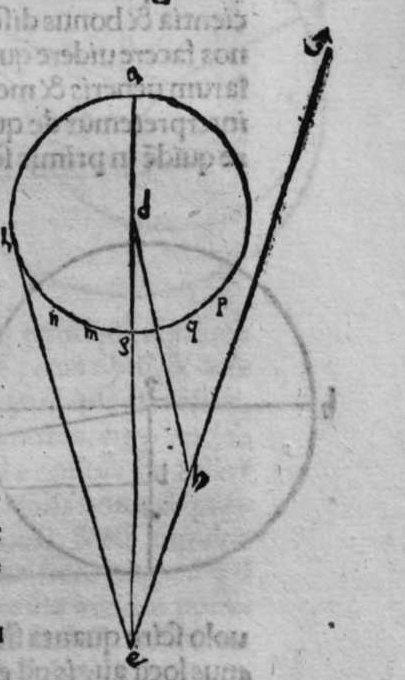centrum d, et centrum orbis signorum punctum e, et centrum motus aequalis punctum et longitudinem longiorem z, et continuabo centrum orbis signorum cum centro orbis reuolutionis per lineam a d g e, et sit stella in statione sua prima super punctum b, et sit centrum orbis reuolutionis in eo quod est inter punctum longitudinis longioris et transitum medium. Sequitur ergo propter illud, ut punctum g quod est longitudo propior uisibilis permutetur per motum centri orbis reuolutionis ad contrarium motus stellae, mouetur ergo usquequo perueniat stella in habitudine quae nominatur extremitas noctis per arcum g m ipsum punctum, quod diuidit illud quod est inter duo loca stationis, in duo media, quoniam quando stella peruenit ad punctum stationis secundae, perambulat punctum longitudinis propioris arcum aequalem arcui g m, qui sit arcus m n, et est longitudo puncti stationis secundae a puncto n aequalis longitudini puncti stationis primae a puncto m. Sequitur ergo propter illud, ut punctum m diuidat quod est inter duo loca stationis in duo media, non punctum g, sicut ipse putauit, oportet ergo propter illud, ut duplum arcus b g addat in hoc loco super longitudinem quae est inter duo loca stationis per duplum arcus g m, quod est arcus g n. Sequitur ergo propter illud in hoc loco, scilicet, quando est centrum orbis reuolutionis inter longitudinem longiorem et transitum medium primum, ut minuatur de arcu b g qui est longitudo stationis primae a puncto longitudinis propioris uisibilis arcus g m, qui est superfluitas diuersitatis arcus quam abscindit centrum orbis reuolutionis in tempore in quo abscidit stella arcum b g secundum propinquitatem, sed secundum ueritatem arcum b m, uerum ipse est quaesitus, quod ergo erit post diminutionem duplabimus illud, erit ergo illud quod est inter duo loca stationis, et similiter sequitur etiam, quando centrum orbis reuolutionis est in eo quod est inter transitum medium secundum et longitudinem longiorem. At uero, quando est in una duarum stationum, quae sunt a duabus partibus longitudinis propioris, tunc sequitur contrarium illius, et est, ut addatur quantitas arcus g m super arcum qui est inter duo loca stationis primae. Haec autem res si defuerit in stella Martis, perueniet error in ea ut sint inter stationem eius primam secundum ueritatem, et illud quod est secundum opus eius, quasi 9. dies. Et similiter est in statione secunda, quod est, si est centrum orbis reuolutionis in habitudine quae nominatur extremitas noctis super punctum longitudinis longioris, est angulus diuersitatis propter ecentricum in hora stationis primae ipse angulus centri orbis reuolutionis, cui subtenditur arcus g m, et erit angulus diuersitatis in statione secunda augulus cui subtenditur arcus m n. Et summa cuiusque horum duorum angulorum in diuersitate stellae martis a duobus lateribus longitudinis longioris ecentrici, est quasi 4. partes, et stella martis abscidit illud de orbe reuolutionis suae in propinquitate 9. dierum, et tunc incipit retrogradari, et incipit dirigi ante inceptionem suam secundum opus eius nouem diebus alijs, dies ergo retrogradationis eius secundum ueritatem minuuntur ab eo, quod egreditur per opus eius 18. diebus, et quando est in longitudine propiore ecentrici, est res econtrario illius, et hoc apparens est in Venere. Est ergo error in eo quod est inter directionem eius et ipsius retrogradationem circiter diem et quartam, et simile illius est in retrogradatione secunda, dies uero retrogradationis diuersificantur a diebus qui proueniunt secundum opus suum circiter duos dies et medium. Et ego miror de hoc uiro, qualiter cucurrit super eum haec aestimatio, et ipse mensurauit scilicet hanc intentionem secundum motum propinquitatis propioris uisibilis in inuentione punctorum stationis primae in stellis, quando est centrum orbis reuolutionis in hora habitudinis quae nominatur extremitas noctis in ipsa longitudine longiore et propiore ecentrici, et dixit illud, et expergefecit super illud in fine capituli sexti, in quo inuenit antecessionem stellae mercurij, et ponit exemplum in eo per stellam martis, et defuit ei in huiusmodi loco in quo possibile est, ut ingrediatur de errore haec quantitas, et illud in quo non dubito est, quia non fuit ei studium cum sollicitudine in scientia Geometriae, quoniam si fuisset ei in ipsa studium, non deperisset super ipsum tale, quale est hoc, nec deperisset super ipsum in primis in inuentione puncti stationis primae, et aliorum de eis de quibus euigilauimus iam super ipsum. O quam magnus est singularis cum complemento non est deus nisi ipse, neque adorandus praeter ipsum, et ipse est nostra sufficientia et bonus distributor, et ad ipsum est recurrendum. Amplius ipse post illud uoluit nos facere uidere qualiter inueniamus quantitatem longitudinum magnarum a sole duarum stellarum ueneris et mercurij in locis positis orbis signorum secundum radices positas utrisque, ut interpretemur de quantitatibus inuentis per considerationem. Ostendam ergo illud in uenere quidem in primis secundum hunc modum. Sit linea transiens per longitudinem longiorem et 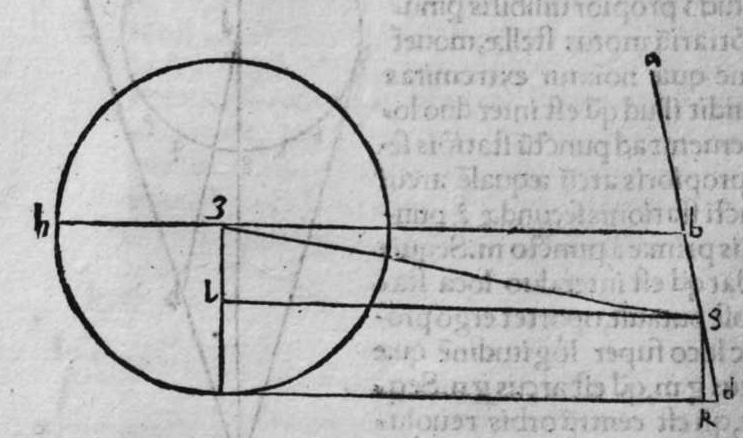propiorem linea a b e, et sit longitudo longior punctum a, et longitudo propior e, et centrum orbis signorum super ipsam punctum d, et centrum deferentis punctum g, et centrum motus aequalis punctum b, et sit orbis reuolutionis circulus h t circa centrum z, et sit stella in maiore longitudine sua a sole super punctum t orbis reuolutionis, et continuabo ipsum cum centro orbis signorum per lineam d t. Est ergo haec linea contingens circulum h t super punctum t, et est haec linea transiens per partem aliquam notam orbis signorum, et est locus stellae, et uolo scire quanta sit longitudo eius in hoc loco a sole, est ergo necessarium in primis, ut sciamus locum augis quod est punctum a de orbe signorum in illa hora. Est ergo propter illud longitudo stellae a puncto augis nota, et est angulus a d t, et continuabo centrum orbis reuolutionis cum puncto t per lineam z t, et cum centro motus aequalis per lineam z b, et cum centro deferentis per lineam z g, a puncto uero g perpendicularem producam super lineam z t quae sit linea g l, et protraham ab eo iterum perpendicularem super lineam t d quae sit linea g k, propterea ergo quod angulus a d t est notus, et angulus k est rectus, et linea g d est nota, est latus g k notum, et angulus k g d notus. Et propterea quod angulus t est rectus, et similiter angulus l et angulus k, erit angulus l g k iterum rectus, ergo angulus l g d est notus, et linea l t est aequalis lineae g k, ergo est nota. Quamobrem remanet linea l z nota, et linea z g quae est medietas diametri deferentis est 60. et angulus l est rectus, erit ergo angulus z g l notus, et iam fuit angulus d g l notus, ergo angulus z g b est notus, et unumquodque duorum laterum z g, g b trianguli z g b est notum, ergo angulus z b g est notus, ergo et angulus z b a est notus, et iste angulus est aequalis semper longitudini medij solis a puncto longitudinis longioris, ergo longitudo medij solis a puncto a est nota, et similiter locus eius uerus iterum, et longitudo stellae a puncto a nota, ergo longitudo eius a loco solis uero iterum est nota, completa est eius declaratio. In stella autem mercuij reiterabo formam secundum dispositionem suam, praeter quod ponam punctum g centrum motus aequalis, et punctum b centrum reuoluens deferentem, et sit orbis deferens circulus q o f circa centrum m, quoniam indigemus in inuentione quantitatis anguli a g z ex angulo a d t, quando est datus singulariter cognitione quantitatis longitudinis centri orbis reuolutionis ab uno centrorum trium, scilicet centro reuoluente deferentem, et centro motus aequalis, et centro orbis signorum, et illud non scimus nisi ita, ut sciamus quantitatem anguli a g z, tunc propter illud, non quando ponitur singulariter cursus huius stellae uerus ex orbe signorum, est cursus eius medius notus. Et quando ponitur cursus eius medius, scilicet angulus a g z, tunc cursus eius uerus est notus, ergo propter illud est necesse in cognitione quantitatis maioris longitudinis eius a sole in loco singulariter posito orbis signorum, ut ponamus duo puncta orbis signorum nota, ita, ut quando est medius solis in eis utrisque, sint duo loca stellae in duabus longitudinibus suis maioribus a sole propinqua puncto posito, quorum unum sit transiens ipsum, et alterum minoratum ab eo. Inueniam ergo per proportionem superfluitatum inter duas longitudines maiores quantitatem longitudinis maioris stellae, quando est in puncto dato orbis signorum secundum hunc modum. Sit ergo orbis signorum circulus a l r circa centrum d, et sit punctum positum in 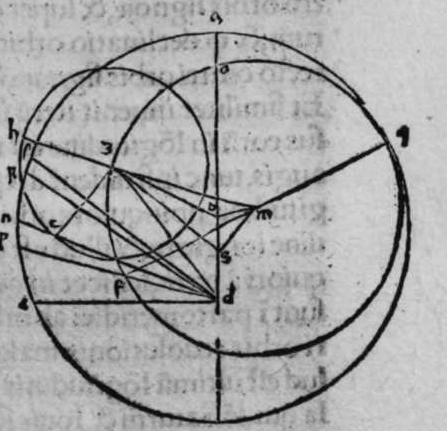quo uolo scire maiorem longitudinem stellae punctum l, et continuabo lineam d l, erit ergo angulus a d l notus, et erit angulus a d s notus, et punctum s punctum super quod cum fuerit medius solis erit stella in longitudine sua maiore propinqua puncto l, aut pertransiens ipsum, aut diminutum ab eo. Sit itaque in primis diminutum ab eo, et continuabo lineas m z, m g, d z, et quoniam angulus a d s est notus, et est aequalis angulo a b m, ergo trianguli b m g angulus b est notus, et unumquodque duorum laterum eius b m, b g est notum per quantitatem qua est linea m z, quae est medietas diametri deferentis 60. Est ergo latus m g notum per illam quantitatem, et unusquisque duorum angulorum reliquorum notus, ergo angulus m g z trianguli m g z est notus, et unumquodque duorum laterum m g, m z est notum, ergo latus g z est notum per quantitatem qua est medietas diametri deferentis 60. propterea quod trianguli d g z unumquodque duorum laterum g z, g d est notum, et angulus d g z eius est notus, est latus d z eius notum, et angulus eius a d z notus. Et propterea quod trianguli d z t angulus t est notus, quoniam ipse est rectus, et unumquodque duorum laterum eius z t, z d est notum, est angulus eius z d t notus, ergo angulus a d t totus est notus. Cum ergo fuerit cursus solis medius angulus a d s positus singulariter, erit locus stellae de orbe signorum in longitudine sua maiore a medio solis notus, et propter illud erit longitudo eius maior a sole nota, ergo angulus t d l est notus, et est angulus quo minuitur stella a puncto l posito singulariter. Et similiter ponamus iterum angulum a d k notum, et est angulus cursus medij solis, a quo est stella in longitudine sua maiore propinqua puncto l posito singulariter de orbe signorum, et pertransiens ipsum, et sit stella in illa longitudine super punctum e, et ostendam sicut praemissum est quantitatem anguli a d s, ergo erit longitudo stellae maior a sole nota, et angulus e d l notus, et est ille, quo stella pertransiens punctum l positum singulariter. Cum ergo nos acceperimus ex superfluitate supefluitate ed., quae est inter duas longitudines stellae maiores a sole, quando est super punctum t, et similiter punctum e, quod sit aequale proportioni anguli t d l ad angulum t d e, tunc si fuerit longitudo in puncto t minor longitudine in puncto e, addemus super ipsam illam partem, et si fuerit maior, minuemus eam ab ipsa, ergo erit illud secundum propinquitatem quantitatis longitudinis maioris stellae, quando est super punctum l positum singulariter. completa est eius declaratio.

⟨IX⟩ LIBER NONVS. DE LATITVDINIBVS ET APparitionibus atque occultationibus quinque planetarum.

ET propterea quod remanserunt de scientia stellarum quinque haesitantium duae res, quarum una est scientia eius quae accidit eis ex cursibus in latitudinibus per cursum ipsarum in orbe signorum, et altera est speculatio in quantitatibus longitudinum earum a sole in apparitione earum et ipsarum occultatione, et oportet, ut scientia de longitudinibus earum in latitudine praemittatur, quoniam cadit propter diuersitatem harum longitudinum in longitudinibus earum a sole in apparitione earum et ipsarum occultatione diuersitas, cui est quantitas sensibilis, oportet propter illud, ut antecedat speculatio in cursibus earum in latitudine ab orbe signorum. Dixit ergo, quod ipse inuenit unicuique harum stellarum duas diuersitates in latitudine, sicut sunt ei in longitudine, quarum una est secundum partes orbis ecentrici, et secunda secundum partes orbis reuolutionis, scilicet longitudinis eius a sole. Significauit ergo ei illud, quod superficies orbis ecentrici est declinata a superficie orbis signorum, et quod superficies orbis reuolutionis est declinata iterum a superficie orbis ecentrici, et dixit, quod ipse reperit per considerationes in unaquaque harum quinque stellarum, quia longitudo et diuersitas aequatae, quando unaquaeque earum est quarta circuli, in longitudine quidem aequata a finibus septentrionalibus aut meridianis orbis ecentrici, et numerus quidem diuersitatis a longitudine longiore aut propiore orbis reuolutionis quae uidentur, tunc uidetur in superficie orbis signorum. Significauit ergo ei illud, quod declinatio orbium ecentricorum non est nisi a centro orbis signorum, et super diametros transeuntes per fines septentrionales et meridianos eorum, et quod declinatio orbium reuolutionum non est nisi super diametros ipsorum quae sunt in directo centri orbis signorum, scilicet super quas sunt longitudo longior et propior quae uidentur. Et similiter inuenit iterum in stellis tribus earum, scilicet Saturno et Ioue et Marte, quod quando cursus eorum in longitudine est in sectione longiori a terra ecentrici, scilicet in qua est punctum augis, tunc ipsi uidentur a septentrione ab orbe signorum, et longitudo earum ab eo, quando sunt in longitudine propinquiore orbis reuolutionis, est maior longitudine eorum ab eo, quando sunt in longitudine longiore, et illud est ultimitas longitudinis eorum. Et quando est in sectione ecentrici propinquiori a terra, scilicet in qua est punctum magis profundum, est res econtrario illius, scilicet, quia sunt in parte meridiei ab orbe signorum, et est longitudo eorum ab eo, quando sunt in longitudine propiori orbis reuolutionis maior longitudine eorum ab eo, quando sunt in longitudine longiori, et illud est ultimum longitudinis eorum. Et quod fines orbium eorum ecentricorum septentrionales in stella quidem Saturni et Iouis sunt in principijs signi librae, et in stella quidem Martis in postremis signi cancri, et forsitan sunt in ipsa longitudine longiore eius. Significant ergo omnia illa, quod declinatio orbium ecentricorum est fixa, et quod illud quod est ex plagis eorum super partes praedictas orbis signorum, est declinatum ad septentrionem semper, et quod ex finibus eorum est super partes oppositas eis, est declinatum ad meridiem semper cum aequalitate illius declinationis quantitatis. Et quod superficies orbium reuolutionum sunt declinatae iterum a superficiebus orbium reuolutionum ecentricorum, et quod longitudo propinquior est in parte declinationis orbium ecentricorum, diametros uero eorum orthogonaliter erectas super has diametros, inuenit facere semper aequedistantiam superficiei orbis signorum, et si reflectuntur ab ea, est earum reflexio insensibilis. In duabus autem stellis Venere et Mercurio inuenit per considerationes, quod quando cursus earum in longitudine est in parte longitudinis longioris aut propioris ecentrici, tunc cursus ambarum in longitudine propinquiore orbis reuolutionis est aequalis in latitudine cursui utrarumque in longitudine longiori eius, et in parte una. Sed in Venere quidem in septentrione semper ab orbe signorum, et in Mercurio quidem in meridie semper ab eo. Cursus autem utrarumque in maioribus longitudinibus ipsarum a sole sunt ita, quod longitudines ambarum matutinales sunt diuersae a longitudinibus earum uespertinis in latitudine ultima diuersitate. Et similiter habitudo cuiusque duarum longitudinum alicuius stellae ex eis duabus in longitudine longiore ecentrici est diuersa ab habitudine sua in longitudine propiori eius ultima diuersitate ad contrarium partis, quia erit longitudo uespertina sequens, in stella quidem ueneris in longitudine longiori ecentrici decliuior ad septentrionem, et in longitudine propinquiori decliuior ad meridiem, et in stella quidem mercurij econtrario illius. In longitudine quidem longiori ecentrici decliuior ad meridiem, et in longitudine quidem propiori decliuior ad septentrionem. Sed quando cursus utriusque in longitudine aequatus, scilicet centri orbis reuolutionis, est in duobus nodis, tunc erunt longitudines, quarum summa a longitudine longiori aut propiori a duobus lateribus orbis reuolutionis ambarum est quarta circuli simul in superficie orbis signorum, et erit cursus utriusque in longitudine propiori orbis reuolutionis in ultimo diuersitatis a cursu utriusque in longitudine longiori, et erit declinatio longitudinis propioris cum stella ueneris quidem, quando est in nodo, qui est in medietate circuli quae est ad diminutionem, et est ille super quem sunt transitus ad plagam meridianam ab ecentrico ad meridiem semper a superficie orbis signorum, et quando est in nodo contrario ei ad septentrionem semper ab ea. In stella autem mercurij est econtrario illius quidem cum est in medietate circuli, quae est ad diminutionem ad septentrionem semper ab ea, sed cum est in nodo opposito ei, tunc ad meridiem semper. Significauit ergo ei illud, quod declinationes duorum orbium eorum ecentricorum sunt motae, et redeunt in motibus earum cum reditione reuolutionum duorum orbium reuolutionis earum, donec centra duorum orbium reuolutionis, quando sunt in duobus nodis, fiunt ambo in superficie orbis signorum, et quando sunt in longitudine longiori aut propiori ecentrici, tunc sunt in ultimo longitudinis ab orbe signorum, in uenere quidem in septentrione semper ab eo. Duo uero orbes reuolutionis eorum faciunt duos modos diuersitatis, quorum unus est in duobus nodis orbis ecentrici, et secundus in longitudine longiori et propiori. Nam ipsi duo faciunt declinare duas diametros transeuntes per longitudinem longiorem et propiorem, quae uidentur ultima declinatione ambarum, quando sunt in duobus nodis, et ponunt duas diametros orthogonaliter erectas super eas ambas in superficie orbis signorum, et mouent istas duas diametros ultima reflexione ambarum, quando sunt in longitudine longiori aut propiori ecentrici, et ponunt illas duas diametros transeuntes per longitudinem longiorem et propiorem in superficie ecentrici, et non nominatur iste modus diuersitatis reflexio, nisi ad distinguendum inter ipsum et modum secundum. Modus autem secundum quem currit res in ordine harum diuersitatum in latitudine, est in stellis quidem tribus, scilicet Saturno et Ioue et Marte, quod orbes eorum ecentrici sunt declinati a superficie orbis signorum, et super centrum eius super diametros transeuntes per fines septentrionales et meridianos declinatione fixa immobili, per quos utrosque duo cursus diametrales orbium reuolutionum permutantur in latitudine ad septentrionem et ad meridiem ab orbe signorum. In sectione quidem ecentrici longiore a terra ad septentrionem semper, et in sectione propinquiore a terra ad meridiem semper, et quod orbes reuolutionum eorum sunt declinati a superficie orbis ecentrici super centra ipsorum, et super diametros transeuntes per longitudinem longiorem et propiorem quae uidentur, et quod longitudo propior uisibilis cuiusque eorum est posita super circumferentiam circuli parui, cuius centrum est in superficie orbis ecentrici, et est erecta super eam orthogonaliter, et isti circuli sunt aequales recessionibus in latitudine, et mouetur illa propinquitas propior super circumferentiam horum circulorum paruorum secundum aequalitatem motus aequalis motui longitudinis mediae, et redit per motum suum superficies orbis reuolutionis in reuolutione quidem sua in quarta prima huius circuli, a superficie orbis ecentrici ad plagam septentrionalem eius, et in quarta secunda a plaga septentrionali ad superficiem ecentrici, et in quarta tertia ab illa superficie ad plagam meridionalem, et in quarta quarta a plaga meridionali ad locum a quo incepit, scilicet superficiem orbis ecentrici. Inceptio autem huius separationis et reditionis eius in unaquaque harum stellarum trium est a nodo, qui est in medietate circuli, qui est ad directionem scilicet super quam sunt transitus ad plagam septentrionalem orbis ecentrici, et sunt extremitates harum diametrorum quidem, quando centrum orbis reuolutionis est in duobus nodis in superficie orbis ecentrici. Et quidem, quando est in longitudine longiore aut propiore in ultimo declinationis earum ab ea. In longitudine quidem longiore ecentrici fit longitudo propior uisibilis in ultimo longitudinis a superficie ecentrici in septentrione. In longitudine uero propiori in ultimo longitudinis ab ea in meridie, diametri uero eorum erectae super has diametros orthogonaliter, faciunt semper aequedistantiam superficiei orbis signorum, et si reflectantur ab ea, earum reflexio est insensibilis. Duorum uero ecentricorum duarum stellarum declinationes mouentur ad partem ad quam mouetur centrum orbis reuolutionis in latitudine, cum quidem centrum orbis reuolutionis est in longitudine longiori ecentrici, tunc sunt in ultimo longitudinis suae ab orbe signorum, et mouentur cum eo ad superficiem orbis signorum. Cum ergo perueniunt ad nodum, peruenit etiam superficies orbis ecentrici ad superficiem orbis signorum, et quando peruenit centrum orbis reuolutionis ad longitudinem propiorem ecentrici, fit illa longitudo propior in ultimo declinationis suae ab orbe signorum ad partem, in qua fuit decliuior longitudo longior in primis, deinde redit ad superficiem orbis signorum, quando peruenit centrum orbis reuolutionis ad nodum secundum. Cum ergo redit ad longitudinem longiorem, fit illa longitudo longior in fine longitudinis suae ab orbe signorum secundum illud super quod fuit in primis. Est ergo propter illud centrum orbis reuolutionis utriusque ab orbe signorum semper, in uenere quidem centrum orbis reuolutionis eius in septentrione semper, et in mercurio quidem in meridie semper. Longitudo uero propior uisibilis diametrorum duorum orbium reuolutionis utriusque sunt in rectitudine centri orbis signorum, quando est posita super circumferentiam circuli parui, cuius centrum cenrum ed. est positum in superficie orbis ecentrici, et est erecta orthogonaliter, et mouetur super circumferentiam eius, et mouetur cum ea superficies orbis reuolutionis a superficie orbis ecentrici ad plagam septentrionalem eius, sicut fuit in stellis tribus, praeter quod inceptio huius motus reditionis eius est in uenere quidem a longitudine propiori ecentrici. Et in mercurio quidem a longitugine longiori eius, et fit illa longitudo propior in ultimo longitudinis suae a septentrione, quando centrum orbis reuolutionis est in duobus nodis, non in longitudine longiori et propiori ecentrici, sicut fuit in stellis tribus. In uenere quidem in nodo, qui est in medietate circuli quae est ad additionem, et in mercurio quidem in nodo opposito ei. Diametrorum uero erectarum super has diametros orthogonaliter extremitates sequentes, sunt positae super duas circumferentias circulorum paruorum aequalium summe recessionum in latitudine, et eorum centra sunt posita etiam super superficies aequedistantes superficiei orbis signorum, et mouentur extremitates harum diametrorum super circumferentias ctrcumferentias ed. eorum cum superficiebus orbium reuolutionum motu aequali, et aequali in uelocitate motui medio in longitudine, et motui extremitatum diametrorum primarum ab uno duorum principiorum, quae sunt super sectiones horum circulorum et superficierum, in quibus eorum centra sunt posita uersus septentrionem, et inceptio huius motus et reditionis eius in uenere quidem est a nodo, qui est in medietate circuli, quae est ad additionem, et in mercurio quidem a nodo opposito ei. Est ergo longitudo uespertina sequens, quando est centrum orbis reuolutionis in longitudine longttudine ed. longiori, et ueneri quidem in ultimo longitudinis suae in septentrione, et mecurio quidem in ultimo longitudinis suae in meridie, et quando centrum orbis reuolutionis est in longitudine propiori, res est econtrario illius, scilicet, quia est longitudo uespertina tunc ueneri quidem in ultimo longitudinis suae in meridie, et mercurio quidem in ultimo longitudinis suae in septentrione, et sunt istae duae diametri in superficie orbis ecentrici, et in superficie orbis signorum, quando centrum orbis reuolutionis est in unoquoque duorum nodorum. Motus autem aequalis extremitatum harum diametrorum est super circumferentias horum circulorum paruorum in omnibus stellis. Non sunt ergo in circuitu centrorum eorum, sed in circuitu punctorum, quorum egressio a centris eorum est similis egressioni centrorum orbium ecentricorum a centro orbis signorum, et significo per assimilationem, ut sit proportio eius quod est inter duo centra ad medietatem diametri circuli parui, sicut proportio eius quod est inter duo centra in orbe ecentrico ad medietatem diametri suae, et ut sit locus augis eus a parte septentrionali eius cum loco augis ecentrici a parte septentrionali, per hoc enim praeparatur, ut sint extremitates harum diametrorum in quartis horum circulorum conuenientes centro orbis reuolutionis in quartis orbis signorum. Et postquam declaratus est ei modus secundum quem currit res in istis declinationibus et motibus earum, incepit post illud declarationem quantitatum cuiusque earum, scilicet quantitatum arcuum circulorum magnorum transeuntium per orbem signorum, et per duos polos orbium ecentricorum. Dixit ergo, quod ipse considerauit unamquanque duarum stellarum ueneris et mercurij orbibus reuolutionum earum ambarum in longitudine longiore et propiori ecentrici, et ipsae ambae erant propinquae longitudini longiori et propiori orbis reuolutionis. Inuenit ergo longitudinem utrisque ab orbe signorum, ueneris quidem ad septentrionem semper quasi sextam partis, et mercurij quidem ad meridiem semper quasi medietatem et quartam partis, et hoc est ultimum declinationis orbium ecentricorum duorum utriusque. Et similiter considerauit ambas, et ipsae erant in ultimo longitudinis suae a sole, quae sunt contrariae, inuenit ergo aggregationem duarum longitudinum earum quae sunt contrarie ab orbe signo rum quasi quinque partium. Stellae quidem ueneris minus in iu ed. longitudine longiori ecentrici quinque partibus, et plus eis in longitudine propiori eius per illud, de quo non curatur, Mercurium uero ipse inuenit addere super quinque partes in longitudine propiori, et minuere ab eis in longitudine longiori quasi medietatem partis unius, donec reflexio duorum orbium reuolutionis in uno duorum laterum superficiei orbis ecentrici subtenditur apud centrum orbis signorum super quod est uersus angulo, cuius summa est secundum mediationem fere duarum partium et medietas. Et considerauit eas ambas centro orbis reuolutionis existente in duobus nodis ecentrici. Inuenit ergo stellam ueneris, quando est in longitudine longiori orbis reuolutionis elongatam ab orbe signorum ad septentrionem et ad meridiem quasi parte una, et quando est in longitudine propiori ipsius sex partibus et tertia partis, donec fit, quod declinatio orbis reuolutionis eius propter illud tenet de circulo, qui sequitur quandoque super polos eius et super longitudinem eius longiorem et propiorem duas partes et medietatem partis secundum propinquitatem, quoniam istae partes quando separantur apud longitudinem logiorem et propinquiorem orbis reuolutionis ueneris, subtenduntur apud uisum in longitudinibus medijs fere istis partibus praedictis, quod est, quia duae partes et medietas quando separantur ab eo quod sequitur longitudinem longiorem orbis reuolutionis, subtenduntur angulo, cuius summa est pars una et duo minuta, et quando separantur apud longitudinem propiorem, subtenduntur angulo, cuius summa est 6. partes et 22. minuta. Et inuenit stellam mercurij elongari ab orbe signorum, quando est in longitudine longiori orbis reuolutionis ad septentrionem parte una et 3. quartis partis, et quando est in longitudine propiori eius 4. partibus fere secundum quod stetit super illud cum computatione accepta propter apparitionem suam propinquam istis locis, donec fit, quod declinatio orbis reuolutionis eius propter illud tenet de circulo, qui signatur quandoque super polos eius, et super longitudinem eius propiorem et longiorem 6. partes et 4. partis, quod est, quia istae partes quando separantur ex longitudine longiore orbis reuolutionis, subtenduntur apud uisum in illis longitudinibus medijs angulo, cuius summa est pars una et 46. minuta et quando separantur ab eo quod sequitur longitudinem propiorem, inueniuntur subtendi apud uisum secundum illud exemplum angulo cuius summa est 4. partes et 5. minuta. In stellis autem tribus, scilicet saturno et ioue et marte, non fuit possibile per hanc uiam peruenire ad cognitionem quantitatum declinationum earum, quoniam declinationes orbium eorum ecentricorum, et declinationes orbium reuolutionis sunt semper permixtae. Est ergo longitudo longituo ed. stellae ab orbe signorum composita ex declinatione orbis ecentrici, et ex declinatione orbis reuolutionis adiuncta ad ipsam, aut diminuta ab ea, uerum ipse inuenit illud propter superfluitates, et inter quantitates earum in longitudine longiori et propiori ecentrici ex orbibus reuolutionum secundum hunc modum. Sit in superficie erecta orthogonaliter super superficiem orbis signorum sectio 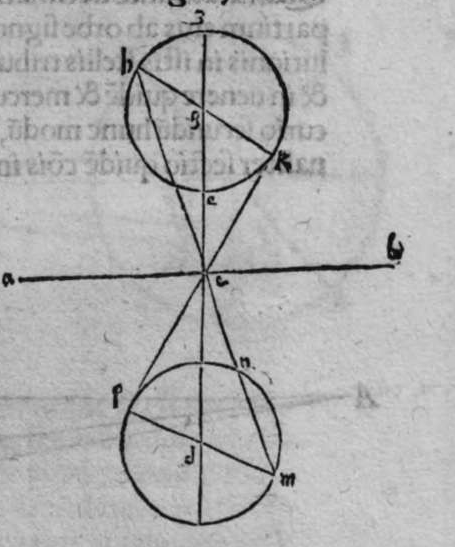communis inter ipsam et superficiem orbis signorum a b, et sectio communis inter ipsam et inter or bem ecentricum linea g c, et punctum e sit centrum orbis signorum in sectione communi superficiebus, et signabo circa punctum g, et est plaga septentrionalis orbis ecentrici, et circa punctum d, et est plaga meridiana eius in superficie posita, duos circulos z h t k, m n s aequales, sicut duos circulos, qui sunt transeuntes per polos orbium reuolutionis, et inclinentur super eos ambos duae superficies orbium reuolutionis per lineam h g k, et lineam m d s per quantitatem duorum angulorum, qui sunt apud duo puncta g d, et manifestum est, quod ipsi sunt aequales, et faciam continuari inter punctum e, quod est centrum orbis signorum, et inter duas longitudines longiores per duas lineas e h et e m. Sed inter ipsum et inter duas longitudines propiores per duas lineas e k et e s. Et manifestum est, quod duo puncta k s comprehendunt duos cursus proportionatos ad extremitatem noctis, et duo puncta m h comprehendunt duos cursus duarum coniunctionum. In stella uero martis, propterea quod superfluitas inter cursus, qui sunt orbis reuolutionis in longitudine longiori ecentrici, et inter cursus, qui sunt ei in longitudine propiori eius, est manifesta sensui ualde, et illud est, quia inuenit hanc stellam elongari ab orbe signorum in habitudinibus extremitatis noctis, scilicet in longitudine sua propinquiori orbis reuolutionis quidem, quando centrum orbis reuolutionis est in longitudine longiori ecentrici 4. partibus et tertia partis in septentrione, et quidem, quando est in longitudine propiori cius 7. partibus in meridie cum propinquitate, donec fit, quod angulus a e k est 4. partes et tertia partis, per partes quibus 4. anguli recti sunt 360. partes, et est angulus b e s per istas partes 7. partes, uerum superfluitas inter istos duos angulos est nota, et proportio unius eorum ad alterum est nota, tunc oportet propter illud, ut sit unusquisque eorum notus. In duabus uero stellis saturno et ioue, superfluitas inter eos ambos est parua, propter propinquitatem duorum centrorum motuum amborum aequalium a centro orbis signorum. In stella uero martis propter longitudinem quae est inter motum eius aequalem et centrum orbis signorum, sunt superfluitates inter istos duos angulos multae, et illud est, quia proportio unius eorum ad alterum est sicut proportio quinque partium ad 9. partes, prouenit ergo per computationem summa anguli g e k  in marte 3. partes et tertia partis cum propinquitate per partes, quibus 4. anguli recti sunt 60. partes, et angulus d e s 6. partes, et oportet, ut sit unusquisque duorum angulorum a e g et b e d aequalium notus. Erit ergo unusquisque eorum secundum quod egreditur per computationem pars una secundum propinquitatem, et propterea quod unusquisque duorum angulorum g e k, d e s est notus, et unaquaeque duarum longitudinum g e, d e est nota, et unumquodque duorum laterum g k et d s est notum, et est medietas diametri orbis reuolutionis, erit unusquisque duorum angulorum k g t, n d s aequalium notus, declinatio ergo orbis ecentrici, et declinatio orbis reuolutionis etiam sunt notae. In stellis uero saturni et iouis, propterea quod superfluitates inter duos angulos g e k et d e s sunt paruae ualde, utitur in inuentione illius uia alia, et est, quia sciuit in unoquoque amborum proportionem angulorum, qui sunt apud centrum orbis signorum, quibus subtenduntur arcus aequales orbis reuolutionis separati apud longitudinem longiorem eius, ad angulos separatos apud longitudinem propiorem eius, scilicet proportionem anguli g e h ad angulum g e k. inuenit ergo eam in saturno quidem proportionem 18. ad 23. secundum propinquitatem, et in ioue quidem proportionem 29. ad 43. et aggregatio horum duorum angulorum est nota, scilicet angulus k e h, quoniam est superfluitas quae est inter duos angulos a e k, a e h notos. Oportet ergo ut sit unusquisque duorum angulorum g e h, g e k notus, et oportet propter illud, ut sit angulus a e g, et est declinatio orbis ecentrici notus. Exiuit ergo ei angulus iste in stella quidem saturni duae partes et medietas partis secundum propinquitatem. Angulus autem k g e, qui est declinatio orbis reuolutionis, est notus in unaquaque duarum stellarum, propter quantitatem anguli g e k, secundum quod praemissum in stella martis. In saturno quidem 4. partes et medietas partis secundum propinquitatem, et in ioue quidem duae partes et medietas partis secundum propinquitatem, et illud est cuius uoluimus declarationem. Quantitatum autem declinationum particularium orbis reuolutionis, scilicet longitudinis alicuius partium eius ab orbe signorum in declinationibus suis magnis, scilicet quando centrum orbis reuolutionis in istis stellis tribus est in plaga septentrionali et meridiana orbium ecentricorum, et in uenere quidem et mercurio in duobus nodis est possibilis inuentio, et in uenere et mercurio secundum hunc modum, ut sit in superficie erecta super superficiem orbis signorum orthogonaliter sectio quidem communis inter ipsam et superficiem orbis signorum linea a b g, et sectio quidem communis inter ipsam et inter orbem reuolutionis linea d b e, et sit centrum orbis signorum punctum a, et centrum orbis reuolutionis punctum b, et sit linea a b longitudo duorum orbium reuolutionis harum duarum stellarum in declinatione eorum maior, et est longitudo eius, quando est in transitu medio ecentrici, et signabo circa punctum b or bem reuolutionis d z e h, et producam diametrum z b h erectam orthogonaliter super lineam d e, et ponam ut superficies orbis reuolutionis sit erecta etiam orthogonaliter super superficiem narratam positam, ita, ut omnes lineae protractae orhogonaliter super lineam d e in superficie orbis reuolutionis sint aequedistantes superficiei orbis signorum, praeter z, ipsae enim sunt in superficie orbis signorum. Et sit punctum, cuius declinationem uolumus scire, punctum t notum, et protrahamus ab ipso ad superficiem orbis signorum perpendicularem, et sit linea t m, et continuabo duo puncta t m cum centro orbis signorum per duas lineas a m, a t, et sit intentio nostra, quando angulus a b e, qui est finis declinationis, est notus, et proportio longitudinis a b ad medietatem diametri b e nota, ut sciamus quantitatem anguli t a m. Protraham ergo super lineam b e perpendicularem t k, et super superficiem orbis signorum perpendicularem k l, et continuabo lineas duas t b, l m, declaratur ergo ex proximo, quod figura l m t k quadrilatere est aequedistantium laterum et rectorum angulorum, propterea ergo quod angulus e b t est notus, et linea b t est nota, et angulus b k t est rectus, et unumquodque duorum laterum k t, b k notum, ergo latus l m etiam est notum, propterea quod angulus k b l est notus, et angulus l est rectus, et latus b k est notum, est latus k l notum, et latus t m aequale ei notum, et similiter est iterum latus b l notum. Remanet ergo a l nota, et latus l m notum, et angulus a l m est rectus, ergo linea a m est nota, et angulus m a l est notus, et propterea quod linea t m iam ostensum est quod est nota, et angulus a m t est rectus, est linea a t nota, et angulus t a m notus, et est longitudo puncti t a superficie orbis signorum, et angulus m a l notus, est angulus additionis aut diminutionis in longitudine. Et ut interpretando significemus illud quod cadit de superfluitate propter additionem aut diminutionem in longitudine, signabo huius formae similem secundum quod orbis reuolutionis in utrisque sit non declinatus, et quoniam longitudo a b est nota per illud, quo medietas diametri b t est nota, et angulus a b t est datus, est angulus b a t notus, et ipse est angulus superfluitatis, quae additur aut minuitur secundum quod sit superficies orbis reuolutionis in superficie orbis signorum, et angulus b a m figurae praecedentis est angulus superfluitatis in ueritate. Accipitur ergo diuersitas inter istos duos angulos in uenere quasi duo minuta, et in mercurio quasi tria minuta, et illud est cuius uoluimus declarationem. In stellis autem tribus superioribus, scilicet saturno et ioue et marte, propterea quod declinationes orbium reuolutionis eorum sunt permixtae cum declinationibus orbium earum ecentricorum, tunc ipse inuenit quantitates harum declinationum particularium in eis secundum hunc modum, ut sit, sicut praemissum est in figura nuper, sectio communis inter superficiem positam et superficiem orbis signorum linea a b, et sectio communis inter ipsam et superficiem orbis reuolutionis linea d g e, et sit centrum orbis signorum punctum a, et centrum orbis reuolutionis punctum g, et signabo circa punctum g or bem reuolutionis d e z h, 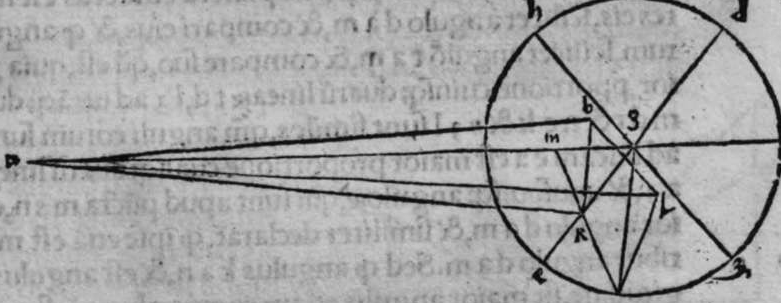secundum quod sit diameter z g h ex lineis quae sunt productae orthogonaliter super lineam d e in superficie ecentrici, et fiunt aequedistantes superficiei orbis signorum, et sit arcus e t orbis reuolutionis datus, et protraham a puncto t super lineam e g perpendicularem t k, et ex duobus punctis t k etiam super superficiem orbis signorum duas perpendiculares k b, t l, et continuabo lineas b l, a l, a t, et sit intentio nostra, quando angulus declinationis orbis reuolutionis, et angulus deelinationis orbis ecentrici est notus, et est proportio longitudinis centri orbis reuolutionis ex medietate diametri eius, scilicet proportio lineae a g ex linea g e nota, qualiter ineniamus numerum additionum aut diminutionum in longitudine, et est ille, quem comprehendit angulus t a l, et protraham iterum super lineam a g a puncto k perpendicularem k m, et continuabo duas lineas g t et a k, propterea ergo quod angulus t g k est datus, et angulus t k g est rectus, et latus g t est notum, et unumquodque duorum laterum t k, k g notum. Et propterea quod angulus k g m est notus, et est angulus declinationis orbis reuolutionis, et angulus k m g est rectus, et latus g k est notum, est unumquodque duorum laterum k m, m g notum, et propterea quod centrum orbis reuolutionis est positum in declinationibus magnis orbium reuolutionis harum stellarum trium in una duarum plagarum septentrionalium aut meridionalium, et longitudo cuiusque harum duarum plagarum a longitudine longiore et propiore orbium ecentricorum est nota, est linea a g nota. Remanet ergo linea a m nota, et linea m k  iam fuit ostensum quod est nota, et angulus a m k est rectus, tunc linea a k est nota, et angulus k a m est notus, et angulus g a b, et est declinatio orbis ecentrici, est notus, ergo angulus k a b est notus, et angulus a k b est rectus, et latus a k est notum, ergo latus b k est notum. Et similiter latus b a etiam est notum, et latus b l est notum, quoniam est aequale lateri k t noto, quoniam quadratum b k t l est rectorum angulorum et aequedistantium laterum, et angulus a b l est rectus, ergo linea a l est nota, et est angults b a l notus, et est angulus qui comprehendit additionem in longitudine. Et propterea quod linea a l est nota, et linea l t nota, quoniam est aequalis lateri b k, de quo iam ostensum est quod est notum, et angulus a l t est rectus, est linea a t nota, et angulus t a l est notus, et est angulus, qui comprehendit cursum in latitudine. Inuenit ergo superfluitatem inter angulum b a l, et inter angulum additionis aut diminutionis arcus e t orbis reuolutionis, in saturno quidem et ioue quasi minutum unum secundum propinquitatem, sed in marte insensibilem penitus, et illud est cuius uoluimus declarationem. Cursuum autem in latitudine propter reflexionem duorum orbium reuolutionis ueneris et mercurij, qui sunt centro orbis reuolutionis existente in longitudine longiori et propiori ecentrici, secundum quod praemissum est, inuenit quantitates particulares harum reflexionum secundum hunc modum, ut sit linea a b g sectio 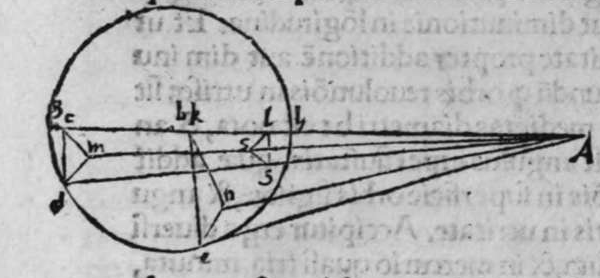communis superficiei orbis signorum, et superficiei orbis reuolutionis, et punctum a centrum orbis signorum, et sit orbis reuolutionis circulus g z h circa centrum b, et sit superficies eius reflexa a superficie orbis signorum, et ponam quaerendo facilitatem in opere centrum eius super superficiem orbis signorum super lineam a b g, et protraham lineam a e tangentem circulum g z h super punctum e, et lineam a z d secantem ipsum, qualitercunque accidat super duo puncta z d, et protraham a punctis d e z perpendiculares, super superficiem quidem orbis signorum perpendiculares d m et e n et z s, et super lineam quidem a b g perpendiculares d t et e k et z l, et continuabo lineas m t, n k, s l, et similiter continuabo iterum lineas a n, a s, a m, ergo linea a s m est linea una recta, quoniam puncta a s m sunt super sectionem communem superficiei orbis signorum, et superficiei erectae super eam orthogonaliter transeunti per lineam a z d. Manifestum est ergo in hac declinatione, quod illud quod comprehendit additiones aut diminutiones harum duarum stellarum, in longitudine quidem est angulus t a m, et angulus k a n, et in latitudine quidem angulus d a m, et angulus e a n. Et declarabitur ex proximo, quod angulus e a n, et est angulus cursus in latitudine, apud punctum contactus est maior angulis omnibus qui sunt compares eis, scilicet angulo d a m, et compari eius, et quod angulus k a n est maior compare suo iterum, scilicet angulo t a m, et compare suo, quod est, quia proportio lineae k e ad lineam e a est maior proportione cuiusque duarum linearum t d, l z ad utramque duarum linearum d a, z a, et quia trianguli m d t et n e k et s z l sunt similes, quoniam anguli eorum sunt aequales, ergo proportio lineae n e ad lineam e a est maior proportione cuiusque duarum linearum m d, s z ad unamquanque duarum a d a z, et unusquisque angulorum, qui sunt apud puncta m s n, est rectus, ergo angulus e a n est maior angulo d a m, et similiter declaratur, quod ipse etiam est maior reliquis angulis omnibus comparibus angulo d a m. Sed quod angulus k a n, et est angulus additionis aut diminutionis in longitudine, sit maior angulis etiam comparibus ei est manifestum. Et similiter declara tur etiam quod proportio plurimi eius, quod est ex additione aut diminutione in longitudine, scilicet anguli e a k ad maiorem cursum in latitudine, scilicet angulum e a n, est secundum propinquitatem aequalis proportioni, quae est sectionum orbis reuolutionis omnium quae sunt additionum aut diminutionum in longitudine in unaquaque sectione earum ad cursus in latitudine, scilicet proportionem anguli d a t, et comparium eius ad angulum d a m, et compares eius, quod est, quia proportio lineae k e ad lineam e n est sicut proportio cuiusque duarum linearum t d et l z, et comparium utrarumque ad unamquanque duarum linearum d m et z s, et compares utrarumque. Verum proportiones quae sunt inter istas lineas secundum propinquitatem, sunt proportiones quae sunt inter arcus earum, quibus ipsae subtendunt. Erit ergo propter illud proportio anguli k a e ad angulum e a n existens secundum propinquitatem proportio anguli d a t, et comparium eius ad angulum d a m et compares eius. Sermo autem eius, quod superfluitates quae sunt additionum et diminutionum in longitudine propter illas reflexiones, scilicet superfluitas anguli e a k, et comparium eius super angulum n a k et compares eius, est maior superfluitas quae cadit apud cursus magnos, qui sunt apud punctum e, scilicet superfluitate e a k super angulum n a k, non est consequens, et hoc est de summa eius in quo errauit, quoniam sequitur hoc, ut sit angulus e a k minor medietate recti. In mercurio non ipse est minor medietate recti, in uenere autem est maior. Fabricauit ergo hanc rem secundum hunc modum, quod est, quia ipse dixit, quod istas superfluitates comprehendunt anguli, quibus subtenduntur superfluitas inter lineas t d et k e et l r, et inter lineas t m et k n et l s, et propterea quod proportio cuiusque harum linearum ad illud quo superfluunt, est proportio una et eadem, tunc iam sequitur inde, ut sit proportio superfluitatum inter duas lineas e k, k n ad lineam e a maior proportione superfluitatum inter omnes duas lineas harum linearum comparium his duabus lineis comparibus lineae a e, et non sequitur ex hoc absolute, ut sit maior angulorum ipse angulus, cui subtenduntur illae superfluitates, cuius proportio ad lineam e a est maior proportionum, nisi ita, ut angulus a e k non sit minor angulo a d t et comparibus eius, et non est ita, imo est minor angulis comparibus ei. Verum sequitur illud per proprietatem, quando latus a k est maius latere k e, sequitur ergo ex illo, propterea quod angulus k est rectus, ut sit angulus k a e minor medietate recti, reliqui ergo anguli compares ei, scilicet angulus d a t et compares ei, sunt multum minores medietate recti. Ab hoc ergo tantum sequitur, ut sit superfluitas anguli maioris horum angulorum, scilicet superfluitas anguli e a k super angulum n a k maior superfluitatum comparium ei. Ponamus ergo ad ostendendum illud in superficie duos triangulos a k e, a t d figurae, et ponam eos utrosque communicantes in puncto 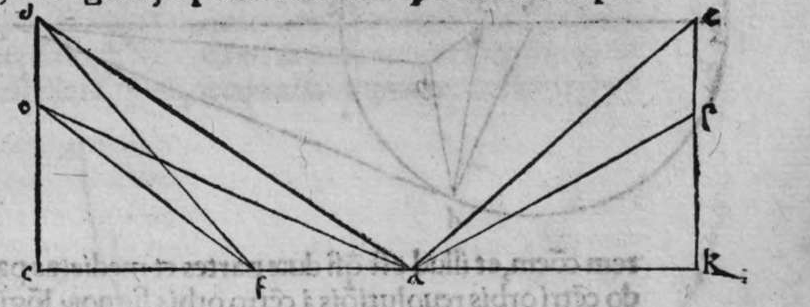a, propter occupationem formae, et abscidam lineam q k aequalem lineae k n, et lineam o t aequalem lineae t m, et continuabo q a et o a, oportet ergo ut ostendam quod angulus e a q est maior angulo d a o et comparibus eius, manifestum est ergo, quod angulus q e a est minor angulo a d o, et reliquis comparibus ei. Sit ergo angulus o d f aequalis angulo q e a et continuabo lineam o f, ergo triangulus k e a est similis triangulo t d f, ergo proportio lateris k e ad latus e a, est sicut proportio lateris t d ad latus d f. Sed proportio k e ad q e est sicut proportio t d ad o d, ergo proportio q e ad e a est sicut proportio a d ad d t, et duo anguli c et d sunt aequales, ergo duo trianguli q e a et d o f sunt similes, ergo angulus d f o est aequalis angulo q a e. Si ergo fuerit angulus e a k minor medietate recti, erit angulus a q e minor recto et medietate, ergo angulus d o f aequalis ei, et est minor recto et medietate. Verum angulus d a t est minor medietate recti, quoniam est minor angulo e a k, ergo aggregatio duorum angulorum d o f, d a f est minor duobus angulis rectis. Sit ergo aggregatio duorum angulorum d r f, d o f aequalis duobus rectis. Erit ergo circulus continens triangulum d o f transiens 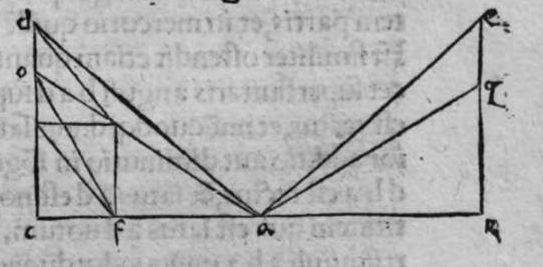etiam per punctum r, erit continens figuram d o f r quadrilateram, et erit d r o aequalis angulo d f o, ergo angulus d f o aequalis angulo q a e, est maior angulo d a o. Et similiter sequitur contrarium illius, quando est unusquisque angulorum e a k et d a t, et compares amborum maior medietate recti, et similiter anguli, ex quibus diminutus est angulus a n k figurae primae, et compares eorum. Sequitur enim ex illo, ut sit angulus e a q, et est ille, cui subtenditur superfluitas, cuius proportio est ad lineam e a, est maior minor ed. proportionibus angulo d a o. In mercurio uero angulus e a k, et est maior angulorum diuersitatis, est minor medietate recti, sequitur ergo in ipso, ut sit maior superfluitatum apud punctum e, scilicet superfluitas anguli e a k super angulum n a k. In uenere autem unusquisque duorum angulorum e a k et n a k est maior medietate recti, propter illud ergo non est maior superfluitatum apud punctum e, quoniam si angulus d a t est maior medietate recti, tunc angulus d a o est maior angulo e a q, et illud est quod uoluimus declarare, et forma eius est, super quam est q. Et postquam declaratae sunt ei res istae, incepit declarare quantitates anguli reflexionis duorum orbium reuolutionis harum duarum stellarum, quod est, quia iam inuenit per considerationem, quod unaquaeque harum duarum stellarum, quando est in maiori longitudine sua a sole, est tunc decliuior ad septentrionem et ad meridiem a longitudine contraria ei, quasi quinque partibus secundum rem mediam, quod est, quia stella ueneris facit hanc contrarietatem in latitudine unius quinque partibus in longitudine longiori ecentrici, et plus quinque partibus in longitudine propiori per id, de quo non curatur. Mercurius uero diuersificatur in illa quasi medietate partis unius, scilicet, quia facit hanc contrarietatem in latitudine, in longitudine quidem longiori minus 5. per medietatem partis, propter illud ergo unusquisque duorum angulorum, quos determinat reflexio orbis reuolutionis a duobus lateribus orbis ecentrici, subtenditur secundum rem mediam quasi duabus partibus et mediae circuli erecti super superficiem orbis signorum orthogonaliter. Inuenit ergo ex hoc angulo quantitatem anguli reflexionis orbis reuolutionis secundum hunc modum, ut sit sectio communis orbis signorum et superficiei, in qua est orbis reuolutionis linea a b g, et signabo circa punctum b orbem reuolutionis g d e, reflexum a superficie 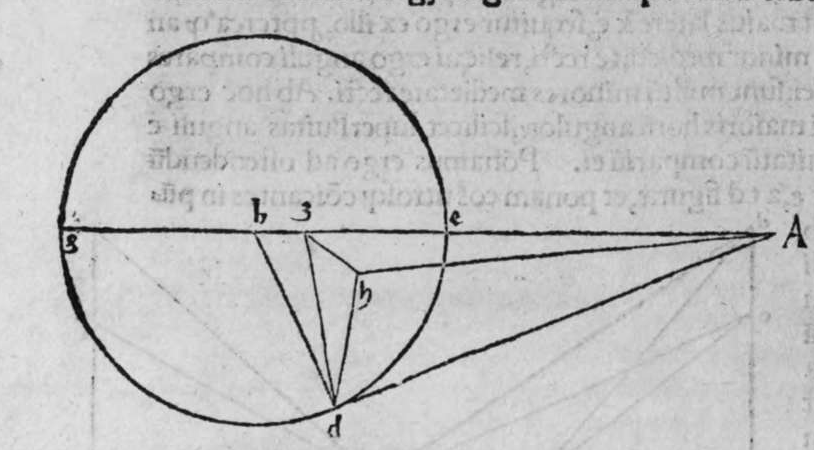orbis signorum, et sit reflexio eius super lineam a b g, et protraham a puncto a, et est centrum orbis signorum, lineam contingentem or bem reuolutionis super punctum d, et est linea a d, et protraham a puncto d super lineam quidem g e perpendicularem d z, et super superficiem quidem orbis signorum perpendicularem d h, et continuabo lineas b d, z h, a h et sit angulus d a h quantitas medietatis elongationis in latitudine in unaquaque duarum stellarum secundum rem communem, et ilud est quasi duae partes et medietas partis, et ponam lineam a b, quae est longitudo centri orbis reuolutionis a centro orbis signorum, longitudinem mediam inter maiorem longitudinem eius et minorem ipsius longitudinem, et illud est 60. Propterea ergo quod unumquodque duorum laterum a b et b d est notum, et angulus a d b est rectus, est latus a d notum, et proportio eius ad lineam a b notam, est sicut proportio lineae z d ad lineam d b notam, erit propter illud linea z d nota per quantitatem qua est unumquodque laterum trianguli a b d notum, et erit linea z b nota. Remanet ergo linea a z nota, et propterea quod angulus d a h est datus, et angulus a h d est rectus, et latus a d est notum, est latus d h notum per quantitatem qua latus a d est notum, et iam fuit per illam quantitatem latus d z notum, ergo trianguli d z h angulus h est rectus, et unumquodque duorum laterum z d et d h eius est notum, ergo angulus d z h est notus, et est angulus reflexionis orbis reuolutionis. Inuenit ergo quantitatem huius anguli in uenere quidem tres partes et medietatem partis, et in mercurio quidem 7. partes per partes quibus angulus rectus est partes 90. Et similiter ostendit etiam quantitatem superfluitatis, quae est propter hanc reflexionem, scilicet superfluitatis anguli b a d super angulum z a h, et illud est, quoniam propterea quod angulus a d b est rectus, et unumquodque duorum laterum a b et b d est notum, est angulus d a b notus, et est maior additio aut diminutio in longitudine, et propterea quod angulus d a h est notus, et angulus d h a est rectus, et latus a d est notum, est unumquodque duorum laterum d h et h a notum per quantitatem qua est latus a d notum. Et propterea quod latus a z iam ostensum est, quod est notum, et trianguli a h z unumquodque duorum laterum a h, a z est notum, et angulus eius a h z est rectus est propter illud angulus z a h notus, ergo superfluitas inter ipsum et inter angulum 3 a d est nota. Inuenit ergo quantitatem huius superfluitatis qua minuitur angulus z a h ab angulo z a d, in uenere quidem minutum unum, et in mercurio quidem minuta 7. completa est eius declaratio. Deinde post illud uoluit scire, quando ponitur angulus d z h, et est angulus reflexionis orbis reuolutionis, quantitates quas inuenit in uenere quidem tres partes et medietas partis, et in mercurio quidem 7. partes, sicut diximus, an sint quantitates recessionum in latitudine in longitudine longiori et propiori ecentrici, scilicet quantitas anguli d a h conueniens quantitatibus quas inuenit per considerationem, ostendit ergo illud quod praemissum est secundum quod longitudo centri orbis reuolutionis, et est linea a b, sit maior longitudinum eius, deinde minor earum. Inuenit ergo quantitatem anguli d a h in maiori quidem longitudine orbis reuolutionis ueneri duas partes et 27. minuta, et in minori quidem longitudine eius duas partes et 34. minuta. Non ergo diuersa facta est haec reflexio secundum maiorem longitudinem et minorem eius ab eo, quod posuit eam secundum longitudinem mediam nisi 3. minutis tantum, et hoc est ex eis, quod impossibile fuit consequi per considerationem, et reperit in stella mercurij quidem, quando est centrum orbis reuolutionis in maiori longitudine sua duas partes partrs ed. et 17. minuta, et quidem, quando est in minori longitudine sua duas partes et 47. minuta. Iam ergo diuersa fit haec reflexio secundum maiorem longitudinem et minorem eius ab eo quod posita est secundum longitudinem mediam quasi quarta partis unius secundum quod ipse inuenit per considerationem.

⟨IX.1⟩ De apparitionibus et occultationibus planetarum quinque.

ET postquam declaratum est ei illud quod praemissum est de cognitione habitudinum stellarum quinque in latitudine, fuit ei possibile post illud inuenire quantitates longitudinum earum a sole in apparitione earum et ipsarum occultatione. Istae autem longitudines sunt arcus orbis signorum, qui sunt inter duo loca solis et stellae uera apud principium apparitionis earum, aut initium occultationis ipsarum, et oportet necessario, ut longitudines istae diuersificentur in stellis quinque propter diuersitatem earum in magnitudine et paruitate, quoniam maiores earum oportet ut appareant ex arcu minore, et minores ex arcu maiore, et oportet iterum, ut diuersificetur arcus longitudinis in una et eadem stella propter intentiones multas, quarum una est diuersitas declinationis partium orbis signorum in horizonte dato, et secunda est diuersitas horizontum in declinatione, et tertia est diuersitas latitudinis stellarum, quod est, ut nos aestimemus arcum a e b portionem 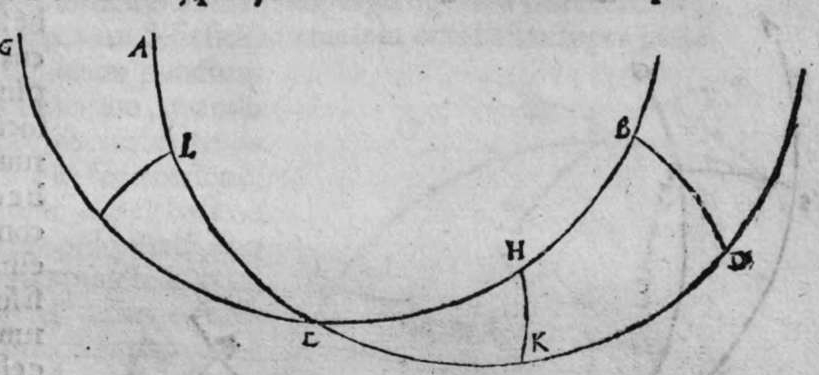horizontis, et arcum g e d portionem orbis signorum, et ponamus stellam in primis super ipsum orbem signorum, sicut si ipsa fit super punctum e, quod est sectio communis apud initium apparitionis eius, aut initium occultationis ipsius, et ponamus solem super punctum d, et sit arcus d b erectus super horizonta orthogonaliter, ipse arcus cui, quando est longitudo solis ab horizonte aequalis, est initium apparitionis stellae, aut initium occultationis eius, propterea ergo quod arcus b d diuersificatur secundum diuersitatem stellae in magnitudine et paruitate, oportet etiam, quamuis reliquae res sint remanentes secundum habitudinem unam, ut arcus e d diuersificetur etiam in stella una et eadem secundum partes orbis signorum, quamuis reliquae res sint remanentes secundum habitudinem unam, quoniam angulus b e d diuersificatur secundum partes orbis signorum, et secundum diuersitatem huius anguli diuersificatur arcus e d, fit ergo quod quanto plus magnificatur angulus iste, minoratur iste arcus, et quanto plus minoratur, magnificatur iste arcus, et similiter iterum diuersificatur iste angulus in parte una orbis signorum secundum diuersitatem declinationum horizontum. Sequitur ergo ex illo diuersitas arcus e d etiam, quod si fuerit stellae latitudo stella existente super punctum h, et latitudo eius arcus k h, tunc sequitur, quamuis latitudo sit una, ut diuersificetur arcus e k secundum diuersitatem anguli h e k, et iam ostensum fuit, quod arcus e d diuersificatur per diuersitatem eius iterum. Sequitur ergo ab illo, quod arcus e k, et est longitudo inter duo loca stellae et solis, diuersificatur, et ut latitudo stellae in una parte et in horizonte uno sit diuersa. Nam sequitur ab illo etiam, ut longitudo loci eius ueri a sole diuersificetur, quod est, quia quamuis angulus e sit unus, tamen sequitur a diuersitate arcus h k, quae est latitudo, ut diuersificetur etiam arcus e k, sequitur ergo, ut arcus d k etiam sit diuersus. Iam ergo ostensum est, quod arcus longitudinis loci stellae a sole in initio apparitionis eius, aut initio occultationis ipsius diuersificatur in partibus orbis signorum, et secundum diuersitatem declinationum horizontum, et secundum diuersitatem latitudinis stellae, et non sciuit illud, scilicet quantitatem longitudinis eius in omnibus partibus orbis signorum, et in horizontibus, nisi per hoc, ut sciret quantitatem arcus b d totalis, et non est possibile, ut sciat quantitatem arcus b d, nisi ita, ut sciat per considerationem quantitatem longitudinis stellae a sole in initio apparitionis suae et suae occultationis in horizonte dato, et in parte data, ex partibus orbis signorum quicunque horizon fuerit aut quaecunque pars fuerit, uerum electum in illo est, ut sit illa pars orbis signorum in principijs signi cancri, quoniam aer est tunc clarus subtilis. Dixit ergo, quod inuenit per considerationes Chaldeorum, et sunt considerationes quae fuerunt in climatibus, quae transeunt per terram conakie de Syria, quod stella saturni, quando est in principijs cancri, tunc oritur in diluculis, scilicet, quando est exiens ex tegumento, et longitudo loci eius a sole 14. partes. Stella autem iouis oritur cum diluculis secundum illam similitudinem, et longitudo eius a sole 12. partes et tres quartae partis. Stella uero martis oritur cum diluculis secundum illam similitudinem, et longitudo eius a sole 14. partes et medietas partis. Stella autem ueneris oritur cum uesperis, scilicet, quando est secundum illud exemplum, exiens ex tegumento, et longitudo loci eius a sole quinque partes et duae tertiae partis. Stella uero mercuij oritur in uesperis secundum illud exemplum etiam, et longitudo loci eius a sole 11. partes et duae tertiae partis. Quando ergo istud expositum est, tunc iterabo figuram praecedentem, et sit punctum e punctum quod oritur uel occidit cum stella, quando locus eius uerus est in principijs signi cancri, et propterea quod longitudo eius quae est inter locum cuiusque harum quinque stellarum et locum solis uerum est nota per considerationem, et est arcus e d, si est in superficie orbis signorum, aut arcus d k, si fuerit eius latitudo septentrionalis, aut arcus l d, si fuerit eius latitudo meridiana, et est locus stellae uerus ex orbe signorum notus, et est principium cancri, et propter illud locus solis notus, et est propter illud longitudo stellae a longitudine longiore orbis reuolutionis nota. Est ergo propter illud latitudo eius ab orbe 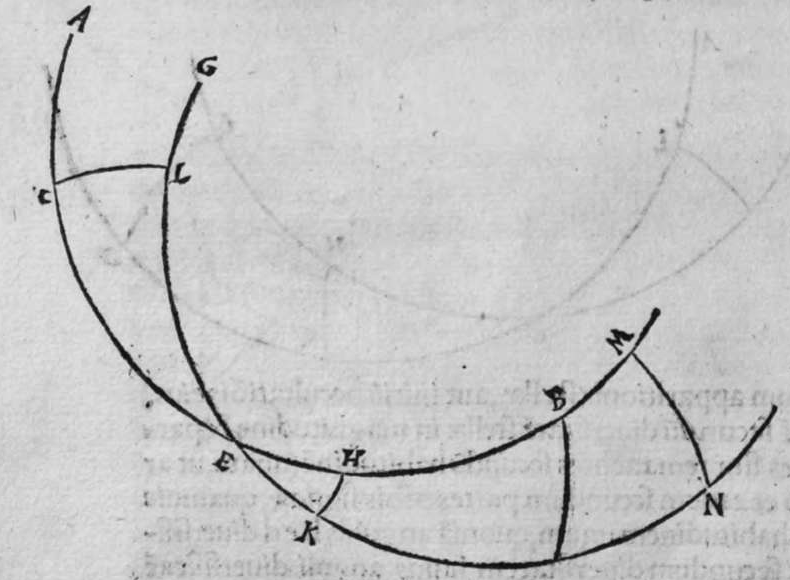signorum nota, et est arcus h k, aut arcus t l, et angulus b e d est secundum propinquitatem aequalis angulo qui est loci stellae, scilicet uni duorum punctorum k l. Erit ergo propter proper ed. illud angulus b c d notus in illo horizonte in quo est consideratio, et angulus d b e est rectus. Quod si non fuit stellae latitudo, et si fuerit locus eius uerus ex orbe signorum punctum e, tunc triangulus b d e est ex arcubus circulorum magnorum, ergo proportio sinus anguli b eius noti, quoniam est rectus ad sinum anguli eius e noti in horizonte in quo fuerit consideratio, est sicut proportio sinus lateris e d noti ad sinum lateris b d, sed arcus b d est minor quarta circuli. Erit ergo propter illud arcus b d notus, quod si stellae latitudo ab orbe signorum septentrionalis sit aut meridiana, tunc scitur quantitas b d secundum hunc modum. Ponam ergo in primis ut latitudo eius sit septentrionalis, et est arcus k h, et ut stella oriatur aut occidat apud initium suae apparitionis, aut occultationis suae apud punctum h horizontis, et locus eius uerus ex orbe signorum, et est initium cancri punctum k, ergo erit triangulus h k e ex arcubus circulorum magnorum, ergo proportio sinus anguli k eius noti, quoniam est rectus ad sinum anguli e eius noti, etiam est sicut proportio sinus lateris e h ad sinum lateris h k noti. Erit ergo propter illud latus h e notum, et propterea proterea ed. etiam quod triangulus h k e est orthogonius, est proportio sinus complementi lateris e h subtensi recto, quod est notum, ad sinum complementi lateris h k noti, etiam sicut proportio sinus complementi lateris e k residui ad sinum quartae circuli, qui est notus, est ergo propter illud e k notum, et arcus k d notus per considerationem, et est longitudo eius, quod est inter loca duo stellae et solis uera, ergo arcus e d est notus. Inuenitur ergo ex eo quod praemissum est, etiam quantitas arcus b d, et similiter si est latitudo latudo ed. eius meridiana, quasi ipsa sit super punctum t, et latitudo eius t l et locus eius uerus punctum l, declaratur per illud idem, quod arcus l e est notus, et arcus l d est notus, remanet ergo arcus e d notus. Declaratum est ergo ei, quod quantitas arcus d b in saturno quidem est 11. partes, et in ioue quidem 10. partes, et in marte 11. partes et medietas partis, cum propinquitate, et in uenere quidem 5. partes, et in mercurio quidem 10. partes, et praeparatur in stella ueneris solum, propterea quod quantitas arcus d b in ea est minor maiore latitudine sua, et illud est, quia latitudo eius ab orbe signorum signoum ed., quando ortus eius aequatus est in uno duorum nodorum orbis ecentrici, scilicet in principijs signi piscis, aut in principijs signi uirginis, et est in longitudine propiore orbis reuolutionis suae 6. partes et tertia partis, et illud est plus latitudinis eius, et est plus 5. partibus, quae sunt quantitas arcus d b, ut oriatur cum diluculis, et est abbreuiata a longitudine propiori orbis reuolutionis suae. Est ergo locus eius uerus ad partem successionis signorum a loco solis, sicut si sit super circumferentiam horizontis super punctum m huius figurae, et locus eius uerus super punctum n orbis signorum, et est latitudo eius, et est arcus m n maior arcu b d, et illud est, quia non praeparatur in alia harum stellarum, quoniam quantitas arcus b d in unaquaque reliquiarum est maior maiori latitudine eius. Et postquam declaratum est ei illud, uoluit uidere, si illud quod inuenit ex proprietatibus in apparitionibus ueneris et mercurij et occultationibus utriusque, sit conueniens radicibus politis utrisque, quod est, quia  in stella ueneris tempus quod est ab occasu eius uespertino ad ortum eius matutinum, tunc quidem, quando est in initijs piscis, est quasi duorum dierum, et quando quidem est in initijs uirginis, est 16. dies. In stella autem mercurij, quando est in principijs scorpionis eius apparitionis uespertinae, destruuntur et euanescunt, et quando est in principijs signi tauri, tunc apparitiones eius matutinae euanescunt et destruuntur, et declaratio eius praeparatur secundum hunc modum. Iterabo ergo figuram praecedentem, 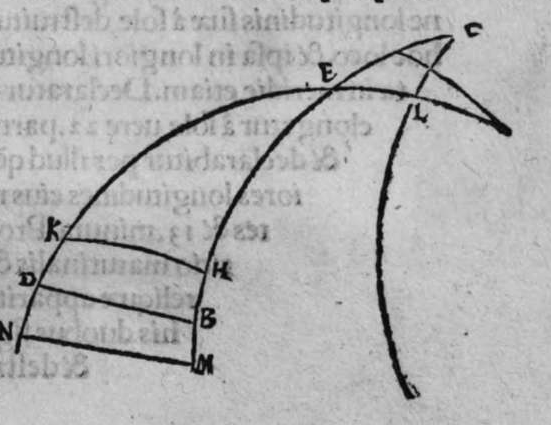et ponam ipsam figuram occasus uespertini, et sit stella ueneris in occasu suo super punctum h, et locus eius uerus ex orbe signorum punctum k, et quoniam in initijs signi piscis, et est in quo, quando stella ueneris est ex longitudine propiori orbis reuolutionis, est in maiori latitudine sua in septentrione, et illud est 6. partes et tertia partis, tunc arcus k h est notus, et angulus e est notus secundum propinquitatem, quoniam est propinquius angulo qui est a puncto k dato, quoniam est super horizonta, et angulus k est rectus, erit secundum quod ostensum est in figura praecedenti, arcus e k notus. Et similiter etiam, propterea quod latus b d est notum, et duo anguli b et e sunt noti, est, quod latus d e est notum, remanet ergo arcus d k, et est illud quod est inter duo loca stellae et solis uera, notus. Longitudo ergo loci stellae ueri, et est punctum k a longitudine propiori orbis reuolutionis est nota, et per simile huius inuenit etiam longitudinem eius ab ea in ortu suo matutino. Sciuit ergo ex illo quantitatem arcus quam abscidit stella ex partibus orbis signorum in tempore quod est inter occasum eius uespertinum, et inter ortum ipsius matutinum. Exiuit ergo ei quantitas huius arcus pars una et quarta partis, et stella ueneris abscidit hanc quantitatem de partibus orbis reuolutionis quasi in duobus diebus, et per simile illius ostenditur quantitas temporis quod est inter duas apparitiones, quando est in initijs uirginis, ueruntamen latitudo stellae est tunc meridiana, et est quantitas sex partium et tertia partis. Est ergo quasi stella sit in hac figura super punctum t circumferentiae horizontis, et locus eius uerus, et est principium uirginis super punctum l orbis signorum, et latitudo eius l t. Declaratur ergo per simile eius quod praemissum est ex demonstratione quantitas arcus d l, et est longitudo eius quod est inter duo loca stellae et solis uera in occasu eius uespertino. Et similiter etiam sciuit quantitatem eius in ortu ipsius matutino, et inuenit ex illo per simile eius quod praemissum est, quantitatem arcus orbis reuolutionis quem abscidit stella ueneris in tempore quod est inter has apparitiones, exiuit ergo ei quantitas harum partium orbis reuolutionis 10. partes, et stella abscidit illud quasi in 16. diebus. completa est eius declaratio. Stella autem mercurij, quando est in initijs scorpionis, tunc apparitiones eius uespertinae destruuntur et pereunt, et quando est in initijs tauri, tunc apparitiones eius matutinae destruuntur et pereunt, illud enim declaratur secundum hunc modum. Iterabo ergo figuram praecedentem, et intendam ad apparitionem uespertinam, quae est ei in initijs signi scorpionis, et ipsa est in ultimo longitudinis suae a sole. Nam quando declaratur, quod ipsa apparitio destruitur et perit, est illud dignius in apparitionibus quae sunt ei in longitudinibus, quae sunt minores hac longitudine, et quoniam quando stella mercurij est in initijs scorpionis, et est in maiori longitudine sua uerspertina a sole, tunc est latitudo eius in meridie quasi tres partes, tunc quasi stella occidat super punctum 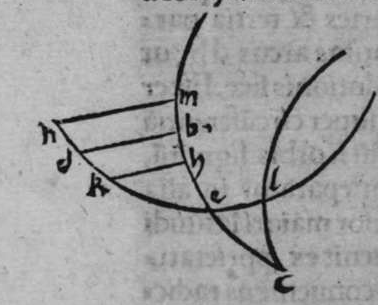t horizontis, et locus eius uerus de orbe signorum, et est initium scorpionis, sit punctum l, et latitudo eius meridiana arcus t l, et propterea quod punctum l est datum, est angulus per quem est super horizonta notus. Erit ergo propter illum angulum angulus e secundum propinquitatem notus, sed angulus b est rectus, et arcus b d, et est longitudo totalis, est datus, et illud est decem partes. Erit ergo per simile eius quod praemissum est arcus d e notus, et similiter etiam, propterea quod arcus l t et est latitudo stellae, est notus, et unusquisque duorum angulorum e l est notus, erit arcus l e notus, ergo arcus l c d est notus, et est illud quod  est inter duo loca stellae et solis uera. Declaratur ergo, quod quantitas huius arcus est 22. partes secundum propinquitatem. Haec est ergo quantitas qua oportet elongari hanc stellam a sole uere in initijs signi scorpionis in uesperis, et tunc uidetur uerum, declaratur per illud quod diximus in postremo tractatus octaui huius libri, quod maiores longitudines huius stellae uespertinae in hoc loco a sole uero sunt 20. partes et 52. minuta. Propter illud ergo destruitur haec uespertina apparitio in hoc loco et perit, et per simile istius declaratur iterum, quod quando haec stella est in initijs signi tauri, tunc apparitio eius matutinalis quae est ei et ipsa in fine longitudinis suae a sole, destruitur etiam et euanescit, et illud est, quia latitudo eius est in hoc loco, et ipsa in longiori longitudine sua matutinali, est quasi tres partes et 10. minuta in meridie etiam. Declaratur ergo per simile eius quod praemissum est, quod oportet, ut elongetur a sole uere 22. partibus et 16. minutis, et tunc uidetur in diluculis duluculis ed., et declarabitur per illud quod diximus in fine sermonis octaui etiam, quod maiores longitudines eius matutinales in initio signi tauri sunt 22. partes et 13. minuta. Propter illud ergo euanescit etiam haec apparitio matutinalis et destruitur, et quando illud est ita, tunc reliquae apparitiones uespertinae et matutinales in his duobus signis sunt digniores, ut euanescant et destruantur. Completa est eius declaratio. Finis nouem librorum Gebri, Arabice primo scripti, et per magistrum Girardum Cremonensem in latinum uersi.